Protein-folding landscapes in multichain systems

Abstract

Computational studies of proteins have significantly improved our understanding of protein folding. These studies are normally carried out by using chains in isolation. However, in many systems of practical interest, proteins fold in the presence of other molecules. To obtain insight into folding in such situations, we compare the thermodynamics of folding for a Miyazawa–Jernigan model 64-mer in isolation to results obtained in the presence of additional chains. The melting temperature falls as the chain concentration increases. In multichain systems, free-energy landscapes for folding show an increased preference for misfolded states. Misfolding is accompanied by an increase in interprotein interactions; however, near the folding temperature, the transition from folded chains to misfolded and associated chains is entropically driven. A majority of the most probable interprotein contacts are also native contacts, suggesting that native topology plays a role in early stages of aggregation.

Lattice-model proteins have played a key role in developing our understanding of protein folding. These model proteins contain enough detail to capture the essential physics of the folding process, yet are amenable to rigorous calculation of free-energy landscapes used to describe the folding pathway. Such calculations have provided a conceptual solution to the Levinthal Paradox, which ponders the ability of a protein to navigate a vast amount of conformational space to reach its native state on time scales of seconds or less (1–3). The funnel-like nature of the free-energy landscapes, first calculated from lattice models, shows that proteins only need to sample a small fraction of conformations to reach the native state. The energetic bias toward the native state exists because native interactions are, on average, more stable than nonnative ones. Similar features are observed in folding landscapes generated from experiments, validating results from model calculations (1).

Most computational studies of protein folding have examined a single chain in isolation (4–7). However, in many systems of practical interest, including in vivo folding, proteins fold in crowded environments. In such situations, interactions with other biological molecules compete with the intraprotein interactions that bias a protein's conformation toward its native state. Some biological molecules, such as molecular chaperones, promote folding (8). However, intermolecular interactions can also induce misfolding and aggregation (9, 10), resulting in loss of protein function (11). Further, protein aggregates can be toxic. Protein association has been linked to >20 human diseases, including Alzheimer's, Parkinson's, and Huntington's diseases (12, 13).

We report simulations for systems containing one-, two-, or four-lattice model 64-mers. This chain length is greater than that in most model studies of multichain systems and correspondingly provides a more realistic surface area/volume ratio than that for smaller models (14, 15). Free-energy landscapes have been calculated for the folding of chains in isolation and in systems where individual chains may also form intermolecular interactions. Throughout all simulations, we use a fixed protein sequence. We increase the number of neighbor molecules to monitor association in addition to folding.

Methods

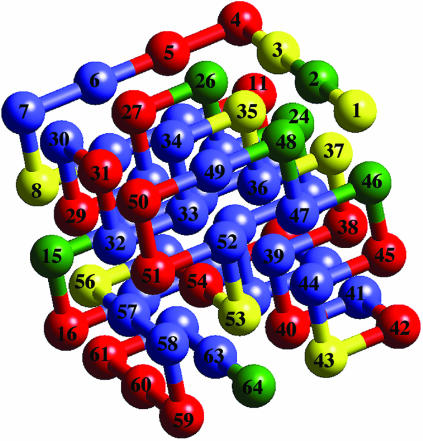
Protein Sequence and Potential Function. We use the conventional on-lattice representation (Fig. 1). Protein molecules are represented as self-avoiding chains comprised of amino acid residues (beads on the chain) interacting through a renormalized Miyazawa–Jernigan (MJ) potential (16, 17). MJ potentials are empirically derived: 20 different amino acids are possible. The renormalization of the solvent–solute interactions introduced by Leonhard et al. (16) corrects for some of the inconsistencies resulting from the approximations underlying the original MJ model. Empirical energy scales such as the present one can at best be used to capture qualitative aspects of protein behavior (18, 19). For a detailed description of the potential function see ref. 16. Each chain consists of 64 beads with the following sequence: KEKSTAGRVASGVLDSVACGVLGDIDTLQGSPIAKLKTFYGNKFNDVEASQAHMIRWPNYTLPE (Fig. 1). Solvent effects are included implicitly in the Hamiltonian. Studies of different sequences suggest that our present conclusions are qualitatively general and not limited to the chosen sequence.

Fig. 1.

Lowest-energy structure of the model protein.

Simulation Details. All simulations were of the standard Monte Carlo form and conducted in the canonical (N,V,T) ensemble. Boundary effects are taken into account by applying periodic (minimum image) conditions. We use standard simulation moves including: (i) displacements of either one of the end beads to one of the available four neighboring sites; (ii) corner flips for beads characterized by a right angle between the directions to both contour neighbors; and (iii) crankshaft moves of bead pairs located at the bottom of a U turn. We also allow forward and backward slithering-snake reptation moves (20), as well as translations of entire chains or groups of chains. Moves are attempted at random with a priori probabilities as specified in ref. 15, where further details of the (N,V,T) simulations are available.

To alleviate problems related to local trapping on a rugged free-energy landscape, we apply a replica exchange Monte Carlo simulation technique (15). Systems are allowed to swap between adjacent temperature levels with probabilities that preserve canonical (Boltzmann) statistics within each level. Assuming an approximate Arrhenius dependence of first passage times from the local minimum, the chance of escape of a trapped system is significantly improved during the time it spends at an elevated temperature. A temperature swap was attempted after every simulation pass. The attempted exchange of systems i and j with energies V_i and V_j between temperature levels m and n was accepted with the probability (21)

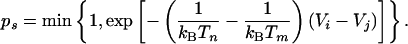[1]

In most calculations, the number of replicas (and temperature levels) was six, with reduced temperature T ranging between 1.0 and 1.3 and typical swapping acceptances between 8% and 30%. Reduced temperature T is normalized by the reference temperature T_o such that k_BT_o represents the energy unit pertinent to our system. The size of the cubic box equals 12, 14, and 16 monomer lengths corresponding to volume fractions of ≈3.7, 4.7, and 6.3% in one, two-, and four-chain systems, respectively. To alleviate finite-size effects, periodic boundary conditions are applied in all directions.

Weighted Histogram Analysis Method (WHAM). WHAM was used to analyze simulation data (22). WHAM minimizes the error in the density-of-states function and facilitates the calculation of free-energy surfaces. With the number of native contacts N_Nat and the number of interprotein contacts N_Inter as example reaction coordinates, the density-of-states function has the form

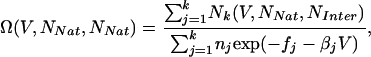[2]

where N_k is the number of occurrences for samples with (V, N_Nat, N_Inter), f_j = βA_j, where A_j is the free energy of simulation j, and β is 1/k_BT, k is the number of simulations, n_j is the number of samples from simulation j. The density of states can then be used to calculate thermodynamic averages (using N_Nat as an example) by

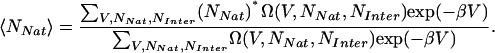[3]

Apart from an undetermined constant, free-energy surfaces are calculated by

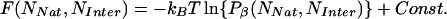[4]

where P_β(N_Nat, N_Inter) is the probability of observing a system with (N_Nat, N_Inter) at temperature T = (k_Bβ)^–1. A more complete description of the application of the weighted histogram analysis method (WHAM) equations is in ref. 23.

Results

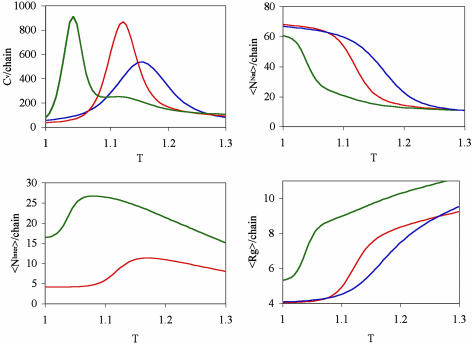
Unfolding Occurs at Lower Temperatures in Multichain Systems. Fig. 2 Upper Left shows heat capacities as a function of temperature for one-, two-, and four-chain systems. In all three cases, a single, strong peak is observed, suggesting a single phase transition. As the number of chains increases, the peak is shifted to lower temperatures. For a one-chain system, the peak occurs at T = 1.155, for a two-chain system at 1.12, and for a four-chain system at 1.05.

Fig. 2.

Thermodynamic data for systems of one, two, or four lattice-model proteins. (Upper Left) Heat capacities for single-chain (blue), two-chain (red), and four-chain systems (green) as functions of temperature. (Upper Right) Average number of native contacts (per chain) for single-chain (blue), two-chain (red), and four-chain systems (green) as functions of temperature. (Lower Left) Average number of interprotein contacts (per chain) for two-chain (red) and four-chain systems (green) as functions of temperature. (Lower Right) Average radius of gyration (per chain) for single-chain (blue), two-chain (red), and four chain systems (green) as functions of temperature.

Further insight into the phase-transition data is obtained from plots of the average number of native contacts (N_Nat, Fig. 2 Upper Right), interprotein contacts (N_Inter, Fig. 2 Lower Left), and radius of gyration (R_g, Fig. 2 Lower Right) as a function of temperature. When multiple chains are present, thermal denaturation takes place at lower temperatures, a result corroborated by findings from more realistic models (24). For all three cases, the midpoint temperature of unfolding essentially coincides with the heat-capacity-peak temperature. These data show that the heat-capacity peaks are associated with unfolding events. Further, for multichain systems, there are sharp increases at the melting temperatures in the number of interprotein contacts. Thus, the loss of intraprotein interactions, to some extent, is compensated by an increase in (attractive) interprotein interactions. Finally, the R_g vs. T plot indicates that protein unfolding and association are accompanied by chain expansion.

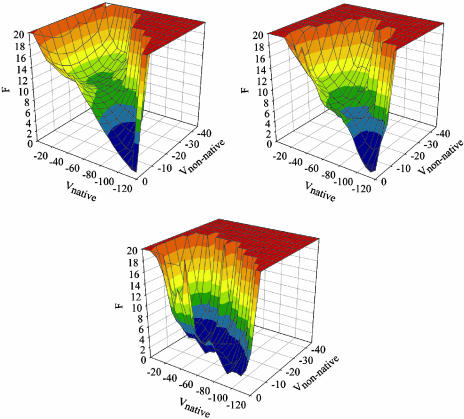
Free-Energy Landscapes for Folding. Fig. 3 shows free-energy landscapes for chains simulated in isolation (Upper Left), in the presence of a second chain (Upper Right), and in the presence of three other chains (Lower). Progress variables are the native energy (per chain) and nonnative energy (per chain). Because these two quantities do not explicitly include interchain effects, they allow direct comparison of the landscapes. Further, our progress variables are similar to those used in other lattice model studies (1).

Fig. 3.

Free-energy landscapes for one-chain (Upper Left), two-chain (Upper Right), and four-chain systems (Lower). V_native and V_nonnative are the potential energy contributions from intraprotein native and nonnative interactions, respectively.

The plots were produced for systems at T = 1.05. At this temperature, chains simulated in isolation populate the native state ≈99% of the time (23). This result is reflected in the landscape for a single chain in isolation that exhibits a funnel-like shape with only a small barrier to folding. When a second chain is present, the landscape is more rugged and exhibits two local minima with modest free-energy barriers (≈k_BT) that slow progression toward the native state. However, the funnel-like shape of the landscape is retained, and a noticeable bias toward the native state exists. When a chain can interact with three possible partners, the landscape is remarkably different. There is little bias toward the native structure, as chains spend about half the time populating misfolded states. The barrier separating the misfolded states from the native state is small, ≈1.5 k_BT.

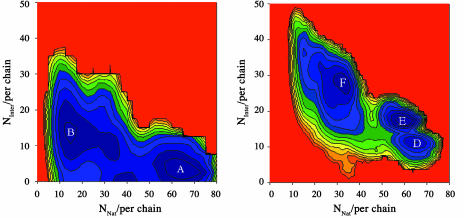
Thermodynamics of Association. Fig. 4 shows free-energy contours versus the number of native and interprotein contacts for two-chain (Left) and four-chain systems (Right). The data are plotted at the phase transition temperatures (T = 1.12 for the two-chain system, T = 1.05 for the four-chain system).

Fig. 4.

Free-energy contours for multichain systems. (Left) Free-energy contours for a two-chain system at T = 1.12. (Right) Free-energy contours for a four-chain systems at T = 1.05. N_Nat and N_Inter are the number of native and interprotein contacts per chain, respectively. The contours are in increments of 2 k_BT₀.

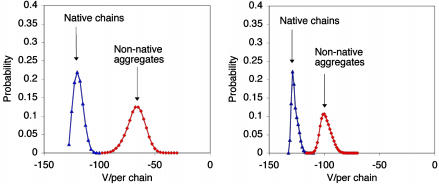
In the two-chain system, we see two minima of equal (relative) free energy (F). The first, found in the region of Fig. 4 characterized by a large number of native contacts, corresponds to a pair of native chains that interact through surface residues (labeled A in Fig. 4 Left). The second corresponds to nonnative chains that interact predominantly through residues that are buried in the native state (labeled B in Fig. 4 Left). Fig. 5 Left shows the probability distribution of the potential energy for these two states. The pair of native chains populates states with a potential energy much lower than the nonnative aggregate, showing that association is entropically driven. Using the average potential energy for each state, and the fact that the free-energy difference between the two states is zero, we estimate that the average entropy difference between the two states is (47 ± 9) k_B per chain. This finding is similar to the entropy difference (43 ± 11) k_B between the unfolded and folded states at the phase-transition temperature for chains in isolation.

Fig. 5.

Potential energy distributions (per chain) for a two-chain system at T = 1.12 (Left) and a four-chain system at T = 1.05 (Right).

Fig. 4 Right shows free-energy contours for the four-chain system at T = 1.05. Two adjacent minima (labeled D and E in Fig. 4 Right) exist with large numbers of native contacts; they represent states where all four chains are native. The third minimum (labeled F in Fig. 4 Right) exists at a region in the diagram with a large number of interprotein contacts, but at a much smaller number of native contacts; this minimum represents an aggregate of misfolded chains. The two minima corresponding to systems of native proteins were grouped together to generate a state of free energy equal to that of the aggregate. As with the two-chain system, in the vicinity of the transition temperature, aggregate states have potential energies significantly higher than those for states corresponding to native proteins (Fig. 5 Right). However, because of opportunities for interprotein interactions with multiple partners, the entropy difference (27 ± 6)k_B per chain is lower than that in one-chain and two-chain systems.

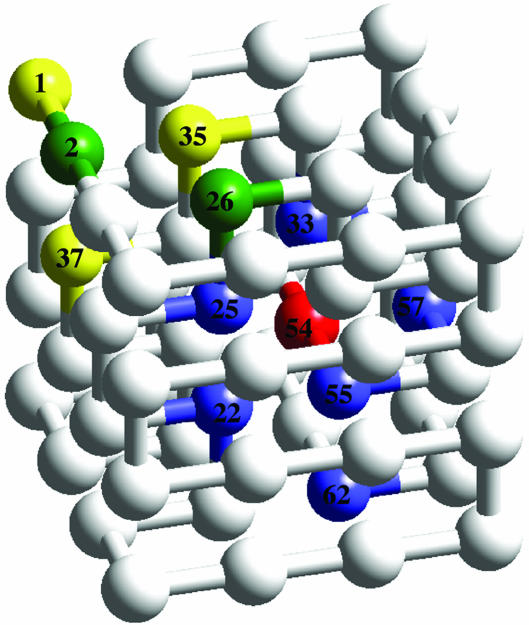
Contacts Leading to Aggregation. To obtain a more complete picture of the association process, we have investigated the specific amino acid residues and residue contacts that contribute most significantly to the protein–protein interaction potential. Despite the increased entropy of the aggregated state, certain amino acid residues do play an enhanced role in association. The 12 beads listed in Table 1, and shown within the context of the native state in Fig. 6, are involved in interactions that (on average) contribute 50% of the interprotein potential for aggregates in two-chain and four-chain systems. Five of these beads are buried in the native state. This finding is consistent with the experimental observation that unfolding facilitates aggregation (25–28).

Table 1. Amino acids that, on average, contribute 50% of the interprotein interaction potential for two- and four-chain systems.

Amino acid	Amino acid identity	Buried in lowest-energy structure
1	K	No
2	E	No
22	L	Yes
25	I	Yes
26	D	No
33	I	Yes
35	K	No
37	K	No
54	M	Yes
55	I	Yes

Fig. 6.

Highlighted beads contribute, on average, 50% of the interprotein interaction potential.

Tables 2 and 3 list the 10 most probable interprotein contacts found in aggregates. In both two-chain and four-chain systems, 9 of the 10 contacts are also native contacts, which indicates domain swapping, which has been observed as a mechanism of aggregation in numerous other systems (29–33).

Table 2. Most probable interprotein contacts found in aggregates for two-chain systems.

Amino acid	Amino acid	Occurrences per snapshot
54M	55I	0.60
54M	57W	0.59
36L	55I	0.30
25I	36L	0.26
33I	54M	0.26
28L	55I	0.26
26D	35K	0.25
55I	62L	0.22
24D	37K	0.21
54M	63P	0.21

Table 3. Most probable interprotein contacts found in aggregates for four-chain systems.

Amino acid	Amino acid	Occurrences per snapshot
26D	35K	2.69
2E	37K	1.99
24D	37K	1.80
1K	24D	1.49
1K	2E	1.42
25L	36I	1.24
55I	62L	1.23
3K	26D	1.15
2E	35K	1.12
54M	55I	1.05

Discussion

Free-energy landscapes show that the presence of multiple chains can impede the folding process under conditions where the native state is favored for isolated chains. In two-chain systems, the landscape is more rugged, but the bias toward the native state remains. When the number of chains increases to four, the bias is removed, and individual molecules spend equivalent times in native and misfolded conformations. In systems of practical interest, such as in vivo folding (12) and inclusion-body protein refolding (34), such changes in the free-energy landscape have a deleterious effect. If proteins cannot reach their native state, they are generally unable to carry out their biological function. In in vivo folding, molecular chaperones (8) are present to ensure that proteins can attain their native state. Insight into chaperone behavior could be obtained if chaperone sequences that return the folding landscape to its natural form were identified.

The origins of the misfolding behavior observed in multichain simulations can be attributed to interprotein interactions. Intramolecular energy is traded for intermolecular energy, thus stabilizing misfolded states. However, in the vicinity of the transition temperature, the loss in intraprotein energy is not fully compensated by interprotein interactions and the process of association is entropically driven. We are unaware of any experimental results that confirm this finding, and it is difficult to imagine the formation of large aggregates such as inclusion bodies or amyloid fibrils accompanied by an increase in protein entropy. Because our Hamiltonian does not explicitly account for hydrogen bonds, it is possible that we underestimate the effect of such interactions, known to be important in the formation of both inclusion bodies and amyloid fibrils (35, 36). Further, because our systems contain a small number of chains, it is possible that for systems with more than four chains a phase transition from disordered to ordered aggregates could take place. Such behavior has been observed for more detailed models found in ref. 24 (C. Hall, personal communication). A decrease in the entropy gain is indeed observed in our model upon increasing the number of associated chains. However, experimental and computational studies have shown that amorphous aggregates (24, 37) can act as precursors to ordered assemblies of proteins, such as amyloid fibrils. Because such amorphous aggregates lack the apparent order of fibrils, it seems more feasible that their formation is favored entropically. Thus if an increase in protein entropy is a driving force for aggregation, it is likely that this increase occurs during the early steps of the association process, before the formation of a quaternary structure that can be propagated such that ordered aggregation starts to occur en masse.

Despite increased disorder characterizing the aggregated state, some amino acids and amino acid contacts play a persistent role in folding and aggregation. Most of these amino acids are hydrophobic beads normally buried in the native state. This finding is not surprising, because we observe an increase in interprotein association upon protein unfolding. Our finding is also in good agreement with experimental data showing that proteins are particularly prone to aggregation when destabilized, and natively buried, sticky residues become available for residue–residue interactions (25–28). Further, the majority of the most probable interprotein contacts are also native contacts. Not surprisingly, these contacts occur between pairs of residues that are strongly interacting. However, although many pairs of the same interaction energy can be formed between chains, there is a significant bias toward amino acid pairs that are also formed in the native state. As shown in a previous study (11), interprotein contacts between strings of complementary residues tend to form or rupture simultaneously, suggesting that a mechanism akin to pattern recognition can operate both intramolecularly and intermolecularly. Native topology therefore plays a role in determining which amino acids play a dominant role in association.

In summary, we have extended a common approach to studying protein folding in isolation to investigate protein folding in the presence of multiple chains. This extension has not only yielded insight into the folding process, but also insight into misfolding and aggregation.