Mechanical control of tissue growth: Function follows form

Early biologists sought to identify vital life forces they believed responsible for the exquisite intricacy of tissue pattern and functional control. Later forms of “vitalism” downplayed the role of mystical powers and focused more on the importance of internal forces that emerged from the specific arrangement of tissue components, with particular emphasis on the role of reciprocal mechanical interactions among the material elements that constitute living systems. Many of these ideas were discarded when reductionist approaches became dominant, and, for the past 30 years, we have “explained” organogenesis and pattern formation almost exclusively in terms of the genes that control developmental signaling pathways. But we still do not understand how nature builds tissues with specialized form and function. Perhaps in part for this reason, there has been a recent resurgence of interest in mechanical forces as morphogenetic regulators. The work of Nelson et al. (1) in this issue of PNAS advances our understanding of the role of physics and architecture in developmental biology by focusing on a mechanical form of morphogenetic control that was proposed in the past (2, 3) but never before tested directly. Specifically, they experimentally address the question of whether the architectural form of a tissue can feed back to control cell growth patterns as a result of local variations of internal mechanical stresses that are distributed through the cytoskeleton and resisted by cell–cell and cell–extracellular matrix (ECM) adhesions.

Local Growth Patterns

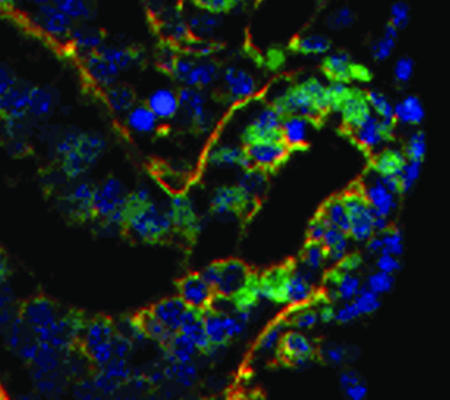
The various 3D forms that tissues exhibit (e.g., tubular, branched, lobular, acinar, etc.) often result from establishment of localized differentials in cell growth during embryogenesis (4, 5). Cells at the tips of expanding epithelial buds, for example, proliferate more rapidly than cells located only micrometers away in the clefts of the same gland and thereby produce regional tissue expansion (Fig. 1). Reiteration of this simple building rule over time and space leads to the fractal patterns characteristic of all epithelial and endothelial tissues. The “positional information” responsible for spatially constrained cell growth patterns in the embryo is commonly thought to be due to gradients of soluble morphogens (6) or local production of growth factors (7). However, cell and tissue distortion are observed before growth is initiated in some developing tissues (8, 9), and it is difficult to explain how soluble gradients of mitogens can produce discrete growth boundaries over the length scale of a single cell, especially in microenvironments saturated with multiple mitogens.

Fig. 1.

A fluorescence view of a tissue section of embryonic lung showing a localized focus of proliferating epithelial cells (green) in a region of high tissue curvature, which drives outward tissue expansion during budding morphogenesis (red, basement membrane; blue, nuclei; adapted from ref. 18). Tissue geometry may feed back to establish and maintain local growth patterns.

Another possibility is that these local growth differentials have a mechanical basis because the form of any structure, whether a skyscraper or a living tissue, is determined through a dynamic equilibrium of physical forces, and every architectural form will be characterized by its own distinct pattern of internal forces. The shape stability of epithelial tissues requires that tensional stresses generated in the cytoskeleton of each cell be balanced by cell–cell and cell–ECM anchoring sites. As cells pull against these resistance sites, they will spontaneously remodel their shape and internal cytoskeletal structure to minimize local stresses and strains, and this response will differ depending on the cell's position and the overall shape of the whole tissue. Cell shape and cytoskeletal structure are tightly coupled to cell growth, with more highly distorted (stretched) cells exhibiting an enhanced sensitivity to soluble mitogens (10, 11). Thus, the internal mechanical stresses characteristic of a tissue's 3D conformation may convey a physical form of positional information that feeds back to spatially constrain cell proliferation and thereby drive tissue morphogenesis (2–4, 12).

Tissue Form Governs Growth

To directly address the question of whether the form of a tissue can feed back to regulate patterns of cell proliferation, Nelson et al. (1) spatially constrained the growth and form of endothelial cell aggregates by culturing them on microfabricated ECM islands of different shapes. When cells were allowed to grow to form a square monolayer, DNA labeling indices of the cells along the sides and in the center of the aggregate dropped to undetectable levels, as expected in confluent cells; however, the cells in the corners continued to proliferate. By culturing cells on differently shaped ECM islands, they were able to demonstrate that the geometry of the entire tissue dictates the growth pattern: stable foci of proliferating cells were consistently positioned in discrete regions of the monolayer, including along the short edges of rectangles and outer periphery of circles and annular rings. Computational modeling using a finite-element method revealed that the positions of most rapid growth corresponded to sites where mechanical stresses were most highly concentrated. This is because isotropic contraction of a cell layer against fixed adhesions on these differently shaped ECM islands results in the highest stress concentrations in these particular regions.

Nelson et al. (1) then directly measured traction forces within cells cultured on similar ECM islands that were microstamped on the tops of an array of flexible microneedles that constituted an elastomeric force sensor (13). By using optical techniques to measure the deflection of each microneedle, it was possible to measure small-scale (pN to nN) forces exerted by cells with subcellular resolution. These studies confirmed that distinct stress patterns can be generated within a cell monolayer as a result of isotropic cell contraction, and that these stress distributions correlate directly with cell growth patterns. Importantly, the spatially localized foci of cell proliferation were lost when cytoskeleton tension was dissipated by using inhibitors of Rho-associated kinase or myosin function, whereas increasing cytoskeletal contraction using a recombinant adenovirus to express constitutively active RhoA accentuated the gradients of proliferation. These proliferation gradients also were significantly reduced when cell–cell adhesions were disrupted by using an adenovirus encoding a cytoplasmic-deletion mutant of VE cadherin, even though it had no effect on the proliferation of cells at subconfluent densities. These findings unequivocally demonstrate that mechanical tension generated within the cytoskeleton and resisted by cell–cell and cell–ECM adhesions is directly responsible for generating spatially constrained cell growth patterns within these monolayers.

One last question remained to be resolved. Must an edge be present for these growth patterns to emerge in a cell monolayer, or is the presence of an edge merely one mechanism for concentrating stress gradients? This is an important question because cells within normal epithelial tissues effectively have no “edge,” yet they are able to generate localized growth foci that drive regional tissue expansion during morphogenesis. To address this question, the investigators used an elegant but simple approach: they cultured the cells on a microfabricated ECM surface containing an undulating tessellation of microscale tetrahedral pyramids. Computational modeling predicted that cells in the regions overlying the valleys between the pyramids will experience more traction force than those at the peaks, and experiments confirmed that cell proliferation rates were again preferentially enhanced in these more highly stressed regions. Thus, the distribution of physical forces characteristic of a particular tissue architectural conformation that are transmitted through the cytoskeleton to cell–cell and cell–ECM adhesions do indeed act as informative forces that regulate cell growth patterns (2–4).

Mechanical Control of Morphogenesis

These seminal findings by Nelson et al. (1) reaffirm that living tissues are governed by the same architectural principles that define the nonliving natural world and remind us how important it is to reintegrate physics into cell and developmental biology. Some of the earliest findings to suggest that tissue geometry can feed back to regulate cell growth came from studies of tumor cells grown as spheroids (14). Tumor cell proliferation was limited to cells in the outer few layers of these spherical cell aggregates, much like the pattern exhibited by cell monolayers grown on circular ECM islands (1). Although the restriction of growth to the outer edge of the spheroid was interpreted to be largely due to diffusion limitations, it was noted that cells in these regions would experience the greatest surface tension and hence physically stretch more than the rest. This observation led to later studies that revealed the tight correlation between cell shape and growth (10). Interestingly, some of the microfabrication techniques used by Nelson et al. also were instrumental in demonstrating that cell spreading per se is required for mitogen-stimulated cells to undergo cell cycle progression (11, 15). Cell distortion-dependent changes in cytoskeletal structure that feed back to regulate the Rho signaling pathway are key to this mechanical form of growth control (16). Cell–cell adhesion molecules, such as VE-cadherin, influence cytoskeletal organization and cell growth by feeding into this same signaling pathway (17). Thus, tissue form may feed back to control cell proliferation by concentrating stresses at particular sites and mechanically restructuring the actin cytoskeleton inside cells within these regions, thereby altering Rho signaling. The possibility that this type of physical control mechanism operates in vivo is supported by the finding that the local gradients of cell proliferation that drive epithelial budding during embryonic lung morphogenesis (Fig. 1) can be enhanced or inhibited by altering cytoskeletal tension by using Rho signaling modulators (18), just as Nelson et al. did in cultured cells (1).

Cells also may use their ability to contract to drive other types of morphogenetic processes, including cell sorting (19), cell movements, and convergent extension during gastrulation (20, 21), neurulation (22), mesenchymal patterning (23), and sheet migration (24) that result from stress-induced changes of cell shape or ECM organization. Mechanical stresses caused by increases in cell packing density also can activate genes that control axis formation in early Drosophila embryos (25). But in all cases, cell-generated mechanical stresses drive the process, and tissue form and function are always inextricably linked. The ability to switch on or off specific developmental sequences by altering expression of particular genes is aweinspiring, and thus it is not surprising that genetic analysis has dominated the field of embryogenesis. However, living cells likely use mechanical cues or changes in cytoskeletal organization to control the switching of many of these very same genes and signaling pathways (25, 26). Apparently, in the developing embryo, sometimes function follows form, and not the other way around.