Abstract
This paper investigates the influence of different parameters on the open circuit voltage of an organic solar cell (OSC) and how the open circuit voltage impacts the cell's power conversion efficiency. These parameters include temperature, light intensity, recombination, charge carrier density, charge carrier mobility ratio, and the reverse saturation current. Organic solar cells' power conversion efficiency is still far from ideal and is currently about 20 %. In the approach, mathematical expressions governing these parameters are established and simulations are then performed in which all other parameters are held at their optimal values and one parameter of interest is varied within a predetermined range. It is shown that the open circuit voltage (Voc) can theoretically reach a value of about 2.34 V if the following parameters are maintained optimal: light intensity, charge-carrier density (1 × 1018cm−3), charge carrier mobility ratio (10) and cell temperature (320 K). It is shown that the open circuit voltage (Voc) is negatively impacted by recombination (up to 30 Ω). Lastly, the power conversion efficiency is predicted to be 20 % at 0.63 V and can reach a theoretical value of 37 % at a Voc of 1.0 V, at a power intensity input of 6.578 w/m2, and a fill factor of 0.89 (max for silicon).
Keywords: Organic solar cell, Open circuit voltage, Recombination, Charge carrier density, Charge carrier mobility ratio, Reverse saturation current
1. Introduction
Organic photovoltaic is a recent technology that portrays a wide range of advantages such as: having modules built with lightweight and flexible organic materials rendering them appropriate for attachment as an accessory to clothing and purses; exhibiting partial transparency; simple incorporation into additional goods; having new market prospects, such as wearable photovoltaics; much-reduced production costs when compared to traditional inorganic technologies; continuous manufacturing of OPV with cutting-edge printing equipment; minimal environmental risks and quick energy payback periods and because they are multicoloured, they may be made to match the colour of purses and clothes.
Organic solar cells have been demonstrated as the potential choice for the next generation of photovoltaic (PV) devices. From the manufacturing perspective, the device processing of an organic solar cell (OSC) is easier, compared to other recent PV technologies [1]. The high absorption coefficients demonstrated in organic semiconductors [2] allow the use of extremely thin films [3,4]. The manufacturing costs of OSCs are cheaper, and this combined with fewer materials required for their production, put OSCs in an advantaged position in the future PV market. Organic photovoltaic (OPV) devices are also characterised by a system of aggregate small molecules which have boosted the power conversion efficiency by up to 12 % as reported in Ref. [5]. The bulk heterojunction (BHJ) type of OPV devices, which is a blend of an electron-donor small molecule material and an electron-acceptor material is now the standard choice for applications, owing to the above advantages and presenting the best performance efficiency (PCE) [6].
Despite these advantages coupled with the flexibility of OPV cells and lower cost, a major shortcoming according to recent research on the technology remains their low power conversion efficiency.
When an OPV device is not connected to any circuit, the electrical potential difference between its two terminals is known as the open circuit voltage (Voc). The highest value of Voc measures the approximate energy difference between the donor's HOMO level and the acceptor's LUMO level [7]. The link between the energy levels at the donor-acceptor (D-A) interface and the open circuit voltage for various bulk heterojunction solar cells was investigated by Scharber et al. in 2016 [8]. One of the most significant fullerene derivatives, PCBM, was utilized as the acceptor material for each device, whereas different donor materials were used. This work led to the derivation of a straightforward relationship between the HOMO of the donor material and the Voc of the device, expressed in Eq. (1) [9].
| (1) |
where (potential difference being work done per unit charge), q is the elementary charge, is the energy level of the highest occupied molecular orbital of the donor material, is the energy level of the Lowest unoccupied molecular orbital of the acceptor material
But rather than being theoretically derived, these results are based on practical analysis. This link is however implicitly questioned by other researchers on the genesis of Voc [10], highlighting the fact that, unlike silicon p-n junction solar cells, the formation of Voc in bulk heterojunction organic solar cells is still poorly understood. In effect it is pointed out in Ref. [10] that, models which perceive polymer semiconductors materials as undoped need some revision to capture the effect of band bending (depletion zones) and the injection of minority carrier and storage in the diode bulk. Currently, research effort is being done to increase the open-circuit voltage (Voc), which is now slightly greater than 1 V for single junction OSC and about 2.03 V for some tandem cells [29]. It is intended in this work to contribute to this on-going effort through theoretical analyses and numerical simulations with the target to improve the open-circuit voltage (Voc).
This work focuses on modelling an Organic Solar Cell (a belt equivalent circuit model). The model of the OSC taken into consideration here is derived from the Mazhari's model of the OSC [11]. In the DC analysis of the equivalent circuit model, recombination effects and charge extraction resistances are captured as diodes (that is, small voltage sources and resistors) and not just resistors. Using the model, various parameters that affect Voc are studied through equations derived from the electrical circuit model. The model is formulated based on electrical circuit equations. All derived equations are substituted into the electrical equations of the OSC both in the dark condition and light conditions where simulations are done to see the trends on various parameters that affect Voc of the OSC. The main limitation of the model is the generic nature that does not offer the possibility to test specific OSC materials, which take into consideration some morphological parameters. The results obtained are in agreement qualitatively in all cases with experimental predictions from literature and quantitatively in some cases. It is believed that by enhancing the properties of organic solar cells and driving the efficiency to comparable levels as that of inorganic solar cells will greatly shift technology towards the production more of OSC as they are much cheaper to produce as highlighted above.
2. Modelling of an organic solar cell
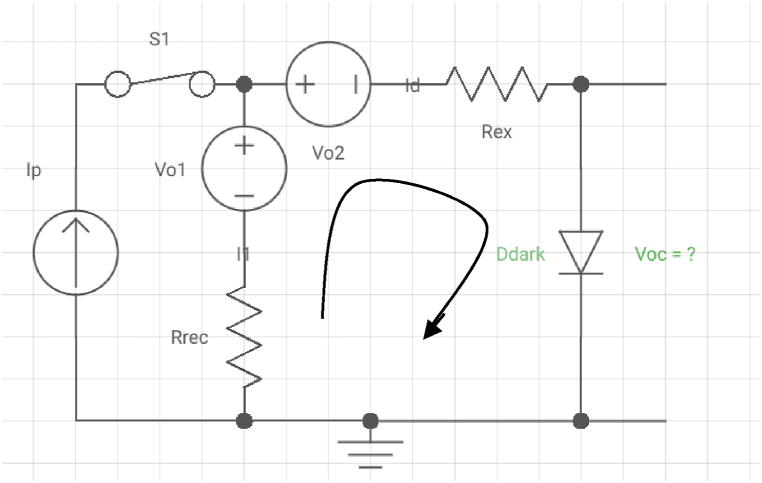
Mazhari's organic solar cell model is adopted in the foregoing analyses [11]. The organic solar cell is modelled as a circuit element operating as a light-regulated current source. In the circuit, this current source generates a given amount of direct current at a fixed light intensity that transits through a Shockley's Diode, which is connected in parallel to the current source. An OSC's ability to generate current is impeded jointly by the phenomenon of exciton recombination and charge carrier extraction at the electrodes. In the model, these recombination effects are represented by a forward-biased diode Drec (silicon diode V01 = 0.7 V and Rrec = 25 Ω) connected in parallel to the current source. A second diode, Dex (germanium diode V02 = 0.3 V and Rex = 5Ω) models the impact of the resistance triggered by charge extraction at the electrodes.
In Fig. 1, Ddack, also known as Shockley's Diode, is regarded as a perfect diode governed by Shockley's diode equation. This diode equation is derived based partly on the presumption that the diode would not have a depletion layer or built-in potential. In the forward bias mode, an ideal diode provides resistance to the flow of current and has a built-in potential of 0.7 V for silicon-based diodes and 0.3 V for germanium-based diodes. The impact of recombination in OSCs is modelled by this resistance. The diodes' inherent potential will have an impact on the cell's open circuit voltage.
Fig. 1.
Equivalent circuit model for an organic solar cell in the absence of parasitic series and shunt resistances.
An organic solar cell generates no current when it is in the dark condition because it produces no excitons, has no recombination effects, and has no exciton dissociation. Within the cell, there is a built-in potential difference. This is a type of diode capacitor because the donor and acceptor materials have different energy potentials, which causes an internal electric field to build up between the two plates. As seen in Fig. 2, this can be represented as an Ideal Shockley's diode in an open circuit.
Fig. 2.
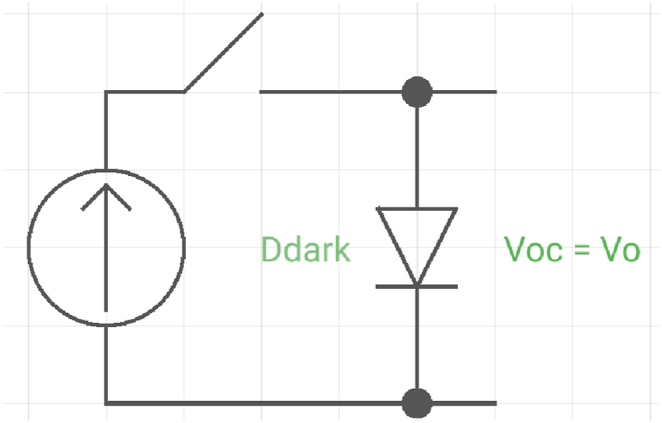
The circuit diagram of the modelled organic solar cell in the dark.
The current flowing through the diode ID if the circuit is closed in the absence of the current source (short circuit current Isc) is given by Ref. [12]:
| (2) |
where I0 is the reverse saturation current, R is the Boltzmann's constant, q is the electronic charge, and T is the temperature. Eq. (2) indicates that the cell will behave as an intrinsic semiconductor whereby the number of holes (Pp) and electrons (Pn) increase with increasing temperature in the absence of light. Further evidence for this comes from the Boltzmann's equation [22].
| (3) |
where Pp is the number of holes, Pn the number of electrons, V0 the build in potential of the diode and VT is the thermal voltage of the diode.
2.1. Relationship between temperature (T), recombination effects (Rrec), and open circuit voltage (Voc)
An OSC illuminated by light of a certain frequency and intensity will generate some direct current, which will in turn initiate some resistance and will be subjected to some recombination effects as the charge carriers reach the electrodes. As a consequence, the net short-circuit current of the OSC will drop, decreasing the solar cell's power conversion efficiency. An OSC under illumination is modelled as presented in Fig. 3.
Fig. 3.
Model of organic solar cell under light condition.
An application of Kirchhoff's Current and voltage laws result in the open circuit voltage expressed as:
| (4) |
Eq. (4) establishes the relationship between the open circuit voltage (Voc), temperature (T), and recombination effects (). has a value of 0.7 V for silicon diodes and take a value of 0.3 V for Germanium diodes. The silicon diode is preferred here to model recombination effects because it offers a higher resistance compared to other diodes. Rex represents the resistance at the electrodes, I0 is the reverse saturation current, Ip is the generated current, and VT is the thermal voltage. VT is expressed as:
| (5) |
and has a value of approximately at room temperature (300 K). The rate of exciton generation is denoted as Ip and the rate of exciton recombination as Rrec. The highest forward-biased resistance of a silicon diode is 25 Ω, while a germanium diode may operate at a maximum temperature of 363 K and has a maximum forward-biased resistance of 5 Ω. A silicon solar cell can produce a maximum current of 46 mA/cm2.
In what follows, the factors that influence exciton generation Ip like temperature and light intensity will be investigated.
2.2. The impact of light intensity on the open-circuit voltage of the organic solar cell
Light intensity is described as the number of photons in a beam, that is [13]:
| (6) |
In Eq. (6), denotes the light intensity, h is the Planks constant (6.62559 × 10−34Js), and ∅ph is the photon flux. The short circuit current (Isc) produced by a photovoltaic material is directly proportional to the intensity of the incident light. This is referred to as the number of suns (X), according to G. Bunea et al. [13], where 1 sun is equivalent to a standard lighting power of 1 kW/m2. Mathematically, this implies that:
| (7) |
Combining Eq. (2) with Eq. (7) results in an ideal model of an OSC operating in the dark, which is expressed as,
| (8) |
Eq. (12) can be rearranged to express as:
| (9) |
In the case where , can be expressed for convenience as:
| (10) |
where
| (11) |
In the event of exciton recombination and charge collection at the electrodes Eq. (4) now becomes
| (12) |
where X is the number of suns.
2.3. The effect of charge density on Voc of an organic solar cell
In the dark condition, or the open circuit voltage is equal to the built-in potential of Shockley's diode V0. The energy gap is defined as [9]
| (13) |
when the OSC is in dark conditions (Open circuit mode with zero recombination and electrode resistance effects)
| (14) |
where, the value of , depends on the type of the Donor/Acceptor material used.
Denoting the electron concentration as n, holes concentration as p, charge carriers concentration in the conduction band as Nc, and charge carriers concentration in the valence band as Nv, then is expressed as [23]
| (15) |
The law of mass action also permits the alternative expression:
| (16) |
The HOMO-LUMO band gap energy can then be expressed as:
| (17) |
and it follows that
| (18) |
From Eq. (13), which represents the model OSC in the dark condition is then expressed as,
| (19) |
hence
| (20) |
where K is the Boltzmann's constant, T is the temperature, q is the electronic charge, ni is the intrinsic charge carrier density, ND is the donor material charge density, and NA is the acceptor material charge density. For silicon, the maximal intrinsic carrier concentration is . Voc is dependent on the log of the Donor and acceptor concentration in the organic molecule, according to Eq. (20).
2.4. Effect charge carrier mobility on the open circuit voltage
Charge carrier mobility is governed by drift and diffusion effects. The movement of charge carriers (holes or electrons) driven by concentration gradients generates a diffusion current. Hence there is a direct proportionality between the diffusion current density and the concentration gradient.
The proportionality is expressed for electrons and holes as:
| (21) |
and
| (22) |
Where and are the diffusion current densities generated by electrons and holes respectively.
They can be further expressed as:
| (23) |
and
| (24) |
where Dn and Dp denote the diffusion current coefficients of the electrons and holes respectively. Taking into consideration the drift velocity, the total current densities due to the electrons and the holes are expressed respectively as [14]:
| (25) |
and
| (26) |
These can be combined into a single expression as:
| (27) |
or,
| (28) |
where are the electrons and holes mobility respectively and n and p are respectively the electron and hole concentration.
Unlike the diffusion current which is driven by the concentration gradients of the holes and the electrons, the drift current is caused by an internal field at the donor-acceptor interface, acting on the excitons. The energy associated with this field is expressed as [15]:
| (29) |
where is the intrinsic energy level of p-type material (acceptor material), is the Fermi energy level of p-type material, is the Fermi energy level of n-type material and is the intrinsic energy level of n-type material. The Fermi energy level (Ef), is that energy level that has 50 % probability of occupation by an electron at any temperature. The intrinsic energy level (Ei) is the average internal energy of the n-type or p-type material.
From semiconductor theory, the concentrations of majority charge carriers; n and p in the N-type and P-type materials are respectively expressed as [23]:
| (30) |
and
| (31) |
Putting these various contributions into Eq. 28 give:
| (32) |
or,
Considering the model of our OSC in the dark condition, from equation (29)
| (33) |
However, the current does not flow under open circuit conditions, expressed as:
| (34) |
or,
| (35) |
Choosing an optimum operating condition characterised in this situation by, , leads to:
| (36) |
from which it can be concluded that the charge carriers mobility ratio is a multivariable function of temperature, electric field strength, electrons and holes concentrations, and impurities which increase resistance.
2.5. The impact of exciton recombination on Voc
Exciton current Ip is lowered by recombination effects. A rising Rrec in an organic solar cell system will provoke a decrease in Ip which is accompanied by a linear decrease in Voc. The variation of Voc against Ip is obtained by rearranging Eq. (12) as expressed in Eqs. (37), (38)). A feasible and reasonable range of Ip is obtainable from Eq. (38) by substituting the lowest and highest values of the recombination factor Rrec, while all other parameters are maintained at their optimal values.
| (37) |
from which,
| (38) |
Eqs. (37), (38)) demonstrate that exciton recombination is a parameter that will impact the value of Voc in an organic solar cell. The Recombination parameter is very important in the cell because it prevents an imminent disintegration of the organic material by avoiding an uncontrollable increase of the majority charge carriers.
2.6. Effects of the reverse saturation current on Voc
The reverse saturation current is made up of a portion of the reverse current in a semi-conductor diode resulting from the minority charge carriers that diffuse from the neutral to the depletion areas. This diffusion process goes on until the depletion layer is built up preventing further diffusion. At this stage, an internal electric field is set up causing hole diffusion from the p-type region to the N-type region and electron diffusion in the reverse direction.
When the OSC is illuminated or subjected to some finite temperature, the bonds will break causing a rise in the reverse saturation current.
In the dark state, the organic solar cell is modelled as a Shockley's diode given by Eq. (2); from which is expressed as:
| (39) |
Knowing that , this expression simplifies to:
| (40) |
This equation gives the relationship between the open circuit voltage and reverse saturation current . For a given Ip, representing the current source value, and from the current divider rule, is expressed from Fig. 3 as:
| (41) |
Where is the current through the Shockley's diode
3. The effect of open circuit voltage on the power conversion efficiency (PCE) of an organic solar cell
An organic solar cell's power conversion efficiency (PCE) is expressed as a function of the fill factor (FF), the short circuit current, the open circuit voltage, and the incident light intensity. The fill factor (FF) here is a measure of the maximum electric power production per unit active area of the OSC. Eqn. (38) is used to calculate PCE as follows [16].
| (42) |
| (43) |
where FF is the fill factor, Jsc is the short circuit current and Pin is the intensity of incident light. Silicon solar cells present a maximum short circuit current of 0.042 A/cm2. The maximum fill factor for a silicon solar cell is approaching 0.89. The average intensity of one sun on Earth's surface is 1000 W/m2.
4. Simulation results and discussions
Simulations are done in this section where all other parameters are maintained at their optimal values while one parameter is changed within a specified range.
4.1. Variation of Voc with temperature
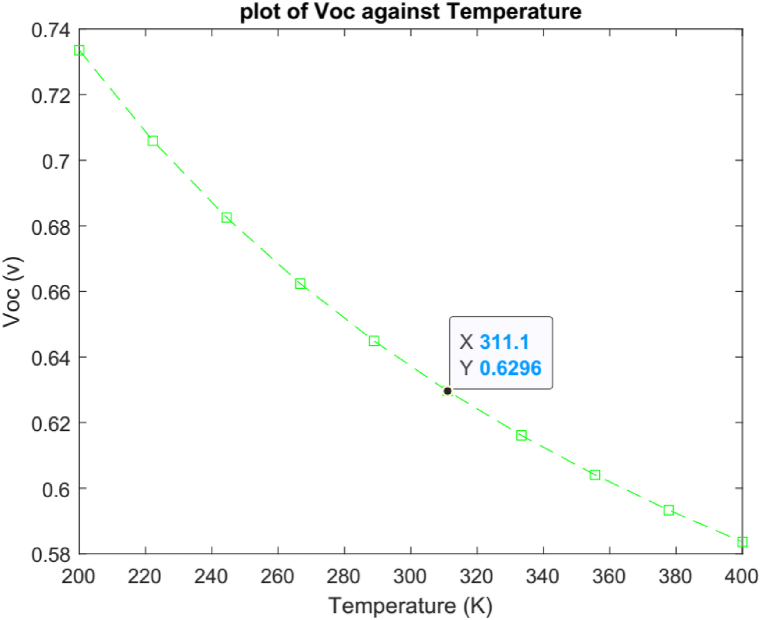
Eq. (4) is used in Fig. 4 to display the trend of Voc with temperature. The recombination parameter is represented by a silicon-based diode with a built-in voltage (V01) of 0.7 V and resistance of 25 Ω in this equation, while the extraction resistance at the electrodes is represented by a germanium diode with a built-in voltage (V02) of 0.3 V and an internal resistance of 5 Ω. At an Ip value of 0.02 A, the current source is retained. The temperature fluctuates between 200 K and 340 K. We see that the open circuit voltage of the simulated organic solar cell decreases from a maximum value of 0.74 V when the temperature is 200 K.
Fig. 4.
Variation of Voc with temperature.
Eq. (1)'s representation of the open circuit voltage serves as the foundation for an explanation of Fig. 4. The open circuit voltage of organic solar cells is a measure of the widening of the band gap between the LUMO and HOMO at low temperatures [[9], [17]]. When comparing these findings to experimental studies, it can be seen that (Brus et al., 2021) observed a similar tendency where Voc drops with temperature, in their study on Temperature and Light Modulated Open-Circuit Voltage in Nonfullerene Organic Solar Cells [25]. The same trend was also experience by (tang et al. 2020) showing a decrease in Voc from low temperatures to increasing temperatures [26]. Thus the relationship of temperature with the open circuit voltage can be pursued so that cell performance may be optimized when used in realistic applications. Ideally, the target is to engineer OSC's to work under standard conditions. Except for low temperature application, attempts to incorporate cooling mechanisms to enhance Voc in OSC's is a possibility but will however add to the complexity and the cost of system.
4.2. The relationship between Voc and light intensity (number of suns) in an OSC
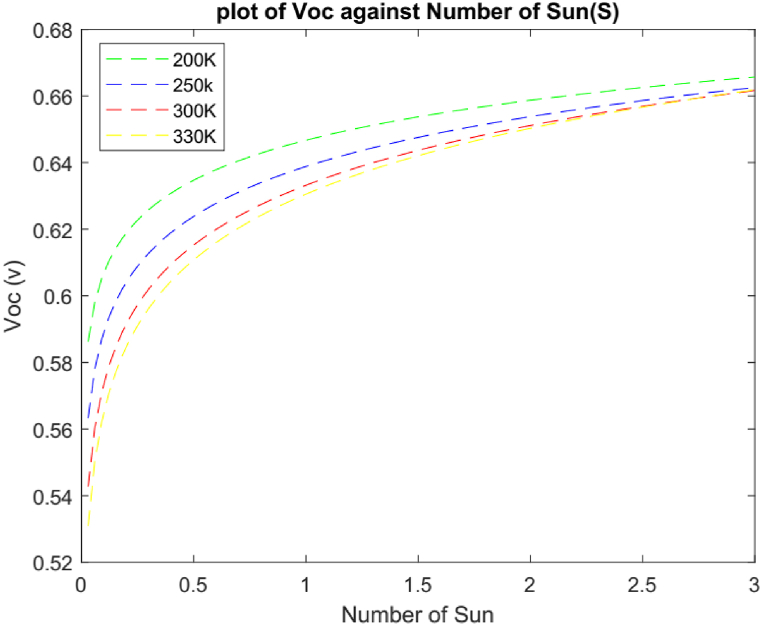
Eq. (12) can be used to increase the number of suns, which will consistently raise Voc, to higher values at different temperature, as shown in Fig. 5.
Fig. 5.
The variation of Voc with light intensity.
Exciton concentration rises with light intensity (more charge carriers are photo-generated in the active layer with an increase in the number of suns), which explains the result seen in Fig. 5. This pattern is consistent with the findings of Naveen Kumar et al. (2015) [18]. According to their review, for polymer: fullerene BHJ solar cells, the open-circuit voltage varies logarithmically with illumination intensity (Voc vs ln(I)). This demonstrated a linear rise in Voc with light intensity. The trend is validated by the experimental works carried out by (Ryu et al., 2021, Benesperi et al. 2022) who experimentally recorded an increase in Voc with an increase in the percentage of light intensity [30,31].
4.3. The relationship between current generated by the cell (Ip) and recombination
The dependency of Ip with recombination effects Rrec is depicted in Fig. 6. Eq. (38) is used in the simulation to get this outcome. The current generated by the cell decreases from an optimal value of 1.5 A to vanishingly small values when the recombination increases from near zero to 25 Ω, which is the actual resistance of a silicon diode, and when all other parameters are kept at optimal values (i.e., V0 = 0.3 V, q = −1.6 × 10-19 C, T = 330 K, R = 1.38 × 10−23 J/K, Rex = 5 Ω, V1 = 0.3 V, V2 = 0.7 V, I0 = 1.82 × 10−11 A, and VOC = 1 V).
Fig. 6.
The variation of cell current generated (short circuit current) (Ip) with recombination Rrec (Ω).
The explanation for the results shown in Fig. 6 is that an organic solar cell can only produce a significant amount of current when a significant quantity of exciton dissociation occurs at the donor-acceptor interface of the cell. The free charge carriers that make up the cell's current won't be produced if dissociation doesn't happen. The distance between the exciton and the D/A interface (which may be adjusted by selecting the cell's morphology), the diffusion rate of the exciton, the concentration of charge carriers, and the exciton lifetime all impede this separation. An organic solar cell will provide a higher current if recombination is kept to a minimum. This outcome is consistent with research conducted by Frédéric Laqua et al. (2017), who found that exciton recombination is the primary cause of power losses in organic solar cells [19]. These results are validated by experimental results obtain by (Liu and Li, 2011) who revealed that monomolecular recombination is the primary loss mechanism in OSCs [32].
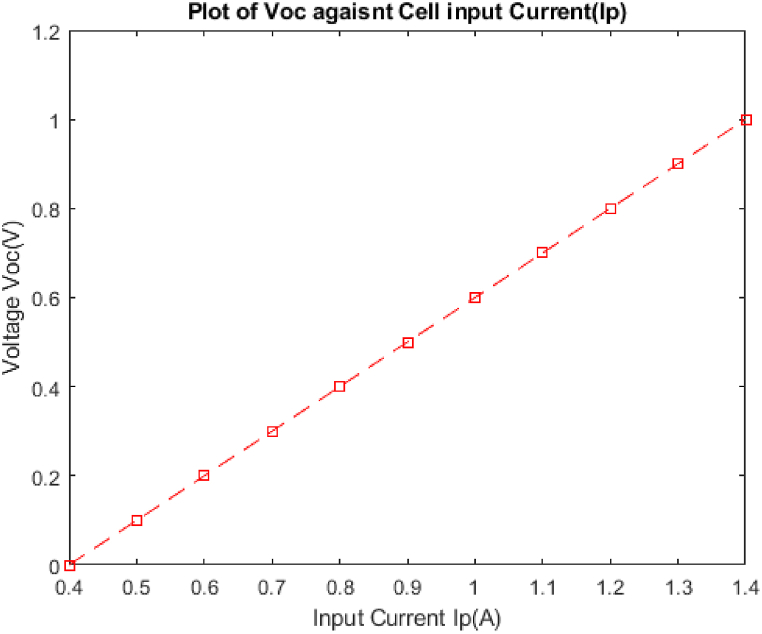
4.4. The relationship between Voc and input current of organic solar cell (Ip)
The result in Fig. 7 shows the influence of Ip on the open circuit voltage Voc. This result was obtained using Eq. (37). With every other parameter kept constant (i.e V0 = 0.3 V, q = −1.6 × 10−19 C, T = 330 K, R = 1.38 × 10−23 J/K, Rex = 5 Ω, V1 = 0.3 V, V2 = 0.7 V, I0 = 1.82 × 10−11 A) and Ip varied from 0.4 A to 1.4 A, Voc increases linearly from zero to 1 V.
Fig. 7.
The variation of Voc with input current.
The idea that the concentration of free charges placed at the electrode which is comparable to the charges placed on a capacitor's plates and determines the current it will drive through helps to explain the results in Fig. 7. It also determines the strength of the current that can be pushed through. The findings of Pankaj Kumar et al. (2009) [20] with their studies utilizing an indium tin oxide (ITO)/copper phthalocyanine (CuPc) (20 nm), C60 (40 nm), bathophenanthroline (BPhen) (8 nm), and Al (150 nm) OPV device are comparable to this one. According to their findings, Ip increases linearly with illumination intensity, which is related to Voc's increase with light intensity. Pankaj Kumar et al. (2009) [20] further report that Voc is nearly saturated at high light intensities, also corroborate this result as well. This result is also validated by the experimental work carried out by (Parhi et al., 2021) on organic solar cells. They found that, Voc increases, exhibiting a higher slope at lower intensities (less than 20 mW/cm2) and lower slope at higher intensities from 20 mW/cm2 to 100 mW/cm2 [33]. In conclusion, the targeted goal of this paper has been accomplished in this instance since Voc rises in response to light intensity, and light intensity and input current are directly correlated.
4.5. The relationship between the donor/acceptor concentration and Voc
From Fig. 8 we see that for a given material with intrinsic carrier concentration ni of amount at a temperature of 300 K, an increase in the concentration of donor and acceptor material from 0 to 1 × 1017 at a temperature of 300 K will lead to a sharp increase in the value of Voc, then approaching a saturation point where Voc increases at a lower rate.
Fig. 8.
Variation of Voc with donor, acceptor material concentration.
The quality of an organic material's conductivity makes it favourable to be used to build a solar cell, this explains the results in Fig. 8. Stated otherwise, a higher amount of charge carrier injection into the active layer will result in a higher Voc. This pattern is consistent with the findings of Kyohei Nakano et al. [24] from 2019, who reported a linear rise in Voc with carrier concentration; however, they did not address the point of saturation, which is the case in this instance. It is also critical to remember that, recombination rises linearly with donor acceptor concentration. This is a constraint on an extraordinarily high Voc.
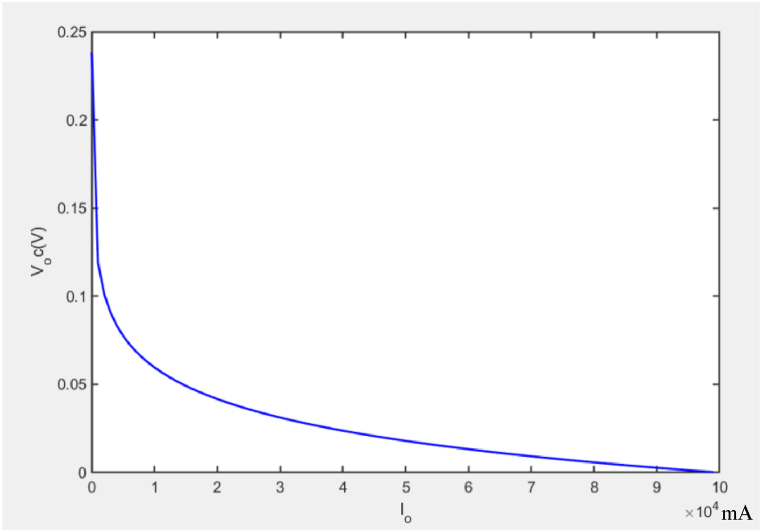
4.6. The relation between Voc and reverse saturation current?
Fig. 9 shows the results obtained for a constant (1 × 105 mA) through Shockley's diode in our model at a constant temperature of 300 K. It is observed that Voc decreases from 0.25 V to 0 V) for a variation of from 0 to 1 × 105 mA.
Fig. 9.
Variation of Voc with reverse saturation current.
Fig. 9 findings can be explained by the fact that minority charge carriers diffuse, causing reverse saturation current to flow. As more bonds in the organic molecule are broken at the Donor-Acceptor/Interface in the organic cell, the built-in potential generates an electric field that functions as an energy barrier to the flow of minority charge carriers, increasing the flow of reverser saturation current. This finding is consistent with the finding by Sean Sehyun et al. (2008) [21], who showed that reverse saturation current density causes Voc to decrease.
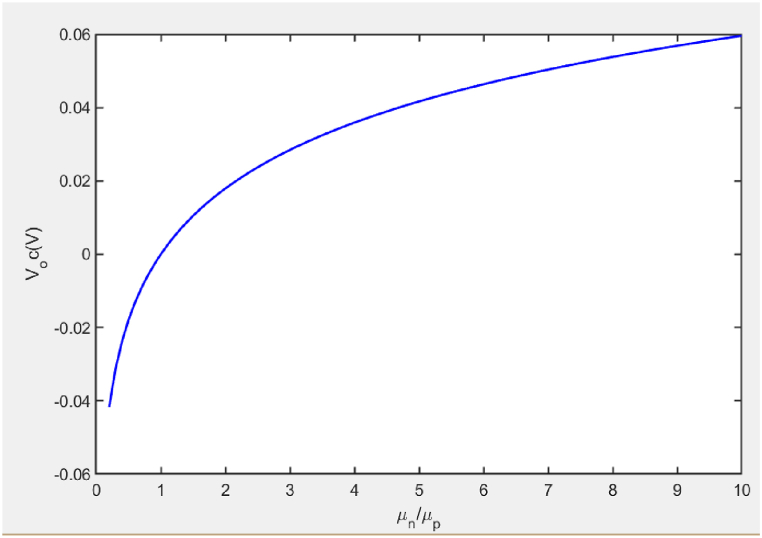
4.7. The relationship between charge carrier mobility ratio with open circuit voltage
Fig. 10 shows the variation of charge carrier mobility ratio in the modelled organic solar cell with Voc. This analysis is done bearing in mind that the charge carrier mobility ratio of silicon diode ranges from 0.22 to 5.55 and the mobility of electrons is 1400 cm2/Vs and that of holes is 450 cm2/Vs.
Fig. 10.
Variation of Voc with charge carrier mobility ratio.
Since low charge mobility indicates high cell resistance and high charge mobility indicates low cell resistance, the curve in Fig. 10 makes sense. The recombination rate is high at high cell resistance, which lowers Voc. Similar results are recoded by Ompong et al. [14]. When the electron mobility is greater than the hole mobility, Voc increases if the ratio >1. When the mobility of electrons and holes in a material are identical, the transport term's contribution to the Voc disappears. Recombination and charge carrier mobility factors as observed in the forgoing analysis can play a major role for the scalability of organic solar cell technology. In effect, recombination of charge carriers reduce efficiency since the charge carriers will not be picked up at electrodes to contribute in power production. Once the optimal values of recombination and charge carrier mobility factors are achieved for a single OSC, scalability will be done as it is the case with inorganic solar cells by arranging the cells in series or in parallel depending on the overall Voc or Isc that is desired.
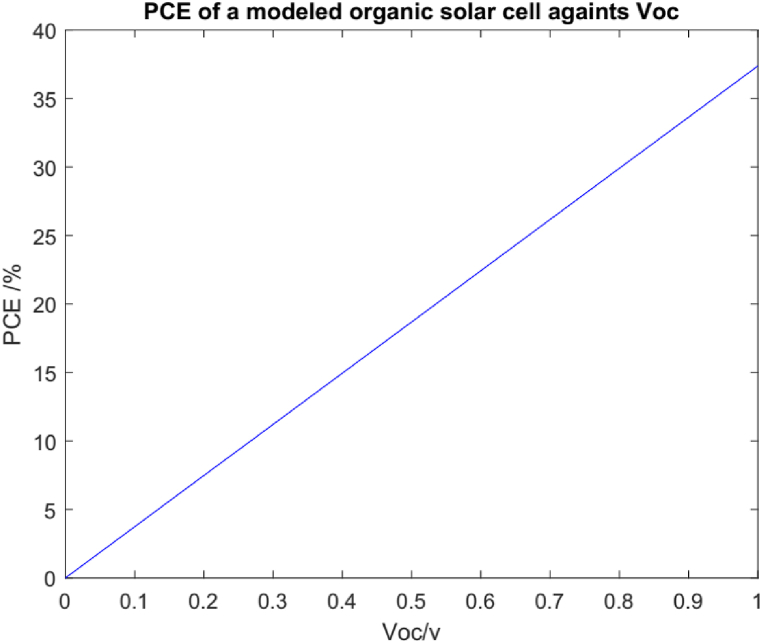
4.8. Open circuit voltage variation with a power conversion efficiency of an organic solar cell?
Fig. 11 illustrates how an organic solar cell's power conversion efficiency is reliant on the open circuit voltage. Eq. (38) is used to get this numerical result, and the range of values for Voc is [0 V–1 V]. This range of Voc is the outcome of simulating an organic solar cell according model's Eq. (4).
Fig. 11.
Variation of PCE with Voc.
Fig. 11 shows that from the equivalent circuit model of the OSC, we record a theoretical value of PCE of 20 % at temperatures closer to 330 K, and when Voc is 0.63 V (see Fig. 4). The increase in PCE with Voc is the trend observed in OSC technology, (Zhou M et al.), in 2023 recorded PCE of 19.10 % of an OSC [27]. This trend of increase in PCE of OSC with Voc is confirmed with the experimental work carried out by Kang et al., in 2020 who obtained an increased in PCE from 15.7 % to 16.3 % [28]. Wang et al., in 2023 with a Voc of 1.09 for single junction OSC and 2.03 V for tandem cells experimentally recorded a certified PCE of 19.1 % and 20.3 % respectively of the constructed single and tandem OSCs [29]. Table 1 presents some optimal data of the maximum PCE for different Voc.
Table 1.
Some typical data on PCE for different Voc based on single junction OSC.
From Table 1 we see that theoretical predictions of the current paper giving a PCE of 20.23 % for a corresponding Voc of 0.63 is within range and can give more hope for the enhancement of the PCE of organic solar cells. Organic solar cells with optimum open circuit voltage will have their efficiencies enhanced. The build in voltage in the diodes that modelled recombination and charge extraction resistance at the electrode were considered in Mazhari's model of organics solar cell.
5. Conclusion
The Open circuit voltage of an organic solar cell (a model considered in this work) cell actually depends on: Temperature, Number of suns (illumination intensity), Charge carrier mobility ratio and Donor & Acceptor Concentration. When temperature increase from 200 K to 320 K, Voc drops from 0.74v to 0.63 V. Increase in the number of suns from 0 to the solar constant (∼1.3suns) will lead to increase in Voc to 0.63 V, this value drops when temperature increase from 200 K to 330 K. Voc increases with increases in the charge carrier mobility ratio of electrons to holes. A Voc of nearly 1 V will be produced by donor and acceptor concentrations of the order of 1 × 1018 cm−3. In addition, a rise in recombination effects within the temperature (273 K–330 K) will cause the short circuit current to drop from 1.5 A to almost zero, which will lower the voltage from 1 V to 0 V. Finally, the PCE is observed to rise from 0 to a theoretical value of 20 % as Voc increases from 0 to 0.63 V. Hence PCE of an OSC is directly proportional to Open circuit voltage.
CRediT authorship contribution statement
Pelote Elvis Pepa: Writing – original draft, Software, Methodology, Investigation, Formal analysis. David Afungchui: Writing – review & editing, Validation, Supervision, Project administration, Methodology, Investigation, Conceptualization. Olivier Holtomo: Validation, Supervision, Project administration. Joseph Ebobenow: Validation, Supervision, Conceptualization.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Contributor Information
Pelote Elvis Pepa, Email: peloteelvis@ahoo.com.
David Afungchui, Email: afungchui@yahoo.fr.
Olivier Holtomo, Email: holtomo@yahoo.fr.
Joseph Ebobenow, Email: ebobenow@gmail.com.
Nomenclature
| CT | Charge transfer |
| FF | Fill factor |
| h | Plank's constant (m2kg/s) |
| J | current density (A/cm2) |
| OPVC | Organic photo voltaic cells |
| OSC | Organic Solar Cells |
| PCE | Power conversion efficiency (%) |
| q | Elementary charge (C) |
| R | Boltzmann's constant (J/K) |
| SC | solar cell |
| v | Frequency of incident light (Hz) |
| IL | Light intensity (cd) |
| Ddack | Shockley's Diode in the dark |
| Dex | Diode modeling extraction resistance (ꭥ) |
| Dn | diffusion current coefficients of the electrons (cm2/s) |
| Dp | diffusion current coefficients of holes (cm2/s) |
| Drec | Diode modeling recombination effects (ꭥ) |
| ID | Current through the Shockley's diode (A) |
| Io | Reverse saturation current (A) |
| Jo | Reverse saturation current density (A) |
| Jsc | Sort circuit current density (A) |
| Pin | Power of incident light (W) |
| Pn | Electron concentration (electrons/cm3) |
| Pp | Holes concentration (holes/cm3) |
| Rex | Build-in-resistance of germanium diode (ꭥ) |
| Rrec | Build-in-resistance of silicon diode (ꭥ) |
| V01 | Build-in-voltage of silicon diode (V) |
| V02 | Build-in-voltage of germanium diode (V) |
| Vo | The build in voltage of a diode (V) |
| Voc | Open circuit Voltage (V) |
| VT | Thermal Voltage (V/K) |
| Homo energy of Donor material (eV) | |
| Lumo energy of acceptor material (eV) | |
| ∅ph | Photon flux. (/sm2) |
| Electron mobility (cm2/Vs) | |
| Hole mobility (cm2/Vs) |
References
- 1.Facchetti A. π-Conjugated polymers for organic electronics and photovoltaic cell applications. Chem. Mater. 2011;23:733–758. [Google Scholar]
- 2.Cheng X.-F., Li J., Hou X., et al. One-dimensional π-d conjugated coordination polymers: synthesis and their improved memory performance. Sci. China Chem. 2019;62:753–760. [Google Scholar]
- 3.Yu G., Gao J., Hummelen J.C., et al. Polymer photovoltaic cells: enhanced efficiencies via a network of internal donor-acceptor heterojunctions. Science. 1995;270:1789–1791. [Google Scholar]
- 4.Tang C.W. Two-layer organic photovoltaic cell. Appl. Phys. Lett. 1986;48:183–185. [Google Scholar]
- 5.Riede M., Spoltore D., Leo K. Organic solar cells—the path to commercial success. Adv. Energy Mater. 2011;11 [Google Scholar]
- 6.Bundgaard E., Krebs F. Low band gap polymers for organic photovoltaics. Sol. Energy Mater. Sol. Cells. 2007;91:954–985. [Google Scholar]
- 7.Kim Myung-Su. 2009. Understanding Organic Photovoltaic Cells: Electrode, Nanostructure, Reliability, and Performance. [Google Scholar]
- 8.Scharber M.C. On the efficiency limit of conjugated polymer: fullerene‐based bulk heterojunction solar cells. Adv. Mater. 2016;28:1994–2001. doi: 10.1002/adma.201504914. [DOI] [PubMed] [Google Scholar]
- 9.Hammouti Belkheir. Physical and Chemical News ·; 2014. Organic Photovoltaic Cells: Operating Principles, Recent Developments and Current Challenges - Review. [Google Scholar]
- 10.Garcia-Belmonte G., Munar A., Barea E.M., et al. Charge carrier mobility and lifetime of organic bulk heterojunctions analyzed by impedance spectroscopy. Org. Electron. 2008;9:847–851. [Google Scholar]
- 11.Mazhari B. An improved solar cell circuit model for organic solar cells. Sol. Energy Mater. Sol. Cells. 2006;90:1021–1033. [Google Scholar]
- 12.From Wikipedia, the free encyclopedia. Shockley diode equation Shockley diode equation. 2023 https://en.wikipedia.org/wiki/Shockley_diode_equation [Google Scholar]
- 13.Brandl M. The Photoelectric Efiect. Michigan State University; 2001. http://www.skpaths.net/modules/pdf_modules/m213.pdf [Google Scholar]
- 14.Ompong D., Singh J. Charge-carrier-mobility-dependent-open-circuit-voltage-in-organic-and-hybrid-solar-cells. Front Nanosci Nanotechnol. 2016;2 doi: 10.15761/FNN.1000108. Epub ahead of print. [DOI] [Google Scholar]
- 15.Energy band structure of open circuited pn junction. https://ashwinjs.files.wordpress.com/2019/02/energy-band.pdf
- 16.Gmbh H., Dresden T.U., Whereas V., Heliatek Open circuit voltage of organic solar cells. An in-depth review. 2013:1–3. [Google Scholar]
- 17.Thakur A.K., Wantz G., Garcia-Belmonte G., et al. Temperature dependence of open-circuit voltage and recombination processes in polymer–fullerene based solar cells. Sol. Energy Mater. Sol. Cells. 2011;95:2131–2135. [Google Scholar]
- 18.Elumalai N.K., Uddin A. Open circuit voltage of organic solar cells: an in-depth review. Energy Environ. Sci. 2016;9:391–410. [Google Scholar]
- 19.Laquai F, Andrienko D, Deibel C, et al. Charge carrier generation, recombination, and extraction in polymer–fullerene bulk heterojunction organic solar cells. In: Leo K (ed) Elementary Processes in Organic Photovoltaics. Cham: Springer International Publishing, pp. 267–291.
- 20.Kumar P., Jain S.C., Kumar H., et al. Effect of illumination intensity and temperature on open circuit voltage in organic solar cells. Appl. Phys. Lett. 2009;94 [Google Scholar]
- 21.Potscavage W.J., Yoo S., Kippelen B. Origin of the open-circuit voltage in multilayer heterojunction organic solar cells. Appl. Phys. Lett. 2008;93 [Google Scholar]
- 22.The pn junction. http://www.univasf.edu.br/∼joseamerico.moura/index_arquivos/Analog20151/pninjection.pdf&ved=2ahUKEwjGk7q2wbeGAxXmQ6QEHcXgBpwQFnoECCEQAQ&usg=AOvVaw3Egy4_TPVJXWdYbXrmFxmj
- 23.Lecture 5 Intrinsic semiconductors-conductivity. https://staff-old.najah.edu/sites/default/files/Lec5.pdf&ved=2ahUKEwjYztapzreGAxVhRaQEHeW1CXUQFnoECBsQAQ&usg=AOvVaw0SFF0PXHe8j-CJXZtiDKqd
- 24.Nakano K., Chen Y., Tajima K. Quantifying charge carrier density in organic solar cells by differential charging techniques. AIP Adv. 2019;9 [Google Scholar]
- 25.Brus V.V., Schopp N., Ko S., et al. Temperature and light modulated open‐circuit voltage in Nonfullerene organic solar cells with different effective bandgaps. Adv. Energy Mater. 2021;11 doi: 10.1002/aenm.202003091. Epub ahead of print January. [DOI] [Google Scholar]
- 26.Tang Y., Bjuggren J.M., Fei Z., et al. Origin of open‐circuit voltage turnover in organic solar cells at low temperature. Sol. RRL. 2020;4 doi: 10.1002/solr.202000375. Epub ahead of print November. [DOI] [Google Scholar]
- 27.Zhou M., Liao C., Duan Y., et al. 19.10% efficiency and 80.5% fill factor layer‐by‐layer organic solar cells realized by 4‐bis(2‐Thienyl)Pyrrole‐2,5‐dione based polymer additives for inducing vertical segregation morphology. Adv. Mater. 2023;35 doi: 10.1002/adma.202305240. [DOI] [PubMed] [Google Scholar]
- 28.Kang Q., Zu Y., Liao Q., et al. An inorganic molecule-induced electron transfer complex for highly efficient organic solar cells. J. Mater. Chem. A. 2020;8:5580–5586. [Google Scholar]
- 29.Wang J., Zheng Z., Bi P., et al. Tandem organic solar cells with 20.6% efficiency enabled by reduced voltage losses. Natl. Sci. Rev. 2023;10 doi: 10.1093/nsr/nwad085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ryu S., Ha N.Y., Ahn Y.H., et al. Light intensity dependence of organic solar cell operation and dominance switching between Shockley–Read–Hall and bimolecular recombination losses. Sci. Rep. 2021;11 doi: 10.1038/s41598-021-96222-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Benesperi I. RETRACTED: cathode interlayer engineering for efficient organic solar cells under solar illumination and light-emitting diode lamp. Coatings. 2022;12:816. [Google Scholar]
- 32.Liu L., Li G. Investigation of recombination loss in organic solar cells by simulating intensity-dependent current–voltage measurements. Sol. Energy Mater. Sol. Cells. 2011;95:2557–2563. [Google Scholar]
- 33.Parhi A.P., Tripathi D.C., Kataria D. Study of the open circuit voltage dependence on incident light intensity of planar heterojunction organic solar cell. Mater. Today Proc. 2021;38:1267–1271. [Google Scholar]
- 34.Gao W, Liu T, Li J, et al. Simultaneously increasing open-circuit voltage and short-circuit current to minimize the energy loss in organic solar cells via designing asymmetrical non-fullerene acceptor. J. Mater. Chem. A. 2019;7:11053–11061. [Google Scholar]
- 35.Cai G, Chen Z, Xia X, et al. Pushing the Efficiency of High Open‐Circuit Voltage Binary Organic Solar Cells by Vertical Morphology Tuning. Adv. Sci. 2022;9:2200578. doi: 10.1002/advs.202200578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Xu R, Jiang Y, Liu F, et al. High Open‐Circuit Voltage Organic Solar Cells with 19.2% Efficiency Enabled by Synergistic Side‐Chain Engineering. Adv. Mater. 2024;36:2312101. doi: 10.1002/adma.202312101. [DOI] [PubMed] [Google Scholar]