Abstract
A recent consensus to achieve carbon neutrality is promoting interest in the use of hydrogen and management of its production system. Among the several types of hydrogen, green hydrogen is of most interest which is produced using power generated from renewable energy sources (RES). However, several challenges are encountered in the stable operation of green hydrogen production systems (GHPS) owing to the inherent intermittent and variable characteristics of RES. Although the implementation of energy storage systems (ESS) can aid in compensating for this variability, large-scale ESS installations can be economically infeasible. Thus, this study seeks an operation strategy suitable for GHPS, considering the expected variability of RES and the operational conditions of a relatively small-sized ESS. In particular, as state-of-charge management is crucial for operating an ESS with limited capacity, this study presents a method to conduct coordinated control between the ESS and electrolyzer. Furthermore, considering the characteristics of the GHPS, the expected short-term variability analyzed using the copula-based approach is utilized. The proposed method is validated based on various RES generation scenarios. By applying the developed method, operational continuity to GHPS is expected to increase with efficiency.
Keywords: Green hydrogen production system (GHPS), Copula-based analysis, Short-term forecast, SOC management, Coordinated control, Alkaline water electrolyzer
Highlights
-
•
Operation strategy for green hydrogen production systems (GHPS) is proposed.
-
•
Coordination between electrolyzer and energy storage systems is employed.
-
•
Variable characteristics of renewable energy sources is considered for operation.
-
•
The proposed method can aid in efficient operation and planning of GHPS.
1. Introduction
In recent years, hydrogen has been noted as a major resource in the era of carbon neutrality. It is expected to be used for transportation, heating, and feedstock for industry. It is also expected to be utilized in power system operations, such as long-term energy storage systems [1,2].
From the perspective of power systems, an electrolyzer is often regarded as a load with high potential to aid in system operation and provide flexibility. In Ref. [3], the authors analyzed the feasibility of utilizing electrolyzer for power quality improvement. In a system configuration in which wind turbines and electrolyzers are connected in parallel, which potentially can be further controlled for green hydrogen production, the voltage quality at the point of common coupling was improved by implementing dynamic control of the electrolyzer with flexible operating capabilities. Authors of [4] developed a method to implement energy storage systems (ESS) with an electrolyzer to comply with low-voltage ride-through requirements. The proposed method includes an examination of the ESS capacity considering both the grid-side and DC-link voltages. In Ref. [5], the maximum penetration level of renewable energy sources (RES) is analyzed when an electrolyzer is installed in an existing distribution system. The authors used an optimal power flow-based approach to determine the appropriate size and location of the electrolyzer as well as a control strategy for the electrolyzer and its performance. While operating the electrolyzer, the management scheme proposed in Ref. [6] can be applied to a multi-electrolyzer system considering the energy balancing and switching strategy.
Some studies have investigated the frequency regulation and dynamic response capability of electrolyzers. In Ref. [7], the dynamic characteristics of alkaline and proton exchange membrane (PEM) electrolyzers were analyzed. The authors verified the ramping capability of the electrolyzer and further evaluated its ability to regulate the power system frequency through experiments. Authors of [8] proposed an analytical model to quantitatively evaluate the dynamic frequency regulation provided by a grid-scale alkaline electrolyzer. In Ref. [9], the authors proposed a coordinated power allocation method between wind turbines and an electrolyzer for secondary frequency regulation, and further developed a multi-timescale control scheme to participate in secondary frequency regulation and the energy market. In Ref. [10], the authors focused on the provision of frequency containment reserves and evaluated their economic efficiency. In Ref. [11], authors developed a generic model with frequency regulation capability applicable for real-time simulations.
Several studies have focused on configuring an optimal operation schedule applicable to systems with electrolyzers. In Ref. [12], a multi-step scheduling method to maximize the profit of the electrolyzer was presented considering the time-of-use price. In Ref. [13], authors proposed an operation management framework with optimization procedures to meet hydrogen demand and also provide ancillary services to the grid. Similarly, the authors of [14] presented a day-ahead dispatch method for a system that included an electrolyzer and wind turbines. In the study, optimal scheduling was performed to maximize the economic benefits of the operation. In Ref. [15], authors highlighted the increasing need for the operation of a system that produces green hydrogen. The authors presented a chance-constrained stochastic optimization model for day-ahead and intra-day operation scheduling of a photovoltaics (PV)-ESS-electrolyzer system participating in the energy and ancillary services markets. These studies focused more on the operational benefits of the electrolyzer while considering the power exchange with the transmission grid.
From the viewpoint of the techno-economic analysis of hydrogen, in the long term, the maturation of the electrolyzer and its operation technology will benefit by lowering a levelized cost of hydrogen (LCOH). The authors of [16] focused on an off-grid electrolyzer system equipped with an RES and ESS and analyzed the optimal control and capacity of each facility to minimize the LCOH. In Ref. [17], the authors used a Monte Carlo-based approach to evaluate the LCOH of an off-grid PV-electrolyzer system. In Ref. [18], a detailed estimation of the cost of hydrogen under various scenarios is presented. The authors considered the impacts of the natural gas price, levelized cost of electricity, tax, and capital expenditures as well as the types and operating conditions of the electrolyzer.
As noted from the literature, electrolyzers have been identified as capable of providing beneficial effects by producing clean fuel, working as a controllable load to aid power system operation, providing short-term load control, and contributing as long-term energy storage. However, although the electrolyzer possesses fast response capability, consecutive rapid changes in the operating point during normal operation may not be beneficial to the electrolyzer. The authors of [19] noted that a short-timescale event that would occur during operation from an unsteady resource such as wind power can potentially lead to rapid performance degradation of an electrolyzer compared to steady-state operation. Moreover, accelerated degradation may occur in the electrolyzer catalyst owing to the instantaneous fluctuating power, as well as degradation caused by consecutive start/stop operations [20]. In addition, consecutive changes in the electrolyzer operating point shall present multi-timescale nonlinear characteristics, such as temperature and efficiency management [21].
With the recent movement toward an era of carbon neutrality, green hydrogen produced by electrolyzers and electrical power from RES is becoming increasingly crucial. However, only a few studies have focused on the operational strategy for green hydrogen production systems (GHPS), which require further development, particularly when the dynamic operation of the electrolyzer is limited. Thus, in this study, a method to operate the electrolyzer with a limited control time step is proposed to enhance the operational continuity of the GHPS with efficiency. The proposed method considers the expected variability of the RES and the coordination between the ESS and the electrolyzer within the system. The main contributions of this study are summarized as follows. (i) The asymmetrical operational characteristics of the GHPS is analyzed and further utilized to configure the coordinated control method. (ii) A copula-based approach is employed to analyze the dependency structure between the forecast data and the actual power generated by the RES, and the analysis results are implemented in configuring the coordinated control. (iii) A coordinated control method that considers both the variability of the RES and state-of-charge (SOC) management of the ESS is configured. (iv) A detailed electro-chemical model of the electrolyzer is included to verify the effectiveness of the coordinated control with respect to hydrogen production.
The remainder of this paper is organized as follows. Section 2 presents a detailed analysis of the GHPS and the electrolyzer model. In Section 3, a control strategy that considers the operational environment of the GHPS is presented. Subsequently, a method to further manage the electrolyzer considering the variable nature of the RES and the SOC of the ESS during operation is proposed. Section 4 presents case study results to verify the effectiveness of the proposed method. Finally, Section 5 presents the conclusions of this study.
2. Green hydrogen production systems
2.1. Classification of hydrogen
Generally, hydrogen can be classified into several groups based on the applied method for the production, as shown in Fig. 1. Grey hydrogen refers to hydrogen produced using natural gas. At high operating temperatures, natural gas is converted into and via steam reformation. Grey hydrogen has the problem of producing both greenhouse gases and clean fuel simultaneously; thus, emission problem should be resolved for future use and sustainability. Blue hydrogen is produced using a procedure similar to that for grey hydrogen. The essential feature of blue hydrogen is the implementation of carbon capture, utilization, and storage to resolve problems related to emissions. Both pink and green hydrogen are produced using electrolyzers. As the electrolysis process splits water into and , no further emissions occur during the conversion process. The difference between pink and green hydrogen is the resource to generate electrical power. Pink hydrogen is produced using the electrical power generated by nuclear power plants, whereas green hydrogen utilizes the power generated from RES. With a growing global consensus to achieve carbon neutrality goals, the need for green hydrogen is rapidly increasing.
Fig. 1.
Categories of hydrogen.
2.2. Operation of green hydrogen production systems
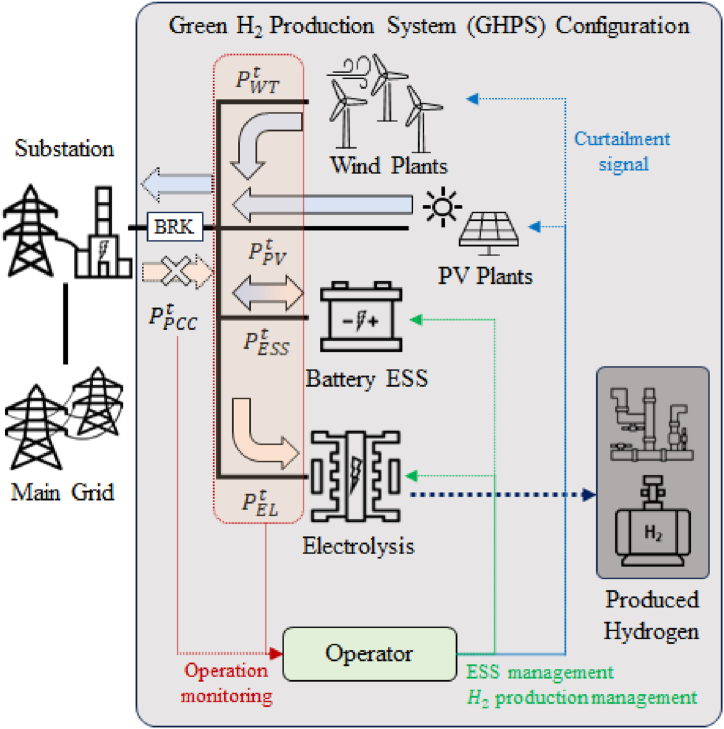
Green hydrogen should be produced using the power generated by RES. Thus, the most common approach is to configure a microgrid with electrolyzers where solar irradiance or wind is abundant, as illustrated in Fig. 2. The produced hydrogen can be stored or sent through pipelines for further applications. The configured system can be operated in either grid-connected or islanded modes. Under the islanded operation mode, the GHPS should manage the power balance within the system solely using the equipped facilities. In Fig. 2, the islanded operating mode refers to the situation in which the breaker installed between the main grid and production system is opened. Here, it is worth noting that the role of the ESS in managing the power balance becomes increasingly important. If the ESS operation is limited by SOC constraints, the operator should curtail the power generated from the RES or further change the operating point of electrolyzer while taking charge for the degradation. On the other hand, if the production system operates in the grid-connected mode, power flow from the production system to the main grid, which corresponds to the surplus power from the RES, can be allowed. Thus, the operator can choose to produce surplus power for the main grid under contract with the transmission system operator rather than implementing curtailment on the RES. However, in the grid-connected mode, the power flow from the main grid to the GHPS should be strictly limited as the system should produce green hydrogen.
Fig. 2.
Green hydrogen production system configuration.
2.3. Operation of green hydrogen production systems
The major types of electrolyzers include alkaline, PEM, solid oxide (SO), and anion exchange membrane (AEM) electrolysis. Among these, AEM and SO electrolysis are not sufficiently mature for utility applications, whereas PEM electrolysis has the drawbacks of high cost and corrosive electrolytes. Currently, alkaline electrolysis is considered suitable for utility-scale applications, considering the maturity of electrolysis technology [[22], [23], [24]]. As an electrode, potassium hydroxide (KOH) can be used. Hydroxide ions () can move through the diaphragm and aid in the anodic and cathodic reactions. Consequently, oxygen and hydrogen gases can be obtained at the anode and cathode, respectively.
The electrical equivalent circuit can be configured as follows based on the model presented in Refs. [[25], [26], [27]]. The voltage for a single cell, , can be defined using a nonlinear voltage-current curve as (1), where denotes the reversible voltage, denotes the operating temperature, denotes the current, and denotes the area. The total voltage can then be computed as (2), by considering the number of cells connected within the system.
| (1) |
| (2) |
Here, the reversible cell voltage refers to the electrical energy required to split water in a molar basis. is defined by the Faraday's law as given in (3), in which denotes the change in Gibbs energy, refers to Faraday constant () and refers to the number of electrons transferred at each reaction. The relationship between the change in Gibbs energy, change in enthalpy, , and change in entropy can be expressed as in (4), where expresses thermal irreversibility. At standard condition, is equal to [25].
| (3) |
| (4) |
The Faraday efficiency of the electrolyzer can be expressed as in (5), which refers to the ratio between the actual and theoretical amount of hydrogen production. In this study, and were set as and , as in Ref. [25]. Based on the computed , the expected hydrogen production rate per hour can be computed as (6) in molar basis. Notably, the production rate can be assumed to be directly proportional to the current as is nearly constant under a normal operation range. The flow rate (6), given in can be further modified to (7), which returns the production rate in normal cubic meters per hour (), where denotes the volume of an ideal gas under standard conditions given as .
| (5) |
| (6) |
| (7) |
3. Short-term forecast data-based control
3.1. Electrolyzer operation for green hydrogen production
In this section, a control strategy applicable to GHPS is analyzed, and a further coordination strategy within the facilities is proposed. As previously noted, it is crucial to manage the power balance within the system and the power flow between the system and the main grid. As the provision of surplus power or curtailment of the RES within the GHPS can be implemented, the best strategy for GHPS operation is to track the power generated from the RES and change the operating point of the electrolyzer. Particularly, if the ESS is not included within the system, the power consumed by the electrolyzer should always be lower than the power generated by the RES during the entire operation period. Considering the degradation of the electrolyzer, a limited control time step shall be applied during the operation. If an ESS is included, a GHPS can be operated with increased flexibility. Nevertheless, considering economic efficiency, the total capacity of the ESS shall be relatively small compared to the capacity of the RES or electrolyzer installed within the GHPS. Thus, the operator should continue to operate it conservatively and use the ESS as a supplementary resource to provide flexibility when the gap between the generated power and the electrolyzer increases.
Under the given operational conditions, a short-term forecast data-based control approach can be effective considering the operational environment of the GHPS, as illustrated in Fig. 3. In this study, the operating point of the electrolyzer was set to be changed at predetermined time intervals. Every time the electrolyzer is capable of changing the operating point, the operator can adjust the power according to (8) by considering the variability of the RES. In compliance with the time step in decision to adjust electrolyzer operating point for real-time operation, a 15-min time interval can be adopted [14].
Fig. 3.
Short-term forecast data-based electrolyzer operation strategy.
By scheduling the electrolyzer power based on short-term forecast data, which show a small error compared to the day-ahead forecast data, the operator will benefit by producing maximum hydrogen under the given weather condition. Although short-term forecasting tends to guarantee high accuracy, the operator still needs to control unexpected change of RES generation, which should be compensated through the equipped ESS. Here, if the SOC of the ESS is not managed appropriately, or if the capacity of the installed ESS is too small, problems related to uncompensated power may arise, that is, a situation in which the GHPS needs to import power from the main grid may arise when the SOC is not well managed.
| (8) |
This problem arises due to asymmetrical flexibility in managing surplus power and power shortages. When the surplus power occurs, the GHPS can choose to charge the ESS, provide surplus power to the main grid, or curtail the surplus RES power. However, when power shortage problems occur, the equipped ESS should be discharged, especially if the RES are operating in maximum power point tracking (MPPT) mode. This asymmetry emphasizes that the ESS should focus on its discharging capability to aid in sustainable and continuous system operation. Thus, this study aims to maximize the operational flexibility of small-sized ESS and enhance the operational continuity of GHPS by managing the SOC based on a coordinated control scheme for the ESS and electrolyzer. A detailed description of the proposed control scheme is presented in the following sections.
3.2. Copula-based short-term forecast data analysis
The coordinated control scheme is set to utilize both the expected variability of the RES and the SOC of the ESS. In this study, a copula-based approach is implemented to analyze the dependence structure between given forecast and measurement data.
The widely used Pearson's correlation coefficient can be computed as shown in (9). Although the correlation coefficient can be easily computed and provides information on the strength of the linear relationship between the given variables, it cannot fully represent the interdependency or correlational characteristics between variables.
| (9) |
Therefore, a copula-based approach is adopted for further analysis. The configuration process of the copula function between the variables can be summarized as follows: (i) Load raw data. (ii) Estimate the probabilistic distribution curve (PDF) for each variable. (iii) Convert the data into a uniform distribution using the computed PDF data. (iv) Define the copula function and analyze the correlational characteristics.
The copula function is a multivariate distribution function that can be defined for variables following a uniform distribution which can model the dependence structure [28,29]. For the bivariate case, the joint distribution can be expressed as (10) based on Sklars's theorem [30], where denotes the copula function with a definition domain of , denotes the joint distribution, and and represent the cumulative distribution function, which is equivalent to the uniform rank distribution of each variable.
| (10) |
As noted, copula function can be defined for variables with a uniform distribution in the range of . In order to conduct an analysis with the copula function, the variables should first be transformed into cumulative distribution functions, after which the transformed data provide information on the rank in uniform distribution. This transformation procedure is performed based on the PDF of each variable. In general, the PDF can be configured in two different methods: parametric estimation and nonparametric estimation. If the information on the distribution for a certain variable is available in advance, PDF estimation procedures can be performed by determining the parameters of the given PDF function that best represent the given data. For instance, the Weibull distribution is generally known to be appropriate for modeling the PDF of wind speed. On the other hand, a nonparametric estimation can be implemented if information on the distribution is unavailable [31]. Kernel density estimation (KDE) illustrated in (11) is a nonparametric estimation method that represents the PDF of the given data with a kernel function. As the kernel function for KDE, , Gaussian function, uniform function or Epanechikov function can be utilized. Among these kernel functions, the Gaussian kernel function expressed in (12) is most commonly used [29]. Thus, in this study, considering that PDF of forecast data measurement data should be estimated for specific renewable energy farm, KDE is implemented with Gaussian kernel function [32].
| (11) |
| (12) |
Subsequently, once the copula function is computed using the estimated PDF for each variable, a confidence interval (CI) can be computed with respect to the defined confidence level, as in (13), (14), where and refer to the upper and lower boundaries corresponding to the confidence level .
| (13) |
| (14) |
3.3. Proposed control method for GHPS
Coordination between ESS and electrolyzer can be achieved by modifying the operating point of the electrolyzer rather than implementing control methods for the ESS, as depicted in Fig. 4(a). Nevertheless, as the basic operating principle of the ESS is to compensate for the variability of the power generated from the RES and manage the power flow between the GHPS and the main grid, the adjustment of the electrolyzer operating point can aid in managing the SOC of the ESS. Meanwhile, if the expected variability of the power generated from the RES increases, that is, if the confidence interval that corresponds to the forecast data increases, the operator can adjust the electrolyzer operating point to enhance operational continuity.
Fig. 4.
(a) Power adjustment scheme for GHPS operation. (b) Power adjustment with respect to SOC of ESS and CI. (c) Comprehensive flowchart of the proposed control scheme.
Considering the ESS operation and the expected variability of the RES, the power adjustment can be conducted as (15) and (16), respectively, where refers to the SOC of the ESS during operation and refers to the power conversion system (PCS) capacity of ESS. In Table 1, specific parameters for the power adjustment are illustrated. The power adjustment considering the expected variability of the RES is modelled as negative value as the rapid ramp-down of output of RES should be well managed to avoid power shortage within the GHPS. In this paper, power adjustment is implemented when the expected uncertainty range is larger than the rated power of the inverter of ESS (), and maximum power adjustment is implemented when the expected uncertainty range is larger than as illustrated in Table 1. On the other hand, the power adjustment considering the SOC of ESS, a power adjustment is modelled as droop control with a deadband near SOC of 0.5. In this paper, deadband of 0.4–0.6 is adopted, and peak power adjustment is applied when SOC reaches 0.1 or 0.9. By adding two equations with equal weights and applying specific parameters to Table 1, the proposed method can be illustrated as Fig. 4(b).
| (15) |
| (16) |
Table 1.
Parameters for power adjustment.
| parameters | parameters | ||||
|---|---|---|---|---|---|
| 0.1 | 0.4 | 0.6 | 0.9 | ||
A comprehensive flowchart of the proposed GHPS control scheme is illustrated in Fig. 4(c). It is worth noting that the proposed method can be directly implemented without further modification of existing facilities when the RES farm owner, who is generally equipped with an ESS, plans to install an electrolyzer to produce green hydrogen.
4. Case study
In this section, case study results are presented to verify the effectiveness of the proposed method. The test system was configured to include a wind farm, electrolyzer, and ESS with a specific capacity indicated in Table 2. The parameters for the electrolyzer model are listed in Table 3, where the electrolyzer is assumed to be operated at a constant temperature of 80 °C with its minimum load of 10 % of its capacity [26]. In this study, the electrolyzer was set to change its operating point every 15 min to represent a limited control time step, while the maximum adjustment power was set to 0.2 MW. The initial SOC for the simulation was set to 0.5. Historical forecast and measurement data for 365 days were used in the case study [33]. A short-term forecast of a 15-min interval was applied for the simulation [34]. In this study, additional noise which follows uniform distribution ranging from −0.5 MW to 0.5 MW was added to the measurement data to further verify the robustness of proposed method with respect to variability within RES. Root mean square error and mean absolute error of the forecast data are found as 1.843 MW and 1.286 MW, respectively. Considering the applicability of the proposed method, which can be implemented on existing RES farms without modification, the RES within the GHPS was set to be operated in the MPPT mode. In analyzing the historical forecast and measurement data, a confidence level of 90 % was implemented while utilizing the Student's t-copula, which is appropriate for data with elliptical correlation.
Table 2.
Test system configuration data.
| Wind Farm | Electrolyzer | ESS PCS | ESS Battery |
|---|---|---|---|
| 30 MW | 15 MW | 4 MW | 4 MWh |
Table 3.
Parameters for electrolyzer model.
| 8.05e−5 | −2.5e−7 | 0.185 | −0.1002 | 8.424 | 247.3 |
4.1. Simulation case without power surplus or shortage
This section presents a simulation case in which there is no power surplus or shortage. This simulation case corresponds to cases in which the ESS can compensate for the variability of the RES for the entire operation period, even when the proposed method is not implemented. The simulation results for May 31 are depicted in detail in Fig. 5. Here, the base case presented in the simulation results refers to the simulation case without proposed power adjustment, which operate as presented in Fig. 3, Fig. 8. As depicted in Fig. 5(a), the electrolyzer load appears similar in both cases as the maximum power adjustment is limited to 0.2 MW. Nevertheless, in terms of SOC management, the SOC of the proposed method remained closer to 0.5, which ensures a better response for long-term operation, as depicted in Fig. 5(c). The power output of the ESS is depicted in Fig. 5(b), where the positive sign corresponds to the discharging operation. The adjusted power and the corresponding CI and SOC are depicted in Fig. 5(d). Here, the adjusted power and CI in Fig. 5(d) are each normalized with and .
Fig. 5.
Simulation results of May 31. (a) Electrolyzer load and RES generation, (b) ESS operation, (c) SOC of ESS, and (d) power adjustment result.
Fig. 8.
Box plot for (a) power surplus, (b) power shortage during the operation, (c) electrolyzer load, and (d) produced hydrogen.
4.2. Simulation cases with power surplus
Fig. 6 depicts the simulation cases in which surplus power occurs, which shall be provided to the transmission system or controlled through RES curtailment. Fig. 6(a)–(e) shows the simulation results for April 29. In this simulation case, the RES power lies in the area with a large CI. Thus, to secure the discharging capability of the ESS to handle RES variability, a power adjustment was conducted to shift the ESS into charging mode. Consequently, compared with the base case, the SOC reached its maximum level earlier. Nevertheless, as surplus power can be managed without charging the ESS, the system can be continuously operated.
Fig. 6.
Simulation results of April 29. (a) Electrolyzer load and RES generation, (b) ESS operation, (c) SOC of ESS, (d) power adjustment result, and (e) surplus power. Simulation results of October 26. (f) Electrolyzer load and RES generation, (g) ESS operation, (h) SOC of ESS, (i) power adjustment result, and (j) surplus power.
On the other hand, Fig. 6(f)–(j) corresponds to the case with a smaller CI, as depicted in Fig. 6(i). Therefore, in this simulation case, the SOC management became more dominant. As illustrated in Fig. 6(h), without the proposed method, the SOC remains close to its maximum limit. As noted, although the SOC of the ESS reaches its maximum limit, the GHPS can be operated continuously. However, this operation may be inefficient when the CI is small. For the simulation results using the proposed method, it was found that the SOC slowly decreased after it reached its maximum limit. Through this operation, the GHPS can limit unnecessary power curtailment.
These simulation cases can be summarized as Fig. 6(e) and (j), which shows the surplus power for each simulation case. As noted, for the case of April 29, the GHPS faces a larger CI and thus attempts to take charge of curtailment to enhance its operational continuity as shown in Fig. 6(e). On the other hand, when a smaller CI is computed, the SOC management scheme can contribute to the GHPS operation by effectively limiting the surplus power as illustrated in Fig. 6(j).
4.3. Simulation cases with power shortage due to limited ESS capacity
Fig. 7 depicts the simulation cases in which a power shortage occurs during operation, which violates the condition of green hydrogen production. Fig. 7(a)–(e) shows the simulation case for June 8. In this simulation case, it can be found that the proposed method successfully managed the GHPS operation when CI is large as depicted in Fig. 7(d). For the base case, it is shown that the ESS exhaustion occurred between 6 a.m. and 7 a.m. During this period, the ESS cannot discharge any power to the GHPS; thus, a power shortage occurs. However, when the proposed method was applied for operation, the results show that no power shortage occurred and the GHPS operated successfully as illustrated in Fig. 7(e).
Fig. 7.
Simulation results of June 8. (a) Electrolyzer load and RES generation, (b) ESS operation, (c) SOC of ESS, (d) power adjustment result, and (e) power shortage. Simulation results of March 16. (f) Electrolyzer load and RES generation, (g) ESS operation, (h) SOC of ESS, (i) power adjustment result, and (j) power shortage.
Fig. 7(f)–(j) depicts the simulation results for March 16, which presents more severe results. In this simulation, the SOC reached its lower limit near 8 a.m. and did not recover for approximately 10 h. This case reflects a situation where short-term forecast data are not sufficiently accurate and the power generated from the RES decreases faster than expected. In such a severe case, the proposed method showed a dramatic improvement by adjusting the electrolyzer based on the CI results and SOC of the ESS. Consequently, the proposed method successfully managed most of the power shortages, except for the 40 min of operation time. Detailed results are depicted in Fig. 7 (j). The power shortage problem is mainly caused by insufficient compensation capability of ESS due to limited capacity, especially in discharging mode. Thus, this could be resolved by increasing the capacity of the installed ESS or adjusting the maximum adjustment power of the proposed method to lower the load of ESS in compensation. Furthermore, a deloaded operation of connected RES can be included [35,36]. Impacts of the capacity of ESS and maximum adjustment power of the proposed method are further illustrated in Section 4.5.
4.4. Summary on the simulation cases
The overall simulation results are summarized as follows. Box plots illustrating the surplus and shortage of energy per day are depicted shown in Fig. 8(a) and (b). In Fig. 8(a), the boxplot for surplus cases is configured by extracting the days that show surplus power (308 days). Similarly, in Fig. 8(b), the box plot was constructed by extracting the days that exhibit a power shortage (27 days). The detailed parameters of the box plots are listed in Table 4, Table 5, respectively. According to the results, the proposed method shows a dramatic decrease in power shortage cases and the number of days with power shortages decreased from 27 days to 9 days. For the cases in which surplus power occurs, slight decreases in median and quartiles are captured when the proposed method is implemented. The maximum surplus of 287 MWh on February 5 is captured in both cases, in which RES generation is sufficient.
Table 4.
Surplus box plot data.
| Unit: MWh/day | Median | Quartile | Whiskers | Minimum | Maximum |
|---|---|---|---|---|---|
| Base Case | 7.923 | [3.015, 15.05] | [0, 32.67] | 0 | 287 |
| Proposed | 7.693 | [2.774, 14.62] | [0, 29.98] | 0 | 287 |
Table 5.
Shortage box plot data.
| Unit: MWh/day | Median | Quartile | Whiskers | Minimum | Maximum |
|---|---|---|---|---|---|
| Base Case | 0.4409 | [0.1287, 1.359] | [0.03827, 2.537] | 0.03827 | 2.357 |
| Proposed | 0 | [0, 0.09709] | [0, 0.1234] | 0 | 1.733 |
Fig. 8(c) shows a box plot that depicts the power consumed by the electrolyzer, which is directly related to the amount of hydrogen produced. Overall, the expected production of hydrogen has not changed significantly, even though the proposed method is set to take charge of the surplus power for operational continuity. It was found that the median increased by 0.77 MWh when the proposed method was applied. The whiskers were found to be at [0, 360] for both cases. Here, a maximum load of 360 MWh/day corresponds to the case in which the power generated from the RES is sufficient and the electrolyzer operates at its maximum operating point for the entire day. Similarly, in Fig. 8(d), the hydrogen produced is depicted by considering the electrochemical characteristics presented in Section 2. These simulation results clearly show that the proposed method can enhance the operational continuity of the GHPS. Through the implementation of the proposed strategy, more efficient utilization of facilities within GHPS is expected without significantly deteriorating the expected hydrogen production.
4.5. Evaluation of the required ESS capacity
In the previous sections, representative simulation cases are illustrated in detail to demonstrate the effectiveness of the proposed method. In this section, the required capacity of the ESS for continuous GHPS operation and the effect of the maximum adjustment power within the proposed method are analyzed. As presented in Table 6, the number of days with a power shortage (i.e., the violated case for GHPS operation) decreases with respect to the increasing maximum adjustment power.
Table 6.
Number of days with violation (4 MWh ESS case).
| [MW] | 0.1 | 0.2 | 0.3 | 0.4 |
|---|---|---|---|---|
| Base Case | 27 | |||
| Proposed | 16 | 9 | 6 | 4 |
The required capacity for the continuous operation of the GHPS is shown in Table 7, which depicts the change in days with violations with respect to the ESS capacity. It was found that the 8.92 MWh of ESS is required in the case without the proposed control. However, with the implementation of the proposed method, the required capacity was found to be 7.35 MWh. Compared with the base case, the ESS capacity decreased by 17.6 %. It can be concluded that the proposed control strategy aids in increasing the operational continuity of GHPS and also helps GHPS invest in facilities efficiently.
Table 7.
Number of days with violation ( = 0.2 MW).
| ESS Capacity [MWh] | 2 | 4 | 6 | 7.35 | 8.92 |
|---|---|---|---|---|---|
| Base Case | 113 | 27 | 7 | 5 | 0 |
| Proposed | 64 | 9 | 2 | 0 | 0 |
4.6. Simulation results for monthly consecutive operation
In this section, monthly consecutive simulation results are presented. Through the consecutive operation, the SOC at the end of each day is represented as the initial SOC of the next day. The initial SOC for each month is set as 0.5. In Table 8, number of days with violation are presented for each month. In this simulation case, ESS capacity illustrated in Table 2 and maximum power adjustment of 0.2 MW is considered. The results show that the proposed method showed smaller violation days except for January, February, and December.
Table 8.
Number of days with violation for monthly consecutive operation.
| Month | January | February | March | April | May | June |
| Base Case | 2 | 1 | 3 | 3 | 3 | 4 |
| Proposed | 2 | 1 | 1 | 1 | 1 | 0 |
| Month | July | August | September | October | November | December |
| Base Case | 2 | 2 | 2 | 5 | 2 | 0 |
| Proposed | 0 | 1 | 1 | 1 | 0 | 0 |
5. Conclusions
With global efforts to achieve carbon neutral goals, green hydrogen is gaining importance. In this study, a method for operating the electrolyzer to enhance operational continuity of GHPS was proposed by considering its asymmetric operational characteristics. The proposed method includes a copula-based analysis for the evaluation of the RES characteristics and coordinated control to manage the SOC of the ESS. The case study showed that the proposed method could effectively manage the GHPS without significantly deteriorating the expected curtailment and hydrogen production. As the required capacity of the ESS can be decreased by implementing the proposed method, it can aid in more efficient GHPS planning and operations. Moreover, the distinguishing feature of the proposed method is that it can be directly implemented without significant modification to existing facilities when the RES farm owner newly installs an electrolyzer to produce green hydrogen.
CRediT authorship contribution statement
Sungwoo Kang: Methodology, Software, Writing – original draft. Seungmin Jung: Conceptualization, Validation, Writing – review & editing. Dongwon Lee: Investigation, Resources, Software. Yeuntae Yoo: Data curation, Formal analysis, Validation. Gilsoo Jang: Conceptualization, Supervision, Writing – review & editing.
Data availability
Data would be available on reasonable request.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. RS-2023-00218377) and the Nuclear Safety Research Program through the Korea Foundation Of Nuclear Safety (KoFONS) using the financial resource granted by the Nuclear Safety and Security Commission (NSSC) of the Republic of Korea (No. 2204009).
References
- 1.Ruth M.F., Jadun P., Gilroy N., Connelly E., Boardman R., Simon A.J., et al. National Renewable Energy Lab (NREL); 2020. The Technical and Economic Potential of the H2@ Scale Hydrogen Concept within the United States. [Google Scholar]
- 2.Mayyas A., Wei M., Levis G. Hydrogen as a long-term, large-scale energy storage solution when coupled with renewable energy sources or grids with dynamic electricity pricing schemes. Int J Hydrog Energy. 2020;45:16311–16325. [Google Scholar]
- 3.Chiesa N., Korpås M., Kongstein O.E., Ødegård A. Proc of. International Conference on Power Systems Transients (IPST2011) 2011. Dynamic control of an electrolyser for voltage quality enhancement. [Google Scholar]
- 4.Saha P., Zhao W., Stroe D.I., Iov F., Munk-Nielsen S. Enabling LVRT compliance of electrolyzer systems using energy storage technologies. Batteries. 2023;9:527. [Google Scholar]
- 5.Kiaee M., Infield D., Cruden A. Utilisation of alkaline electrolysers in existing distribution networks to increase the amount of integrated wind capacity. J. Energy Storage. 2018;16:8–20. [Google Scholar]
- 6.Li Y., Deng X., Zhang T., Liu S., Song L., Yang F., Ouyang M., Shen Exploration of the configuration and operation rule of the multi-electrolyzers hybrid system of large-scale alkaline water hydrogen production system. Appl. Energy. 2023;331 [Google Scholar]
- 7.Eichman J., Harrison K., Peters M. National Renewable Energy Lab (NREL); 2014. Novel Electrolyzer Applications: Providing More than Just Hydrogen. [Google Scholar]
- 8.Huang C., Zong Y., You S., Traholt C. Analytical modeling and control of grid-scale alkaline electrolyzer plant for frequency support in wind-dominated electricity-hydrogen systems. IEEE Trans. Sustain. Energy. 2022;14:217–232. [Google Scholar]
- 9.Cheng X., Lin J., Liu F., Qiu Y., Song Y., Li J., Wu S. A coordinated frequency regulation and bidding method for wind-electrolysis joint systems participating within ancillary services markets. IEEE Trans. Sustain. Energy. 2023;14:1370–1384. [Google Scholar]
- 10.Samani A.E., D'Amicis A., De Kooning J.D.M., Bozalakov D., Silva P., Vandevelde L. Grid balancing with a large‐scale electrolyser providing primary reserve. IET Renew. Power Gener. 2020;14:3070–3078. [Google Scholar]
- 11.Tuinema B.W., Adabi E., Ayivor P.K.S., García Suárez V., Liu L., Perilla A., Ahmad Z., Torres J.L.R., Meijden M.A., Palensky P. Modelling of large‐sized electrolysers for real‐time simulation and study of the possibility of frequency support by electrolysers. IET Gener. Transm. Distrib. 2020;14:1985–1992. [Google Scholar]
- 12.Yang Y., De La Torre B., Stewart K., Lair L., Phan N.L., Das R., D Gonzalez Lo RC. The scheduling of alkaline water electrolysis for hydrogen production using hybrid energy sources. Energy Convers. Manag. 2022;257 [Google Scholar]
- 13.Farag H.E.Z., Al-Obaidi A., Khani H., El-Taweel N., El-Saadany E.F., Zeineldin H.H. Optimal operation management of distributed and centralized electrolysis-based hydrogen generation and storage systems. Electr Power Syst Res. 2020;187 [Google Scholar]
- 14.Zheng Y., You S., Bindner H.W., Münster M. Optimal day-ahead dispatch of an alkaline electrolyser system concerning thermal–electric properties and state-transitional dynamics. Appl. Energy. 2022;307 [Google Scholar]
- 15.Maluenda M., Córdova S., Lorca Á., Negrete-Pincetic M. Optimal operation scheduling of a PV-BESS-Electrolyzer system for hydrogen production and frequency regulation. Appl. Energy. 2023;344 [Google Scholar]
- 16.Ibáñez-Rioja A., Järvinen L., Puranen P., Kosonen A., Ruuskanen V., Hynynen K., Ahola J., Kauranen P. Off-grid solar PV–wind power–battery–water electrolyzer plant: simultaneous optimization of component capacities and system control. Appl. Energy. 2023;345 [Google Scholar]
- 17.Yates J., Daiyan R., Patterson R., Egan R., Amal R., Ho-Baille A., Chang N.L. Techno-economic analysis of hydrogen electrolysis from off-grid stand-alone photovoltaics incorporating uncertainty analysis. Cell Rep Phys Sci. 2020;1 [Google Scholar]
- 18.Nami H., Rizvandi O.B., Chatzichristodoulou C., Hendriksen P.V., Frandsen H.L. Techno-economic analysis of current and emerging electrolysis technologies for green hydrogen production. Energy Convers. Manag. 2022;269 [Google Scholar]
- 19.Bergen A., Pitt L., Rowe A., Wild P., Djilali N. Transient electrolyser response in a renewable-regenerative energy system. Int J Hydrog Energy. 2009;34:64–70. [Google Scholar]
- 20.Kojima H., Nagasawa K., Todoroki N., Ito Y., Matsui T., Nakajima R. Influence of renewable energy power fluctuations on water electrolysis for green hydrogen production. Int J Hydrog Energy. 2023;48:4572–4593. [Google Scholar]
- 21.Haoran C., Xia Y., Wei W., Yongzhi Z., Bo Z., Leiqi Z. Safety and efficiency problems of hydrogen production from alkaline water electrolyzers driven by renewable energy sources. Int J Hydrog Energy. 2024;54:700–712. [Google Scholar]
- 22.Xing X., Lin J., Song Y., Zhou Y., Mu S., Hu Q. Modeling and operation of the power-to-gas system for renewables integration: a review. CSEE J Power Energy Syst. 2018;4:168–178. [Google Scholar]
- 23.Martinez Lopez V.A., Ziar H., Haverkort J.W., Zeman M., Isabella O. Dynamic operation of water electrolyzers: a review for applications in photovoltaic systems integration. Renew. Sustain. Energy Rev. 2023;182 [Google Scholar]
- 24.Daoudi C., Bounahmidi T. Overview of alkaline water electrolysis modeling. Int J Hydrog Energy. 2024;49:646–667. [Google Scholar]
- 25.Ulleberg O. Modeling of advanced alkaline electrolyzers: a system simulation approach. Int J Hydrog Energy. 2003;28:21–33. [Google Scholar]
- 26.Khan M.J., Iqbal M.T. Analysis of a small wind-hydrogen stand-alone hybrid energy system. Appl. Energy. 2009;86:2429–2442. [Google Scholar]
- 27.Hong Z., Wei Z., Han X. Optimization scheduling control strategy of wind-hydrogen system considering hydrogen production efficiency. J. Energy Storage. 2022;47 [Google Scholar]
- 28.Papaefthymiou G., Kurowicka D. Using copulas for modeling stochastic dependence in power system uncertainty analysis. IEEE Trans. Power Syst. 2008;24:40–49. [Google Scholar]
- 29.Hou Q., Zhang N., Du E., Miao M., Peng F., Kang C. Probabilistic duck curve in high PV penetration power system: concept, modeling, and empirical analysis in China. Appl. Energy. 2019;242:205–215. [Google Scholar]
- 30.Sklar M. Fonctions de répartition à n dimensions et leurs marges. Ann ISUP. 1959;8:229–231. [Google Scholar]
- 31.Parzen E. On estimation of a probability density function and mode. Ann Math Statist. 1962;33:1065–1076. [Google Scholar]
- 32.Song S., Kang S., Lee S., Kim C. Korean renewables management system: copulas model-based adaptive droop control strategy for energy storage systems. IEEE Access. 2023;11:134604–134613. [Google Scholar]
- 33.50 Hertz Transmission GmbH, Berlin, Germany: Grid Data, https://www.50hertz.com/en/Transparency/GridData/Production/Windpower, accessed 21st Nov. 2023.
- 34.Jing K., Liu C., Cao X., Sun H., Dong Y. Analysis, modeling and control of a non-grid-connected source-load collaboration wind-hydrogen system. J Electr Eng Technol. 2021;16:2355–2365. [Google Scholar]
- 35.Yoo Y., Jang G., Jung S. Stochastic assessment of frequency support from wind power plants for power system with high wind penetration using correlation between wind farms. IET Renew. Power Gener. 2022;16:2372–2383. [Google Scholar]
- 36.Sangwongwanich A., Yang Y., Blaabjerg F., Sera D. Delta power control strategy for multistring grid-connected PV inverters. IEEE Trans. Ind. Appl. 2017;53:3862–3870. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data would be available on reasonable request.