Abstract
Electroosmosis, originating in the double-layer of a small liquid-filled pore (size R) and driven by a voltage V, is shown to be effective in pumping against the capillary pressure of a larger liquid droplet (size B) provided the dimensionless parameter σR2/ε|ζ|VB is small enough. Here σ is surface tension of the droplet liquid/gas interface, ε is the liquid dielectric constant, and ζ is the zeta potential of the solid/liquid pair. As droplet size diminishes, the voltage required to pump eletroosmotically scales as V ∼ R2/B. Accordingly, the voltage needed to pump against smaller higher-pressure droplets can actually decrease provided the pump poresize scales down with droplet size appropriately. The technological implication of this favorable scaling is that electromechanical transducers made of moving droplets, so-called “droplet transducers,” become feasible. To illustrate, we demonstrate a switch whose bistable energy landscape derives from the surface energy of a droplet–droplet system and whose triggering derives from the electroosmosis effect. The switch is an electromechanical transducer characterized by individual addressability, fast switching time with low voltage, and no moving solid parts. We report experimental results for millimeter-scale droplets to verify key predictions of a mathematical model of the switch. With millimeter-size water droplets and micrometer-size pores, 5 V can yield switching times of 1 s. Switching time scales as B3/VR2. Two possible “grab-and-release” applications of arrays of switches are described. One mimics the controlled adhesion of an insect, the palm beetle; the other uses wettability to move a particle along a trajectory.
Keywords: bistability, controlled adhesion, electroosmotic pump, palm beetle, electro-capillary transducer
The natural tendencies of surface tension alone can move liquid between two small droplets. Droplets initially of different curvatures and connected by a liquid-filled conduit come to rest in one of two stable configurations owing to capillarity (recognized for connected bubbles, by ref. 1). The pumping action of electroosmosis can move liquid against this capillary force. A voltage signal applied to an electroosmotic pump positioned between the two droplets precisely controls toggling between the two configurations. This action characterizes the “electroosmotic droplet switch” (EODS), whose behavior and potential applications are the subject of this work.
This work begins with a description of the system, including a discussion of the bistable nature of the two-droplet system and the model of flow in the EODS. Next, we provide validating data for the model based on time-dependent operation of the device. Model predictions include the parameter limits for successful switching and the time needed to switch the system between stable states. Scaling laws, indicating favorable operation of the EODS down to micrometer-size droplets, are then discussed. Finally, two examples of applications are suggested through demonstrations of unit operations of the system.
EODS: Description
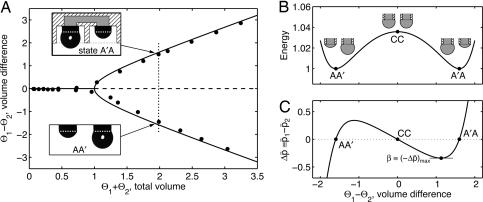
Consider a system of two droplets of the same liquid, each pinned on a circular contact line (radius B) and connected by internal pressure. Equilibrium states are described by volume difference Θ1–Θ2 and total volume Θ1 +Θ2 of the two droplets (Fig. 1A). In our model, droplet shapes are assumed to be spherical caps, as surface tension σ dominates in small systems (Bond number, Bo ≡ ρgB2/σ ≪ 1, where g is gravitational acceleration and ρ is liquid density). Equilibrium between droplets occurs when the interdroplet pressure difference Δp ≡ p1 – p2 vanishes, resulting in identical curvatures of the interfaces κ = κ1 = κ2 in view of the Young–Laplace equation, pi = 2σκi. The bifurcation diagram for the system shows bistability for total volumes greater than the two-hemisphere case (2, 3). For these volumes, there coexist two symmetric stable equilibria, each consisting of complementary pieces of the same sphere. Located between the stable equilibria is a barrier of unstable equilibria corresponding to a ridge in the energy landscape.
Fig. 1.
Behavior of bistable system of coupled droplets, showing droplet 1 of volume Θ1, at left, and 2 of Θ2, at right. Volume is scaled by 4 π B3/3; only liquid below the contact-line (white dots in A Insets) is counted. (A) Equilibrium bifurcation diagram showing bistability for Θ1 + Θ2 > 1 (line, model; circles, experiments). (Insets) Image of droplets on nozzles (radius B = 0.85 mm). (Upper Inset) Schematic superposed on image demonstrates shielding (right) and exposure (left) that are used in applications. (Lower Inset) Image alone. Data were obtained with a threshold edge detection algorithm. (B and C) Nonequilibrium response for constant total volume (Θ1 +Θ2 = 2), assuming spherical-cap droplets. Note that switching from top to bottom along dotted line in A means right to left in B and C. (B) Normalized energy landscape (droplet surface areas) shows the barrier to switching at the unstable equilibrium CC. (C) Interdroplet pressure difference (normalized here only, p̄ = p·B/σ), with maximum resistance indicated by β.
Switching between stable equilibria follows some nonequilibrium path over the barrier. One such path, obtained by assuming pressure internal to the droplets equilibrates much more quickly than the pressure between the droplets, illustrates the double-well energy landscape (Fig. 1B). The corresponding Δp shows the capillary driving force for flow between droplets (Fig. 1C). As switching proceeds from A′A to AA′, capillarity first resists (Δp < 0) and then, beyond the barrier, assists (Δp > 0) in driving the system toward the other equilibrium. There is a maximum resisting pressure (–Δp)max = βσ/B that must be overcome for switching to be successful. Here β is a scaling factor that depends only on the total volume of the droplets, straightforward to calculate from geometry.
To actuate the switch, we use an electroosmotic pump, which can overcome the resisting pressure without limiting the practical usefulness of the system. Other techniques that have been tried include a pressure pulse (awkward for addressability) and an electrochemical trigger (slow to switch) (3). Electroosmosis relies on a layer of excess ions, the electric double layer or Debye layer, naturally present in the liquid adjacent to a solid for many solid/liquid pairs. An electric field imposed in the surface-parallel direction moves the ions, which drag the liquid along a tube or channel by means of viscosity. The net velocity in a tube can be expressed as the superposition of Poiseuille and Smoluchowski electroosmotic velocities when the electric double layer is much smaller than the tube size (of radius R and length L here) (4–7)
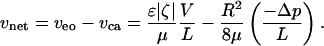 |
[1] |
The fluid has dynamic viscosity μ and dielectric constant ε, while the solid/liquid pair has zeta potential ζ (generally a negative value). For the sake of discussion, net velocity is counted positive (favorable to switching) for flow toward the initially smaller droplet (i.e., for reverse flow, droplet identity must alternate to \maintain consistency of the signs). The electroosmotic velocity veo is always favorable for positive voltage drop (V > 0). For this system, the dominant contribution to Δp is the capillary pressure difference. Positive capillary velocity vca ≡ (R2/8μ)(–Δp/L) occurs for a resisting capillary pressure.
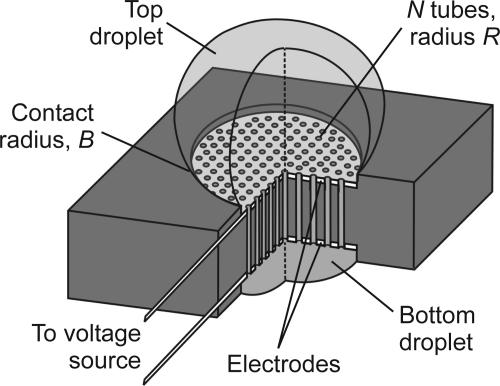
The single-tube electroosmotic flowrate must be amplified by using a large number N of tiny tubes feeding in parallel into the larger-scale droplets (see Fig. 4). The EODS prototype reported here (8) (Fig. 2A) effectively achieves this goal by using a porous glass disk as the pumping medium (CG-201-33, Chemglass, Vineland, NJ; 50-mm diameter, 4.6-mm thickness, 4- to 5.5-μm nominal pore diameter). The electric field is applied to electrodes at either end of the glass disk. It should be noted that all voltages reported in this work reflect the effective drop across the disk.¶
Fig. 4.
Compact EODS design concept in cutaway schematic. Top and bottom droplets (pinned contact circles) are connected by a bundle of tubes with electrode surfaces coating both ends. The switch toggles between big droplet on top and on bottom.
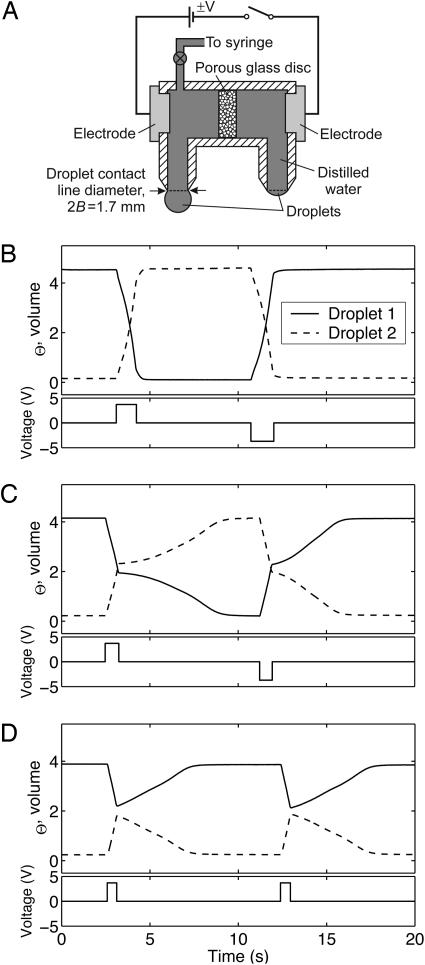
Fig. 2.
EODS device and operation. (A) Prototype in cross-section (not to scale). A porous glass disk is positioned between copper electrodes in a chamber filled with water connected to the droplet nozzles. (B–D) Response of droplet volume over time (Upper) to ±3.7 V square-wave voltage signal (Lower). (B) Voltage maintained constant throughout the transition from one equilibrium to the other. (C) Voltage interrupted just beyond the energy barrier. (D) Voltage interrupted just before the barrier. Note the curvatures in the volume response in C and D where, after the interruption, the system is driven to equilibrium by capillarity.
Results and Discussion
EODS Time-Dependent Operation. The capability of precise switching is demonstrated by turning the voltage off at various stages of the switching event (Fig. 2 B–D). Movement of the droplets is seen to respond precisely to the voltage signal. If interruption occurs just before (just after) the energy maximum, capillarity alone moves the system backward (forward) down the energy landscape to the nearest stable equilibrium. This capillary relaxation has practical implications for low-power devices as power-saving protocols become possible. That is, power is needed only to get the system over the barrier after which it can be turned off.
For successful switching, the EODS design must provide an electroosmotic pressure that exceeds the maximum resistive capillary pressure. For the discussion hereafter, applied voltage is held constant during switching (contrast to Fig. 2 C and D) so that veo is constant and vca depends on time only through Δp. For any switching trajectory, vca initially increases from vca = 0 (at equilibrium). If at some instant vca = veo (vnet = 0), the system must stall.∥ It follows that max (vca/veo) can be used as a criterion for switching/nonswitching because, if vca/veo ever reaches 1, the volume transfer stops. By using the approximation (–Δp)max ≈ βσ/B in vca, a nondimensional indicator emerges, a measure of capillary resistance to electroosmotic pump strength
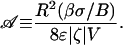 |
[2] |
For 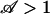 , the pump is too weak to switch, whereas for
, the pump is too weak to switch, whereas for 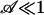 the electroosmotic pumping dominates capillary resistance.
the electroosmotic pumping dominates capillary resistance.
Setting 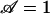 in Eq. 2 gives a critical pore radius,
in Eq. 2 gives a critical pore radius, 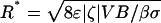 . For all else fixed, switching will not be possible for R > R*. For a voltage drop of 10 V across the pump, one can estimate R*1 ≈ 8.3 μm for nominal values of parameters (set 1; see Table 1). If parameters based on in-house characterization are used (set 2),
. For all else fixed, switching will not be possible for R > R*. For a voltage drop of 10 V across the pump, one can estimate R*1 ≈ 8.3 μm for nominal values of parameters (set 1; see Table 1). If parameters based on in-house characterization are used (set 2), 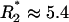 μm. An upper limit on the pore-size for switching is not surprising because electroosmotic pumping is enhanced by large surface-to-volume ratios of the porous pump medium. Implications for designing switches with specified size and performance follow from Eq. 2. For example, down-scaling system size B must be accompanied by a reduction in pore size R for the system to operate at the same applied voltage V.
μm. An upper limit on the pore-size for switching is not surprising because electroosmotic pumping is enhanced by large surface-to-volume ratios of the porous pump medium. Implications for designing switches with specified size and performance follow from Eq. 2. For example, down-scaling system size B must be accompanied by a reduction in pore size R for the system to operate at the same applied voltage V.
Table 1. Parameter values used in model calculations.
| Parameter | Set 1† | Set 2‡ |
|---|---|---|
| Contact line radius, B, mm | 0.85§ | 0.85 |
| Surface tension, σ, dyne/cm | 72¶ | 72 |
| Maximum pressure, β | 0.90∥ | 0.90 |
| Effective pore length, L, mm | 5.5†† | 5.5 |
| Effective pore radius, R, μm | 2.4‡‡ | 1.9 |
| Effective number of pores, N | 28.3 × 106§§ | 24.8 × 106 |
| Dielectric constant × zeta potential, ε|ζ|, V·C2/J·m | 6.56 × 10-11¶¶ | 2.74 × 10-11 |
Parameters are listed in order of increasing uncertainty.
Nominal values
In-house characterization; details to be reported elsewhere.
Measured value.
From ref. 9.
Calculated for Θtotal = 6.5.
From the measured frit thickness and a typical value of tortuosity (7).
Mean of manufacturer's specifications.
Via porosity measurement.
From ref. 7.
To test the prediction of critical upper pore size, one needs only to test the limit of 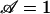 , which can be done in any number of ways according to the law of dimensional similitude. For convenience, we choose to vary voltage. Setting
, which can be done in any number of ways according to the law of dimensional similitude. For convenience, we choose to vary voltage. Setting 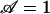 , one finds V* = βσR2/8Bε|ζ|, which evaluates to
, one finds V* = βσR2/8Bε|ζ|, which evaluates to 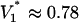 V for set 1 or
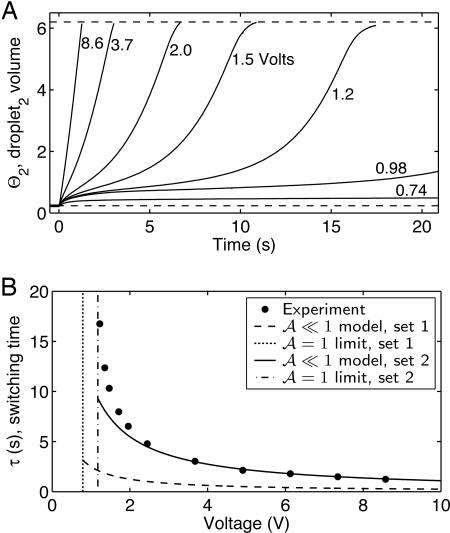
V for set 1 or 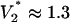 V for set 2 parameters. We now compare with observation. The change in droplet volume over time was measured for different constant voltages applied to the system (Fig. 3A). At the largest voltages, the pump dominates the flow, as seen by the nearly constant slope. For lower voltages, the effects of the capillary pressure are evident. As expected (e.g., see V = 1.2 V), the flow is retarded for the first half of the switching event and enhanced for the second half. Switching takes longer with lower voltages. The experiments indicate a critical voltage between 0.74 and 0.98 V. Switching fails for all smaller voltages.
V for set 2 parameters. We now compare with observation. The change in droplet volume over time was measured for different constant voltages applied to the system (Fig. 3A). At the largest voltages, the pump dominates the flow, as seen by the nearly constant slope. For lower voltages, the effects of the capillary pressure are evident. As expected (e.g., see V = 1.2 V), the flow is retarded for the first half of the switching event and enhanced for the second half. Switching takes longer with lower voltages. The experiments indicate a critical voltage between 0.74 and 0.98 V. Switching fails for all smaller voltages.
Fig. 3.
Time course of switching at constant voltage. At the start of each test, Θ1 ≈ 6.2 and Θ2 ≈ 0.3. The same droplets are used for all data, and total volume loss over the 20-min duration of the entire experiment was ≈5%. (A) Volume change over time (various voltages). The system stalls at 0.74 V, but 0.98 V is sufficient for switching (limited image storage precluded more data). (B) Summary of A: switching time τ against voltage (symbols). Model curves (solid) plot Eq. 4 (set 1 and set 2 parameters). Vertical limits (dashed) plot V* according to 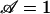 . Several data shown do not appear in A.
. Several data shown do not appear in A.
We shall now focus on time to switch from equilibrium to equilibrium. The total time τ needed to transfer the requisite volume ΔΘ from one droplet to the other depends on the effective number N of pores
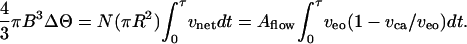 |
[3] |
Here, Aflow ≡ Nπ R2 is the cross-sectional area available for flow, proportional to the porosity ψ times the cross-sectional area available for pumping in a porous structure. A reasonable estimate for τ may be obtained by replacing (1 – vca/veo) by (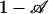 ) in Eq. 3 to yield in the limit
) in Eq. 3 to yield in the limit 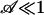 ,
,
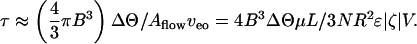 |
[4] |
The utility of this estimate is demonstrated in Fig. 3B, where this model is plotted with the experimental switching times read from Fig. 3A. Also plotted is V* predicted by the model, discussed above. Even for off-the-shelf parameters (set 1), the approximation in the pump-dominated limit captures the observed switching time to within an order-of-magnitude over the whole range, even for the longest times (near  ). The curve based on in-house pump characterization (set 2) does much better.
). The curve based on in-house pump characterization (set 2) does much better.
EODS Down-Scaling. For fixed materials, the voltage required for electroosmosis to counter capillary pressure depends only on single pore size and droplet size, according to Eq. 2. This dependence is because the pores act in parallel. Eq. 2 predicts V ∼ R2/B, which has been verified experimentally by varying V (Fig. 3). In contrast to the voltage required, switching time depends on N and L according to Eq. 4 because volume transferred per unit time depends on number of pores and resistance to transfer depends on pore length. For N and L fixed, switching time scales as τ ∼ B3/(R2V). Thus, if B diminishes in scale and R is arranged to diminish also, say, as R2 ∼ B, the voltage required for switching remains constant and the switching time decreases as B2. In summary, down-scaling of droplets to submillimeter sizes is favorable, regarding both the required voltage and time-to-switch.
Either time-to-switch or voltage (or some combination) can be used as a design criterion. Table 2 lists the time-to-switch and voltages for several combinations of droplet size and pore size. Values in the second and third rows are obtained from the measured values (first row) by using simple ratios following the similitude dictated by the model. Hence, they apply to the same experimental setup with changes only in B and R (i.e., same N, L, pump material, and working liquid). At some small scale the Debye layer will become a significant fraction of the pore size, invalidating the model. However, it is well known that Debye layers of <10 nm are common (indeed, it takes some care to create larger Debye layers). The scaling predicts submillisecond switching for a droplet diameter of 17 μm with 5 V.
Table 2. Examples: Scaling from experiment.
| Criterion: V = 5 V
|
Criterion: τ = 2.5 s
|
|||
|---|---|---|---|---|
| B, μm | R, μm | τ | R, μm | V, V |
| 850 | 1.9 | 2.5 s | 1.9 | 5 |
| 85 | 0.6 | 25 ms | 0.19 | 0.5 |
| 8.5 | 0.19 | 250 μs | 0.019 | 0.05 |
The EODS prototype demonstrated in the figures was intentionally designed with a large radius porous glass disk (frit) as pump to allow fast switching. Can the disk radius D be scaled down to match the droplet radius to obtain an overall EODS of compact volume, as suggested by the schematic of Fig. 4? Here, we shall assume a pump of cylindrical volume (Vfrit = π D2L) with porosity ψ. From the definition of porosity (void fraction) it follows that 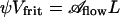 . Because N varies in this design example (D ∼ N1/2R), one must use Eqs. 2 and 4 rather than measured values and similitude as in the previous paragraph. Suppose a droplet of diameter 2B = 100 μm is desired. Choose Θtot = 2 (for which one can calculate ΔΘ = 1.6 and β = 0.34) with a goal of 10 V activation and τ ≤ 100 ms, still using the air/water/glass system. By using nominal values of ε|ζ| and tortuosity (Table 1), Eq. 2 gives the maximum pore radius that allows switching, R* = 3.27 μm. Choose R = 1.8 μm, conservatively, to yield A = 0.3 (compare 3.7 V in Fig. 3B). The pump radius required is then obtained from Eq. 4. By using a glass frit with L = 1mmand ψ = 0.36 (replace NR2 with ψD2) yields D > 530 μm. The point here is that the frit radius approaches the droplet radius, even before optimization. A wide variety of porous materials are available off-the-shelf and, alternatively, a range of fabrication techniques is available if a custom porous structure is needed. Eqs. 2 and 4 also provide the framework for optimization of an EODS system [e.g., varying pore size to nanoscale, or zeta potential and liquid/solid chemistry (10)].
. Because N varies in this design example (D ∼ N1/2R), one must use Eqs. 2 and 4 rather than measured values and similitude as in the previous paragraph. Suppose a droplet of diameter 2B = 100 μm is desired. Choose Θtot = 2 (for which one can calculate ΔΘ = 1.6 and β = 0.34) with a goal of 10 V activation and τ ≤ 100 ms, still using the air/water/glass system. By using nominal values of ε|ζ| and tortuosity (Table 1), Eq. 2 gives the maximum pore radius that allows switching, R* = 3.27 μm. Choose R = 1.8 μm, conservatively, to yield A = 0.3 (compare 3.7 V in Fig. 3B). The pump radius required is then obtained from Eq. 4. By using a glass frit with L = 1mmand ψ = 0.36 (replace NR2 with ψD2) yields D > 530 μm. The point here is that the frit radius approaches the droplet radius, even before optimization. A wide variety of porous materials are available off-the-shelf and, alternatively, a range of fabrication techniques is available if a custom porous structure is needed. Eqs. 2 and 4 also provide the framework for optimization of an EODS system [e.g., varying pore size to nanoscale, or zeta potential and liquid/solid chemistry (10)].
EODS Application. The capillary switch is an electromechanical transducer with applications envisioned in the areas of mechanics, microfluidics, and optics, among others. Presently, we focus on controllable adhesion and particle-moving applications, two examples from mechanics that are inspired by nature. These applications may be viewed as opening examples illustrating the class of capillary transducers.
Control of the wetting nature of a surface can be achieved by using an array of switches that “expose” or “shield” the droplets. It is well known that interfacial properties of a solid substrate on the macroscale, such as wetting and adhesion, are determined by features of the surface on smaller scales. A number of examples of small-scale influence have been reported, both reversible (11–13) and nonreversible (14–18). Each of these modifies the surface by a mechanism different from the exposure and shielding of droplets.
If a collar is placed around the end of each tube of an EODS, then a droplet is either exposed or shielded depending on whether or not it extends beyond the collar (Fig. 1 A Inset). Imagine an array of these capillary switches imbedded in a substrate (Teflon, for example) where droplet partners are not necessarily adjacent to each other. A region of shielded droplets will allow the substrate to retain its intrinsic nature (hydrophobic) and present a nonwetting behavior. Alternatively, a region of exposed droplets will cause the substrate surface to exhibit a wetting nature (hydrophilic) provided these droplets dominate the surface contact. Because each switch is individually addressable and switching times are fast, instantaneous control of gradients of exposure/shielding is possible. The potential is for precise temporal and spatial modifications of substrate wettability. Spatial and temporal resolution is limited by the droplet size and switching time, discussed above.
Adhesion by capillarity using a large array of droplet contacts is known to provide dramatic amplification of the otherwise relatively weak surface tension force. The palm beetle (Hemisphaerota cyanea) defends against attacking ants by “hunkering down” on the palm leaf with an adhesion strength approaching 102 times its own body weight (19, 20). The secret of the beetle's adhesive strength comes from down-scaling its capillary contacts. The millimeter-size beetle deploys up to 105 micrometer-size droplets made of an oil that it secretes. Noteworthy is that the beetle can attach and detach itself at will on the timescale of a second. It is this combination of reversibility and strength that is most remarkable (man-made bonds, such as epoxy, are stronger but not easily reversed).
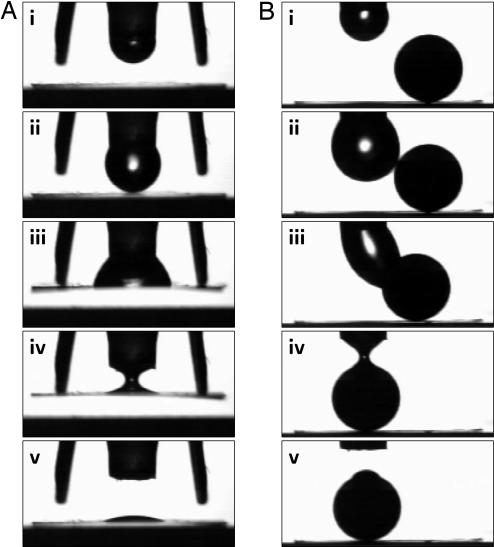
EODS-controlled adhesion happens through exposure and shielding of a single contact. Fig. 5A illustrates the unit EODS action of grabbing and releasing a substrate where the shielding is achieved by spacers. A 2D array of such EODS will enable tunable “superadhesion.” A 1-cm2 array of micrometer-size droplets will carry a load of nearly 1 kg, according to scaling. Decreasing droplet size B increases overall contact length as 1/B because a greater number of droplets can be packed in the same area. If this scaling were to hold to the nanometer scale, nanometer contacts would lead to a bond strength approaching the yield strength of aluminum. Adhesion by an EODS array can be turned quickly on and off like the beetle, although by a different mechanism.
Fig. 5.
Unit EODS actions for array applications. Snapshots from two dynamical sequences show a water droplet (e.g., half an EODS) pumped out from (i to ii) and back into (iv to v) the nylon nozzle. The entire sequence takes one switching cycle. (A) Controllable adhesion and release (compare the palm beetle) of a flat piece of aluminum foil (7 × 7mm × 10 μm). Upon contact with the foil (ii), wetting occurs and the foil is pulled up (iii) where it is held by surface tension against a pair of solid spacers. On droplet retraction (iv), the capillary adhesion is broken and the foil falls back (v). (B) Moving a solid Teflon sphere (2.4-mm diameter). Upon contact with the sphere (ii), wetting occurs (iii) after which the sphere is moved laterally one diameter. On droplet retraction (iv), the sphere is released (v). Repetition of this cycle by an adjacent EODS would continue the lateral movement of the sphere.
Movement of a particle around a 2D trajectory is an application that takes advantage of individual addressability of the EODS. The unit action of the EODS, as illustrated in Fig. 5B, moves a spherical solid particle one diameter laterally in a single switching cycle. A grid of EODS switches with characteristic array spacing of one diameter could sequentially move the sphere to an arbitrary position on the grid. With appropriate attention to wetting and miscibility issues, the same EODS unit action can move a droplet instead of a solid particle. This example illustrates a “bucket brigade” strategy of moving liquids around as packets for lab-on-a-chip applications (with surface tension as the bucket). The advantage is that, in contrast to pressure-driven single-phase liquid movement, moving droplets involves less viscous dissipation with consequent reduced power requirements on the device scale.
Ease of manufacture of arrays of EODS is favored by the absence of solid moving parts and the use of simple materials (“green” chemistry). Immiscible organic droplets can replace the exposed water droplets (retaining water in the pump) to limit evaporation. Large numbers of addressable EODS can be combined in series or parallel arrangements, interacting by means of planar or 3D network topologies.
Summary
The EODS is introduced to test the extent to which electroosmosis can counter capillary pressures, by using a Poiseuille–Smoluchowski model as a guide. Model predictions include (i) switching times as a function of system parameters and (ii) a critical pore size above which switching fails (other parameters fixed). Both predictions are in reasonable agreement with observation. The electrical double layer is assumed small relative to pore size in the model, an assumption straightforward (and likely necessary) to relax to extend to nanoporous pumps and liquid pH effects.
For the electroosmotic pressure to successfully overcome the capillary pressure of a droplet of size B, pore size R must be sufficiently small (for fixed voltage), as mentioned, or, equivalently, applied voltage V must be sufficiently large (for fixed pore size). These critical values have been reported for millimeter-scale droplets. For smaller droplets, similitude dictates that applied voltage and time-to-switch scale as V ∼ R2/B and τ ∼ B3/R2V, respectively. Thus, low voltage and fast switching are anticipated for a range of droplet switches, 1 μm < B < 1 mm. Furthermore, size of the pump also scales favorably with diminishing droplet size. Technological implications of these scalings are noteworthy.
We have created a previously undescribed switch that combines the stable states determined by the surface energy of droplet surfaces with electrokinetic control over the toggling from one configuration to another. Applications are inspired by the palm beetle, which proves the functionality of an array of micrometer-sized droplet switches in controlling adhesion (controlled by nonelectronic means). For such “grab-and-release” applications, droplets are exposed and wettability is crucial. Two unit actions of the EODS illustrate possible grab-and-release applications. For applications that are not grab-and-release, but that still exert a force, droplets could be covered by a thin flexible polymeric film, or the liquid might be otherwise isolated from the object of the droplet's action.
Acknowledgments
We thank D. P. J. Barz for design suggestions and A. H. Hirsa for useful comments. P.H.S. and M.J.V. thank the Forschungszentrum Karlsruhe and were supported by NASA Grant NAG32-2713 and National Science Foundation Grant DMI-0335000. M.J.V. was supported by the Deutscher Akademischer Austausch Dienst.
Author contributions: M.J.V., P.E., and P.H.S. designed research; M.J.V., P.E., and P.H.S. performed research; M.J.V. and P.H.S. analyzed data; and M.J.V. and P.H.S. wrote the paper.
Abbreviation: EODS, electroosmotic droplet switch.
Footnotes
The voltage applied to the electrodes Vapp results in a smaller effective voltage across the glass disk Veff because of a decomposition potential [electrochemistry at the electrodes (7)] and a voltage drop across the gaps on either side of the disk in the pump chamber (Fig. 2 A). The decomposition potential is measured at V = 2.5 V. The voltages are linearly related as Veff = 0.49(Vapp – 2.5). All voltages reported in this work are Veff, from which Vapp can be readily obtained by this equation, which depends only on chamber geometry, electrode, and liquid materials (measurement details to be reported elsewhere).
Consider switching from A′A to AA′ as a 1D dynamical system: dΘ2/dt ∝ vnet = c1+c2· Δp(Θ2), with c1 and c2 positive. It can be shown (graphically or by linear stability analysis) that the first fixed point (veo = vca) is stable, because at that point dΔp/dΘ2 ∝–dΔp/d(Θ1 – Θ2) < 0 (compare Fig. 1C).
References
- 1.Boys, C. V. (1959) Soap Bubbles, Their Colors and Forces Which Mold Them (Dover, New York).
- 2.Wente, H. C. (1999) Pac. J. Math. 189, 339–376. [Google Scholar]
- 3.Hirsa, A. H., López, C. A., Laytin, M. A., Vogel, M. J. & Steen, P. H. (2005) Appl. Phys. Lett. 86, 014106. [Google Scholar]
- 4.von Smoluchowski, M. (1914) in Handbuch der Elektrizität und des Magnetismus, ed. Graetz, L. (Barth, Leipzig, Germany), Vol. 2, pp. 366–428. [Google Scholar]
- 5.Rice, C. L & Whitehead, R. (1965) J. Phys. Chem. 69, 4017–4023. [Google Scholar]
- 6.Probstein, R. F. (1994) Physicochemical Hydrodynamics: An Introduction. (Wiley, New York).
- 7.Zeng, S, Chen, C.-H, Mikkelson, J. C. & Santiago, J. G. (2001) Sens. Actuator B 79, 107–114. [Google Scholar]
- 8.Steen, P. H., Ehrhard, P. & Vogel, M. J. (2004) German Patent Appl. 102 004 034 839.1, filed 19 July 2004.
- 9.Weast, B., ed. (1980) Handbook of Chemistry and Physics (CRC, Boca Raton, FL), 60th Ed.
- 10.Kirby, B. J & Hasselbrink, E. F. (2004) Electrophoresis 25, 187–202. [DOI] [PubMed] [Google Scholar]
- 11.Abbott, N. L., Gorman, C. B. & Whitesides, G. M. (1995) Langmuir 11, 16–18. [Google Scholar]
- 12.Abbott, S., Ralston, J., Reynolds, G. & Hayes, R. (1999) Langmuir 15, 8923–8928. [Google Scholar]
- 13.Lahann, J., Mitragotri, S., Tran, T.-N., Kaido, H., Sundaram, J., Choi, I. S., Hoffer, S., Somorjai, G. A. & Langer, R. (2003) Science 299, 371–374. [DOI] [PubMed] [Google Scholar]
- 14.Shibuichi, S., Onda, T., Satoh, N. & Tsujii, K. (1996) J. Phys. Chem. 100, 19512–19517. [Google Scholar]
- 15.Quéré, D. (2002) Physica A 313, 32–46. [Google Scholar]
- 16.Darhuber, A. A., Valentino, J. P., Troian, S. M. & Wagner, S. (2003) J. Microelectromech. Syst. 12, 873–879. [Google Scholar]
- 17.Geim, A. K., Dubonos, S. V., Grigorieva, I. V., Novoselov, K. S., Zhukov, A. A. & Shapoval, S. Y. (2003) Nat. Mater. 2, 461–463. [DOI] [PubMed] [Google Scholar]
- 18.Daniel, S., Sircar, S., Gliem, J. & Chaudhury, M. K. (2004) Langmuir 20, 4085–4092. [DOI] [PubMed] [Google Scholar]
- 19.Eisner, T. & Aneshansley, D. J. (2000) Proc. Natl. Acad. Sci. USA 97, 6568–6573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Eisner, T. (2003) For Love of Insects (Belknap Harvard, Cambridge, MA).