Temperature dependence of membrane viscosity of ternary lipid GUV with L_o domains

Abstract

In the cell membrane, it is considered that saturated lipids and cholesterol organize liquid-ordered (L_o) domains in a sea of liquid-disordered (L_d) phases and proteins relevant to cellular functions are localized in the L_o domains. Since the diffusion of transmembrane proteins is regulated by the membrane viscosity, we investigate the temperature dependence of the membrane viscosity of the ternary giant unilamellar vesicles (GUVs) composed of the saturated lipid 1,2-dipalmitoyl-sn-glycero-3-phosphocholine, the unsaturated lipid 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), and cholesterol to understand the effect of the phase separation on the membrane viscosity using a microinjection technique. In the microinjection method, membrane viscosity is estimated by comparing the flow pattern induced on a spherical membrane with a hydrodynamic model. For phase-separated GUVs, the flow pattern is visualized by the motion of the domains. In this study, we developed a method to visualize the flow patterns of homogeneous GUVs above the phase separation temperature by using beads attached to the GUVs. We succeeded in measuring the membrane viscosity of ternary GUVs both above phase separation temperature and in the phase-separated region and found that the membrane viscosity decreases dramatically by phase separation. In the phase-separated region, i.e., GUVs with L_o domains, the membrane viscosity is determined by that of the L_d phase, ${\eta }_{\text{Ld}}$, and shows weak temperature dependence compared to that of the DOPC single-component GUV, which is a main component of the L_d phase. We revealed that the Moelwyn-Hughest model, which takes into account the effects of the membrane composition, viscosity of the pure component, and interaction between components, well describes the obtained membrane viscosity of the ternary GUV both above the phase separation temperature and in the phase-separated region. The drastic decrease of the membrane viscosity by the phase separation plays an important role in regulating the mobility of constituents in multi-component membranes.

Significance

Cell membranes are considered to show phase separation, where saturated lipids and cholesterol organize liquid-ordered domains, localizing specific proteins relevant to cellular functions. Since the membrane fluidity controls cellular functions, phase separation of the cell membranes is expected to play important roles in regulating not only the distribution of proteins but also the membrane viscosity. In this study, we find that the membrane viscosity decreases drastically by phase separation due to the changes in the membrane composition and viscosity of the pure component by decreasing the temperature. We believe that this study will provide new insight into the effect of phase separation on the viscosity of the cell membrane.

Introduction

In the cell membrane, functional molecules such as peptides, proteins, and polysaccharides are embedded in the lipid bilayer, which is composed of saturated and unsaturated lipids and cholesterol (CHOL). In the lipid raft hypothesis (1,2,3,4,5,6,7,8,9,10,11,12,13,14), sphingolipid-CHOL-protein assemblies or liquid-ordered (L_o) domains composed of saturated lipid and CHOL that localize specific proteins in a sea of liquid-disordered (L_d) phases may play a crucial role in signal transduction, cell recognition, protein sorting, and other processes (1,2,7,8). Although the direct observation of lipid rafts has not yet succeeded due to their submicron size, the lipid raft model is supported by phase separation into the L_o and L_d phases observed in micrometer-sized model cell membranes (giant unilamellar vesicles [GUVs]) composed of saturated and unsaturated phospholipids and CHOL (15,16,17,18,19,20). One plausible explanation for the lack of phase separation observed in living cells is that the actin cytoskeleton inhibits L_o domain growth so that the L_o domains remain at a submicron scale. Recently, L_o domains have also been observed in giant plasma membrane vesicles, which are isolated from the cell membrane, retaining the lipid diversity and protein content of living cell membranes but lacking the actin cytoskeleton (21,22,23,24,25). These studies indicate that the cell membrane may have L_o domains. Phase separation of the ternary GUVs and giant plasma membrane vesicles is governed by the balance between the mixing free energy and the interaction energy among lipids (26,27,28,29,30,31,32).

In this context, phase separation of the cell membranes is expected to play important roles in regulating not only the distribution of lipids and proteins but also the mobility of these molecules. The functional molecules or lipid rafts diffuse in the cell membrane and interact with molecules outside/inside the cell to realize cellular functions (1,2,3,4,5,6,7). Thus, the membrane viscosity, which is a measure of the membrane fluidity, is a key parameter to regulate cellular functions. Since the structure of the cell membrane is too complex to measure the membrane viscosity, the viscosity of lipid GUVs has been investigated both experimentally and theoretically (33,34,35,36,37,38,39,40,41,42,43,44,45,46). Still, measuring the viscosity of phase-separated lipid membranes is difficult, and much effort has been made to develop methods to measure it (47,48,49). For example, Cicuta et al. estimated the diffusion coefficient of the L_d domains on the phase-separated ternary GUV composed of the saturated lipid 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), the unsaturated lipid 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), and CHOL (49), and the obtained diffusion constant was converted to the membrane viscosity using the Saffman-Delbrück (SD) model (43). The SD model is valid when the tracer size $a$ is smaller than the SD length, which is defined by the ratio of the membrane viscosity to the viscosity of surrounding water, ${\eta }_{\mathrm{m}}/{\eta }_{\mathrm{w}}$. The GUV with L_d domains is in the range of $a<{\eta }_{\mathrm{m}}/{\eta }_{\mathrm{w}}$, while that with L_o domains (a model of lipid rafts) is often out of this range. For the range of $a>{\eta }_{\mathrm{m}}/{\eta }_{\mathrm{w}}$, the diffusion coefficient is mainly governed by the viscosity of the solvent, but Petrov et al. propose an approximation of the Hughes, Pailthorpe, and White model (44) expressing the relationship between membrane viscosity and diffusion coefficient (45). Despite these efforts, the systematic measurement of the membrane viscosity of ternary GUVs has been limited because the viscosity measurement method that could cover both above the phase separation temperature (miscibility transition temperature [$T_{\text{misc}}$]) and in the phase-separated region has not been established. Then, to systematically measure the membrane viscosity of ternary GUVs, we recently developed a membrane viscosity measurement method using microinjection (50). In this technique, we induce a fluid velocity field on a spherical GUV by applying a point force using the microinjection. The membrane viscosity is then obtained by comparing the observed flow pattern with the hydrodynamic model proposed by Henle and Levine (HL model) (51) (details of the HL model are described in supporting material S1). Since our measurement technique uses the information only on the fluid velocity pattern on the membrane, both homogeneous and phase-separated GUVs can be measured as long as the membrane flow can be visualized.

In this study, to reveal the effect of the phase separation on the membrane viscosity, we measure the temperature dependence of the membrane viscosity of DPPC/DOPC/CHOL ternary GUVs both above the phase separation temperature and in the phase-separated region using the microinjection technique. Due to the phase separation, membrane viscosity decreases dramatically, which plays an important role in regulating the mobility of constituents in multi-component membranes. Our previous work has revealed that the viscosity of the L_d phase governs that of the ternary GUVs with L_o domains (50). In this case, the viscosity of the L_d phase is well described by the Einstein viscosity equation for the two-dimensional fluid using the area fraction of L_o domains (52,53),

$${\eta }_{\mathrm{m},\text{demix}}={\eta }_{\text{Ld}}\left(1+2{\mathrm{\Phi }}^{\text{Lo}}\right)$$ (1)

Here, ${\eta }_{\text{Ld}}$ is the membrane viscosity of the L_d phase and ${\mathrm{\Phi }}^{\text{Lo}}$ is the area fraction of L_o domains on the GUV. We shall refer to the membrane viscosity in the phase-separated region as an apparent membrane viscosity, ${\eta }_{\mathrm{m},\text{demix}}$. Using Eq. 1, we estimate ${\eta }_{\text{Ld}}$ from the obtained ${\eta }_{\mathrm{m},\text{demix}}$. To describe the obtained membrane viscosity above $T_{\text{misc}}$, which we denote as ${\eta }_{\mathrm{m},\text{mix}}$, and that of the L_d phase in the phase-separated region, ${\eta }_{\text{Ld}}$, we employ the Moelwyn-Hughest (MH) model used for the viscosity of a binary fluid composed of A and B, given by

$$\eta =\left(x_{\mathrm{A}}{\eta }_{\mathrm{A}}+x_{\mathrm{B}}{\eta }_{\mathrm{B}}\right)\left(1-2\frac{\Delta H^E}{RT}\right)$$ (2)

where $x_i\left(i=\mathrm{A},\mathrm{B}\right)$ and ${\eta }_i$ are the molar fraction and viscosity of A and B, respectively; $\Delta H^E$ is the excess mixing enthalpy, which is relevant to the interaction energy between two components; $R$ is the ideal gas constant; and $T$ is the temperature (54) (details are described in supporting material S2). We find that the obtained membrane viscosity is well described by the MH model, indicating that the membrane viscosity of ternary GUVs is determined by the membrane composition, viscosity of the pure component, and interaction between components. We believe that these observations will provide new insight into the effect of phase separation on the viscosity of the multi-component membrane, such as the cell membrane.

Materials and methods

Materials

The phospholipids used in this study were DPPC (purity >99%) and DOPC (purity >99%), and both of them were purchased from Avanti Polar Lipids (Alabaster, Alabama) and used without further purification. CHOL (purity ≥99%) was obtained from Sigma-Aldrich (St. Louis, Missouri). To visualize phase-separated domains, Texas Red-DPPE (TR-DPPE) purchased from Molecular Probes (Eugene, Oregon) was used. Ultrapure water purified with a Direct-Q 3 UV apparatus (Merck Millipore, Darmstadt, Germany) was used for the preparation of GUVs and the microinjection. Fluorescence bead Fluoresbrite YG Microspheres with a 1.00 μm diameter purchased from Polysciences Asia Pacific (Taipei, Taiwan), which are fluorescence monodispersed polystyrene microspheres that have carboxylate groups on their surfaces, were used as a tracer to visualize the membrane flow of GUVs above the phase separation temperature and GUVs with a single phase. We removed detergents in the fluorescence bead suspension before use. Details are described in the adhesion of colloidal particles to the GUV membrane section.

GUV preparation

GUVs were prepared by a gentle hydration method (55,56). First, we dissolved the prescribed amounts of lipids, i.e., DPPC, DOPC, and CHOL, in 10 μL of chloroform (in total 10 mM). To dye GUVs, TR-DPPE was added to the lipid solution with a molar concentration of 0.36 mol % to total lipids. Phospholipids used in this study exhibit melting temperatures at 41°C for DPPC and −17°C for DOPC. The GUVs composed of DPPC/DOPC/CHOL show a homogeneous phase in the high-temperature region (∼50°C). By decreasing the temperature, the ternary GUV shows phase separation into the L_d phase, mainly composed of DOPC and CHOL, and the L_o phase, mainly composed of DPPC and CHOL, at the phase separation temperature (15,16,17,18,19,20). The fluorescence dye TR-DPPE is excluded from the L_o phase and localized in the L_d phase when phase separation occurs. Therefore, the L_d and L_o phases can be distinguished under a fluorescence microscope. Although the size of Texas Red is ∼2 nm, the molar fraction of Texas Red is small enough so as to not affect the membrane viscosity. Details are described in our previous work (57). The organic solvent was evaporated in a stream of nitrogen gas, and the obtained lipid film was kept under vacuum for one night to remove the remaining solvent completely. The dried lipid film was prewarmed at 50°C, and then the sample was hydrated with 1 mL of ultrapure water at 50°C (0.1 mM lipids/water). During the hydration process, the lipid films spontaneously form a GUV suspension, where the diameters of the GUVs are 10–60 μm.

Adhesion of colloidal particles to the GUV membrane

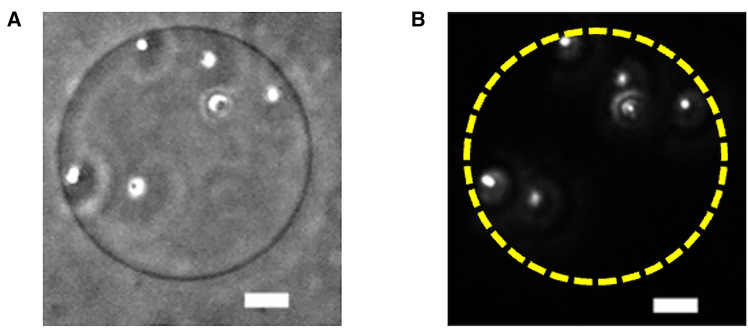
To visualize the membrane flow of the GUV without phase separation, fluorescence beads were adhered to the GUVs as a tracer using centrifuge method proposed by Hamada’s group (58,59). In this method, to adhere beads onto GUVs, a mixture of fluorescence beads and phospholipid GUVs was subjected to centrifugation. The adhesion mode of the beads on the GUV membrane is controlled by the size of the beads and the centrifugal force. When beads with a diameter larger than 200 nm are subjected to the centrifugal force of 1600 rcf (relative centrifugal force) for 3 min, the beads are partially wrapped, whereas when beads with a diameter smaller than 200 nm are subjected to a centrifugal force of 1600 rcf for 8 min, the beads are fully wrapped. We adhered fluorescence beads of a diameter of 1 μm with a centrifugal force of ∼1600 rcf and centrifuging time of ∼3 min, i.e., in a partially wrapped manner. The bead-adhering procedure is as follows. We first removed detergents in the fluorescence bead suspension. The fluorescence bead suspension was 100 times diluted by ultrapure water. Then, the diluted solution was centrifuged at 14,500 rpm during 5 min using Centrifuge Mini Spin︎ plus (Eppendorf, Hamburg, Germany), and the supernatant was replaced with the same volume of ultrapure water. After repeating this procedure three times, we obtained 0.025 vol % of fluorescence bead suspension. The diluted fluorescence bead suspension and GUV suspension were mixed in a 1:1 volume ratio and centrifuged with 1600 rcf for 3 min. The supernatant, excluding the sedimented beads, was collected, and GUVs with attached beads were retrieved for the membrane viscosity measurement. Fig. 1 shows the phase contrast and fluorescence images of the GUV with adhering fluorescence beads.

Figure 1.

Microscope images of the beads adhered on a GUV. (A) Phase contrast image. (B) Fluorescence image. The broken circle denotes the contour of the GUV. Scale bars represent 10 μm.

Membrane viscosity measurement of GUVs

In order to measure the membrane viscosity, we applied the point force at the north pole on the spherical GUV (Fig. S1 a). To apply the point force to a GUV membrane, we used the microinjection method. The target GUV was held by the holding pipette VacuTip I (Eppendorf) with a flat edge and a hole with a 15 μm inner diameter. The suction pressure was kept as low as possible to hold the GUV (∼1 Pa) by the microinjector Cell Tram Vario (Eppendorf). The membrane tension induced by the suction pressure of the holding pipette did not significantly affect the observed membrane viscosity. Details are described in our previous work (50). An injection pipette FemtoTip II (Eppendorf) with a hole of 0.5 ± 0.2 μm diameter was filled with ultrapure water and then inserted into the observation chamber. The microinjection pressure was 15–100 hPa using the microinjection system FemtoJet (Eppendorf, Hamburg, Germany) for the membrane viscosity measurement. Estimation of the injection flow velocity is described in our previous work (50). Then, we placed the tip of an injection pipette on the north pole of the GUV using a hydraulic micromanipulator (MMO-202ND, MN-4; Narishige, Tokyo, Japan). The positioning of the tip of the injection pipette on the north pole, which is explained in our previous publication (50), is important to accurately determine the vortex center. Then, the injection flow was applied to the target GUV. The injection flow induced the vortex flow on the GUV. Then, we obtained the position of the vortex center, which depends on the membrane viscosity (Fig. S1 b). The relationship between the vortex center and the membrane viscosity is described by the theoretical prediction made by the HL model (51). Details of the HL model are described in supporting material S1. The GUV suspension prepared at 50°C was placed on a temperature-controlled stage for microscope observation (PE120; Linkam Scientific Instruments, Tadworth, United Kingdom) set at the prescribed temperature. We measured the membrane viscosity 5 min after the sample reached the prescribed temperature. We confirmed that the observed membrane viscosity was independent of the waiting time between 5 and 15 min. Although it is known to take several hours to reach full thermal equilibrium (17), no significant change in domain size was observed between 5 and 15 min after the observation temperature was reached in this study. The membrane flow induced by microinjection was observed using a fluorescence microscope (Axiovert Z1; Carl Zeiss Microscopy, Jena, Germany) with an objective (LD Plan-NEOFLUAR 20×/0.4; Carl Zeiss Microscopy) and recorded with a CMOS camera (ORCA-Flash 4.0; Hamamatsu Photonics, Shizuoka, Japan). We performed the membrane viscosity measurements with more than 10 GUVs for one composition and obtained the mean membrane viscosity, ${\eta }_{\mathrm{m}}$, and standard error of the mean of the membrane viscosity, $\sigma$.

Determination of the position of the vortex center

In this study, the membrane viscosity was estimated from the position of the vortex center. We express the vortex center in the spherical coordinate ($r$, $\theta$, $\varphi$). Since the radius of the spherical GUV, $R$, and the azimuth angle of the vortex center, $\varphi$, are constant (details are described in supporting material S1), the position of the vortex center is determined solely by the polar angle, ${\theta =\theta }_{\mathrm{v}}$. The relationship between ${\theta }_{\mathrm{v}}$ and the membrane viscosity ${\eta }_{\mathrm{m}}/R{\eta }_{\mathrm{w}}$ is shown in Fig. S1 b. Here, ${\eta }_{\mathrm{m}}$ is the membrane viscosity, and ${\eta }_{\mathrm{w}}$ is the viscosity of surrounding water. To measure the position of the vortex center, the time series of the positions of tracers, such as phase-separated domains or adhering fluorescence beads on the GUV, were recorded for about 300 snapshots (10 frames/s). The domain trajectories were tracked using the tracking plugin Track Mate StarDist (60) of an open-source platform for the biological image analysis package Fiji (61). The trajectory of a L_o domain or a fluorescence bead drew a deformed ellipse path line around the vortex center. The smallest path line was approximated by an ellipse, and the vortex center ${\theta }_{\mathrm{v}}$ was obtained from the intersection of the major and minor axes of the ellipse. More details are described in our previous work (57).

Results

Membrane viscosity measured by bead-based method

In this study, membrane flow on a spherical GUV was induced by microinjection (point force), and the flow pattern was compared with that of the HL model to estimate the membrane viscosity of the GUV. So far, flow patterns have been visualized by tracing the movement of domains formed by the phase separation of GUVs (Fig. 2) (50). In this study, membrane flow was also visualized by tracing the movement of fluorescence beads attached to GUVs, which also made it possible to measure the membrane viscosity of GUVs without phase separation.

Figure 2.

Snapshots of raw (top row) and analyzed (bottom) data. A vortex flow is induced by microinjection. A domain indicated by an arrow draws the smallest path line. In the analyzed data, the contour of the domains is indicated by a yellow line, and the domain trajectory is denoted by a light blue line. The vortex center is estimated from the smallest path line. Scale bars represent 10 μm.

To examine the reliability of a new membrane viscosity measurement method that visualizes membrane flow using beads attached onto the GUV, we measured the membrane viscosity of the phase-separated GUV composed of DPPC/DOPC/CHOL = 30:50:20, on which beads were adhered. First, the flow pattern on the GUV induced by microinjection was visualized by the motion of a bead (Fig. 3 A). Beads adhered to the L_d phase of the phase-separated GUV. Using the same GUV, we then traced the domain motion and visualized the flow pattern (Fig. 3 B). As shown in Fig. 3 A and B, the movements of the bead and the domain showed nearly the same trajectory. The membrane viscosities obtained from five independent measurements were 12.1 ± 3.0 nP · s · m for the bead-based method and 12.5 ± 0.9 nP · s · m for the domain-based method. This result shows that bead-based and domain-based methods give the same membrane viscosity with excellent accuracy and that, regardless of phase separation, our method can cover the measurement of membrane viscosity over a wide range of membrane compositions.

Figure 3.

The flow field visualized by a bead attached onto the GUV membrane (A) and by a domain formed by phase separation (B). The membrane viscosity measurement was performed with the same GUV composed of DPPC/DOPC/CHOL = 30:50:20 at 13°C. Scale bars represent 10 μm.

Temperature dependence of the membrane viscosity

In this study, we prepared the three compositions of the ternary GUVs composed of DPPC/DOPC/CHOL = (composition a) 40:40:20, (composition b) 30:50:20, and (composition c) 20:60:20 (molar ratio), DPPC/CHOL = 1:1 and 2:1 binary GUVs, and pure DOPC GUVs. First, we examined the phase separation temperature, $T_{\text{misc}}$, of the GUVs with compositions a, b, and c and obtained $T_{\text{misc}}=$ 33.7°C ± 1°C, 32.0°C ± 1°C, and 29.3°C ± 0.9°C, respectively. These $T_{\text{misc}}$s agree well with those reported in the literature (17,57). Below $T_{\text{misc}}$, GUVs with compositions a, b, and c form L_o domains in a sea of L_d phases, as shown in the insets of Fig. 4 A. Then, we applied a point force at the north pole of the target GUV, which induced a pair of vortices. We visualized the vortex flow by the motion of L_o domains for the phase-separated GUV and that of beads for homogeneous GUVs and determined the vortex center, which gave the membrane viscosity based on the HL model. Fig. 4 B and Table 1 show the temperature dependence of ${\eta }_{\mathrm{m},\text{mix}}$ of the GUVs with compositions a, b, and c and in the phase-separated region, ${\eta }_{\mathrm{m},\text{demix}}$, as well as that of the GUVs composed of DPPC/CHOL, ${\eta }_{\text{DPPC}/\text{DOPC}}$, and those composed of only DOPC, ${\eta }_{\text{DOPC}}$. When the temperature of the phase-separated GUVs was increased from 13°C, the apparent membrane viscosity decreased gradually but increased abruptly at the phase separation temperature. Near the phase separation temperature $T_{\text{misc}}$, ${\eta }_{\mathrm{m},\text{mix}}$ of the ternary GUV is four times larger than that in the phase-separated region.

Figure 4.

Membrane viscosity of the GUV. (A) GUV compositions in which membrane viscosity measurement was performed. The green square, yellow diamond, and red circle indicate compositions DPPC/DOPC/CHOL= (a) 40:40:20, (b) 30:50:20, and (c) 20:60:20, respectively. The dashed line denotes the boundary of the L_d-L_o coexistence region at 20°C taken from (17). Violet, blue, green, and orange lines are the tie lines through composition a at 19°C, 23°C, 27°C, and 32°C, respectively, obtained by SANS measurements (see supporting material S3). Inset: microscope images of the GUVs at 20°C with compositions a, b, and c from right to left. Scale bars represent 10 μm. (B) Temperature dependence of ${\eta }_{\mathrm{m},\text{mix}}$ of the GUV with compositions a, b, and c and that of ${\eta }_{\mathrm{m},\text{demix}}$, as well as that of ${\eta }_{\text{DPPC}/\text{DOPC}}$ and ${\eta }_{\text{DOPC}}$. Squares, diamonds, and circles indicate the membrane viscosity of GUVs with compositions a, b, and c, respectively. Up triangles and down triangles denote the membrane viscosity of the GUVs composed of DPPC/CHOL and DOPC, respectively. Dashed lines are drawn to guide the eye. The temperature dependence of ${\eta }_{\text{DOPC}}$ has a steep slope compared to the other compositions. The error bars express mean ± SE.

Table 1.

Temperature dependence of measured membrane viscosities for compositions a, b, and c, DPPC/CHOL = 1:1 and 2:1, and DOPC

Temperature (°C)	${\eta }_{\mathrm{m},\text{mix}}\pm \sigma ,{\eta }_{\mathrm{m},\text{demix}}\pm \sigma ,{\eta }_{\text{DPPC}/\text{CHOL}}\pm \sigma ,{\eta }_{\text{DOPC}}\pm \sigma \left[\text{nPa}·\mathrm{s}·\mathrm{m}\right]$
	a	b	c	DPPC/CHOL = 1:1	DPPC/CHOL = 2:1	DOPC
13	12.4 ± 2.3	10.9 ± 2.3	8.8 ± 1.4	46.1 ± 6.7	–	6.0 ± 2.1
15	–	–	–	–	–	4.0 ± 1.5
18	10.6 ± 1.9	11.3 ± 2.4	9.0 ± 2.5	–	–	5.2 ± 2.0
20	–	–	–	–	–	3.2 ± 1.5
23	8.5 ± 1.0	7.5 ± 5.7	6.2 ± 1.2	29.9 ± 8.8	–	1.7 ± 0.6
27	5.8 ± 2.9	5.3 ± 0.7	6.0 ± 2.3	–	–	–
32	6.6 ± 1.8	5.4 ± 1.2	–	33.6 ± 3.0	–	–
35	27.2 ± 2.3	21.8 ± 3.3	–	–	–	–
37	26.3 ± 2.4	26.1 ± 1.3	–	–	51.1 ± 6.9	–
39	21.6 ± 2.4	–	–	–	–	–

$\sigma$, standard error of the mean.

Membrane viscosity of the L_d phase

Here, we show that the apparent membrane viscosity of phase-separated DPPC/DOPC/CHOL GUVs is governed by the viscosity of the L_d phase; that is, the viscosity of the phase-separated membranes obeys the theoretical prediction expressed by Eq. 1 (52,53). For this purpose, the membrane viscosity experiments were performed with three compositions, DPPC/DOPC/CHOL = (i) 20:60:20, (ii) 27:53:20, and (iii) 37.5:37.5:25, which are on the same tie line at 20°C. Compositions i, ii, and iii, the tie line through these three compositions, and the boundary of the L_d-L_o coexistence region of the DPPC/DOPC/CHOL system at 20°C taken from the literature (17) are shown in Fig. 5 A. The obtained ${\eta }_{\mathrm{m},\text{demix}}$s with compositions i, ii, and iii are listed in Table 2. Then, ${\mathrm{\Phi }}^{\text{Lo}}$ of the GUVs with compositions i, ii, and iii at 20°C were estimated from the microscope images and obtained as 0.10 ± 0.041, 0.18 ± 0.015, and 0.45 ± 0.040, respectively, as shown in Table 2. As shown in Fig. 5 B, the ${\mathrm{\Phi }}^{\text{Lo}}$ dependence of ${\eta }_{\mathrm{m},\text{demix}}$ is well fitted by ${\eta }_{\mathrm{m},\text{demix}}={\eta }_{\text{Ld}}\left(1+\epsilon {\mathrm{\Phi }}^{\text{Lo}}\right)$, with ${\eta }_{\text{Ld}}=7.9\pm 0.2$ nPa · s · m and $\epsilon =2.0\pm 0.1$, which agrees well with the prediction of Einstein viscosity equation for two-dimensional fluid (Eq. 1). Thus, the effect of ${\mathrm{\Phi }}^{\text{Lo}}$ on ${\eta }_{\mathrm{m},\text{demix}}$ was corrected by Eq. 1, and ${\eta }_{\text{Ld}}$ was obtained. It should be noted that the viscosity of the L_d phase depends on not only the area fraction of the L_o domains but also their size in general. Since the L_o domains have a stick boundary, when the liquid molecules (the molecules that constitute the L_d phase) and domains are of similar sizes, it also depends on the domain size. In this study, the liquid molecules are nanometer sized, whereas L_o domains are micrometer sized. Therefore, the effect of the domain size is negligible. In fact, as shown in Fig. 6, for composition a at 23°C, the average domain radius of 10 GUVs, $R_{\mathrm{d}}$, is 5.3 ± 0.9 μm and almost uniform in size. It is also clear that the apparent membrane viscosity does not depend on the domain radius. Therefore, in this study, ${\eta }_{\text{Ld}}$ can be obtained from the apparent membrane viscosity by Eq. 1 using only the area fraction of the L_o domains.

Figure 5.

Membrane viscosity of the GUV with L_o domains. (A) The phase diagram of DPPC/DOPC/CHOL ternary system at 20°C. Cross symbols denote compositions DPPC/DOPC/CHOL = (i) 20/60/20, (ii) 27/53/20, and (iii) 37.5/37.5/25 on the same tie line indicated by a solid line. The dashed line denotes the boundary of the L_d-L_o coexistence region at 20°C taken from (17). The red circle indicates the composition DPPC/DOPC/CHOL = 12:70:18, which is in a single phase. Inset: microscope image of the GUV with composition i. Scale Bar represents 10 μm. (B) ${\mathrm{\Phi }}^{\text{Lo}}$ dependence of the membrane viscosity of the GUVs composed of DPPC/DOPC/CHOL, which are on the same tie line at 20°C. The dashed line denotes the fitting curve expressed by ${\eta }_{\mathrm{m},\text{demix}}={\eta }_{\text{Ld}}\left(1+\epsilon {\mathrm{\Phi }}^{\text{Lo}}\right)$. The fitting gives ${\eta }_{\text{Ld}}=7.9\pm 0.2$ nPa · s · m and $\epsilon =2.0\pm 0.1$. The error bars express mean ± SE.

Table 2.

Measured apparent membrane viscosities, area fraction of L_o domains, and calculated membrane viscosity of the L_d phase at 20°C for compositions i, ii, and iii

Composition DPPC/DOPC/CHOL	${\mathrm{\Phi }}^{\text{Lo}}$	${\eta }_{\mathrm{m},\text{demix}}\pm \sigma \left[\text{nPa}·\mathrm{s}·\mathrm{m}\right]$	${\eta }_{\text{Ld}}\pm \sigma \left[\text{nPa}·\mathrm{s}·\mathrm{m}\right]$
(i) 20:60:20	0.10 ± 0.041	9.6 ± 3.2	8.0 ± 2.7
(ii) 27:53:20	0.18 ± 0.015	10.6 ± 2.3	7.8 ± 1.7
(iii) 37.5:37.5:25	0.45 ± 0.040	15.0 ± 3.0	7.9 ± 1.6

$\sigma$, standard error of the mean.

Figure 6.

Relation between domain radius, $R_{\mathrm{d}}$, and apparent membrane viscosity for composition a at 23°C. There is no correlation between the domain radius and the apparent membrane viscosity at the same composition and temperature. Error bars express mean ± SE.

We also measured the membrane viscosity of the GUV composed of DPPC/DOPC/CHOL = 12:70:18 (red circle in Fig. 5 A), which is just outside the L_d-L_o coexistence phase boundary, close to the tie-line endpoint at 20°C. Since the GUV composed of DPPC/DOPC/CHOL = 12:70:18 is in a single phase, the viscosity measurement was performed using the beads attached to the GUV surface. The obtained membrane viscosity was 8.4 ± 2.2 nPa · s · m at 20°C, which agrees with the membrane viscosity of the L_d phase, ${\eta }_{\text{Ld}}$ = 7.9 ± 0.2 nPa · s · m, obtained from the apparent membrane viscosities in the phase-separated region using Eq. 1. This also indicates that the composition of the L_d phase determines the viscosity of the GUV in the phase-separated region and that the membrane viscosity obtained by the bead-based method is consistent with that obtained by domain-based methods. Hereinafter, we discuss the temperature dependence of the membrane viscosity of ternary GUVs in the phase-separated region using ${\eta }_{\text{Ld}}$.

Membrane viscosity of the ternary GUV in the phase-separated region

The obtained ${\eta }_{\mathrm{m},\text{demix}}$ was converted to ${\eta }_{\text{Ld}}$ using Eq. 1, and we show the temperature dependence of ${\eta }_{\text{Ld}}$ in Fig. 7. At each temperature, the obtained ${\eta }_{\text{Ld}}$s for the GUVs with compositions a, b, and c have almost the same values. This indicates that the L_d phase has almost the same composition at each measurement temperature, although the compositions are not on the same tie line at any measurement temperature. Previous study shows that the compositions of the L_d phase at 20°C are DPPC/DOPC/CHOL = ∼21:61:18 for composition a and DPPC/DOPC/CHOL = ∼19:62:19 for compositions b and c (57), which is consistent with the present study. Near the phase separation temperature $T_{\text{misc}}$, the membrane viscosity of the ternary GUV above $T_{\text{misc}}$ is six times larger than that of the L_d phase. We also displayed the temperature dependence of the membrane viscosity of a binary GUV composed of DPPC/CHOL = 1:1 (molar ratio), ${\eta }_{\text{DPPC}/\text{CHOL}=1:1}$, and that of a single-component GUV composed of DOPC, ${\eta }_{\text{DOPC}}$, in Fig. 7. DPPC/CHOL = 1:1 and DOPC are the minority and majority components of the L_d phase, respectively. The obtained ${\eta }_{\text{DOPC}}$ at 23°C was consistent with that in the literature (41). The temperature dependence of ${\eta }_{\text{DPPC}/\text{CHOL}=1:1}$, ${\eta }_{\text{Ld}}$s of compositions a, b, and c, and ${\eta }_{\text{DOPC}}$ shown in Fig. 7 are fitted with ${\eta }_{\text{Ld}}=A\exp \left(B/T_{\text{abs}}\right)$, where $A$ is the numerical constant, $B$ is the slope of temperature dependence of membrane viscosity, and $T_{\text{abs}}$ is the absolute temperature. Slope $B$ of ${\eta }_{\text{DPPC}/\text{CHOL}=1:1}$, ${\eta }_{\text{Ld}}$s of compositions a, b, and c, and ${\eta }_{\text{DOPC}}$ are $B=1.6\times {10}^3$, $2.2\times {10}^3$, $2.2\times {10}^3$, $1.8\times {10}^3$, and $9.1\times {10}^3$ 1/K, respectively. The temperature dependence of the weighted average of the membrane viscosities of DOPC and the DPPC/CHOL complex for composition a is expressed by ${\eta }_{\text{Ld}}=\left(x_{\text{DOPC}}^{\text{Ld}}{\eta }_{\text{DOPC}}+x_{\text{DPPC}/\text{CHOL}}^{\text{Ld}}{\eta }_{\text{DPPC}/\text{CHOL}}\right)$, where we assume that the L_d phase is composed of DOPC and the DPPC/CHOL complex. Using the estimated molar fraction of each component for composition a from small-angle neutron scattering (SANS) measurement (details are described in supporting material S3), we obtained the slope $B=1.7\times {10}^3$ 1/K (black solid line in Fig. 7), which is close to that of ${\eta }_{\text{Ld}}$ of composition a, $B=2.2\times {10}^3$ 1/K. However, the value of the weighted average of the membrane viscosity does not agree with the value of ${\eta }_{\text{Ld}}$ of the ternary GUV obtained experimentally (Fig. 7). This discrepancy is discussed in the membrane viscosity of the ternary GUVs in the phase-separated region section.

Figure 7.

${\eta }_{\text{Ld}}$s for compositions a, b, and c, ${\eta }_{\text{DOPC}}$, and ${\eta }_{\text{DPPC}/\text{CHOL}=1:1}$ as a function of the temperature. Solid lines denote the fitting results by ${\eta }_{\text{Ld}}=A\exp \left(B/T_{\text{abs}}\right)$, where $A$ is the numerical constant, $B$ is the slope of the temperature dependence of membrane viscosity, and $T_{\text{abs}}$ is the absolute temperature. The temperature dependence of ${\eta }_{\text{DOPC}}$ has a steep slope compared to the other compositions. The black solid line and dashed line denote the calculated ${\eta }_{\text{Ld}}$ by simply taking the weighted average of the DPPC/CHOL complex and DOPC and the MH model, respectively. The error bars express mean ± SE.

Discussion

Differences in membrane viscosity by measurement methods

By introducing the bead-based method, we are now able to study the difference in membrane viscosity obtained by our method and other methods using DOPC single-component vesicles. It has been reported that the same lipid vesicles have different membrane viscosities depending on the measurement method. Faizi et al. summarized the membrane viscosities of DOPC at 25°C measured by various methods (41). The viscosities obtained from the lifetime or spectra of the fluorescence molecules embedded in the lipid membrane are in the range of 0.15–0.84 nPa · s · m (62,63,64). On the other hand, the viscosities determined from the response of the membrane to external forces such as electric field (41) or point force (this study) are about 4–5 nPa · s · m, which is an order of magnitude larger than the viscosity obtained by the fluorescence methods. Since the membrane viscosities obtained from the fluorescence methods are derived by the interaction of the fluorescence molecule with the surrounding molecules, the viscosities are based on the responses at local (nanometer-scale) and short (nanosecond) timescales. In contrast, the external force methods evaluate the membrane viscosity from the membrane deformation or membrane flow on a micrometer length scale that occurs in a few seconds. Thus, the former is useful for evaluating diffusion behavior at the molecular level, while the latter evaluates the fluidity of the whole GUV. Therefore, it is important to choose the measurement method according to the time and spatial scales of interest and to compare membrane viscosities using the same measurement method.

Membrane viscosity of the ternary GUVs above phase separation temperature

We estimated ${\eta }_{\mathrm{m},\text{mix}}$ of the ternary GUV by the MH model (54), expressed by

$${\eta }_{\mathrm{m},\text{mix}}=\left(x_{\mathrm{A}}{\eta }_{\mathrm{A}}+x_{\mathrm{B}}{\eta }_{\mathrm{B}}\right)\left(1-2\frac{\Delta H^E}{RT}\right)$$ (3)

where components A and B refer to DOPC and the DPPC/CHOL = 2:1 complex, respectively; $x_i\left(i=\mathrm{A},\mathrm{B}\right)$ is the molar fraction of the $i$ component in the GUV; and ${\eta }_i$ is the viscosity of the $i$ component (details are described in supporting material S2). The excess mixing enthalpy of two components $\Delta H^E$ is given by

$$\Delta H^E=x_{\mathrm{A}}{x}_{\mathrm{B}}\mathrm{\Omega }$$ (4)

using the average gain in potential energy by forming A and B pairs in the solution, $\mathrm{\Omega }$. The average gain in potential energy is expressed by

$$\mathrm{\Omega }=z{\omega }_{\text{AB}}$$ (5)

using the number of neighbor sites, $z$, and the interaction parameter between DOPC and the DPPC/CHOL complex given by ${\omega }_{\text{AB}}$. When the interaction parameter of the DPPC/CHOL complex and DOPC pair is approximated by the interaction parameter of the DPPC and DOPC pair in the mixed state, ${\omega }_{\text{DOPC}/\text{DPPC}}=294$ J/mol (65,66), lipids are hexagonally packed in the two-dimensional membrane, $z=6$, and the membrane viscosity of the GUV with composition a at 35°C (above the phase separation temperature) is calculated by the MH model using the values of $x_{\text{DOPC}}=0.4$, $x_{\text{DPPC}/\text{CHOL}=2:1}=0.6$, ${\eta }_{\text{DOPC}}=0.56\pm 0.35$ nPa · s · m, and ${\eta }_{\text{DPPC}/\text{CHOL}=2:1}=51.0\pm 6.9$ nPa · s · m obtained from experiments. Here, the molar ratio of the DPPC/CHOL complex is assumed to be 2:1 according to their ratio in the GUV composition. The calculated membrane viscosity is 20.1 $\pm$ 2.7 nPa · s · m, which agrees well with the measured membrane viscosity 21.6 ± 2.4 nPa · s · m, suggesting the validity of MH model for describing the membrane viscosity of DPPC/DOPC/CHOL ternary GUVs.

Membrane viscosity of the ternary GUVs in the phase-separated region

Next, we discuss ${\eta }_{\text{Ld}}$ in the ternary GUV with composition a based on the MH model (54), where we assume that the L_d phase is composed of DOPC and the DPPC/CHOL complex. From the SANS measurements, the composition of the L_d phase at 19°C is obtained as DPPC/DOPC/CHOL = 20:70:10, indicating that the DPPC/CHOL molar ratio is 2:1 (details are described in supporting material S3). This DPPC/CHOL molar ratio increases with increasing temperature (DPPC/CHOL = 3:1 at 32°C). Since it is difficult to obtain the stable GUV composed of DPPC/CHOL = 2:1 or 3:1, we approximated ${\eta }_{\text{DPPC}/\text{CHOL}=2:1\text{or}3:1}$ by the membrane viscosity of binary GUVs composed of DPPC/CHOL = 1:1, ${\eta }_{\text{DPPC}/\text{CHOL}=1:1}$, that form stable GUVs. Therefore, ${\eta }_{\text{Ld}}$ is approximated by

$${\eta }_{\text{Ld}}\approx \left(x_{\mathrm{A}}^{\text{Ld}}{\eta }_{\mathrm{A}}+x_{\mathrm{C}}^{\text{Ld}}{\eta }_{\mathrm{C}}\right)\left(1-2\frac{\Delta H^E}{RT}\right)$$ (6)

where components A and C refer to DOPC and the DPPC/CHOL = 1:1 complex, respectively. As shown in Fig. 7, ${\eta }_{\text{Ld}}$ decreases with increasing temperature with the slope of $B=2.2\times {10}^3$ 1/K. Since ${\eta }_{\text{Ld}}$ is described by Eq. 6, the factors contributing to the temperature dependence of ${\eta }_{\text{Ld}}$ are as follows: 1) temperature dependence of the composition of the L_d phase, $x_{\text{DOPC}}^{\text{Ld}}$, and $x_{\text{DPPC}/\text{CHOL}=1:1}^{\text{Ld}}$ and 2) temperature dependence of membrane viscosity, ${\eta }_{\text{DOPC}}$, and ${\eta }_{\text{DPPC}/\text{CHOL}=1:1}$. Note that since $z=6$ and ${\omega }_{\text{AC}}=294$ J/mol do not depend on the temperature, the effect of the interaction term on the temperature dependence of ${\eta }_{\text{Ld}}$ is negligible. These observations indicate that the decrease in ${\eta }_{\text{Ld}}$ with increasing temperature is determined by the composition of the L_d phase and membrane viscosities of DOPC and the DPPC/CHOL complex.

Here, we consider the absolute value of ${\eta }_{\text{Ld}}$. As shown in Fig. 7, the slope of the plot of ${\eta }_{\text{Ld}}$ against temperature in the phase-separated region is explained by the temperature dependence of the weighted average of the membrane viscosities of DOPC and the DPPC/CHOL complex (Fig. 7, black solid line), whereas the value of the weighted average membrane viscosity does not agree with the experimental value of the ternary GUV, ${\eta }_{\text{Ld}}$. When the interaction parameter between DPPC and DOPC, ${\omega }_{\text{DPPC}/\text{DOPC}}$ = 294 J/mol, is introduced instead of that between the DPPC/CHOL complex and DOPC, the calculated ${\eta }_{\text{Ld}}$ using the MH model, Eq. 6, becomes closer to the measured value, as shown by the dashed line in Fig. 7. Therefore, it is suggested that the interaction parameters between components need to be taken into account based on the MH model rather than simply superimposing the membrane viscosity of each component. The difference between the experimental results and the theoretical prediction is mainly attributed to the assumption that the L_d phase is represented as a binary system composed of DOPC and the DPPC/CHOL complex, where the membrane viscosity of the DPPC/CHOL complex is approximated by that of DPPC/CHOL = 1:1 GUVs and the interaction parameters are represented by the interaction parameters between DPPC and DOPC.

In this study, the membrane viscosity of ternary GUVs was measured above the phase separation temperature and in the phase-separated region, and we found that phase separation causes a drastic decrease in membrane viscosity. The L_o domain area fraction dependence of the apparent viscosity of phase-separated ternary GUVs with L_o domains, ${\eta }_{\mathrm{m},\text{demix}}$, obeys the Einstein viscosity equation for two-dimensional fluid, indicating that ${\eta }_{\mathrm{m},\text{demix}}$ is governed by the viscosity of the L_d phase. The membrane viscosities obtained in this study can be described by the MH model both above the phase separation temperature and in the phase-separated region, indicating that the dramatic decrease in the membrane viscosity near the phase separation temperature is due to a significant change in the membrane composition, which governs the membrane viscosity.

While this study succeeded in obtaining the temperature dependence of the ternary GUVs and showed that this could be explained by the MH model, there were some limitations. Firstly, in applying the MH model describing the viscosity of a binary fluid to our DPPC/DOPC/CHOL ternary system, we assumed that DPPC and CHOL form a complex. Secondly, in the description of the MH model in the phase-separated region, the complex of DPPC/CHOL = 2:1 or 3:1 was approximated by that of DPPC/CHOL = 1:1, as stable GUVs composed of DPPC/CHOL = 2:1 or 3:1 were not obtained in this temperature range.

Conclusion

The membrane fluidity plays an important role in regulating cellular functions. According to the lipid raft model, in the cell membrane, the lipid bilayer forms L_o domains in which specific proteins relevant to cellular functions, such as signal transduction, cell recognition, protein sorting, and other processes, are localized (1,2,3,4,5,6,7). The phase separation of the cell membranes is expected to play important roles in regulating not only the distribution of specific proteins but also their mobility. To reveal the effect of L_o domain formation on the membrane fluidity, we systematically measured the membrane viscosity of ternary GUVs composed of DPPC, DOPC, and CHOL. The membrane viscosity of the ternary GUVs abruptly decreases by the L_o domain formation, as the apparent membrane viscosity is governed by that of the L_d phase below the phase separation temperature. The membrane viscosity both above the phase separation temperature and in the L_d phase in the phase-separated region are well described by the MH model, which indicates that the membrane viscosity is determined by the membrane compositions, viscosity of pure membrane components, and interaction between membrane components. The drastic decrease of the membrane viscosity by L_o domain formation should be a great advantage for lipid rafts in regulating the traffic of lipids and proteins. The lipid raft model remains controversial because there has been no success in observing them due to their submicron size. Although we need further basic studies for the nanometer-sized lipid rafts, we believe our study brings new insights into the lipid raft model.

Acknowledgments

The SANS experiments were performed using the instrument C1-2: SANS-U at JRR-3M under the approval of the Neutron Scattering Program Advisory Committee of the Institute for Solid State Physics, the University of Tokyo (proposal numbers 7605, 9586, and 10610). This work was supported by the Japan Society for the Promotion of Science Grant-in-Aid for Scientific Research (grant number JP23K25834).

Author contributions

Y.S. designed the research. J.T. carried out the membrane viscosity measurements. Y.S. carried out the SANS measurements. K.H. analyzed the experimental data. N.U. constructed a calculation program for the form factor of SANS profiles obtained at the matching contrast condition. Y.S. wrote the manuscript with support from M.I.

Declaration of interests

The authors declare no competing interests.

Editor: Frederick Heberle.

Supporting citations

References (67,68,69,70,71,72,73,74,75,76,77,78,79,80) appear in the supporting material.