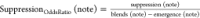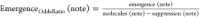Deep Learning for Odor Prediction on Aroma-Chemical Blends

Abstract

The application of deep-learning techniques to aroma chemicals has resulted in models that surpass those of human experts in predicting olfactory qualities. However, public research in this field has been limited to predicting the qualities of individual molecules, whereas in industry, perfumers and food scientists are often more concerned with blends of multiple molecules. In this paper, we apply both established and novel approaches to a data set we compiled, which consists of labeled pairs of molecules. We present graph neural network models that accurately predict the olfactory qualities emerging from blends of aroma chemicals along with an analysis of how variations in model architecture can significantly impact predictive performance.

Introduction

Carefully designed fragrances and flavors appear everywhere in our daily lives, like in our food, drinks, and hygienic products. However, designing fragrant molecules is a laborious and time-consuming process. The forefront of quantitative olfactory research has been the hunt for new and explicable features used in the prediction of perceived olfactory descriptors.

Prior to the application of graph neural networks (GNNs) to odor prediction, researchers featurized aroma chemicals based on specific molecular structures, like aromaticity and the presence of certain functional groups.^1,2 These approaches achieved decent success on benchmarks like the DREAM Olfactory Challenge.² Contemporary deep-learning methods^3,4 which operate on data-intensive graphical or plain text representations of molecules⁵⁻⁸ have led to improvements across drug discovery, material development, molecular property prediction, and de novo molecular design.⁹⁻¹² Recently, Lee et al.¹³ used GNNs to predict aroma labels with high accuracy and precision, building a “Principal Odor Map” from the underlying vector-embedding representations for each molecule.

Despite these breakthroughs in single-molecule understanding, the nonlinear results of aroma-chemical blending remain difficult to predict.¹⁴Figure 1a,b illustrates the nonlinear relationship between constituent aroma chemicals and the overall blend. We adapt contemporary deep-learning methods and apply new techniques to capture and understand these relationships at the blend level.

Figure 1.

(a,b) Data sets—nonlinear relationship between the qualities of constituent aroma chemicals and the overall blend. (c,d) Models—(c) MPNN-GNN for the single-molecule trained model and (d) MPNN-GNN for the mixture model.

The contribution of this work is 2-fold: first, we present a carefully compiled odor mixture data set with both single-molecule and blend-level perceptual descriptors; second, we present a set of publicly available GNN-based models to predict these labels and structure the underlying embedding space. We also present a number of selected experiments which showcase the efficacy of our approach, namely, the capability of our models to transfer from blend prediction to single-molecule prediction and vice versa.¹⁵ Given the predominantly proprietary nature of research using GNNs in chemistry, it was necessary to explore a variety of architectures to obtain these results.

GNN Models

Message-Passing Neural Networks¹⁶

Message-passing neural networks (MPNN) models aim to capture the relationship between neighboring nodes, which has been shown to yield excellent results on molecular property prediction benchmarks. Consider a graph G, where each node v has associated features x_v, representing atomic properties such as formal charge and hybridization. The edges between nodes, defined by e_vw, capture bond-related features, including bond order and ring membership.

The forward pass consists of a message-passing phase and a readout phase. The message-passing phase is characterized by two functions: message functions M_t and vertex update functions U_t, where t refers to the time steps for which message passing occurs. Each node is updated based on the messages from neighboring nodes. When the node h^t_w sends a message to neighboring node h^t_v, it takes into account both the node and edge attributes h^t_w and e_vw. Formally, this can be written as

where N(v) denotes the neighbors of node v in graph G. The readout function R computes a feature vector for the entire graph

where the message functions M_t, vertex update functions U_t, and the readout function R learned differentiable functions. Notably, the readout function R, which operates on the set of node states, must be permutation-invariant. Figure 1c,d provides a graphical representation of the MPNN-GNN model for single molecules and mixtures, respectively.

Graph Isomorphism Network¹⁷

This framework is inspired from the Weisfeiler–Lehman (WL) graph isomorphism test, which distinguishes graphs by iteratively updating node features through injective aggregation. A GNN can match the WL test’s discriminative power if its aggregation scheme is sufficiently expressive to model injective functions. In order to obtain strong representational power, GNNs must aggregate distinct multisets into unique representations. The Graph Isomorphism Network (GIN) accomplishes this, demonstrating that its power equals that of the WL test. The graph isomorphism problem remains challenging, but the GIN effectively captures the uniqueness of graph structures for practical tasks. If ϵ is a learnable parameter or a fixed scalar, then, the GIN updates node representations as

where N(v) denotes the neighbors of the node.

GIN node embeddings can be used for node classification and link prediction. For graph classification, a “readout” function aggregates embeddings across iterations, refining subtree representations as iterations increase. To utilize structural information from all depths, features from every iteration are combined by using a Jumping Knowledge architecture, improving generalization. This aggregation can be represented as

Results

Data Set Characteristics

To build the blended pair data set, molecular structures (SMILES) and odorant labels were gathered from the GoodScents online chemical repository.¹⁸ While the GoodScents Web site cataloged ∼3.5k individual molecules, each aroma chemical’s page suggested complementary odorants (called “blenders”) which, when mixed together, yielded distinct aromas. Molecule pages often contained more than 50 such recommendations, enabling us to gather over 160k molecule-pair data points.

We built an adaptive Web crawler that parsed the names, olfactory labels, and recommended blenders for all odorants across GoodScents using the Python package BeautifulSoup. Non-aroma-chemicals odorants, like essential oils and flavor extracts, were filtered out. Across the database, 0.05% of entries lacked SMILES or contained malformed structures. These entries were dropped.

The data set generated contains discrete labels for 109 olfactory notes, which we standardized. There were no data available for relative concentrations in the blends. Some entries contained pairs with no labels (marked as “No odor group found for these”), and these nonlabeled pairs were removed. Additionally, “anisic” was substituted with the more common “anise”, “medicinal,” (with a trailing comma) was adjusted to “medicinal”, and “corn chip” was replaced with “corn”. These modifications led to a final set of 104 notes.

This data set is one of the first of its kind for blends of aroma chemicals and by far the largest of any publicly available machine-olfaction data set. While there are data sets of aroma-chemical blends with concentrations,¹⁹⁻²¹ they lack descriptive labels. On the other hand, though the GoodScents¹⁸ and Leffingwell²² data sets contain continuous ratings, they only cover single molecules. The ideal data set in this domain would consist of many blended aroma chemicals with varying concentrations, labeled by a panel of human experts on continuous descriptors. Nothing like this is publicly available, although they likely exist in some proprietary form within major flavor and fragrance houses.

Further complicating this data scarcity is the fact that there is no universal, canonical set of odor descriptors. Previous works have used sets of 138 labels,²³ 131 labels,²⁴ and as few as 19 labels.²⁵ Though it is possible to predict ratings on one set of labels from another,^26,27 a canonical set would allow direct comparison between different approaches. Researchers in this domain would need to unify neurological, linguistic, and sociological approaches to olfaction in order to produce this universal descriptor set.^28,29

To examine the transfer learning capabilities of our models, we derived the single odorant data sets from Leffingwell and GoodScents, which were available as a combined data set.³⁰

Figure 2a shows the co-occurrence matrix for the 25 most common descriptors. While the top 15 descriptors (up to “creamy”) all co-occur at least once, the matrix becomes increasingly sparse for less frequent descriptors. The node degree distribution is also examined in Figure 2b. The majority of nodes have hundreds of edges, with the most connected node having 807 edges, while 23 nodes have only a single edge; Figure 2c shows the occurrences of the 25 most common descriptors ordered by their frequency. This frequency (blue, on the left) represents the count of all pairs in which the descriptor appears, and the support set (red, on the right) represents the number of unique molecules across all pairs labeled with that descriptor.

Figure 2.

Data set features for the molecules and their resultant blends. (a) Co-occurrence matrix for the 25 most common descriptors. The co-occurrence values are normalized to sum to 1 for each row and column. The color scale is logarithmic. The top 15 notes (up to “creamy”) all co-occur at least once, but the matrix becomes increasingly sparser for the less frequent elements. The total co-occurrence matrix for all 104 descriptors is available in the Supporting Information section. (b) Distribution of node degree, on a log scale. The majority of nodes have on the order of hundreds of edges, with the most connected node having 807 edges, and 23 nodes have only a single edge. (c) Occurrences for the 25 most common descriptors, ordered by the most frequent notes. The frequency (blue, on the left) for each note is the count of all pairs for which the descriptor appears. The support set (red, on the right) is the number of unique molecules across all pairs labeled with that note.

Data Separation

In order to accurately measure the predictive power of our model, we examined a number of data split techniques. The simplest approach to this task would be to split up the data set by blends, so the 160k molecule-pair data points would be separated uniformly at random. However, this would lead to significant data leakage, as molecules that appeared in training set blends would be components in the evaluation set blends, resulting in a highly overestimated performance metric.³¹

To alleviate this, we attempted to extend the concept of scaffold splits to the multimolecule domain. In short, scaffold splits break the train, test, and validation sets up by the molecular structure, in order to evaluate the model’s ability to transfer to new kinds of molecules.³² As our data set consists of pairs of molecules, enforced separation by constituent components means that models would be evaluated on unseen molecules, not just unseen blends. In order to achieve this separation, the meta graph was carved into two components with the following requirements: first, in order to prevent distribution shift, each component must contain blended pair data points covering every label; second, in order to maximize the amount of useable data, the number of edges between the components (known as the edge-boundary degree) should be minimized, as these data points are thrown out to ensure train/test separation. Efficiently minimizing the edge-boundary degree is NP hard in the general case,³³ although previous research demonstrates that some special cases can be solved in polynomial time.³⁴

Graph Carving

The collection of all molecule pairs in the database forms a metagraph (Figure 4a), where each node is itself a molecular graph, with edges between nodes if there are odor labels for the blended pair.

Figure 4.

Meta-graph backbone consisting of the 15 most used molecules (nodes labeled by CID) and their combinations (edges). This figure is best viewed in color. (a) Aromatic combinations of molecules. Though each molecule has an aroma (node color) of its own, the blend (edge color) may smell different. (b) Graph carving for train/test separation. Using a 50:50 train/test split (node colors) allows the train/test data points (colored dashed edges) to cover similar descriptor distributions but results in some discarded data points (solid gray edges).

We carved the meta graph by randomly partitioning the set of molecules into train and test splits. The carving algorithm was repeated until we generated a carving with at least one train and test data point for every label. We decided to optimize the number of useable data points rather than the similarity between the components. While raising the training fraction would result in less discarded data points, it would be impossible to carve a test set of molecules that covered all labels. Uneven splits also exacerbated the label imbalance issue, such that less even splits had larger Kullback–Leibler divergences between the label distributions of the train and test sets with each other, and the data set as a whole (Figure 5).

Figure 5.

Kullback–Leibler similarity for label distributions between carved train/test components and the full data set. Similarity is calculated using KL(P∥Q) = exp(−KL_divergence(P∥Q)) which quantifies how much information is lost when approximating one distribution with another. To avoid distributional shift, only carvings very close to 50:50 are useable.

Because we aimed to maximize the number of useable labels and minimize the distribution shift, we selected a 50:50 split (Figure 4b). Though it would be possible to focus on carvings which minimize label imbalance, this would reduce the total number of useable data points.

This carving procedure resulted in a final data set with 44,000 training pairs and 40,000 test pairs, discarding 83,000 data points to satisfy the separation requirements. Out of the 109 odor labels, only 74 appeared across enough molecules to be carved. We attempted 250k further carvings but never found one that covered more labels. While better carvings would result in more total data points, it is unlikely that a carving that covers more labels exists.

Note Canonicalization

There are labels that are difficult to predict because they appear across multiple structural classes. “musk” is one such label, and though “floral musk” and “soft musk” are frequently used to distinguish between different kinds of “musky” odors, difficulty arises when “musk” is used directly as a note, instead of as a family of notes. Researchers and perfumers may benefit from using labels specific to each structural class. Future work could task a panel of experts to determine if two molecules, both labeled “musk”, come from the same or different structural class. If “musks” from different classes are easily separable, then new descriptive words are called for.

As shown in Table 1, there were 11 notes that were strict subsets of other notes, i.e., they exclusively linked to a parent note, while there were 3 notes as shown in Table 2 that existed independently.

Table 1. Notes That Occurred Exclusively in Association with a Parent Note.

dependent note	parent note	frequency
estery	fruity	739
cherry	floral	443
toasted	butterfly	218
juicy	sulfurous	185
tomato	vegetable	138
tobacco	nutty	101
potato	vegetable	51
celery	lactonic	34
lactonic	celery	34
dusty	fruity	32
tarragon	anise	28

Table 2. Isolate Note with the Frequency.

isolate note	frequency
ammoniacal	9
salty	1
hay	2

Descriptor Patterns

In order to numerically measure the influence of constituent notes on the odor of the blend, we calculated the Jaccard coefficient between the labels of the molecules prior to combination and the labels of the final blend. If blending follows additive mixing, then the final blend would resemble the union of molecular labels. On the other hand, if blending follows subtractive mixing, the final blend would be closer to the intersection of molecular labels. Through analysis, we found low Jaccard coefficients observed for both methods of combination. Utilizing the set union resulted in a Jaccard coefficient of 0.12, while employing the set intersection resulted in a Jaccard coefficient of 0.24.

It is not possible to simply examine the individual labels of the constituents and predict how the blend will smell. We observed the emergence of notes that did not appear in either molecule and the suppression of notes that appeared across both constituent molecules. On average, 0.2 notes emerged, and 1.2 notes became suppressed in the blend.

In order to capture which notes were more likely to emerge or be suppressed, we calculate the odds ratio for these occurrences for every note. Let:

• Blends (note) be the number of blends a note appears in

• Molecules (note) be the number of molecules a note appears in.

• Suppression (note) be the occurrences when the note appears in either molecule but not in the blend, across every blend.

• Emergence (note) be the occurrences when a note appears in the blend but not in either constituent molecule.

Because a descriptor can appear in the blend if it appeared in the individual molecules and was not suppressed, or if it emerged

• 

• 

The table containing all suppression and emergence odds ratios is available in the Supporting Information. Tables 3 and 4 present the top and bottom five notes for suppression and emergence, respectively.

Table 3. Suppression Odds Ratio for Notes (Top 5 and Bottom 5).

note	suppression odds-ratio
alliaceous	0.892
floral	0.963
fruity	1.17
sulfurous	1.60
moldy	1.62
peach	1010
fresh	1300
mushroom	1460
juicy	1640
celery	1840

Table 4. Emergence Odds Ratio for Notes (Top 5 and Bottom 5).

note	emergence odds-ratio
woody	0.022
honey	0.023
sulfurous	0.024
green	0.038
fruity	0.043
celery	16.0
eggy	19.0
juicy	45.2
malty	50.0
cabbage	54.5

There were 32 notes that never appeared through emergence, including “vanilla”, “musk”, “camphoreous”, and “coconut”.

The emergence odds-ratio quantifies additive or synergistic interactions. The suppression odds ratio, on the other hand, captures the likelihood of one odor note being masked or diminished in a blend and highlights the antagonistic interactions. Both of these metrics together describe how molecular interactions influence perceptual outcomes. Perfumers could benefit from studying these odds ratios, as they may observe unpleasant emergent notes, like “eggy” and “cabbage”, which cannot be predicted simply by examining all components. They may also be surprised to see some notes, like “peach” or “fresh”, disappear from the final composition, even though they were explicitly included in the blend through aroma chemicals.

There were other notable patterns in the odor descriptors. First, a number of notes occurred only in conjunction with more frequent notes (Table 1). Second, there were three isolated notes that only appeared on their own (Table 2).

Models

We trained a variety of GNN models for predicting the blended odor labels from the structures of pairs of aroma chemicals. These models were derived from two primary architectures. First, we extended the popular GIN¹⁷ based model, to generate embeddings for each molecule in a pair. We combine these individual molecule embeddings during the final pair prediction step. Second, we trained several variations on the MPNN inspired by Lee et al.²³ Here, the molecular structures for pairs of molecules are grouped into a unified two-component graph before being fed into the message-passing layers. The aggregation layer treats all of the atoms as though they belong to a single molecule. Both architectures generate novel permutation-invariant embeddings such that the ordering of components in the pair does not affect the final predictions.

Blended Pair Prediction

To measure the predicting powers of the various models, we used the area under the receiver operating characteristic curve (AUROC) for each of the 74 odor labels. To compare the results, we took the macroaverage across all test data points. The ROC-AUC 95% confidence interval (t distribution) for 20 trials on the test set for MPNN-GNN and GIN-GNN was 0.7627 ± 0.00467 and 0.7359 ± 0.02218, respectively (95% confidence level). The MPNN models achieved a precision of 0.536 ± 0.001, recall of 0.648 ± 0.004, and accuracy of 93.98% ± 0.01%, while the GIN model achieved a precision of 0.534 ± 0.001, recall of 0.636 ± 0.004, and accuracy of 93.93% ± 0.02%. For context, a naive 0-R model using the mean frequency of each label across all molecules as a constant prediction achieves an AUROC of 0.5 for every label by definition. As a baseline model, we generated 2048-bit Morgan fingerprints (MFP) with radius = 4 for each molecule in a pair, which were concatenated and then used as input for a support vector machine (SVM) which predicted the blended pair’s labels. We also attempted to fit a logistic regression and random forest model but found that the SVM predicted the descriptors most accurately. See Tables 5 and 6.

Table 5. Top 10 Predicted Labels by the Model^a.

label	MPNN-GNN	GIN-GNN	logistic regression	SVM	random forest
acidic	0.98	0.99	0.94	0.88	0.89
honey	0.95	0.97	0.98	0.98	0.88
mossy	0.94	0.97	0.94	0.99	0.77
sour	0.99	1.00	0.80	0.95	0.49
vanilla	0.98	0.92	0.97	0.98	0.93
amber	0.95	0.96	0.86	0.94	0.91
coffee	0.94	0.92	0.88	0.96	0.78
buttery	0.95	0.93	0.83	0.93	0.81
fresh	0.91	0.90	0.92	0.98	1.00
chocolate	0.95	0.81	0.97	0.96	0.54

^aFor the other labels, please refer to Table S1 of the Supporting Infomation section

Table 6. Bottom 10 Predicted Labels by the Model^a.

label	MPNN-GNN	GIN-GNN	logistic regression	SVM	random forest
dairy	0.56	0.43	0.12	0.69	0.49
earthy	0.37	0.42	0.44	0.50	0.44
orris	0.29	0.46	0.45	0.33	0.49
cocoa	0.57	0.56	0.29	0.53	0.50
rummy	0.56	0.45	0.47	0.41	0.50
tropical	0.52	0.55	0.45	0.55	0.49
bitter	0.45	0.17	0.58	0.50	0.47
cooling	0.35	0.33	0.58	0.42	0.50
musty	0.62	0.57	0.48	0.41	0.56
sweet	0.58	0.17	0.65	0.42	0.57

^aFor the other labels, please refer to Table S1 of the Supporting Infomation section.

While the GIN-GNN model predicts some labels very accurately, it significantly underperforms the random baseline on other labels. On the other hand, the MPNN-GNN model performs consistently across all labels. One of the easiest descriptors to predict was “alliaceous” (garlic), reflecting previous work²³ which suggested that this note straightforwardly correlated with the presence of sulfur in the molecule. Unlike in previous work, our models accurately predicted the label “musk”, which is normally difficult to predict, as it occurs across many different structural classes of molecules. However, direct comparison between benchmarks is not straightforward, as previous work predicted continuous ratings for odor, and our data set contains discrete labels. There were some descriptors (like “orris” and “earthy”) which none of the models were able to accurately predict. The Morgan fingerprint model did outperform our models on occasion, likely due to the hand-crafted nature of these fingerprints, which explicitly incorporate structural details like functional groups and steric effects that our model must implicitly learn from our data set.

Single-Molecule Prediction

We also measured the performance of our models on the single-molecule prediction task. To adapt the GIN-GNN model to this task, we generated graph-level embeddings for each molecule and trained a logistic regression classifier to predict the same 74 odor labels. Because the graph-level and original pair-level embeddings were of different dimensionalities, the MLP portion of the architecture could not be transferred. For the MPNN-GNN, the only modification necessary was inputting a single molecule instead of a pair of molecules into the passing phase. The entire trained architecture was able to be reused. On the single-molecule task, the MPNN-GNN achieved a mean AUROC score of 0.888, while the GIN-GNN and Morgan fingerprint models achieved scores of 0.852 and 0.821, respectively.

The significant improvement of all models on the single-molecule prediction task as compared to the blended pair task suggests that the former task is much harder than the latter. We hypothesize that the widened gap between the MPNN-GNN and the GIN-GNN on this task is due to the fact that the GIN-GNN’s prediction layers could not be reused.

Regardless, the descriptor “alliaceous” remained easy to predict across the board, but surprisingly, “musk” was one of the easiest descriptors to predict. In our data set, “musk” molecules, regardless of the structural class, were often combined with each other in blends. This likely produced similar embeddings in our GNN models for the molecules even though they were structurally dissimilar. This provided an advantage over previous work in which models had to learn the olfactory similarity for “musk” molecules from their labels alone. One notable exception was the label “aromatic”, which the GIN-GNN and Morgan fingerprint models failed to accurately predict.

In order to test and identify the best performing models, we performed various sets of experiments on the carved train and test components of the data sets. These experimental procedures are documented in Figure 3. The following steps were done to perform the cross validation:

• 15-fold split and hyperparameter search: we conducted further searches to obtain five train–test split carvings, which were fully separated as above. Because each component had fewer constituent molecules, the number of odor labels that were possible to carve was only the range of 41–44 per fold. We used these 5-fold splits to conduct hyperparameter optimization, hypothesizing that the best models would transfer well to the original 74 label 50:50 carving.
• 250:50 split on the model based on mixture data: In this experiment, we trained 3 MPNN-GNN models, with different random seeds, on the original 50:50 train–test split using the best hyperparameters found. We observed an average AUROC score on the test set of 0.7609 ± 0.00736 (95% confidence level).

Figure 3.

Experiment overview. (a,b) Schema of the experiment. (c) Graph carving schematic.

Discussion

MPNN-GNN Performance

Several experiments were conducted to understand the MPNN-GNN’s performance on individual labels, focusing on the best and worst performing odor labels. MPNN-GNN’s edge conditioning, which passes information along molecular graph edges, offers an advantage over GIN-GNN, which focuses on updating node states based on node features. Our goal was to analyze how model predictions correlated with the co-occurrence patterns of odor descriptors in blended pairs across both the training and test sets. Figure 8 shows the kernel density estimation (KDE) plots of the MPNN-GNN’s most accurate and least accurate predictions on both the single-molecule and blended pair prediction task, alongside the ground-truth values.

Figure 8.

Analysis of odor labels by conducting experiments. (a) KDE plots for top 5 descriptors by predictive accuracy in the training set of the single-molecule task. (b) KDE top 5 single molecules as above, for the test set. (c) KDE plots for bottom 5 descriptors by predictive accuracy in the training set of the single-molecule task. (d) KDE bottom 5 single molecules as above, for the test set. (e) KDE plots for top 5 descriptors by predictive accuracy in the training set of the blended pair prediction task. (f) KDE top 5 blended pairs as above, for the test set. (g) KDE plots for bottom 5 descriptors by predictive accuracy in the training set of the blended pair task. (h) KDE bottom 5 blended pairs as above, for the test set.

Interestingly, the MPNN-GNN’s predictive scores for the top 5 and bottom 5 are not correlated with the descriptors’ occurrences in the training data, contradicting the findings of Lee et al.²³ We conducted detailed analysis for a small set of descriptors which is briefed in the Supporting Information section under the MPNN-GNN Performance section.

From the analysis of the odor mix model, the top five predicted labels provide the following insights: “sour”, “acidic”, “vanilla”, “mossy”, and “cheesy” perform as expected with the highest prediction scores for their respective odor labels. Even their mixture components exhibit a high percentage of these odor labels. For further details, please reference the Supporting Information.

The top 5 predicted labels from the odor mix model analysis reveal that “sour”, “onion”, “meaty”, “alliaceous”, and “roasted” perform as expected, with the highest prediction scores for their respective odor labels. Even their mixture components show a high percentage of these odor labels. However, it is worth noting that odors like “onion”, “alliaceous”, and “roasted” have a second set of odor labels with high co-occurrence in the single-molecules data set. While this strong co-occurrence is not observed in mixture labels, the model predicts them with high scores. This suggests that the model may struggle to prioritize dominant odors in mixtures, often predicting labels of individual components. More sophisticated research from linguists or neuroscientists exploring hierarchies within the odor space³⁵ would allow our models to leverage a hierarchical multilabel classification network.³⁶ In this way, future models could leverage strong predictions on common odors to reduce uncertainty for more scarce labels.

In our analysis, we aimed to address two questions: first, how GNNs capture the relationship between the molecular structure and odor? second, how GNNs combine their underlying models, captured in the embedding space, for individual molecules into blended pairs? To answer the second question, we analyzed the embedding space.

There seems to be semantic spillover across labels with regards to their co-occurrences in both the blended pair and single-molecule tasks. To a certain degree, this is expected, as olfactory labels are often nebulous and overlapping.

Incorporating additional odor-relevant information beyond molecular structure, exploring alternative GNN architectures that better capture non-linear relationships, and refining the olfactory vocabulary are necessary for further research into a definitive olfactory vocabulary, where all descriptors are semantically distinct from each other.^23,37 and could lead to significant improvements. We implemented integrated gradients (IG) as a state-of-the-art attribution technique to enhance interpretability. IG attributes predictions to molecular features by quantifying their contribution along a gradient path from a baseline to the input, providing theoretical guarantees such as sensitivity and implementation invariance. Specifically, we interpret the model at both the node (atom) and edge (bond) levels. Node-level attribution identifies critical atoms contributing to predictions, while edge-level attribution reveals influential molecular bonds. These contributions are normalized for clarity and visualized using RDKit, where color coding highlights the importance of structural features in the molecular graph. When binary aroma blends are mixed, the resulting odor can be dominated by the first aroma, the second, a new aroma, or an odor common to both. Through an explainability analysis, we observed no consistent molecular structure pattern determining odor dominance. Interestingly, the dominance is not always linked to molecules with higher edge and node importance; contrary cases were also observed. Clearly, there is no single representation that describes a particular molecule’s scent. In fact, the mosaic of molecular substructures for an odor descriptor also overlaps, i.e., similar fragments can be found for different perceptual descriptors. It is akin to molecule–receptor interactions in which many parts of a single molecule activate multiple receptors. Additionally, this approach aligns well with chemical intuition, aiding in the validation and design of odorant molecules. Examples can be found in the Supporting Information. The code for this is open-source and is available in the GitHub repository mentioned in the data availability statement.

GIN-GNN Performance

Across both the blended pair and single-molecule prediction tasks, the GIN-GNN underperforms compared to the MPNN-GNN. We hypothesize this is primarily due to a number of differences in the architectures.

First, molecules are fed into the GNNs in different ways. As stated above, the MPNN-GNN applies the message-passing function across the pairs of molecules as if they were a single graph with two disconnected components. The readout layer combines all of the nodes across both graphs simultaneously. From there, additional feedforward layers generate the prediction, and this feedforward neural network can be reused for the single-molecule prediction task. On the other hand, the GIN-GNN generates component embeddings separately and concatenates them together prior to the final feedforward layers. We hypothesize that this leads to weaker underlying representations for component molecules in the GIN-GNN. As shown in the performance comparison in Figure 7a,b, the difference is especially noticeable for the single-molecule prediction task, where a new feedforward network must be trained from scratch. Figure 6a,b shows the ROC values for both GIN and MPNN 5 folds. The AUROC scores of all labels for both the blended pair and the single-molecule trained model tasks are available in the Supporting Information.

Figure 7.

Predictive power of our GNN models and the Morgan fingerprint baseline across all labels with random baseline (dashed line). (a) Blended pair task AUROC scores per descriptor, by the model. (b) Single-molecule task AUROC scores per descriptor, by the model.

Figure 6.

ROC values for both GIN and MPNN 5 folds. The figures show ROC values separately for each fold and also the mean value. (a) ROC value for the GIN model. The colored line shows the mean ROC value. (b) ROC value for the MPNN model. The colored line shows the mean ROC value.

We also propose that the additional information provided by edge conditioning in the MPNN-GNN results in a higher predictive capacity than in the GIN-GNN, which updates the hidden states of nodes based only on the node’s own features.

Finally, we note that the set2set readout method provided better results than simply concatenating the mean and max pooling results of the node-level embeddings.³⁸

Embedding Space

Although the relationship between the odors of individual molecules and the blended pairs in which they occur is nonlinear, previous work has shown that embedding spaces can represent nonlinear relationships with linear transformations.^39,40 Please refer to Figure S2, which illustrates four pairs of molecules, representing different blending outcomes.

In order to explore the relationships between the latent space of individual molecules and that of the blended pairs, we generated three vector embeddings per data point: e₁ (the embedding of the first molecule in the pair), e₂ (the embedding of the second molecule in the pair), and e_p (the embedding of the blended pair), using the MPNN-GNN. To determine if the blended pair embeddings were simply linear combinations of the constituent embeddings, we fit a number of linear regression models, one per pair in the data set

where α₁ and α₂ are constant coefficients. We measured how well the linear regression model fits the relationship using the coefficient of determination (r²). Across all blended pair data points, the average (r²) was 0.47, and the p value for the F statistic is 4.68 × 10^–5  (Figure 9a).

Figure 9.

Scatter-plots of fit-coefficients for predicting the blended pair’s embedding using the GNN embeddings. (a) Scatter-plot of the fit coefficient using the MPNN-GNN model, with zoom on centroid. Notably, the distribution is not centered on the origin. In some cases, the blended pair’s embedding consists of equal combinations of each individual embedding, while in other cases, one particular embedding predominates. (b) Scatter-plot, as above, using the GIN-GNN embedding. The distribution is centered on the origin, suggesting that for many points, neither molecule’s embedding factors into the pair-level embedding. The vertical and horizontal lines represent where one component predominates, but the other molecule is not factored in at all.

The process was repeated with the GIN-GNN, though the component embedding space could not be directly compared due to differing dimensionality, so we reduced the component embedding space to the same dimension as the pair embedding space and fit linear regressors as above. The resultant average r² was 0.021, with a p value for the F statistic of 0.45 (Figure 9b).

This difference in the predictive power of the constituent–blend relationship in the embedding spaces of the MPNN-GNN and the GIN-GNN may explain the differences in model performance. While for the MPNN-GNN, there was a significant portion of the relationship between constituent and blended pairs that could be explained linearly in the embedding space, the GIN-GNN fails to produce an embedding space with the same capability.

This suggests certain, well-structured embedding spaces can represent nonlinear relationships through linear transformations, but it is not guaranteed for any arbitrary model. Though some of this may be due to the dimensionality reduction technique, perhaps the selected readout phase for the MPNN-GNN allows the shape of the embedding space to be preserved. This aligns with previous research, which suggests that slight changes in GNN architecture can significantly affect the embedding space.⁴¹

Notably, for both models, α₁ and α₂ had mixed correlations. While they were often inversely correlated, there were many occasions where they were positively correlated. Though a number of blended pair embeddings were weighted combinations of the constituent molecules, just as often, when the influence of one molecule increased in the blend, the other molecule’s influence decreased or became negative. This may be explained by the odorant receptor-level phenomena of agonism and antagonism, wherein some molecules intensify certain notes when combined, while other molecules may mute each other in combination.⁴² Though previous works have explored combinatorial⁴³ and nonbinding⁴⁴ interactions between odorant molecules and the receptors, a careful study of antagonism is required to get a complete picture of how odorants behave in blends. Future researchers could apply blend-level models across odorant–receptor databases like “M2OR”⁴⁵ to understand these interactions.

Conclusions

By applying deep-learning techniques to a novel data set, we trained a number of models capable of accurately predicting the nonlinear olfactory qualities of aroma-chemical blends while strongly transferring to single-molecule prediction tasks. They are available on GitHub for further exploration.

This is the first public extension of structure–odor relationship prediction to the multimolecule domain. We provide empirical analysis of how certain notes can emerge or become suppressed in blends, though the exact physical and neurological interactions behind these phenomena remain unexplored. Researchers who aim to understand agonistic and antagonistic odor–receptor interactions can leverage our models during ligand discovery. Given the strong performance of our models across a challenging benchmark, perfumers and food scientists can now confidently leverage our GNNs during formulation to reduce unexpected surprises resulting from aroma-chemical combinations. During aroma-chemical discovery, our model can predict how novel odorants interact with commonly used aroma chemicals, reducing churn.

The underlying embedding spaces of our models capture the nonlinear structure of the odor blending. These embeddings translate both additive and subtractive blends into linear transformations. Our exploration of message-passing convolutions and readout techniques demonstrates how architecture choices can affect the usefulness of these embeddings. We showcase some of the intricacies around blending empirically through emergence and suppression odds ratios.

These embeddings have already been used with great success in mixture similarity prediction. This task requires a statistical model to predict the perceptual similarities of two intensity-matched blends, as rated by panels of experts. During the DREAM Olfactory Mixtures Prediction Challenge,⁴⁶ the blend-level embeddings from the GIN-GNN were used as input to an XGBoost model that predicted the ratings and this combination resulted in competition-winning results.⁴⁷

We also introduce a rigorous train/test separation for the multimolecule domain, where the meta graphs of all molecules and blends are partitioned into two separate graphs. Because different research groups use different molecular subsets for evaluation, comparing the relative performance between approaches is infeasible. Our method maximizes the number of useable data points, minimizes label shifts, and can also be used for single-molecule prediction.

In our opinion, the ultimate research goal in machine olfaction is to produce a model capable of predicting continuous labels for blends of many aroma chemicals at varying concentrations. This would mirror the real-life work done by food scientists and perfumers. Unfortunately, well-labeled public olfactory data sets that enable this research remain scarce even for the single-molecule case. Though fragrance companies likely have extensive libraries of blend recipes, these data sets remain proprietary. Our work stands as a proof of concept: one stepping stone from single molecules in-silico to real-world blends. Beyond olfaction, the GNN architectures we present can be leveraged to predict drug–drug pharmaceutical interactions or in alloyed material design.

Data Availability Statement

The source code is available at https://github.com/BioMachineLearning/openpom and https://github.com/Odor-pair/odor-pair. The data is available at https://github.com/odor-pair/odor-pair/tree/main/dataset. The Python scripts of charts and other forms of analysis can also be found on these GitHub repositories. We have also made the data set available in a standardized form in the Pyrfume database https://github.com/pyrfume/pyrfume-data/pull/224

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.4c07078.

• Table of AUROC scores for all labels predicted; combined scatter plot of the regressors for both the MPNN-GNN and the GIN-GNN; and four pairs of molecules, representing different blending outcomes (PDF)

The authors declare no competing financial interest.