Asymmetry in centrosome maturation revealed through AIR-1 dynamics in the early Caenorhabditis elegans embryo

Abstract

Centrosomes are critical organelles associated with the nucleus, consisting of a pair of centrioles surrounded by a cloud of pericentriolar material. They serve as key nucleation sites for microtubule arrays and are essential for positioning the nucleus prior to cell division, but mechanisms for ensuring proper centrosome positioning are not well understood. Previous research has identified asymmetries in microtubule arrays nucleated by centrosomes prior to cell division, including during the first cell cycle in Caenorhabditis elegans, as playing a critical role in centrosome positioning, however the origin of this asymmetry remains unclear. To explore potential sources of centrosome asymmetry, we developed a mathematical model of centrosome maturation, distinct from prior models by not presuming any inherent symmetry or asymmetry. We determined model parameters using in vivo data on the recruitment and recovery of GFP-tagged AIR-1 (Aurora kinase A) in early C. elegans embryos, enabling precise parameter estimation. Our results reveal an intrinsic asymmetry in centrosome dynamics that highlights the potential for variability in physical centrosome characteristics. These dynamics produce highly consistent microtubule arrays, independent of specific structural details. These findings offer novel insights into centrosome behavior and positioning during cell division and early embryonic development.

Introduction

The centrosome, consisting of a pair of centrioles surrounded by a cloud of pericentriolar material (PCM), is the cell’s primary microtubule organizing center^1,2. The centrosome nucleates microtubule arrays within the cytoplasm, which are required for fundamental cellular processes including establishing intracellular polarity, and driving cellular division. Precise regulation of the timing and placement of cellular division is critically important for proper cell fate determination, and defects in centrosome positioning are associated with disease processes including cancer metastasis³. Asymmetries in microtubule arrays are thought to play an important role in centrosome positioning⁴; however, it remains unclear whether this microtubule array asymmetry is related to asymmetries within the centrosomes themselves.

Exploiting the high conservation of centrosome-associated factors, the early embryos of the nematode Caenorhabditis elegans provide an ideal model for investigating potential centrosome asymmetries⁵. During fertilization in the C. elegans zygote, two centrioles are contributed by the sperm along with the paternal pronucleus⁶. These centrioles undergo duplication and maturation, accumulating pericentriolar material (PCM) to form fully functional centrosomes⁷. These developing centrosomes serve as nucleation sites for microtubule (MT) arrays that interact with motor proteins at the cell periphery to position the nucleus prior to cell division⁸. Previous modeling studies have assumed that centrosomes have equal nucleation capabilities, in the absence of conclusive evidence regarding the composition of PCM^9–12. Current research suggests that the PCM may exist in solid, liquid, or gel-like states (a combination of solid and liquid), highlighting the complexity and potential variability in centrosome structure⁵.

In many systems, centrioles possess age-specific markers such as distal appendage proteins, allowing the older (mother) and younger (daughter) centrioles to be segregated to specific cells during division to promote particular cell fates^13,14; inheritance of the mother centriole is linked to stem cell maintenance in the Drosophila germline^15,16 and the developing mouse neocortex¹⁷. In C. elegans embryos, the P-lineage, which gives rise to the germline, undergoes a series of asymmetric divisions, resulting in a larger anterior cell and a smaller posterior germline cell (Fig. 1a). These divisions are critical for development of the worm, as perturbations in the division plane by as little as 10% can be lethal¹⁸. However, it remains unclear whether C. elegans centrioles possess age related markers, and whether the mother and daughter centrioles are specifically segregated during these early asymmetric divisions.

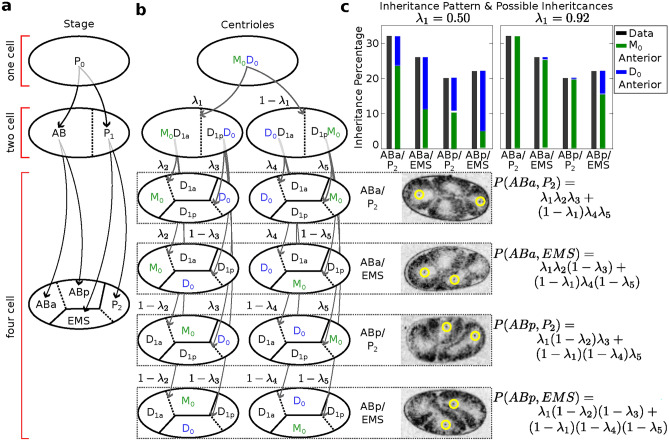
Figure 1.

Ambiguous identity of sperm-derived centrioles at the two and four cell stages. (a) The divisions leading up to the four-cell stage follow the predetermined pattern shown. (b) Schematic of potential inheritance patterns. (c) The inheritance pattern percentages for the four possible observable configurations, represented by the black bars, are not significantly different from a uniform distribution. The black bars correspond to experimental data obtained from 65 embryos, each exhibiting two distinct GFP+ centrioles. The colored bars indicate the potential inheritance patterns for the paternal mother centriole (Green) and paternal daughter centriole (Blue), as determined by different choices for 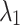. Example images of the four possible distributions of GFP+ centrioles and their associated probabilities are shown.

Previously, our lab demonstrated an asymmetry in the microtubule (MT) arrays nucleated by the two centrosomes in the early C. elegans embryo, which play a crucial role in positioning the pronuclear complex before the first division⁴. The lagging centrosome, inherited by the germline cell, forms a smaller and less dense MT array, an asymmetry which our mathematical model indicated as essential for proper centrosome positioning. To investigate a possible unrecognized asymmetry in the associated centrioles and centrosomes, we characterize the inheritance of paternal centrioles through the first two divisions of the C. elegans embryo and the recruitment and recovery dynamics of centrosome-associated proteins. Using a novel mathematical model of centrosome maturation calibrated and validated by in vivo data, our results reveal potential intrinsic asymmetries in centriole identity and centrosome dynamics, highlighting significant variability in physical centrosome characteristics while still producing similar microtubule arrays. This indicates a high degree of flexibility in centrosome dynamics, enabling consistent and reproducible MT array asymmetry, independent of specific structural details.

Results

Patterns of centriole inheritance

To assess for potential bias in centriole inheritance during the initial divisions of the C. elegans embryo, we tracked SAS-4, a stable core protein specific to centrioles. Using GFP-tagged SAS-4 expressed in paternal centrioles, distinguishable up to the 550-cell stage¹⁹, we crossed males with GFP-tagged SAS-4 with feminized hermaphrodites lacking fluorescence. We then monitored paternal centriole inheritance up to the four-cell stage (Fig. 1a). Due to the visual indistinguishability of the mother and daughter sperm-derived centrioles, there are four observable fluorescence patterns among the eight possible configurations (Fig. 1b). Using these patterns, we constructed a probabilistic model (Eq. 10) to determine the probability of centriole inheritance, 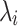, for each division outcome. Imaging 72 embryos revealed two distinct GFP+ centrioles in 65 cases. The most prevalent inheritance pattern, observed in 21 cases (32.3% of observable patterns), is paternal centriole inheritance to the ABa and P2 cells (Fig. 1c), although the overall distribution is not significantly different from uniform according to the Kolmogorov-Smirnov test, consistent with other reports²⁰. A wide range of probability values can produce the same distribution of paternal centriole inheritance, ranging from purely random inheritance of the mother and daughter centrioles (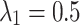) to highly biased and directed inheritance (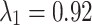) in the first cell division that still results in the same pattern of fluorescence (Fig. 1c).

Centrosomal AIR-1 recruitment

To determine if the observed asymmetry in microtubule (MT) arrays is associated with centrosome asymmetry, we investigate centrosome protein recruitment during the first cell cycle. The movement of centrosomes leading up to the first asymmetric division is highly regulated and controlled by the MT arrays they nucleate. Immediately after fertilization, the centrioles duplicate and initiate MT nucleation, which facilitate the migration of the maternal pronucleus. The pronuclei meet at the posterior end of the embryo and form the pronuclear complex (PNC). The PNC then migrates to the center of the embryo and rotates 90 degrees to align the centrosomes along the anterior-posterior axis, a process known as centration and rotation (C&R), which is crucial for establishing the orientation and position of the division plane for first division (Fig. 2a).

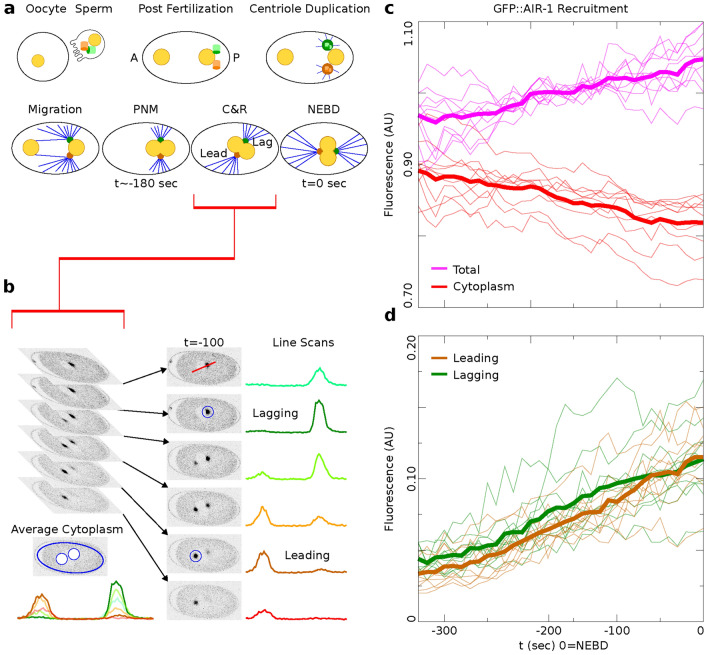
Figure 2.

Recruitment of AIR-1/AURKA revealed by precise quantification of 4D microscopy. (a) C. elegans development steps leading up to the first division. The sperm donates the two centrioles and marks the posterior (P) of the embryo. Centrioles duplicate, and their centrosomes mature during migration, pronuclear meeting (PNM), centration and rotation (C&R), and nuclear envelope breakdown (NEBD). (b) Quantification of the centrosome using the brightest fluorescent signal. Line scans are used to visualize the fluorescence of the centrosomes; circles denote the measured area. (c,d) Individual time courses are plotted (thin lines) and averages (solid lines). (c) The cytoplasm (red) and the total (magenta). (d) The leading centrosome (orange) and the lagging centrosome (green) with mean lagger trajectory significantly higher than the mean leader trajectory (p-value for the difference is 0.0097 as detailed in Results).

AIR-1, a protein homologous to Aurora Kinase A (AURKA), plays a key role in centrosome maturation by regulating the recruitment of pericentriolar material (PCM) proteins via protein phosphorylation. Depletion of AIR-1/AURKA in early C. elegans embryos via RNA interference results in malformed spindles and impaired centrosome maturation^21,22. AIR-1/AURKA also acts to repress microtubule nucleation by activating KLP-7, a kinesin-like protein that inhibits microtubule nucleation at the centrosome²³. Following a quantification and normalization protocol (Materials & Methods, Fig. 2b), we analyze time-lapse microscopy images of centrosomal GFP::AIR-1 fluorescence, allowing us to identify potential asymmetries in centrosomes during the critical positioning period, from pronuclear migration to nuclear envelope breakdown (NEBD). Our analysis reveals that both leading and lagging centrosomes undergo maturation by recruiting proteins such as AIR-1/AURKA, but lagging centrosomes exhibit higher average intensity of GFP::AIR-1 compared to the leaders (Fig. 2d). This observation is confirmed with statistical analysis by fitting a regression model with AR(1) within-subject correlation structure and indicator variable for the centrosome type (leading=0, lagging = 1) as detailed in Materials & Methods. The mean trajectories of the two centrosome types have similar slopes (Wald’s test statistic for the difference in slopes is 1.09 with a p-value of 0.2973) but different intercepts, with the lagging centrosome’s intercept significantly higher than the leader’s intercept (Wald’s test statistic for the difference in intercepts is 6.69 with p-value of 0.0097), indicating that the mean trajectory of the lagger is significantly above the mean trajectory of the leader. Additionally, while the cytoplasmic pool of GFP::AIR-1 decreases over this period, the total amount of GFP::AIR-1 slightly increases (Fig. 2c).

Centrosomal AIR-1 recovery

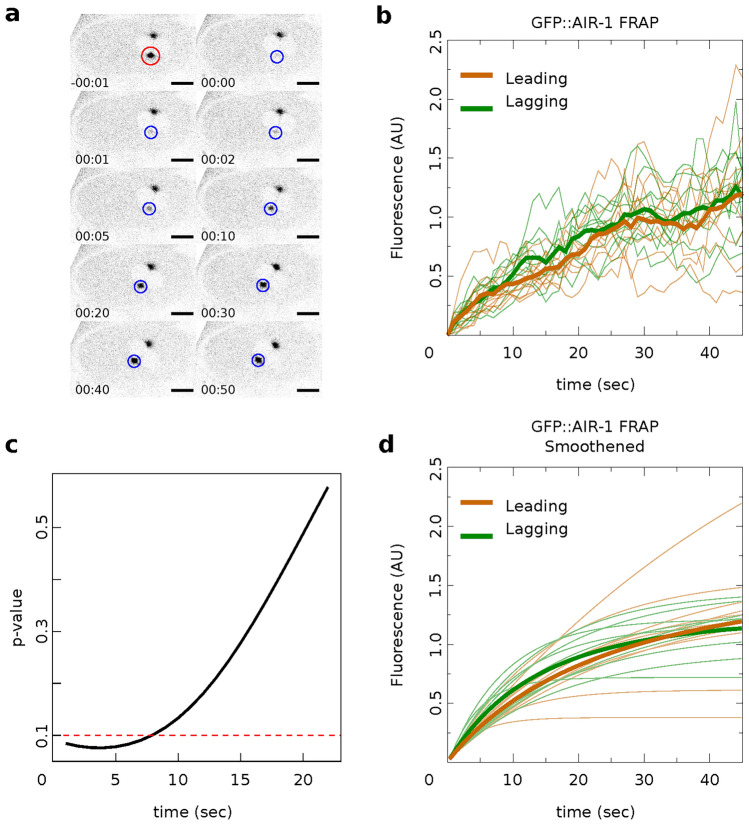
Centrosome maturation and asymmetric recruitment of AIR-1/AURKA discussed above occurs over a long timescale of approximately 330 s. To identify any asymmetries on a faster timescale, we use Fluorescence Recovery After Photobleaching (FRAP) shortly after pronuclear meeting (PNM), a time window not previously explored²⁴. Using the C. elegans strain expressing GFP labeled AIR-1, we photobleached either the leading or lagging centrosome (10 of each) and tracked their recovery until AIR-1/AURKA levels stabilized, approximately 50 s (Fig. 3a). Individual time course data (Fig. 3b) was smoothed by fitting the exponential recovery model as detailed in the Methods. The computed recovery curve parameters indicate similar median values for the maximum recovery amount, 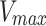(1.5 for the leader and 1.4 for the lagger), and different median values for the half recovery time, 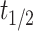(20.2 s for the leader and 15.7 s for the lagger). These values suggest a faster recovery for the lagger, potentially reflecting differences in the initial recovery dynamics (Fig. 3d). This observation is supported by mild statistical significance between the shapes of the average FRAP curves of leader versus lagger centrosomes during the initial period of recovery, assessed using a FRAP-specific statistical procedure.²⁵ As previously discussed,²⁵ testing for differences in specific parameters from fitted FRAP trajectories may be too restrictive to reveal differences in overall shapes of the recovery curves and may overlook biologically relevant differences. Instead, considering p-values from t-tests between means at each time point provides a more flexible method to detect differences in FRAP trajectory shapes. In our case, the p-values increase with time but show mild significance during the initial recovery stage (Fig. 3c), indicating a potential difference between the two centrosomes.

Figure 3.

Recovery of AIR-1/AURKA observed on a short timescale using FRAP. (a) Example image of photobleaching of a single centrosome. Photobleaching was performed shortly after PNM and imaged every second for a total of 50 s (Scale bar: 10 m). (b) Recovery curves (thin lines) and their averages (solid lines) for ten leading centrosomes (orange) and ten lagging centrosomes (green). Measurements were taken from 20 centrosomes (10 leader and 10 lagger) across 20 embryos. (c) p-values for FRAP-specific statistical procedure developed in²⁵. Red line indicates significance level 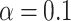. (d) Smoothed version of the data in (b) used to compute p-values in (c).

The model requires distinct centrosomes

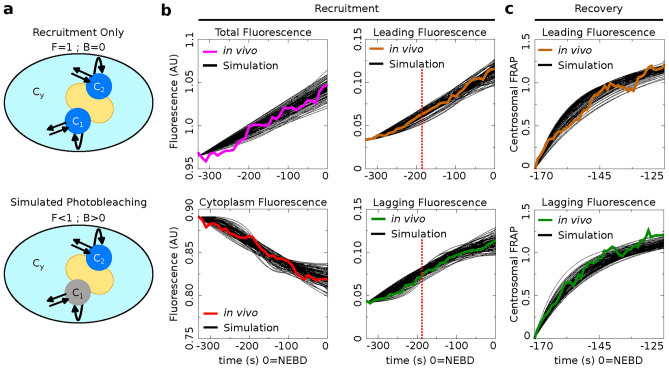
To identify the specific dynamic factors underlying the observed asymmetry over extended time scales, we develop a comprehensive mathematical model of centrosome maturation that avoids bias from assumptions about centrosome identity. Our model consists of three compartments: two representing the centrosomes and a third representing the free supply of the model factor found in the cytoplasm (Fig. 4a). The model incorporates a dynamic cytoplasmic concentration, and centrosomes characterized by cooperativity, carrying capacity, and cytoplasmic flux (Eq. 6). Parameter sets were identified that best fit our in vivo AIR-1/AURKA data²⁶. Model variants that assume the centrosomes have identical kinetics are not able to match the in vivo data as effectively as those model variants that treat centrosomes as distinct compartments (Extended Data Fig. 1), suggesting that the leader and lagger centrosomes have distinct AIR-1/AURKA recruitment dynamics.

Figure 4.

Simulations recapitulate the observed recruitment and recovery dynamics. (a) Schematic of our three-compartment centrosome maturation model and example of photobleaching compartment 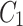. The model factor can transfer from the two centrosome compartments to the cytoplasm compartment as controlled by the model parameters. (b–c) Parameter sets produce simulated curves that match to (b) recruitment and (c) recovery. Red dotted lines indicate the time of PNM, when the FRAP analysis started.

The dynamics of the mathematical model

As the best fit to our model requires us to consider centrosomes as distinct compartments with their own dynamics, we construct three variants of the model representing different interactions to assess their impact on model fit. All three model variants produce comparable parameter distributions, yet the dynamic cytoplasm model consistently demonstrates a twofold reduction in fitting error to the in vivo data (Extended Data Fig. 1, Extended Data Fig. 2).

We continue our investigation with a mathematical model of centrosome dynamics by extending the dynamic cytoplasm model to include fluorescent (F) and bleached (B) versions of the model factor to simulate photobleaching (Eq. 1a–f, Fig. 4a). We identify 112 independent parameter sets that minimize error in simulations of recruitment (Fig. 4b) and recovery dynamics (Fig. 4c).

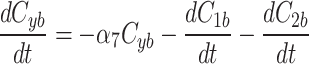1a

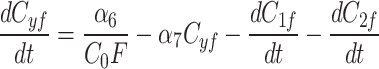1b

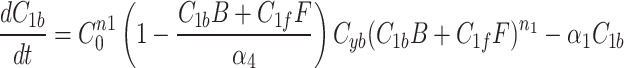1c

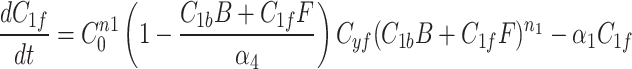1d

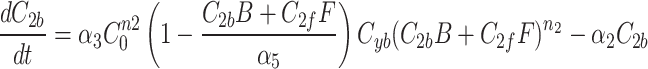1e

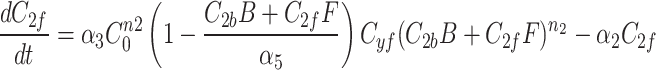1f

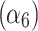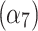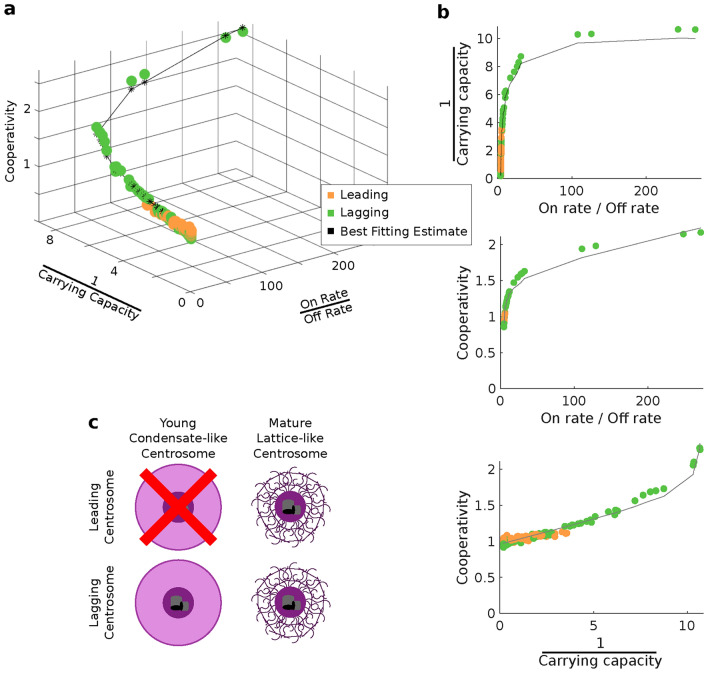
In the cytoplasmic compartment, the on rate and off rate exhibit a remarkably high linear correlation with an 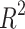value of 0.9995 (Extended Data Fig. 4), indicating tightly regulated protein production and decay dynamics. By fitting these centrosome dynamics parameters to a 3D curve, we achieved precise estimation of cooperativity with minimal error relative to the other parameters of interest (Fig. 5a). Parameters governing the centrosome compartments, specifically cooperativity, inverse of the carrying capacity, and the ratio of the on rate to off rate, also show significant correlations (Fig. 5b). This suggests that the model parameters must be highly constrained in order to replicate dynamics that closely resemble the observed in vivo behavior. In particular, we find that the leader and lagger centrosomes can inhabit distinct regions of the space defined by these three distinct features. The parameter space associated with the leading centrosome compartment appears to be a subset of that associated with the lagging compartment, suggesting that the leading centrosome predominantly exists in an older, lattice-like state, while the lagging centrosome is able to adopt a younger, condensate-like form⁵ (Fig. 5c, Table 1).

Figure 5.

Parameter Analysis reveals tight regulation of simulated centrosome dynamics. (a) 3D plot and (b) of all parameter sets (on rate/off rate, 1/carrying capacity, cooperativity) fit to 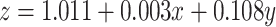with an 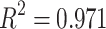and RMSE of 0.040. Best fit estimates correspond to the calculated cooperativity values; see Extended Data Figure 6 for the full surface generated by the best-fit equation. (c) The four possible identities of the leading and lagging centrosome in terms of its centriole age. Our model indicates that the leading centrosome is not found in the younger and condensate-like state.

Table 1.

Comparison of model features using the parameter sets that best fit the experimental data, with the characteristics of different types of centrosome structures as reported in previous studies.⁵.

	Cooperativity	Turnover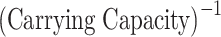
Leader	Low	Low	Low
Lagger	Low to High	Low to High	Low to High
Lattice	Low	Low	Low
Condensate	High	High	High

Discussion

Understanding the structure and dynamics of maturing centrosomes is crucial for unraveling their role in cell fate decisions. To achieve this, we conducted targeted experiments examining the centriole and pericentriolar material (PCM), and developed a data validated mathematical model to elucidate the mechanisms underlying the distinct dynamics between the two centrosomes. Together, our results contribute to our understanding of the structural intricacies and the unique maturation dynamics of both centrosomes during early embryonic development.

We tracked centriole inheritance up to the four-cell stage to detect any potential bias in their distribution to the daughter cells. Our probability model indicates that the first division can yield either random or biased outcomes while still matching experimentally observed distributions, aligning with similar reports²⁰. In various organisms, centriole maturation involves acquiring distal appendage proteins (DAPs), leading to structural and functional differences between mother and daughter centrioles^27,28, and age-related inheritance in specific cell types^13,14,17. Unlike human cells, C. elegans centrioles are believed to lack orthologs of these DAPs. Instead, C. elegans centrosomes feature a unique structure known as the paddlewheel, which spans the entire length of mature centrioles^29,30. Unlike DAPs, which are dispensable for division in human cells^30–33, paddlewheels are essential for proper cell division in C. elegans. However, the extent to which paddlewheel features affect centriole inheritance remains unclear.

To further investigate potential asymmetries in centrosome maturation, we quantified AIR-1/AURKA dynamics during this critical developmental process. We focused on the intensity of the GFP-AIR-1 signal rather than the size of the PCM because the boundaries of the centrosome are not well-defined. While centrosomes are thought to evolve from a dynamic, liquid-like state to a more solid, stable state with lower turnover⁵, this change in centrosome state is not proposed to be associated with a change in the size of the centrosomes. To minimize potential confounding effects from centrosome growth and movement, we measured GFP fluorescence within a fixed area, using fluorescence intensity as a proxy for AIR-1/AURKA density in that region. The distinct long timescale recruitment and short timescale FRAP recovery dynamics of the leading and lagging centrosomes reveal that centrosomes are highly dynamic during maturation leading to the first division of the C. elegans embryo. The experimental data for both the recruitment and the recovery show differences between the leading and the lagging centrosomes dynamics in both processes. These differences were highlighted by modeling results, where initially unbiased mathematical model fits the data significantly better when we accounting for different kinetics between the two centrosome compartments.

The parameters for our model analysis were identified through a comprehensive parameter search designed to explore a wide range of values with the only constraint being that the parameters are positive³⁴. This approach ensures that the resulting parameter sets are not biased toward any specific range or relationships. Our mathematical model reveals three distinct parameter regimes capable of producing dynamics consistent with the observed recruitment and recovery of centrosomal AIR-1/AURKA. The model demonstrates that within a single simulation, the two centrosomes can possess vastly different characteristics while still producing recruitment and recovery curves that align with our experimental data. In particular, the leading and lagging centrosomes have distinct dynamics, with the lagging centrosome having lower cooperativity in its AIR-1/AURKA recruitment dynamics compared to the leader. This is consistent with the lower density of microtubules in the lagging centrosome, possibly due to AIR-1/AURKA’s activation of KLP-7, an inhibitor of microtubule nucleation at centrosomes²³. In contrast, the leading centrosome exhibits higher cooperativity in its AIR-1/AURKA recruitment dynamics, resulting in lower levels of AIR-1/AURKA and KLP-7 during the early stages of centrosome maturation, promoting higher microtubule nucleation and highlighting the complex role of AIR-1/AURKA.

This study employs an interdiscplinary multiscale approach to investigate how structural variations at different scales affect centrosome characteristics. Our centriole inheritance data indicates that preferential centriole inheritance may occur while preserving observed centriole distributions at the four cell stage, and any differences in paternally derived centrioles could either be amplified or suppressed at the macroscale level of the centrosome’s PCM. There are three prevailing biological models for centrosome structure: lattice, condensate, and transition, each supported by distinct experimental evidence⁵. Our combined use of multi-scale microscopy and mathematical modeling reveals distinct dynamic behaviors between the leading and lagging centrosomes (Table 1). Our analysis shows that the leading centrosome operates within a more restricted parameter space, indicating less dynamic behavior, while the lagging centrosome occupies a more dynamically variable state. This aligns with prior findings that centrosomes mature from a dynamic condensate-like state to a stable lattice-like state.

In future work, we will investigate whether asymmetries are present in other centrosome-associated proteins, including AIR-1/AURKA’s upstream regulator SPD-5 and its downstream effectors TBG-1 and ZYG-9. SPD-5 plays a crucial role in assembling the pericentriolar material³⁵, while TBG-1 and ZYG-9 are involved in microtubule nucleation and stabilization.^36,37 Using similar analyses, we will determine whether the asymmetry observed with AIR-1/AURKA is unique or reflects a broader pattern of asymmetric recruitment at the centrosomes, providing additional insights into the mechanisms underlying asymmetries during centrosome maturation. We will further explore whether age-related differences or specific cues designate the paternally contributed mother and daughter centrioles as leading or lagging, and how this influences the centrosome’s structure leading up to the first division of the C. elegans embryo. This study suggests that a more nuanced understanding of centrosome dynamics is necessary to fully understand cell fate determination and centrosome biology in C. elegans and other organisms.

Methods

Experimental methods

Nematode strains

The OD142 (ltIs78 [(pKO5) pie-1::GFP::TEV::Stag::air-1 spliced coding + unc-119(+)]), BA17 (fem-1(hc17) IV) strains were provided by the Caenorhabditis Genetics Center, which is funded by the National Institutes of Health (NIH) Office of Research Infrastructure Programs (P40 OD010440). The OD574 (unc-119(ed9)III; ltSi81[pY024; Psas-6::GFP::SAS-4 reencoded; cb-unc-119(+)]II) strain was a gift from Karen Oegema. Strains were maintained on nematode growth media agar plates seeded with OP50 Escherichia coli as a food source. Strain stocks were maintained at 20C by chunking or picking wild-type worms as needed and were stored at -80C according to standard practices.

Centriole tracking

Male OD574 GFP::SAS-4 worms were picked from starved plates to propagate. Feminized worms were generated from the BA17 strain by growing at 25C. Male OD574 organisms were picked to plates containing female BA17 worms and then, after mating overnight, were dissected and imaged as described below.

Fluorescence microscopy

Hermaphrodite worms were transferred to a coverslip with egg salts buffer (118 mM NaCl, 48 mM KCl, 2 mM MgCl2, 2 mM CaCl2, 0.025 mM HEPES, pH 7.4) and dissected to release embryos. Coverslips were then inverted onto slides with 2% agar pads (in egg salts buffer) and sealed with Petrolatum.

Centrosomal recruitment

Time-lapse z-stacks were taken with 1.5 m spacing, spanning 15 m centered at the midplane of the embryo, with a 10s delay between stacks. Images were always collected from 100 s before PNM to second division to ensure the embryos divided with normal timing, indicating that they were healthy.

Centriole inheritance tracking

z-stacks were taken with 1.0 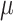m spacing, spanning 7 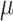m centered at the midplane of the embryo. Images that did not capture two distinct centrioles were removed before analysis. 3 embryos had no identifiable GFP+ centrioles, and 4 only had one GFP+ centriole.

Image analysis

Image analysis and maximum-intensity projections shown in the figures were made in FIJI (Fiji Is Just ImageJ).

AIR-1 intensity plots

Embryo images were rotated and flipped as necessary so that the anterior was at the left and the MTOC that went to the anterior started on the bottom. For each time point a single slice of the 10 slice z-stack was chosen to be analyzed, this slice represents the middle and brightest slice of the MTOC and we required 1 slice of the z-stack on both sides of it to ensure we were capturing the brightest slice possible. This was done independently for the leading and lagging MTOCs, and a new image sequence containing only these slices to be analyzed was generated.

Fluorescence recovery after photobleaching (FRAP)

Standard FRAP protocols were followed as previously described²⁴.

Recovery curve and fitting to an exponential

Recovery parameters were calculated as follows:

1

where 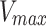represents the Mobile Fraction of the fluorophore.

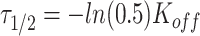2

where 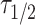represents the half time of recovery.

Theoretical methods

Normalization of data

The calculated fluorescence values with background removed were individually normalized by dividing each point by the average value of the total fluorescence, giving values that we can simulate in our model.

Error calculation

We defined the error between our simulated data and the AIR-1 fluorescence data as the point-wise sum of the differences between the two data sets.

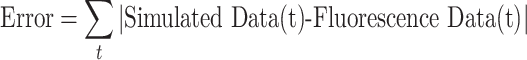3

Model selection

MTOC factor is capable of flowing from the cytoplasm to each of the compartments, 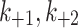and back to the cytoplasm, 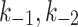, where it is available for further patterning. The recruitment to each MTOC was limited by saturation, , but promoted by the cooperativity of the compartment 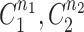. The following three models were implemented with different cytoplasmic dynamics to determine the best for our investigation.

To simulate the conservation of the MTOC factor, we used 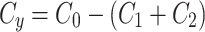such that the amount of factor was equal to at all time points.

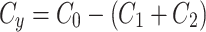4a

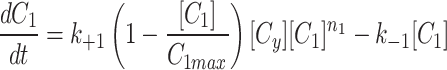4b

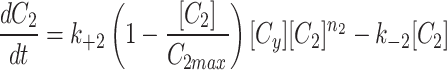4c

When we simulate a quasi-steady state we use 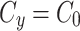such that the amount of factor in the cytoplasm is equal to 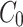at all time points.

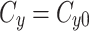5a

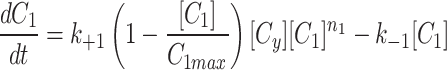5b

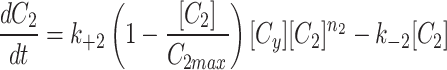5c

The cytoplasm can gain and lose model factor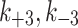

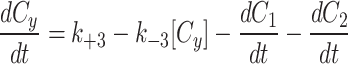6a

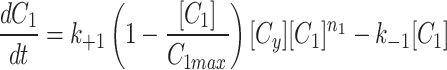6b

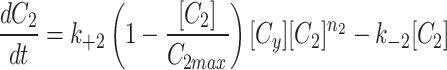6c

As described in the results, the Dynamic cytoplasm had a two fold better fit by our error metric and the parameter sets were all consistent between the three models (Extended Data Fig. 1, Extended Data Fig. 2).

Mathematical model

With the dynamic cytoplasm model chosen, we then wanted to simulate the photobleaching of the MTOCs. This required constructing a set of equations for two separate populations of model factor, a fluorescent population and a bleached population. We included a bleached factor and a fluorescent factor to account for the simulated photobleaching. We required this model to account for the photobleaching without changing the dynamics of the original model. The sum of bleached factor 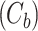and fluorescent factor 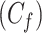would behave exactly as in a model with just a fluorescent factor. These features are incorporated into a set of differential equations describing the change in concentration of the MTOC factor in each compartment over time, resulting in Eq. 7. We converted these equations into their dimensionless forms, as the specific parameter values for these generic MTOC factors cannot be directly estimated, resulting in Eq. 1.

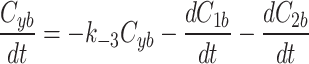7a

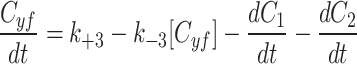7b

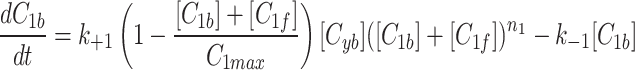7c

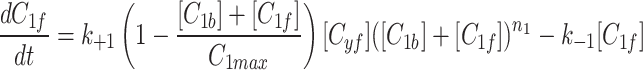7d

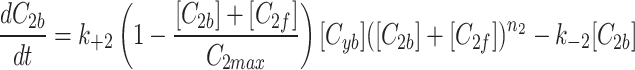7e

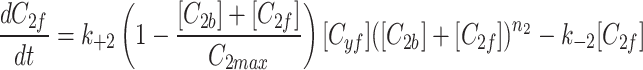7f

At any specified time, we can simulate photobleaching in the model by transferring all, or a proportion, of the fluorescent model factor to the bleached factor in a compartment.

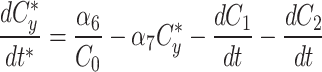8a

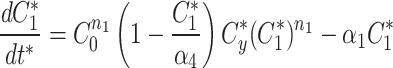8b

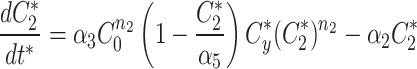8c

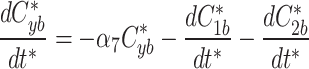9a

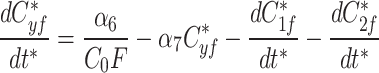9b

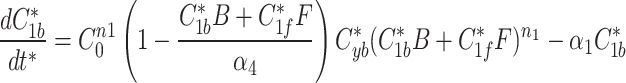9c

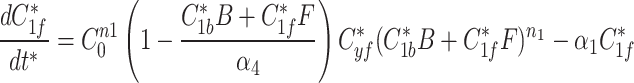9d

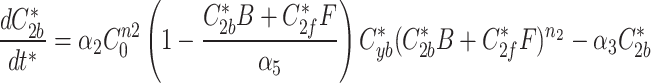9e

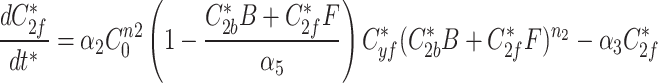9f

Modified metropolis hastings

The modified Metropolis-Hastings (MMH) algorithm is an iterative algorithm with the goal of minimizing some measurable quantity. Starting from an initial random parameter set as the seed, the MMH algorithm randomly generates a new parameter set where each parameter is selected from a normal distribution centered on the seed’s value with a standard deviation we set to be 90% of that value. The total error from the simulated fluorescence data to the actual fluorescence of AIR-1 was calculated and compared to the error calculated from the seed parameter set. If the new parameter set had a lower error it was selected as the seed for future iterations, if the error was higher it was discarded and the previous seed remained. This process was repeated until the error satisfied our end condition giving us a single parameter set that produced simulated data matching our AIR-1 fluorescence.

Inheritance analysis

Given the distribution of the fluorescent centrioles follows a series of independent Bernoulli trials, the probability of each possible fluorescence profile can be written as in Eq. 10.

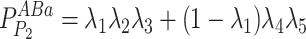10a

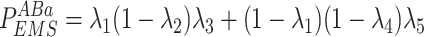10b

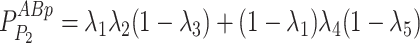10c

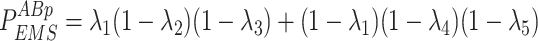10d

Statistical analysis

The standard statistical tests performed in this paper (paired T-test, Pearson correlation, Kolmogorov-Smirnov test) were implemented in Matlab or R using standard built-in functions.

Two additional methods were implemented for analysis of the AIR-1 recruitment (Fig. 2) and recovery (Fig. 3). For the recruitment data, we fit the linear model

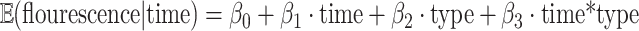where the “type” is the indicator variable which equals to 0 if type = leading and equals to 1 if type = lagging (see, e.g., Sect. 5.1 of³⁸ for the description of this type of models). We used the AR(1) correlation structure to account for correlations between observations that belong to the same embryo (see, e.g., Sect. 7.3 of³⁸ for correlation structures in models of this type). Coefficient estimation and testing was performed using the R package geepack³⁹.

For the recovery data, we smoothed the raw trajectories by fitting the exponential recovery model as detailed in Sect. 4.2 (Fig. 3d). Adopting the FRAP-specific methodology developed in²⁵, we performed pairwise t-testing between mean trajectories for each time point and reported the p-value over time (Fig. 3c).

Author contributions

S.M.P. contributed conceptualization, methodology, formal analysis, coding, investigation, visualization, writing-original draft, writing-review and editing. N.K. contributed Methodology and formal analysis. A.T.D. contributed conceptualization, methodology, formal analysis, investigation, writing-original draft, writing-review and editing, and supervision.

Data availability

Our data and code are available in the following public GitHub repository. https://github.com/Shayne-Falco/CentrosomeStructure_ModelsData.

Declarations

Competing interests

All other authors declare no competing interests.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-025-86548-0.