“Seeing is believing.” Fluorescence microscopy facilitates highly specific imaging of bioprocesses with detailed spatiotemporal information. However, classic optical microscopy is fundamentally constrained by the diffraction limit, preventing fine details in organelles and macromolecules from being resolved.1 This limitation has led to the development of super-resolution (SR) methods.
The most well-known SR methods include super-resolution fluorescence microscopy2 such as stimulated emission depletion microscopy (STED)3 and single-molecule localization microscopy (SMLM),4,5 which were awarded with the Nobel Prize in Chemistry in 2014. Although not well recognized in 2014, structured illumination microscopy (SIM)6 is also a prominent SR technique for live-cell SR imaging. Moreover, other methods such as super-resolution optical fluctuation imaging (SOFI)7 and expansion microscopy8 have also emerged recently.
A holistic view of dynamic biological phenomena in their native states is essential for understanding life, necessitating live-cell SR imaging capabilities. However, the live-cell SR imaging scheme remains constrained due to the compromise between the imaging speed and the resolution. As many SR imaging methods rely on prolonged exposure to collect more photons to improve resolution, an increase in physical resolution may lead to blurred images of fast-moving subcellular structures in live-cell imaging conditions.9 Meanwhile, fluorescent molecules emit a finite number of photons before irreversibly photobleaching, and biological samples can withstand only limited light exposure. In this context, the photon budget—the maximum flux of photons that can be emitted and detected—limits the practical resolution achievable in live cells. Enhancing resolution often requires excessive illumination power, causing compromised sample integrity. Thus, live-cell SR imaging entails a delicate balance among spatial resolution, the signal-to-noise ratio (SNR), and structural integrity.
Recently, computational super-resolution (CSR), which enhances image resolution through computational processes without modifying microscope hardware, has expanded the possibilities for capturing detailed biological information in live systems. CSR enables SR in a postprocessing phase, preserving imaging speed and sample integrity while extending the potential imaging properties set by the photon budget. Advances in conventional analytical algorithms10 and deep learning models11 have significantly broadened CSR’s capabilities, enabling applications across diverse imaging modalities.12−14
Historically, the idea of CSR predates the advent of SR microscopy,15 once referred to as “data inversion” or “mathematical band exploration”.16 Despite its potential, CSR remains under-appreciated within the biological research community. One primary reason is the absence of a unified concept, resulting in fragmented terminology such as deconvolution algorithms, image deblurring, noise filtering, and artificial intelligence methods. After data inversion was summarized early,16 traditional deconvolution methods for fluorescence imaging were discussed in 2006.17 Regarding the mathematical concepts of optical super-resolution, Lindberg put forth a review in 2012,18 and the latest one focusing on algorithms appeared in 2020.19 Although these reviews are insightful, they focus on only specific aspects and do not incorporate the latest advances. To the best of the authors’ knowledge, there has been no comprehensive review that explicitly defines CSR in microscopy or integrates existing methods under a single framework, as listed here in Figure 1.
Figure 1.
Key milestones in the development of super-resolution fluorescence microscopy and CSR methods. All of the CSR methods in the diagram are covered in this Review. Computational techniques dedicated to a specific SR fluorescence microscopy are not listed. Adapted in part with permission from ref (25). Copyright Prakash Kirti, Diederich Benedict, Heintzmann Rainer, and Schermelleh Lothar, licensed under a Creative Common Attribution (CC BY) 4.0 license.
Another barrier lies in the interdisciplinary nature of CSR, existing at the intersection of computation, mathematics, and physics. Mastering CSR requires an understanding of imaging systems,20 optimization,21 and deep learning,22 making it akin to a “black box” for many microscopists and biologists or, worse, often misinterpreted as mere image enhancement or “photoshopping”.
This Review aims to address these challenges by conceptualizing CSR as a framework that exploits priors to recover high-frequency spectrum information and organize its existing methods into a unified system. We will provide an in-depth explanation of the principles of CSR, with particular emphasis on the historical evolution of CSR methods. Equally important, we highlight the biological applications of CSR, either alone or in combination with other SR techniques, with a focus on overcoming the limitations imposed by photon budgets. We hope this Review serves as a Hitchhiker’s Guide to CSR for microscopists and biologists alike.
The Review is structured as follows: The first section defines resolution and SR, establishing a precise definition of the CSR and introducing its core concepts. This foundational section sets the stage for the remainder of the Review. Following this, we explore CSR methods from a historical perspective, dividing the development into four overlapping stages: early explorations, model-based CSR, data-driven CSR, and the latest advancements. The latter two sections discuss applications of CSR in live-cell SR imaging, biological discovery, and objective resolution evaluation in CSR. We conclude with a discussion of the challenges and future prospects of CSR. Table 1 summarizes all of the discussed methods along with their pros and cons.
Table 1. CSR Methods in This Review.
| methods | priors | algorithms | advantages | drawbacks | application |
|---|---|---|---|---|---|
| inverse filters | imaging is a linear system | linear system | easy-to-use | noise infeasible | deblurring, denoising |
| analytical continuation | finite spatial size | not restricted | theoretical guarantees | noise infeasible | low practicality |
| PWSFs decompose | finite spatial size | truncated PWSFs | improvement of noise robust | still noise infeasible | low practicality |
| Gerchberg–Papoulis Algorithm | finite spatial size | iterative algorithm | theoretical guarantees, improvement of noise robust | still noise infeasible | SR, phase retrival155 |
| Landweber iteration | smoothness | iterative algorithm | improvement of noise robust | still noise overfitting, iteration number choose | mainly noise filter |
| Tikhonov–Miller | smoothness | iterative algorithm | improvement of noise robust | still noise overfitting, iteration number choose | noise filter, deconvolution, background light remove |
| Richardson–Lucy Deconvolution | poisson noise model | iterative algorithm | positive, photon conserving | noise susceptibility; pattern artifacts | general, mainly deconvolution, deblurring, denoising |
| maximal entropy deconvolution | maximal entropy of data information | iterative algorithm | positive, smooth | resolution impaired | deconvolution |
| total variation | edges of image are sparse | proximal operator splitting algorithm | edge preserving; efficient algorithms | cartoon-like artifacts | mainly denoising |
| multi-resolution analysis | multiresolution nature in images | not specifically | theoretical guarantees | nonstationarity sensitivity, edge effects | general, mainly denoising |
| MRA75 | edge continuity and across-edge sparsity | proximal operator splitting algorithm | fidelity | rely on the prior | SR, deconvolution |
| l0 minimization | sparsity prior | specific algorithms | theoretical guarantees | no efficient algorithm | signal processing, including SR |
| l1 minimization | ISTA or FISTA(see Supporting Information) | theoretical guarantees; efficient algorithms | not general feasible in SR | signal processing, including SR | |
| analytical framework (see Supporting Information) | proximal operator splitting algorithm | generality | handcraft prior | general, most low-level processing | |
| sparse coding (see Supporting Information) | proximal operator splitting algorithm; machine learning | generality | handcraft prior | general, most low-level processing | |
| sparse-deconvolution10 | continuation and sparsity | proximal operator splitting algorithm | versatility in SR | parameters tuning, computation burden | SR, background light remove |
| Wang et al.11 | data prior | supervised learning | high performance, fast and flexible for deployment | data dependency, generalization, stability, black-box | cross-modalities SR |
| RCAN121 | denoising, SR | ||||
| DFCAN110 | SR | ||||
| XTC114 | SR | ||||
| VCD-Net115 | light-field microscopy reconstruction and isotropic resolution | ||||
| Task-GAN125 | SR | ||||
| SISRM111 | SR | ||||
| rDL139 | SIM SR | ||||
| UniFMIR146 | foundation model | ||||
| RLD156 | improve RL, parameters autotuning, acceleration | ||||
| ZS-DeconvNet112 | unsupervised learning | partially alleviate data collection issues | lack one-size-fits-all approach | SR | |
| Li et al.113 | isotropic resolution | ||||
| Park et al.127 | |||||
| Deep image prior | neural network architecture | classic optimization | totally alleviate data collection issues | early stopping issue, prone to low frequency | general |
| TDV-SIM154 | data prior + SIM | SIM reconstruction and ANN optimization | suppressing artifacts | computation burden | SIM SR |
| SUPPOSe157 and A-PoD13 | virtual points | genetic algorithms and Adam | clever prior model | nonconvex, points number determination | SR, especially in Raman microscopy |
| SRRF and eSRRF | fluorescence fluctuation | specific operation | versatility | need fluctuation | SOFI and other multi-images SR |
| MSSR158 | process of photon emission | derived from the mean shift (MS) theory | versatility in SR | artifacts | SR |
| Zhao et al.159 | High resolution means narrower PSF | pixel-reassignment | easy-to-use | lack fidelity | SR |
This Review strives to balance rigorous principles with accessibility for application-focused readers. Given the interdisciplinary nature of CSR, the use of mathematical language is essential. Yet, we have minimized technical details in the main text and provided critical mathematical content in the Supporting Information. Readers only need a basic understanding of linear algebra23 and Fourier transform analysis24 to follow the key ideas.
Lastly, two points regarding the scope of this Review need emphasis:
First, this Review focuses specifically on CSR. We do not discuss more general microscopy image restoration methods, which are covered in earlier26 and recent reviews.27 Similarly, we exclude computational techniques closely associated with certain SR fluorescence microscopy such as localization, clustering, and drift estimation. Readers interested in these computational techniques may refer to refs (28) and (29).
Second, SR is a frequently misunderstood term, as it encompasses various definitions. Notably, SR in computer vision,30−33 referred to as natural image super-resolution, is distinct from CSR in microscopy. For the sake of completeness, the Supporting Information elaborates on the distinction between CSR and natural image SR.
We invite readers to explore the exciting historical developments of the CSR through this lens.
Notions
In this Review, we use the terms “image”
and “signal”
interchangeably. Lowercase italic letters x denote
continuous function (or random variable), lowercase Roman letters
x denote discrete (digital) image. Lowercase bold Roman x represents a vector and uppercase bold X represents
a matrix. Because discrete image can be mathematically represented
by a vector, x and bold x would be used intercahngeably. A dash on
the letter x̅ denotes its Fourier transform, a star on the letter
x* denotes the result of a certain algorithm; the inner product of
two functions f(r) and g(r) is ⟨f, g⟩≔ ∫ f(r)g(r) dr. The 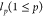 norm of n-dimension vector x is
norm of n-dimension vector x is 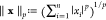 . The total number of nonzero elements in
vector x corresponds to its l0 norm, although it does not meet the mathematical definition of a
norm. For matrix A, its null space is null (A):{x|A·x = 0 }; the Fourier
matrix F of order n is a n × n matrix in which Fjk = e2πijk/n where j, k ∈ {0,1,···, n – 1} and i2 = −1; I denotes the identity matrix; UT is
the transpose of U; U† is the conjugate transpose of U; and matrix U is unitary if U†U = UU† = I.
. The total number of nonzero elements in
vector x corresponds to its l0 norm, although it does not meet the mathematical definition of a
norm. For matrix A, its null space is null (A):{x|A·x = 0 }; the Fourier
matrix F of order n is a n × n matrix in which Fjk = e2πijk/n where j, k ∈ {0,1,···, n – 1} and i2 = −1; I denotes the identity matrix; UT is
the transpose of U; U† is the conjugate transpose of U; and matrix U is unitary if U†U = UU† = I.
Concepts and Principles of CSR
This section serves as the foundational basis for the Review. It begins by defining the concepts of resolution and SR and then formalizes the notion of CSR. Next, it analyzes the core challenges of CSR and explains underlying principles, with a focus on the use of priors. Finally, it summarizes the main approaches for modeling priors.
Imaging and Resolution
This Review uses fluorescence microscopy as an example, although CSR is applicable to other imaging modalities. Fluorescence microscopy relies on a laser to excite fluorophores, which emit fluorescence signals collected by a photomultiplier or a camera to form an image. Despite its mechanical complexity, the imaging process of a fluorescence microscope can be abstracted as a 4f optical system, explained below.
As illustrated in Figure 2(A), the core of the microscope consists of two lenses (an objective lens and a tube lens) separated by their focal lengths. The intermediate (virtual) plane between these lenses is referred to as the conjugate plane. The focal plane, where the sample is positioned, is located at the front focal plane of the objective lens, while the image plane, where the camera is placed, lies at the back focal plane of the tube lens. The system is termed a 4f system because the focal plane and image plane are separated by four focal lengths.
Figure 2.
Key concepts of optical imaging. (A) An abstract representation of a fluorescence microscope. The fluorescence emitted from the focal plane is collected by a camera, such as a CCD, at the image plane to form an image. (B) Overlap of the Airy functions. Rayleigh determined that the human eye can resolve a ± 20% decrease in intensity, which corresponds to the overlap of the Airy disk of one Airy function with the first minimum of another. On the left, two resolved Airy functions are shown. On the right, two unresolved Airy functions are depicted. The middle image represents two Airy functions separated by the Rayleigh limit. (C) Spatial and frequency domain representations of the imaging process. (Top) The imaging process can be modeled as the convolution of the sample with the PSF, shown here in a 2D plane. CCD: charge coupled device. (B) is reprinted with permission from ref (34). Copyright 2018 IOP Publishing Ltd., licensed under a Creative Common Attribution (CC BY) 3.0 license. (A) and (C) were created in https://BioRender.com.
Due to the wave nature of light, an infinitesimal point source in the focal plane is imaged as a blurred spot in the image plane, known as an Airy disk for a circular aperture. Figure 2(B) shows two Airy disk functions. Generally, the spatial distribution of this spot is termed the point spread function (PSF).
An imaging target can be modeled as a collection of infinitesimal points, which, after passing through the microscope, become superimposed PSFs. This superposition resulted in a blurred image.
Mathematically, this process is described as
| 1 |
Here, r represents spatial coordinates, x is the unknown sample with a fluorescence distribution in the focal plane, and y is the resulting blurred image in the image plane. The imaging process is characterized by the PSF. We assume a shift-invariant PSF, meaning its shape remains unchanged with spatial shifts, which is valid for most optical microscopes. Thus, eq 1 is a convolution process, where ⊗ denotes convolution. This is depicted in Figure 2(C), which shows initially sharp lines becoming blurred after imaging.
In practice, y will be reconstructed into a digital image that can be represented as a 2D (or three-dimensional) vector. Each element of the vector corresponds to an image pixel.
Therefore,
all continuous functions in eq 1 are replaced with discrete vectors 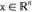 and
and 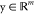 , and the imaging equation transitions from
an integral to a discrete convolution. Additionally, noise will inevitably
appear, leading to the complete imaging equation:
, and the imaging equation transitions from
an integral to a discrete convolution. Additionally, noise will inevitably
appear, leading to the complete imaging equation:
| 2 |
where e represents the noise. Note that although noise is represented additively here, it can take more complex forms, such as Poisson noise in photon-limited cases, and can be even more nuanced in SR fluorescence microscopy.35 The detailed derivation can be found in the Fourier optics textbook.36 Additionally, we provide further details in the “Details of Imaging Process” section of the Supporting Information.
It is well-known that the Rayleigh resolution limit corresponds to the overlap of two Airy disks (Figure 2(B)). It is calculated that a ±20% decrease in intensity can barely be resolved by the human eye. This occurs when the center of one Airy function overlaps with the first minimum of the second Airy function (Figure 2(B) middle). However, this is an empirical criterion. Another resolution definition is the full width at half-maximum (FWHM) of the PSF. However, it is challenging to identify independent PSFs in a single fluorescence image. This poses practical difficulties in defining the SR.
On the other hand, the core of “Fourier
optics” resides
in the Fourier transform, which decomposes signals into a weighted
sum of sinusoidal components. This provides a frequency-domain definition
of the imaging resolution. Figure 3(A–C) illustrate how a step function is approximated
using an infinite series of sinusoidal functions 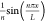 . Notably, as n increases,
the sharp edges of the superimposed signal become increasingly clear.
This indicates that a larger n corresponds to a sharper
signal.
. Notably, as n increases,
the sharp edges of the superimposed signal become increasingly clear.
This indicates that a larger n corresponds to a sharper
signal.
Figure 3.
Imaging in the perspective of the Fourier domain. (A–C) Signal decomposition in Fourier theory. (A) A step function representing an arbitrary signal. (B) This complex shape can be approximated by a sum of sine functions. (C) To approximate the original signal faithfully, a large number of sinusoidal signals (blue) need to be summed (red). (D) (Left) Wavelength of a sine wave. (Right) High-frequency (short-wavelength) waves correspond to higher resolution. Intuitively, high-frequency waves are less able to bypass small objects, thereby resolving smaller features. (E) Fourier transforms of two-dimensional images. The top and middle show two 2D sine waves with different orientations and frequencies, which can be combined to form the image shown at the bottom. (F) Two-dimensional frequency spectrum and the optical transfer function (OTF). In the 2D frequency domain, sine waves are represented by their frequency and orientation (only 1D components are shown here, so orientation is not explicitly indicated). Higher frequencies are located farther from the origin. The OTF is a function limited to low-frequency components (yellow circle) with a cutoff frequency of ωl (red arrow). (G) Spatial and frequency domain representations of the imaging process. (Bottom) In the frequency domain, the convolution corresponds to multiplication. The sample’s frequency domain signal is multiplied by the OTF, leading to the loss of high-frequency components beyond the cutoff frequency ωl. (A–C, E) are reprinted with permission from ref (34). Copyright 2018 IOP Publishing Ltd., licensed under a Creative Common Attribution (CC BY) 3.0 license. (D, F, G) were created in https://BioRender.com.
As shown on the left side of Figure 3(D), the distance between two peaks of a
sine wave
is called the wavelength λ, and the reciprocal of the wavelength
is the frequency 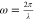 . A larger n also implies
a higher-frequency signal, which corresponds to a sharper signal or,
in other words, a higher resolution. Although there are complex physical
implications behind this, it can be intuitively understood as follows:
longer-wavelength (lower-frequency) sine waves can more easily bypass
large objects, whereas shorter-wavelength (higher-frequency) waves
are more likely to interact with smaller objects, thereby resolving
underlying structures (Figure 3(D)).
. A larger n also implies
a higher-frequency signal, which corresponds to a sharper signal or,
in other words, a higher resolution. Although there are complex physical
implications behind this, it can be intuitively understood as follows:
longer-wavelength (lower-frequency) sine waves can more easily bypass
large objects, whereas shorter-wavelength (higher-frequency) waves
are more likely to interact with smaller objects, thereby resolving
underlying structures (Figure 3(D)).
The same principle can be easily extended to 2D images, which are essentially a superposition of spatial frequencies with varying orientations. As shown in Figure 3(E), the top and middle images represent two 2D sine waves with different orientations and frequencies. Their superposition (bottom) results in a more complex 2D image.
These 2D sine waves can be represented in a 2D frequency-domain image based on their orientation and frequency. As illustrated in Figure 3(F) (note that the orientation is not shown in the figure; therefore, 1D sine waves are used to represent 2D sine waves with a specific orientation), the origin point represents a plane wave with no intensity variation. Along a given line, 2D sine waves with higher frequencies are located farther from the origin. Just like in 1D, 2D sine waves with higher frequencies correspond to higher image resolution.
Therefore, the Fourier transform links the resolution to the frequency domain: the resolution of an image is defined as the reciprocal of the highest frequency component in its spectrum. This frequency-domain analysis allows resolution to be defined objectively, independent of specific imaging details, which is an advantage over other definitions.37
This allows the imaging process to be understood from a frequency-domain perspective. The Fourier transform of the PSF is known as the Optical Transfer Function (OTF). The OTF describes how different frequency components of the true image are modulated as they pass through the optical system. The most significant property of the OTF is that it is band-limited (Figure 3(F), yellow circle), meaning that only 2D frequency components with frequencies below the cutoff frequency ωl (Figure 3(F), red arrow) can pass through the imaging system. This ultimately limits the imaging resolution.
Mathematically, in Fourier space, convolution becomes a multiplication, simplifying the imaging equation to
| 3 |
where ω is frequency variable. The high-frequency components of the true image beyond the cutoff frequencies ωl are filtered out by the OTF, making the microscope effectively act as a low-pass filter (Figure 3(G)). This low-pass filtering effect fundamentally limits the resolution. As described by Abbe’s criterion, the diffraction limit resolution d is
| 4 |
where NA is the numerical aperture. For biological research, this limit typically corresponds to ∼250 nm of lateral resolution and ∼750 nm of axial resolution.
On the other hand, the OTF is three-dimensional. Another property of the OTF is the “missing cone”, meaning classical optical microscopy cannot distinct in-focus light and out-of-focus photons. More detail is provided in the Supporting Information under “Details of Imaging Process”.
Computational Super-Resolution as an Ill-Posed Problem
The resolution limit defines the SR problem as the recovery of high-frequency components of the true image beyond the cutoff frequency. This process is often referred to as “out-of-band extrapolation”. The concept of SR was first introduced by Toraldo di Francia in 1952,38 who described it as enhancing the angular resolution of an optical system beyond the diffraction limit. This aligns with the modern definition of the SR.
We define computational super-resolution (CSR) as follows: given a low-resolution image y and the PSF in the imaging eq 2, CSR aims to derive or approximate the true high-resolution image using specific algorithms. In this Review, x is referred to as the true image or true signal, y as the (imaging) data, and the algorithm’s output as the model image or model signal, denoted as x*.
In the literature, CSR is frequently conflated with terms such as deconvolution and even deblurring. While CSR inherently involves countering the effects of convolution, it specifically focuses on out-of-band extrapolation. Note that, by this definition, filling the missing cone of the OTF, that is, enhancing the optical sectioning capability of the microscope, is also a form of SR. In contrast, deconvolution may also refer to normalizing the contrast within the cutoff frequency due to OTF attenuation, which aligns with the concept of deblurring, and resolving previously unresolved high-frequency information due to low signal-to-noise contrast. In this Review, we define deconvolution as focusing on out-of-band extrapolation and deblurring as enhanced contrast within the OTF.
Since the OTF limits high-frequency information beyond the cutoff frequency, an infinite number of possible high-frequency models could correspond to the same low-resolution data. As shown in Figure 4(a), after passing through the microscope imaging system, fine lines originally become blurred and thicker and an infinite number of possible images can result in the same thick-line image when processed by the imaging system. Furthermore, we do not directly observe the low-resolution data; instead, it is affected by noise and aberrations.
Figure 4.
The framework of computational SR (CSR). (a) CSR as an ill-posed problem. Due to the low-pass filtering effect of microscopes, the true image is degraded into a low-resolution image. The loss of high-frequency information results in infinitely many possible high-resolution images corresponding to the same low-resolution image. (b) Solving CSR with priors. The introduction of priors helps address the ill-posed nature of CSR by constraining the set of possible solutions. Through specific algorithms, these priors enable the recovery of a high-resolution image that closely approximates the true image. (c) Iterative optimization for solving the CSR. This panel illustrates the iterative process of solving an optimization problem. The target is to minimize an objective function (denoted by the green dot as the object point). Starting from an initial guess (red dot, often the low-resolution image), the optimization algorithm takes steps toward the minimum point according to a specified rule, such as gradient descent. After several iterations, the algorithm converges to the minimum point. (d) The basic framework of CSR. The CSR framework involves defining a prior (regularization term), determining the data fidelity term, and solving the corresponding objective function through optimization. This figure was created in https://BioRender.com.
This reveals the central challenge of CSR: it is an ill-posed problem. In mathematics, a problem is considered well-posed39 if it satisfies three conditions:
-
1.
A solution exists.
-
2.
The solution is unique.
-
3.
The solution process is stable (if the reader wants a formal mathematical definition, please see ref (40)).
An ill-posed problem fails to satisfy at least one of these conditions. In the case of the CSR, the last two conditions are not met.
Linear Algebra View of Computational Super-Resolution
The core idea to solve ill-posed problems is to impose a “priori” constraint, allowing a stable algorithm to select a unique image from all those that are consistent with the data. This process is illustrated in Figure 4(b). This has a clear mathematical meaning in linear algebra. The imaging eq 2, that is, the convolution process, can be represented as matrix multiplication:
| 5 |
where P is the PSF matrix. (Readers unfamiliar with this can refer to the Supporting Information section “Convolution as Matrix Multiplication” for the derivation.) In this context, the CSR problem transforms into a least-squares (LS) problem:
| 6 |
Here ∥•∥2 is the l2 norm, with vector z as the independent variable. The term “arg min” means obtaining the value of the independent variable that minimizes the function on the right (l2 norm takes its minimum value). In mathematics, finding this extremum is termed solving an optimization problem. If the matrix P is full rank, it allows for a solution named direct inversion:
| 7 |
However, two problems arise: first, matrix P is not full rank. It has a nontrivial null space, containing infinitely many vectors that, when added to x*, still satisfy the equation. This corresponds to the previous issue: due to the loss of high-frequency information, there are infinitely many possible high-resolution images that map to the same low-resolution image. Second, P is related to submatrices of the Fourier matrix, which have very large condition numbers.41 Consequently, the presence of noise exacerbates the difficulty of solving the LS problem, as even small perturbations in the observed data can lead to significant deviations in the solution.
In linear algebra, solving this (named under-determined) equation typically requires “regularization”. Generally, regularization is a process that simplifies the solution of a problem by introducing constraints or additional information. Specifically, regularization introduces an additional penalty term to the LS problem:
| 8 |
where 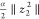 is the penalty term and α > 0
is
the penalty parameter. This modification ensures that PTP + αI is symmetric and
positively definite, providing a unique solution:
is the penalty term and α > 0
is
the penalty parameter. This modification ensures that PTP + αI is symmetric and
positively definite, providing a unique solution:
| 9 |
This regularized approach also helps stabilize the solution and address the issues arising from noise.
The Basic Function in Computational Super-Resolution
Beyond the source of prior information, a unified mathematical framework
is needed to model them. Without loss of generality, we define a prior
as a constraint modeled by a penalty function R(x),
which measures the agreement of the image with the priors: the lower R(x), the better the agreement. For example, true high-resolution
images tend to be noise-free, so the prior reason can be that the
pixel values in the model image should be smooth. The 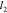 norm of a differential operator is a good
choice to impose this constraint, a method known as classic Tikhonov
regularization.42 The smoother the image,
the smaller the penalty function
norm of a differential operator is a good
choice to impose this constraint, a method known as classic Tikhonov
regularization.42 The smoother the image,
the smaller the penalty function 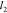 should be.
should be.
However, priors alone are not sufficient (as the smoothest possible image, for example, would be a constant image). The model image also needs to be constrained by the observed data. The objective is to find a model image x* that aligns with the observed low-resolution data y and satisfies the priors. This leads to a constrained optimization problem:
 |
10 |
However, due to the presence of noise, ensuring the model image exactly matches y would be misleading. Therefore, some expected discrepancy between the model and the observed data is considered acceptable. We set η(e) as the error level according to the real noise e, and modify the optimization problem to
 |
11 |
Here, F(P·z-y)
≔ F(z, y) represents the expected discrepancy,
quantifying the fidelity of the model to the observed data. Ideally,
the result depends on the noise model, but for simplicity, it is often
taken as the square of the 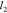 norm.
norm.
Using the Lagrange multiplier method (see Supporting Information on the “Lagrange Multiplier Method”), the constrained optimization problem can be reformulated as an unconstrained optimization problem:
| 12 |
In this Review, we refer to this optimization problem as the “basic function”, with F(z, y) representing the “data fidelity” term and R(z) representing the “regularization” term. Here, λ ≥ 0 is the Lagrange multiplier, which balances the data fidelity and prior adherence. Under suitable conditions, the solutions to both optimization eqs 11 and 12are equivalent. Notably, eq 8 is a special case of this basic function.
Unlike direct inversion, the basic function in CSR is typically complex, making a direct analytical solution infeasible. Instead, iterative algorithms are employed (Figure 4(c)). The exact shape of the basic function is often unknown; in this example, it is represented as a parabolic curve with a minimum point. The algorithm begins at an initial point, usually the low-resolution image, and iteratively moves closer to the minimum point by following optimization rules. If conditions are suitable, such as when the objective function is convex, the algorithm will converge to the minimum point after a finite number of iterations. (Readers unfamiliar with convex and nonconvex optimization can refer to the Supporting Information on “Convex and Non-Convex Optimization”).
The process for solving the CSR using the basic function is summarized in Figure 4(d). First, the prior (regularization term) and the data fidelity term are determined. Then, an iterative algorithm is applied. In each iteration, the algorithm generates a predicted image, compares it to the observed data through the forward process, and evaluates its consistency with the priors. The error feedback is used to adjust the predicted image according to specific optimization rules. While this explanation is intuitive, rigorous mathematical derivations can validate this process in concrete implementations.
The core of CSR is the use of priors. There are alternative ways to model priors using different mathematical frameworks. One widely used approach treats the unknown high-resolution image as a random variable, with the prior represented as its probability distribution; this is known as the Bayesian framework. Further details on this modeling approach are provided in the Supporting Information section titled “Bayesian Views of Priors” for the readers’ reference.
The choice of priors determines the various methods utilized in CSR. Given CSR’s close integration with microscopy, the proposal of both common and specific priors has significantly shaped its developmental trajectory. In the following sections, we will trace the fascinating history of CSR’s evolution, organized around its key methodological advancements.
Early Explorations
We will first review the development of CSR from the mid-20th century to the 1980s, a period before the emergence of SR fluorescence microscopy, highlighting key methods and analyzing their limitations. Figure 5 shows the performance of several algorithms discussed in this section on simulated images.
Figure 5.
Orthogonal sections of the maximum intensity projection (MIP) of a degraded 3D synthetic volume after deconvolution using various algorithms. From top left to bottom right: ground-truth volume, degraded volume (after convolution with PSF and simulate noise), naïve inverse filter (NIF), regularized inverse Filter (RIF), Tikhonov regularization (TR), Landweber iteration (LW), Richardson–Lucy (RL), Tikhonov–Miller (TM), Fast Iterative Shrinkage-Thresholding Algorithm (FISTA, l1 minimization), and Richardson–Lucy with total variation (RL-TV). A non-negativity constraint was used for all algorithms. The setting of the optimal parameters for each deconvolution algorithm was performed through visual assessment. Reprinted from with permission from ref (54). Copyright 2017 Elsevier.
Inverse Filters
In the early 20th century, the theory of linear systems was established. Early attempts to solve CSR treated it as a linear signal recovery problem.
Without additional information, the only way to recover input x from output y is to approximate x as a linear superposition of y:
| 13 |
This linear solver or estimator is characterized by the function M(r, r′), in Fourier space:
| 14 |
Here, M̅ is termed a filter in signal processing. Ideally, M̅ = [OTF] –1, so such processing is called an inverse filter.
The simplest inverse filter is the naïve inverse:
| 15 |
However, this naïve inverse approach has two major problems. First, the OTF is band-limited, meaning that frequencies beyond the cutoff are zero. This makes direct inversion impossible for these frequencies. A workaround is to constrain the inverse operation to within the cutoff frequency. Second, and more critically, noise in the data is significantly amplified in frequency regions where the OTF(ω) is small, especially near the cutoff frequency. As a result, the naïve inverse fails to preserve meaningful image information. The performance of the naïve inverse filter is shown in Figure 5 (NIF), where the result is full of noise.
The classical Wiener filter43 improves noise suppression by providing the best linear estimate in the least-squares sense (eq 6). Setting M̅ as the Wiener filter, the result is
| 16 |
where OTF* is the conjugate of the OTF, |OTF|2 is power spectrum of OTF, and w is the Wiener parameter. This method is also known as Wiener deconvolution. If the noise is assumed to be white, then an optimal Wiener filter can be derived. Wiener deconvolution is equivalent to Tikhonov regularization, as shown in Figure 5 (TR).
To further suppress noise, additional linear regularization can be applied, transforming the least-squares problem into a regularized least-squares problem:
| 17 |
where C a is transform matrix. The inverse filter in this case is
| 18 |
Here, CTC acts as a filter. Equation 9 is a special case of this formulation.
These algorithms are often used to suppress noise for the initial recovery of x. In SIM reconstruction, Wiener deconvolution is a standard method.9 More precisely, inverse filters are used to correct attenuation within the cutoff frequency and improve contrast, similar to how the human eye enhances resolution; this is essentially what deblurring means.
However, the fundamental flaw of linear algorithms is that they can only provide information based on their input. Since the data does not contain any high-frequency information, the linear superposition of data still cannot generate new information. Consequently, inverse filters are not effective in recovering the out-of-band spectrum. Thus, more advanced approaches are needed.
Analytic Continuation
When Francia introduced the concept of super-resolution in 1952, he realized, “achieving image resolution greater than the diffraction limit lies in the ambiguity which generally attends the extension of a complex spectrum which is known over a finite interval only”.38
However, in 1964, Harris proposed a method based on a straightforward prior: the imaging object has a finite spatial extent.44 Under this assumption, it can be proven that ambiguity does not exist. In such cases, the true image spectrum is an entire analytic function and is uniquely determined by the part of the spectrum transmitted by the optical system. Therefore, the required out-of-band extrapolation— SR—can be performed, at least in theory. This concept is known as “analytical continuation”. A precise definition is provided in the Supporting Information section on the “Analytical Continuation of CSR”. However, in practice, noise renders this theory ineffective.
Prolate Spheroidal Wave Functions
Analytic continuation inspired the theoretical foundation for out-of-band extrapolation, with the extent of extrapolation determined by a set of special functions known as prolate spheroidal wave functions (PSWFs),45 denoted as ψn(c, r), where c is the space–bandwidth parameter determined by ωl. Detailed mathematical explanations are provided in the Supporting Information section titled “Mathematical Meaning of PSWFs”.
Under the assumption of a finite spatial extent and a box-like OTF (no attenuation within the cutoff frequency, which can also be achieved through deblurring), the true image can be represented as46
| 19 |
This equation indicates that the true image is uniquely determined by the data, aligning with the theory of the analytic continuation. In principle, the coefficients ⟨y, ψn(c)⟩ can be derived from y using PSWFs and then used to reconstruct true image. However, as n increases, the coefficient approaches zero and, after a certain point, falls below the noise level. The effective number of recoverable coefficients depends on the SNR.
Conversely, we can approximate the true image using a truncated expansion according to the effective number of coefficients. The goal is for the approximated image to have a resolution higher than the cutoff frequency. Historically, PSWFs provided theoretical insight by demonstrating that even though infinite extrapolation is not feasible, limited SR improvement is possible. This redefined CSR as an extrapolation problem, aiming to recover the out-of-band spectrum given the noisy spectrum within the cutoff.
Gerchberg–Papoulis Algorithm
A simple iterative algorithm for the extrapolation problem, based on the finite spatial extent prior, is the Gerchberg–Papoulis (GP) algorithm, proposed in the 1970s.47,48 We defer the details of the algorithm to the Supporting Information section titled “Gerchberg–Papoulis Algorithm”.
In the absence of noise, this algorithm theoretically converges to the correct solution,49 as the uniqueness implied by analytic continuation guarantees. However, in the presence of noise, the algorithm risks overfitting. Often, early termination yields better results, while adding regularization can further suppress noise. Despite its limitations, the GP algorithm was a pioneering method and its iterative approach inspired future developments in CSR.
In the 1970s and 1980s, it seemed that the CSR problem had been addressed, from theory to algorithm, based on the finite spatial extent prior. However, in practice, it was found that the increase in resolution was very limited, falling short of achieving SR. The main reason for this shortfall is that the prior’s modeling was too simple, leading to a limited constraint effect. As noted in the famous textbook Introduction to Fourier Optics, “While the fundamental mathematical principles are most easily stated in terms of analytic continuation...this method has not proven successful in practice”.36
From this point on, CSR gradually transitioned from being an extrapolation problem to one solved through optimization-based methods.
Iterative Deconvolution
For historical reasons, CSR methods based on iterative algorithms are often referred to as “deconvolution”, and the field is also known as deconvolution microscopy.
The first type of method replaces direct inversion with gradient descent. Directly applying gradient descent to solve the least-squares (LS) problem in eq 6 yields the Landweber iteration (LW):50
| 20 |
where γ is the step size. Occasionally, to ensure non-negativity, additional calculations max{x(k+1), 0 } are performed in each step (Figure 5, LW). Similar to the GP algorithm, LW can suffer from overfitting if the iteration count is too high. At first glance, LW does not seem to provide additional priors compared with the inverse filter. However, the iterative process itself bypasses the divided by zero operation and serves as a form of constraint. This helps ensure that the solution is closer to the true solution, which also justifies the use of deconvolution methods. Later studies demonstrated that the number of iterations can serve as a regularization parameter,51 and it was further proved that GP is a special case of LW.16
LW demonstrated the ability to enhance optical sectioning in conventional microscopy. In 1983, Agard and Sedat used LW to enhance the resolution of the observed three-dimensional distribution of nuclear chromosomes.52 Similarly, applying gradient descent to solve a regularized LS problem leads to the Tikhonov–Miller iteration53 (Figure 5, TM):
| 21 |
where λ is a regularization parameter and CTC represents a transform. Although LW and TM originated in earlier decades, their application in image processing became practical much later due to computational limitations. When the transform matrix C is related to the properties of the image, a popular choice is smoothness, implying that adjacent image pixels tend to have similar values. Thus, C can be the discretization of a differential operator such as the Laplacian operator.
Richardson–Lucy Deconvolution
Another class of iterative SR algorithms is based on assumptions about the probabilistic distribution of random variables. Richardson–Lucy deconvolution (RL) proposed by Richardson (1972)55 and Lucy (1974)56 has played a pivotal role in CSR. Its formulation is as follows:
 |
22 |
where ⊗̅ denotes the transpose of convolution and 1 represents a vector of ones with the same size as vector y. Sometimes, the numerator and denominator in the RL formulation are referred to as the “inverse projector” and the “projector”, respectively. The RL method assumes that noise follows a Poisson distribution, which is a fundamental characteristic of photon detection. The detailed derivation of RL can be found in the Supporting Information section titled “Richardson-Lucy Deconvolution Detail”.
RL exhibits SR capabilities on simulated data (Figure 5, RL). Unlike other iterative algorithms, RL has been shown in many studies to achieve SR, particularly in radio astronomy.57,58 Specifically, RL has demonstrated the ability to surpass the Rayleigh criterion in separating double stars in astronomical imaging. As RL lacks an explicit regularization term, it must possess some inherent regularization properties. Like other iterative algorithms, the number of iterations itself acts as a form of regularization.59 At the same time, RL naturally ensures non-negativity and preserves the total photon count, aligning with the physical meaning of the PSF.60
However, RL also has its unique weaknesses. It has been observed in practice that RL is sensitive to noise and prone to produce pattern-like artifacts, such as the ringing effect61 and sparsity effect.62 The understanding of these artifacts is still unsatisfactory, and they limit the practical application of RL in achieving SR. For example, RL has been proven to be infeasible for solar system imaging.63 Some studies have introduced additional regularization terms to suppress noise,64 but these efforts have achieved only limited success. It was not until recent developments, which combined several methods, that significant breakthroughs were achieved,10 as will be discussed later. Another problem with the RL is its slow convergence rate. Recently, modifications to the inverse convolution operator with an unmatched back projector have achieved a speedup of several thousand-fold.65
Unfortunately, first proposed as an engineering approach, the mechanisms by which RL achieves super-resolution and exhibits its other demonstrated characteristics are still not fully understand. In fact, it was noted in 2015 that “The understanding of the RL algorithm and proper stopping is still an open issue and has not been solved satisfactorily”.35 Despite these challenges, RL remains one of the most commonly used deconvolution algorithms in biological imaging. It is frequently employed in confocal and wide-field microscopy to deblur images and enhance contrast. As will be shown in the applications section, RL has recently been used for fluctuation-based SR fluorescence microscopy,12 light sheet microscopy,65 and spatial transcriptomics.14
Summary on Early Explorations
In this section, we present the key achievements and limitations of early CSR. The two main approaches explored were analytical continuation theory and iterative deconvolution. To be honest, these methods have achieved only limited progress. Perhaps the most appropriate annotation for this comes from the autobiography of STED inventor and Nobel laureate Stefan W. Hell, who stated:66 “[before invention of STED] it was widely believed that the route towards higher resolution in the far-field was data processing, which typically required some assumptions about the object...Yet, none of these concepts were practical, or got beyond a factor of two.”
This underscores the challenges faced by early CSR methods in achieving substantial improvements in resolution. On the other hand, these pioneering efforts have left a rich legacy and paved the way for the next stage of CSR: model-based CSR.
Model-Based CSR
A major flaw of early iterative algorithms such as LW, TM, and RL is their lack of regularization terms or reliance on linear regularization. Since the 1990s, model-based CSR has evolved significantly, with a focus on nonlinear regularizations that enhance prior modeling and address the limitations of early deconvolution methods.
In this section, we chronologically introduce milestone works in model-based CSR, focusing on sparsity priors and leading up to recent breakthroughs such as sparse-deconvolution.
Maximal Entropy Deconvolution
A classical nonlinear regularization method is maximal entropy deconvolution (ME),67 expressed as
| 23 |
Here, the regularization term represents the maximum entropy regularization term. Entropy, a physical concept measuring system disorder, is used in this context. The fundamental idea behind maximum entropy regularization is to select the solution that is the least biased or assumes the least amount of additional information beyond what is provided by the data. For fluorescence imaging, maximum entropy assumes that the most probable distribution of fluorescence intensity is the smoothest distribution that still matches the observed data.
Like the RL, maximum entropy regularization preserves positivity. It is widely used in microscopy to suppress noise while preserving the sample structure. For instance, Arigovindan et al. (2013) proposed ER-Decon (entropy-regularized deconvolution) to enhance low-dose wide-field fluorescence imaging, enabling high-resolution in vivo imaging under extremely low phototoxicity conditions.68
Total Variation
While smoothness suppresses noise, it also damages high-frequency information, conflicting with CSR objectives. A more refined approach utilizes nonsmooth regularizations. The most classic of these is total variation (TV), introduced in the 1990s.69 Originally proposed from a functional space and partial differential perspective,70 the discrete form of TV is
| 24 |
where ∂i represents the differential operator in direction i (the row and column orientations of the image).
When used as a regularization term, the TV-regularized problem becomes
| 25 |
TV assumes that the image consists of piecewise-constant regions separated by sharp boundaries. In biological imaging, this means that TV tends to reconstruct a sharp fluorescence image by assuming that the true image has relatively smooth regions (e.g., cytoplasm) and sharp boundaries (e.g., cell membranes). With this prior, TV is effective for preserving edges while reducing noise.
TV was first applied to the CSR for deblurring and denoising. For instance, it has been combined with RL to enhance confocal microscopy deconvolution71 (also shown in Figure 4, RL-TV). However, TV’s preference for piecewise-constant representations can lead to “cartoon-like” effects in reconstructions. To address these limitations, advanced versions such as higher-order TV have been developed.72
Multi-Resolution Analysis
Biological images capture resolution information across multiple scales such as organelles, protein complexes, and molecular structures. This multiscale nature can itself serve as a prior. Multiresolution analysis (MRA), originating in the late 1980s with wavelets,73 is a method to analyze an image’s features at various resolutions.
A major tool of MRA is the discrete wavelet transform (DWT), which relies on recursively decomposing an image into low- and high-frequency components as follows:
| 26 |
where {bi(r)}i=1···N are the wavelet functions and {ui}i=1···N are wavelet coefficients. A wavelet function is a mathematical function that resembles a small wave. Unlike traditional sine waves used in Fourier analysis, wavelets are localized in both space and frequency, allowing them to capture fine details of a signal in specific regions. (The detailed mathematical definition is beyond the scope of this Review and will not be covered here.) The key property of wavelets, orthogonality, ensures that each level of detail is independent.
DWT can analyze images at different levels of resolution, similar to zooming in and out of a picture. In CSR, the high-resolution image contains more frequency components in the wavelet domain compared with the low-resolution image. Thus, CSR can be reformulated as a problem of reconstructing the missing high-frequency components. This is achieved by transforming the low-resolution data into the wavelet domain and iteratively refining the detail coefficients.
However, DWT is primarily used for denoising in microscopy, as noise often has small coefficients in the wavelet domain due to its incoherent structure. By applying thresholding to remove these small coefficients, the signal can be separated from the noise. When combined with iterative algorithms, this approach can improve the resolution. For example, Boutet de Monvel et al. applied wavelet denoising to confocal microscopy and combined it with maximum entropy regularization, achieving better resolution in biological applications of imaging the organ of hearing.74
Framelets and curvelets extend the capabilities of wavelets, allowing for more flexible signal decomposition, especially in handling geometric features, such as edges and curves, in images. Assume high-resolution fluorescence images often exhibit characteristics such as edge continuity and cross-edge sparsity,75 it is proposed to use framelet and curvelet transforms as the prior:
| 27 |
Here, W denotes the framelet transform and C denotes the curvelet transform. The authors claim that this framework may improve the SNR and can provide up to a 2-fold increase in fidelity-ensured resolution improvement. However, this assertion also critically depends on the assumption of edge continuity and cross-edge sparsity.
Sparsity Prior
We do not delve into the above nonlinear
regularizations in detail because, in CSR, they only show significance
when combined with a sparsity prior. Sparsity prior, or sparse regularization—particularly
convex approaches based on 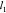 norm minimization (well-known in Compressed
Sensing theory)—is a cornerstone for addressing ill-posed problems
and has become foundational also in CSR. In the following sections,
we will introduce CSR based on the sparsity prior. We include only
the necessary concepts, deferring precise mathematical concepts to
the Supporting Information section titled
“Mathematical Concepts in Sparsity Prior”.
norm minimization (well-known in Compressed
Sensing theory)—is a cornerstone for addressing ill-posed problems
and has become foundational also in CSR. In the following sections,
we will introduce CSR based on the sparsity prior. We include only
the necessary concepts, deferring precise mathematical concepts to
the Supporting Information section titled
“Mathematical Concepts in Sparsity Prior”.
In general, a sparsity prior refers to the knowledge that the real-world data can be represented as a combination of only a few significant terms. Sparsity is closely tied to the famous Razor principle.
In biology, sparsity is very common. For example, the retina encodes images using a sparse set of ganglion cells; the olfactory system utilizes a sparse set of receptor proteins to detect a wide variety of odors; and within a given cell, only a sparse number of genes exhibit notable expression. Most importantly, designated molecules are sparsely labeled and excited to produce highly contrasted and sensitive fluorescence images as opposed to the comprehensive view provided by an electron micrograph.
The simplest sparsity is 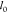 norm sparsity. For a vector
norm sparsity. For a vector 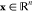 , if it contains only a small number of
nonzero elements, that is,
, if it contains only a small number of
nonzero elements, that is, 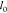 norm of x is small, it is
considered sparse. As shown in Figure 6(B(a)), the image (a 2D vector) has only a few significant
points, making it a sparse image.
norm of x is small, it is
considered sparse. As shown in Figure 6(B(a)), the image (a 2D vector) has only a few significant
points, making it a sparse image.
Figure 6.
Results of three algorithms using the
sparsity prior. (A) 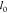 minimization on Mitochondria imaging. Wide-field
image: average live-cell image with local magnification. SPIDER:
minimization on Mitochondria imaging. Wide-field
image: average live-cell image with local magnification. SPIDER: 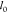 minimization with a specific solve algorithm.
Note that the membranes are recovered. (B)
minimization with a specific solve algorithm.
Note that the membranes are recovered. (B) 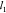 minimization on coherent diffractive imaging.
(a) A scanning electron microscope (SEM) image of the sample. (b)
Blurred image, as seen in the microscope. The individual holes cannot
be resolved. (c) The measured spatial power spectrum of the field.
The color map is identical to that in the other panels: only the background
has been removed for clarity. (d) The reconstructed 2D information
algorithmically recovered from the measured power spectrum (c) and
the blurred image (b). (C) Sparse-deconvolution on SIM achieves ∼60
nm resolution on the COS-7 cell labeled with (a) LifeAct–EGFP
with (b) an enlarged region. (c) The concept of Sparse-deconvolution,
see main text for details. (A) is reprinted by permission from ref (80). Licensed under a Creative
Common Attribution (CC BY) 4.0 license. (B) is reprinted with permission
from ref (82). Copyright
2012 Springer Nature. (C) Reprinted with permission from ref (10). Copyright 2021 The Authors.
minimization on coherent diffractive imaging.
(a) A scanning electron microscope (SEM) image of the sample. (b)
Blurred image, as seen in the microscope. The individual holes cannot
be resolved. (c) The measured spatial power spectrum of the field.
The color map is identical to that in the other panels: only the background
has been removed for clarity. (d) The reconstructed 2D information
algorithmically recovered from the measured power spectrum (c) and
the blurred image (b). (C) Sparse-deconvolution on SIM achieves ∼60
nm resolution on the COS-7 cell labeled with (a) LifeAct–EGFP
with (b) an enlarged region. (c) The concept of Sparse-deconvolution,
see main text for details. (A) is reprinted by permission from ref (80). Licensed under a Creative
Common Attribution (CC BY) 4.0 license. (B) is reprinted with permission
from ref (82). Copyright
2012 Springer Nature. (C) Reprinted with permission from ref (10). Copyright 2021 The Authors.
As mentioned, the CSR problem can be reformulated as an underdetermined equation-solving problem, written as
| 28 |
where 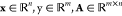 , with m < n. The sparsity prior assumes that the true solution is sparse. This
type of problem is generally called a spare recovery problem. We refer
to all solutions that satisfy the equation as feasible solutions.
A reasonable approach is to find the sparsest solution among these
feasible solutions. This approach can be formulated as a constraint
optimization problem:
, with m < n. The sparsity prior assumes that the true solution is sparse. This
type of problem is generally called a spare recovery problem. We refer
to all solutions that satisfy the equation as feasible solutions.
A reasonable approach is to find the sparsest solution among these
feasible solutions. This approach can be formulated as a constraint
optimization problem:
 |
29 |
This is commonly referred to as 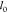 minimization. Suppose there is an algorithm
that can solve this optimization problem , theoretical studies have
shown that if the true solution is sufficiently sparse and the matrix A satisfies certain properties (see the mathematical definition
in Supporting Information on
minimization. Suppose there is an algorithm
that can solve this optimization problem , theoretical studies have
shown that if the true solution is sufficiently sparse and the matrix A satisfies certain properties (see the mathematical definition
in Supporting Information on 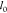 minimization), then the solution to
minimization), then the solution to 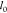 minimization is unique and exactly the
true solution.76,77
minimization is unique and exactly the
true solution.76,77
Although this appears promising
in theory, it misses a critical
element: an efficient algorithm to solve 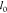 minimization. In fact, even before the
theoretical research on uniqueness, by the 1990s it had been proven
that
minimization. In fact, even before the
theoretical research on uniqueness, by the 1990s it had been proven
that 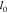 minimization is an NP-hard problem,78 meaning it cannot be solved in polynomial time.
The only available methods involved exhaustive search or highly specialized
algorithms, which limited its application to even moderately sized
problems, let alone processing images in CSR.
minimization is an NP-hard problem,78 meaning it cannot be solved in polynomial time.
The only available methods involved exhaustive search or highly specialized
algorithms, which limited its application to even moderately sized
problems, let alone processing images in CSR.
This necessitated
an alternative approach to 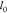 minimization. Before delving into that,
it is worth noting that delineating the boundaries between tractable
and intractable instances of
minimization. Before delving into that,
it is worth noting that delineating the boundaries between tractable
and intractable instances of 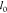 minimization remains an active research
topic. In recent years, direct solutions to
minimization remains an active research
topic. In recent years, direct solutions to 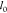 minimization have seen renewed interest.79 For example, a 2016 study80 introduced a deconvolution algorithm for high-density emissive
fluorophores in single-frame wide-field super-resolution imaging.
This approach modeled high-density localization as
minimization have seen renewed interest.79 For example, a 2016 study80 introduced a deconvolution algorithm for high-density emissive
fluorophores in single-frame wide-field super-resolution imaging.
This approach modeled high-density localization as 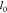 norm regularization and proposed an iterative
algorithm called sparse image deconvolution and reconstruction (SPIDER)
to solve
norm regularization and proposed an iterative
algorithm called sparse image deconvolution and reconstruction (SPIDER)
to solve 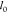 minimization. The study achieved SR imaging
for mitochondria using total internal reflection fluorescence (TIRF)
data (Figure 6(A)).
minimization. The study achieved SR imaging
for mitochondria using total internal reflection fluorescence (TIRF)
data (Figure 6(A)).
The difficulty of solving 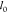 minimization lies primarily in the properties
of the
minimization lies primarily in the properties
of the 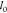 norm itself. In contrast, because the
norm itself. In contrast, because the 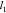 norm is convex, its optimization is much
easier:
norm is convex, its optimization is much
easier:
 |
30 |
In the literature, this is referred to as
the basis pursuit (BP) problem. This raises a fundamental question:
can 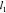 minimization replace
minimization replace 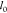 minimization? Using the concept of mutual
coherence, it has been shown that if the true solution is sufficiently
sparse and the matrix A satisfies certain properties,
then the solution to
minimization? Using the concept of mutual
coherence, it has been shown that if the true solution is sufficiently
sparse and the matrix A satisfies certain properties,
then the solution to 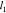 minimization is unique and corresponds
to the true solution.76,81 Detailed definitions are provided
in the Supporting Information on
minimization is unique and corresponds
to the true solution.76,81 Detailed definitions are provided
in the Supporting Information on 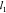 minimization.
minimization.
However, real-world signals are often not strictly sparse; they may not contain only a few nonzero elements. Instead, they are often “soft sparse”, meaning a small number of elements are large while many others are small but not exactly zero. This leads to the concept of compressibility.
In simple terms, a vector is considered compressible if setting most of its smaller elements to zero and retaining only the largest ones introduces only a small error compared to the original vector. Compressibility is closely related to sparsity, and vectors that are compressible but not strictly sparse are referred to as inexact sparse vectors.
Another source of inexactness is noise, which is not considered in the BP model. To address this, we introduce an error level η(e) corresponding to the real noise and modify BP into the following form:
 |
31 |
This optimization problem is named the quadratically constrained basis pursuit (QCBP). Notably, the minimizer of QCBP is not guaranteed to be unique.
The question then becomes, if the true signal is compressible, can QCBP recover or approximate the true image? Mathematically, is the error between any minimizer x* of QCBP and the true image bounded?
Compressed Sensing
In 2006, milestone work by Donoho, Candès, Justin Romberg, and Terence Tao provided conclusive answers to these questions.83,84 Their contributions collectively became known as compressed sensing (CS) Theory, starting a revolution in signal processing.
The seminal works of Candès and Tao introduced the famous restricted isometry property (RIP).85,86 The detailed definition is presented in the Supporting Information on RIP. Briefly, if the true signal is compressible and matrix A satisfies the RIP (with a certain constant), then the error between any minimizer of QCBP and the true signal is bounded by a constant. This constant depends on factors such as sparsity, SNR, the RIP constant, and the compressibility error. When the true signal is sufficiently compressible and the SNR is high, this error becomes very small, meaning the solution recovered by QCBP is close to the true signal. Moreover, QCBP can be solved efficiently using existing algorithms.
With this, another problem remains: do matrices exist or can they be designed to satisfy the necessary properties for sparse recovery?
In practice, the ability to design matrix A is crucial, as the rows of A often have physical interpretations. For example, in magnetic resonance imaging (MRI), matrix A is a partial Fourier matrix, where each row represents a single MRI scan. Similarly, in other forms of imaging, the number of rows in A (denoted as m) corresponds to the number of samples taken. This is why A is referred to as the “sensing” matrix in CS. Traditionally, the minimal sampling required was constrained by the Shannon-Nyquist sampling theory.87
Thus, the refined version of the question becomes do matrices exist in practice that satisfy the requirements for sparse recovery, and what is the minimum number of samples required to guarantee this property?
Donoho, Candès, and Tao addressed this question using a special class of matrices: random matrices.83,84 Simply put, for three types of random matrices—randomly chosen rows from a unitary matrix, random Gaussian matrices, and random Bernoulli matrices—the required number of samples m can be much smaller than the dimension n while still satisfying RIP with high probability. Combined with earlier results, this means that if the true signal is sparse or compressible, then even when m ≪ n, QCBP can recover the true signal with high probability. This allows sparse signals to be reconstructed using far fewer samples than traditional methods require, which is the essence of the term “compressed” sensing. The mathematical definitions are provided in the Supporting Information on RIP Matrices.
With this, CS theory addresses a major question: it challenges the long-held Shannon–Nyquist sampling limit, revolutionizing the field of signal processing.
Naturally, CS has also impacted fluorescence imaging88 and super-resolution fields. In 2009, CS was first proposed as a method to recover sub-wavelength information from far-field optical images under coherent light imaging.89 The study assumed the object was spatially sparse and simulated low-pass filtering at different cutoff frequencies on the synthetic data. Using eq 30 for recovery, the results demonstrated SR, validating the feasibility of the method. Subsequently, the same team applied CS to partially incoherent light imaging,90 incoherent light,91 and coherent diffractive imaging82 (Figure 6(B)). In all cases, assuming sparsity, sparse recovery enabled SR to some extents.
From this point on, many subsequent works have directly applied CS to achieve SR, especially in cases like SMLM, where the data are genuinely sparse. For instance, the pioneering proposed CS-STORM, employing sparse recovery methods to reconstruct higher-density frames and reduce the number of frames needed for SMLM.92
On the other hand, the primary goal of CS itself is to reduce sampling rates. A more direct application involves designing optical devices to lower the number of elements or imaging instances required. A representative example is single-pixel imaging.93 In fluorescence microscopy, point-scanning techniques are often employed to encode sparsity, such as using CS to accelerate two-photon acquisition.94 These applications, yet, extend beyond the scope of CSR and can be explored in related references.95
However, a gap persists between the CS theory and CSR within the field of microscopy. The imaging matrix P in microscopy functions as a low-pass filter with deterministic sampling, which omits high frequencies and has not been demonstrated to meet the RIP. Indeed, to date, no deterministic matrix has been proven to satisfy RIP; all sensing matrices known to align with CS theory exhibit random elements. This issue has already been recognized within the CS field itself. In 2012, Candès remarked in another paper,96 “This (super-resolution) is very different from a typical compressed sensing problem in which we wish to interpolate—and not extrapolate—the spectrum.”
To address this issue, more advanced extensions of CS theory have been developed.96 Given the technical complexity of this topic, we provide a brief discussion in the Supporting Information.
Generalized Sparsity Prior
As previously mentioned, sparsity refers to the knowledge that the true solution can be represented using only a few terms. In the context of the l0 norm, sparsity implies that the term is a single element of a vector. In this sense, both TV and DWT can also be considered forms of sparsity priors. Specifically, TV can be interpreted as a sparse transform in the gradient domain, where discontinuities in the image, such as edges, are sparse. Similarly, DWT achieves sparsity by representing an image in the wavelet domain. The combination of Compressed Sensing and DWT has been a significant success in MRI.97 Utilizing wavelet transformations to encode MRI images sparsely allows for reconstruction from undersampled data, greatly reducing the number of required scans and, consequently, saving both time and cost. This advancement has had significant historical importance in promoting CS.
The success of CS, particularly
through the application of the 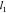 norm, has inspired the development of CSR
methods that incorporate generalized forms of sparsity. These models
are collectively referred to as low-dimensional sparse models.98 Given that this topic is beyond the scope of
this Review and remains highly technical, with applications in biological
imaging still under development, we will not delve into further details
here. Interested readers are encouraged to consult the Supporting Information on “Generalized
Sparsity Prior”.
norm, has inspired the development of CSR
methods that incorporate generalized forms of sparsity. These models
are collectively referred to as low-dimensional sparse models.98 Given that this topic is beyond the scope of
this Review and remains highly technical, with applications in biological
imaging still under development, we will not delve into further details
here. Interested readers are encouraged to consult the Supporting Information on “Generalized
Sparsity Prior”.
Optimization and Parameter Tuning
The introduction
of nonlinear regularization terms brings new challenges to optimization.
For example, TV and 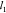 minimization involve nonsmooth functions
that cannot be directly addressed using gradient descent. This necessitates
the development of specialized optimization algorithms. Another challenge
is parameter tuning, particularly the adjustment of λ in the
objective function. Given the technical complexity of these topics,
interested readers are encouraged to refer to the Supporting Information on “Operator Splitting Optimization
Methods and Parameter Tuning”.
minimization involve nonsmooth functions
that cannot be directly addressed using gradient descent. This necessitates
the development of specialized optimization algorithms. Another challenge
is parameter tuning, particularly the adjustment of λ in the
objective function. Given the technical complexity of these topics,
interested readers are encouraged to refer to the Supporting Information on “Operator Splitting Optimization
Methods and Parameter Tuning”.
Sparse-Deconvolution
One major advancement in model-based CSR is sparse-deconvolution, proposed by Zhao et al. in 2022.10 This method marks a breakthrough in general-purpose CSR.
As mentioned earlier, RL deconvolution has inherent super-resolution capabilities; however, its performance degrades in the presence of noise. Sparse-deconvolution leverages a priori knowledge about the sparsity and continuity of biological structures to enhance the resolution through deconvolution algorithms. This principle is illustrated in Figure 6(C).
The continuity
prior assesses the relationship between pixel values
along both spatial and temporal axes. According to sampling theory,
the FWHM of the PSF is at least two pixels in the data, making sparse
pointillist structures continuous within that region spatially. Additionally,
if the movement of the biological sample between two consecutive time
points is smaller than the lateral resolution, then the structures
are considered continuous along the temporal axis. In contrast, noise
typically lacks continuity along these axes. The continuity prior
to this is quantified using the Hessian matrix continuity, which regularizes
second-order gradients. This approach is derived from Hessian–Schatten
regularization99,100 but employs the 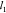 norm instead:
norm instead:
 |
32 |
where ∂pqx represents the second-order differential operator along image directions p and q.
Compared to TV, the Hessian prior represents a significant advancement in reducing nonimage features. It indeed shows that the “Hessian-based regularizer is most effective for describing locally smooth features present in biological specimens”.101 Prior to the advent of sparse-deconvolution, Hessian regularization was combined with Wiener-SIM to propose Hessian-SIM.9 This approach achieves artifact-minimized super-resolution (SR) images using less than 10% of the photon dose required by conventional SIM, while substantially outperforming current algorithms at low signal intensities.
Another important prior is sparsity, but it differs
from 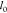 norm sparsity. An increase in spatial resolution
in any fluorescence microscope always results in a smaller PSF. Compared
with conventional microscopy, the convolution of the object with this
smaller PSF in SR imaging leads to a relative increase in sparsity.
This sparsity prior is modeled using the
norm sparsity. An increase in spatial resolution
in any fluorescence microscope always results in a smaller PSF. Compared
with conventional microscopy, the convolution of the object with this
smaller PSF in SR imaging leads to a relative increase in sparsity.
This sparsity prior is modeled using the  norm. (Note that this background is different
from compressed sensing.)
norm. (Note that this background is different
from compressed sensing.)
Additionally, sparse deconvolution accounts for the removal of background light by decomposing the image using wavelets and retaining only the first few coefficients. This approach has proven to be a crucial factor in the success of the algorithm.
The basic function of sparse-deconvolution is
 |
33 |
where b is background light to remove and λ and ξ are regularization parameters.
Different from iterative deconvolution, sparse-deconvolution does not solve the optimization function directly but iteratively solves it in two steps:
 |
34 |
The second step corresponds to RL. Experiments show that the best super-resolution effect can be achieved only by two-stage optimization.
Sparse-deconvolution improves resolution and contrast compared to raw RL. The resolving power of sparse-deconvolution was verified by comparing the results of known structures (nuclear pores) with SMIM. Combined with SIM, sparse-deconvolution achieves ultrafast 60 nm resolution in live cells (Figure 6(C)). Sparse-deconvolution has universal live-cell super-resolution and improved resolution of spinning-disc confocal SIM (SD-SIM), wide-field, confocal, two-photon, and expansion microscopes.
Subsequent research has explored one-stage optimization approaches, but it consistently demonstrates that combining sparsity and continuity priors is the most effective method.102 However, the impact of sparse-deconvolution also raises additional questions, such as its theoretical foundation and parameter adjustment, among other concerns.
Note on Model-based CSR
Model-based CSR represents substantial progress compared with earlier explorations. However, several significant challenges remain. First, while model-based CSR employs handcrafted priors that are effective, these priors lack a unified design approach and may not generalize well across diverse applications. Second, stronger theoretical foundations are needed to justify the use of these priors and their outcomes. Additionally, parameter tuning and ensuring computational feasibility remain difficult challenges. Notably, there is no effective method for solving nonconvex regularization.
Despite these hurdles, model-based CSR has laid a strong foundation for the field. While it is still too early to draw definitive conclusions about model-based CSR, we can refer to the famous quote: “All models are wrong, but some are useful.”
Data-Driven CSR
While model-based CSR relies on manually designed priors, an entirely different approach avoids explicitly modeling these priors and instead uses genuine high-resolution images as examples. By leveraging the features of these images to constrain the super-resolution results, the data itself serve as the prior; these are known as “data priors”.
To implement this approach, tools capable of directly extracting features from the data are essential. In computer science, machine learning is one such tool. This shift has been accelerated by the rise of deep learning22 (DL), a specific machine learning method that relies on data to optimize artificial neural networks (ANNs) to approximate complex function mappings. DL has revolutionized various fields, including CSR.
This section introduces deep learning for CSR (DL-CSR). For readers unfamiliar with DL, we briefly explain its foundational concepts (Figure 7(A)), although a comprehensive understanding will require consulting more detailed tutorials.103
Figure 7.
Concepts and representative works in DL-CSR. (A) Workflow of deep learning for CSR. Details are provided in the main text. (B–D) Supervised learning CSR. (B) Representative two-color DFCAN images of the mitochondrial inner membrane (green) and nucleoids (magenta). Top left: a fraction of the corresponding wide-field image. Scale bar, 2 μm. (C) SFSRM’s performance on immunostained microtubules in fixed Beas2B cells. WF: wide-field; ANNAPALM is a deep learning model for SMLM reconstruction.108 Scale bar: 1 μm. (D) Super-resolved images of bovine pulmonary artery endothelial cells (BPAECs) by a GAN SR model. (E) Unsupervised learning CSR. Representative SR images reconstructed by ZS-DeconvNet of the F-actin cytoskeleton (cyan) and myosin-II (orange). DeepCAD is a self-supervised denoising model.109 Scale bar: 5 μm. (F) Self-supervised CSR for 4D SR with isotropic resolution. Results of the cascaded deep learning process on live U2OS cells expressing lysosomal marker LAMP1-GFP (cyan) and additionally labeled with LysoTracker Red to mark the lysosome interior (magenta). Scale bars: 5 μm (left large subfigure) and 500 nm (right small subfigures). (A) was created in https://BioRender.com. (B) is reprinted with permission from ref (110). Copyright 2021 The Authors. (C) is reprinted with permission from ref (111). Copyright 2023 The Authors, licensed under a Creative Common Attribution (CC BY) 4.0 license. (D) is reprinted with permission from ref (11). Copyright 2019 The Authors. (E) is reprinted with permission from ref (112). Copyright 2024 The Authors, licensed under a Creative Common Attribution (CC BY) 4.0 license. (F) is reprinted with permission from ref (113). Copyright 2023 The Authors, licensed under a Creative Common Attribution (CC BY) 4.0 license.
Deep-Learning
Suppose we have a large data set of paired low-resolution (LR, e.g., wide-field microscopy) and high-resolution (HR, e.g., super-resolution fluorescence microscopy) images. Denote the LR images as {yi}Ni = 1 (termed data) and their corresponding HR images as {xi}Ni = 1 (termed labels or ground truths). The imaging process that connects them can be approximated by yi ≈ psf⊗xi, where the approximation accounts for noise.
Supervised machine learning refers to fitting a model using these paired data to transform yi to xi. Typically, the model is parametrized, and these parameters are learned by minimizing the average value of a loss function that quantifies discrepancies between the predicted HR output and the true HR label. This process is called training. If the training process uses a data set without labels but only data, it is called unsupervised machine learning. A special unsupervised learning is self-supervised learning; it generates pseudo-labels from data only and trains the model as supervised learning. After training, we expect the trained model to infer accurate HR outputs for new LR inputs outside the training set, a phase known as inference. The ability of the model to perform well on unseen data that were not part of the training set is called generalization.
A major challenge in machine learning is the risk of overfitting.114 Overfitting occurs when a model memorizes the training data too well but fails to generalize to unseen data. To determine whether the model can generalize and to guide training, a validation data set is needed. Additionally, to address overfitting, alongside increasing the amount of training data, regularization techniques are required, a concept familiar in CSR.
DL is a type of machine learning in which the model is an artificial neural network (ANN). Inspired by the structure of neural connectivity in the brain, we designed an ANN consisting of multiple layers of artificial neurons. Each artificial neuron, known as a node, maps inputs to outputs through a mathematical function:
| 35 |
where xi represents a single input variable (among n such inputs), wi represents a weight for that input, b represents a learnable bias term, and σ represents a nonlinear activation function that takes a single input and returns a single output. The weights and biases are the parameters to be fitted in an artificial neuron. Collectively, the parameters of all artificial neurons are the parameters to be fitted in an entire ANN.
A key property of ANNs is that a two-layer ANN is sufficient to approximate almost any (with a slight request) mathematical function to an arbitrary level of accuracy, provided there are enough artificial neurons. This capability may explain the success of DL. In a simple ANN, the output of one layer serves as the input to the next (Figure 7(A)). Alternatively, there are various approaches for arranging artificial neurons in more complex structures. For image applications, a popular architecture is a convolutional neural network (CNN).
Supervised deep learning uses data and corresponding labels to train an ANN. The primary tool for this process is stochastic optimization. In each iteration, the ANN randomly selects a small batch of the data set, uses the data in the batch as input, and computes the output. The error between the output and labels is back-propagated to each node in the network in a process called backpropagation. The ANN then uses gradient descent to update the parameters based on the calculated error. After a sufficient number of iterations, the ANN reduces the loss function on the training set to a sufficiently small value.
If the ANN learns all transformations automatically during training, mapping raw data directly to the desired output, the framework is called end-to-end. Yet, it proves to be suboptimal when a particular prior occurs for specific task, such as in CSR. Thus, useful model priors can be designed to enhance DL performance and sometimes even essential for generalization.104
Once training is complete, the ANN can be deployed to generate new low-resolution images for SR. DL-CSR can also be integrated into the broader framework of the basic function:
 |
36 |
where f represents the ANN and θ are its parameters.
The main flow of the DL is outlined above. Due to its powerful feature extraction capabilities, these principles are fundamentally the same across different domains. In fact, the primary difference between DL-CSR in microscopy and DL natural image SR lies in the data used to train the DL models. Therefore, readers interested in the broader scope of DL-based SR can directly refer to reviews on natural image SR.105−107 Here, we focus specifically on representative advancements in DL-CSR for microscopy.
Supervised Learning CSR
Variations in supervised learning CSR methods typically arise from three main aspects: the training data, the neural network architecture, and the specific model priors used.
First, the quality and nature of the training data significantly influence the performance of the DL model. The most straightforward approach is to collect paired data using bimodal methods. For example, one of the earliest works in DL-CSR utilized two data sets: one used different numerical apertures (10×/0.4-NA and 20×/0.75-NA) in wide-field microscopy, and another used confocal and STED imaging to generate paired LR and HR images.11 In some cases, specific protocols are required to generate matched data; for instance, Xu et al. performed in vitro imaging of acute slices of SEP-GluA2 brains to produce a paired data set, aiming to improve the resolution of in vivo two-photon imaging.114
However, obtaining paired data is very challenging, especially when imaging with different modalities, where registration becomes difficult. Additionally, maintaining the consistency of the sample before and after imaging is hard. When physical methods for generating paired data are impractical, computational approaches can be employed. One strategy is to collect high-resolution images and simulate the corresponding low-resolution counterparts. For example, Qiao et al. used SIM to acquire high-resolution images of four cellular structures under varying illumination conditions.110 They averaged these SIM images to generate wide-field images at different SNR levels, thus creating paired data sets. Similarly, Wang et al. first acquired high-resolution point-scanning images and then used a wave optics model of light-field microscopy to project these high-resolution 3D images into 2D light-field images for training.115 Despite this progress, acquiring high-resolution images is still time-consuming and resource-intensive, especially when SR fluorescence microscopy is required.
Another significant aspect is the evolution of neural network architectures. Using CNNs as basic building blocks, various complex structures can be constructed. Among these, the most commonly used architectures for image processing tasks are U-Net116 and 3D-Unet,117 which follow an encoder–decoder architecture. CARE (content-aware image restoration) was one of the earliest works to apply U-Net to microscopy image restoration118 and has since become the benchmark for many subsequent DL-CSR models. For example, XTC (cross-trained CARE) utilized the CARE structure for SR tasks using previously mentioned data from ex vivo super-resolution and in vivo imaging modalities.114 Another structural advancement involves the use of attention mechanisms,119 which dynamically adjust the weights between artificial neurons, allowing the network to learn more representative features. A representative work in computer vision that employs this technique is RCAN (residual channel attention networks).120 Later, it was used in SR microscopy to denoise and extend resolution121 and was extended to DFCAN (deep Fourier channel attention network) incorporating attention mechanisms in the frequency domain.110
U-Net has also been integrated into generative adversarial networks (GANs).122 By combining a generator and a discriminator, GAN-based models enhance the network’s capabilities. For instance, Wang et al. used a GAN model to transform diffraction-limited input images into super-resolved ones.11 Chen et al. proposed single-frame super-resolution microscopy (SFSRM), further employed enhanced super-resolution generative adversarial networks (ESRGAN),123 and introduced improved loss functions to enhance the reliability of CSR training results.111 In addition to these advancements, network architectures also vary in the design of loss functions, specific network layers, and other implementation details; for details, see more comprehensive reviews.105−107
The third major development is task prior utilization, modeled as a regularization term. Since SR is inherently an ill-posed problem, deep learning models are particularly prone to overfitting. Introducing explicit regularization can improve the model generalizability. Beyond the commonly used regularization methods in DL,124 incorporating domain-specific priors has been shown to be highly effective.104 These priors can be embedded into the network structure or the loss function. A prime example is DFCAN, which uses a Fourier channel attention (FCA) mechanism to exploit the characteristics of the power spectrum of distinct feature maps in the Fourier domain, resulting in more stable training and improved generalization. Additionally, Chen et al. used edge maps from low-resolution images as guidance to design a multicomponent regularizer.111 Bouchard et al. proposed TA-GAN (task-assisted generative adversarial network), which employs auxiliary tasks, such as segmentation or localization, to guide SR training.125 These results demonstrate that while DL-based methods are inherently data-driven, introducing priors is a critical step in stabilizing networks and improving generalizability, similar to model-based CSR.
Unsupervised Learning CSR
The lack of sufficient paired data is a major bottleneck in broadly applying supervised learning to CSR. In the context of live-cell imaging, obtaining SR images as ground truths is often infeasible. Unsupervised learning provides a potential solution to this challenge but introduces additional difficulties. Currently, applications of unsupervised learning in CSR are much less common than supervised approaches and are not yet developed enough to form a conceptual category; we can discuss only existing case studies.
One typical scenario stems from the high cost of acquiring high-resolution images, while it is generally easier to obtain abundant low-resolution data. Qiao et al. proposed ZS-DeconvNet (zero-shot deconvolution networks), where the objective function is given as112
| 37 |
Here, θ represents the neural network parameters, fθ denotes the network, and ↓ refers to downsampling. Zero-shot implies that high-resolution data are not used to train fθ. However, directly training with this objective can lead to instability. To address this, ZS-DeconvNet employs an additional denoisingr network and a Hessian regularization term to stabilize convergence. The denoisingr network, named R2R, is trained in a self-supervised manner, which will be introduced in the following paragraph. ZS-DeconvNet enhances the resolution of microscope images by more than 1.5-fold over the diffraction limit, with 10-fold lower fluorescence than ordinary super-resolution imaging conditions. Nevertheless, even though it is labeled as zero-shot, training the neural network still requires a large amount of data, and generalization confers still a problem.
Self-supervised learning is a special case of unsupervised learning, where pseudolabels are generated from unlabeled data and used to train neural networks in a supervised fashion. In the R2R (recorrupted-to-recorrupted) example above, a single noisy image is transformed to generate two new noisy versions, which are then treated as data-label pairs for network training.126 Under certain assumptions, R2R is theoretically proven to be equivalent to supervised learning. The principle behind self-supervised learning is that supervision signals are inherently present in the data and can be extracted by specific methods.
A notable application of self-supervised learning in CSR is improving the axial resolution. Axial resolution in microscopy is typically much lower than the lateral resolution. By treating lateral 2D slices from 3D data sets as high-resolution images and simulating low-resolution images computationally, neural networks can be trained and later applied to infer axial 2D images. For example, Li et al. combined this approach with optical setup adjustments to enhance SIM to achieve ∼120 nm isotropic resolution.113 Park et al.127 further employed cycleGAN to eliminate the need for computationally generated low-resolution images, training directly on unpaired lateral and axial 2D images.128 Although unsupervised and self-supervised CSR research remains limited, these approaches hold promise for future advancements.
Note on Deep-Leaning CSR
DL-CSR employs a data-driven framework, extracting priors directly from training data unlike model-based CSR, which relies on handcrafted prior modeling. Given abundant data, an appropriate network architecture, and well-tuned training processes, DL-CSR often surpasses traditional methods. Moreover, once trained, DL-CSR models are both fast and flexible, making them suitable for specific tasks.
We present the results of several representative studies mentioned above in Figure 7(B–F). As shown for supervised learning examples, the SR images generated by DFCAN from wide-field mitochondrial images can clearly resolve mitochondrial inner membranes and nucleoids110 (Figure 7 (B)), SFSRM achieves super-resolution of wide-field images to match the results of SMLM111 (Figure 7 (C)), and cross-modality SR digitally enhances low numerical aperture (10×/0.4-NA) images to high numerical aperture quality11 (Figure 7 (D)). Figure 7(E) illustrates unsupervised CSR, showcasing long-term SR imaging by using ZS-DeconvNet. It achieves super-resolution of the F-actin cytoskeleton and myosin-II, which are dynamic and photosensitive biological processes.112Figure 7(F) demonstrates the application of self-supervised learning CSR to achieve isotropic 4D SIM resolution.113
However, the comparison between model-based CSR and DL-CSR is nuanced. DL-CSR’s performance is highly dependent on the quality and size of the training data. Obtaining large, high-quality, diverse data sets for CSR is challenging, particularly in live-cell imaging scenarios requiring ultrafast and ultrahigh-resolution imaging. In such cases, SR ground truth data are often entirely unavailable, rendering DL-CSR incapable of learning the SR mapping. While unsupervised learning in CSR offers some promise, progress in this area is still limited. Conversely, model-based CSR can be applied under these challenging conditions.
Another significant challenge is generalization. Training data for DL-CSR often include only a limited set of cellular structures. When faced with the task of super-resolving novel structures, the performance of DL-CSR can degrade significantly. In contrast, model-based CSR typically exhibits much better generalization capabilities.
Stability is another growing concern for DL methods, particularly in CSR. For instance, experiments have shown that DL models for MRI reconstruction can produce unstable outputs—minor changes in the test image can lead to drastic differences in the reconstruction, or vice versa.129 This instability could result in severe clinical consequences, such as misidentifying tumors or overlooking critical pathological features. As DL models become increasingly complex, instability issues may worsen, leading to hallucinations, a topic we will explore further in the next section on Foundation models.
A more fundamental issue is that DL-CSR remains a black box to this day, which is particularly challenging for the field of SR, where interpretability is paramount.130 We concur with the view131 that “if based on a solid mathematical model of the imaging and noise processes, carefully executed deconvolution should be the preferred choice for post-processing techniques”.
Despite these challenges, several promising trends are emerging to address these issues. The field of DL itself is progressing toward solutions, as researchers across various disciplines work on adopting DL responsibly. Research on interpretable DL aims to demystify the “black box” nature of these models.132 Until significant breakthroughs are achieved, a practical approach involves providing uncertainty metrics to inform users of potential risks, with Bayesian DL offering a viable pathway.133
For CSR, the key challenge is data dependency, highlighting the need for more high-quality, publicly available data sets; data sets like BioSR serve as an inspiring example.110 Additionally, further applications of unsupervised learning can help mitigate some of these data-related constraints.
Finally, considering the complementary strengths and weaknesses of model-based and data-driven approaches, a promising direction is their integration. Combining these methodologies could leverage their respective advantages, leading to more robust and effective CSR solutions. This leads us to the latest advancements in CSR, which will be introduced in the next section.
The Future of Convergence of Models and Data
Since the 2010s, there has been a growing advocacy for a “fourth paradigm”134 of research driven by data-based scientific discovery.135 The debate between models and data is not new. A historical example is the contrast between fitting planetary orbits using detailed observational data and Newton’s derivation of laws. In the context of CSR, we, like many across various fields, believe that these approaches are not mutually exclusive.136 Rather, their integration and complementary advancement present the most promising path forward.
Emerging as the cutting-edge trend in CSR is the convergence of model-based and data-driven methods. We will draw on recent works from the past several years to trace this trend and illustrate how combining these methodologies can lead to significant progress.
Image Pre-Processing
Fluorescence imaging faces fundamental limitations due to various degrading factors, particularly stochastic shot-noise inherent in photon detection, which restricts the quality of images recorded by cameras. CSR is especially sensitive to noise; as the analytical continuation theorem suggests, deconvolution can theoretically achieve infinite resolution under noise-free conditions. However, in live-cell imaging, photon budgets are often restricted, necessitating the use of moderate or low light intensities, which increase noise levels.
Recent advancements in DL image preprocessing have led to transformative improvements.137 Sophisticated self-supervised denoising methods enable high SNR imaging with significantly fewer photons and in some cases even surpass the shot-noise limit.138 This has made the combination of advanced DL denoising techniques and CSR algorithms a highly promising trend.
One work by Qiao et al. proposed a rationalized deep learning (rDL) approach.139 By leveraging the physical properties of SIM patterns to constrain network outputs, this method significantly enhances the denoising of raw SIM images. This results in over 10-fold improved SR reconstruction at lower illumination intensities compared to other computational approaches. Another notable example introduced a novel DL-based denoising method using specific fluorescence label methods with reduced data dependency.140 This method is combined with sparse-deconvolution to achieve single-frame live-cell super-resolution imaging, demonstrating the potential of integrating advanced DL techniques with CSR methodologies.
In addition to noise, background light—comprising defocused signal light and scattered light—significantly affects imaging quality. Effective background removal is crucial for sparse-deconvolution to achieve robust CSR. However, methods like wavelet-based background suppression often improve the resolution at the expense of removing weak signals or altering reconstruction linearity. A notable example is BF-SIM, which introduced a physical model-based background suppression algorithm optimized for 2D-SIM. This approach demonstrated that effective background removal can enhance the fidelity of sparse-deconvolution results.141
Other factors, such as defocusing and fluorescence drift, also impact the image quality. Continued advancements in DL-based low-level image processing are anticipated to yield increasingly higher-quality images. Therefore, obtaining the highest-quality images before applying CSR algorithms is crucial to achieving optimal results.
Foundation Models
Recently, two novel neural network architectures, namely, transformers142 and the diffusion model,143 have driven significant progress in DL, supported by large data sets and specialized training methods. This progress has culminated in the emergence of Foundation Models.
Originally developed for natural language processing, transformers employ complex attention mechanisms. When combined with massive data sets, transformers enable a new training paradigm called pretraining. This approach relies on unsupervised techniques, especially self-supervised learning, to extract intrinsic data structures from large data sets prior to fine-tuning for specific downstream tasks. Due to their enormous parameter sizes and remarkable generalization capabilities, these models are referred to as foundation models,144 with large language models (LLMs) being a prime example. Transformers have since been adapted for imaging tasks, leading to the development of image foundation models.145
In microscopy, traditional supervised learning methods are often limited to specific tasks such as CSR, requiring task-specific data sets for optimal performance. Ma et al. applied foundation model methods to microscopy restoration,146 leveraging the Swin transformer (an improved version of the transformer).147 They developed a foundation model called UniFMIR, which was trained on various restoration tasks using an aggregated large data set comprising 196 418 training samples from 14 public data sets (approximately 30 GB). UniFMIR demonstrated a strong performance on downstream single-image SR tasks, effectively reconstructing details in wide-field images to achieve SIM-level resolution. This success was evident across diverse cellular structures, including clathrin-coated pits, endoplasmic reticulum, microtubules, and actin filaments.
Another architecture, the diffusion model, is based on highly dimensional sampling processes and is particularly well-suited for image data. Beyond serving as discriminative foundation models, diffusion models support generative learning,148 an unsupervised approach that learns the probability distribution of data from large unlabeled data sets. This capability enables the generation of new, unseen data.
For supervised CSR, where obtaining high-resolution images can be challenging, generative learning offers a potential solution by creating new data sets from limited existing high-resolution data. Saguy et al. provided a proof-of-concept in bioimaging by training a diffusion model on SR fluorescence data of several organelles.149 The generated data were then used to train new supervised models for single-image SR, yielding results comparable to those from traditional data collection approaches.
However, generative approaches remain contentious in scientific research due to the risk of hallucinations, a common issue found in foundation models.
Hallucination of the Foundation Model
Foundation models have introduced a new challenge: hallucination.150 In practice, these models may generate outputs that are misaligned with their training data or actual phenomena. For example, large language models sometimes produce a nonsensical text. This phenomenon, which is akin to DL instability, currently lacks a comprehensive explanation. In CSR, this uncertainty limits the broader adoption of foundation models as it becomes difficult to discern whether the results represent genuine SR details or artifacts.
Despite these challenges, foundation models have already made a significant impact globally; just consider the widespread recognition of ChatGPT.151 Their potential in CSR remains promising, and ongoing research may address these limitations to fully leverage their capabilities.
Hybrid of Model and DL Methods
Combining the strengths of physical priors and data-driven DL capabilities has emerged as a key trend in CSR. Here are some notable recent approaches:
Deep Image Prior (DIP)
Traditionally, the power of DL is attributed to priors derived from training data. Contrary to this belief, DIP demonstrates that the architecture of an untrained neural network itself can capture significant low-level image statistics, functioning as a form of regularization.152 In CSR, DIP replaces traditional regularization terms with an untrained neural network:
| 38 |
Here, z is a fixed random noise vector and fθ represents the network structure. The minimizer θ* is obtained using an optimizer such as gradient descent starting from a random initialization of parameters θ. The result of the high-resolution image is obtained as x* = fθ*(z). Without any training data, DIP showed remarkable SR performance. Incorporating model-based regularization (e.g., TV) further enhances results, highlighting the potential of DIP to mitigate DL-CSR’s dependency on data.
Learned Prior
Learned priors use DL to design regularization terms in the basic function. An instance is total deep variation (TDV).153 TDV is a convolutional neural network that extracts local features on multiple scales and in successive blocks. TDV is set as regularization term in the basic function, and optimization is performed in optimal control formulation. The integrated TDV and SIM reconstruction in ref154 , named TDV-SIM, outperforms conventional or DL methods in suppressing artifacts and hallucinations while maintaining resolutions.
Plug-and-Play Method
Plug-and-play (PnP) methods160 integrate DL-based denoisiers as proximal operators in model-based CSR optimization, enhancing stability while retaining the original CSR structure. Though widely used in general image restoration, their application in microscopy-specific CSR remains underexplored.
Algorithm Unrolling
Algorithm unrolling replaces iterative optimization steps in traditional methods with neural network layers.161 This approach automates parameter tuning using data, improving stability and inference speed. For example, Li et al. developed the Richardson–Lucy network (RLN), a 3D microscopy deconvolution method that combines the forward/backward projector structure of RL deconvolution with DL.156 Benchmarks show that RLN produces fewer artifacts compared to RL or purely data-driven models while requiring fewer parameters.
These examples illustrate the trend of integrating model-based and data-driven frameworks. For a more comprehensive overview, readers can refer to ref (136).
Miscellaneous Specialized Methods
Emerging CSR methods also leverage unique physical priors. For example, SUPPOSE (super position of virtual point sources) is similar to optimization-based deconvolution but models the SR target as a collection of virtual points of identical intensity.157 This approach results in a nonconvex optimization problem, which is originally solved using genetic algorithms. Subsequently, Jiang et al. replaced genetic algorithms with gradient descent to develop A-PoD (adaptive moment estimation optimization-based pointillism deconvolution).13 A-PoD demonstrates a superior SR performance in Raman imaging. Another major class of CSR algorithms departs from deconvolution-based structures, utilizing fluorescence fluctuation information for SR. SRRF (super-resolution radial fluctuations) achieve SR imaging by analyzing radial gradient variations in fluorescence fluctuation signals,164 while eSRRF redefines key principles for estimating radiality and temporal analysis to enhance image reconstruction quality.165 By optimizing parameter ranges and acquisition configurations, eSRRF minimizes artifacts and nonlinear distortions, improving the overall fidelity to the underlying structure. MSSR (mean-shift super resolution) is a combination of SRRF and single-molecule deconvolution.158 MSSR enhances image resolution by iteratively shifting pixel intensities toward the local mean within a defined neighborhood, achieving approximately 2-fold resolution improvement.
Inspired by fluorescence fluctuations, an image-sharpening approach based on pixel reassignment was introduced to general microscope modalities and various fluorophore types.159 The main steps involve first preconditioning the raw image and then performing pixel reassignment, where pixel values are reassigned to neighboring locations according to the direction and magnitude of the localized image gradient.
Applications
In this section, we show the applications of CSR in biological imaging, particularly in advancing live-cell SR imaging and enabling biological discoveries.
Breaking the Photon Budget limit
Live-cell SR imaging poses significant challenges as it requires a delicate balance within a certain photon budget. CSR effectively addresses these barriers by extracting super-resolved information computationally while retaining the advantages of lower-resolution imaging methods, such as higher acquisition speed, improved SNR, and reduced phototoxicity.
For example, traditional deconvolution algorithms enhance the photon utilization efficiency of conventional microscopy. By incorporating advanced priors, such as continuation and sparsity constraints, sparse-deconvolution on SIM achieves approximately 60 nm resolution at frame rates up to 564 Hz.10 This capability allows researchers to resolve intricate structures, including small vesicular fusion pores, ring-shaped nuclear pores formed by nucleoporins, and the relative movements of inner and outer mitochondrial membranes in live cells.
Thanks to these advantages, CSR has been successfully applied to studies of mitochondrial nucleoid dynamics within mitochondrial cristae,110 rotational streaming of mitochondrial tubes, mitochondrial fission, cell division,121 and cytoskeletal dynamics in immune cells,113 as well as subcellular growth cone dynamics in living C. elegans embryos.166 The inferred high-resolution images provide more accurate segmentation and reveal finer details than those available from lower-resolution raw data, driving new insights into dynamic cellular processes.
Facilitating Biological Discoveries
CSR has powered live-cell SR imaging, enabling new observations and insights. Here, we illustrate its transformative impact through four examples spanning subcellular structures (actin), functional proteins (nuclear pore complexes), neural cells, and preclinical disease studies.
Actin
Actin forms gel-like, dynamic networks under the cell cortex with pore diameters of 50–200 nm. Resolving these networks requires both high spatial and temporal resolution, which is challenging for conventional live-cell SR methods. Using Sparse-SIM,10 researchers achieved sub-70 nm resolution and visualized weakly labeled actin filaments in live macrophages. Enhanced with advanced background subtraction,141 this technique facilitated the discovery of transient actin dynamics, including “actin blips” (localized puncta that emerge and disassemble), “actin clouds” (collaborative assemblies of actin spreading laterally), and “actin vortexes” (ring-like structures with spiral brightening) (Figure 8 (a)). These confirm CSR’s ability to reveal intricate cytoskeletal behaviors critical for cellular function.
Figure 8.
Biological discoveries enabled by CSR. (a) Three types of localized transient actin dynamics: an actin blip event that was small in size, an actin cloud event that was large, and an actin vortex event that was medium in size. (b) A representative example of nuclear pores labeled with POM121-Halo or POM121-3xmCherry in a live MCF7 cell. Two-dimensional structured illumination microscopy (2D-SIM) was reconstructed with the Wiener algorithm (first column), and sparse-SIM was reconstructed with the sparse-deconvolution algorithm (second column). NPC morphology and morphological dynamics (third column). (Top) A representative example of different nuclear pore structures labeled by POM121-Halo. (Bottom) A snapshot of the petaled gathering nuclear pore structure enclosed by a white box. The white box on the right is enlarged and shown at four time points to show the dynamic changes of nuclear pores. (c) XTC super-resolves SEP synapses in vivo. Comparison of the same in vivo 2p image before (left) and after XTC (middle). All images show a single axial slice. (d) Live-cell super-resolution pathology enables precise identification of genotype–phenotype correlations with different PLP1 mutations. The images show that MO3.13 cells were cotransfected with different proteins (green) and the ER marker protein Sec 61β (red). The scheme shows defects at different steps of the trafficking of PLP1 mutants to the plasma membrane in different PMD subtypes and the function of cholesterol or curcumin in facilitating the escape of the severe PLP1 mutants from ER. (a) is reprinted by permission from ref (141). Copyright 2023 The Authors, licensed under a Creative Common Attribution (CC BY) 4.0 license. (b) is reproduced with permission from ref (162). Licensed under a Creative Common Attribution (CC BY) 4.0 license. (c) is reprinted with permission from ref (114). Copyright 2023 The Authors, licensed under a Creative Common Attribution (CC BY) 4.0 license. (d) is reprinted with permission from ref (163). Copyright Science China Press, licensed under a Creative Common Attribution (CC BY) 4.0 license.
Nuclear Pore Complexes (NPCs)
NPCs are enormous, 8-fold symmetrical protein assemblies. The limited number of fluorophores labeling these proteins, which correlates with their few copy numbers, sets an upper limit on the photon budget for conventional SR fluorescence microscopy. Using labeled NPC proteins with Halo-SiR fluorophores and employing Sparse-SIM, 20 Hz imaging with enhanced contrast and photostability is achieved.162 This method resolved fine NPC structures and uncovered atypical morphological changes in the NPC clusters (Figure 8(b)). These findings demonstrate CSR’s capability to study dynamic protein assemblies in live cells at extreme spatiotemporal resolutions.
Synaptic Plasticity
Learning involves changes in glutamate receptors at synapses, which mediate neuronal communication. However, the sub-micrometer size and high density of synapses make them difficult to resolve in vivo, limiting the study of receptor dynamics during behavior. To address this challenge, a transgenic mouse line (SEP-GluA2) was developed, along with a computational pipeline that combines a DL image-restoration algorithm (XTC) with in vivo imaging114 (Figure 8(c)). This approach enabled super-resolution tracking of AMPA receptor (AMPAR) dynamics at synapses during behavior. By linking spatiotemporal changes in AMPAR content to synaptic strength and behavior, CSR has provided new insights into the molecular underpinnings of learning and memory.
Pelizaeus–Merzbacher Disease (PMD)
CSR has also made significant contributions to clinical research, as demonstrated by its application to Pelizaeus–Merzbacher disease (PMD), a hypomyelination leukodystrophy disorder.163 Using sparse-SIM, researchers investigated PLP1 mutations associated with PMD, identifying three distinct cellular phenotypes linked to clinical subtypes (Figure 8(d)): severe phenotypes resulting from ER retention, intermediate phenotypes involving lysosomal missorting, and mild phenotypes related to vesicle trafficking defects. This study provided the first cellular-level characterization of PMD subtypes, uncovering their pathogenic mechanisms and paving the way for targeted therapeutic strategies.
In summary, the transformative applications of CSR across diverse biological contexts demonstrate its immense potential to revolutionize biological research.
Integrating CSR with Multimodal Imaging
CSR can be seamlessly integrated with various imaging modalities. Below, we highlight CSR’s applications in several advanced imaging techniques, including SOFI, Raman microscopy, spatial omics, and expansion microscopy, showcasing its transformative impact on biological research.
SOFI
CSR methods have been employed to improve SOFI by addressing noise and background artifacts. For example, the SACD (autocorrelation with two-step deconvolution) technique introduces RL deconvolution to preprocess raw image sequences before calculating autocorrelated cumulants.12 This preprocessing step effectively removes out-of-focus and cytoplasmic background noise, enhances the effective switching contrast, and reduces random pixel-level noise while maintaining linearity across frames. By incorporating Fourier interpolation and advanced postprocessing, SACD achieves 2-fold improvements in lateral and axial resolution with as few as 20 raw image frames (Figure 9(a)). This integration exemplifies how CSR can significantly enhance the spatiotemporal resolution of the SOFI.
Figure 9.
Integration of CSR with multimodal imaging. (a) Application of SACD (with 20 frames) to high-throughput SR imaging of an ∼2.0 mm × 1.4 mm area containing more than 2000 cells. Microtubules are identified in COS-7 cells labeled with QD605. Scale bar, 0.1 mm. (b) (Top) DO-SRS images of LDs in CH2 and CD channels. The CH2 channel represents the distribution of old LDs (left), and the CD vibration image shows the distribution of newly synthesized LDs (middle). To compare the two images (left and middle), the images were overlaid (right). (Bottom) DO-SRS images were deconvolved using A-PoD, and the results clearly separate the signals of two different types of LDs, old versus newly synthesized (left, middle, and right) (c) Human SKBR3 cells stained with smFISH probes targeting GAPDH transcripts (white) (left) and after deconvolution with DW (right). Imaging: widefield, ×100 oil objective (NA 1.45). Maximum z-projection is shown. Blue, DNA. Scale bars, 20 μm in top panel, 5 μm in middle panel. (d) Superimposition of ONE microscopy images and cryo-EM data. The overview panel shows an exemplary ONE image (from a total of 648 ONE images, acquired from at least six gels) of GABAAR–Nb that are postexpansion labeled with NHS-ester dyes, followed by a magnified region of a single receptor. The last panel shows a cryo-EM–ONE overlay. [(a) is reproduced with permission from ref (12). Copyright 2023 The authors. (b) is reproduced with permission from ref (13)). Copyright 2023 The Authors. (c) is reproduced with permission from ref (14). Copyright 2024 The Authors, licensed under a Creative Common Attribution (CC BY) 4.0 license. (d) is reproduced with permission from ref (167). Copyright 2024 The Authors, licensed under a Creative Common Attribution (CC BY) 4.0 license.
Raman Microscopy
Stimulated Raman scattering (SRS) microscopy enables imaging of metabolic dynamics with high signal-to-noise ratios but is spatially constrained by the numerical aperture of the objective and the scattering cross-section of molecules. CSR addresses these limitations through algorithms such as the A-PoD.13 A-PoD achieved a spatial resolution below 59 nm on lipid droplet membranes, enabling a detailed analysis of protein and lipid distributions within cells. Further, A-PoD-enhanced deuterium oxide-probed SRS (DO-SRS) imaging differentiated newly synthesized lipids in lipid droplets and revealed metabolic changes in Drosophila brain samples under different diets (Figure 9(b)). This integration demonstrates CSR’s capability to enhance vibrational spectroscopy, offering nanoscopic insights into biomolecular dynamics and spatial localization.
Spatial Omics
CSR has proven to be particularly impactful in microscopy-based spatial transcriptomics, where densely packed molecular targets often exceed the diffraction limit. For instance, Deconwolf, an open-sourced accelerated version of the RL algorithm,14 improves the identification of transcripts in wide-field fluorescence microscopy. Applied to DNA and RNA fluorescence in situ hybridization (FISH) images, Deconwolf enhances transcript detection more than 3-fold and facilitates chromosome tracing with fluorescence in situ sequencing of barcoded probes (Figure 9(c)). By enabling robust quantification of diffraction-limited fluorescence dots, CSR expands the utility of spatial omics techniques, offering a detailed molecular view of biological systems.
Expansion Microscopy
CSR also enhances expansion microscopy (ExM) by further improving resolution and SNR. For instance, when SRRF is combined with ExM, it achieves near-molecular-scale precision (Figure 9(d)).167 Using an isotropically expandable X10 gel and acquiring thousands of frames, SRRF analyzes radial symmetries and higher-order temporal statistics to reconstruct high-resolution images. By mitigating imaging drift and optimizing the SNR, this approach can separate fluorophores found at distances of approximately 20 nm, achieving resolutions close to 10 nm in ideal conditions. This combination of CSR and ExM allows for detailed visualization of biological structures, with significant implications for studying complex molecular assemblies.
These advancements unlock new possibilities for studying dynamic biological processes, revealing insights into molecular, cellular, and tissue-level structures with unparalleled precision.
Artifacts and Resolution Quantification in CSR
In scientific research, the primary goal of SR imaging is fidelity. With the rapid development of SR technologies, objectively measuring the resolution achieved by SR methods has become a critical challenge in the field.131
Systematically, the uncertainty (or error) of resolution can arise from two main sources: “model bias” and “data bias”. Model bias results from discrepancies between the estimation model and the physical reality that it aims to represent. In CSR, the mismatch between prior models and the actual biological structures is an inherent limitation that affects the SR results. Data bias primarily stems from noise, mechanical inaccuracies of the imaging system, and other random factors. Both model bias and data bias can introduce artifacts, undermining the fidelity of the SR imaging.
Traditionally, analytical formulations have been used to analyze microscopy resolution by modeling factors such as system aberrations and noise. Yet, for CSR, relying solely on theoretical analysis to quantify resolution is often impractical. This challenge is further exacerbated in DL-CSR, where the underlying models are more opaque.
The most objective approach to validate resolution and detect artifacts is to compare CSR results against a ground-truth (GT) reference. Calibration samples such as DNA origami structures168 or known biological structures like nuclear pore complexes169 can serve this purpose. For biological samples, higher-resolution techniques such as electron microscopy can sometimes be used as a reference.
However, in most biological and chemical studies, GT is often unavailable due to either technical limitations or the nature of the experiment (e.g., live-cell imaging).
A classical method for assessing data bias without GT is Fourier ring correlation (FRC),170 which has been adapted for the SR domain:171
 |
39 |
The FRC method measures the statistical correlation between two signals over a series of concentric rings in the Fourier domain. Here, f1 and f2 are statistically independent images of the object by like imaging the identical object with the same configurations. ∑ωϵqi represents the summation over the pixels on the perimeter of circles of the corresponding spatial frequency qi.
The bias of the data can be highlighted by the difference between f1 and f2. However, the “absolute differences” is susceptible to the intensity fluctuation and subpixel structural motions, so classical FRC has difficult detecting the local heterogeneity of resolution.
To address this, rolling FRC (rFRC)172 was proposed. This approach applies FRC locally using a rolling block, akin to a moving filter, with thresholds chosen for specific spatial frequencies. Validation in different SR imaging shows the effectiveness and stability of rFRC.
While FRC and rFRC are effective for detecting data bias, they are not feasible for identifying model bias, which is often embedded in SR reconstructions. A notable method for addressing this issue is SQUIRREL (super-resolution quantitative image rating and reporting of error locations).173 SQUIRREL evaluates SR errors by comparing them to a simultaneously acquired high-SNR wide-field reference.
rFRC can further be combined with SQUIRREL using a rolling block map to create a composite map known as PANEL (pixel-level analysis of error locations), which pinpoints regions with low reliability for subsequent biological profiling.
Nevertheless, detecting the model bias remains extremely challenging without a GT reference. For instance, there has been a long-standing debate in SR regarding whether the honeycomb artifacts observed in SIM arise from system design or background light.174,175 When fidelity cannot be directly assessed, reproducibility becomes the next best measure of SR reliability. CSR has an advantage here: compared to experimental environments that are prone to uncontrollable variability, the physical randomness in the CSR is minimal. By thoroughly documenting all parameters and intermediate processes, reproducibility can be ensured—except for methods involving stochastic elements such as certain DL-based CSR approaches.
On the other hand, CSR, particularly model-based methods, offers an advantage in dealing with artifacts through its foundation in mathematical principles. These methods allow researchers to detect and reduce patterned artifacts systematically, compensating for gaps in the biological knowledge. For example, systematic patterns in textures can often be traced back to their computational origins and corrected.
Finally, even if certain phenomena observed in SR images cannot be fully validated, CSR still has a unique advantage: low cost and nondestructive processing. Unlike experimental methods that may consume samples or require costly resources, CSR preserves the original image data while providing valuable insights. This makes CSR an excellent “compass” for guiding exploratory biological research. Researchers can use CSR to identify potential areas of interest before committing to more complex and expensive techniques.
Challenges and Outlook of CSR
After reviewing more than half a century of development in CSR, its future appears to be promising. Of course, challenges remain. This section outlines the current major challenges and prospects for future advancements.
Ultra-High Resolution Ultra-Fast Live-Cell Imaging
Ultrahigh-resolution and ultrafast live-cell imaging remains a critical frontier in the field of CSR. Achieving this ambitious goal requires the ability to visualize dynamic cellular processes in real-time with nanometer-scale resolution while preserving cell viability and minimizing phototoxicity. Although significant progress has been made, CSR is still far from fully realizing this objective, which presents both key challenges and exciting opportunities.
First, achieving ultrahigh-resolution and ultrafast imaging demands the development of more advanced algorithms, which in turn requires foundational theoretical research. Key areas include the design of innovative priors, theoretical guarantees for reconstruction accuracy, improved model interpretability, and algorithmic stability under challenging conditions.
The emergence of foundation models presents another promising avenue. With sufficiently large data sets and computational resources, could CSR reach a singularity point where the problem is fundamentally solved? Testing this hypothesis requires the construction of large biomedical imaging models, which necessitates overcoming challenges, such as data sharing, multimodal data integration, and large-scale data processing.
Second, CSR must evolve alongside the latest advancements in optical microscopy. For example, MINFLUX (MINimal photon FLUXes), a breakthrough in fluorescence microscopy, achieves nanometer-scale resolution and has enabled live tracking of motor proteins.176 However, it faces challenges such as low throughput and limited temporal resolution. Integrating CSR with MINFLUX’s localization algorithms could reduce the number of images required, enhance SNR, and increase imaging speed.
Additionally, CSR can be paired with light-sheet microscopy to minimize photobleaching by selectively illuminating only the imaging plane. This integration could enable high-resolution imaging with reduced phototoxicity, preserving the sample integrity during long-term observations. Another exciting prospect lies in expanding CSR-compatible imaging modalities to include label-free methods.177 Techniques such as phase imaging or label-free scattering hold promise for minimally invasive live-cell imaging. By reducing the reliance on fluorescent labels, these methods could enable CSR to be applied in scenarios in which fluorescence imaging is impractical or detrimental to the sample.
Quantitative CSR
The ultimate goal of improving resolution is to enable quantitative analysis of biological processes on finer scales. The fundamental requirements for quantitative live-cell CSR are preserving the integrity of delicate structures and maintaining the linearity of fluorescence signals. Although this area largely remains uncharted territory, model-based CSR grounded in accurate mathematical and physical models holds significant promise.
Moreover, CSR algorithms should aim to facilitate enhanced quantitative processing and the segmentation of biological phenomena. In this context, DL-based detection and segmentation methods have already demonstrated remarkable capabilities. Integrating advanced CSR algorithms with DL for quantitative analysis is an essential step toward making CSR a universal tool for life sciences.
Unknown or Spatially Variant PSF
Most methods discussed in this Review rely on the assumption in imaging (eq 1) that the PSF is precisely known and spatially invariant. However, this assumption often presents challenges in practice.178 Aberrations and scattering can make it difficult to accurately obtain the PSF, and local PSF variations may arise—especially in advanced microscopy techniques like light-sheet or light-field microscopy, where the PSF is inherently spatially variant.
Addressing unknown or spatially variant PSFs in CSR remains a difficult problem. Blind deconvolution179 offers a potential solution by simultaneously estimating the PSF and performing deconvolution, though this significantly increases the complexity. DL may bypass this issue by learning PSF information directly from data; however, acquiring sufficient ground-truth data remains infeasible. Adaptive optics180 can correct the PSF to reduce uncertainties. Recently, advancements in deconvolution theory for a spatially varied PSF181 have opened new avenues of exploration.
Computational Imaging
Historically, CSR and fluorescence SR microscopy have developed largely independently. One notable exception is SIM, which encodes high-frequency signals into the imaging system and uses CSR algorithms to recover them. Recently, similar approaches—combining algorithm and hardware design—have gained increasing attention under the umbrella of computational imaging.182
Computational imaging integrates computation as a fundamental part of the image-formation process. CSR leverages priors, and the introduction of more suitable priors through system design can foster a symbiotic relationship between algorithms and hardware, potentially enabling the next generation of SR imaging systems. A successful precedent is single-pixel imaging, which incorporates CS theory into a system design. The development of more controllable hardware systems has accelerated this trend. For instance, metamaterials allow for precise tailoring of light–matter interactions at subwavelength scales, opening up possibilities for designing more controllable and reliable systems in conjunction with CSR algorithms.183
Orientation to Practical Applications
Every biotechnique should ultimately aim for practical applicability. Perhaps the greatest challenge for CSR lies in how to make it accessible to end-users (e.g., biologists and chemists) for their research. Like SR fluorescence microscopy, CSR faces high adoption barriers due to its complexity. To address this, CSR researchers must engage in an interdisciplinary collaboration with biologists and chemists. Additionally, designing more user-friendly hardware and software systems is imperative.
Beyond the integration of more reliable algorithmic tools, a promising trend is leveraging foundation language models to create intuitive user interfaces. Such interfaces could allow users to operate CSR-based smart microscopy184 systems without requiring in-depth understanding of the underlying principles, significantly lowering the barrier to entry.
Summary
In the pursuit of breaking imaging barriers, the CSR represents a testament to the boundless ingenuity of science. This Review has traced the odyssey of CSR. Starting with fluorescence microscopy as a model, we introduced the process of optical imaging. Using Fourier transform as a tool, we derived the frequency-domain definition of resolution and, subsequently, the meaning of super-resolution. CSR achieves super-resolution through algorithms, with its core relying on the introduction of priors to solve ill-posed problems. We have unified diverse CSR methods under a single conceptual framework, defined by the rule of priors and the interplay of computation. Within this framework, we have traced the historical development of CSR, beginning with its roots in analytical continuation and early iterative deconvolution, moving through paradigm-shifting advancements in model-based and data-driven methods and culminating in recent breakthroughs such as sparse-deconvolution and deep-learning-based CSR. Along the way, we highlighted the biological applications of CSR in overcoming photon budget limitations and extending the boundaries of live-cell super-resolution imaging. Besides, we discussed the objective resolution quantification method.
Yet, as much as CSR has advanced, its journey is far from complete. The challenges of achieving ultrahigh resolution and ultrafast live-cell imaging require more advanced theories and algorithms. Additionally, integrating interdisciplinary knowledge, designing interpretable models, and overcoming barriers to adoption among biologists remind us that CSR is not just a computational endeavor but a dynamic collaboration between physics, biology, and computation.
Alongside state-of-the-art super-resolution fluorescence microscopy, CSR promises to be integrated into the next generation of SR imaging systems. This integration is poised to deliver unprecedented precision and detail with the potential to revolutionize biological research.
Swiss-born American naturalist, geologist Louis Agassiz (1807–1873) once wrote a poem that thought-provokingly revealed the evolution of scientific breakthroughs, which is displayed in the entrance area of the Nobel Museum in Stockholm:185
“Every great scientific truth goes through three stages. First, people say it conflicts with the Bible. Next they say it had been discovered before. Lastly they say they always believed it.”
Even in the era of artificial intelligence, CSR stands as a profound reminder that it is not algorithms or data but our ideas, wisdom, curiosity, and boundless courage to challenge the limits of nature that shape the future.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (81925022, T2288102, and 32227802), The National Key Research and Development Program of China (2022YFC3400600), and the High-Performance Computing Platform of Peking University. L.C. is also supported by New Cornerstone Science Foundation.
Biographies
Wenfeng Tian received a BE degree in biomedical engineering from Shanghai Jiao Tong University and a ME degree in biomedical engineering from Tsinghua University. He is currently working toward a Ph.D. degree in biophysics in the College of Future Technology, Peking University. His current research interests include super-resolution live-cell imaging, data science in biology, literature and the art of loving. Now, he is searching for self.
Riwang Chen received a BE degree in electrical engineering and automation from University of Electronic Science and Technology of China and a ME degree in software engineering from Peking University. He is currently working toward a Ph.D. degree in integrated life sciences (physics) at the Academy for Advanced Interdisciplinary Studies, Peking University. His current research interests include single-molecule localization precision analysis and the super-resolution principle and algorithm.
Liangyi Chen is Boya Professor of Peking University and a New Cornerstone Investigator. He obtained his undergraduate degrees in biomedical engineering in Xi’an JiaoTong University, then majored in biomedical engineering while pursuing Ph.D. degree in Huazhong University of Science and Technology. His lab focused on two interweaved aspects: the development of new imaging and quantitative image analysis algorithms and the application of these technologies to study how glucose-stimulated insulin secretion is regulated in health and disease at multiple levels (single cells, islets, and in vivo) in health and disease animal models. His lab developed Hessian SIM, SR-FACT for live-cell holistic superresolution imaging, fast high-resolution miniature two-photon microscopy (FHIRM-TPM) for brain imaging in freely behaving mice, and the sparse-deconvolution for extending the spatial resolution of fluorescence microscopes limited by the optics in general.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.analchem.4c07047.
All mathematical concepts and proofs that are covered in the main text but not specifically elaborated (PDF)
Author Contributions
Wenfeng Tian: investigation, formal analysis, visualization, writing–original draft and review and editing. Riwang Chen: formal analysis, writing–review and editing. Liangyi Chen: conceptualization, writing–review and editing, project administration, funding acquisition, supervision.
The authors declare no competing financial interest.
Special Issue
Published as part of Analytical Chemistryspecial issue “Fundamental and Applied Reviews in Analytical Chemistry 2025”.
Supplementary Material
References
- Born M.; Wolf E.. Elements of the theory of diffraction. In Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press, 2019; pp 412–516. [Google Scholar]
- Schermelleh L.; Ferrand A.; Huser T.; Eggeling C.; Sauer M.; Biehlmaier O.; Drummen G. P. C. Super-resolution microscopy demystified. Nat. Cell Biol. 2019, 21 (1), 72–84. 10.1038/s41556-018-0251-8. [DOI] [PubMed] [Google Scholar]
- Hell S. W.; Wichmann J. Breaking the diffraction resolution limit by stimulated emission: stimulated-emission-depletion fluorescence microscopy. Opt. Lett. 1994, 19 (11), 780–782. 10.1364/OL.19.000780. [DOI] [PubMed] [Google Scholar]
- Betzig E.; Patterson G. H.; Sougrat R.; Lindwasser O. W.; Olenych S.; Bonifacino J. S.; Davidson M. W.; Lippincott-Schwartz J.; Hess H. F. Imaging Intracellular Fluorescent Proteins at Nanometer Resolution. Science 2006, 313 (5793), 1642–1645. 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
- Rust M. J.; Bates M.; Zhuang X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM). Nat. Methods 2006, 3 (10), 793–796. 10.1038/nmeth929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gustafsson M. G. L. Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy. J. Microsc. 2000, 198 (2), 82–87. 10.1046/j.1365-2818.2000.00710.x. [DOI] [PubMed] [Google Scholar]
- Dertinger T.; Colyer R.; Iyer G.; Weiss S.; Enderlein J. Fast, background-free, 3D super-resolution optical fluctuation imaging (SOFI). Proc. Natl. Acad. Sci. U. S. A. 2009, 106 (52), 22287–22292. 10.1073/pnas.0907866106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen F.; Tillberg P. W.; Boyden E. S. Expansion microscopy. Science 2015, 347 (6221), 543–548. 10.1126/science.1260088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang X.; Fan J.; Li L.; Liu H.; Wu R.; Wu Y.; Wei L.; Mao H.; Lal A.; Xi P.; et al. Fast, long-term, super-resolution imaging with Hessian structured illumination microscopy. Nat. Biotechnol. 2018, 36 (5), 451–459. 10.1038/nbt.4115. [DOI] [PubMed] [Google Scholar]
- Zhao W.; Zhao S.; Li L.; Huang X.; Xing S.; Zhang Y.; Qiu G.; Han Z.; Shang Y.; Sun D.-e.; et al. Sparse deconvolution improves the resolution of live-cell super-resolution fluorescence microscopy. Nat. Biotechnol. 2022, 40 (4), 606–617. 10.1038/s41587-021-01092-2. [DOI] [PubMed] [Google Scholar]
- Wang H. D.; Rivenson Y.; Jin Y. Y.; Wei Z. S.; Gao R.; Günaydin H.; Bentolila L. A.; Kural C.; Ozcan A. Deep learning enables cross-modality super-resolution in fluorescence microscopy. Nat. Methods 2019, 16 (1), 103. 10.1038/s41592-018-0239-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao W.; Zhao S.; Han Z.; Ding X.; Hu G.; Qu L.; Huang Y.; Wang X.; Mao H.; Jiu Y.; et al. Enhanced detection of fluorescence fluctuations for high-throughput super-resolution imaging. Nat. Photonics 2023, 17 (9), 806–813. 10.1038/s41566-023-01234-9. [DOI] [Google Scholar]
- Jang H.; Li Y.; Fung A. A.; Bagheri P.; Hoang K.; Skowronska-Krawczyk D.; Chen X.; Wu J. Y.; Bintu B.; Shi L. Super-resolution SRS microscopy with A-PoD. Nat. Methods 2023, 20 (3), 448–458. 10.1038/s41592-023-01779-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wernersson E.; Gelali E.; Girelli G.; Wang S.; Castillo D.; Mattsson Langseth C.; Verron Q.; Nguyen H. Q.; Chattoraj S.; Martinez Casals A.; et al. Deconwolf enables high-performance deconvolution of widefield fluorescence microscopy images. Nat. Methods 2024, 21 (7), 1245–1256. 10.1038/s41592-024-02294-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diaspro A.; Bianchini P. Optical nanoscopy. Riv. Nuovo. Cim. 2020, 43, 385. 10.1007/s40766-020-00008-1. [DOI] [Google Scholar]
- Bertero M.; De Mol C. III Super-Resolution by Data Inversion. Prog. Optics 1996, 36, 129–178. 10.1016/S0079-6638(08)70314-7. [DOI] [Google Scholar]
- Sarder P.; Nehorai A. Deconvolution methods for 3-D fluorescence microscopy images. IEEE Signal Processing Magazine 2006, 23 (3), 32–45. 10.1109/MSP.2006.1628876. [DOI] [Google Scholar]
- Lindberg J. Mathematical concepts of optical superresolution. Journal of Optics 2012, 14 (8), 083001. 10.1088/2040-8978/14/8/083001. [DOI] [Google Scholar]
- Kaderuppan S. S.; Wong E. W. L.; Sharma A.; Woo W. L. Smart Nanoscopy: A Review of Computational Approaches to Achieve Super-Resolved Optical Microscopy. IEEE Access 2020, 8, 214801–214831. 10.1109/ACCESS.2020.3040319. [DOI] [Google Scholar]
- Mertz J.Introduction to Optical Microscopy; Cambridge University Press, 2019. 10.1017/9781108552660. [DOI] [Google Scholar]
- Boyd S.; Vandenberghe L.. Convex Optimization; Cambridge University Press, 2004. 10.1017/CBO9780511804441. [DOI] [Google Scholar]
- LeCun Y.; Bengio Y.; Hinton G. Deep learning. Nature 2015, 521 (7553), 436–444. 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- Strang G.Introduction to linear algebra, 6th ed.; Wellesley-Cambridge Press: Wellesley, MA, 2023. [Google Scholar]
- Delsuc M.-A.; O’Connor P. The Fourier transform in analytical science. Nature Reviews Methods Primers 2024, 4 (1), 49. 10.1038/s43586-024-00326-2. [DOI] [Google Scholar]
- Prakash K.; Diederich B.; Heintzmann R.; Schermelleh L. Super-resolution microscopy: a brief history and new avenues. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2022, 380 (2220), 20210110. 10.1098/rsta.2021.0110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puetter R. C.; Gosnell T. R.; Yahil A. Digital Image Reconstruction: Deblurring and Denoising. Annu. Rev. Astron. Astrophys. 2005, 43, 139–194. 10.1146/annurev.astro.43.112904.104850. [DOI] [Google Scholar]
- Shroff H.; Testa I.; Jug F.; Manley S. Live-cell imaging powered by computation. Nat. Rev. Mol. Cell Biol. 2024, 25 (6), 443–463. 10.1038/s41580-024-00702-6. [DOI] [PubMed] [Google Scholar]
- Kervrann C.; Sorzano C. Ó. S.; Acton S. T.; Olivo-Marin J. C.; Unser M. A Guided Tour of Selected Image Processing and Analysis Methods for Fluorescence and Electron Microscopy. IEEE J. Sel. Top. Signal Process. 2016, 10 (1), 6–30. 10.1109/JSTSP.2015.2505402. [DOI] [Google Scholar]
- Zeng Z.-p.; Xie H.; Chen L.; Zhanghao K.; Zhao K.; Yang X.-s.; Xi P. Computational methods in super-resolution microscopy. Frontiers of Information Technology & Electronic Engineering 2017, 18 (9), 1222–1235. 10.1631/FITEE.1601628. [DOI] [Google Scholar]
- Park S. C.; Park M. K.; Kang M. G. Super-resolution image reconstruction: a technical overview. IEEE Signal Process. Mag. 2003, 20 (3), 21–36. 10.1109/MSP.2003.1203207. [DOI] [Google Scholar]
- Li X.; Dong W.; Wu J.; Li L.; Shi G. Superresolution Image Reconstruction: Selective milestones and open problems. IEEE Signal Processing Magazine 2023, 40 (5), 54–66. 10.1109/MSP.2023.3271438. [DOI] [Google Scholar]
- Lepcha D. C.; Goyal B.; Dogra A.; Goyal V. Image super-resolution: A comprehensive review, recent trends, challenges and applications. Information Fusion 2023, 91, 230–260. 10.1016/j.inffus.2022.10.007. [DOI] [Google Scholar]
- Chen H.; He X.; Qing L.; Wu Y.; Ren C.; Sheriff R. E.; Zhu C. Real-world single image super-resolution: A brief review. Information Fusion 2022, 79, 124–145. 10.1016/j.inffus.2021.09.005. [DOI] [Google Scholar]
- Vangindertael J.; Camacho R.; Sempels W.; Mizuno H.; Dedecker P.; Janssen K. P. F. An introduction to optical super-resolution microscopy for the adventurous biologist. Methods and Applications in Fluorescence 2018, 6 (2), 022003. 10.1088/2050-6120/aaae0c. [DOI] [PubMed] [Google Scholar]
- Aspelmeier T.; Egner A.; Munk A.. Modern Statistical Challenges in High-Resolution Fluorescence Microscopy In Annual Review of Statistics and Its Application, Vol 2; Fienberg S. E., Ed.; Annual Reviews, 2015; pp 163–202. [Google Scholar]
- Goodman J. W.Introduction to Fourier Optics, 3rd ed.; Roberts and Company Publishers, 2005. [Google Scholar]
- Masters B. R.Concepts and Criteria of Resolution In Superresolution Optical Microscopy: The Quest for Enhanced Resolution and Contrast; Springer International Publishing, 2020; pp 13–32. [Google Scholar]
- Toraldo di Francia G. Nuovo pupille superrisolvente. Atti Fond. Giorgio Ronchi 1952, 7, 366–372. [Google Scholar]
- Hadamard J. Sur les problèmes aux dérivées partielles et leur signification physique. Princeton Univ. Bul. 1902, 13, 49–52. [Google Scholar]
- Bertero M.; Boccacci P.; Koenig A. M. Introduction to inverse problems in imaging. Optics and Photonics News 2001, 12 (10), 46–47. [Google Scholar]
- Barnett A. H. How Exponentially Ill-Conditioned Are Contiguous Submatrices of the Fourier Matrix?. SIAM Review 2022, 64 (1), 105–131. 10.1137/20M1336837. [DOI] [Google Scholar]
- Tikhonov A. N. On the stability of inverse problems. Proc. USSR Acad. Sci. 1943, 39, 195–198. [Google Scholar]
- Wiener N.Extrapolation, interpolation, and smoothing of stationary time series: with engineering applications; MIT Press, 1964; pp 1043–1054.
- Harris J. L. Diffraction and Resolving Power*. J. Opt. Soc. Am. 1964, 54 (7), 931–936. 10.1364/JOSA.54.000931. [DOI] [Google Scholar]
- Slepian D. S.; Pollak H. O. Prolate spheroidal wave functions, fourier analysis and uncertainty — II. Bell System Technical Journal 1961, 40, 43–63. 10.1002/j.1538-7305.1961.tb03976.x. [DOI] [Google Scholar]
- Bertero M.; Pike E. R. Resolution in Diffraction-limited Imaging, a Singular Value Analysis. Optica Acta: International Journal of Optics 1982, 29 (6), 727–746. 10.1080/713820912. [DOI] [Google Scholar]
- Gerchberg R. W. Super-resolution through Error Energy Reduction. Optica Acta: International Journal of Optics 1974, 21 (9), 709–720. 10.1080/713818946. [DOI] [Google Scholar]
- Papoulis A. A new algorithm in spectral analysis and band-limited extrapolation. IEEE Transactions on Circuits and Systems 1975, 22 (9), 735–742. 10.1109/TCS.1975.1084118. [DOI] [Google Scholar]
- De Santis P.; Gori F. On an Iterative Method for Super-resolution. Optica Acta: International Journal of Optics 1975, 22 (8), 691–695. 10.1080/713819094. [DOI] [Google Scholar]
- Landweber L. An Iteration Formula for Fredholm Integral Equations of the First Kind. American Journal of Mathematics 1951, 73 (3), 615–624. 10.2307/2372313. [DOI] [Google Scholar]
- Hansen P. C.Toward Real-World Problems: Iterative Regularization. In Discrete Inverse Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, 2010; pp 109–134. 10.1137/1.9780898718836.ch6. [DOI] [Google Scholar]
- Agard D. A.; Sedat J. W. Three-dimensional architecture of a polytene nucleus. Nature 1983, 302 (5910), 676–681. 10.1038/302676a0. [DOI] [PubMed] [Google Scholar]
- Barakat V.; Guilpart B.; Goutte R.; Prost R.. Model-based Tikhonov-Miller image restoration. In Proceedings of International Conference on Image Processing, Santa Barbara, CA, October 26–29, 1997; IEEE, 1997; pp 310–313. 10.1109/ICIP.1997.647768. [DOI]
- Sage D.; Donati L.; Soulez F.; Fortun D.; Schmit G.; Seitz A.; Guiet R.; Vonesch C.; Unser M. DeconvolutionLab2: An open-source software for deconvolution microscopy. Methods 2017, 115, 28–41. 10.1016/j.ymeth.2016.12.015. [DOI] [PubMed] [Google Scholar]
- Richardson W. H. Bayesian-Based Iterative Method of Image Restoration. J. Opt. Soc. Am. 1972, 62 (1), 55. 10.1364/JOSA.62.000055. [DOI] [Google Scholar]
- Lucy L. B. An iterative technique for the rectification of observed distributions. Astron. J. 1974, 79, 745–754. 10.1086/111605. [DOI] [Google Scholar]
- Heintzmann R. Estimating missing information by maximum likelihood deconvolution. Micron 2007, 38 (2), 136–144. 10.1016/j.micron.2006.07.009. [DOI] [PubMed] [Google Scholar]
- Bertero A.; Boccacci P. Super-resolution in computational imaging. Micron 2003, 34 (6–7), 265–273. 10.1016/S0968-4328(03)00051-9. [DOI] [PubMed] [Google Scholar]
- Benvenuto F. A Study on Regularization for Discrete Inverse Problems with Model-Dependent Noise. SIAM Journal on Numerical Analysis 2017, 55 (5), 2187–2203. 10.1137/15M1049051. [DOI] [Google Scholar]
- Bertero M.; Boccacci P.; Ruggiero V.. Inverse Imaging with Poisson Data; IOP Publishing, 2018. 10.1088/2053-2563/aae109. [DOI] [Google Scholar]
- van Kempen G.M.P.; van der Voort H.T.M.; Bauman J.G.J.; Strasters K.C. Comparing maximum likelihood estimation and constrained Tikhonov-Miller restoration. IEEE Eng. Med. Biol. Mag. 1996, 15 (1), 76–83. 10.1109/51.482846. [DOI] [Google Scholar]
- Pouchol C.; Verdier O. The ML–EM algorithm in continuum: sparse measure solutions. Inverse Problems 2020, 36 (3), 035013. 10.1088/1361-6420/ab6d55. [DOI] [Google Scholar]
- Puschmann K. G.; Kneer F. On super-resolution in astronomical imaging. Astron. Astrophys. 2005, 436, 373–378. 10.1051/0004-6361:20042320. [DOI] [Google Scholar]
- Dey N.; Blanc-Feraud L.; Zimmer C.; Roux P.; Kam Z.; Olivo-Marin J.-C.; Zerubia J. Richardson–Lucy algorithm with total variation regularization for 3D confocal microscope deconvolution. Microscopy Research and Technique 2006, 69 (4), 260–266. 10.1002/jemt.20294. [DOI] [PubMed] [Google Scholar]
- Guo M.; Li Y.; Su Y.; Lambert T.; Nogare D. D.; Moyle M. W.; Duncan L. H.; Ikegami R.; Santella A.; Rey-Suarez I.; et al. Rapid image deconvolution and multiview fusion for optical microscopy. Nat. Biotechnol. 2020, 38 (11), 1337–1346. 10.1038/s41587-020-0560-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stefan W. Hell Biographical. The Nobel Prize. https://www.nobelprize.org/prizes/chemistry/2014/hell/biographical/.
- Narayan R.; Nityananda R. Maximum Entropy Image Restoration in Astronomy. Annu. Rev. Astron. Astrophys. 1986, 24, 127–170. 10.1146/annurev.aa.24.090186.001015. [DOI] [Google Scholar]
- Arigovindan M.; Fung J. C.; Elnatan D.; Mennella V.; Chan Y.-H. M.; Pollard M.; Branlund E.; Sedat J. W.; Agard D. A. High-resolution restoration of 3D structures from widefield images with extreme low signal-to-noise-ratio. Proc. Natl. Acad. Sci. U. S. A. 2013, 110 (43), 17344–17349. 10.1073/pnas.1315675110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudin L. I.; Osher S.; Fatemi E. Nonlinear total variation based noise removal algorithms. Physica D: Nonlinear Phenomena 1992, 60 (1), 259–268. 10.1016/0167-2789(92)90242-F. [DOI] [Google Scholar]
- Benning M.; Burger M. Modern regularization methods for inverse problems. Acta Numerica 2018, 27, 1–111. 10.1017/S0962492918000016. [DOI] [Google Scholar]
- Laasmaa M.; Vendelin M.; Peterson P. Application of regularized Richardson–Lucy algorithm for deconvolution of confocal microscopy images. J. Microsc. 2011, 243 (2), 124–140. 10.1111/j.1365-2818.2011.03486.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bredies K.; Holler M. Higher-order total variation approaches and generalisations. Inverse Problems 2020, 36 (12), 123001. 10.1088/1361-6420/ab8f80. [DOI] [Google Scholar]
- Chan R. H.; Chan T. F.; Shen L.; Shen Z. Wavelet Algorithms for High-Resolution Image Reconstruction. SIAM Journal on Scientific Computing 2003, 24 (4), 1408–1432. 10.1137/S1064827500383123. [DOI] [Google Scholar]
- Boutet de Monvel J.; Le Calvez S.; Ulfendahl M. Image Restoration for Confocal Microscopy: Improving the Limits of Deconvolution, with Application to the Visualization of the Mammalian Hearing Organ. Biophys. J. 2001, 80 (5), 2455–2470. 10.1016/S0006-3495(01)76214-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou Y. W.; Wang W. Y.; Fu Y. Z.; Ge X. C.; Li M. Q.; Xi P. Multi-resolution analysis enables fidelity-ensured deconvolution for fluorescence microscopy. eLight 2024, 4, 14. 10.1186/s43593-024-00073-7. [DOI] [Google Scholar]
- Donoho D. L.; Elad M. Optimally sparse representation in general (nonorthogonal) dictionaries via l1 minimization. Proc. Natl. Acad. Sci. U. S. A. 2003, 100 (5), 2197–2202. 10.1073/pnas.0437847100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen A.; Dahmen W.; DeVore R. A. Compressed sensing and best k-term approximation. Journal of the American Mathematical Society 2009, 22, 211–231. 10.1090/S0894-0347-08-00610-3. [DOI] [Google Scholar]
- Natarajan B. K. Sparse Approximate Solutions to Linear Systems. SIAM Journal on Computing 1995, 24 (2), 227–234. 10.1137/S0097539792240406. [DOI] [Google Scholar]
- Tillmann A. M.; Bienstock D.; Lodi A.; Schwartz A. Cardinality Minimization, Constraints, and Regularization: A Survey. SIAM Review 2024, 66 (3), 403–477. 10.1137/21M142770X. [DOI] [Google Scholar]
- Hugelier S.; de Rooi J. J.; Bernex R.; Duwé S.; Devos O.; Sliwa M.; Dedecker P.; Eilers P. H. C.; Ruckebusch C. Sparse deconvolution of high-density super-resolution images. Sci. Rep. 2016, 6, 6. 10.1038/srep21413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gribonval R.; Nielsen M. Sparse representations in unions of bases. IEEE Transactions on Information Theory 2003, 49 (12), 3320–3325. 10.1109/TIT.2003.820031. [DOI] [Google Scholar]
- Szameit A.; Shechtman Y.; Osherovich E.; Bullkich E.; Sidorenko P.; Dana H.; Steiner S.; Kley E. B.; Gazit S.; Cohen-Hyams T.; et al. Sparsity-based single-shot subwavelength coherent diffractive imaging. Nat. Mater. 2012, 11 (5), 455–459. 10.1038/nmat3289. [DOI] [PubMed] [Google Scholar]
- Donoho D. L. Compressed sensing. Ieee Transactions on Information Theory 2006, 52 (4), 1289–1306. 10.1109/TIT.2006.871582. [DOI] [Google Scholar]
- Candes E. J.; Romberg J.; Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory 2006, 52 (2), 489–509. 10.1109/TIT.2005.862083. [DOI] [Google Scholar]
- Candes E. J.; Tao T. Decoding by linear programming. IEEE Transactions on Information Theory 2005, 51 (12), 4203–4215. 10.1109/TIT.2005.858979. [DOI] [Google Scholar]
- Candès E. J.; Romberg J. K.; Tao T. Stable signal recovery from incomplete and inaccurate measurements. Communications on Pure and Applied Mathematics 2006, 59 (8), 1207–1223. 10.1002/cpa.20124. [DOI] [Google Scholar]
- Unser M. Sampling-50 years after Shannon. Proceedings of the IEEE 2000, 88 (4), 569–587. 10.1109/5.843002. [DOI] [Google Scholar]
- Calisesi G.; Ghezzi A.; Ancora D.; D’Andrea C.; Valentini G.; Farina A.; Bassi A. Compressed sensing in fluorescence microscopy. Prog. Biophys. Mol. Biol. 2022, 168, 66–80. 10.1016/j.pbiomolbio.2021.06.004. [DOI] [PubMed] [Google Scholar]
- Gazit S.; Szameit A.; Eldar Y. C.; Segev M. Super-resolution and reconstruction of sparse sub-wavelength images. Opt. Express 2009, 17 (26), 23920–23946. 10.1364/OE.17.023920. [DOI] [PubMed] [Google Scholar]
- Shechtman Y.; Eldar Y. C.; Szameit A.; Segev M. Sparsity based sub-wavelength imaging with partially incoherent light via quadratic compressed sensing. Opt. Express 2011, 19 (16), 14807–14822. 10.1364/OE.19.014807. [DOI] [PubMed] [Google Scholar]
- Shechtman Y.; Gazit S.; Szameit A.; Eldar Y. C.; Segev M. Super-resolution and reconstruction of sparse images carried by incoherent light. Opt. Lett. 2010, 35 (8), 1148–1150. 10.1364/OL.35.001148. [DOI] [PubMed] [Google Scholar]
- Zhu L.; Zhang W.; Elnatan D.; Huang B. Faster STORM using compressed sensing. Nat. Methods 2012, 9 (7), 721–723. 10.1038/nmeth.1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duarte M. F.; Davenport M. A.; Takhar D.; Laska J. N.; Sun T.; Kelly K. F.; Baraniuk R. G. Single-pixel imaging via compressive sampling. IEEE Signal Processing Magazine 2008, 25 (2), 83–91. 10.1109/MSP.2007.914730. [DOI] [Google Scholar]
- Weisenburger S.; Vaziri A. A Guide to Emerging Technologies for Large-Scale and Whole-Brain Optical Imaging of Neuronal Activity. Annu. Rev. Neurosci. 2018, 41, 431–452. 10.1146/annurev-neuro-072116-031458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern A.Optical compressive imaging; CRC Press, 2016. [Google Scholar]
- Candès E. J.; Fernandez-Granda C. Towards a Mathematical Theory of Super- resolution. Communications on Pure and Applied Mathematics 2014, 67 (6), 906–956. 10.1002/cpa.21455. [DOI] [Google Scholar]
- Lustig M.; Donoho D. L.; Santos J. M.; Pauly J. M. Compressed Sensing MRI. IEEE Signal Processing Magazine 2008, 25 (2), 72–82. 10.1109/MSP.2007.914728. [DOI] [Google Scholar]
- Wright J.; Ma Y.. High-Dimensional Data Analysis with Low-Dimensional Models: Principles, Computation, and Applications; Cambridge University Press, 2022. 10.1017/9781108779302. [DOI] [Google Scholar]
- Lefkimmiatis S.; Ward J. P.; Unser M. Hessian Schatten-Norm Regularization for Linear Inverse Problems. IEEE Transactions on Image Processing 2013, 22 (5), 1873–1888. 10.1109/TIP.2013.2237919. [DOI] [PubMed] [Google Scholar]
- Lefkimmiatis S.; Unser M. Poisson Image Reconstruction With Hessian Schatten-Norm Regularization. IEEE Transactions on Image Processing 2013, 22 (11), 4314–4327. 10.1109/TIP.2013.2271852. [DOI] [PubMed] [Google Scholar]
- Ikoma H.; Broxton M.; Kudo T.; Wetzstein G. A convex 3D deconvolution algorithm for low photon count fluorescence imaging. Sci. Rep. 2018, 8 (1), 11489. 10.1038/s41598-018-29768-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Y.; Sun Y.; Wu H.; Cao W.; Bai L.; Tao S.; Tian Z.; Cui Y.; Hao X.; Kuang C.; et al. Regularized deconvolution for structured illumination microscopy via accelerated linearized ADMM. Optics & Laser Technology 2024, 169, 110119. 10.1016/j.optlastec.2023.110119. [DOI] [Google Scholar]
- Greener J. G.; Kandathil S. M.; Moffat L.; Jones D. T. A guide to machine learning for biologists. Nat. Rev. Mol. Cell Biol. 2022, 23 (1), 40–55. 10.1038/s41580-021-00407-0. [DOI] [PubMed] [Google Scholar]
- Xu H.; Chen Y.; Zhang D. Worth of prior knowledge for enhancing deep learning. Nexus 2024, 1 (1), 100003. 10.1016/j.ynexs.2024.100003. [DOI] [Google Scholar]
- Moser B. B.; Raue F.; Frolov S.; Palacio S.; Hees J.; Dengel A. Hitchhiker’s Guide to Super-Resolution: Introduction and Recent Advances. IEEE Transactions on Pattern Analysis and Machine Intelligence 2023, 45 (8), 9862–9882. 10.1109/TPAMI.2023.3243794. [DOI] [PubMed] [Google Scholar]
- Anwar S.; Khan S.; Barnes N. A Deep Journey into Super-resolution: A Survey. ACM Comput. Surv. 2021, 53 (3), 60. 10.1145/3390462. [DOI] [Google Scholar]
- Wang Z.; Chen J.; Hoi S. C. H. Deep Learning for Image Super-Resolution: A Survey. IEEE Transactions on Pattern Analysis and Machine Intelligence 2021, 43 (10), 3365–3387. 10.1109/TPAMI.2020.2982166. [DOI] [PubMed] [Google Scholar]
- Ouyang W.; Aristov A.; Lelek M.; Hao X.; Zimmer C. Deep learning massively accelerates super-resolution localization microscopy. Nat. Biotechnol. 2018, 36 (5), 460–468. 10.1038/nbt.4106. [DOI] [PubMed] [Google Scholar]
- Li X.; Zhang G.; Wu J.; Zhang Y.; Zhao Z.; Lin X.; Qiao H.; Xie H.; Wang H.; Fang L.; et al. Reinforcing neuron extraction and spike inference in calcium imaging using deep self-supervised denoising. Nat. Methods 2021, 18 (11), 1395–1400. 10.1038/s41592-021-01225-0. [DOI] [PubMed] [Google Scholar]
- Qiao C.; Li D.; Guo Y.; Liu C.; Jiang T.; Dai Q.; Li D. Evaluation and development of deep neural networks for image super-resolution in optical microscopy. Nat. Methods 2021, 18 (2), 194–202. 10.1038/s41592-020-01048-5. [DOI] [PubMed] [Google Scholar]
- Chen R.; Tang X.; Zhao Y.; Shen Z.; Zhang M.; Shen Y.; Li T.; Chung C. H Y.; Zhang L.; Wang J.; et al. Single-frame deep-learning super-resolution microscopy for intracellular dynamics imaging. Nat. Commun. 2023, 14 (1), 2854. 10.1038/s41467-023-38452-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiao C.; Zeng Y.; Meng Q.; Chen X.; Chen H.; Jiang T.; Wei R.; Guo J.; Fu W.; Lu H.; et al. Zero-shot learning enables instant denoising and super-resolution in optical fluorescence microscopy. Nat. Commun. 2024, 15 (1), 4180. 10.1038/s41467-024-48575-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X.; Wu Y.; Su Y.; Rey-Suarez I.; Matthaeus C.; Updegrove T. B.; Wei Z.; Zhang L.; Sasaki H.; Li Y.; et al. Three-dimensional structured illumination microscopy with enhanced axial resolution. Nat. Biotechnol. 2023, 41 (9), 1307–1319. 10.1038/s41587-022-01651-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Y. K. T.; Graves A. R.; Coste G. I.; Huganir R. L.; Bergles D. E.; Charles A. S.; Sulam J. Cross-modality supervised image restoration enables nanoscale tracking of synaptic plasticity in living mice. Nat. Methods 2023, 20 (6), 935–944. 10.1038/s41592-023-01871-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z.; Zhu L.; Zhang H.; Li G.; Yi C.; Li Y.; Yang Y.; Ding Y.; Zhen M.; Gao S.; et al. Real-time volumetric reconstruction of biological dynamics with light-field microscopy and deep learning. Nat. Methods 2021, 18 (5), 551–556. 10.1038/s41592-021-01058-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isensee F.; Jaeger P. F.; Kohl S. A. A.; Petersen J.; Maier-Hein K. H. nnU-Net: a self-configuring method for deep learning-based biomedical image segmentation. Nature Methods 2021, 18 (2), 203–211. 10.1038/s41592-020-01008-z. [DOI] [PubMed] [Google Scholar]
- Çiçek Ö.; Abdulkadir A.; Lienkamp S. S.; Brox T.; Ronneberger O. 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation. arXiv 2016, 1606.06650. 10.48550/arXiv.1606.06650. [DOI] [Google Scholar]
- Weigert M.; Schmidt U.; Boothe T.; Müller A.; Dibrov A.; Jain A.; Wilhelm B.; Schmidt D.; Broaddus C.; Culley S.; et al. Content-aware image restoration: pushing the limits of fluorescence microscopy. Nat. Methods 2018, 15 (12), 1090–1097. 10.1038/s41592-018-0216-7. [DOI] [PubMed] [Google Scholar]
- Chaudhari S.; Mithal V.; Polatkan G.; Ramanath R. An Attentive Survey of Attention Models. ACM Trans. Intell. Syst. Technol. 2021, 12 (5), 53. 10.1145/3465055. [DOI] [Google Scholar]
- Zhang Y.; Li K.; Li K.; Wang L.; Zhong B.; Fu Y. Image Super-Resolution Using Very Deep Residual Channel Attention Networks. Lecture Notes Comput. Comput. Sci. 2018, 11211, 294–310. 10.1007/978-3-030-01234-2_18. [DOI] [Google Scholar]
- Chen J.; Sasaki H.; Lai H.; Su Y.; Liu J.; Wu Y.; Zhovmer A.; Combs C. A.; Rey-Suarez I.; Chang H.-Y.; et al. Three-dimensional residual channel attention networks denoise and sharpen fluorescence microscopy image volumes. Nat. Methods 2021, 18 (6), 678–687. 10.1038/s41592-021-01155-x. [DOI] [PubMed] [Google Scholar]
- Goodfellow I. J.; Pouget-Abadie J.; Mirza M.; Xu B.; Warde-Farley D.; Ozair S.; Courville A.; Bengio Y. Generative Adversarial Networks. arXiv 2014, 1406.2661. 10.48550/arXiv.1406.2661. [DOI] [Google Scholar]
- Wang X.; Yu K.; Wu S.; Gu J.; Liu Y.; Dong C.; Qiao Y.; Loy C. C. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. Lecture Notes Comput. Sci. 2019, 11133, 63. 10.1007/978-3-030-11021-5_5. [DOI] [Google Scholar]
- Kukačka J.; Golkov V.; Cremers D. Regularization for Deep Learning: A Taxonomy. arXiv 2017, 1710.10686. 10.48550/arXiv.1710.10686. [DOI] [Google Scholar]
- Bouchard C.; Wiesner T.; Deschênes A.; Bilodeau A.; Turcotte B.; Gagné C.; Lavoie-Cardinal F. Resolution enhancement with a task-assisted GAN to guide optical nanoscopy image analysis and acquisition. Nature Machine Intelligence 2023, 5 (8), 830–844. 10.1038/s42256-023-00689-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pang T.; Zheng H.; Quan Y.; Ji H.. Recorrupted-to-Recorrupted: Unsupervised Deep Learning for Image Denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE, 2021; pp 2043–2052. 10.1109/CVPR46437.2021.00208. [DOI]
- Park H.; Na M.; Kim B.; Park S.; Kim K. H.; Chang S.; Ye J. C. Deep learning enables reference-free isotropic super-resolution for volumetric fluorescence microscopy. Nat. Commun. 2022, 13 (1), 3297. 10.1038/s41467-022-30949-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J.-Y.; Park T.; Isola P.; Efros A. A. Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks. arXiv 2017, 1703.10593. 10.48550/arXiv.1703.10593. [DOI] [Google Scholar]
- Antun V.; Renna F.; Poon C.; Adcock B.; Hansen A. C. On instabilities of deep learning in image reconstruction and the potential costs of AI. Proc. Natl. Acad. Sci. U. S. A. 2020, 117 (48), 30088–30095. 10.1073/pnas.1907377117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman D. P.; Slavitt I.; Fitzpatrick C. A. The promise and peril of deep learning in microscopy. Nat. Methods 2021, 18 (2), 131–132. 10.1038/s41592-020-01035-w. [DOI] [PubMed] [Google Scholar]
- Prakash K.; Baddeley D.; Eggeling C.; Fiolka R.; Heintzmann R.; Manley S.; Radenovic A.; Smith C.; Shroff H.; Schermelleh L. Resolution in super-resolution microscopy — definition, trade-offs and perspectives. Nat. Rev. Mol. Cell Biol. 2024, 25 (9), 677–682. 10.1038/s41580-024-00755-7. [DOI] [PubMed] [Google Scholar]
- Guidotti R.; Monreale A.; Ruggieri S.; Turini F.; Giannotti F.; Pedreschi D. A Survey of Methods for Explaining Black Box Models. ACM Comput. Surv. 2019, 51 (5), 93. 10.1145/3236009. [DOI] [Google Scholar]
- Wang H.; Yeung D.-Y. A Survey on Bayesian Deep Learning. ACM Comput. Surv. 2021, 53 (5), 108. 10.1145/3409383. [DOI] [Google Scholar]
- Tolle K. M.; Tansley D. S. W.; Hey A. J. G. The Fourth Paradigm: Data-Intensive Scientific Discovery [Point of View]. Proceedings of the IEEE 2011, 99 (8), 1334–1337. 10.1109/JPROC.2011.2155130. [DOI] [Google Scholar]
- Wang H.; Fu T.; Du Y.; Gao W.; Huang K.; Liu Z.; Chandak P.; Liu S.; Van Katwyk P.; Deac A.; et al. Scientific discovery in the age of artificial intelligence. Nature 2023, 620 (7972), 47–60. 10.1038/s41586-023-06221-2. [DOI] [PubMed] [Google Scholar]
- Mukherjee S.; Hauptmann A.; Öktem O.; Pereyra M.; Schönlieb C. B. Learned Reconstruction Methods With Convergence Guarantees: A survey of concepts and applications. IEEE Signal Processing Magazine 2023, 40 (1), 164–182. 10.1109/MSP.2022.3207451. [DOI] [Google Scholar]
- Li X.; Zhang Y.; Wu J.; Dai Q. Challenges and opportunities in bioimage analysis. Nat. Methods 2023, 20 (7), 958–961. 10.1038/s41592-023-01900-4. [DOI] [PubMed] [Google Scholar]
- Li X.; Li Y.; Zhou Y.; Wu J.; Zhao Z.; Fan J.; Deng F.; Wu Z.; Xiao G.; He J.; et al. Real-time denoising enables high-sensitivity fluorescence time-lapse imaging beyond the shot-noise limit. Nat. Biotechnol. 2023, 41 (2), 282–292. 10.1038/s41587-022-01450-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiao C.; Li D.; Liu Y.; Zhang S.; Liu K.; Liu C.; Guo Y.; Jiang T.; Fang C.; Li N.; et al. Rationalized deep learning super-resolution microscopy for sustained live imaging of rapid subcellular processes. Nat. Biotechnol. 2023, 41 (3), 367–377. 10.1038/s41587-022-01471-3. [DOI] [PubMed] [Google Scholar]
- Xue F.; He W.; Xiang Z. a.; Ren J.; Shan C.; Yuan L.; Xu P. Parameter-free clear image deconvolution (CLID) technique for single-frame live-cell super-resolution imaging. bioRxiv 2024, 10.1101/2024.09.11.612552. [DOI] [Google Scholar]
- Mo Y.; Wang K.; Li L.; Xing S.; Ye S.; Wen J.; Duan X.; Luo Z.; Gou W.; Chen T.; et al. Quantitative structured illumination microscopy via a physical model-based background filtering algorithm reveals actin dynamics. Nat. Commun. 2023, 14 (1), 3089. 10.1038/s41467-023-38808-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaswani A.; Shazeer N.; Parmar N.; Uszkoreit J.; Jones L.; Gomez A. N.; Kaiser Ł.; Polosukhin I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Bachimanchi H.; Volpe G. Diffusion Models to Enhance the Resolution of Microscopy Images: A Tutorial. arXiv 2024, 2409.16488. 10.48550/arXiv.2409.16488. [DOI] [Google Scholar]
- Du Y.; Liu Z.; Li J.; Zhao W. X. A Survey of Vision-Language Pre-Trained Models. arXiv 2022, 2202.10936. 10.48550/arXiv.2202.10936. [DOI] [Google Scholar]
- Han K.; Wang Y.; Chen H.; Chen X.; Guo J.; Liu Z.; Tang Y.; Xiao A.; Xu C.; Xu Y.; et al. A survey on vision transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45 (1), 87–110. 10.1109/TPAMI.2022.3152247. [DOI] [PubMed] [Google Scholar]
- Ma C.; Tan W.; He R.; Yan B. Pretraining a foundation model for generalizable fluorescence microscopy-based image restoration. Nat. Methods 2024, 21 (8), 1558–1567. 10.1038/s41592-024-02244-3. [DOI] [PubMed] [Google Scholar]
- Liu Z.; Lin Y.; Cao Y.; Hu H.; Wei Y.; Zhang Z.; Lin S.; Guo B.. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV); IEEE, 2021; pp 9992–10002. 10.1109/ICCV48922.2021.00986. [DOI]
- Tomczak J. M.Why Deep Generative Modeling? In Deep Generative Modeling, 1st ed.; Springer International Publishing, 2022; pp 1–12. 10.1007/978-3-030-93158-2_1. [DOI] [Google Scholar]
- Saguy A.; Nahimov T.; Lehrman M.; Gómez-de-Mariscal E.; Hidalgo-Cenalmor I.; Alalouf O.; Balakrishnan A.; Heilemann M.; Henriques R.; Shechtman Y. This Microtubule Does Not Exist: Super-Resolution Microscopy Image Generation by a Diffusion Model. Small Methods 2024, 2400672. 10.1002/smtd.202400672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang L.; Yu W.; Ma W.; Zhong W.; Feng Z.; Wang H.; Chen Q.; Peng W.; Feng X.; Qin B.; et al. A Survey on Hallucination in Large Language Models: Principles, Taxonomy, Challenges, and Open Questions. ACM Trans. Inf. Syst. 2025, 43, 1. 10.1145/3703155. [DOI] [Google Scholar]
- ChatGPT. OpenAI. https://openai.com/chatgpt/overview/.
- Ulyanov D.; Vedaldi A.; Lempitsky V. Deep Image Prior. International Journal of Computer Vision 2020, 128 (7), 1867–1888. 10.1007/s11263-020-01303-4. [DOI] [Google Scholar]
- Kobler E.; Effland A.; Kunisch K.; Pock T. Total Deep Variation: A Stable Regularization Method for Inverse Problems. IEEE Transactions on Pattern Analysis and Machine Intelligence 2022, 44 (12), 9163–9180. 10.1109/TPAMI.2021.3124086. [DOI] [PubMed] [Google Scholar]
- Wang J.; Fan J.; Zhou B.; Huang X.; Chen L. Hybrid reconstruction of the physical model with the deep learning that improves structured illumination microscopy. Advanced Photonics Nexus 2023, 2 (1), 016012. 10.1117/1.APN.2.1.016012. [DOI] [Google Scholar]
- Sui X.; He Z.; Chu D.; Cao L. Non-convex optimization for inverse problem solving in computer-generated holography. Light: Science & Applications 2024, 13 (1), 158. 10.1038/s41377-024-01446-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y.; Su Y.; Guo M.; Han X.; Liu J.; Vishwasrao H. D.; Li X.; Christensen R.; Sengupta T.; Moyle M. W.; et al. Incorporating the image formation process into deep learning improves network performance. Nat. Methods 2022, 19 (11), 1427–1437. 10.1038/s41592-022-01652-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MARTÍNEZ S.; TOSCANI M.; MARTINEZ O. E. Superresolution method for a single wide-field image deconvolution by superposition of point sources. J. Microsc. 2019, 275 (1), 51–65. 10.1111/jmi.12802. [DOI] [PubMed] [Google Scholar]
- Torres-García E.; Pinto-Cámara R.; Linares A.; Martínez D.; Abonza V.; Brito-Alarcón E.; Calcines-Cruz C.; Valdés-Galindo G.; Torres D.; Jabloñski M.; et al. Extending resolution within a single imaging frame. Nat. Commun. 2022, 13 (1), 7452. 10.1038/s41467-022-34693-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao B.; Mertz J. Resolution enhancement with deblurring by pixel reassignment. Advanced Photonics 2023, 5 (6), 066004. 10.1117/1.AP.5.6.066004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamilov U. S.; Bouman C. A.; Buzzard G. T.; Wohlberg B. Plug-and-Play Methods for Integrating Physical and Learned Models in Computational Imaging: Theory, algorithms, and applications. IEEE Signal Processing Magazine 2023, 40 (1), 85–97. 10.1109/MSP.2022.3199595. [DOI] [Google Scholar]
- Monga V.; Li Y.; Eldar Y. C. Algorithm Unrolling: Interpretable, Efficient Deep Learning for Signal and Image Processing. IEEE Signal Processing Magazine 2021, 38 (2), 18–44. 10.1109/MSP.2020.3016905. [DOI] [Google Scholar]
- Ye X.; Guan M.; Guo Y.; Liu X.; Wang K.; Chen T.; Zhao S.; Chen L. Live-cell super-resolution imaging unconventional dynamics and assemblies of nuclear pore complexes. Biophysics Reports 2023, 9 (4), 206–214. 10.52601/bpr.2023.230010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng X.; Duan R.; Li L.; Xing S.; Ji H.; Yan H.; Gao K.; Wang J.; Wang J.; Chen L. Live-cell superresolution pathology reveals different molecular mechanisms of pelizaeus-merzbacher disease. Science Bulletin 2020, 65 (24), 2061–2064. 10.1016/j.scib.2020.08.016. [DOI] [PubMed] [Google Scholar]
- Laine R. F.; Heil H. S.; Coelho S.; Nixon-Abell J.; Jimenez A.; Wiesner T.; Martínez D.; Galgani T.; Régnier L.; Stubb A.; et al. High-fidelity 3D live-cell nanoscopy through data-driven enhanced super-resolution radial fluctuation. Nat. Methods 2023, 20 (12), 1949–1956. 10.1038/s41592-023-02057-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gustafsson N.; Culley S.; Ashdown G.; Owen D. M.; Pereira P. M.; Henriques R. Fast live-cell conventional fluorophore nanoscopy with ImageJ through super-resolution radial fluctuations. Nat. Commun. 2016, 7, 7. 10.1038/ncomms12471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Y.; Han X.; Su Y.; Glidewell M.; Daniels J. S.; Liu J.; Sengupta T.; Rey-Suarez I.; Fischer R.; Patel A.; et al. Multiview confocal super-resolution microscopy. Nature 2021, 600 (7888), 279–284. 10.1038/s41586-021-04110-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaib A. H.; Chouaib A. A.; Chowdhury R.; Altendorf J.; Mihaylov D.; Zhang C.; Krah D.; Imani V.; Spencer R. K. W.; Georgiev S. V.; et al. One-step nanoscale expansion microscopy reveals individual protein shapes. Nat. Biotechnol. 2024, 10.1038/s41587-024-02431-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dey S.; Fan C.; Gothelf K. V.; Li J.; Lin C.; Liu L.; Liu N.; Nijenhuis M. A. D.; Saccà B.; Simmel F. C.; et al. DNA origami. Nature Reviews Methods Primers 2021, 1 (1), 13. 10.1038/s43586-020-00009-8. [DOI] [Google Scholar]
- Thevathasan J. V.; Kahnwald M.; Cieśliński K.; Hoess P.; Peneti S. K.; Reitberger M.; Heid D.; Kasuba K. C.; Hoerner S. J.; Li Y.; et al. Nuclear pores as versatile reference standards for quantitative superresolution microscopy. Nat. Methods 2019, 16 (10), 1045–1053. 10.1038/s41592-019-0574-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saxton W. O.; Baumeister W. The correlation averaging of a regularly arranged bacterial cell envelope protein. J. Microsc. 1982, 127 (2), 127–138. 10.1111/j.1365-2818.1982.tb00405.x. [DOI] [PubMed] [Google Scholar]
- Nieuwenhuizen R. P. J.; Lidke K. A.; Bates M.; Puig D. L.; Grünwald D.; Stallinga S.; Rieger B. Measuring image resolution in optical nanoscopy. Nat. Methods 2013, 10 (6), 557–562. 10.1038/nmeth.2448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao W.; Huang X.; Yang J.; Qu L.; Qiu G.; Zhao Y.; Wang X.; Su D.; Ding X.; Mao H. Quantitatively mapping local quality of super-resolution microscopy by rolling Fourier ring correlation. Light Sci. Appl. 2023, 12, 298. 10.1038/s41377-023-01321-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Culley S.; Albrecht D.; Jacobs C.; Pereira P. M.; Leterrier C.; Mercer J.; Henriques R. Quantitative mapping and minimization of super-resolution optical imaging artifacts. Nat. Methods 2018, 15 (4), 263–266. 10.1038/nmeth.4605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sahl S. J.; Balzarotti F.; Keller-Findeisen J.; Leutenegger M.; Westphal V.; Egner A.; Lavoie-Cardinal F.; Chmyrov A.; Grotjohann T.; Jakobs S. Comment on “Extended-resolution structured illumination imaging of endocytic and cytoskeletal dynamics. Science 2016, 352 (6285), 527–527. 10.1126/science.aad7983. [DOI] [PubMed] [Google Scholar]
- Li D.; Betzig E. Response to Comment on “Extended-resolution structured illumination imaging of endocytic and cytoskeletal dynamics. Science 2016, 352 (6285), 527–527. 10.1126/science.aad8396. [DOI] [PubMed] [Google Scholar]
- Deguchi T.; Iwanski M. K.; Schentarra E.-M.; Heidebrecht C.; Schmidt L.; Heck J.; Weihs T.; Schnorrenberg S.; Hoess P.; Liu S.; et al. Direct observation of motor protein stepping in living cells using MINFLUX. Science 2023, 379 (6636), 1010–1015. 10.1126/science.ade2676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaked N. T.; Boppart S. A.; Wang L. V.; Popp J. Label-free biomedical optical imaging. Nat. Photonics 2023, 17 (12), 1031–1041. 10.1038/s41566-023-01299-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theer P.; Mongis C.; Knop M. PSFj: know your fluorescence microscope. Nat. Methods 2014, 11 (10), 981–982. 10.1038/nmeth.3102. [DOI] [PubMed] [Google Scholar]
- Liu A.; Liu Y.; Gu J.; Qiao Y.; Dong C. Blind Image Super-Resolution: A Survey and Beyond. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45 (5), 5461–5480. 10.1109/TPAMI.2022.3203009. [DOI] [PubMed] [Google Scholar]
- Booth M. J. Adaptive optical microscopy: the ongoing quest for a perfect image. Light Sci. Appl. 2014, 3 (4), e165 10.1038/lsa.2014.46. [DOI] [Google Scholar]
- Toader B.; Boulanger J.; Korolev Y.; Lenz M. O.; Manton J.; Schönlieb C.-B.; Mureşan L. Image Reconstruction in Light-Sheet Microscopy: Spatially Varying Deconvolution and Mixed Noise. Journal of Mathematical Imaging and Vision 2022, 64 (9), 968–992. 10.1007/s10851-022-01100-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karl W. C.; Fowler J. E.; Bouman C. A.; Çetin M.; Wohlberg B.; Ye J. C. The Foundations of Computational Imaging: A signal processing perspective. IEEE Signal Processing Magazine 2023, 40 (5), 40–53. 10.1109/MSP.2023.3274328. [DOI] [Google Scholar]
- Padilla W. J.; Averitt R. D. Imaging with metamaterials. Nature Reviews Physics 2022, 4 (2), 85–100. 10.1038/s42254-021-00394-3. [DOI] [Google Scholar]
- Carpenter A. E.; Cimini B. A.; Eliceiri K. W. Smart microscopes of the future. Nat. Methods 2023, 20 (7), 962–964. 10.1038/s41592-023-01912-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hell S. W.; Sahl S. J.; Bates M.; Zhuang X.; Heintzmann R.; Booth M. J.; Bewersdorf J.; Shtengel G.; Hess H.; Tinnefeld P.; et al. The 2015 super-resolution microscopy roadmap. J. Phys. D: Appl. Phys. 2015, 48 (44), 443001. 10.1088/0022-3727/48/44/443001. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.











