Abstract

Charge separation is at the heart of solar energy applications, and efficient materials require fast photoinduced electron transfer (ET) and slow charge recombination (CR). Using time-dependent self-consistent charge density functional tight-binding theory combined with nonadiabatic (NA) molecular dynamics, we report a detailed analysis of ET and CR in hybrids composed of photoactive covalent organic polyhedra (COP) and encapsulated fullerenes. The ET occurs on a subpicosecond time scale and accelerates with increasing fullerene diameter, C60 to C70 to C84. As the fullerene size increases, the π-electron system available for interaction with the COP grows, the fullerene-COP separation decreases, and the number of fullerene states available to accept the photoexcited electron increases, accelerating the ET. In comparison, the CR occurs on a nanosecond time scale and correlates with the length of the fullerene shortest axis because the relevant fullerene state is polarized in that direction. The largest and least symmetrical C84 exhibits the fastest ET and the slowest CR, making COP@C84 the most promising hybrid. Both high-frequency bond stretching and bending vibrations and low-frequency breathing modes are involved in the ET and CR processes, with more modes present in the C84 system due its lower symmetry. The 10–20 fs vibrationally induced coherence loss in the electronic subsystem contributes to long lifetimes of the charge-separated states. The comprehensive investigation of the structure–property relationship of the charge carrier dynamics in the COP@fullerene hybrids provides a detailed atomistic understanding of interfacial ET processes and generates guidelines for rational design of high-performance materials for solar energy and related applications.
1. Introduction
Efficient conversion of solar light into electricity remains challenging, and much emphasis is placed on keeping up with the rapidly increasing global energy demand.1 The photoinduced electron transfer (ET) and charge recombination (CR) are the key fundamental processes for the conversion of light to electricity.2−5 Efficient solar energy systems should exhibit fast ET and slow CR.6−9 Keeping this in mind, several strategies have been adopted in recent times to tune ET and CR dynamics at donor–acceptor interfaces.10−16 The architectures of donor–acceptor composites have attracted significant attention in solar energy conversion, optoelectronics, and other fields.17,18 Porphyrins are appealing candidates because of their potential applications as light-harvesting agents,19,20 light emitters in organic light-emitting diodes,21 molecular switches,22 and molecular photocatalysts.23 On the other hand, the three-dimensional π-electronic system of fullerenes is considered an excellent choice for an electron acceptor in hybrid systems.24−26 The extraordinary electron acceptor properties of fullerenes have led to their wide utilization for photoinduced ET in solar energy conversion.4,27,28 Donor–acceptor interactions between the π-systems of porphyrins and fullerenes give rise to a fascinating class of functional materials.29−32 Supramolecular construction of donor–acceptor hybrids allows for selection and interchange the donor and acceptor entities, while preserving their intrinsic structures and electronic features at the interface.29,33 Multiple recent experimental studies focused on photoinduced excited state charge transfer dynamics in porphyrin-fullerene hybrids, reporting charge separation and recombination time scales with transient absorption spectroscopies.34−41 The π–π interaction plays an important role in constructing efficient porphyrin-fullerene hybrid systems by controlling their charge transfer behavior.42 For instance, Caballero et al. demonstrated how the lifetime of the charge-separated state could be extended by controlling supramolecular interaction in porphyrin-fullerene assemblies.43 Although substantial efforts have been dedicated already to the development of light-harvesting devices, the overall device performance remains below the ideal theoretical limit. Therefore, theoretical studies of the photophysics of interfacial ET and CR processes in realistic systems are needed in order to achieve further progress.
In this work, we investigated the photoinduced charge separation and recombination dynamics in the covalent organic polyhedra (COP)@fullerene composites using nonadiabatic molecular dynamics (NAMD). We show that upon photoexcitation of the covalent organic polyhedron COP, an electron is transferred from the COP to the fullerene (C70, C60, and C84). The COP@C70 hybrid exhibits an ultrafast photoinduced ET with a time constant of 585 fs, in agreement with the experiment.44 The incorporation of C60 into the COP slows down the ET to 783 fs, while the ET become extremely fast, 199 fs, in the COP@C84 system. Our analysis suggests that the ET time is strongly related to the size of the fullerene interfaced with the COP, decreasing in the order C60 > C70 > C84. The interfacial ET time depends inversely on the average diameter of the fullerene for several reasons: (1) the extent of the fullerene π-electron system accessible for the π–π interaction with the COP electron donor grows; (2) the donor–acceptor separation distance shortens; (3) the number of fullerene states available to accept the electron increases; and (4) the donor–acceptor energy gap decreases. The first two factors enhance the donor–acceptor electronic interaction. The third factor increases the number of ET pathways, while the last factor increases the NA coupling that is inversely proportional to the energy gap. As a result, the ET is the fastest in COP@C84. The CR dynamics is several orders of magnitude slower than the ET, and its dependence on the fullerene size is somewhat different. In particular, fullerene symmetry plays a key role. The difference in the dependence of the ET and CR rates on fullerene size and symmetry stems from the fact that multiple final states are available for the ET, while only one donor–acceptor state pair participates in the CR. Fullerene states are polarized along the three fullerene axes. The ET involves multiple states and the polarizations are averaged, but the CR occurs from the fullerene lowest unoccupied molecular orbital (LUMO), which is polarized along the shortest fullerene axis. Hence, it is the length of the shortest axis rather than the average diameter that governs the CR. The recombination is the slowest, 8.47 ns, in COP@C84 that exhibits the largest asymmetry, and becomes faster for C60 and C70, 4.57 and 2.54 ns, respectively. Quantum decoherence plays an important role in making the CR time long, while the dependence on the coherence time is complex. Exhibiting the fastest ET and the slowest CR, with the CR/ET time scale ratio exceeding 42,000, the COP@C84 hybrid is particularly promising for solar energy applications. The reported study provides in-depth atomistic insights into the operation of organic solar cells and related devices based on fullerene–porphyrin hybrids, providing fundamental principles and practical guidelines for further progress in this important field.
2. Methods
All the quantum mechanical calculations along with geometry optimization and MD simulations are carried out with the self-consistent charge density functional tight-binding (SCC-DFTB) methodology implemented in the DFTB+ package.45,46 The DFTB parameter set, mio skfs,47,48 used in this study has been successfully applied to a variety of systems. To characterize the van der Waals interactions between the COP and the fullerene, the Lennard-Jones dispersion correction49 is employed. After geometry optimization, the COP@fullerene hybrids are heated to 300 K for 5 ps with velocity rescaling.50 Then 3 ps adiabatic MD trajectories are generated using the Verlet methodology51,52 with the 1 fs atomic time step. The trajectories are used to calculate the time-dependent Kohn–Sham orbital energies NA coupling matrix elements between the energy eigenstates. The NAMD simulation are performed under the classical path approximation (CPA).53,54 The electrons are treated quantum mechanically and the nuclear degrees of freedom semiclassically. The atoms are evolved with classical Newton’s equation of motion, and the influence of the quantum properties of the nuclei on the electronic evolution is captured semiclassically as the decoherence process.55 In the CPA, the electronic degrees of freedom do not affect the nuclear dynamics and parametrically depend on the nuclear evolution given by the MD trajectory. In general, CPA speeds up the simulation by greatly reducing the number of electronic structure calculations and avoiding expensive calculations of excited state forces. The charge transfer dynamics processes are modeled with the fewest switches surface hopping algorithm.56,57 The nonradiative CR is simulated using decoherence induced surface hopping (DISH).58 Both algorithms are implemented in the PYthon eXtension for Ab Initio Dynamics (PYXAID) package.13,59 The methodology60 reproduces well the carrier dynamics times scale obtained from transient absorption spectroscopy experiments, provides important atomistic insights, and has been applied successfully to a variety of systems, including carbon nanotube composites,61−64 cadmium chalcogenide quantum dots65,66 and nanoplatelets,67−69 macromolecular porphyrin systems,70−73 and metal halide perovskites,74−81 etc.82,83
3. Results and Discussions
Excited state dynamics in COP@fullerene hybrids involves multiple steps, as illustrated schematically in Figure 1a. Photoexcitation of the electron-rich COP promotes an electron from its highest occupied molecular orbital (HOMO) to its LUMO leaving a hole in the HOMO and creating an exciton (e–h pair) (i). Subsequently, the photoexcited electron transfers from the COP excited state to fullerene LUMO (ii). Once the charge separation is achieved, the charge-separated state can undergo CR, leading to relaxation of the COP@fullerene hybrid to the ground state (iii). An efficient photovoltaic hybrid requires a fast ET and slow CR.
Figure 1.
(a) Schematic of energy levels involved in the photoinduced ET and CR dynamics across the (COP)@fullerene interface. (i) Photoexcitation of electron-rich COP promotes an electron from its HOMO to LUMO leaving a hole inside the HOMO and creating an exciton (e–h pair). (ii) Subsequently, the excited electron is transferred to the energetically lower LUMO of the fullerene (C70, C60, and C84) interfaced with COP. (iii) Following the charge separation, the photogenerated carriers can recombine at the interface, returning the system to the ground state. Optimized geometries of the COP with encapsulated fullerenes: (b) COP@C70, (c) COP@C60, and (d) COP@C84. The COP and fullerenes are held together by the van der Waals force of attraction through π–π interaction. C atoms of the fullerenes are denoted by red spheres, while the C, N, and H atoms of COP are shown by brown, light blue, and light pink spheres, respectively.
3.1. Geometric and Electronic Structure
To analyze the photoinduced charge transfer dynamics, we focus first on the geometry of the systems under investigation. In the COP@fullerene hybrids, the fullerene guest occupies the cavity of bis-porphyrin based COP macrocycle host, and the two subsystems interact by van der Waals force of attractions and Pauli (sterical) force of repulsion, as shown in Figure 1b–d. In addition, the porphyrin units of the COP and the fullerene experience an π–π electron interaction. The calculated binding energy of COP@C60 is 2.98 eV. The binding energy of COP@C70 is somewhat larger, 3.6 eV. Encapsulation of C84 inside the COP cavity increases the binding energy further to 4.31 eV.
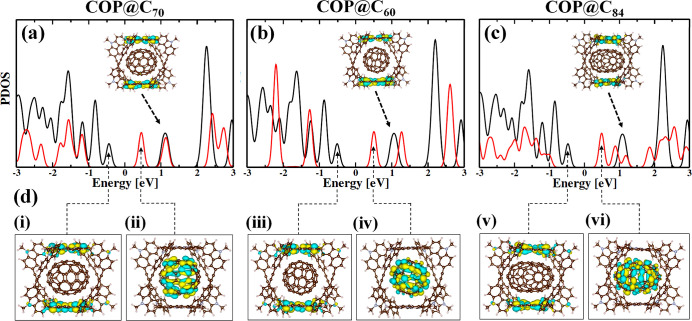
The projected density of states (PDOS) provides qualitative insight regarding the interfacial electronic interaction and charge separation and recombination dynamics at the interface. Figure 2a–c shows the PDOS of the COP@fullerene hybrids, split into contributions from COP and fullerene (C70, C60, and C84). The PDOS demonstrates that the COP@fullerene hybrids form a type-II photovoltaic interface. The observation is consistent with the experiment.44 The COP DOS is larger than the fullerene DOS. The HOMO of the composite systems is contributed by the macrocyclic COP, while the LUMO comes from the fullerenes (C70, C60, and C84) for all of the hybrid systems. The number of electron acceptor states in the fullerene conduction band (CB) grows with increasing fullerene size. Triply degenerate states of C60 can accept electron from the COP. Similarly, only triply degenerate states in C70 can accept the electron, because the COP electron donor states are slightly lower in energy compared to the doubly degenerate states of C70, though the energy difference is small. In comparison, both triply and doubly degenerate states can accept the photoexcited electron in the COP@C84 hybrid. The larger number of acceptor states leads to a faster ET in this composite.
Figure 2.
PDOS of (a) COP@C70, (b) COP@C60, and (c) COP@C84. Zero energy is set to the Fermi level. Black and red lines indicate the density of states of COP and fullerenes, respectively. The inserts show charge densities of the electron donor states. (d) Charge densities of the electron acceptor and hole states. The dotted arrows relate the charge densities to the corresponding energy levels. The PDOS demonstrates a type-II band alignment for all systems. The HOMOs of the composite systems are localized on the COP, while the LUMOs come from the fullerene (C70, C60, and C84). Note that the COP DOS is larger than the fullerene DOS because the COP has more atoms.
The charge densities of the key electronic states involved in the charge separation and recombination dynamics are presented in the insets of Figure 2a–c and in Figure 2d. The photoexcited donor states are localized on the electron-rich COP subunit. Because the COP LUMO can be close in energy of some fullerene states, the photoexcitation process can generate a partially charge-separated state. In contrast, the ET acceptor states are localized entirely over the fullerene units, and the ET process creates a fully charge-separated state. The CR process starts with the photoexcited electron in the fullerene LUMO and ends with the electron relaxing to the COP HOMO.
The absorption spectra of the three COP@fullerene nanohybrids and their individual components, i.e., COP, C70, C60, and C84, were simulated using time-dependent DFTB theory, as shown in Figure S1. The spectra of the individual components (Figure S1a) demonstrate that COP absorbs light much more strongly than fullerenes at low energies. The spectra of the hybrid systems (Figure S1b) show that the highest absorption peak is nearly the same in all three hybrids, arising from COP. Therefore, COP is photoexcited predominantly in the hybrid systems over the relevant energy range, and hence, the process of interest is ET from COP to fullerenes. Hole transfer that would arise if fullerenes were photoexcited is much less important in current systems. As demonstrated by Krajewski et al., the S0 → S1 transition is dipole-forbidden for fullerene or its derivatives.84
The time scales of the nonradiative charge transfer and recombination dynamics depend on the NA coupling between the donor and acceptor states, and the NA coupling strength is inversely proportional to the energy difference between the corresponding states,85,86 leading to the energy gap law.87 The NA coupling can be enhanced by (i) larger overlap of initial and final states, (ii) narrower energy gap, and (iii) faster nuclear motion.75,76,88,89 The electronic energy levels involved in the photoexcited dynamics are perturbed when fullerenes (C70, C60, and C84) interact with the COP subsystem. The computed energy offsets between the donor and acceptor states for the charge separation process are very similar in the COP@C70 and COP@C60 hybrids, 0.65 and 0.64 eV, respectively. The energy offset helps to overcome the exciton binding energy. The excess electronic energy is deposited on vibrations during the ET process. The energy offset values reported above are obtained canonically averaged over the MD trajectories at 300 K and are summarized in Table 1 and Figure 3a. In turn, the C84 fullerene reduces the band offset to 0.38 eV and, consequently, enhances the NA coupling. Thus, the canonically averaged NA coupling value is 29.28 meV for COP@C84, whereas it is 7 times smaller in COP@C70 and COP@C60, 4.21 and 3.99 meV, respectively.
Table 1. Canonically Averaged Energy Gaps, Root-Mean-Square Nonadiabatic Coupling (NAC), and Decoherence/Pure-Dephasing, ET, and CR Times in the COP@fullerene Systems.
| system | process | band offset/gap (eV) | NAC (meV) | decoherence (fs) | time (ps) |
|---|---|---|---|---|---|
| COP@C70 | ET | 0.65 | 4.21 | 28 | 0.585 |
| COP@C60 | 0.64 | 3.99 | 20 | 0.783 | |
| COP@C84 | 0.38 | 29.28 | 24 | 0.199 | |
| COP@C70 | CR | 0.77 | 0.51 | 14 | 2.540 |
| COP@C60 | 0.85 | 0.39 | 12 | 4.570 | |
| COP@C84 | 0.86 | 0.28 | 25 | 8.470 |
Figure 3.
(a) Schematic of the energy levels of the key states involved in the photoinduced dynamics in the COP@fullerene hybrids. The energy levels are color-coded for the COP and fullerene in each hybrid. Dual color lines represent states with contributions from both components. The electron donor and acceptor states of COP@C70 are separated by 0.65 eV. The gap is narrowed to 0.38 eV, when C84 interfaced with the COP. The smaller energy gap results in a stronger NA coupling and faster charge separation. In contrast, the energy gap for CR is 0.77 eV in COP@C70, and is widened to 0.85 and 0.86 eV in COP@C60 and COP@C84, respectively. The NA coupling is weakened, and the lifetime of the charge separated state becomes longer. Spectral densities obtained from Fourier transforms of the energy gaps between the donor and acceptor states involved in the photoinduced ET in (b) COP@C70, (c) COP@C60, and (d) COP@C84. Both low and high frequency phonon modes are involved in the C70 and C60 hybrids, while in C84, high-frequency modes dominate over low frequency modes, enhancing the NA coupling and accelerating the ET. (e) Pure-dephasing functions for the ET processes in COP@C70 (black), COP@C60 (red), and COP@C84 (blue).
Considering the recombination, the energy gap between the fullerene LUMO and COP HOMO is the smallest in the COP@C70 hybrid, 0.77 eV. The COP HOMO is downshifted in the COP@C60 hybrid, whereas the C60 LUMO is upshifted, increasing the gap to 0.85 eV. Similarly, the energy gap involved in the CR is 0.86 eV in the COP@C84. Since the NA coupling is inversely proportional to the gap, the NA coupling of 0.51 meV in the COP@C70 composite is larger than the NA coupling of 0.39 meV in the COP@C60 composite. The hybrid COP@C84 shows an even weaker NA coupling of 0.28 meV. The increased energy gaps between the COP HOMO and fullerene LUMO slow down the electron-hole recombination.
Analysis of the electronic structure of the COP@fullerene hybrids shows that the energy gap involved in the ET process is the smallest, while the gap involved in the CR is the largest in the C84 system, suggesting that it should exhibit the most favorable excited state dynamics. That is, one can expect the fastest ET and the slowest CR in COP@C84 among the three systems under consideration.
In addition to fixing the COP size and varying the fullerene, we considered the C70 fullerene embedded into larger COPs, as studied experimentally by Yang et al.90Figure S4 demonstrates that these systems also exhibit the type-II energy alignment. As the COP size increases from COP to COP-2 to COP-3, the fullerene-COP interaction weakens because the fullerene cannot approach all parts of the COP simultaneously, and the COP distorts to adjust its cavity to the fullerene size. This result suggests that both charge separation and recombination should slow with increasing COP size.
To test the accuracy of the SCC-DFTB calculations, we calculated the electronic structure of COP@C60, COP@C70, and COP@C84 using ab initio density functional theory (DFT) with the Perdew-Burke-Ernzerhof (PBE) functional.91 The PBE data were obtained with Vienna Ab initio Simulation Package using a converged plane-wave basis set. The data shown in Figure S5 demonstrate a good agreement between the tight-binding and ab initio data.
3.2. Electron–Vibrational Interactions and Electronic Coherence
The motion of the nuclei affects electronic motion, and electron–phonon interactions generate elastic and inelastic scattering.71 Inelastic scattering is characterized by the NA coupling that induces energy exchange between the electronic and vibrational subsystems.64,70 Elastic electron–phonon scattering randomizes phases of electronic wave functions, inducing the loss of coherence between electronic state pairs. Both types of scattering directly influence the excited state dynamics. Fourier transforms of phonon-induced fluctuation of the energy gaps between donor and acceptor states generate spectral densities that identify active phonon modes associated with the ET and CR processes, as shown in Figures 3b–d and S2, respectively. The low 250 cm–1 frequency is assigned to be the out-of-plane skeletal vibration of porphyrin, and the signals in the 250–500 cm–1 range are due to the breathing modes of the porphyrin. The signals in the high frequency range, from 1400 to 1800 cm–1, originate from C–C and C–N bond stretching of the porphyrin unit. The spectral density characterizing the ET process in COP@C70 exhibits few dominant signals at ∼550 cm–1 and ∼1650 cm–1, as shown in Figure 3b. The high frequency signals become weaker in COP@C60, and a strong low frequency signal appears, as shown in Figure 3c. The large C84 fullerene introduces several high-frequency modes that actively participate in the ET, as shown in Figure 3d. These high frequency modes contribute strongly to the NA coupling. The fast modes create large nuclear velocities that enter into the NA coupling matrix element,60 rationalizing the larger NA coupling for ET in COP@C84 compared to the other two systems, as shown in Table 1. Thus, involvement of multiple high frequency modes in COP@C84, together with the reduced donor–acceptor energy gap, favors fast charge separation.
To characterize coherence loss in the electronic subsystem due
to elastic electron–phonon scattering, we obtain pure-dephasing
times using optical-response theory and the second order cumulant
approximation.92Figure 3e presents the pure-dephasing curves for
ET dynamics. The pure-dephasing times, τgau, are
obtained by Gaussian fitting of the curves, 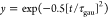 . The coherence times are similar in all
three systems, indicating that it is not a major factor distinguishing
the three fullerenes.
. The coherence times are similar in all
three systems, indicating that it is not a major factor distinguishing
the three fullerenes.
3.3. Interfacial ET Dynamics in COP@fullerene Hybrids
In the COP@fullerene hybrids, the electron-rich COP serves as an
electron donor, whereas the fullerenes act as electron acceptors.
Absorption of a photon by the COP molecule leads to ET from COP to
the fullerene. Figure 4a shows decay of populations of the donor states during the photoinduced
ET in the COP@fullerene systems. The dynamics are not purely exponential
and contain a notable Gaussian component at an early time. The data
were fitted by the linear combination of Gaussian and exponential
functions 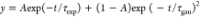 . The ET time constants shown in Table 1 are obtained as the
weighted averages of the Gaussian and exponential times. In COP@C70, photoexcitation of COP leads to an ultrafast, 585 fs ET
to C70, in good agreement with the experiment.44 The ET is slower in COP@C60, at 783
fs. In comparison, incorporation of C84 into the COP cavity
accelerates the ET nearly by a factor of 4, with a time constant of
199 fs.
. The ET time constants shown in Table 1 are obtained as the
weighted averages of the Gaussian and exponential times. In COP@C70, photoexcitation of COP leads to an ultrafast, 585 fs ET
to C70, in good agreement with the experiment.44 The ET is slower in COP@C60, at 783
fs. In comparison, incorporation of C84 into the COP cavity
accelerates the ET nearly by a factor of 4, with a time constant of
199 fs.
Figure 4.

(a) Decay of population of the donor states in COP@C70 (black), COP@C60 (red), and COP@C84 (blue) during the ET dynamics. The time scales are obtained by fitting the simulated data by combination of Gaussian and exponential functions. The interfacial ET time decreases with increasing average diameter (d) of the fullerene, which is 7.12, 7.31, and 8.21 Å for C60, C70, and C84, respectively. As fullerene size increases, it can approach the COP more closely, enhancing the electronic communication between the subunits, and thereby, the NA coupling that promotes ET. NA coupling and band offset values for ET are shown in the doughnut representation in the inset. The same color code is used for each system. (b) Schematic of charge distributions in the acceptor states for ET in COP@C70, COP@C60, and COP@C84. There are more acceptor states in C84 compared to C60 and C70, favoring the charge separation.
The photoexcited electrons undergo photoexcitation from the COP donor states to the fullerene acceptor states. COP has a stable and rigid structure, and therefore, the proximity between COP and fullerene depends on the fullerene size. Since C84 is the largest among the three fullerenes, it remains closest to the COP, enhancing the donor–acceptor interaction. Further, only the first three unoccupied states of C60 and C70 can accept the electron since they are below the COP CB in energy. In contrast, five unoccupied states can act as electron acceptor states in C84, as shown in Figures 2 and 3. Schematic charge distributions of the fullerene acceptor are presented in Figure 4b, and the corresponding charge density isosurface plots are shown in Figure S3. Although individual acceptor states exhibit pronounced asymmetries relative to the spherical symmetry of the fullerenes, on average the acceptor states cover the whole fullerene. Therefore, the directionality of the donor–acceptor interaction is insignificant, and the overlap of the donor and acceptor states can be characterized by the average fullerene diameter (d). The latter is obtained by averaging the lengths of the three fullerene axes. The values reported in Figure 4b and Table S1 agree with the previous results.93 As expected, the average fullerene diameter increases with the number of atoms, C84 > C70 > C60. The donor–acceptor separation decreases as the fullerene diameter increases, and therefore, the photoinduced ET should be faster for larger fullerenes.
Further, a larger d value corresponds to a larger area of the π-electron surface of the fullerene unit. The enhanced electronic communication with the COP also strengthens the NA coupling between the donor–acceptor subunits; see Table 1 and the inset of Figure 4a, favoring faster charge separation. Therefore, we can conclude that the ET from the COP macrocycle to fullerene in the COP@fullerenes hybrids depends upon the fullerene and can be inversely correlated with the average fullerene diameter. The fullerene diameter can be used as a predictive tool for the kinetics of the photoinduced ET.
3.4. Electron–Hole Recombination at COP@fullerene Interfaces
Nonradiative electron–hole recombination is the prime source of charge and energy losses in solar energy applications. Therefore, along with a fast charge separation, a slow CR is key to the high photon-to-electric conversion efficiency of photovoltaics. Figure 5a illustrates the CR dynamics of the COP@fullerene composites, obtained using the DISH technique.58 The decay of the populations of the charge-separated states is fitted with the short-time linear approximation to the exponential function: y = exp(−t/τ) ≈ 1 – t/τ, and the time constants are summarized in Table 1. The NAMD simulations demonstrate that the nonradiative CR between the fullerene LUMO and COP HOMO is fastest. 2.54 ns, in the COP@C70 hybrid. The CR slows to 4.57 ns in the COP@C60 system. The NAMD simulations performed with ab initio DFT using the PBE functional show a similar trend, as shown in Figure S6. The CR is the slowest, 8.47 ns, for the largest fullerene system, COP@C84. In all systems, the CR process is several orders of magnitude slower than the charge separation. The combination of the fastest charge separation with the slowest CR makes this system the most favorable for photovoltaic applications.
Figure 5.
(a) Decay of population of the donor state during CR in COP@C70 (black), COP@C60 (red), and COP@C84 (blue). The recombination dynamics are simulated by the DISH technique, and the time scales are in nano second time regime, obtained from short-time linear approximation to exponential decay. The two major factors, energy gaps and NA coupling, contributing to the CR dynamics are compared in the inset of (a). The same color code is used for each system. (b) Lengths of fullerene axis along the direction between the porphyrin units (green) of the COP. The axis length is inversely related to the recombination time scale; the longer the axis, the faster the recombination. The orientations of fullerene LUMO charge densities are represented schematically by red. Distribution of charge in proximity with the porphyrin units of the COP accelerates the recombination.
The electron vibrational influence spectra characterizing the phonon modes that drive the nonradiative CR and accommodate the electronic energy are shown in Figure S2. The spectra for the C70 and C60 systems are quite analogous. Several high- and low frequency vibrational modes drive the nonradiative CR in the hybrid containing C70, while in COP@C60, very low frequency modes dominate the spectrum. The strongest signals are related to fullerene bouncing against the COP cage, allowed by the relatively small size of the fullerene. The weak participation of high frequency phonons in C60 relative to C70 makes the charge-separated state longer-lived. In comparison, the C84 hybrid exhibits multiple signals at both low and high frequencies, as shown in Figure S2c.
The pure-dephasing functions, calculated based on the phonon-induced fluctuations of the electronic energy gaps,94,95 are shown in Figure S2d. The pure-dephasing times are similar for the C70 and C60 systems, 12 and 14 fs, respectively, as shown in Table 1. The loss of coherence occurs twice as slowly in COP@C84. This may appear surprising, since more vibrational modes couple to the electronic transition in this case (Figure S2c) than in the other two cases (Figure S2a,b), and phase randomization is faster if multiple frequencies contribute to the signal. However, the time scale of pure-dephasing also depends on the absolute magnitude of the energy gap fluctuation,96 and that value is smaller for COP@C84, because the system is more spatially constrained and fluctuates less. According to the quantum Zeno effect,97 quantum transitions stop in the limit of infinitely fast decoherence, and close to that limit, shorter coherence time favors longer transition time. The current system is not sufficiently close to the quantum Zeno limit and does not follow this trend, because the coherence times are longer than the Rabi oscillation times, as analyzed in detail in ref. (97).
The fullerene LUMO and the COP HOMO represent the initial and final states of the nonradiative CR. The COP HOMO is localized in porphyrin units and is the same in all three cases; however, the properties of the fullerene LUMO depend on the size and symmetry of fullerene. The orientations of the LUMO in the three systems are represented schematically in Figure 5b, and the corresponding iso-surface charge density plots are shown in Figure S3. The C70 LUMO is localized in the middle of the fullerene and is close to the two porphyrin units of the COP. This situation enhances the donor–acceptor coupling and accelerates the CR, relative to the other systems. In comparison, the C60 LUMO is tilted relative to that of the two porphyrins. Further, C60 is smaller than C70, and therefore, the donor–acceptor interaction is weaker, resulting in a smaller NA coupling and slower CR, as shown in Table 1. C84 is not spherically symmetric. Its LUMO is along the minor axis, and therefore, its overlap with the porphyrin wave functions is decreased compared to the other two systems. As a result, the NA coupling is the smallest and the lifetime of the charge-separated state is the longest. Thus, the size and orientation of the fullerene moiety play a key role in the CR process. C60 is spherically symmetric, and the lengths of the three axes are the same in all directions, 7.12 Å, as shown in Table S1. C84 is oriented between the two COP porphyrin units along its minor axis, 6.34 Å, and generates the weakest NA coupling. C70 is more symmetric than C84 and all its axes are longer than the C60 axis. As a result, C70 approaches the COP porphyrin units the closest, and the NA coupling is the strongest, as shown in Table 1. Therefore, the current simulation established the axis length as the predictive tool for designing fullerene-based photovoltaic devices. Shorter length of the relevant axis extends the lifetime of the charge-separated state.
Finally, the performance of photovoltaic devices depends on the ratio of the CR and ET times, τCR/τET. Good performance requires the ratio to be high.44 For the C70-encapsulated hybrid, the computed τCR/τET ratio is ∼4300. The corresponding value for COP@C60 is ∼5800. Most notably, COP@C84 exhibits a very large ratio, ∼42,500, nearly an order of magnitude higher than that of the other two systems, making COP@C84 hybrids particularly promising for solar energy applications.
4. Conclusions
Motivated by recent experimental results, we have investigated the ET and CR dynamics in COP@fullerene hybrids using atomistic quantum dynamics simulations. By considering several fullerenes of different sizes and shapes, we have unraveled the role of the fullerene encapsulated inside the COP cavity on the charge carrier dynamics. The analysis of the simulation results allowed us to establish the factors that make the ET fast and the CR slow, as required for efficient solar energy materials. The NAMD simulation demonstrates that through-space ET from the COP to C70 takes 585 fs, in agreement with the experiment.44 The COP@C60 hybrid exhibits a slower, 783 fs ET. In contrast, the COP@C84 system generates a very fast ET process, 199 fs. The analysis of the NAMD results has revealed that the ET depends strongly on the average diameter of the fullerene: The larger the diameter, the faster the ET. As the fullerene size increases, the extent of the fullerene π-electron surface accessible for electronic communication with the COP grows, enhancing the donor–acceptor interaction. In addition, larger fullerenes make a tighter fit inside the COP, decreasing the donor–acceptor distance. Further, the number of states, available in the fullerene for accepting the electron, grows with increasing fullerene size, and the donor–acceptor energy gaps decrease. All these factors make the NA coupling stronger for larger fullerenes, facilitating the charge separation process.
The simulations demonstrate that the CR in the COP@fullerene hybrids is 5 orders of magnitude slower than the charge separation, as required of efficient solar energy materials. The CR time depends on the fullerene geometry but in a different way compared to the ET. Only a single pair of donor–acceptor states is involved in the CR process, while multiple fullerene acceptor states participate in the ET process. As a result, the ET depends on the average fullerene diameter, while the CR correlates with the fullerene dimension, along which the relevant orbital is localized. In particular, the LUMO of the asymmetrical C84 fullerene is localized along its short axis. Therefore, the LUMO is far from the COP moiety, leading to the smallest NA coupling and the longest CR time, 8.47 ns. The fullerene LUMOs are closer to the COP in the COP@C60 and COP@C70 hybrids, resulting in a larger NA coupling and faster CR, 4.57 and 2.54 ns, respectively. The fastest ET and slowest CR, with a CR/ET time ratio of 42,500, make COP@C84 the best material for solar energy applications.
The reported study has also identified the vibrational motions that drive the nonradiative ET and CR, accommodate the excess energy lost during these processes, and induce the loss of quantum coherence within the electronic subsystem. A broad range of vibrations, from high-frequency bond stretching and bending modes to very low-frequency sub-100 cm–1 motions, couple to the electronic degrees of freedom, with a larger number of modes participating in the C84 system due to its lower symmetry. Similar vibrational modes participate in the ET and CR processes for each system, with differences more pronounced among the three fullerenes than between ET and CR for a particular fullerene. Quantum coherence within the electronic subsystem is lost on a 10–20 fs time scale. The rapid coherence loss ensures long lifetimes of the charge-separated states.
The reported NAMD simulations highlight the role of the encapsulated guest molecule in the photoinduced charge transfer dynamics and provide a detailed atomistic understanding of the photophysics of the supramolecular ensembles. The reported results underscore the following points. First, the theoretical approach employed in this work provides a good description of the experimental observations, supporting the methodology. Second, the simulations unravel the key factors that govern ultrafast ET and slow CR. Third, the mechanism and means of control of the charge carrier dynamics by modulation of the electronic energy levels are demonstrated and discussed in depth. Fourth, the study demonstrates that the average diameter of the fullerene in the hybrid can be used as a predictive tool for the photoinduced ET kinetics: the larger the diameter, the faster the rate. At the same time, the length of the shortest fullerene axis correlates with the CR time: the shorter the axis, the longer-lived is the charge-separated state. Fifth, a promising strategy for achieving high τCR/τET ratios is prescribed. Sixth, the reported results can motivate experiments to design novel efficient hybrid materials for solar energy and related applications and to probe the ensuing charge carrier dynamics.
Acknowledgments
S.M. acknowledges UGC-NFSC for her Junior Research Fellowship (211610143614). U.C. thanks UGC for his Junior Research Fellowship. S.P. is grateful for the financial support from CSIR (01(2956)/18/EMR-II), Govt. of India. O.V.P. acknowledges support of the US National Science Foundation (grant CHE-2154367).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.4c05856.
Charge densities of fullerene acceptor states, electron-vibrational influence spectra and pure-dephasing functions for charge recombination, and geometric parameters of fullerenes (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Battersby S. News Feature: The Solar Cell of the Future. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 7–10. 10.1073/pnas.1820406116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao L.; Pütz A. M.; Vignolo-González H.; Lotsch B. V. Covalent Organic Frameworks as Single-Site Photocatalysts for Solar-to-Fuel Conversion. J. Am. Chem. Soc. 2024, 146, 9479–9492. 10.1021/jacs.3c11539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Kreijger S.; Ripak A.; Elias B.; Troian-Gautier L. Investigation of the Excited-State Electron Transfer and Cage Escape Yields between Halides and a Fe(Iii) Photosensitizer. J. Am. Chem. Soc. 2024, 146, 10286–10292. 10.1021/jacs.4c02808. [DOI] [PubMed] [Google Scholar]
- Ponseca C. S.; Chabera P.; Uhlig J.; Persson P.; Sundstrom V. Ultrafast Electron Dynamics in Solar Energy Conversion. Chem. Rev. 2017, 117, 10940–11024. 10.1021/acs.chemrev.6b00807. [DOI] [PubMed] [Google Scholar]
- Pensack R. D.; Scholes G. D. Managing Complex Photophysical Pathways for Solar Energy Conversion. J. Phys. Chem. Lett. 2014, 5, 2380–2381. 10.1021/jz501241q. [DOI] [PubMed] [Google Scholar]
- Xue J. W.; Fujitsuka M.; Tachikawa T.; Bao J.; Majima T. Charge Trapping in Semiconductor Photocatalysts: A Time- and Space-Domain Perspective. J. Am. Chem. Soc. 2024, 146, 8787–8799. 10.1021/jacs.3c14757. [DOI] [PubMed] [Google Scholar]
- Ponseca C. S.; Savenije T. J.; Abdellah M.; Zheng K.; Yartsev A.; Pascher T. r.; Harlang T.; Chabera P.; Pullerits T.; Stepanov A.; et al. Organometal Halide Perovskite Solar Cell Materials Rationalized: Ultrafast Charge Generation, High and Microsecond-Long Balanced Mobilities, and Slow Recombination. J. Am. Chem. Soc. 2014, 136, 5189–5192. 10.1021/ja412583t. [DOI] [PubMed] [Google Scholar]
- Fisher J. M.; Williams M. L.; Palmer J. R.; Powers-Riggs N. E.; Young R. M.; Wasielewski M. R. Long-Lived Charge Separation in Single Crystals of an Electron Donor Covalently Linked to Four Acceptor Molecules. J. Am. Chem. Soc. 2024, 146, 9911–9919. 10.1021/jacs.4c00201. [DOI] [PubMed] [Google Scholar]
- Ihly R.; Dowgiallo A.-M.; Yang M.; Schulz P.; Stanton N. J.; Reid O. G.; Ferguson A. J.; Zhu K.; Berry J. J.; Blackburn J. L. Efficient Charge Extraction and Slow Recombination in Organic–Inorganic Perovskites Capped with Semiconducting Single-Walled Carbon Nanotubes. Energy Environ. Sci. 2016, 9, 1439–1449. 10.1039/C5EE03806E. [DOI] [Google Scholar]
- De A.; Perez C. M.; Liang A. H.; Wang K.; Dou L. T.; Prezhdo O.; Huang L. B. Tunneling-Driven Marcus-Inverted Triplet Energy Transfer in a Two-Dimensional Perovskite. J. Am. Chem. Soc. 2024, 146, 4260–4269. 10.1021/jacs.4c00236. [DOI] [PubMed] [Google Scholar]
- Shi Y.; Prezhdo O. V.; Zhao J.; Saidi W. A. Iodine and Sulfur Vacancy Cooperation Promotes Ultrafast Charge Extraction at Mapbi3/Mos2 Interface. ACS Energy Lett. 2020, 5, 1346–1354. 10.1021/acsenergylett.0c00485. [DOI] [Google Scholar]
- Wei Y.; Li L.; Fang W.; Long R.; Prezhdo O. V. Weak Donor–Acceptor Interaction and Interface Polarization Define Photoexcitation Dynamics in the Mos2/Tio2 Composite: Time-Domain Ab Initio Simulation. Nano Lett. 2017, 17, 4038–4046. 10.1021/acs.nanolett.7b00167. [DOI] [PubMed] [Google Scholar]
- Akimov A. V.; Neukirch A. J.; Prezhdo O. V. Theoretical Insights into Photoinduced Charge Transfer and Catalysis at Oxide Interfaces. Chem. Rev. 2013, 113, 4496–4565. 10.1021/cr3004899. [DOI] [PubMed] [Google Scholar]
- Das A.; Liu D. Y.; Wary R. R.; Vasenko A. S.; Prezhdo O. V.; Nair R. G. Enhancement of Photocatalytic and Photoelectrochemical Performance of Zno by Mg Doping: Experimental and Density Functional Theory Insights. J. Phys. Chem. Lett. 2023, 14, 4134–4141. 10.1021/acs.jpclett.3c00736. [DOI] [PubMed] [Google Scholar]
- Liu D. Y.; Wu Y. F.; Samatov M. R.; Vasenko A. S.; Chulkov E. V.; Prezhdo O. V. Compression Eliminates Charge Traps by Stabilizing Perovskite Grain Boundary Structures: An Ab Initio Analysis with Machine Learning Force Field. Chem. Mater. 2024, 36, 2898–2906. 10.1021/acs.chemmater.3c03261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu C.; Barden N.; Alexeev E. M.; Wang X. L.; Long R.; Cadore A. R.; Paradisanos I.; Ott A. K.; Soavi G.; Tongay S.; Cerullo G.; Ferrari A. C.; Prezhdo O. V.; Loh Z. H. Ultrafast Charge Transfer and Recombination Dynamics in Monolayer–Multilayer WSe2 Junctions Revealed by Time-Resolved Photoemission Electron Microscopy. ACS Nano 2024, 18, 1931–1947. 10.1021/acsnano.3c06473. [DOI] [PubMed] [Google Scholar]
- Zhang J.; Liu W.; Chen S.; Xu S.; Yang C.; Zhu X. One-Pot Synthesis of Electron-Acceptor Composite Enables Efficient Fullerene-Free Ternary Organic Solar Cells. J. Mater. Chem. A 2018, 6, 22519–22525. 10.1039/C8TA08961B. [DOI] [Google Scholar]
- Poelking C.; Andrienko D. Design Rules for Organic Donor–Acceptor Heterojunctions: Pathway for Charge Splitting and Detrapping. J. Am. Chem. Soc. 2015, 137, 6320–6326. 10.1021/jacs.5b02130. [DOI] [PubMed] [Google Scholar]
- Son H.-J.; Jin S.; Patwardhan S.; Wezenberg S. J.; Jeong N. C.; So M.; Wilmer C. E.; Sarjeant A. A.; Schatz G. C.; Snurr R. Q.; et al. Light-Harvesting and Ultrafast Energy Migration in Porphyrin-Based Metal–Organic Frameworks. J. Am. Chem. Soc. 2013, 135, 862–869. 10.1021/ja310596a. [DOI] [PubMed] [Google Scholar]
- Fiankor C.; Nyakuchena J.; Khoo R. S. H.; Zhang X.; Hu Y.; Yang S.; Huang J.; Zhang J. Symmetry-Guided Synthesis of N, N′-Bicarbazole and Porphyrin-Based Mixed-Ligand Metal–Organic Frameworks: Light Harvesting and Energy Transfer. J. Am. Chem. Soc. 2021, 143, 20411–20418. 10.1021/jacs.1c10291. [DOI] [PubMed] [Google Scholar]
- Minotto A.; Bulut I.; Rapidis A. G.; Carnicella G.; Patrini M.; Lunedei E.; Anderson H. L.; Cacialli F. Towards Efficient near-Infrared Fluorescent Organic Light-Emitting Diodes. Light Sci. Appl. 2021, 10, 18. 10.1038/s41377-020-00456-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y.; Zhao Y.; Han Z.; Zhang R.; Du P.; Wu Y.; Lu X. Switching the Photoluminescence and Electrochemiluminescence of Liposoluble Porphyrin in Aqueous Phase by Molecular Regulation. Angew. Chem., Int. Ed. 2020, 59, 23261–23267. 10.1002/anie.202010216. [DOI] [PubMed] [Google Scholar]
- Shang S.; Xiong W.; Yang C.; Johannessen B.; Liu R.; Hsu H.-Y.; Gu Q.; Leung M. K.; Shang J. Atomically Dispersed Iron Metal Site in a Porphyrin-Based Metal–Organic Framework for Photocatalytic Nitrogen Fixation. ACS Nano 2021, 15, 9670–9678. 10.1021/acsnano.0c10947. [DOI] [PubMed] [Google Scholar]
- Imahori H.; Yamada H.; Guldi D. M.; Endo Y.; Shimomura A.; Kundu S.; Yamada K.; Okada T.; Sakata Y.; Fukuzumi S. Comparison of Reorganization Energies for Intra-and Intermolecular Electron Transfer. Angew. Chem., Int. Ed. 2002, 41, 2344–2347. . [DOI] [PubMed] [Google Scholar]
- Guldi D. M.; Prato M. Excited-State Properties of C60 Fullerene Derivatives. Acc. Chem. Res. 2000, 33, 695–703. 10.1021/ar990144m. [DOI] [PubMed] [Google Scholar]
- Diederich F.; Gómez-López M. Supramolecular Fullerene Chemistry. Chem. Soc. Rev. 1999, 28, 263–277. 10.1039/a804248i. [DOI] [Google Scholar]
- Ostroverkhova O. Organic Optoelectronic Materials: Mechanisms and Applications. Chem. Rev. 2016, 116, 13279–13412. 10.1021/acs.chemrev.6b00127. [DOI] [PubMed] [Google Scholar]
- Akimov A. V.; Prezhdo O. V. Nonadiabatic Dynamics of Charge Transfer and Singlet Fission at the Pentacene/C60 Interface. J. Am. Chem. Soc. 2014, 136, 1599–1608. 10.1021/ja411800n. [DOI] [PubMed] [Google Scholar]
- Zarrabi N.; Seetharaman S.; Chaudhuri S.; Holzer N.; Batista V. S.; Van Der Est A.; D’Souza F.; Poddutoori P. K. Decelerating Charge Recombination Using Fluorinated Porphyrins in N, N-Bis (3, 4, 5-Trimethoxyphenyl) Aniline—Aluminum (Iii) Porphyrin—Fullerene Reaction Center Models. J. Am. Chem. Soc. 2020, 142, 10008–10024. 10.1021/jacs.0c01574. [DOI] [PubMed] [Google Scholar]
- Luo C.; Guldi D. M.; Imahori H.; Tamaki K.; Sakata Y. Sequential Energy and Electron Transfer in an Artificial Reaction Center: Formation of a Long-Lived Charge-Separated State. J. Am. Chem. Soc. 2000, 122, 6535–6551. 10.1021/ja993959z. [DOI] [Google Scholar]
- Kahnt A.; Kärnbratt J.; Esdaile L. J.; Hutin M.; Sawada K.; Anderson H. L.; Albinsson B. Temperature Dependence of Charge Separation and Recombination in Porphyrin Oligomer–Fullerene Donor–Acceptor Systems. J. Am. Chem. Soc. 2011, 133, 9863–9871. 10.1021/ja2019367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton L. R.; Scheloske M.; Pirner K. S.; Hirsch A.; Guldi D. M.; Gisselbrecht J.-P. Unexpected Change in Charge Transfer Behavior in a Cobalt(Ii) Porphyrin–Fullerene Conjugate That Stabilizes Radical Ion Pair States. J. Am. Chem. Soc. 2004, 126, 10370–10381. 10.1021/ja048983d. [DOI] [PubMed] [Google Scholar]
- Badgurjar D.; Seetharaman S.; D’Souza F.; Chitta R. One-Photon Excitation Followed by a Three-Step Sequential Energy–Energy–Electron Transfer Leading to a Charge-Separated State in a Supramolecular Tetrad Featuring Benzothiazole–Boron-Dipyrromethene–Zinc Porphyrin–C60. Chem.—Eur. J. 2021, 27, 2184–2195. 10.1002/chem.202004262. [DOI] [PubMed] [Google Scholar]
- Arpaçay P.; Maity P.; El-Zohry A. M.; Meindl A.; Akca S.; Plunkett S.; Senge M. O.; Blau W. J.; Mohammed O. F. Controllable Charge-Transfer Mechanism at Push–Pull Porphyrin/Nanocarbon Interfaces. J. Phys. Chem. C 2019, 123, 14283–14291. 10.1021/acs.jpcc.9b03718. [DOI] [Google Scholar]
- D’Souza F.; Chitta R.; Gadde S.; Zandler M. E.; McCarty A. L.; Sandanayaka A. S.; Araki Y.; Ito O. Effect of Axial Ligation or Π–Π-Type Interactions on Photochemical Charge Stabilization in “Two-Point” Bound Supramolecular Porphyrin–Fullerene Conjugates. Chem.—Eur. J. 2005, 11, 4416–4428. 10.1002/chem.200500186. [DOI] [PubMed] [Google Scholar]
- D’Souza F.; Deviprasad G. R.; Zandler M. E.; El-Khouly M. E.; Fujitsuka M.; Ito O. Photoinduced Electron Transfer in “Two-Point” Bound Supramolecular Triads Composed of N, N-Dimethylaminophenyl-Fullerene-Pyridine Coordinated to Zinc Porphyrin. J. Phys. Chem. A 2003, 107, 4801–4807. 10.1021/jp030363w. [DOI] [Google Scholar]
- D’Souza F.; Ito O. Supramolecular Donor–Acceptor Hybrids of Porphyrins/Phthalocyanines with Fullerenes/Carbon Nanotubes: Electron Transfer, Sensing, Switching, and Catalytic Applications. Chem. Commun. 2009, 4913–4928. 10.1039/b905753f. [DOI] [PubMed] [Google Scholar]
- Kaur R.; Possanza F.; Limosani F.; Bauroth S.; Zanoni R.; Clark T.; Arrigoni G.; Tagliatesta P.; Guldi D. M. Understanding and Controlling Short-and Long-Range Electron/Charge-Transfer Processes in Electron Donor–Acceptor Conjugates. J. Am. Chem. Soc. 2020, 142, 7898–7911. 10.1021/jacs.0c01452. [DOI] [PubMed] [Google Scholar]
- Megiatto J. D.; Schuster D. I.; de Miguel G.; Wolfrum S.; Guldi D. M. Topological and Conformational Effects on Electron Transfer Dynamics in Porphyrin-[60] Fullerene Interlocked Systems. Chem. Mater. 2012, 24, 2472–2485. 10.1021/cm3004408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf M.; Costa J. I.; Minameyer M. B.; Drewello T.; Tomé A. C.; Guldi D. M. Efficient Low Driving Force Charge Separation in an Electron Deficient Zn-Porphyrin– Fullerene Donor–Acceptor Conjugate. J. Phys. Chem. C 2019, 123, 28093–28099. 10.1021/acs.jpcc.9b09790. [DOI] [Google Scholar]
- Yu M.-L.; Wang S.-M.; Feng K.; Khoury T.; Crossley M. J.; Yang F.; Zhang J.-P.; Tung C.-H.; Wu L.-Z. Photoinduced Electron Transfer and Charge-Recombination in 2-Ureido-4 [1 H]-Pyrimidinone Quadruple Hydrogen-Bonded Porphyrin–Fullerene Assemblies. J. Phys. Chem. C 2011, 115, 23634–23641. 10.1021/jp207852j. [DOI] [Google Scholar]
- Takai A.; Chkounda M.; Eggenspiller A.; Gros C. P.; Lachkar M.; Barbe J.-M.; Fukuzumi S. Efficient Photoinduced Electron Transfer in a Porphyrin Tripod– Fullerene Supramolecular Complex Via Π– Π Interactions in Nonpolar Media. J. Am. Chem. Soc. 2010, 132, 4477–4489. 10.1021/ja100192x. [DOI] [PubMed] [Google Scholar]
- Caballero R.; Barrejon M.; Cerda J.; Arago J.; Seetharaman S.; de la Cruz P.; Orti E.; D’Souza F.; Langa F. Self-Assembly-Directed Organization of a Fullerene–Bisporphyrin into Supramolecular Giant Donut Structures for Excited-State Charge Stabilization. J. Am. Chem. Soc. 2021, 143, 11199–11208. 10.1021/jacs.1c05133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ortiz M.; Cho S.; Niklas J.; Kim S.; Poluektov O. G.; Zhang W.; Rumbles G.; Park J. Through-Space Ultrafast Photoinduced Electron Transfer Dynamics of a C70-Encapsulated Bisporphyrin Covalent Organic Polyhedron in a Low-Dielectric Medium. J. Am. Chem. Soc. 2017, 139, 4286–4289. 10.1021/jacs.7b00220. [DOI] [PubMed] [Google Scholar]
- Aradi B.; Hourahine B.; Frauenheim T. Dftb+, a Sparse Matrix-Based Implementation of the Dftb Method. J. Phys. Chem. A 2007, 111, 5678–5684. 10.1021/jp070186p. [DOI] [PubMed] [Google Scholar]
- Hourahine B.; Aradi B.; Blum V.; Bonafé F.; Buccheri A.; Camacho C.; Cevallos C.; Deshaye M.; Dumitrică T.; Dominguez A.; et al. Dftb+, a Software Package for Efficient Approximate Density Functional Theory Based Atomistic Simulations. J. Chem. Phys. 2020, 152, 124101. 10.1063/1.5143190. [DOI] [PubMed] [Google Scholar]
- Elstner M.; Porezag D.; Jungnickel G.; Elsner J.; Haugk M.; Frauenheim T.; Suhai S.; Seifert G. Self-Consistent-Charge Density-Functional Tight-Binding Method for Simulations of Complex Materials Properties. Phys. Rev. B 1998, 58, 7260. 10.1103/PhysRevB.58.7260. [DOI] [Google Scholar]
- Krüger T.; Elstner M.; Schiffels P.; Frauenheim T. Validation of the Density-Functional Based Tight-Binding Approximation Method for the Calculation of Reaction Energies and Other Data. J. Chem. Phys. 2005, 122, 114110. 10.1063/1.1871913. [DOI] [PubMed] [Google Scholar]
- Rappé A. K.; Casewit C. J.; Colwell K.; Goddard W. A.; Skiff W. M. Uff, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. 10.1021/ja00051a040. [DOI] [Google Scholar]
- Bussi G.; Donadio D.; Parrinello M. Canonical Sampling through Velocity Rescaling. J. Chem. Phys. 2007, 126, 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Verlet L. Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. 1967, 159, 98. 10.1103/PhysRev.159.98. [DOI] [Google Scholar]
- Grubmüller H.; Heller H.; Windemuth A.; Schulten K. Generalized Verlet Algorithm for Efficient Molecular Dynamics Simulations with Long-Range Interactions. Mol. Simul. 1991, 6, 121–142. 10.1080/08927029108022142. [DOI] [Google Scholar]
- Augustin S. D.; Rabitz H. The Classical Path Approximation in Time-Dependent Quantum Collision Theory. J. Chem. Phys. 1978, 69, 4195–4200. 10.1063/1.437100. [DOI] [Google Scholar]
- Miller W. H. Classical Path Approximation for the Boltzmann Density Matrix. J. Chem. Phys. 1971, 55, 3146–3149. 10.1063/1.1676560. [DOI] [Google Scholar]
- Nijjar P.; Jankowska J.; Prezhdo O. V. Ehrenfest and Classical Path Dynamics with Decoherence and Detailed Balance. J. Chem. Phys. 2019, 150, 204124. 10.1063/1.5095810. [DOI] [PubMed] [Google Scholar]
- Parandekar P. V.; Tully J. C. Mixed Quantum-Classical Equilibrium. J. Chem. Phys. 2005, 122, 094102. 10.1063/1.1856460. [DOI] [PubMed] [Google Scholar]
- Tully J. C. Molecular Dynamics with Electronic Transitions. J. Chem. Phys. 1990, 93, 1061–1071. 10.1063/1.459170. [DOI] [Google Scholar]
- Jaeger H. M.; Fischer S.; Prezhdo O. V. Decoherence-Induced Surface Hopping. J. Chem. Phys. 2012, 137, 22A545. 10.1063/1.4757100. [DOI] [PubMed] [Google Scholar]
- Akimov A. V.; Prezhdo O. V. Advanced Capabilities of the Pyxaid Program: Integration Schemes, Decoherence Effects, Multiexcitonic States, and Field-Matter Interaction. J. Chem. Theory Comput. 2014, 10, 789–804. 10.1021/ct400934c. [DOI] [PubMed] [Google Scholar]
- Pal S.; Trivedi D. J.; Akimov A. V.; Aradi B.; Frauenheim T.; Prezhdo O. V. Nonadiabatic Molecular Dynamics for Thousand Atom Systems: A Tight-Binding Approach toward Pyxaid. J. Chem. Theory Comput. 2016, 12, 1436–1448. 10.1021/acs.jctc.5b01231. [DOI] [PubMed] [Google Scholar]
- Chaban V. V.; Pal S.; Prezhdo O. V. Laser-Induced Explosion of Nitrated Carbon Nanotubes: Nonadiabatic and Reactive Molecular Dynamics Simulations. J. Am. Chem. Soc. 2016, 138, 15927–15934. 10.1021/jacs.6b08082. [DOI] [PubMed] [Google Scholar]
- Pal S.; Casanova D.; Prezhdo O. V. Effect of Aspect Ratio on Multiparticle Auger Recombination in Single-Walled Carbon Nanotubes: Time Domain Atomistic Simulation. Nano Lett. 2018, 18, 58–63. 10.1021/acs.nanolett.7b03150. [DOI] [PubMed] [Google Scholar]
- Sarkar R.; Habib M.; Pal S.; Prezhdo O. V. Ultrafast, Asymmetric Charge Transfer and Slow Charge Recombination in Porphyrin/Cnt Composites Demonstrated by Time-Domain Atomistic Simulation. Nanoscale 2018, 10, 12683–12694. 10.1039/C8NR02544D. [DOI] [PubMed] [Google Scholar]
- Sarkar R.; Habib M.; Pal S.; Prezhdo O. V. Tuning Charge Transfer and Recombination in Exttf/Cnt Nanohybrids by Choice of Chalcogen: A Time-Domain Density Functional Analysis. J. Appl. Phys. 2021, 129, 025501. 10.1063/5.0034561. [DOI] [Google Scholar]
- Habib M.; Kar M.; Pal S.; Sarkar P. Role of Chalcogens in the Exciton Relaxation Dynamics of Chalcogenol-Functionalized Cdse Qd: A Time-Domain Atomistic Simulation. Chem. Mater. 2019, 31, 4042–4050. 10.1021/acs.chemmater.9b00605. [DOI] [Google Scholar]
- Gumber S.; Eniodunmo O.; Ivanov S. A.; Kilina S.; Prezhdo O. V.; Ghosh D.; Tretiak S. Hot Carrier Relaxation Dynamics in Non-Stoichiometric Cdse Quantum Dots: Computational Insights. J. Mater. Chem. A 2023, 11, 8256–8264. 10.1039/D3TA00149K. [DOI] [Google Scholar]
- Dong S.; Pal S.; Lian J.; Chan Y.; Prezhdo O. V.; Loh Z.-H. Sub-Picosecond Auger-Mediated Hole-Trapping Dynamics in Colloidal Cdse/Cds Core/Shell Nanoplatelets. ACS Nano 2016, 10, 9370–9378. 10.1021/acsnano.6b04210. [DOI] [PubMed] [Google Scholar]
- Pal S.; Nijjar P.; Frauenheim T.; Prezhdo O. V. Atomistic Analysis of Room Temperature Quantum Coherence in Two-Dimensional Cdse Nanostructures. Nano Lett. 2017, 17, 2389–2396. 10.1021/acs.nanolett.6b05368. [DOI] [PubMed] [Google Scholar]
- Nguyen H. L.; Do T. N.; Durmusoglu E. G.; Izmir M.; Sarkar R.; Pal S.; Prezhdo O. V.; Demir H. V.; Tan H.-S. Measuring the Ultrafast Spectral Diffusion and Vibronic Coupling Dynamics in Cdse Colloidal Quantum Wells Using Two-Dimensional Electronic Spectroscopy. ACS Nano 2023, 17, 2411–2420. 10.1021/acsnano.2c09606. [DOI] [PubMed] [Google Scholar]
- Sarkar R.; Habib M.; Kar M.; Pramanik A.; Pal S.; Sarkar P. Structural Rigidity Accelerates Quantum Decoherence and Extends Carrier Lifetime in Porphyrin Nanoballs: A Time Domain Atomistic Simulation. Nanoscale Adv. 2020, 2, 1502–1511. 10.1039/D0NA00001A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarkar R.; Habib M.; Kovalenko S. M.; Pal S.; Prezhdo O. V. Mixed Metals Slow down Nonradiative Recombination in Saddle-Shaped Porphyrin Nanorings: A Time-Domain Atomistic Simulation. J. Phys. Chem. C 2021, 125, 16620–16628. 10.1021/acs.jpcc.1c04749. [DOI] [Google Scholar]
- Sarkar R.; Habib M.; Pal S. Symmetrical Linkage in Porphyrin Nanoring Suppressed the Electron–Hole Recombination Demonstrated by Nonadiabatic Molecular Dynamics. J. Phys. Chem. Lett. 2022, 13, 7213–7219. 10.1021/acs.jpclett.2c02073. [DOI] [PubMed] [Google Scholar]
- Mondal S.; Chowdhury U.; Dey S.; Habib M.; Mora Perez C.; Frauenheim T.; Sarkar R.; Pal S.; Prezhdo O. V. Controlling Charge Carrier Dynamics in Porphyrin Nanorings by Optically Active Templates. J. Phys. Chem. Lett. 2023, 14, 11384–11392. 10.1021/acs.jpclett.3c03304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao X.; Vasenko A. S.; Prezhdo O. V.; Long R. Anion Doping Delays Nonradiative Electron–Hole Recombination in Cs-Based All-Inorganic Perovskites: Time Domain Ab Initio Analysis. J. Phys. Chem. Lett. 2022, 13, 11375–11382. 10.1021/acs.jpclett.2c03072. [DOI] [PubMed] [Google Scholar]
- Shi R.; Fang Q.; Vasenko A. S.; Long R.; Fang W.-H.; Prezhdo O. V. Structural Disorder in Higher-Temperature Phases Increases Charge Carrier Lifetimes in Metal Halide Perovskites. J. Am. Chem. Soc. 2022, 144, 19137–19149. 10.1021/jacs.2c08627. [DOI] [PubMed] [Google Scholar]
- Tong C.-J.; Cai X.; Zhu A.-Y.; Liu L.-M.; Prezhdo O. V. How Hole Injection Accelerates Both Ion Migration and Nonradiative Recombination in Metal Halide Perovskites. J. Am. Chem. Soc. 2022, 144, 6604–6612. 10.1021/jacs.2c02148. [DOI] [PubMed] [Google Scholar]
- Liu D. Y.; Perez C. M.; Vasenko A. S.; Prezhdo O. V. Ag–Bi Charge Redistribution Creates Deep Traps in Defective Cs2AgBiBr6: Machine Learning Analysis of Density Functional Theory. J. Phys. Chem. Lett. 2022, 13, 3645–3651. 10.1021/acs.jpclett.2c00869. [DOI] [PubMed] [Google Scholar]
- Tong C. J.; Li L. Q.; Liu L. M.; Prezhdo O. V. Synergy between Ion Migration and Charge Carrier Recombination in Metal-Halide Perovskites. J. Am. Chem. Soc. 2020, 142, 3060–3068. 10.1021/jacs.9b12391. [DOI] [PubMed] [Google Scholar]
- Liu L. H.; Fang W. H.; Long R.; Prezhdo O. V. Lewis Base Passivation of Hybrid Halide Perovskites Slows Electron-Hole Recombination: Time-Domain Ab Lnitio Analysis. J. Phys. Chem. Lett. 2018, 9, 1164–1171. 10.1021/acs.jpclett.8b00177. [DOI] [PubMed] [Google Scholar]
- Liu Y. L.; Long R.; Fang W. H.; Prezhdo O. V. Nuclear Quantum Effects Prolong Charge Carrier Lifetimes in Hybrid Organic-Inorganic Perovskites. J. Am. Chem. Soc. 2023, 145, 14112–14123. 10.1021/jacs.3c04412. [DOI] [PubMed] [Google Scholar]
- Yin J. W.; Xu Z. F.; Hu Q.; Teobaldi G.; Liu L. M.; Prezhdo O. V. Tuning Octahedral Tilting by Doping to Prevent Detrimental Phase Transition and Extend Carrier Lifetime in Organometallic Perovskites. J. Am. Chem. Soc. 2023, 145, 5393–5399. 10.1021/jacs.2c13593. [DOI] [PubMed] [Google Scholar]
- Zhou Z. B.; Zheng Z. F.; He J. J.; Wang J. L.; Prezhdo O. V.; Frauenheim T. Ultrafast Laser Control of Antiferromagnetic-Ferrimagnetic Switching in Two-Dimensional Ferromagnetic Semiconductor Heterostructures. Nano Lett. 2023, 23, 5688–5695. 10.1021/acs.nanolett.3c01350. [DOI] [PubMed] [Google Scholar]
- Zhu Y. H.; Prezhdo O. V.; Long R.; Fang W. H. Twist Angle-Dependent Intervalley Charge Carrier Transfer and Recombination in Bilayer WS2. J. Am. Chem. Soc. 2023, 145, 22826–22835. 10.1021/jacs.3c09170. [DOI] [PubMed] [Google Scholar]
- Krajewski M.; Piotrowski P.; Mech W.; Korona K. P.; Wojtkiewicz J.; Pilch M.; Kaim A.; Drabińska A.; Kamińska M. Optical Properties and Light-Induced Charge Transfer in Selected Aromatic C60 Fullerene Derivatives and in Their Bulk Heterojunctions with Poly (3-Hexylthiophene). Mater. 2022, 15, 6908. 10.3390/ma15196908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habenicht B. F.; Prezhdo O. V. Ab Initio Time-Domain Study of the Triplet State in a Semiconducting Carbon Nanotube: Intersystem Crossing, Phosphorescence Time, and Line Width. J. Am. Chem. Soc. 2012, 134, 15648–15651. 10.1021/ja305685v. [DOI] [PubMed] [Google Scholar]
- Tretiak S. Triplet State Absorption in Carbon Nanotubes: A Td– Dft Study. Nano Lett. 2007, 7, 2201–2206. 10.1021/nl070355h. [DOI] [PubMed] [Google Scholar]
- Englman R.; Jortner J. The Energy Gap Law for Non-Radiative Decay in Large Molecules. J. Lumin. 1970, 1, 134–142. 10.1016/0022-2313(70)90029-3. [DOI] [Google Scholar]
- Sarkar R.; Kar M.; Habib M.; Zhou G.; Frauenheim T.; Sarkar P.; Pal S.; Prezhdo O. V. Common Defects Accelerate Charge Separation and Reduce Recombination in Cnt/Molecule Composites: Atomistic Quantum Dynamics. J. Am. Chem. Soc. 2021, 143, 6649–6656. 10.1021/jacs.1c02325. [DOI] [PubMed] [Google Scholar]
- Qiao L.; Fang W.-H.; Prezhdo O. V.; Long R. Suppressing Oxygen-Induced Deterioration of Metal Halide Perovskites by Alkaline Earth Metal Doping: A Quantum Dynamics Study. J. Am. Chem. Soc. 2022, 144, 5543–5551. 10.1021/jacs.2c00319. [DOI] [PubMed] [Google Scholar]
- Yang X.; Huang S.; Ortiz M.; Wang X.; Cao Y.; Kareem O.; Jin Y.; Huang F.; Wang X.; Zhang W. Truxene-Based Covalent Organic Polyhedrons Constructed through Alkyne Metathesis. Org. Chem. Front. 2021, 8, 4723–4729. 10.1039/D1QO00685A. [DOI] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Mukamel S.Principles of Nonlinear Optical Spectroscopy; Oxford University Press on Demand, 1999. [Google Scholar]
- Wang P.; Ni J.-f.; Meng L.; Wang X.-B.; Sheng C.-Q.; Zhang W.-H.; Xu Y.; Xu F.-Q.; Zhu J.-F.; Li H.-N. Valence Photoemission Intensity Oscillations of C84. Carbon 2012, 50, 1762–1768. 10.1016/j.carbon.2011.12.023. [DOI] [Google Scholar]
- Hyeon-Deuk K.; Prezhdo O. V. Photoexcited Electron and Hole Dynamics in Semiconductor Quantum Dots: Phonon-Induced Relaxation, Dephasing, Multiple Exciton Generation and Recombination. J. Phys.: Condens. Matter 2012, 24, 363201. 10.1088/0953-8984/24/36/363201. [DOI] [PubMed] [Google Scholar]
- Liu J.; Kilina S. V.; Tretiak S.; Prezhdo O. V. Ligands Slow down Pure-Dephasing in Semiconductor Quantum Dots. ACS Nano 2015, 9, 9106–9116. 10.1021/acsnano.5b03255. [DOI] [PubMed] [Google Scholar]
- Akimov A. V.; Prezhdo O. V. Persistent Electronic Coherence Despite Rapid Loss of Electron–Nuclear Correlation. J. Phys. Chem. Lett. 2013, 4, 3857–3864. 10.1021/jz402035z. [DOI] [Google Scholar]
- Gumber S.; Prezhdo O. V. Zeno and Anti-Zeno Effects in Nonadiabatic Molecular Dynamics. J. Phys. Chem. Lett. 2023, 14, 7274–7282. 10.1021/acs.jpclett.3c01831. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.