FAItH: Federated Analytics and Integrated Differential Privacy with Clustering for Healthcare Monitoring

Abstract

Monitoring physical activity is crucial for assessing patient health, particularly in managing chronic diseases and rehabilitation. Wearable devices tracking physical movement play a key role in monitoring elderly individuals or patients with chronic diseases. However, sharing of this data is often restricted by privacy regulations such as GDPR, as well as data ownership and security concerns, limiting its use in collaborative healthcare analysis. Federated analytics (FA) offers a promising solution that enables multiple parties to gain insights without sharing data, but current research focuses more on data protection than actionable insights. Limited exploration exists on analyzing privacy-preserved, aggregated data to uncover patterns for patient monitoring and healthcare interventions. This paper addresses this gap by proposing FAItH, a dual-stage solution that integrates privacy-preserving techniques - Laplace, Gaussian, Exponential and Locally Differentially Private (LDP) noise - on statistical functions (mean, variance, quantile) within a federated analytics environment. The solution employs feature-specific scaling to fine-tune the privacy-utility trade-off, ensuring sensitive features are protected while retaining utility for less sensitive ones. After applying federated analytics (FA) with differential privacy (DP) to generate insights, we introduce clustering to identify patterns in patient activity relevant to healthcare. Using the Human Activity Recognition (HAR) dataset, FAItH shows that privacy-preserving configurations achieve clustering utility nearly equal to non-DP setups, outperforming privacy-preserving clustering algorithms. This balances privacy with effective insights. These results validate FA with DP as a viable solution for secure collaborative analysis in healthcare, enabling meaningful insights without compromising patient privacy.

Introduction

User privacy and security remain a primary concern for users of wearable device technology¹. Sharing personal data, such as movement or activity information, poses risks as it can be highly exposed to adversaries². However, a number of life-saving applications could benefit from this data in health and aging. There is a vast amount of medical data within healthcare facilities that remain distributed and isolated from innovative health solutions³. Numerous solutions across different healthcare industries, such as pharmacy, health-tech, and academic labs, struggle to aggregate this data⁴. Although aggregating healthcare data from different sources may seem like a technical challenge, the primary obstacle to data collection is regulations around patient privacy⁵. Regulations such as Health Insurance Portability and Accountability Act (HIPAA) and Saudi Arabia’s Personal Data Protection Law (PDPL), prohibit the sharing of patient data across facility borders. Even when facilities receive approval to share data, it is still a time-consuming and labor-intensive process.

Recently, emerging technology in federated analytics has gained attention in various sensitive domains such as healthcare and finance⁶. Federated analytics allows different parties to collaborate on analyzing and aggregating their data without sharing raw data between them-only aggregated data is shared. Federated analytics is similar to federated learning⁷; both paradigms require client collaboration without exchanging their underlying data. However, federated analytics does not require optimization or learning as federated learning does. In other words, federated learning requires intelligence, such as deep learning or simple machine learning, to be involved in the learning rounds. On the other hand, federated analytics focuses on running analytics operations, such as calculating the mean, sum, or histograms among the participating clients. This paradigm was first proposed by Google with its application in Gboard (Google’s smart keyboard)⁸.

Federated analytics is merely a paradigm and not yet an end-to-end privacy-preserving technology. To ensure security and privacy, federated analytics should implement additional privacy-enhancing technologies such as homomorphic encryption, differential privacy, and multi-party computation^9–11. The choice of technology depends on the scalability of the parties involved. For instance, homomorphic encryption works well with cross-silo scenarios, where the number of parties is low, while differential privacy is more suited for cross-device applications¹².

Although these paradigms show promising outcomes, their adoption in the healthcare domain is still hesitant for various reasons. Implementing privacy-enhancing technologies is challenging and requires experts within healthcare facilities. Even with these technologies, a number of security risks, such as data leaks and exploits, can arise when aggregating data^13,14. Risks like re-identification, membership inference, and feature reconstruction remain a concern¹⁵. However, privacy-preserving methods such as homomorphic encryption (HE) and multi-party computation (MPC) have significant limitations in practice. HE ensures perfect privacy by allowing computations on encrypted data, but it introduces substantial computational overhead, making it impractical for large-scale real-time applications. Similarly, MPC guarantees exact results without exposing data but incurs high communication costs due to multiple rounds of secure communication. These drawbacks limit their scalability and efficiency in distributed environments with numerous participants.

Our focus in this paper is to adapt these technologies and make them accessible for researchers and doctors within healthcare centers. Given the limitations of HE and MPC, we adopt differential privacy (DP) as a lightweight and scalable privacy-preserving mechanism for federated analytics. Although DP introduces a privacy-utility trade-off, where higher privacy reduces accuracy, it remains highly efficient for distributed systems requiring real-time analytics and scalability. By systematically evaluating various DP mechanisms (Laplace, Gaussian, Exponential, and LDP) and privacy budgets, we aim to demonstrate configurations that balance privacy and utility effectively in healthcare scenarios.

Current open-source implementations of privacy enhancement technologies, such as differential privacy¹⁶, homomorphic encryption¹⁷, and federated analytics^18,19, are available online. These tools show promising results across various fields but often lack comprehensive analysis features and remain primarily suited for domain experts. In federated analytics, several statistical functions-such as histograms, means, and others-are employed to summarize data insights. Adding noise to these functions using differential privacy requires carefully balancing the trade-off between utility and privacy. This trade-off is addressed in our work by systematically tuning the privacy budgets (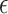) and comparing their impact on both utility and security. For instance, we analyze configurations with values of 10 and 50, illustrating how tighter privacy budgets reduce data utility while providing stronger privacy guarantees. Configuring and setting these privacy budgets is challenging, as more noise enhances security but reduces insight accuracy, and vice versa. Additionally, selecting an appropriate noise distribution adds further complexity. To mitigate this complexity, we evaluate multiple noise mechanisms (Laplace, Gaussian, Exponential) and their effectiveness in preserving utility for statistical functions such as mean, variance, and quantile.

Moreover, while existing work supports privacy-preserving technologies, to the best of our knowledge, our study is the first to extend the use of aggregated insights and explore how such privacy-protected data can be further analyzed to uncover actionable patterns that support patient monitoring and intervention. Our approach addresses this gap by applying DP to raw data for privacy protection and then leveraging clustering techniques to extract valuable patterns from aggregated data, specifically within human activity data. This dual-stage integration of privacy mechanisms and clustering ensures that privacy noise minimally impacts actionable insights by separating the privacy protection from the clustering process. This dual-stage approach enables healthcare providers to gain insights into activity trends-such as patterns in elderly patient movement-without risking individual privacy.

Therefore, this paper aims to evaluate the impact of various noise mechanisms on the accuracy-privacy trade-offs of essential statistical functions, offering insights for secure healthcare data analytics. We applied privacy-preserving mechanisms, including centralized and local differential privacy, using Laplace, Gaussian, and Exponential noise on a federated analytics setup. To enable healthcare providers to derive meaningful insights from aggregated and privacy-protected data, we further introduce a clustering stage in our analysis. By applying clustering to the differentially private aggregated outputs, healthcare organizations can identify important patterns related to patient activity, movement, and other metrics relevant to monitoring health conditions. For instance, clustering results can reveal activity trends among elderly patients, supporting preventive care and intervention strategies for chronic disease management. By quantitatively evaluating the trade-offs between privacy budgets and clustering utility, and employing feature-specific scaling to fine-tune noise levels across features, our results highlight practical configurations that maintain both privacy and data utility. This clustering stage adds significant value to federated analytics, allowing healthcare stakeholders to gain actionable insights without compromising patient confidentiality. The Human Activity Recognition (HAR) dataset is used to demonstrate that privacy-preserving configurations can effectively reduce data leakage risks while maintaining data utility.

The contributions of this paper are as follows:

• We propose a dual-stage integration of privacy-preserving techniques (Laplace, Gaussian, Exponential, and LDP noise) with federated analytics to protect statistical functions while enabling collaborative analysis.

• We employ feature-specific scaling to fine-tune the privacy-utility trade-off, ensuring that sensitive features receive adequate protection while retaining utility for less sensitive features.

• We introduce both KMeans and Agglomerative clustering on differentially private outputs, allowing healthcare providers to derive actionable insights for patient monitoring and health management from privacy-preserving data analytics.

• We evaluate the impact of different noise mechanisms and privacy budgets (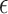) on clustering performance using Silhouette Scores, demonstrating practical configurations that balance privacy and utility effectively.

• We compare our results with state-of-the-art methods in federated analytics and privacy-preserving clustering.

The organization of this paper is as follows. In section “Related works”, related works are discussed. In section “System design and architecture”, the design and architecture are explained. In section “Proposed model”, the proposed model is presented. In section “Experiment”, the experimental setup is summarized, and the results of the experiments are evaluated. In section “Limitations and future directions”, we present the limitations and future work. Finally, section “Conclusion” concludes our study.

Related works

Patient and health data is a major concern in privacy technology research. There are a number of methodologies and techniques proposed and used to accommodate the full service with this data. As sharing this data outside of health centers is prohibited due to regulations such as HIPAA and the recent PDPL, algorithms such as homomorphic encryption, differential privacy, and multi-party computation have been used along with distributed systems such as federated learning and analytics.

Froelicher et al.¹⁵ introduced FAMHE, a federated analytics system utilizing multiparty homomorphic encryption (MHE) to enable privacy-preserving computations across distributed biomedical datasets. Unlike traditional federated approaches, FAMHE ensures that only encrypted intermediate results are shared, thereby mitigating privacy risks inherent in clear-text data exchange. Their method was demonstrated on two key biomedical tasks: Kaplan–Meier survival analysis for cancer studies and genome-wide association studies (GWAS) for identifying genetic variants associated with diseases. The scalability of FAMHE was highlighted through its ability to handle datasets comprising millions of genetic variants and thousands of patient records, achieving high computational efficiency with minimal error. Moreover, Froelicher et al. developed optimization techniques to enhance FAMHE’s performance, such as ciphertext packing and polynomial approximations for complex operations like matrix inversion. These techniques facilitated efficient parallel computations while maintaining a high level of data confidentiality. The study successfully replicated results from centralized analyses, illustrating FAMHE’s potential to replace centralized workflows in real-world clinical settings where data sharing restrictions apply. By combining secure computation with federated analytics, FAMHE bridges the gap between data privacy regulations and large-scale collaborative biomedical research. The authors noted that FAMHE’s design could be extended to other privacy-sensitive fields, suggesting future work in broader multi-institutional collaborations beyond healthcare

Zhao et al.²⁰ introduced CrowdFA, a novel privacy-preserving mobile crowdsensing paradigm that leverages federated analytics (FA) to address key challenges in data aggregation, incentive mechanisms, and privacy protection simultaneously. The proposed platform consists of two main components: the Sensing Platform (SP), which is responsible for managing participants, data aggregation, and distributing incentives; and the users or participants, who locally compute statistical functions such as mean, variance, and p-order moments on their data. CrowdFA incorporates the PRADA protocol, which supports various aggregation operations while ensuring data privacy through additive secret sharing, eliminating the need to introduce noise for privacy. PRADA comprises four key stages: initialization, federated computation, transmission, and aggregation. The initialization step involves the recruitment of participants and the configuration of aggregation functions. In the federated computation stage, participants perform local computations on their data, which are then securely shared with the SP in the transmission step. Finally, the SP aggregates the shared results to generate global statistics without accessing individual raw data. In addition to PRADA, CrowdFA includes PRAED, a privacy-preserving incentive mechanism designed to ensure truthful and fair reward distribution among participants. This mechanism not only safeguards bid privacy but also maximizes rewards for participants based on their contributions. Compared to traditional approaches, CrowdFA achieves significant improvements in computational efficiency, with theoretical analysis and experimental results indicating up to a 22x reduction in computation time. CrowdFA stands out as the first platform to integrate a comprehensive privacy-preserving data aggregation mechanism with an incentive platform, ensuring both participant data confidentiality and fair compensation. Its unified framework highlights practical applications in mobile crowdsensing, enabling secure and efficient aggregation of sensitive data in scenarios such as urban management, healthcare, and environmental monitoring.

Welten et al.²¹ proposed a Privacy-Preserving Federated Analytics Platform for healthcare, utilizing the Personal Health Train (PHT) paradigm to enable distributed analytics while ensuring data privacy and autonomy of healthcare centers. In their design, the PHT infrastructure comprises three main components: Containerization, Station Autonomy, and a Central Service (CS). Containerization encapsulates analytic tasks into portable containers, which are transmitted to different healthcare centers (stations) for execution, ensuring that no raw data leaves the centers. Station Autonomy grants full control to each healthcare center over incoming analytic tasks, allowing them to accept, execute, or reject tasks based on local policies. The CS oversees orchestration, routing tasks to the appropriate stations, and managing the metadata repository. One significant contribution of this work is its ability to provide transparency in data analytics by employing a monitoring dashboard and metadata-driven workflows. Additionally, the platform supports a variety of analytical tasks, including complex machine learning models and lightweight statistical operations, as demonstrated through a pneumonia detection case study involving distributed X-ray data. This approach shows practical potential for large-scale healthcare applications, addressing regulatory and operational challenges by enabling compliance with GDPR and HIPAA through secure task execution and encryption. Welten et al. emphasized the flexibility of their platform by adopting containerization technology, allowing seamless integration with different data formats and programming languages. Moreover, the infrastructure incorporates robust privacy-preserving features, including public-private key encryption and station-specific result masking, to safeguard sensitive patient information during distributed analytics.

The Work in²² The authors propose a survival analysis framework for heart failure and breast cancer genomics in a federated environment. Their algorithm achieves a one-shot training approach by selecting the best trees from each client, evaluated using metrics such as the Concordance Index, Integrated Brier Score (IBS), and Cumulative AUC. This method overcomes common drawbacks in federated learning by reducing communication rounds and maintaining robust model performance. The results outperform several baseline models, even under highly skewed data distributions. Chaulwar et al.²³ proposed the SAFE protocol, a Bayesian Federated Analytics approach for detecting trending keywords. SAFE uses Bayesian theorem to calculate the prior and likelihood probabilities for identifying trending keywords locally on users’ devices. The computed summaries are then shared through secure aggregation, ensuring that the actual data remains on the local device. Finally, the protocol ranks the trending keywords based on total count and pooled trends, preserving user privacy throughout the process. Bagdasaryan et al.²⁴ present a similar approach where they apply federated analytics to aggregate location data from millions of users. They employ privacy-preserving technologies such as differential privacy and secure multi-party computation. Their work is effective for spatial and geolocation data. Liu et al.²⁵ propose Colo, a privacy-preserving federated graph analytics method. The approach is suitable for COVID-19 cases, where each node performs computations locally, only interacting with its neighborhood, while all data remains on-site. Each node applies random masking to protect its data. Colo pre-computes a list of all possible results before securely performing computations with its neighbors to obtain the final result. The model is both lightweight and efficient, thanks to its specialized localized data processing, metadata-hiding communication, and optimized aggregation techniques.

In distributed systems, Luo et al.²⁶ propose a communication-efficient collaborative model for distributed linear mixed models. Unlike federated learning that requires multiple rounds of communication, their model runs in one-shot. They used the length of stay (LOS) of hospitalized COVID-19 patients across 11 international data sources with 120,609 patients. The result produced by DDLM is accurate as the data is optimized in a centralized system. There are a number of works focusing on clustering data within human activity recognition. Ali et al.²⁷ propose using CNN and Naive Bayes for activity detection, focusing on motion patterns within indoor activity recognition. Ariza Colpas et al.²⁸ aim to enhance the recognition of daily living activities, with a strong emphasis on improving HAR model performance in terms of clustering quality and feature selection. None of these approaches consider privacy or apply federated analytics over sensors or resources.

There are several studies on human activity recognition using federated learning. FedSiKD²⁹ applies clustering techniques on clients to group them based on data distribution. The clustering is used to address the non-IID (non-independent and identically distributed) nature of data in federated learning, rather than to observe patterns in movement. HAR datasets are also utilized in this work.. The work in³⁰ proposes a fog computing approach combined with federated learning and blockchain to develop an accurate and secure classification model for human activity. FedHealth³¹ introduces a federated transfer learning framework to create personalized classification models for human activity. The authors employ transfer learning and homomorphic encryption, demonstrating that FedHealth significantly improves recognition accuracy by 5.3% compared to traditional learning methods. Work³² presents an approach to ensure data privacy, security, and scalability in Internet of Medical Things (IoMT) applications. The authors integrate different technologies to deliver a privacy-preserving solution for processing sensitive medical data in a scalable environment using federated learning and blockchain. An interesting study proposes a framework similar to federated learning, known as Swarm Learning³³. In this work, the authors introduce a new decentralized learning paradigm called Swarm Learning, which combines federated learning with blockchain technology to train machine learning models on local data without centralizing the data. The paper presents experimental results on four use cases, including leukemia prediction, tuberculosis (TB) detection, lung disease classification, and COVID-19 detection.

Despite progress in federated analytics and privacy-preserving techniques like differential privacy, current methods still struggle to strike a balance between protecting privacy and preserving data utility. Notably, previous research has paid little attention to applying privacy-preserving methods in the realm of human activity recognition (HAR) clustering. Most studies in human activity recognition (HAR) focus on improving accuracy and clustering quality, but they often ignore the privacy risks of sensitive data from wearable sensors and IoT devices. Table 1 discusses the comparison of our work with different approaches in the literature review. Additionally, setting up noise distributions can be complex, making it hard for non-experts to perform secure data analysis. This paper addresses this gap by testing federated statistical functions with different noise distribution methods. We examine how each method balances privacy and data usefulness in HAR applications.

Table 1.

Comparison of related work on privacy-preserving federated analytics and clustering.

Category	Study	Approach	Privacy mechanism	Federated analytics	Clustering
Location Heatmap	Bagdasaryan et al.24	Sparse federated analytics for location data	Dist. DP, SMPC (Pólya noise)	Yes	Limited to spatial data (non-HAR)
Healthcare	Welten et al.21	Distributed analytics (PHT)	SMPC	Yes	No
Precision Medicine	Froelicher et al.15	Federated analytics for biomedical data	Multiparty HE (MHE)	Yes	No
Human Activity Recognition	Ariza Colpas et al.28	Unsupervised HAR analysis using clustering	None	No	Extensive (multiple clustering methods)
Indoor Activity Recognition	Ali et al.27	CNN and Naive Bayes for activity detection	No privacy mechanism	No	Yes (CNN-based on motion patterns)
Healthcare	Our Work	Privacy-preserving federated analytics on wearable data	Laplace, Gaussian, Exponential	Yes	Yes (KMeans, Agglomerative)

System design and architecture

In this section, we describe the design and architecture of our proposed system. We start by introducing federated analytics (FA). Then, we walk through the system workflow using diagrams to show how healthcare centers and the health department interact to generate insights. Finally, we explain the models and notations used in this research.

Preliminary: introduction to federated analytics

Federated analytics (FA) is the core paradigm within our work. FA is a distributed paradigm that allows different parties to collaborate on analytics without exchanging their data. Unlike centralized analytics, where raw data is sent to a central server, FA enables parties, such as healthcare centers, to cooperate by sharing only statistical summaries. This ensures that sensitive data remains local, reducing privacy risks and helping participants comply with privacy regulations like GDPR.

FA differs from federated learning in that it focuses on computing and aggregating statistical summaries rather than training machine learning models. Its main goal is to enable privacy-preserving data analysis while maintaining high utility and scalability across multiple data sources.

System workflow

Figure 1 illustrates the system and workflow architectures of a healthcare system using a federated analytics infrastructure. It consists of different components, where at the bottom are healthcare centers, such as hospitals and laboratories, that agree to collaborate and share summaries of specific domains they aim to study. This layer communicates with the health department or health authority, which collaborates with these centers and aggregates the required insights.

Fig. 1.

The system and workflow architectures.

Figure 1 illustrates the system and workflow architectures of healthcare system using a federated analytics infrastructure. It consists of different components, where at the bottom are healthcare centers, such as hospitals and laboratories, that agree to collaborate and share summaries of specific domains they aim to study. This layer communicates with the health department or health authority, which aims to collaborate with these centers and aggregate the required insights. First, the health department (Step 1) requests federated statistics and distributes them to all participants (e.g., healthcare centers, patients) in this project. Second, the healthcare centers compute specific functions locally (Step 2), using privacy-preserving technology like differential privacy. Depending on configuration, this differential privacy can be applied either locally at the healthcare centers or centrally during aggregation. Third, these healthcare centers or patients share their summaries (Step 3) with the health department for aggregation. Fourth, the health department aggregates the collected summaries (Step 4) to obtain global results. Finally, the health department applies clustering (Step 5) to the aggregated data from different sources to analyze physical activity levels, highlighting subgroups among elderly patients with similar movement patterns.

Models and notation

We model the federated statistics system as consisting of a collection of 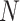patients, each represented by a local dataset 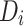, and a global server acting as a health department. In this system, statistical summaries are computed on individual datasets 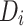without sharing raw data. In federated analytics, there are a number of statistical functions that can be used during the analysis of health data. In this work, we focus on mean, variance, and quantile.

Each instance in 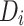represents individual data points, such as medical test results, age, or activity levels (e.g., data from wearable devices). The aim is to compute local statistics and aggregate them across all patients. Depending on the configuration, the key operations are either performed locally by each patient or healthcare center or centrally at the health department. These operations are denoted by 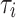when computed locally, with the aggregated statistic for all patients denoted by 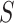, computed after global aggregation. Noise mechanisms (Laplace, Gaussian, Exponential, and Local Differential Privacy (LDP)) are applied to the data; in the case of LDP, noise is added to the local data before sharing.

Finally, clustering is applied to the DP-protected aggregated data 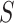to identify patterns in patient activity and other health metrics. This step allows the health department to group similar patient profiles, providing insights such as physical activity trends among subgroups without compromising individual privacy.

.

Proposed model

Our solution involves a dual-stage process. First, local computations are performed to derive statistical summaries (mean, variance, quantile) from sensitive data. Differential privacy noise is applied either locally or globally, depending on the required level of privacy. Next, once the privacy-preserving summaries are aggregated at the global level, clustering methods (KMeans and Agglomerative) are applied to uncover patterns and trends, such as patient activity levels or chronic disease progression. This dual-stage integration ensures that noise is added after local computation, preserving individual privacy while minimizing utility loss. It also allows healthcare providers to derive meaningful insights from aggregated data without directly accessing raw patient data.

Privacy-preserving statistical functions

Federated statistics functions such as mean, variance, and quantile-are computed locally on patient data in a privacy-preserving manner. Health departments, acting as the global authorities, rely on these functions to derive insights without breaching patient confidentiality. By applying privacy-preserving noise mechanisms at the local or global level, our approach ensures individual-level privacy while enabling meaningful aggregation and analysis. This integration focuses on preserving the balance between utility and privacy, which is particularly crucial for sensitive health data.

We explore four well-known privacy-preserving noise mechanisms: Laplace, Gaussian, and Exponential for centralized DP, and random noise for LDP. Each of these mechanisms adds noise to local data or statistics before sharing, thus protecting individual data. However, each noise mechanism also impacts the accuracy of the statistical functions, which makes balancing privacy and utility a challenge. To address this, we evaluate how varying privacy budgets (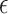) impact clustering utility and statistical function accuracy. For instance, we analyze configurations where 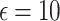ensures strong privacy at the cost of utility, while 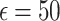achieves better utility with relaxed privacy. This systematic analysis identifies practical configurations for healthcare use cases.

For example, in a healthcare scenario where wearable devices track patient movements, healthcare centers may use federated statistics to analyze trends in physical activity among patients with chronic conditions. The statistical functions (e.g., average steps per day, variance in activity levels) are computed locally, and the noise mechanisms ensure privacy is maintained. The aggregated insights can then be used by the health department to improve patient care, while the underlying data remains protected.

Differential privacy

Differential Privacy (DP) is a commonly used approach that incorporates the analysis of personal or sensitive data while ensuring the privacy of individuals. The key idea is that the presence or absence of an individual’s data in the dataset has a minimal effect on the output of a function, providing strong privacy guarantees. Additionally, we introduce feature-specific sensitivity scaling by incorporating a scaling factor, where represents the feature index and is the total number of features. This scaling mechanism ensures that more sensitive features are assigned greater noise, thereby enhancing privacy protection while retaining utility for less sensitive features. For example, in the case of mean estimation, features with higher sensitivity (e.g., patient heart rate) receive proportionally higher noise, whereas less sensitive features (e.g., step count) retain more accuracy. In this work, DP is not applied uniformly; instead, privacy mechanisms are tuned based on function sensitivity and data characteristics. This ensures that utility is maximized for key metrics, such as variance and quantiles, while maintaining privacy for sensitive patterns in healthcare data.

Where:

• and are neighboring datasets differing by one element,

• is the function or query applied to the dataset (e.g., mean, sum),

• is the output,

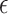• is the privacy budget, controlling the level of privacy; smaller values provide stronger privacy guarantees.

Each mechanism can be applied in two configurations, centralized or local, depending on the stage at which noise is added. In centralized DP, aggregated summaries are perturbed at the global server, optimizing group-level privacy and analysis accuracy. In contrast, local DP applies noise directly at the data source, ensuring stronger individual privacy but introducing higher noise levels. Our experiments demonstrate how these configurations influence clustering outcomes and utility.

Laplace mechanism

The Laplace mechanism adds noise sampled from a Laplace distribution to ensure differential privacy (DP) by adding randomness to statistical summaries such as the mean. This helps prevent the exact values of individual data points from being inferred.

In a centralized DP setting, noise is applied to the aggregated result at the global server, while in a local DP setting, noise is added directly to each patient’s computed statistic before sharing, ensuring that private data remains protected from the start.

For example, in a healthcare scenario, if the goal is to compute the average heart rate of patients, applying noise sampled from a Laplace distribution to the computed mean ensures that the shared result does not reveal precise individual data, thereby protecting patient confidentiality.

The Laplace noise added to a function is given by:

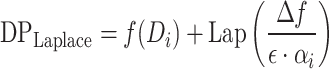Here, 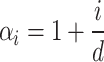is a feature-specific scaling factor, where 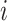represents the index of the feature, and is the total number of features. This factor ensures that features with higher sensitivity (e.g., heart rate) receive more noise, while less sensitive features (e.g., step count) receive less noise. This fine-tuning helps maintain accuracy for less sensitive features while ensuring stronger privacy for sensitive ones.

Gaussian mechanism

The Gaussian mechanism, suitable for 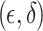-DP, adds noise from a Gaussian distribution. It is often preferred when a slight relaxation in privacy is acceptable. Like Laplace, Gaussian noise can be applied at the local level by adding noise before data sharing or centrally during aggregation.

The Gaussian noise added to a function is defined as:

where and provides a scaling factor by feature, optimizing privacy and utility trade-offs across data types. Similar to the Laplace mechanism, 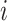represents the feature index, and 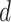denotes the total number of features.

Exponential mechanism

The Exponential mechanism is typically used for discrete choices or functions like quantile estimation. By introducing noise based on the exponential distribution, it allows differentially private selection while preserving the utility of the selected result. In our evaluation, the Exponential mechanism, particularly for quantile functions, demonstrates a strong balance between privacy and utility when 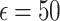, achieving clustering quality close to non-DP setups.

The Exponential noise added to a function is given by:

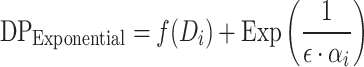where 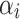scales the noise based on the feature’s sensitivity. The feature-specific scaling factor ensures that functions with varying sensitivities receive appropriate levels of noise.

The noise added to local data before aggregation with the global server is crucial for highly sensitive health data. Each of these noise mechanisms is applied to statistical functions (mean, variance, quantile) to evaluate their impact on privacy and accuracy in federated analytics, enabling health departments to derive meaningful insights without compromising patient confidentiality.

Clustering on differentially private data

After applying differential privacy (DP) noise to the aggregated statistical summaries in the federated analytics environment, we introduce a clustering stage. This stage is used to derive actionable patterns from the privacy-protected data. It enables healthcare providers to identify and group similar activity patterns among patients. By separating privacy protection and clustering into distinct stages, our approach ensures that noise minimally impacts the clustering process, preserving utility while maintaining strong privacy guarantees. We employ two different clustering methods, KMeans and Agglomerative Clustering, to analyze patterns in the differentially private aggregated data. Both methods are effective at identifying underlying structures in high-dimensional data. They also handle the noise introduced by privacy mechanisms well.

KMeans clustering

Now, after all participants share their summaries with the global entity, which, in our case, is the health department, the health department aggregates these summaries to obtain global results. Consequently, clustering is applied at the global level to identify common patterns. In this research, we apply two different clustering algorithms. First, we discuss the partitioning algorithm, KMeans. KMeans clustering partitions the data into clusters by minimizing the variance within each cluster. Given a dataset of differentially private aggregated statistics , KMeans seeks to minimize:

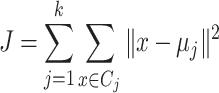where:

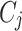• is the 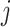-th cluster,

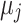• is the centroid of ,

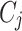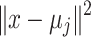• represents the squared Euclidean distance between a data point 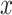and its cluster centroid .

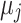This clustering method is applied to the DP-protected outputs (mean, variance, quantile) to identify common patterns, such as activity levels across patient groups, which could inform interventions or preventive care strategies in healthcare.

Agglomerative clustering

The Agglomerative clustering aim to group the data into different clusters, this call dendrogram. This method does not require the number of clusters k as an input, but needs a termination condition Initially, each data point is count as a separate cluster. The merging process happens gradually, grouping similar data points together step-by-step. This continues until all data points are combined into a single cluster. This approach is especially useful for analyzing data in layers, as it allows different levels of grouping to reveal complex patterns within patient populations.

For Agglomerative clustering, we use Euclidean distance to measure similarity between data points within the differentially private (DP) dataset. At each step, a linkage criterion, such as Ward linkage, determines how close clusters are to each other. These choices help the clustering method adapt to the structure of the data, even when privacy-related noise is added.

Applying clustering to federated analytics allows healthcare providers to derive meaningful insights into patient activity patterns without accessing individual raw data. This dual-stage integration enables healthcare stakeholders to balance privacy and utility effectively, leveraging the strengths of federated analytics for secure and actionable insights. For example, clustering results reveal activity trends, such as subgroups among elderly patients with similar movement patterns, which support personalized health management while ensuring compliance with privacy requirements.

Experiment

n this experiment, we first evaluated the performance of various differential privacy (DP) mechanisms. Next, we compared the results of FAItH with state-of-the-art methods, specifically clustering techniques used in federated analytics³⁴ and federated learning frameworks^35,36, which share similarities with our approach but differ in their clustering strategy and how they integrate within the federated learning and machine learning pipeline. The dataset used for this purpose was the Human Activity Recognition (HAR) dataset, which is typical for sensor data on mobile devices³⁷. The HAR dataset captures three-dimensional measurements from both an accelerometer and a gyroscope. Which uses these sensor information to anticipate user behavior with high accuracy. There are around 10,299 cases in all, and 561 characteristics characterize each one.

Experiment parameters

The federated analytics environment was simulated with 510 clients in most cases, and with 980 clients for a specific test to evaluate the scalability of FAItH. Two different privacy budgets, represented by epsilon () values of 10 and 50, were tested. These values determine the level of privacy control, with smaller values providing stronger privacy guarantees but potentially reducing accuracy. Additionally, the performance of various differential privacy mechanisms was evaluated under highly distributed data, and the effectiveness of FAItH was assessed and compared with state-of-the-art methods across different degrees of distribution to test its novelty and effectiveness. Therefore, to mimic the highly imbalanced or non-identical (non-i.i.d.) data distribution across participants, we employed the Dirichlet distribution with parameters . As 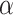decreases, the label distribution becomes more heterogeneous, indicating a shift towards a more pronounced non-i.i.d. data distribution.

To evaluate the first stage, which includes federated analytics and differential privacy (DP), we used three key metrics: membership inference attack success rates, attack accuracy, and overall accuracy. In the second stage, to assess the clustering performance, we employed the silhouette score.

The first metric, Membership Inference Attack Success Rates, was used to evaluate the vulnerability of DP mechanisms to adversarial attacks. We explored three types of membership inference attacks: simple, complex, and advanced. The simple membership inference attack is a basic approach that attempts to determine whether a specific data point was part of the training set. To measure its success, we calculated the true statistic (mean, sum, variance, or quantile) on the original client data and compared it to the DP result. If the difference between the two was below a threshold (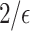), the attack was considered successful. The attack success rate was determined by the percentage of successfully attacked clients.

In contrast, the Complex Membership Inference Attack employed machine learning techniques, particularly logistic regression, to predict membership. This method involved preparing a dataset by computing DP results for each client and obtaining their true statistics. These values were then used to train a logistic regression model, which predicted membership based on the deviation from the true statistic. The model’s success rate reflected the privacy mechanism’s susceptibility to advanced attacks. However, the effectiveness of this attack can be limited by the diversity of the training dataset.

Furthermore, to capture complex patterns and non-linear relationships in the data, we incorporated an Advanced Membership Inference Attack (Neural Network-based). This attack model utilizes a deep learning approach to predict membership more accurately. The neural network model takes the differentially private outputs, compares them with the true statistics, and learns to predict membership based on these comparisons. The network is trained on the DP results, and the accuracy of its predictions serves as an advanced measure of the privacy protection offered by the DP mechanism. The success rate of this advanced attack was evaluated based on the ability of the neural network to distinguish between members and non-members of the dataset, providing a deeper insight into the privacy mechanism’s robustness against more sophisticated attacks.

Accuracy was used to measure the closeness of the statistical functions (mean, variance, and quantile) to the true values when applying differential privacy. A high accuracy score indicates that, despite the noise introduced by DP, the function still approximates the actual value closely. This metric balances the trade-off between maintaining privacy and preserving the utility of the data. In this experiment, an attack is considered to fail when it cannot correctly predict if a specific data point was part of the original dataset. For simple attacks, failure happens when the difference between the real value and the differentially private (DP) result is too big. If the difference is larger than , the attack fails. This means the added noise makes it harder for the attacker to figure out the original value.

For complex attacks, failure is measured by how well a machine learning model (such as logistic regression) can predict if a data point was in the dataset. If the model can’t predict well, the attack is less successful, meaning the privacy protection is stronger. Finally, the advanced attack is evaluated based on the neural network’s ability to learn the membership prediction task. A failed advanced attack indicates that the deep learning model could not identify the original data point, signaling that the privacy-preserving mechanism is effective.

In this work, several clustering evaluation metrics are employed to assess the performance of the clustering algorithms. The silhouette score is used to measure the quality of the clustering by comparing how similar each data point is to its own cluster versus neighboring clusters, with higher scores indicating better-defined clusters. Along with the silhouette score, the confidence interval for silhouette score is provided to quantify the uncertainty of the clustering results, offering a range within which the true Silhouette Score is likely to lie. The Davies–Bouldin Index (DBI) is another metric that evaluates the compactness and separation of clusters, where a lower DBI indicates more distinct and compact clusters. Finally, the computation time is measured to assess the efficiency of the clustering process, including both model training and evaluation, providing insight into the algorithm’s performance in terms of time efficiency.

Evaluated the performance of various differential privacy (DP) mechanisms

First we discuss results for centralized and local DP with different noise mechanisms. Then We discuss clustering and compare with non-DP results.

Analysis of results for centralized and local DP with different noise mechanisms

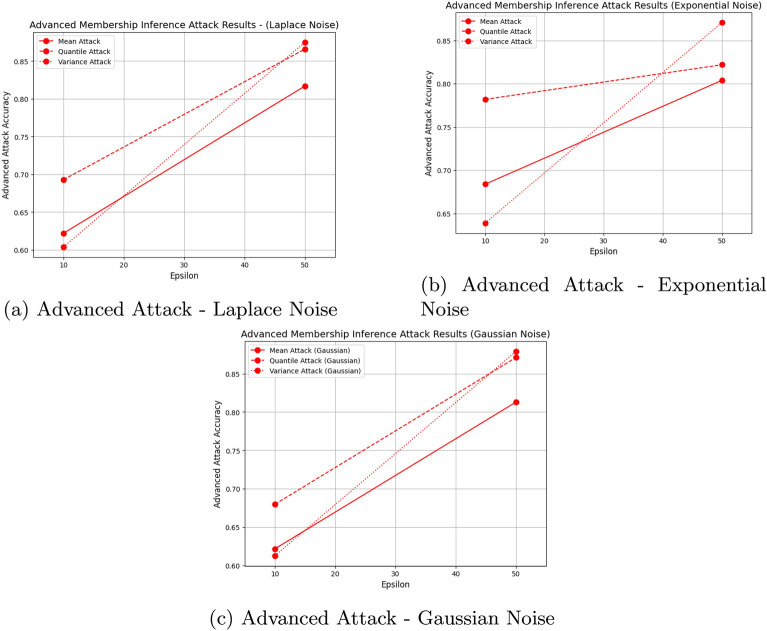
In Fig. 2, we illustrate the comparison of Accuracy and Attack Levels across Noise Types. The figure displays the accuracy of different noise mechanisms alongside the results of the regression attack. In Fig. 3, the figures exclusively present the attack accuracy for the deep learning model. This presentation highlights the distinct performance of the advanced deep learning model in evaluating privacy, offering a more sophisticated measure of attack success compared to traditional regression model Under Central DP with Laplace noise, accuracy improves as the privacy budget increases. At epsilon 10, Mean and Quantile have lower accuracy values (− 1.5886 and − 0.0769, respectively), indicating notable information distortion due to noise addition. At epsilon 50, however, accuracy is positive for all functions, with Variance achieving the highest accuracy (0.9584), suggesting that Laplace noise is effective in preserving accuracy with a higher privacy budget. This result demonstrates the inherent trade-off between privacy and utility, where higher privacy budgets reduce noise distortion but increase the potential for attack vulnerability. Nonetheless, attack levels also increase with a higher epsilon, with Quantile showing the highest susceptibility to attack (0.92) at epsilon 50 in the regression attack. In contrast, for the advanced attack using the deep learning model, the attack success rate at epsilon 10 reaches 0.69, which is higher than the 0.65 achieved by the regression model. This suggests that the deep learning model is better equipped at capturing complex relationships in the data, particularly at lower privacy budgets, as compared to the simpler regression models, which struggle more under higher privacy budgets.

Fig. 2.

Comparison of accuracy and attack levels across noise types.

Fig. 3.

Membership attack levels across noise types.

For Exponential noise under Center DP, accuracy also improves with a higher epsilon value. Mean and Quantile have relatively lower accuracies at epsilon 10 (− 0.6505 and − 0.1521, respectively), while at epsilon 50, accuracy is positive for all functions, with Variance achieving the highest (0.9571). The improved performance with Exponential noise demonstrates its potential for preserving utility in statistical functions, particularly when privacy constraints are relaxed. Nevertheless, Exponential noise shows a notable increase in vulnerability from epsilon 10 to epsilon 50, suggesting a similar trade-off between accuracy and privacy. For instance, when the attacker uses a deep learning model, the attack accuracy for the Quantile function at epsilon 10 reaches 0.68, which is higher than the regression model’s accuracy of around 0.6. This highlights the importance of using advanced attack models in privacy evaluations, as they are better equipped to exploit complex patterns in the data.

With Gaussian noise under Center DP, Mean and Quantile exhibit negative accuracies at epsilon 10, which are less severe than those under Laplace but still indicate substantial noise impact. At epsilon 50, accuracy improves across all functions, with Variance reaching the highest (0.9603), demonstrating that Gaussian noise can better maintain accuracy at higher privacy budgets. However, as with other noise types, the increased epsilon correlates with higher attack probabilities. This finding further underscores the critical balance between privacy and utility across all mechanisms. For different attack evaluations, both regression and deep learning attacks show accuracy around 0.6 and 0.8 for different epsilon values. However, the results in Figs. 2 and 3 demonstrate that the deep learning attack observes significantly higher accuracy compared to regression, proving the importance of including deep learning in privacy evaluations

In summary, accuracy consistently improves across all noise types as epsilon increases, with Variance demonstrating the most resilience and highest accuracy overall. However, attack probability also increases with a higher epsilon. These results underscore the critical need to balance privacy and utility by selecting appropriate privacy budgets and noise mechanisms. For instance, Variance achieves a favorable trade-off between accuracy and attack resistance, while Quantile remains more vulnerable under relaxed privacy budgets, emphasizing the importance of tailoring configurations to specific application needs.

Analysis of results for local DP with different noise mechanisms. In Fig. 4, under Local DP with Laplace noise, accuracy improves as the privacy budget increases. At epsilon 10, Mean and Quantile have lower accuracy values (− 2.6517 and − 0.0601, respectively), indicating notable information distortion due to noise addition. At epsilon 50, however, accuracy is positive for all functions, with Variance achieving the highest accuracy (0.9591), suggesting that Laplace noise is effective in preserving accuracy with a higher privacy budget. However, this improvement comes at the expense of increased vulnerability, with attack levels rising as the privacy budget is relaxed. Nonetheless, attack levels also increase with a higher epsilon, with Quantile showing the highest susceptibility to attack (0.92). This outcome highlights a trade-off between accuracy and privacy, as greater accuracy at epsilon 50 correlates with an increase in attack vulnerability.

Fig. 4.

Comparison of accuracy and attack levels across noise types for local differential privacy methods.

For Exponential noise under Local DP, accuracy also improves with a higher epsilon value. Mean and Quantile have relatively lower accuracies at epsilon 10 (− 2.2975 and − 0.1556, respectively), while at epsilon 50, accuracy is positive for all functions, with Variance achieving the highest (0.9601). The results for Exponential noise highlight its ability to maintain strong accuracy retention while balancing privacy, although attack levels also increase as privacy constraints loosen. Nevertheless, attack levels also rise with epsilon, reaching 0.92 for Quantile. Exponential noise shows a notable increase in vulnerability from epsilon 10 to epsilon 50, suggesting a similar trade-off between accuracy and privacy.

With Gaussian noise under Local DP, Mean and Quantile exhibit negative accuracies at epsilon 10, which are less severe than those under Laplace but still indicate substantial noise impact. At epsilon 50, accuracy improves across all functions, with Variance reaching the highest (0.9593), demonstrating that Gaussian noise can better maintain accuracy at higher privacy budgets. As with other mechanisms, the increased epsilon correlates with higher attack probabilities, particularly for Quantile, which remains most vulnerable under relaxed privacy settings.

In summary, accuracy consistently improves across all noise types as epsilon increases, with Variance demonstrating the most resilience and highest accuracy overall. However, attack probability also increases with a higher epsilon. These findings emphasize the importance of tailoring noise mechanisms and privacy budgets to specific application requirements, balancing the need for privacy with the utility of the results. For example, Variance offers a favorable balance of accuracy and attack resistance, while Quantile requires careful consideration due to its higher susceptibility to attacks. In comparison to non-DP configurations, the trade-offs in our approach highlight the practicality of achieving sufficient clustering utility while preserving strong privacy guarantees. These findings are particularly relevant for healthcare applications, where balancing data confidentiality with actionable insights is essential.

Clustering analysis

Mean function analysis. Interestingly, for Agglomerative clustering, the Centralized DP with Gaussian noise at 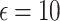yields a score of 0.3598, and Local DP with Exponential noise at 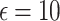yields a score of 0.3556, both of which are higher than the non-DP baseline score of 0.3089.

The results in Table 2 show that clustering quality can sometimes even improve with noise added through differential privacy, indicating robust clustering potential while maintaining privacy. These findings demonstrate that differential privacy mechanisms can achieve competitive clustering utility with mean-based functions, even in privacy-preserving configurations, making them suitable for sensitive data applications such as healthcare.

Table 2.

Silhouette scores for mean function by DP type and epsilon. Significant values are in bold.

DP type	Noise type
		KMeans	Agglomerative	KMeans	Agglomerative
Centralized	Laplace	0.2747	0.2722	0.3021	0.3021
	Exponential	0.2629	0.2733	0.3019	0.3077
	Gaussian	0.2824	0.3598	0.3018	0.3076
Local	Laplace	0.2757	0.2736	0.3021	0.3080
	Exponential	0.2816	0.3556	0.3014	0.3014
	Gaussian	0.2733	0.2714	0.3019	0.3019
None (No DP)		KMeans 0.3031		Agglomerative 0.3089

Variance function analysis. Interestingly, for Agglomerative clustering, the local DP with Gaussian noise at 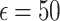yields a score of 0.3930, which is higher than the non-DP baseline score of 0.3089.

The results in Table 3 show that adding differential privacy noise doesn’t always reduce clustering quality; in some cases, it can even enhance it. This indicates a favorable balance between privacy and utility, as variance-based functions exhibit minimal utility loss even under privacy constraints. The findings indicate only a minor utility trade-off when applying DP to variance-based functions, which actually perform better than both non-DP and mean-based functions (with a score of 0.3598). This highlights how specific noise mechanisms and privacy budgets can be carefully selected to optimize clustering performance while maintaining strong privacy guarantees. The inherent data structure captured by Agglomerative clustering further contributes to this balance, demonstrating its effectiveness in privacy-preserving scenarios.

Table 3.

Silhouette scores for variance function by DP type and epsilon. Significant values are in bold.

DP type	Noise type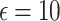
		KMeans	Agglomerative	KMeans	Agglomerative
Centralized	Laplace	0.3529	0.3851	0.3692	0.3607
	Exponential	0.3533	0.3859	0.3608	0.3608
	Gaussian	0.3528	0.3720	0.3608	0.3608
Local	Laplace	0.3532	0.3626	0.3605	0.3930
	Exponential	0.3530	0.3530	0.3607	0.3607
	Gaussian	0.3530	0.3853	0.3607	0.3931
None (No DP)		KMeans 0.361		Agglomerative 0.361

Quantile function analysis. The results show that for the Quantile function, the local DP with Exponential noise at 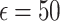performs very closely to the non-DP baseline, achieving silhouette scores of 0.4378 for both KMeans and Agglomerative clustering, compared to the non-DP score of 0.4387. Although this mechanism does not outperform the non-DP baseline, the similarity in scores suggests minimal loss in clustering utility. Although the Quantile function doesn’t outperform non-DP, it shows the highest score and provides the most robust support for privacy-preserving clustering in healthcare applications.

The results in Table 4 indicate that the Quantile function with Local DP and Exponential noise at achieves the highest clustering quality while preserving privacy, nearly matching the non-DP baseline. This configuration offers a strong balance for healthcare monitoring in applications like chronic disease tracking, where both privacy and accurate clustering are essential. When greater privacy is required, the variance function with Local DP and Gaussian noise at 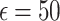provides a reliable alternative, demonstrating robust clustering performance with minimal utility loss under stricter privacy constraints. Agglomerative clustering plays a key role by effectively capturing the underlying structure of the data, resulting in superior clustering quality.

Table 4.

Silhouette scores for quantile function by DP type and epsilon. Significant values are in bold.

DP type	Noise type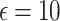
		KMeans	Agglomerative	KMeans	Agglomerative
Centralized	Laplace	0.4154	0.4154	0.4377	0.4377
	Exponential	0.3996	0.4137	0.4375	0.4375
	Gaussian	0.3985	0.4120	0.4368	0.4368
Local	Laplace	0.4130	0.4130	0.4376	0.4376
	Exponential	0.4144	0.4144	0.4378	0.4378
	Gaussian	0.3988	0.4144	0.4376	0.4376
None (No DP)		KMeans 0.4387		Agglomerative 0.4387

Overall, these findings show that our privacy-preserving clustering approach is both effective and highly suitable for healthcare applications such as patient activity monitoring and chronic disease management. By balancing privacy and utility through careful selection of configurations, our approach ensures actionable insights without compromising patient confidentiality. By focusing on federated analytics rather than accessing actual patient data, our approach builds trust and encourages adoption in privacy-sensitive environments.

Comparison results

In this experiment, we compared FAItH against two other approaches: federated analytics (without differential privacy) and federated learning (FL). In this experiment, we use the Variance function with the Laplace privacy mechanism as a candidate function to compare against other approaches, as it demonstrates a good trade-off between accuracy and privacy. We used a few important metrics to evaluate the clustering performance, including the silhouette score, Davies–Bouldin Score, and computation time. FAItH does not expect to outperform federated analytics; instead, FA shows a great guideline. As FA does not introduce noise to the results.

First, we discuss results when we set 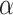= 3. When we looked at the Silhouette Score, which measures how well the clusters are formed, federated analytics (without privacy) showed the best results with a score of 0.59 for 510 clients, indicating the best cluster separation. FAItH, which adds differential privacy, naturally had lower Silhouette Scores, with a score of 0.53 for 510 clients, because of the noise introduced for privacy reasons. Still, FAItH performed better than federated learning, which had the lowest Silhouette Scores overall, with a score of 0.31 for 510 clients. Interestingly, as the number of clients increased, federated learning improved slightly, but it still lagged behind FAItH and federated analytics. Next, we looked at the Confidence Intervals (CIs) for the Silhouette Scores to get a sense of how consistent the clustering results were for each approach. For federated analytics (FA), the CIs were more consistent with a higher upper bound, showing stable cluster formations. In contrast, FAItH’s CIs were a bit narrower, which is expected since adding differential privacy introduces some noise, but the results still stayed within a reasonable range. Federated learning (FL) showed much wider CIs, pointing to more uncertainty in its clustering. This is especially clear because the upper bounds for FL were generally higher, meaning its clustering was less predictable compared to FA and FAItH.

Next, we checked the Davies–Bouldin Score, a measure of cluster quality-lower values are better. As we expected, federated analytics had the best performance here, with the lowest Davies–Bouldin Scores (0.53 for 510 clients), indicating it had the most distinct clusters. FAItH was a bit higher due to the noise from differential privacy, but still performed better than federated learning, which had the highest Davies–Bouldin Scores (1.47 for 510 clients) and the least distinct clusters.

Lastly, we compared computation time. For all numbers of clients involved, both FA and FAItH took less than a minute; however, for federated learning, the time consumption was significantly higher, ranging between approximately 1.43 min (86.02 s for 10 clients) to 16.11 min (966.72 s for 510 clients) due to the training overhead inherent in the nature of FL. In typical simulations, we usually work with around 100 clients. However, to test how well FAItH scales, we extended the experiment up to 980 clients. Since FAItH doesn’t have the extra overhead from optimization, it doesn’t take much longer to process, which made it possible to test such a large number of clients. The results showed that the Silhouette Scores remained stable throughout the experiment. FA showed a small improvement, reaching 0.61, while FAItH reached 0.54. The Davies–Bouldin Score stayed the same for both methods. Since both FA and FAItH finished in under a minute, we decided not to include the federated learning (FL) approach in this part of the experiment, as its communication time was much higher. This demonstrates how scalable FAItH is, even with large numbers of clients.

Fig. 5.

Comparison of clustering performance for FAItH, federated analytics, and federated learning across different metrics where .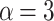

First, we discuss the results when we set . When we looked at the Silhouette Score, which measures how well the clusters are formed, federated analytics (without privacy) showed the best results with a score of 0.60 for 510 clients, indicating the best cluster separation. FAItH, which adds differential privacy, naturally had lower Silhouette Scores, with a score of 0.53 for 510 clients, because of the noise introduced for privacy reasons. Still, FAItH performed better than federated learning, which had the lowest Silhouette Scores overall, with a score of 0.31 for 510 clients. Interestingly, as the number of clients increased, federated learning improved slightly, but it still lagged behind FAItH and federated analytics.

Next, we looked at the Confidence Intervals (CIs) for the Silhouette Scores to get a sense of how consistent the clustering results were for each approach. For federated analytics (FA), the CIs were more consistent with a higher upper bound, showing stable cluster formations. In contrast, FAItH’s CIs were a bit narrower, which is expected since adding differential privacy introduces some noise, but the results still stayed within a reasonable range. Federated learning (FL) showed much wider CIs, pointing to more uncertainty in its clustering. This is especially clear because the upper bounds for FL were generally higher, meaning its clustering was less predictable compared to FA and FAItH.

Next, we checked the Davies–Bouldin Score, a measure of cluster quality-lower values are better. As we expected, federated analytics had the best performance here, with the lowest Davies–Bouldin Scores (0.5263 for 510 clients), indicating it had the most distinct clusters. FAItH was a bit higher due to the noise from differential privacy, but still performed better than federated learning, which had the highest Davies–Bouldin Scores (1.490308 for 510 clients) and the least distinct clusters.

Lastly, we compared computation time. For all numbers of clients involved, both FA and FAItH took less than a minute; however, for federated learning, the time consumption was significantly higher, ranging between approximately 1.65 min (98.85 s for 10 clients) to 16.86 min (1011.73 s for 510 clients) due to the training overhead inherent in the nature of FL. Similar to the previous experiment when 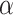=3 we increased the number of clients to 980, and the results remained steady. This consistency further proves that FAItH is a suitable solution for large-scale environments

Fig. 6.

Comparison of clustering performance for FAItH, federated analytics, and federated learning across different metrics where .

In this section, we compared FAItH, federated analytics (FA), and federated learning (FL) using key clustering metrics such as the Silhouette Score, Davies–Bouldin Score, Dunn Index, and computation time. The results clearly show that while FAItH performs well, its clustering quality is slightly lower than federated analytics due to the noise introduced by differential privacy (DP). However, even with this reduction, FAItH outperformed federated learning in terms of clustering quality, as FL had the lowest scores overall.

One of the most significant findings is that FAItH remains stable and performs consistently even as the number of clients increases. When we pushed the experiment to 980 clients, the results still held steady, proving that FAItH is a highly scalable solution. Federated analytics showed a slight improvement in the Silhouette Score, but FAItH’s performance was still close behind, showing the effectiveness of DP without compromising too much on clustering quality. Furthermore, unlike federated learning, which has higher computation time due to training overhead, both FA and FAItH took less than a minute, confirming that FAItH is suitable for large-scale environments.

This makes FAItH a great choice for privacy-preserving federated analytics, especially in large-scale scenarios that require strong privacy protection. DP is becoming the best practice for such environments, as it provides necessary privacy guarantees without introducing significant computational overhead. This highlights FAItH’s potential as a scalable and efficient privacy-enhanced solution for federated analytics.

Limitations and future directions

The proposed approach assumes that participants (e.g., healthcare centers) behave honestly and adhere to the protocol. In real-world federated systems, however, adversarial participants may submit manipulated or malicious summaries, potentially compromising the aggregated insights. Addressing this challenge would require incorporating adversarial resilience techniques, which is beyond the current scope of this work. Future research will focus on addressing these limitations and testing the approach in a broader range of environments.

In future research, we will look into how to combine different privacy-preserving techniques, including differential privacy (DP), secure multi-party computation (SMC), and homomorphic encryption (HE). While DP offers scalable and efficient solutions with low computing overhead, HE and SMC provide stronger privacy protection by ensuring that all intermediate calculations remain private or encrypted. A hybrid approach combining the scalability of DP with the stronger privacy guarantees of HE and SMC could result in a complete federated analytics system capable of handling more sensitive and complex applications in fields like healthcare, finance, and the Internet of Things.

Conclusion

In this paper, we investigate the impact of various privacy-preserving clustering techniques within a federated analytics framework for health monitoring systems. Initially, we applied privacy-preserving mechanisms, including centralized and local differential privacy, using Laplace, Gaussian, and Exponential noise on a federated analytics setup. At this stage, the variance function achieved an effective balance between accuracy and privacy. We then performed clustering on the aggregated results and found that applying differential privacy on statistics consistently showed competitive results compared to non-differentially private configurations in both privacy and utility. This method proves to be an effective approach for enabling healthcare organizations to make informed decisions while ensuring sensitive data remains protected through secure collaborative analytics. Furthermore, we compared our approach, FAItH, with two other state-of-the-art techniques: Federated Analytics (without privacy) and federated learning (FL). The results confirmed that while FAItH’s clustering quality was slightly lower than federated analytics due to the noise from differential privacy, it still performed significantly better than FL, which exhibited the lowest clustering quality. FAItH also showed strong scalability, remaining stable even with an increase in the number of clients, making it well-suited for large-scale environments. As the demand for privacy-preserving technologies grows, particularly in large-scale federated environments, we conclude that differential privacy remains the best practice for protecting sensitive data. FAItH provides an effective balance between privacy and utility and offers a scalable solution for secure collaborative analytics. Researchers can access the code for secure analytics experimentation on GitHub at https://github.com/SimuEnv/Federated-Analytics.

Author contributions

Y.A. (Yousef Alsenani) conceptualized and designed the study, performed the data analysis, developed the differential privacy techniques, prepared the Human Activity Recognition (HAR) dataset for federated analytics, and wrote the manuscript. Y.A. also prepared all figures and reviewed the manuscript.

Data availability

The datasets analyzed during the current study are publicly available as the Human Activity Recognition (HAR) dataset. It can be accessed³⁷. This dataset was used as provided, without any modifications.

Declarations

Competing interests

The authors declare no competing interests.