Abstract
Our research addressed the question of whether sensitivity to relative reinforcer magnitude in concurrent chains depends on the distribution of reinforcer delays when the terminal-link schedules are equal. In Experiment 1, 12 pigeons responded in a two-component procedure. In both components, the initial links were concurrent variable-interval 40 s variable-interval 40 s, and the terminal links were both 20-s interval schedules in which responses were reinforced by either 4 s of grain in one, or 2 s of grain in the other. The only difference between the components was whether the terminal-link schedules were fixed interval or variable intervals. For all subjects, the relative rate of responding in the initial links for the terminal link that produced the 4-s reinforcer was greater when the terminal links were fixed-interval schedules than when they were variable-interval schedules. This result is contrary to the prediction of Grace's (1994) contextual choice model, but is consistent with both Mazur's (2001) hyperbolic value-added model and Killeen's (1985) incentive theory. In Experiment 2, 4 pigeons responded in a concurrent-chains procedure in which 4-s or 2-s reinforcers were provided independently of responding according to equal fixed-time or mixed-time schedules. Preference for the 4-s reinforcer increased as the variability of the intervals comprising the mixed-time schedules was decreased. Generalized-matching sensitivity of initial-link response allocation to relative reinforcer magnitude was proportional to the geometric mean of the terminal-link delays.
Keywords: reinforcer magnitude, concurrent chains, contextual choice model, hyperbolic value added model, incentive theory, key peck, pigeons
One of the most fundamental issues for behavioral psychology has been to discover how different aspects of reinforcer value, such as rate, magnitude, and delay, combine to determine choice. The importance of this issue is demonstrated by the significant research topics it has generated. For example, extension of the matching law to situations in which alternatives differ in both reinforcer delay and magnitude led to the development of models for “self-control” (Rachlin & Green, 1972; see Rachlin, 1995, for a review). Moreover, because reinforcement in natural contexts often varies along multiple dimensions, the determination of such combination rules is critically important to building models for behavior that are applicable outside the laboratory.
Perhaps the simplest assumption is that different dimensions of reinforcement combine multiplicatively, which allows variables that are measured in different physical units to be combined into new variables. The concatenated matching law (Baum & Rachlin, 1969), developed to account for response allocation between two alternatives that can differ in terms of several reinforcer dimensions, provides a good example:
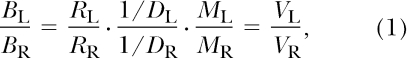 |
in which B represents behavior, and R, M and D the reinforcer rate, magnitude, and delay associated with a choice alternative (subscripted L and R). According to Equation 1, response allocation matches the relative value (V) associated with the choice alternatives, with value being determined by a multiplicative combination of rate, magnitude, and the reciprocal of delay (i.e., immediacy). Equation 1 implies that a logarithmic transformation will render the ratios of different dimensions of reinforcement additive:
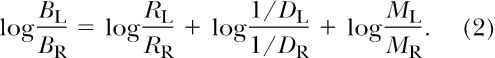 |
Equation 2 is a special case of a linear relation between log response ratio and the log ratios of reinforcement variables,
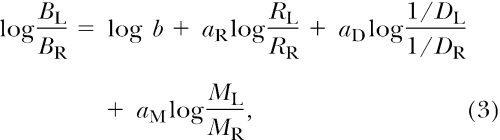 |
known as the concatenated generalized matching law (Baum, 1974; Killeen, 1972; Logue, Rodriguez, Peña-Correal, & Mauro, 1984). The relation has been generalized through the inclusion of an additive constant, log b, which represents bias, and sensitivity parameters for relative reinforcer rate (aR), delay (aD), and magnitude (aM). Equation 3 predicts that the effects of log ratios of reinforcer rate, delay, and magnitude should be additive and independent.
What is the evidence for additivity of log ratios of reinforcer rates, delays, and magnitudes? Different groups of studies have varied rate and magnitude, and delay and magnitude. Neuringer (1967) reported that response-allocation ratios in concurrent-schedule performance matched relative log ratios of reinforcement times (i.e., product of reinforcer rate and magnitude), supporting the additivity prediction. Subsequently, Todorov (1973; see also Keller & Gollub, 1977) found that response ratios were more sensitive to variation in reinforcer rate than magnitude in concurrent schedules, which is consistent with Equation 3 if aR is more than aM. Leon and Gallistel (1998) used electrical brain stimulation as a reinforcer for rats, and varied absolute and relative reinforcer rate and magnitude in concurrent schedules. They found no evidence for an interaction and concluded that rate and magnitude combined multiplicatively. Recently, McLean and Blampied (2001) varied relative reinforcer rate parametrically for two absolute levels of magnitude in concurrent schedules, and found that sensitivity to rate was approximately constant. Overall, these studies suggest that the assumption of the generalized matching law (Equation 3) that reinforcer rate and magnitude combine multiplicatively can be sustained for concurrent schedules, at least when overall reinforcer rate is not varied. But when overall reinforcer rate is varied, sensitivity to reinforcer magnitude ratios changed (Davison, 1988).
By contrast, researchers who have varied reinforcer delay and magnitude have found consistent evidence of interaction. For example, Navarick and Fantino (1976) found that preference in the initial link of concurrent chains for the terminal-link schedule that delivered the larger reinforcer magnitude increased as the duration of equal terminal-link fixed-interval (FI) schedules increased. Similar results were reported by Ito and Asaki (1982) and White and Pipe (1987). Green and Snyderman (1980) and Snyderman (1983) studied pigeons' preference for large versus small reinforcer magnitude (6 s vs. 2 s of access to grain). For several delay ratios, they increased the absolute duration of the delays while keeping the ratio constant (note that the shorter delay always led to the 2-s reinforcer). Both studies found that preference for the large reinforcer terminal link changed systematically with increases in absolute duration. For delay ratios of 6:1 and 3: 1, Green and Snyderman (1980) and Snyderman (1983) reported that preference for the large magnitude decreased, whereas with a delay ratio of 1:1, Snyderman found that preference for the large magnitude increased. Results from the studies disagreed for 3:2 delay ratios, with Green and Snyderman finding an increase in preference for the large magnitude whereas Snyderman reported the opposite. Apparently, sensitivity to magnitude depends on both the absolute and relative delay durations, indicating that these dimensions of reinforcer value may combine in a complex way. However, several models are able to account for the empirical interaction between delay and magnitude reported by Snyderman and the other studies reviewed above.
Grace (1994) proposed a model for concurrent-chains performance based on the generalized matching law (Equation 3). According to the contextual choice model (CCM), sensitivity to terminal-link reinforcement variables depends on the overall temporal context of reinforcement, specifically the ratio of the average terminal- and initial-link durations (Tt/Ti). Written in terms of power functions:
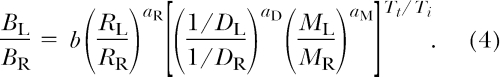 |
Because of the laws of exponents, the effective sensitivities to terminal-link delay and magnitude, respectively, are aD(Tt/Ti) and aM(Tt/Ti). This means that CCM is able to predict the interactions between delay and magnitude in the studies mentioned previously. For example, if the terminal links are equal, preference for the larger magnitude reinforcer will increase as absolute duration of the terminal links increases, because aM(Tt/Ti) increases (Navarick & Fantino, 1976). CCM is also able to predict the differential changes in preference depending on the terminal-link delay ratio reported by Green and Snyderman (1980) and Snyderman (1983). If sensitivity to delay (aD) is greater than sensitivity to magnitude (aM; which is generally the case when the terminal links are FI schedules), then increases in Tt will enhance sensitivity to delay for more extreme ratios (i.e., 3:1, 6:1), thus increasing preference for the smaller-magnitude reinforcer; whereas for lower delay ratios (i.e., 3: 2, 1:1), the magnitude ratio (3:1) dominates as Tt is increased. When fitted to the average data from Snyderman, CCM accounted for 90% of the variance.
CCM shares with the generalized matching law the assumption that the effects of relative delay and magnitude are additive in logarithmic terms. The delay-magnitude interactions reported in the studies above are due to changes in terminal-link duration. Thus CCM specifies that delay and magnitude should be additive and independent when the ratio of terminal- to initial-link durations (Tt/Ti) is kept constant. Grace (1995) and Grace, Bedell, and Nevin (2002) have tested this assumption using factorial designs in which sensitivity to delay was obtained at three different levels of relative magnitude (1:3, 3:1, and 1:1). They varied the terminal-link immediacy ratios while keeping the average programmed initial- and terminal-link durations constant, and concluded that delay and magnitude were independent dimensions of reinforcer value. Grace (1999) tested whether sensitivity to delay depended on the absolute magnitude of the reinforcer and also found independence. Thus CCM is able to account for the existing studies that provide apparent evidence of interaction, and correctly predicts independence under a restricted set of conditions.
Another model for concurrent-chains performance has recently been proposed by Mazur (2001). Building on evidence that a hyperbolic relationship describes the effects of delayed reinforcers (Mazur, 1984), he suggested that the strength of preference during the initial links depended on the relative value added when a transition into a terminal link occurred. His hyperbolic value-added (HVA) model is given by:
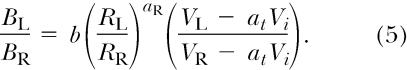 |
In Equation 5, VL and VR are the values of the left and right terminal-link stimuli, respectively, Vi is the value of the initial links, and at is a sensitivity parameter. Thus VL – atVi is the amount of “value added” when the left terminal link is entered. Note that HVA builds on the generalized matching law in a way similar to CCM, because the term for relative terminal-link value added is concatenated with a power function representing the relative entry rates into the terminal links. The values of the terminal and initial links are computed by applying the hyperbolic-decay model of Mazur (1984) to the distributions of reinforcer delays (Di) associated with each stimulus:
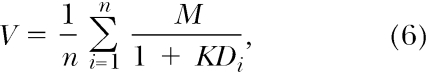 |
where K is a delay-discounting parameter (usually set equal to 0.2 in the analyses reported by Mazur, 2001), and M is reinforcer magnitude. Mazur (2001) showed that the HVA model accounted for about the same percentage of variance in relative initial-link responding as CCM. It is also able to predict Snyderman's (1983) results (accounting for 87% of the variance according to Mazur, 2001) and the other studies cited above. However, there is an important distinction between HVA and CCM. Although both assume that delay and magnitude combine multiplicatively, CCM specifies a set of conditions under which independence can be observed. In contrast, HVA predicts that delay and magnitude will interact (although depending on parameter values it can predict approximate independence).
A third model that can account for delay-magnitude interactions is Killeen's (1985) incentive theory (IT). According to the original version of this theory (Killeen, 1982), the overall strengthening effect of reinforcers (incentives) consists of the product of arousal, which is proportional to reinforcer rate, R, and a “directive” effect, which for concurrent chains is determined by the sum of the effects of primary and conditioned reinforcement. In order to account for Snyderman's (1983) results, Killeen (1985) modified IT so that the value (V) of an incentive would affect the steepness of the reinforcement delay gradient:
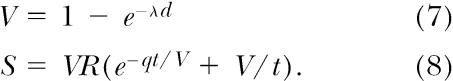 |
Equation 7 defines value as a function of reinforcer duration (d), with λ as a parameter. The strengthening effect of reinforcement (S) is represented by Equation 8, in which t is the time to reinforcer delivery from terminal-link onset, and q is a sensitivity parameter. Preference is then predicted as the relative strengthening effect. For present purposes, the important point to note is that IT does not assume that delay and magnitude combine in a simple multiplicative way. Rather, sensitivity to delay (the exponential parameter in Equation 8) depends inversely on reinforcer magnitude (scaled as incentive value). Killeen (1985) showed that IT accounted for 93% of the variance in Snyderman's data. It is interesting that Killeen's suggestion that sensitivity to delay depends inversely on magnitude has independently been proposed by researchers in decision making to explain the so-called “magnitude effect” in temporal discounting (Kirby & Marakovic, 1996).
A final model that may account for empirical delay-magnitude interactions is delay-reduction theory (DRT; Fantino, 1969). The basic form of DRT is:
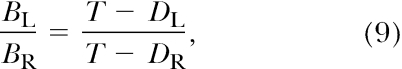 |
is the average time to reinforcement from the onset of the initial links and DL, DR are the average delays to reinforcement signaled by the terminal links. According to DRT, the strength of preference for a terminal link depends on the relative reduction in overall reinforcer delay signaled by its onset (see Fantino, Preston, & Dunn, 1993, for review). Navarick and Fantino (1976) proposed that effects of unequal reinforcer magnitude could be modeled in DRT by combining terminal-link delay (or rate) and magnitude into a single variable: The product of reinforcer rate and magnitude (i.e., the number of seconds per unit time in the terminal links that the organism is able to access the reinforcer). Specifically, they suggested that the delay to the larger reinforcer could be rescaled (i.e., shortened) so that the same value of access time could be obtained if the smaller reinforcer were delivered instead. They showed that with this assumption, DRT was able to predict the obtained increase in preference for the larger magnitude as the terminal links increased.
Thus there are three models that are able to account for the delay-magnitude interaction studies reviewed above (although no doubt a suitable version of DRT with sensitivity parameters could also account for Snyderman's [1983] results). Arguably, CCM is the simplest because it assumes that delay and magnitude combine multiplicatively, and that their effects are additive and independent in logarithmic terms, at least for a restricted range of conditions. HVA also assumes a simple multiplicative combination of delay and magnitude, although their effects are fundamentally nonadditive in terms of the model's structure. Finally, IT is based on a strong interaction in which sensitivity to delay varies inversely with reinforcer magnitude.
The goal of the present research was to explore another situation in which CCM predicts that delay and magnitude should be independent. According to CCM, if the terminal-link schedules are equal, preference for a larger over smaller magnitude (and, hence, aM) will not depend on the distribution of terminal-link reinforcer delays provided that the overall average delay is constant. As shown below, other models for choice, including HVA and IT, predict that preference for the larger magnitude reinforcer will depend on the distribution of delays even if the average delay is constant.
Experiment 1
In Experiment 1, pigeons responded in a two-component concurrent chain in which the initial links were independent concurrent variable interval (VI) 40 s VI 40 s, the terminal-link schedules were equal, and the reinforcer magnitudes were unequal. In one component the terminal links were both VI 20-s schedules, whereas in the other they were both FI 20 s. After sufficient training, the magnitudes were reversed. At issue was whether preference for the larger magnitude reinforcer would be the same or different in the two components. We used 12 subjects, a number sufficiently large enough to provide a fair chance at detecting no difference across the components.
Both CCM and DRT predict that preference should be equal in the VI and FI components because the arithmetic mean delays are the same. In contrast, both HVA and IT (if t in Equation 8 is computed as the harmonic, not arithmetic, mean terminal-link delay) predict that preference for the larger reinforcer should be stronger in the FI component. The reason is that both models use an averaging method that more heavily weights shorter intervals when determining the effects of terminal-link delays, so the delays are effectively longer in the FI component. As a result, these models predict a “terminal-link effect” in which preference for the larger reinforcer is stronger in the FI component (cf. Grace & Bragason, 2004; MacEwen, 1972; Navarick & Fantino, 1976).
Method
Subjects
Subjects were 12 pigeons of mixed breed, and were maintained at 85% of their free-feeding weight ± 15 g through appropriate postsession feeding. Subjects were housed individually in a vivarium with a 12:12 hr light/dark cycle (lights on at 6:00 a.m.), with water and grit always available in the home cages. All subjects were experienced with a variety of experimental procedures.
Apparatus
Eight standard three-key operant chambers, 320 mm deep by 340 mm wide by 340 mm high, were used. The keys were located 210 mm above the floor and arranged in a row. There was a houselight located above the center key that provided general illumination for each chamber, and a grain magazine with an aperture centered 60 mm above the floor. The magazine was illuminated when wheat was made available. A force of approximately 0.15 N was required to operate each key. Chambers were enclosed in sound-attenuating boxes, and ventilation and white noise were provided by attached fans. Experiment control and data collection were accomplished through a computer and MED-PC® interface located in an adjacent room.
Procedure
Because all subjects were experienced, training started immediately on a multiple-component concurrent-chains procedure. Sessions ended when two components had been completed or 75 min had elapsed, whichever occurred first. Each component was a concurrent chain, and lasted until 36 initial- and terminal-link cycles had been completed. All cycles ended with reinforcement. A 3-min blackout during which the keylights and houselight were extinguished separated the components. The order of components varied randomly from session to session. Components differed only in the color of the keylight stimuli used (red or green) and the reinforcement schedules for left and right terminal-link responses. Sessions were conducted 7 days a week at approximately the same time of day.
The side keys were illuminated the same color (red or green, depending on the component) to signal the start of the initial links. Concurrent independent VI VI schedules ran during the initial links, but their timing did not begin in a particular cycle until the first response had been made to either key. In this way, postreinforcement pauses were not counted toward the completion of initial-link schedule requirements. Throughout the experiment, the initial links were always concurrent VI 40-s VI 40-s schedules. Each schedule contained 12 intervals constructed from the exponential progression of Fleshler and Hoffman (1962) and intervals were sampled without replacement.
When an initial-link schedule had timed out, the next response to that key produced an entry into the terminal link associated with that key (provided it was not the first response of the cycle). There was no changeover delay. Terminal-link entry was signaled by a change from continuous to blinking keylight illumination (0.25 s off, 0.25 s on), coupled with the other keylight being extinguished. Terminal-link responses were reinforced by either VI 20-s schedules containing 12 intervals constructed from exponential progressions (Fleshler & Hoffman, 1962), or FI 20-s schedules. Thus the terminal-link schedules were both VI 20 s in one component, and both FI 20 s in the other.
At the start of a terminal link an interval was sampled randomly without replacement from the VI list, or a 20-s timer began (FI). The first response after the delay had elapsed was reinforced. During reinforcement the keylight and houselight were extinguished, and the grain magazine was raised and illuminated for a specified duration. Reinforcer durations were always the same across components but varied within components. For each pair of terminal-link schedules, reinforcer duration was 4 s for one alternative and 2 s for the other. After reinforcement, the houselight and initial-link keylights were illuminated and the next cycle began, unless the 36th reinforcer in the component had just been delivered, in which case either the 3-min intercomponent blackout began or the session ended.
The experiment consisted of two conditions, which differed only in terms of the reinforcer duration associated with the terminal links. For example, in the first condition the terminal links might be VI 20 s (red), and FI 20 s (green), with reinforcer magnitudes of 4 s and 2 s for the left and right terminal links, respectively. For the second condition, the magnitudes were reversed, so that the terminal links would remain VI 20 s (red) and FI 20 s (green), but now with magnitudes of 2 s and 4 s for the left and right schedules. The assignment of VI or FI schedules to each component, and whether the left or right terminal link was associated with the 4-s reinforcer, was counterbalanced across subjects.
Both conditions were run for 36 sessions. A stability criterion was not employed because in the authors' experience this amount of training is usually sufficient for performances to stabilize in multiple-component concurrent chains. Significance tests used the .05 level.
Results
The dependent variable was preference in the initial links, measured as the log of the initial-link response ratio. Because the initial links were independent and equal concurrent VI VI schedules, the obtained relative entry frequency in the terminal links could deviate from 1:1, depending on the subjects' response allocation. Typically, the relative entry frequency will approximate 1:1 for all but very strong levels of preference, when it will shift in favor of the preferred alternative. Because the relative entry frequency can have an effect on preference independent of the terminal links (e.g., Davison & Temple, 1973; Squires & Fantino, 1971; Williams & Dunn, 1991), the following procedure was used. Prior to analysis, the log of the obtained terminal-link entry ratio was subtracted from the log initial-link response ratio. In effect, this sets the sensitivity parameter aR in Equations 3, 4, and 5 equal to 1. (Note that sensitivity to relative terminal-link entry rate is typically close to 1 for initial-link schedule values in the range of VI 30 s to VI 60 s; Alsop & Davison, 1988). This procedure has been used before (e.g., Grace, 1999) and makes the comparison of preference between the components in the present experiment a more conservative test, because subtracting the entry ratio will serve to attenuate preference to a greater extent in relatively extreme conditions.
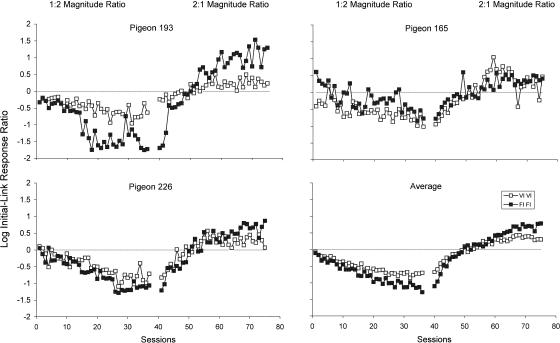
The logarithm of the initial-link response ratios (left/right) for all sessions in both conditions are shown in Figure 1. Data from 3 representative subjects were selected: the pigeon that produced the greatest difference in preference between the VI and FI components (Pigeon 193), the smallest difference (Pigeon 165), and the median difference (Pigeon 226). The log initial-link response ratios averaged across all 12 subjects are shown in the lower-right panel. The data are presented such that for the first condition the 4-s reinforcer was associated with the right terminal link, and for the second condition with the left terminal link.
Fig. 1. Log initial-link response ratios for all sessions in both conditions of Experiment 1. Data are arranged so that negative values in the first condition and positive values in the second condition indicate preference for the terminal link delivering the 4-s reinforcer. Filled symbols indicate data from the FI component; unfilled symbols show data from the VI component. Data are shown for three representative subjects: largest difference between components (Pigeon 193, upper left), smallest difference between components (Pigeon 165, upper right), and median difference between components (Pigeon 226, lower right). The data averaged across all 12 subjects are shown in the lower right panel.
Figure 1 shows that preference developed gradually over the course of each condition, apparently reaching asymptotic levels for the subjects shown between approximately the 20th and 30th sessions. For the average data, preference for the VI component had reached asymptote by about the 25th session in both conditions, but preference might still be changing in the FI component when conditions were terminated. However, it is important to note that systematic increases in preference over the last few sessions were not generally apparent in the individual data.
It is clear from Figure 1 that, on average, preference for the large-magnitude reinforcer was greater in the FI component in both conditions. For both Pigeons 193 and 226 (the subjects with the maximum and median difference between components, respectively), preference was clearly stronger in the FI component in both conditions. Data for Pigeon 165 (smallest difference between components) were more variable, with no clear separation between preference in the FI and VI components.
Table 1 provides asymptotic preference data. Listed are the log initial-link response ratios (corrected for unequal terminal-link entries) for the large magnitude terminal link. Data were summed across the last six sessions of each condition, and then log response ratios were averaged across conditions for each subject. Raw data for all subjects and conditions are listed in Appendix A. For all 12 subjects, preference was greater in the FI component. The difference between components ranged from 0.69 log units (Pigeon 193) to 0.02 log units (Pigeon 165). Averaged across subjects, preference for the large-magnitude terminal link was 0.89 log units for the FI component, and 0.61 log units for the VI component (if the log initial-link response ratios were not corrected for unequal terminal-link entries, the corresponding values would be 1.26 log units for the FI component, and 0.69 log units for the VI component). This is clear evidence that sensitivity of preference to relative magnitude is not independent of the delay distributions comprising the terminal links, but is greater when the terminal links are FI rather than VI schedules.
Table 1. Log initial-link response ratios (corrected for unequal terminal-link entries) for the large magnitude reinforcer for all subjects.
Data were averaged across conditions for each pigeon.
| Component | ||
| Pigeon | VI | FI |
| 191 | 0.43 | 0.85 |
| 192 | 0.67 | 0.73 |
| 193 | 0.48 | 1.17 |
| 194 | 0.89 | 1.24 |
| 225 | 0.68 | 0.73 |
| 226 | 0.51 | 0.85 |
| 227 | 0.44 | 0.82 |
| 228 | 0.16 | 0.48 |
| 165 | 0.47 | 0.49 |
| 166 | 0.95 | 1.06 |
| 167 | 0.72 | 1.01 |
| 168 | 0.90 | 1.24 |
| Average | 0.61 | 0.89 |
| Standard error | 0.07 | 0.08 |
It is important to check that the difference in preference between the components was not confounded by differences in times required to obtain the reinforcers. For example, if terminal-link response rates were greater in the large magnitude terminal links, and the difference in response rates was greater in the FI component, the obtained reinforcer delays could bias preference towards the large magnitude terminal link to a greater extent in the FI component. Thus we computed the obtained reinforcer delays for the terminal links. Data were aggregated over the last six sessions of each condition, and averaged across conditions. Overall, there was no systematic difference in the average reinforcer delays. Averaged across subjects, the delays were: 20.67 s (FI small), 20.61 s (FI large), 20.43 s (VI small), 20.44 s (VI large). The individual data were entered into a repeated-measures analysis of variance (ANOVA) with schedule type and reinforcement magnitude as factors. There were no significant effects or interactions, supporting the conclusion that there were no systematic differences in obtained reinforcer delays across the terminal links.
Discussion
The question addressed by Experiment 1 was whether preference for the larger magnitude reinforcer would depend on whether the terminal-link schedules were VI 20 s VI 20 s or FI 20 s FI 20 s. The results were clear: Although the size of the difference varied considerably across subjects, for all 12 pigeons preference for the 4-s reinforcer was greater with FI terminal links. This is contrary to the prediction of both CCM and the concatenated generalized matching law, and suggests that the independence between delay and magnitude previously reported by Grace et al. (2002) may hold only when the delay distributions are homogeneous across conditions.
Overall, the difference in preference between the FI and VI components was fairly substantial. Averaged across subjects, preference for the larger magnitude reinforcer was 0.89 log units with FI terminal links, compared to 0.61 log units with VI. Because the magnitude ratio was 2:1, this translates into an effective sensitivity to magnitude in CCM (i.e., aM) of 2.96 for FI terminal links and 2.03 for VI terminal links. These sensitivities are higher than the comparable values for VI terminal links from Grace (1995) and Grace et al. (2002), which were 1.52 and 1.71, respectively.
These results provide a parallel with changes in sensitivity to delay (aD) depending on the delay distributions. In the reanalysis of archival data that served as the basis for CCM, Grace (1994) found that estimated aD values averaged 0.90 for VI terminal links (7 studies), compared to 2.68 for FI terminal links (12 studies). Taken together with the present results, the implication is that sensitivities to both delay and magnitude vary with the delay distributions in a similar way.
The difference in preference between the VI and FI components was consistent with the predictions of both Mazur's (2001) HVA model and Killeen's (1985) incentive theory (IT). Both of these models predict greater preference for the larger reinforcer in the FI component because they use methods of aggregating terminal-link delays that give more weight to shorter intervals (i.e., hyperbolic averaging [Equation 6] in HVA, and the harmonic mean in IT). Although the arithmetic mean terminal-link delays are equal across components, they are, according to HVA and IT, effectively longer in the FI compared to the VI terminal links.
An obvious drawback of Experment 1 is that it was limited to a single comparison. Given that sensitivity of response allocation to unequal magnitudes is greater with fixed than with variable equal arithmetic-mean delays, it is important to know how sensitivity varies as a function of the degree of variability. Experiment 2 provides a parametric study of this question.
Experiment 2
In Experiment 2, pigeons again responded in a concurrent-chains procedure with equal terminal-link schedules and unequal reinforcer magnitudes. Reinforcers were delivered independently of responding according to equal mixed-time (MT) or fixed-time (FT) schedules. Across conditions, these schedules were MT 1 s 19 s, MT 4 s 16 s, MT 7 s 13 s, and FT 10 s. Thus the arithmetic mean delay was always constant (10 s) whereas the degree of variability differed across conditions. If preference for the larger reinforcer depends on the degree of variability, then we would expect to find that preference increased monotonically from MT 1 s 19 s to FT 10 s. In addition to providing parametric data on the effect of terminal-link delay distributions, Experiment 2 also tests the generality of the basic result from Experiment 1 by using a different concurrent-chains procedure with (a) interdependent initial-link schedules (Stubbs & Pliskoff, 1969), (b) response-independent terminal-link schedules, (c) a single pair of terminal-link schedules arranged each session, and (d) a changeover delay (COD).
Method
Subjects
Four pigeons from Experiment 1, numbered 165, 166, 167, and 168, served as subjects. They were maintained under identical conditions described above. Training in Experiment 2 commenced several months after the completion of Experiment 1, during which time the pigeons had participated in an unrelated experiment.
Apparatus
The apparatus used was the same as that used in Experiment 1.
Procedure
A concurrent-chains procedure different from Experiment 1 was used. Sessions consisted of 60 initial- and terminal-link cycles, each ending in reinforcement. At the start of a cycle, one side key was lit red and the other was lit green. Either the red or green key was selected pseudorandomly to produce a terminal-link entry. There were four types of cycles: red-left, green-right, red terminal link; red-left, green-right, green terminal link; green-left, red-right, red terminal link; and green-left, red-right, green terminal link. Each cycle type occurred equally often within the session. A single VI 10-s schedule operated during the initial links, but did not begin timing until the first response had been made to either key at the start of a cycle. The initial-link schedule contained 12 intervals constructed from an arithmetic progression, a, a + d, a + 2d, …, where a equals one-twelfth and d equals one-sixth of the schedule value. Intervals were sampled randomly without replacement, and separate lists were maintained for cycles in which terminal links were arranged for the red and green keys. A response produced an entry into a terminal link provided that it was to the preselected key, the initial-link schedule had timed out, and a 1-s COD was satisfied, that is, at least 1 s had elapsed after the first response to the preselected key following a switch from the other alternative.
Terminal-link entry was signaled by the blinking of the preselected key (0.25 s off, 0.25 s on), coupled with extinguishing of the other key. Reinforcers were delivered independently of responding according to FT or MT schedules, which varied across conditions. With an MT x, y schedule, reinforcer delays of x or y seconds were equally likely for a given terminal-link presentaton. During reinforcement, the keylight and houselight were extinguished and the grain magazine was raised and illuminated for a specified duration. After reinforcement, the next initial-link cycle began.
Training continued in a particular condition for at least 20 sessions and until a stability criterion had been met. That criterion required that (a) the highest or lowest choice proportion could not have occurred in the last six sessions, (b) the average choice proportion during the last six sessions was not the highest or lowest six-session average for that condition, and (c) the average choice proportion during the last six sessions did not deviate by more than .05 from the average of the six immediately preceding sessions. Conditions were terminated individually for different pigeons when the above stability criterion was reached.
The terminal-link schedules, reinforcer durations, and sessions of training are listed for all subjects and conditions in Table 2. The schedules were always the same for the red and green terminal links, but varied across conditions from MT 1 s 19 s MT 1 s 19 s to FT 10 s FT 10 s. The reinforcer durations were 4 s and 2 s, and were switched across conditions. Two pigeons (166 and 168) completed the schedules in ascending order (in terms of the shortest reinforcer delay); the other subjects in descending order. The final condition was replicated with reversed reinforcer durations for all subjects except Pigeon 168. Significance tests used the .05 level.
Table 2. Order of conditions and number of sessions of training for each subject in Experiment 2.
| Pigeon | Schedule | Red | Green | Sessions |
| 165 | FT 10 | 4 s | 2 s | 20 |
| MT 7, 13 | 2 s | 4 s | 33 | |
| MT 4, 16 | 4 s | 2 s | 22 | |
| MT 1, 19 | 2 s | 4 s | 34 | |
| MT 1, 19 | 4 s | 2 s | 31 | |
| 166 | MT 1, 19 | 4 s | 2 s | 20 |
| MT 4, 16 | 2 s | 4 s | 28 | |
| MT 7, 13 | 4 s | 2 s | 29 | |
| FT 10 | 2 s | 4 s | 34 | |
| FT 10 | 4 s | 2 s | 31 | |
| 167 | FT 10 | 2 s | 4 s | 34 |
| MT 7, 13 | 4 s | 2 s | 28 | |
| MT 4, 16 | 2 s | 4 s | 35 | |
| MT 1, 19 | 4 s | 2 s | 28 | |
| MT 1, 19 | 2 s | 4 s | 41 | |
| 168 | MT 1, 19 | 2 s | 4 s | 42 |
| MT 4, 16 | 4 s | 2 s | 27 | |
| MT 7, 13 | 2 s | 4 s | 22 | |
| FT 10 | 4 s | 2 s | 64 |
Results
Data were aggregated across the last six sessions of each condition. Initial-link responses were recorded separately for cycles in which the key positions were red-left green-right, and green-left red-right. Thus every condition provided two response ratios (red left/green right; green left/red right). Raw data are listed in Appendix B.
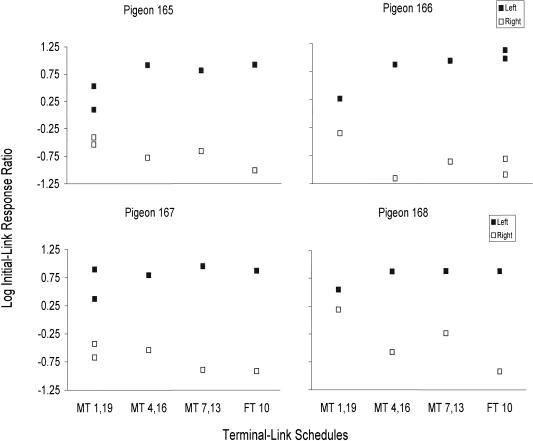
Figure 2 shows the log initial-link response ratios (left/right) for all conditions (including replications) as a function of the shortest reinforcer delay arranged by the terminal-link schedule. With one exception (Pigeon 168, MT 1 s 19 s, large reinforcer on the right), filled data points are greater than zero and unfilled data points are less than zero, indicating preference for the terminal-link associated with the 4-s reinforcer. Across conditions, the data points generally increased in absolute value as the shortest delay increased. For all pigeons, preference for the 4-s reinforcer was more extreme in the MT 7-s 13-s and FT 10-s conditions than the MT 1-s 19-s condition (averaging across replications).
Fig. 2. Log initial-link response ratios for all subjects and conditions in Experiment 2. Data from components in which the large reinforcement magnitude was associated with the left and right terminal link are shown by filled and unfilled squares, respectively.
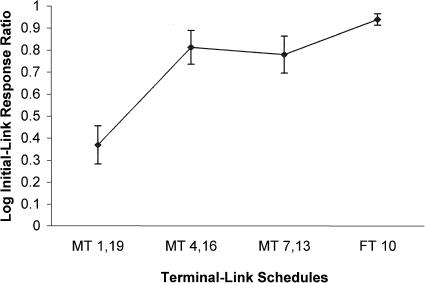
The log initial-link response ratios in Figure 2 were averaged within-subjects across conditions with the same terminal-link schedules, and then across subjects to provide a single measure of preference for each condition. The overall average data are shown in Figure 3. Preference for the 4-s reinforcer increased as the shortest delay increased, although the greatest change appeared to be between the MT 1-s 19-s condition and the other three conditions. Individual data corresponding to Figure 3 were entered into a one-way repeated-measures ANOVA with shortest reinforcer delay as the factor. The main effect of delay was significant, F(1,3) = 14.97, p < .001, as was the linear contrast, F(1,3) = 74.98, p < .01. This result confirms that preference for the 4-s reinforcer increased monotonically with the shortest reinforcer delay.
Fig. 3. Average log initial-link response ratios for all conditions in Experiment 2. Data were averaged within-and across subjects, and are shown as preference for the large magnitude terminal link. Bars indicate one standard error.
To provide a more quantitative assessment of the effect of the terminal-link delays, we conducted a generalized-mean analysis (Killeen, 1968). The generalized mean (Mg) of a distribution of n delays, x1, …, x n is defined as
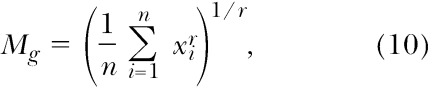 |
where r is a parameter. The arithmetic and harmonic means are given by r values of 1 and −1, respectively; the limit as r approaches zero yields the geometric mean. The analysis was based on a generalized-matching model that assumed the log initial-link response ratio matched relative reinforcer magnitude, with sensitivity proportional to the generalized mean terminal-link delay:
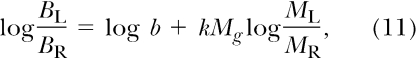 |
where BL, BR are initial-link responses, ML and MR are reinforcer magnitudes, b is bias, k is a parameter that scales the effect of relative reinforcer magnitude (which was constant across conditions), and Mg is defined by Equation 10. In effect, Equation 11 is an extension of Grace's (1994) contextual choice model as applied to the present experiment (i.e., omitting the term for relative terminal-link delay and with initial-link duration constant), in which the arithmetic mean terminal-link delay (Tt in the original model) is replaced by the generalized mean; it is equivalent to CCM if r = 1. The question addressed is what value of r will provide the best prediction of the obtained data.
Equation 11 was fitted to individual and group-mean data in Figure 2 using a nonlinear optimization program. Log response ratios were averaged across replications so that eight data points were fitted for each subject. Best-fitting parameter estimates for b, k, and r and variance accounted for are shown in Table 3. Equation 11 provided an excellent description of the data; variance accounted for was greater than 95% in all cases with the exception of Pigeon 168 (91%). Values of r were small in absolute magnitude (less than 0.40) and, for individual pigeons, unsystematically distributed around zero. The best-fit-ting value of r for the average data was −0.004. This suggests that sensitivity to relative reinforcer magnitude was proportional to the geometric mean of the terminal-link delays. The geometric mean (which is equal to the antilog of the arithmetic mean log delay) weights shorter intervals more heavily than the arithmetic mean, but not to the same degree as the harmonic mean (r = −1). The implication is that generalized-matching sensitivity to relative reinforcer magnitude may increase as a function of the geometric, not arithmetic, mean of the terminal-link delays.
Table 3. Parameter estimates and variance accounted for by the generalized-mean model (Equation 11) applied to the individual and average data from Experiment 2.
| Pigeon | b | k | r | VAC |
| 165 | 0.98 | 0.30 | 0.03 | 0.96 |
| 166 | 0.98 | 0.34 | −0.11 | 0.97 |
| 167 | 1.11 | 0.29 | 0.39 | 0.96 |
| 168 | 1.60 | 0.27 | −0.39 | 0.91 |
| Average | 1.14 | 0.30 | −0.00 | 0.99 |
Discussion
Results of Experiment 2 showed that preference for the larger reinforcer increased as the equal terminal-link schedules were varied from MT 1 s 19 s (maximum variability) to FT 10 s (minimum variability). Because the average terminal-link delay was constant (10 s), CCM and DRT were unable to predict the increase in preference. A generalized-mean analysis showed that allowing sensitivity to magnitude to vary as a function of the geometric mean terminal-link delay provided an excellent account of the data.
This result, however, does not imply that any model not incorporating the geometric mean is unable to account for the data. Both HVA and IT were applied to the average data, and the fits were excellent, accounting for 98% and 99% of the variance, respectively. For IT, the parameter values were b = 1.14, λ = 0.09, and q = 0.07. For HVA, the parameter values were b = 1.14, at = 1.15, and a multiplicative parameter representing the effects of unequal magnitude was 1.55. Thus at least three models based on quite different assumptions (HVA, IT, and Equation 11) can provide an excellent account of the results from Experiment 2; the present data are not sufficient to distinguish among these models.
It is important to note the difference between the generalized-mean analyses reported here and those from previous research on choice. The generalized mean (Equation 10) was first used by Killeen (1968) in an attempt to find a method of averaging reinforcer delays that would account for preference between FI VI and VI VI terminal links. He found that the harmonic mean was a suitable average and was also consistent with results from prior studies (Herrnstein, 1964a, 1964b). However, later researchers found that different values of r were required depending on the terminal-link schedules (e.g., Davison, 1969; Duncan & Fantino, 1970), and the eventual conclusion was that no single value of r was appropriate in all circumstances (see Davison & McCarthy, 1988, for review). All of these studies measured preference for unequal terminal-link schedules with equal reinforcer magnitudes. The present research obtained preference for unequal magnitudes with equal schedules. In terms of the traditional matching-law framework, the former studies were investigating the effects of differences in terminal-link delay, and the present study tested whether the effects of differences in magnitude depend on different distributions of delays.
General Discussion
The goal of this research was to determine whether sensitivity to reinforcer magnitude in concurrent chains was independent of the reinforcer-delay distributions associated with the terminal links. The traditional assumption, based on the matching law, has been that ratios of differing dimensions of reinforcer value, such as rate, immediacy (i.e., reciprocal of delay), and magnitude combine multiplicatively and thus the logarithms of their ratios have additive and independent effects on choice. This assumption is retained in full by the generalized matching law, but has been challenged by consistent findings that preference for a larger versus smaller magnitude reinforcer depends systematically on the absolute duration of the terminal links (e.g., Snyderman, 1983). Grace's (1994) contextual choice model (CCM) is able to account for these interactions, and may be viewed as an attempt to preserve the additivity assumption under restricted cases. Specifically, CCM predicts that effects of delay and magnitude log ratios should be additive so long as the overall average terminal-link duration is kept constant. Prior studies (e.g., Grace, 1995; Grace et al., 2002; see also Rodriguez & Logue, 1986) have provided support for this prediction.
CCM also predicts that the distribution of terminal-link delays should not affect sensitivity to magnitude, provided that the average delays remain constant. Thus the present experiments compared preference for a 4-s versus 2-s magnitude reinforcer when the terminal-link schedules were equal. In Experiment 1, the terminal links were either both VI 20 s or both FI 20 s. For all subjects, preference for the larger reinforcer was stronger with FI terminal links. Experiment 2 varied the degree of variability in terminal-link delays parametrically and found that preference for the larger reinforcer increased as the variability decreased from MT 1 s 19 s to FT 10 s. A generalized-mean analysis showed that sensitivity to magnitude was proportional to the geometric mean of the terminal-link delays.
The present data clearly are at variance with the predictions of CCM, which assumes that sensitivity is proportional to Tt computed as (tL+tR)/2, where t is the arithmetic mean of the terminal-link schedules. However, a suitable revision of that model might be able to account for the results. Computing Tt as the geometric mean accounts for 99% of the variance in the average data from Experiment 2, although it is unclear whether the geometric mean would perform adequately in other situations. Bragason1 has proposed a different modification of CCM, the delay ratio model (DRM). The critical difference between the models is that DRM computes Tt as (VL+VR)/2, where V is the value of the terminal-link schedules, expressed as (3n)/(Σ1/(1 + DIat). The constant 3 is a multiplier of the number (n) of delays (Di) in a distribution; the constant 1 is added to Di to lessen the value of short delays and to avoid the mathematical problem of 0-s delays; and at is a sensitivity parameter of delay. Regardless of the delay distribution, the value of at equals 1 when the preference matches the value of the terminal-link schedules. Applied to terminal links with unequal delays and equal magnitudes, DRM predicts that the preference for the shorter delay is stronger in fixed schedules relative to arithmetic-mean equivalent variable schedules (MacEwen, 1972). DRM predicts this because Tt is larger in fixed schedules. Applied to the present experiment, DRM predicts that the preference for the larger magnitude is stronger in the fixed schedules, again because Tt is larger in fixed schedules. DRM accounts for 99% of the variance in the average data from Experiment 2, with the best-fitting parameter values: b = 1.14, at = .82, and am = 1.33 (setting at = 1, the parameter values are b = 1.14 and am = 0.96, with 98% of the variance accounted for). It should be noted that these parameter values and variance accounted for are based on the assumption that the ratio of the magnitudes concatenates with the other ratio terms in DRM. If, instead, a magnitude term with a corresponding sensitivity parameter replaced the constant 3 in the Equation for V above, DRM accounts for 99% of the variance, with the best-fitting parameter values: b = 1.14, at = .82, aM = 1.14 (setting at = 1, the parameter values are b = 1.14 and aM = 0.98, with 98% of the variance accounted for). Although the different placement of the magnitude term leads to essentially the same results, there are other experimental situations where the placement makes a difference.
Two other models, which do not assume independence of reinforcer delay and magnitude, also were able to describe the data. Mazur's (2001) hyperbolic value-added (HVA) and Killeen's (1985) incentive theory (IT) accounted for 98% and 99% of the variance in the average data, respectively. The present results demonstrate that preference for the larger reinforcer varies inversely with the degree of variability in terminal-link delays, but cannot distinguish between these models.
Thus the fundamental question addressed here is the nature of the combination rule for reinforcement delay and magnitude. The simplest possible rule embodied by the matching law in its original as well as generalized forms—multiplicative combination of ratios, implying strict additivity and independence in log terms, and control by relative, not absolute values—clearly fails empirically. The issue, then, is to determine the simplest set of assumptions that are empirically valid. CCM may be viewed as an attempt to preserve the matching law assumptions under certain restrictions. HVA retains the multiplicative combination rule, but asserts that effects of delay and magnitude log ratios are nonadditive in principle. IT abandons both the multiplicative rule as well as additivity. Although the present data consititute yet another violation of a prediction based on the generalized matching law, it remains to be seen whether the assumptions of additivity and independence can be sustained, perhaps through a suitable modification of CCM, or whether a model based on nonadditive effects of delay and magnitude log ratios is necessary.
APPENDIX A
Raw data from Experiment 1
Shown are the initial-link response (RespL, RespR) and terminal-link entry (EntryL, EntryR) totals for all subjects and conditions. Data were summed across the last six sessions of each condition. Data are shown separately for the VI and FI components.
| VI component | FI component | ||||||||
| Pigeon | Magnitude ratio | RespL | RespR | EntryL | EntryR | RespL | RespR | EntryL | EntryR |
| 191 | 2 to 1 | 5,863 | 1,799 | 120 | 96 | 5,396 | 843 | 120 | 94 |
| 1 to 2 | 1,788 | 5,429 | 103 | 113 | 637 | 7,830 | 96 | 120 | |
| 192 | 2 to 1 | 6,184 | 304 | 133 | 83 | 6,289 | 159 | 163 | 53 |
| 1 to 2 | 1,656 | 3,012 | 105 | 111 | 1,015 | 2,431 | 104 | 112 | |
| 193 | 2 to 1 | 3,998 | 2,152 | 109 | 107 | 6,153 | 283 | 148 | 68 |
| 1 to 2 | 980 | 5,003 | 107 | 109 | 70 | 9,025 | 31 | 185 | |
| 194 | 2 to 1 | 5,819 | 499 | 122 | 94 | 8,141 | 326 | 128 | 88 |
| 1 to 2 | 525 | 6,473 | 77 | 139 | 184 | 9,034 | 57 | 158 | |
| 225 | 2 to 1 | 5,797 | 3,601 | 111 | 105 | 5,098 | 1,953 | 109 | 107 |
| 1 to 2 | 533 | 13,063 | 81 | 135 | 638 | 10,613 | 88 | 128 | |
| 226 | 2 to 1 | 5,641 | 875 | 113 | 103 | 6,972 | 312 | 143 | 73 |
| 1 to 2 | 1,867 | 3,633 | 103 | 113 | 969 | 4,569 | 103 | 113 | |
| 227 | 2 to 1 | 4,808 | 1,352 | 111 | 105 | 5,104 | 1,361 | 113 | 103 |
| 1 to 2 | 1,658 | 3,890 | 107 | 109 | 228 | 6,670 | 66 | 150 | |
| 228 | 2 to 1 | 1,942 | 660 | 114 | 101 | 1,912 | 333 | 128 | 81 |
| 1 to 2 | 1,707 | 1,192 | 116 | 100 | 541 | 1,736 | 94 | 118 | |
| 165 | 2 to 1 | 2,301 | 1,531 | 81 | 72 | 1,178 | 435 | 100 | 85 |
| 1 to 2 | 1,291 | 8,631 | 106 | 110 | 1,067 | 5,946 | 91 | 123 | |
| 166 | 2 to 1 | 5,743 | 711 | 124 | 86 | 7,742 | 14 | 204 | 9 |
| 1 to 2 | 293 | 7,787 | 75 | 141 | 544 | 5,176 | 79 | 137 | |
| 167 | 2 to 1 | 4,851 | 961 | 118 | 97 | 7,706 | 152 | 162 | 47 |
| 1 to 2 | 775 | 6,793 | 89 | 115 | 13 | 8,997 | 2 | 195 | |
| 168 | 2 to 1 | 4,926 | 358 | 128 | 85 | 7,405 | 90 | 173 | 43 |
| 1 to 2 | 781 | 5,731 | 104 | 112 | 203 | 6,457 | 69 | 147 | |
APPENDIX B
Raw data from Experiment 2
Shown are the initial-link response totals for all subjects and conditions. Data were summed across the last six sessions of each condition. Data are shown separately for components in which the red initial and terminal links were on the left key and the green initial and terminal links were on the right key, and for components in which the red/green assignment was reversed.
| Pigeon | Condition | Magnitudes | Red left | Red right | Green left | Green right |
| 165 | MT 1, 19 | Red 2s; Green 4s | 1714 | 2800 | 3519 | 4390 |
| MT 4, 16 | Red 4s; Green 2s | 6028 | 5614 | 938 | 736 | |
| MT 7, 13 | Red 2s; Green 4s; | 986 | 881 | 5801 | 4469 | |
| FT 10 | Red 4s; Green 2s; | 6446 | 9457 | 934 | 770 | |
| MT 1, 19 | Red 4s; Green 2s | 6063 | 4740 | 1377 | 1788 | |
| 166 | MT 1, 19 | Red 4s; Green 2s; | 3654 | 4804 | 2119 | 1984 |
| MT 4, 16 | Red 2s; Green 4s; | 644 | 867 | 6438 | 9165 | |
| MT 7, 13 | Red 4s; Green 2s; | 8148 | 6430 | 894 | 940 | |
| FT 10 | Red 2s; Green 4s; | 1145 | 629 | 8427 | 731 | |
| FT 10 | Red 4s; Green 2s; | 8898 | 7557 | 622 | 934 | |
| 167 | MT 1, 19 | Red 4s; Green 2s | 3026 | 2906 | 619 | 384 |
| MT 4, 16 | Red 2s; Green 4s | 870 | 479 | 2984 | 3015 | |
| MT 7, 13 | Red 4s; Green 2s | 4093 | 4074 | 521 | 456 | |
| FT 10 | Red 2s; Green 4s | 371 | 479 | 3577 | 3045 | |
| MT 1, 19 | Red 2s; Green 4s | 1001 | 863 | 2035 | 2698 | |
| 168 | MT 1, 19 | Red 2s; Green 4s | 2551 | 1151 | 4062 | 1649 |
| MT 4, 16 | Red 4s; Green 2s | 4712 | 4861 | 1292 | 632 | |
| MT 7, 13 | Red 2s; Green 4s | 1771 | 549 | 4168 | 3053 | |
| FT 10 | Red 4s; Green 2s | 5361 | 5484 | 658 | 712 |
Footnotes
Bragason, O. (2000). Is choice determined by the arithmetic or harmonic mean of delayed reward? Poster presented at a symposium of the Japanese Society for Animal Psychology, Tokyo, Japan.
REFERENCES
- Alsop B. Davison M. Concurrent-chain performance: Effects of absolute and relative terminal-link entry frequency. Journal of the Experimental Analysis of Behavior. 1988;49:351–365. doi: 10.1901/jeab.1988.49-351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baum W. M. On two types of deviation from the matching law: Bias and undermatching. Journal of the Experimental Analysis of Behavior. 1974;22:231–242. doi: 10.1901/jeab.1974.22-231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baum W. M. Rachlin H. C. Choice as time allocation. Journal of the Experimental Analysis of Behavior. 1969;12:861–874. doi: 10.1901/jeab.1969.12-861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison M. C. Preference for mixed-interval versus fixed-interval schedules. Journal of the Experimental Analysis of Behavior. 1969;12:247–252. doi: 10.1901/jeab.1969.12-247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison M. Concurrent schedules: Interactions of reinforcer frequency and reinforcer duration. Journal of the Experimental Analysis of Behavior. 1988;49:339–349. doi: 10.1901/jeab.1988.49-339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison M. McCarthy D. The matching law: A research review. Hillsdale, NJ: Erlbaum; 1988. [Google Scholar]
- Davison M. C. Temple W. Preference for fixed-interval schedules: An alternative model. Journal of the Experimental Analysis of Behavior. 1973;20:393–403. doi: 10.1901/jeab.1973.20-393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duncan B. Fantino E. Choice for periodic schedules of reinforcement. Journal of the Experimental Analysis of Behavior. 1970;14:73–86. doi: 10.1901/jeab.1970.14-73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fantino E. Choice and rate of reinforcement. Journal of the Experimental Analysis of Behavior. 1969;12:723–730. doi: 10.1901/jeab.1969.12-723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fantino E. Preston R. A. Dunn R. Delay reduction: Current status. Journal of the Experimental Analysis of Behavior. 1993;60:159–169. doi: 10.1901/jeab.1993.60-159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleshler M. Hoffman H. S. A progression for generating variable-interval schedules. Journal of the Experimental Analysis of Behavior. 1962;5:529–530. doi: 10.1901/jeab.1962.5-529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grace R. C. A contextual model of concurrent-chains choice. Journal of the Experimental Analysis of Behavior. 1994;61:113–129. doi: 10.1901/jeab.1994.61-113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grace R. C. Independence of delay and magnitude of reinforcement in concurrent chains. Journal of the Experimental Analysis of Behavior. 1995;63:255–276. doi: 10.1901/jeab.1995.63-255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grace R. C. The matching law and amount-dependent exponential discounting as accounts of self-control choice. Journal of the Experimental Analysis of Behavior. 1999;71:27–44. doi: 10.1901/jeab.1999.71-27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grace R. C. Bedell M. A. Nevin J. A. Preference and resistance to change with constant- and variable-duration terminal links: Effects of reinforcement rate and magnitude. Journal of the Experimental Analysis of Behavior. 2002;77:233–255. doi: 10.1901/jeab.2002.77-233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grace R. C. Bragason O. Does the terminal-link effect depend on duration or reinforcement rate? Behavioural Processes. 2004;67:67–79. doi: 10.1016/j.beproc.2004.02.006. [DOI] [PubMed] [Google Scholar]
- Green L. Snyderman M. Choice between rewards differing in amount and delay: Toward a choice model of self control. Journal of the Experimental Analysis of Behavior. 1980;34:135–147. doi: 10.1901/jeab.1980.34-135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrnstein R. J. Secondary reinforcement and rate of primary reinforcement. Journal of the Experimental Analysis of Behavior. 1964a;7:27–36. doi: 10.1901/jeab.1964.7-27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrnstein R. J. Aperiodicity as a factor in choice. Journal of the Experimental Analysis of Behavior. 1964b;7:179–182. doi: 10.1901/jeab.1964.7-179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito M. Asaki K. Choice behavior of rats in a concurrent-chains schedule: Amount and delay of reinforcement. Journal of the Experimental Analysis of Behavior. 1982;37:383–392. doi: 10.1901/jeab.1982.37-383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller J. V. Gollub L. R. Duration and rate of reinforcement as determinants of concurrent responding. Journal of the Experimental Analysis of Behavior. 1977;28:145–153. doi: 10.1901/jeab.1977.28-145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Killeen P. On the measurement of reinforcement frequency in the study of preference. Journal of the Experimental Analysis of Behavior. 1968;11:263–269. doi: 10.1901/jeab.1968.11-263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Killeen P. The matching law. Journal of the Experimental Analysis of Behavior. 1972;17:489–495. doi: 10.1901/jeab.1972.17-489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Killeen P. Incentive theory: II. Models for choice. Journal of the Experimental Analysis of Behavior. 1982;38:217–232. doi: 10.1901/jeab.1982.38-217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Killeen P. R. Incentive theory: IV. Magnitude of reward. Journal of the Experimental Analysis of Behavior. 1985;43:407–417. doi: 10.1901/jeab.1985.43-407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirby K. N. Marakovic N. N. Delay-discounting probabilistic rewards: Rates decrease as amounts increase. Psychonomic Bulletin & Review. 1996;3:100–104. doi: 10.3758/BF03210748. [DOI] [PubMed] [Google Scholar]
- Leon M. I. Gallistel C. R. Self-stimulating rats combine subjective reward magnitude and subjective reward rate multiplicatively. Journal of Experimental Psychology: Animal Behavior Processes. 1998;24:265–277. doi: 10.1037//0097-7403.24.3.265. [DOI] [PubMed] [Google Scholar]
- Logue A. W. Rodriguez M. L. Peña-Correal T. E. Mauro B. C. Choice in a self-control paradigm: Quantification of experience-based differences. Journal of the Experimental Analysis of Behavior. 1984;41:53–67. doi: 10.1901/jeab.1984.41-53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacEwen D. The effects of terminal-link fixed-interval and variable-interval schedules on responding under concurrent chained schedules. Journal of the Experimental Analysis of Behavior. 1972;18:253–261. doi: 10.1901/jeab.1972.18-253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazur J. E. Tests for an equivalence rule for fixed and variable reinforcer delays. Journal of Experimental Psychology: Animal Behavior Processes. 1984;10:426–436. [PubMed] [Google Scholar]
- Mazur J. E. Hyperbolic value addition and general models of choice. Psychological Review. 2001;108:96–112. doi: 10.1037/0033-295x.108.1.96. [DOI] [PubMed] [Google Scholar]
- McLean A. P. Blampied N. M. Sensitivity to relative reinforcer rate in concurrent schedules: Independence from relative and absolute reinforcer duration. Journal of the Experimental Analysis of Behavior. 2001;75:25–42. doi: 10.1901/jeab.2001.75-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuringer A. J. Effects of reinforcement magnitude on choice and rate of responding. Journal of the Experimental Analysis of Behavior. 1967;10:417–424. doi: 10.1901/jeab.1967.10-417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rachlin H. Green L. Commitment, choice, and self-control. Journal of the Experimental Analysis of Behavior. 1972;17:15–22. doi: 10.1901/jeab.1972.17-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rachlin H. Self-control: Beyond commitment. Behavioral & Brain Sciences. 1995;18:109–159. (includes commentary) [Google Scholar]
- Rodriguez M. L. Logue A. W. Independence of the amount and delay ratios in the generalized matching law. Animal Learning & Behavior. 1986;14:29–37. [Google Scholar]
- Snyderman M. Delay and amount of reward in a concurrent chain. Journal of the Experimental Analysis of Behavior. 1983;39:437–447. doi: 10.1901/jeab.1983.39-437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Squires N. Fantino E. A model for choice in simple concurrent and concurrent-chains schedules. Journal of the Experimental Analysis of Behavior. 1971;15:27–38. doi: 10.1901/jeab.1971.15-27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stubbs D. A. Pliskoff S. S. Concurrent responding with fixed relative rate of reinforcement. Journal of the Experimental Analysis of Behavior. 1969;12:887–895. doi: 10.1901/jeab.1969.12-887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todorov J. C. Interaction of frequency and magnitude of reinforcement on concurrent performances. Journal of the Experimental Analysis of Behavior. 1973;19:451–458. doi: 10.1901/jeab.1973.19-451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White K. G. Pipe M. E. Sensitivity to reinforcer duration in a self-control procedure. Journal of the Experimental Analysis of Behavior. 1987;48:235–249. doi: 10.1901/jeab.1987.48-235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams B. A. Dunn R. Preference for conditioned reinforcement. Journal of the Experimental Analysis of Behavior. 1991;55:37–46. doi: 10.1901/jeab.1991.55-37. [DOI] [PMC free article] [PubMed] [Google Scholar]