Unsignaled Delay Of Reinforcement, Relative Time, And Resistance To Change

Abstract

Two experiments with pigeons examined the effects of unsignaled, nonresetting delays of reinforcement on responding maintained by different reinforcement rates. In Experiment 1, 3-s unsignaled delays were introduced into each component of a multiple variable-interval (VI) 15-s VI 90-s VI 540-s schedule. When considered as a proportion of the preceding immediate reinforcement baseline, responding was decreased similarly for the three multiple-schedule components in both the first six and last six sessions of exposure to the delay. In addition, the relation between response rates and reinforcement rates was altered such that both parameters of the single-response version of the matching law (i.e., k and R_e) were decreased. Experiment 2 examined the effects of unsignaled delays ranging from 0.5 s to 8.0 s on responding maintained by a multiple VI 20-s VI 120-s schedule of reinforcement. Response rates in both components increased with brief unsignaled delays and decreased with longer delays. As in Experiment 1, response rates as a proportion of baseline were affected similarly for the two components in both the first six and last six sessions of exposure to the delay. Unlike delays imposed between two stimulus events, the effects of delays between responses and reinforcers do not appear to be attenuated when the average time between reinforcers is longer. In addition, the disruptions produced by unsignaled delays appear to be inconsistent with the general finding that responding maintained by higher rates of reinforcement is less resistant to change.

In a variety of classical and operant conditioning preparations, the disruptive effects of delays between environmental stimuli are reduced when the overall time between reinforcers is longer. Williams (1998) referred to this modulation of delay effects by interreinforcement intervals (IRIs) as reflecting the “relative time principle” (see also Balsam, 1984). As an example of relative time effects, autoshaped key pecking of pigeons is a positive function of the ratio of the time between unconditional stimulus (US) deliveries and the time between conditional stimulus (CS) onset and US delivery (i.e., the cycle/trial ratio; see Balsam, 1984; Gibbon & Balsam, 1981 for reviews). Similar effects have been noted in delayed-matching-to-sample (DMTS) procedures in which accuracy is disrupted more by increasing retention intervals when the time between trials is shorter (Grant, 1975; Maki, Moe, & Bierly, 1977; Roberts & Kraemer, 1982; Wilkie, 1984). Additionally, preference in concurrent-chains procedures is determined by the immediacy of a reinforcer following transition to the terminal link relative to the average time between reinforcers (e.g., Fantino, 1977; Squires & Fantino, 1971). Finally, briefly signaled delays of reinforcement reduce behavior maintained by variable-interval (VI) schedules less when the average IRI of the VI schedule is longer (e.g., Schaal, Odum, & Shahan, 2000; Schaal, Schuh, & Branch, 1992).

In the situations described above in which relative time effects occur, a delay is interposed in the relation between two stimuli (i.e., between sample and comparison stimuli, CS and US, or conditioned and primary reinforcer). Based on the results of a series of experiments using a conditional discrimination procedure, Williams (1998) concluded that relative time effects do not occur with delays between responses and contingent reinforcers. In these experiments, the effects of average IRI on rats' acquisition of a conditional discrimination were examined when delays were imposed between sample presentations and choice responses (i.e., retention interval) or between choice responses and reinforcement presentations (i.e., reinforcement delay). The effects of retention interval duration were attenuated with longer IRIs, but the effects of reinforcement delay were not impacted by IRI duration.

The results of the Williams (1998) experiments, however, are difficult to interpret solely in terms of the relation between responses and reinforcers. Lever presses during 4-s sample presentations had no effect, but the first choice response after the 4-s sample presentation resulted in retraction of the lever and started the delay. Thus the response that initiated the delay was associated with a change in stimulus conditions differentially associated with impending reinforcement delivery. The role of these differential stimulus conditions is unclear given that Williams failed to replicate the attenuation of delay of reinforcement effects by longer IRIs obtained by Schaal et al. (1992) in their examination of briefly signaled delays of reinforcement. The difference in results obtained in the two experiments may be due to the fact that Williams examined rats' acquisition of a conditional discrimination whereas Schaal et al. examined steady-state responding of pigeons on VI schedules. Regardless of the sources of the difference in results, neither experiment permits evaluation of relative time effects with delays between operant responses and reinforcers in the absence of stimuli predictive of reinforcement delivery.

The potential modulation of the effects of delays between responses and reinforcers by IRI duration may be examined using unsignaled delays of reinforcement. Unsignaled, nonresetting delays of reinforcement are programmed such that the response that meets a reinforcement schedule requirement starts a delay that is timed independently of further responding during the delay and with no change in stimulus conditions (e.g., Sizemore & Lattal, 1977, 1978; Williams, 1976). Unsignaled delays as short as 1 s decrease steady-state response rates maintained by VI schedules (Catania & Keller, 1981; Sizemore & Lattal, 1978; see Schneider, 1990, for review). In most experiments on the effects of unsignaled delays of reinforcement, only a single IRI has been examined.

Two experiments have examined the potential interaction between the effects of unsignaled, delayed reinforcement and reinforcement rate. Bruner, Avila, Acuna, & Gallardo (1998) compared acquisition of lever pressing of groups of rats when reinforcement occurred either immediately at the completion of different random-interval (RI) schedule requirements or following a 12-s unsignaled, nonresetting delay. Across 20 acquisition sessions, response rates for all groups were low, especially for groups with longer RI schedules. The 12-s delay also reduced acquisition, but this reduction did not interact with the RI schedule in effect. Thus these findings are consistent with Williams' (1998) suggestion that relative time effects do not occur when delays occur between responses and reinforcers.

In their experiment on the effects of briefly signaled delays to reinforcement, Schaal et al. (1992) also examined the effects of a 5-s unsignaled, nonresetting delay of reinforcement on steady-state response rates of pigeons responding on a multiple VI 20-s VI 120-s schedule. Schaal et al. reported that response rates were considerably lower in both components with the 5-s delay than during baseline conditions with immediate reinforcement. Further examination of the Schaal et al. data reveals that when response rates in the delay condition are considered as a proportion of the immediate reinforcement baseline, response rates were decreased less in the VI 20-s than in the VI 120-s component for 3 of 4 pigeons. These results suggest that the effects of unsignaled delays of reinforcement may depend on average IRI, but in the opposite direction predicted by the relative time principle. Thus the findings of Schaal et al. are consistent with studies of behavioral momentum showing that steady-state response rates are more resistant to disruption in components of multiple schedules providing higher rates of reinforcement (e.g., see Nevin, 1992; Nevin & Grace, 2000, for reviews).

Given the limited and discrepant data on the effects of unsignaled delays of reinforcement on responding maintained with different IRIs, the present experiments further examined such effects. Experiment 1 examined the effects of a 3-s unsignaled delay of reinforcement on responding maintained by a wider range of VI schedules than was examined by Schaal et al. (1992). Although the data of Schaal et al. are consistent with the effects of various types of disrupters of operant behavior, they presented only steady-state response rates for the unsignaled delay condition and did not report obtained delay durations. For the sake of consistency with the majority of previous research on the resistance to change of operant behavior (but see Harper & McLean, 1992), we also examined response rates as a proportion of the immediate-reinforcement baseline in the sessions immediately after an unsignaled delay was introduced. Finally, this experiment provided a preliminary assessment of the effects of unsignaled delayed reinforcement on the relation between response rates and reinforcement rates (Catania & Reynolds, 1968; Herrnstein, 1970).

Experiment 1

Method

Subjects

Three retired breeder male White Carneau pigeons were maintained at 80% of free-feeding weight. Pigeons were individually housed in a temperature-controlled colony under a 12:12 hr light/dark cycle and had free access to water and grit. Each had a history of responding on several schedules of reinforcement.

Apparatus

An operant conditioning chamber with internal dimensions of 33 cm across by 30 cm deep by 30 cm high was used. General illumination was provided by two 2.8-W bulbs located behind a 10-cm diameter aperture covered by translucent plastic and located 3 cm above the floor and 9 cm to the right of the midline. A 2-cm diameter response key was mounted on the midline of the work panel 25 cm from the floor. The key required a force of approximately 0.10 N to operate and could be lit from behind with green, red, or white light. A grain hopper was accessible, when raised, through a 4.5 cm by 6 cm aperture located on the midline of the work panel with its center 9.5 cm from the floor. The aperture was illuminated and all other lights were extinguished when the hopper was operated. Reinforcement consisted of 3-s presentations of mixed grain for Pigeons 3742 and 4840 and 2-s presentations of grain for Pigeon 4819. Ventilation was provided through a 5-cm diameter hole in the rear of the chamber, and white noise masked extraneous sounds. Control of experimental events and data recording were conducted with Med-Associates® programming and interfacing.

Procedure

Each pigeon initially was trained to key peck on VI 15-s schedules in the presence of green, red, and white keylights that alternated every 5 min. Mean interreinforcer intervals were increased gradually in the presence of the red and white keylights until the pigeons responded reliably on a multiple VI 15-s (green) VI 90-s (red) VI 540-s (white) schedule (Pigeons 4840 and 3742) or a multiple VI 15-s (green) VI 90-s (red) VI 360-s (white) schedule (Pigeon 4819). The procedure differed for Pigeon 4819 because response rates were not well maintained with the VI 540-s schedule for this pigeon. In the multiple schedule, the three VI schedule components were presented four times each during the session. Components were 5 min long, presented in a random order, and could not end during a reinforcer delivery. There was no intercomponent interval. All VI schedules consisted of 20 intervals (selected without replacement) and were constructed according to the constant probability distribution described by Fleshler and Hoffman (1962).

When baseline response rates were stable (see below), an unsignaled, nonresetting delay between the response that fulfilled the VI schedule requirement and reinforcer delivery was introduced simultaneously into all three multiple-schedule components. Delays were programmed as tandem VI x-s fixed-time (FT) 3-s schedules, where x is the IRI of the VI schedule in baseline minus 3 s. For example, the VI 15-s schedule component was changed to a tandem VI 12-s FT 3-s schedule in the delay condition. The first response after the VI had elapsed started the FT 3-s schedule (hereafter, unsignaled delay) at the end of which food was presented independently of further responding during the FT schedule. No exteroceptive stimulus changes accompanied the delay. Component changes of the multiple schedule did not occur during the timing of the unsignaled delay. If a component was scheduled to end during a delay, the component change was postponed until after the delay ended and food was delivered.

For each subject, the immediate reinforcement baseline condition was followed by the unsignaled delay condition, which in turn was followed by a return to the baseline condition. Response rates were considered stable when, over a 6-day period, the first 3-day and second 3-day means did not differ by more than 6% from the 6-day mean. Due to low response rates, stability in the unsignaled delay condition was judged visually (see Perone, 1991). The number of sessions in the initial baseline condition, the unsignaled delay condition, and the return to baseline, respectively, were 45, 84, and 30 for Pigeon 4840; 22, 64, and 28 for Pigeon 3742; and 65, 70, and 46 for Pigeon 4819. Sessions typically were conducted 6 days per week at approximately the same time each day.

Response rates and reinforcement rates were recorded for each pigeon in each of the three components. During the unsignaled delay condition, response rates were calculated from time and response measures during the VI portion of the tandem VI FT schedules. With unsignaled, nonresetting delays of reinforcement, responses may occur during the delay interval. Thus the time between the last response during the delay and reinforcement delivery (i.e., obtained delay) can be shorter than the programmed delay. Accordingly, mean obtained delays also were recorded for each subject in each component.

Results

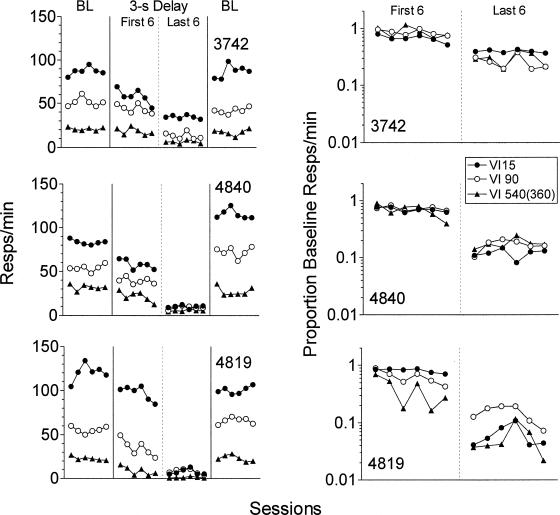
The left panels of Figure 1 show absolute response rates in each component during the last six sessions of the initial baseline condition, the first six sessions after the 3-s unsignaled delay was introduced, the last six sessions of exposure to the unsignaled delay, and the last six sessions of exposure to the return to the baseline condition. For each pigeon, response rates in both exposures to the immediate reinforcement baseline condition were higher in components providing higher reinforcement rates. With the introduction of the unsignaled delay, response rates started to decrease within the first six sessions in each component. Response rates in the last six sessions of exposure to the unsignaled delay were generally quite low, and were lowest in the component with the lowest reinforcement rate (i.e., the VI 540-s or VI 360-s). The right panel of Figure 1 shows response rates in the first six and last six sessions of exposure to the unsignaled delay presented as a proportion of mean response rates in the last six sessions of the preceding immediate reinforcement baseline. Across pigeons, response rates as a proportion of baseline did not vary systematically for responding maintained by different reinforcement rates in either the first six or last six sessions of exposure to the unsignaled delay.

Figure 1. The left panels show response rates for each component in the last six sessions of exposure to the two immediate reinforcement baseline (BL) conditions and the first six and last six sessions of exposure to the 3-s delay condition.

The right panels show response rates in the first six and last six sessions of the 3-s delay condition as a proportion of the preceding immediate reinforcement baseline.

The y axis in the right panels is logarithmic.

Table 1 shows mean obtained delays for each component in the first six and the last six sessions of exposure to the unsignaled delay condition. Mean obtained delays in the first six sessions of exposure to the delay condition tended to be longer for components providing lower reinforcement rates and associated with lower response rates. The only exception was for Pigeon 4840 in the VI 540 component. In the last six sessions of exposure to the unsignaled delay condition, mean obtained delays also were somewhat longer in components with lower reinforcement rates, but this difference across components was small. In addition, with the exception of Pigeon 3742 in the VI 540 component, obtained delays were longer in the last six than in the first six sessions of exposure to the delay condition.

Table 1. Mean obtained delays (s) for each component in the first six and last six sessions of exposure to the unsignaled delay condition. Numbers in parentheses are standard deviations.

Subject	Obtained delay (s)
	First six sessions			Last six sessions
	VI 15	VI 90	VI 540/360	VI 15	VI 90	VI 540/360
3742	0.65	1.19	2.30	0.75	2.08	2.29
	(0.16)	(0.37)	(0.61)	(0.10)	(0.52)	(1.12)
4840	0.56	1.44	1.27	2.42	2.57	2.58
	(0.14)	(0.40)	(0.80)	(0.22)	(0.19)	(0.59)
4819	0.61	1.64	2.25	2.56	2.78	2.92
	(0.14)	(0.41)	(0.54)	(0.16)	(0.17)	(0.10)

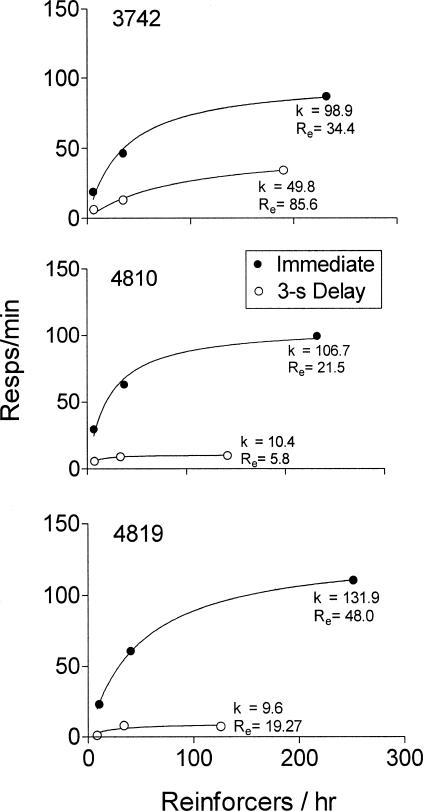
Figure 2 shows response rates as a function of obtained reinforcement rates in conditions with immediate reinforcement and with the 3-s unsignaled delay of reinforcement. Response rates and reinforcement rates typically were similar in the two exposures to the immediate reinforcement baseline and, thus, were combined. With immediate reinforcement, response rates increased with reinforcement rates in a manner consistent with previous findings (e.g., Catania & Reynolds, 1968; see de Villiers, 1977; Herrnstein, 1970, for reviews). In the unsignaled delay condition, response rates also increased with increases in reinforcement rates, but were considerably lower than with responding maintained by immediate reinforcement. The addition of the 3-s unsignaled delay decreased reinforcement rates, especially for the VI 15 component. The decreases in response rates produced by the unsignaled delay, however, were much larger than would be expected based on the decrease in reinforcement rate alone.

Figure 2. Response rates as a function of obtained reinforcement rates in the immediate reinforcement baseline conditions and in the 3-s delay condition. Data were averaged for the two exposures to the immediate reinforcement baseline conditions.

Curves represent least squares fits of Equation 1 to the data.

The fitted functions in Figure 2 represent Herrnstein's (1970) single-response version of the matching law:

where B represents response rate and R represents reinforcement rate. The parameters R_e and k represent extraneous sources of reinforcement and asymptotic response rates, respectively. The function accounted for greater than 97% of the variance in all of the fits with the exception of the fit for Pigeon 4819 in the unsignaled delay condition (i.e., 74%). The goodness of fit is not surprising given the number of data points relative to the number of free parameters. Nonetheless, this analysis provides a preliminary examination of the effects of an unsignaled delay of reinforcement on the parameters of Equation 1. The unsignaled delay of reinforcement produced large decreases in k for each of the pigeons. For Pigeons 4810 and 4819, R_e decreased, but R_e increased for Pigeon 3742.

Discussion

Consistent with previous research, a 3-s unsignaled delay of reinforcement decreased response rates maintained by VI schedules of reinforcement (e.g., Sizemore & Lattal, 1977, 1978; Williams, 1976). When considered as a proportion of response rates in the immediate reinforcement baseline, responding in the first six and the last six sessions of the delay condition was not systematically related to the average IRI. In addition, the unsignaled delay produced dramatic changes in the relation between response rates and reinforcement rates (Figure 2).

The finding that the effects of an unsignaled delay of reinforcement did not depend on the IRI is consistent with Williams' (1998) suggestion that relative time effects do not occur with delays between responses and reinforcers. In addition, both the steady-state and transition data are inconsistent with the steady-state data of Schaal et al. (1992) showing that a 5-s unsignaled delay produced smaller proportional decreases in responding maintained by higher reinforcement rates. Nonetheless, the present experiment differed from Schaal et al. in a potentially important way. In the present procedure, the components remained in effect for a fixed amount of time (i.e., 5 min). In Schaal et al., the components changed after eight reinforcers had been delivered. Consequently, in the present experiment the pigeons were exposed to a larger number of delayed reinforcers in components with higher reinforcement rates. Across the sessions of the unsignaled delay condition, the pigeons experienced an average of 50.7, 11.5, and 2.5 delayed reinforcers per session in the VI 15, VI 90, and VI 540 (VI 360 for Pigeon 4819) components, respectively. Thus responding in the higher reinforcement rate components may have been disproportionately disrupted by this differential exposure to delayed reinforcers. This difference in exposure to the delayed reinforcer may be the source of the difference in results between the present experiment and the experiment of Schaal et al.

To address this issue, Experiment 2 examined the effects of a range of unsignaled delays of reinforcement using a procedure similar to that of Schaal et al. (1992). A multiple VI 20-s VI 120-s schedule was arranged in which components alternated after eight reinforcers. Examination of a range of unsignaled delays at two different IRIs permitted an analysis of the effects of changes in the IRI/delay ratio produced by changes in both terms of the ratio. In addition, previous experiments have suggested that unsignaled delays of reinforcement may produce changes in the functional response unit, as evidenced by changes in interresponse-time (IRT) distributions (e.g., Arbuckle & Lattal, 1988; cf. Schaal, Shahan, Kovera, & Reilly, 1998). Such changes in IRT distributions may be related to the changes in k obtained with a 3-s unsignaled delay in Experiment 1, given that changes in k may be interpreted to reflect changes in response topography. Thus Experiment 2 also examined IRT distributions for both VI schedules at each delay duration.

Experiment 2

Method

Subjects

Four White Carneau pigeons of undetermined sex were maintained at 80% of free-feeding weight. When not in experimental sessions, the pigeons were housed in individual cages in a temperature-controlled colony with a 12:12 hr light/dark cycle (lights on at 6:00 a.m.), and had free access to digestive grit and water in their home cages. Each pigeon had a history of responding on several schedules of reinforcement.

Apparatus

Four BRS/LVE operant-conditioning chambers were used. Chambers were constructed of painted metal with aluminum front panels and measured 35 cm across, 31 cm deep, and 36 cm high. Each front panel had three translucent plastic keys that could be lit from behind with green or red light and that required a force of about 0.10 N to record a response. Only the center of the three keys was used, and it was located in the midline of the work panel. The key was 2.6 cm in diameter and located 24.6 cm from the floor. A shielded 2.8-W bulb mounted 4.4 cm above the center key served as a houselight. A rectangular opening 9 cm below the center key provided access to a solenoid-operated hopper filled with pelleted pigeon chow. During hopper presentations, the opening was lit with white light and the houselight and keylights were extinguished. White noise and ventilation fans masked extraneous sounds. Contingencies were programmed and data collected using Med Associates® interfacing and software.

Procedure

Each pigeon initially was exposed to a multiple VI 15-s (green) VI 15-s (red) schedule. Mean IRIs were increased gradually until the pigeons responded reliably on a multiple VI 20-s (green) VI 120-s (red) schedule. In the multiple schedule, components alternated after every eight reinforcers. Each component was presented three times during the session. The first component of each session was selected with p  =  .5 and the components strictly alternated thereafter. There was no intercomponent interval. All VI schedules consisted of 20 intervals (selected without replacement) and were constructed according to the constant probability distribution described by Fleshler and Hoffman (1962).

When baseline response rates were stable (see below), an unsignaled delay was introduced simultaneously into both multiple-schedule components. Delays were programmed as tandem VI x-s FT y-s schedules in which x is the IRI of the VI schedule in baseline minus the duration of the delay (y). The first response after the VI had lapsed started the FT y-s schedule (i.e., unsignaled delay) at the end of which food was presented independently of further responding. No exteroceptive stimulus changes accompanied the delay. Across conditions, unsignaled delay durations from 0.5 s to 8.0 s were examined for Pigeons 29 and 835 and from 0.5 s to 5.0 s for Pigeons 30 and 32. Each exposure to an unsignaled delay condition was followed by a return to the multiple VI 20-s VI 120-s baseline condition. One unsignaled delay condition was replicated for each pigeon. Each condition was in effect for at least 15 sessions and until responding appeared stable as judged visually for a minimum of six consecutive sessions. The order and number of sessions of exposure to each condition are provided in Table 2.

Table 2. Order of conditions, number of sessions per condition, response rates in successive exposures to the immediate reinforcement baseline condition (multiple VI 20 VI 120), and reinforcement rates in all conditions for Experiment 2. Data are means for the last six sessions of each condition. Numbers in parentheses are standard deviations. Response rates during delay conditions are presented in Figure 3.

Subject	Condition	Sessions	Responses per minute		Reinforcers per minute
			VI 20	VI 120	VI 20	VI 120
29	BL	54	76.27	29.81	2.90	0.49
			(6.76)	(3.63)	(0.02)	(0.00)
	0.5	33			2.92	0.49
					0.01	0.00
	BL	22	55.78	27.63	2.86	0.49
			(6.30)	(4.28)	(0.04)	(0.00)
	1.0	49			2.83	0.49
					(0.03)	(0.00)
	BL	21	61.97	32.41	2.89	0.49
			(4.64)	(2.25)	(0.02)	(0.00)
	2.0	41			2.73	0.48
					(0.02)	(0.00)
	BL	22	65.30	24.31	2.91	0.49
			(3.56)	(2.11)	(0.01)	(0.00)
	3.0	53			2.71	0.48
					(0.08)	(0.00)
	BL	29	67.46	29.73	2.91	0.49
			(2.98)	(3.09)	(0.01)	(0.00)
	5.0	55			2.53	0.48
					(0.14)	(0.00)
	BL	29	63.88	27.99	2.88	0.49
			(3.11)	(3.17)	(0.02)	(0.00)
	5.0	79			2.46	0.46
					(0.09)	(0.01)
	BL	48	40.30	24.20	2.82	0.49
			(3.83)	(1.12)	(0.02)	(0.00)
	8.0	47			1.88	0.40
					(0.16)	(0.02)
	BL	17	39.53	18.66	2.82	0.49
			(3.23)	(1.37)	(0.05)	(0.00)
30	BL	45	63.58	51.55	2.88	0.50
			(10.92)	(5.41)	(0.01)	(0.00)
	0.5	39			2.81	0.49
					(0.04)	(0.00)
	BL	37	54.38	49.26	2.86	0.50
			(6.52)	(3.64)	(0.04)	(0.00)
	1.0	22			2.77	0.48
					(0.04)	(0.01)
	BL	41	65.90	58.23	2.89	0.50
			(7.57)	(2.82)	(0.02)	(0.00)
	2.0	85			2.61	0.48
					(0.06)	(0.00)
	BL	24	47.75	40.05	2.84	0.49
			(3.27)	(3.62)	(0.04)	(0.00)
	3.0	54			2.48	0.46
					(0.13)	(0.01)
	BL	41	42.37	42.48	2.80	0.49
			(5.18)	(5.65)	(0.07)	(0.00)
	5.0	65			1.90	0.36
					(0.40)	(0.03)
	BL	69	47.21	47.03	2.86	0.49
			(3.91)	(3.62)	(0.03)	(0.00)
	3.0	49			1.63	0.45
					(0.30)	(0.02)
	BL	30	64.69	56.47	2.90	0.50
			(5.11)	(3.15)	(0.01)	(0.00)
32	BL	54	41.40	41.12	2.81	0.49
			(6.89)	(5.55)	(0.02)	(0.00)
	0.5	28			2.85	0.49
					0.03	0.00
	BL	28	32.30	30.60	2.76	0.49
			(5.00)	(3.24)	(0.05)	(0.00)
	1.0	46			2.79	0.47
					(0.03)	(0.01)
	BL	59	57.62	24.39	2.82	0.49
			(6.88)	(3.04)	(0.05)	(0.00)
	2.0	48			2.48	0.47
					(0.05)	(0.01)
	BL	69	31.23	19.64	2.74	0.48
			(2.55)	(2.38)	(0.06)	(0.00)
	5.0	45			1.88	0.42
					(0.13)	(0.02)
	BL	25	30.83	14.61	2.72	0.48
			(3.20)	(2.14)	(0.06)	(0.00)
	3.0	57			2.27	0.46
					(0.13)	(0.01)
	BL	29	32.93	23.55	2.73	0.48
			(4.55)	(1.26)	(0.06)	(0.00)
	2.0	81			2.43	0.47
					(0.08)	(0.00)
	BL	22	44.23	21.99	2.78	0.48
			(6.01)	(2.25)	(0.06)	(0.00)
835	BL	38	62.70	43.55	2.91	0.49
			(5.56)	(2.12)	(0.01)	(0.00)
	0.5	19			2.91	0.49
					(0.02)	(0.00)
	BL	17	80.76	46.65	2.93	0.50
			(6.04)	(6.74)	(0.01)	(0.00)
	1.0	22			2.86	0.49
					(0.04)	(0.00)
	BL	25	60.79	38.19	2.89	0.49
			(5.48)	(2.32)	(0.01)	(0.00)
	2.0	58			2.74	0.48
					(0.04)	(0.00)
	BL	37	50.26	38.63	2.88	0.50
			(3.51)	(1.47)	(0.01)	(0.00)
	3.0	48			2.68	0.48
					(0.05)	(0.00)
	BL	18	49.60	35.04	2.88	0.49
			(4.59)	(3.50)	(0.02)	(0.00)
	5.0	51			2.62	0.48
					(0.06)	(0.01)
	BL	19	52.66	40.94	2.87	0.50
			(1.79)	(2.07)	(0.03)	(0.00)
	3.0	32			2.71	0.49
					(0.07)	(0.00)
	BL	49	50.49	43.92	2.88	0.50
			(2.43)	(1.00)	(0.02)	(0.00)
	8.0	46			2.35	0.47
					(0.14)	(0.01)
	BL	32	48.61	41.79	2.87	0.50
			(1.43)	(0.76)	(0.03)	(0.00)

Results

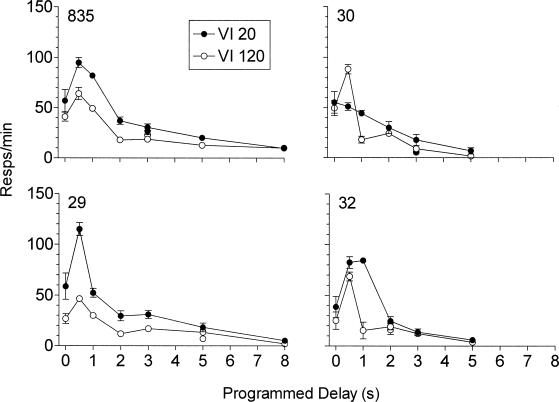
Figure 3 shows average response rates from the last six sessions of exposure to each condition in the VI 20-s and VI 120-s components as a function of the programmed unsignaled delay of reinforcement. Response rates in the repeated immediate reinforcement baseline conditions were averaged for the figure (plotted above zero), but are presented individually in Table 2. In most cases, response rates were higher in the VI 20-s component than in the VI 120-s component in the baseline condition and across delay values. With the exception of Pigeon 30 in the VI 20-s component, response rates increased with the 0.5-s delay. For Pigeons 835 and 32, response rates also were higher with the 1.0-s delay in the VI 20-s component. Response rates with longer delays were lower than during the immediate reinforcement baselines and typically decreased as delay duration increased.

Figure 3. Response rates as a function of programmed delay duration for the VI 20-s and VI 120-s components.

Data plotted over zero represent means of repeated exposures to the immediate reinforcement baseline condition.

Data points not connected by the lines are from the replicated delay condition.

Error bars represent ± 1 SD.

Obtained reinforcement rates in the last six sessions of each condition are presented in Table 2. Reinforcement rates in both components decreased with increases in the programmed delay, but these decreases were relatively smaller for the VI 120 component. For both components, reinforcement rates were lowest in the longer delay conditions in which response rates were quite low. In the VI 20-s component, the largest decreases in reinforcement rates were generally less than one reinforcer per minute (but see Pigeon 30, 3.0-s delay replication). Thus despite the larger decreases in reinforcement rates in the VI 20-s component, reinforcement rates in the two components continued to differ by more than a factor of four.

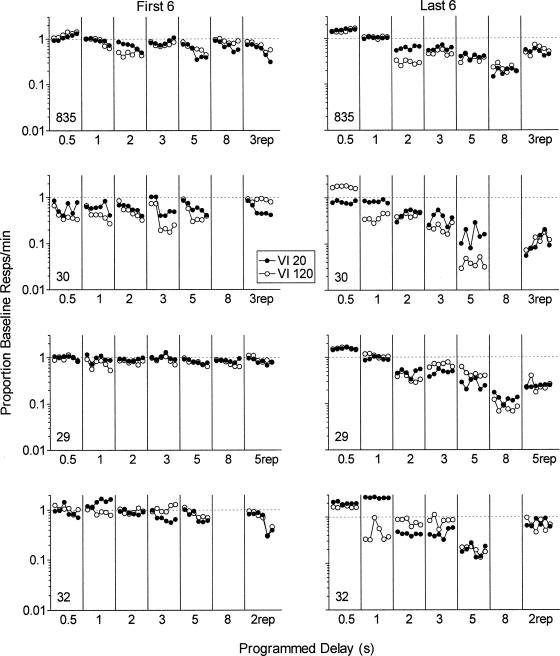
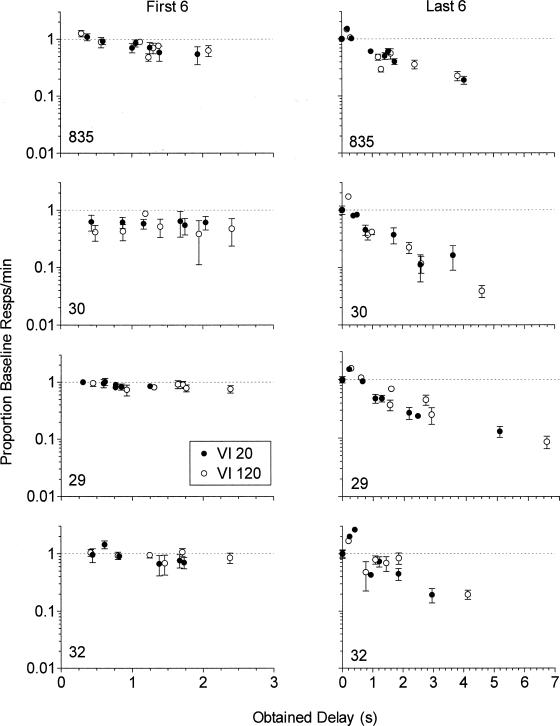
The left panels of Figure 4 show response rates in the first six sessions of exposure to each delay presented as a proportion of the preceding immediate reinforcement baseline. Response rates typically started to decline during the first six sessions, especially for longer delays. The proportional decreases in response rates were not systematically different for the VI 20-s and VI 120-s components. The right panels of Figure 4 show a similar analysis for the last six sessions of exposure to each delay condition. With the exception of increases in response rates at the 0.5-s delay, response rates as a proportion of baseline typically were lower in the last six sessions of each delay condition than in the first six sessions. As with the first six sessions of exposure to the delay condition, proportional decreases in response rates did not differ systematically for the two components.

Figure 4. Response rates in the first six (left panels) and last six (right panels) sessions of exposure to each delay condition plotted as a proportion of the preceding immediate reinforcement baseline condition.

Error bars represent ± 1 SD. The y axes are logarithmic.

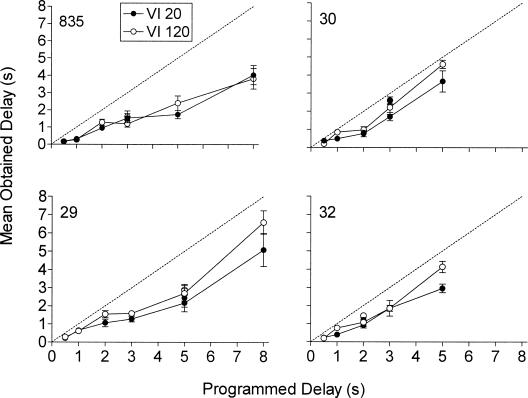
Figure 5 shows mean obtained delays in the last six sessions of exposure to each delay as a function of the programmed unsignaled delay of reinforcement. Obtained delays generally increased with the programmed delay duration but were consistently shorter than the programmed delay. Obtained delays did not differ systematically for the two components across pigeons. Figure 6 shows response rates in the first six (left panels) and last six (right panels) sessions of each delay condition expressed as a proportion of response rates in the preceding immediate reinforcement baseline condition and plotted as a function of mean obtained delay. Obtained delays extended to longer values in the last six sessions of exposure to the delay conditions than in the first six sessions of exposure. Response rates as a proportion of baseline decreased less with increases in obtained delay in the first six than in the last six sessions of exposure to the delay conditions. Proportional decreases in response rate were similar for the VI 20-s and VI 120-s components in both the first six and last six sessions of exposure to the delay conditions.

Figure 5. Mean obtained delays of the last six sessions of exposure to each delay condition as a function of the programmed delay.

Data points not connected by the lines are from the replicated delay condition.

Error bars represent ± 1 SD.

The dotted line denotes equivalence between programmed and obtained delays.

Figure 6. Mean response rates from the first six (left panels) and last six (right panels) sessions of each delay condition presented as a proportion of response rates in the preceding immediate reinforcement baseline condition and plotted as a function of mean obtained delay in those sessions.

Error bars represent ± 1 SD.

The y axes are logarithmic.

Data plotted over zero in the right panels represent means of the repeated exposures to the immediate reinforcement baseline.

Note that the x axes for the left and right panels differ.

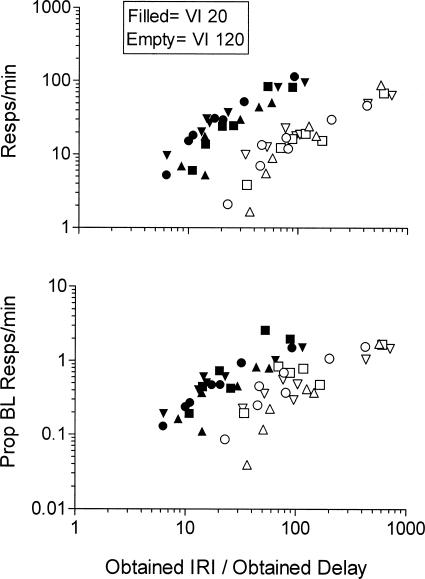
To explicitly examine potential relative time effects with different IRIs and unsignaled delays, response rates were examined as a function of the ratio of the obtained IRI to obtained delay duration. If response rates were determined by the duration of the delay relative to the IRI, then equal IRI/delay ratios should produce similar response rates, regardless of the constituents of the ratio. Figure 7 shows absolute (top panel) and proportion of baseline (bottom panel) responses per minute as a function of the ratio of obtained IRI to obtained delay (i.e., IRI/delay ratio). Figure 7 shows that the functions for the VI 20-s and VI 120-s components did not overlap at equal ratios when response rates were expressed in absolute terms or when they were expressed relative to the immediate reinforcement baseline. Response rates in both components increased with increases in the IRI/delay ratio. Because these increases in the IRI/delay ratio were produced chiefly by decreases in the delay, the increases in response rates with the IRI/delay ratio largely reflect the effects of variations in delay. In addition, it is important to note that even with the largest decreases in obtained reinforcement rates, the average IRI of the two components continued to differ by approximately a factor of four (see above). As a result, the delay for the VI 120 component is necessarily longer when the two components arrange similar IRI/delay ratios. Thus differences in responding in the two components at equal IRI/delay ratios also reflect shorter delays with the VI 20-s component. A similar analysis conducted with programmed delays essentially shifts both functions to the left and yields similar conclusions.

Figure 7. The top panel shows response rates in the last six sessions of exposure to each delay condition plotted as a function of the ratio of the obtained IRI and the obtained delay duration.

The bottom panel shows a similar analysis with responding presented as a proportion of response rates in the preceding immediate reinforcement baseline condition.

In both panels, data for individual pigeons are represented by different symbols.

Pigeons 835, 30, 29, and 32 are represented by inverted triangles, triangles, circles, and squares, respectively.

Both axes are logarithmic.

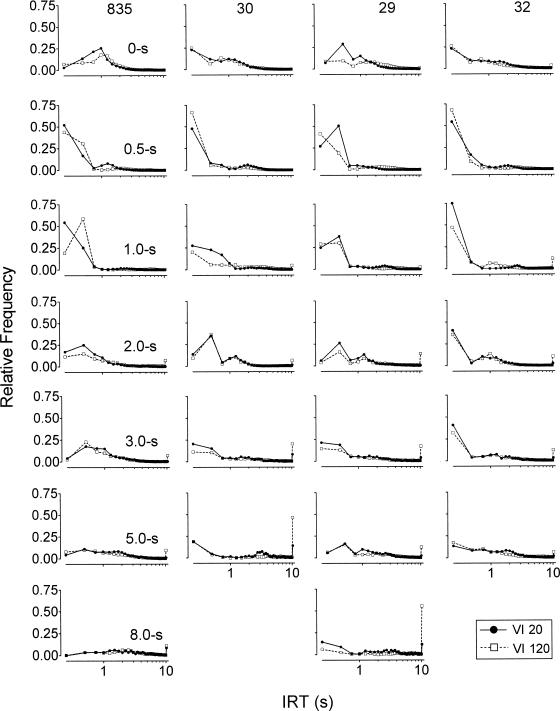
Figure 8 shows the relative frequency of IRTs for each condition in successive 0.25-s bins for the VI 20-s and VI 120-s components. The distributions for repeated immediate reinforcement baseline conditions and for the replicated delay conditions are based on IRTs pooled across successive exposures. Typically, the 0.5-s and 1.0-s delays increased the relative frequency of IRTs less than 0.5 s. The increases in short IRTs with the 0.5-s delay are consistent with the response rate increases observed in this condition (see Figure 3). Despite the sometimes-greater relative frequency of shorter IRTs with delays longer than 0.5 s, response rates in these conditions generally were not higher than in baseline. Nonetheless, there are notable response rate increases for Pigeons 835 and 32 in the 1.0-s delay condition. In all other cases, concomitant increases in the relative frequency of longer IRTs also occurred and response rates were lower than baseline. The distributions tended to spread toward longer IRTs with longer delays. Increases in the relative frequency of IRTs greater than 10 s were generally larger for the VI 120-s component than for the VI 20-s component. Otherwise, changes in the distributions with increases in delay were not systematically different for the two components.

Figure 8. Relative frequency of IRTs plotted in successive 0.25-s bins. Separate distributions are presented for the VI 20-s and VI 120-s components and for each delay condition. The distributions labeled 0-s represent pooled distributions for repeated exposures to the immediate reinforcement baseline condition. Data also were pooled for each of the replicated delay conditions. The data plotted beyond a value of 10 on the x axis represent the relative frequency of IRTs > 10 s. The x axis is logarithmic.

Discussion

The present experiment extends the results of Experiment 1 to a range of unsignaled delays. With the exception of the shortest delays (0.5 and 1.0 s), increases in the obtained duration of unsignaled delays of reinforcement reliably decreased response rates maintained by both a VI 20-s and a VI 120-s schedule of reinforcement. As in Experiment 1, the decreases in response rates did not depend on the average IRI of the VI schedule maintaining responding. Analysis of response rates as a function of a wide range of IRI/delay ratios revealed that response rates in both the VI 20-s and VI 120-s components increased with increases in the IRI/delay ratio, but the two functions did not overlap. Both the increases in response rates with the IRI/delay ratio and the difference in response rates for the two components at similar ratios appeared to be due primarily to differences in obtained delay. Thus the present findings provide no support for relative time effects for delays between responses and reinforcers.

The present results are not consistent with the proportionally smaller decreases in steady-state responding maintained by higher reinforcement rates obtained by Schaal et al. (1992) when unsignaled delays were introduced. In addition, no differences in the disruptive effects of the unsignaled delays were observed when responding was examined in the first six sessions after the unsignaled delay was introduced. The difference in results between the present experiment and those of Schaal et al. occurred despite the use of a nearly identical procedure. Thus the failure to replicate Schaal et al. in Experiment 1 likely was not due to differential exposure to the unsignaled delay resulting from the fixed-duration components in that experiment. It should be noted that Schaal et al. did not report obtained delay durations, but response rates as a proportion of baseline were examined as a function of obtained delays in the present experiment. Nonetheless, an analysis (not presented here) similar to that shown in Figure 6 revealed no consistent difference for the VI 20-s and VI 120-s components as a function of programmed delay (see also Experiment 1).

Finally, examination of the IRT distributions for the VI 20-s and VI 120-s component schedules across delay values revealed that 0.5-s unsignaled delays often increased the relative frequency of short IRTs and led to increases in response rates. This effect is consistent with previous studies that have examined the effects of 0.5-s unsignaled delays of reinforcement (Arbuckle & Lattal, 1988; Lattal & Zeigler, 1982; Sizemore & Lattal, 1978). Typically, longer delays produced spreading of IRTs toward longer values and decreases in response rates. Arbuckle and Lattal and Schaal et al. (1998) obtained similar effects with 5-s and 3-s unsignaled delays, respectively. The present experiment extends these findings to a wider range of unsignaled delays and suggests that the degree of spread of IRTs toward longer values depends on the duration of the delay. In addition, longer delays also sometimes increased the relative frequency of short IRTs, despite the overall lower response rates engendered by these delays. Schaal et al. (1998) obtained a similar result with a 3-s unsignaled delay.

General Discussion

In a number of conditioning preparations, the effects of a delay interposed between a stimulus and a reinforcer depend on the average time between reinforcers in the situation (i.e, the relative time effect). The present experiment examined whether the effects of a delay between a response and a reinforcer depend on the average time between reinforcers in the situation. In Experiment 1, a 3-s unsignaled delay produced similar proportional decreases in response rates with VI schedules arranging average IRIs ranging from 15 s to 540 s. In Experiment 2, unsignaled delays ranging from 0.5 s to 8 s similarly affected responding maintained by VI schedules arranging average IRIs of 20 s and 120 s. Thus the present experiments provide no evidence of relative time effects for delays between responses and reinforcers. Similarly, Bruner et al. (1998) found that the effects of unsignaled delays on the acquisition of rats' lever pressing did not depend on the rate of reinforcement. Together, these data support Williams' (1998) suggestion that relative time effects do not occur with unsignaled delays between responses and reinforcers.

Williams (1998) suggested that the absence of relative time effects with reinforcement delays could reflect a fundamental difference between temporal intervals imposed between two stimuli and temporal intervals imposed between responses and reinforcers. Williams noted, however, that if responses are considered as stimulus events, responses during the IRI could degrade the reinforcement-signaling value of responses and alter the effects of variations in IRI. In the initial baseline of Experiment 1, the mean number of responses per reinforcer was 24, 93, and 269 in the VI 15, VI 90, and VI 540 (VI 360) components, respectively. Similarly, averaged across baselines and subjects in Experiment 2, the number of responses per reinforcer was 19 and 75 for the VI 20-s and VI 120-s components, respectively. The potentially weakened signaling effects of responses in the leaner components could have eliminated any impact the longer IRIs might have had on the effects of the delays.

Based on the considerations above, evaluating relative time effects for delays between responses and reinforcers would require experimental control of response occurrence. The Williams (1998) discrete-trials conditional discrimination procedure better controlled response occurrence and found no evidence of relative time effects for reinforcement delays. Williams obtained this result despite the potential influence of variations in the efficacy of other stimuli associated with impending reinforcement (e.g., lever retraction). The present experiments let the signal value of responses vary, but removed the potential effects of other stimuli signaling reinforcer delivery. The fact that relative time effects were not obtained in either set of experiments provides support for the conclusion that relative time effects do not occur for delays between responses and reinforcers.

In addition to finding no relative time effects for reinforcement delays, the present data are inconsistent with the data of Schaal et al. (1992) showing that an unsignaled delay of reinforcement produced proportionally smaller decreases in response rates for responding maintained by a higher reinforcement rate. In Experiment 1, the ratio of reinforcement rates in the richest (i.e., VI 15 s) and leanest (i.e., VI 540 s) components was 36:1. Nonetheless, response rate decreases as a proportion of baseline in the first six and last six sessions of exposure to the unsignaled delay did not differ across components. Similar results were obtained across a range of delay values in Experiment 2 when number of experienced unsignaled delays was controlled. Thus the disruptive effects of unsignaled delays of reinforcement appear to be inconsistent with the general finding that responding maintained by higher rates of reinforcement is more resistant to change (see Nevin & Grace, 2000).

Similar exceptions to the finding that responding maintained by higher rates or larger magnitudes of reinforcement is more resistant to change have been obtained with disrupters that change the consequences of responding (e.g., Cohen, Riley, & Weigle, 1993; Harper & McLean, 1992; McLean & Blampied, 1995). Based on these exceptions, McLean and Blampied suggested a distinction between disrupters modifying the contingency maintaining responding (i.e., internal disrupters) and those that are remote from the contingency maintaining responding (i.e., external disrupters). Unsignaled delays of reinforcement may provide another example of nondifferential disruption produced by internal disrupters.

As an alternative approach to the present results from the perspective of behavioral momentum theory, consider the likely effects of external disrupters (e.g., presession feeding) on responding maintained by the multiple schedules arranged here. When external disrupters are used, the finding that responding in multiple schedules maintained by higher rates of reinforcement is more resistant to change than responding maintained by lower rates of reinforcement has considerable generality (see Nevin, 1992; Nevin & Grace, 2000). Assuming that large differences in reinforcement rates produce differential susceptibility to disruption, the present findings could suggest that the unsignaled delays produce larger disruptions in higher reinforcement rate components. From this perspective, the question becomes one of how to characterize the effects of an unsignaled delay as a disrupter. Nevin, McLean, and Grace (2001) used a similar approach to account for the apparently weaker resistance to extinction of responding maintained by continuous reinforcement than with intermittent reinforcement (i.e., the partial reinforcement extinction effect). Once the differential impact of extinction was characterized in terms of the termination of the reinforcement contingency and generalization decrement, this apparent exception to behavioral momentum theory was effectively eliminated. Perhaps a similar approach could be used to account for the anomalous effects of other internal disrupters, including unsignaled delays of reinforcement.

One way to characterize the disruptive effects of unsignaled delays is to assume that relative time effects do occur with delays between responses and reinforcers. Unsignaled delays could have a greater disruptive effect on responding maintained by a shorter IRI because, relative to the IRI, the delay is longer. An augmented model like that used by Nevin et al. (2001) could be used to describe the impact of relative delays in the context of differential reinforcement rates. Unfortunately, the lack of consistency of results between Experiment 2 and Schaal et al. (1992) would be problematic for such an approach. In addition, the present and previous data suggest that unsignaled delays may alter response rates through other mechanisms that would be more difficult to characterize in an augmented model of behavioral momentum.

For example, the data from Experiment 1 provided a preliminary examination of the effects of an unsignaled delay on the relation between response rates and reinforcement rates. Figure 2 showed that changes in response rates produced by an unsignaled delay were reflected in decreases in k in Equation 1 and, for 2 of 3 subjects, decreases in R_e. The decreases in both k and R_eare inconsistent with modified versions of Equation 1 that suggest that delays of reinforcement should be reflected primarily in increases in R_e (cf. Williams, 1988). Most important for present purposes, however, is that changes in k can be interpreted to suggest changes in the topography of responding. This interpretation is consistent with an observational analysis conducted by Grace, Schwendiman, and Nevin (1998) that documented altered response topographies when a 3-s unsignaled delay of reinforcement was in effect (e.g., shorter beak-to-key distances, less forceful pecking). In addition, as in previous research with unsignaled delays, Experiment 2 revealed that unsignaled delays altered IRT distributions. An increasing relative frequency of short IRTs was reliably associated with increased response rates when a 0.5-s unsignaled delay was in effect. Based on more extensive analyses, Arbuckle and Lattal (1988) suggested that such increases in the relative frequency of short IRTs occurred as a result of changes in the functional response unit to multiple-key-peck bursts. In Experiment 2, increases in the relative frequency of short IRTs sometimes occurred with longer delays, but were associated with concurrent increases in the relative frequency of longer IRTs (cf. Schaal et al., 1998). Schaal et al. (1998) provided additional data consistent with an interpretation of the spread of IRTs to longer values based on increases in hopper-observing behavior that competes with key pecking.

The findings above suggest that unsignaled delays may alter the structural and functional characteristics of key pecks and generate other responses that compete with key pecks. It is not clear that such effects necessarily should depend on the average IRI of the schedule maintaining responding, and the present data suggest that they may not. Any potential extensions of behavioral momentum theory to account for the disruptive effects of unsignaled delays will require a better understanding of how these delays have their effects.