Geologic constraints on the macroevolutionary history of marine animals

Abstract

The causes of mass extinctions and the nature of taxonomic radiations are central questions in paleobiology. Several episodes of taxonomic turnover in the fossil record, particularly the major mass extinctions, are generally thought to transcend known biases in the geologic record and are widely interpreted as distinct macroevolutionary phenomena that require unique forcing mechanisms. Here, by using a previously undescribed compilation of the durations of sedimentary rock sequences, I compare the rates of expansion and truncation of preserved marine sedimentary basins to rates of origination and extinction among Phanerozoic marine animal genera. Many features of the highly variable record of taxonomic first and last occurrences in the marine animal fossil record, including the major mass extinctions, the frequency distribution of genus longevities, and short- and long-term patterns of genus diversity, can be predicted on the basis of the temporal continuity and quantity of preserved sedimentary rock. Although these results suggest that geologically mediated sampling biases have distorted macroevolutionary patterns in the fossil record, preservation biases alone cannot easily explain the extent to which the sedimentary record duplicates paleobiological patterns. Instead, these results suggest that the processes responsible for producing variability in the sedimentary rock record, such as plate tectonics and sea-level change, may have been dominant and consistent macroevolutionary forces throughout the Phanerozoic.

One of the most striking aspects of the marine animal fossil record is that it preserves a volatile history of biodiversity and rates of taxonomic origination and extinction. Understanding the causes and evolutionary consequences of this volatility is one of the central goals of paleobiology. It has long been recognized, however, that the quantity of preserved sedimentary rock varies over short and long intervals of geologic time (1–3) and that this variation is correlated with several important macroevolutionary patterns in the fossil record, including changes in biodiversity (4–8) and rates of taxonomic extinction (4, 9, 10). The mutual correlations between preserved rock quantity and macroevolutionary patterns have been interpreted as evidence for either preservation biases that distort the apparent timings of extinction and origination in the fossil record (bias hypothesis) (4–7, 10) or a common pattern that is induced by processes, such as sea level fluctuations, plate tectonics, and resultant changes in marine shelf area, that affect both the amount of preserved rock and biological evolution (common-cause hypothesis) (6, 7, 9–12). Nevertheless, some workers have proffered that many intervals of turnover in the fossil record, particularly the major mass extinctions (13), are too substantial to be the result of preservation biases and are sufficiently distinct to require unique forcing mechanisms (14–17).

Evaluating the relative merits of the preservation bias and common-cause hypotheses has been difficult, particularly around mass extinction intervals, because although the total quantity of preserved rock is important, there are many other aspects of variability in the geologic record, such as its temporal continuity and environmental representation, that have not yet been quantified. Moreover, much of this variation is relevant to the interpretation of paleobiological data and results from processes that may directly influence the course of evolution.

Here, I focus on the quantity and temporal continuity of the geologic record by using a previously undescribed compilation of the times of first and last occurrence of gap-bound rock sequences to calculate for the sedimentary record many of the same parameters that are relevant to paleobiological analyses, including sedimentary rock diversity (total number of rock sections), rates of sedimentary basin origination (preserved onset of deposition), and rates of basin extinction (preserved termination of deposition). Such parameters provide a powerful summary of the total amount of preserved sediment and, more importantly, the area-weighted rates of expansion and contraction/erosional truncation of preserved sedimentary basins.

By using this previously undescribed approach, I show that the sedimentary rock record duplicates many aspects of genus first and last occurrences in the marine animal fossil record, including short- and long-term patterns of genus diversity, the average tempo of genus turnover, the frequency distribution of genus durations, and rates of extinction during both “mass extinction” and “background” intervals. Although geologically mediated preservation biases in fossil data have strengthened the apparent similarities between geologic and biologic data, these results provide prima facie evidence for the common-cause hypothesis and offer important constraints on the causes of macroevolutionary patterns in the fossil record.

Data and Methods

Geologic Data. The sedimentary rock record is characterized by packages of sediment that, at a given scale of temporal resolution, accumulated more or less continuously. These packages are known as sequences (18, 19) and are defined by bounding temporal gaps (unconformities) that are recognizable at the same scale of temporal resolution. In the case of marine sedimentary sequences, major gaps result from nondeposition and/or erosion that occur during tectonic uplift and low-stands in sea level. Sequence boundaries that are driven by eustatic sea-level changes are expected to be similarly repeated globally (18, 19). Sequence stratigraphic architecture has been shown to exert a strong control on the distribution of fossil first and last occurrences within local sedimentary basins (9, 20–22). The approach taken here builds on the conceptual framework of sequence stratigraphy and its relationships to paleobiological data.

To quantify the temporal continuity of the geologic record, the times of first and last occurrence of 4,169 gap-bound packages of rock (i.e., sections; see Fig. 7, which is published as supporting information on the PNAS web site) at 541 locations in the USA, including southern Alaska (see Fig. 8, which is published as supporting information on the PNAS web site) were compiled directly from the charts of the Correlation of Stratigraphic Units of North America (COSUNA) (23). These charts provide a comprehensive summary of the known geologic record in the USA that is resolved at a minimum temporal resolution of stages in the Phanerozoic. All told, 2,847 sedimentary sections that are not explicitly designated as nonmarine in origin are present on the COSUNA charts.

Because a single depositional sequence is a 3D rock body that commonly has time-transgressive upper and lower boundaries, individual sequences are represented as sections at the appropriate time intervals for all of the locations that intersect that sequence. Thus, peaks in section origination correspond to the onset of sediment accumulation over a wide region, and peaks in section extinction correspond to the near-simultaneous termination of the sedimentary record over a wide region. The number of sections in a time interval is a measure of the total area of preserved sediment, and rates of section turnover correspond to area-weighted rates of expansion and contraction/erosional truncation of sedimentary rock bodies.

Section first and last occurrences were assigned to the same Phanerozoic time intervals used in Sepkoski's global compendium (24). Because the COSUNA data cannot easily be placed into Sepkoski's stages for the Lower and Middle Cambrian and because the last interval in the COSUNA data is the Pleistocene, most analyses have been conducted for 71 intervals from the Dresbachian to the Pliocene. Median interval duration is 5.5 million years according to modern stage-boundary age assignments (25).

Quantifying the geologic record on the basis of gap-bound packages of sediment is novel, but it has reproduced, at much finer temporal and spatial resolution, a variety of geologic results that derive from different sources of data. For example, the total number of COSUNA sedimentary rock sections is consistent with another estimate of rock quantity in the USA, the number of named formations (10); for first differences, r = 0.61 (P < 0.0001). Estimates of Phanerozoic global rock volume (1) are also congruent with the total number of COSUNA sections. Several other properties of the global geologic record, including long-term rates of sediment accumulation (1, 26) and patterns of lithofacies composition (1) also are reproduced by the COSUNA data. Most importantly for this analysis, the durations of sections documented here are comparable with the durations of sedimentary basins that have been inferred on the basis of other geologic data (27).

Genus Data. Sepkoski's global compendium of marine animals and animal-like protists provided genus data (24). In total, 32,095 fossil genera in the compendium are resolved at a minimum temporal resolution of stages in the Paleozoic–Mesozoic and epochs in the Cenozoic. Sepkoski's genus data can be accessed at http://strata.ummp.lsa.umich.edu/jack. Because proportionally fewer genera are resolved to subepochs in the Cenozoic than are resolved to stages in the Mesozoic, all diversity analyses were conducted at the epoch-level of temporal resolution in the Cenozoic to avoid artificially exaggerating the drop in genus diversity that appears to occur at the Mesozoic–Cenozoic boundary. Because rates of turnover are based on proportions rather than total taxon counts, these measures are less sensitive to a decrease in the number of resolved genera, and therefore Cenozoic subepochs were used in all of the turnover analyses.

Results

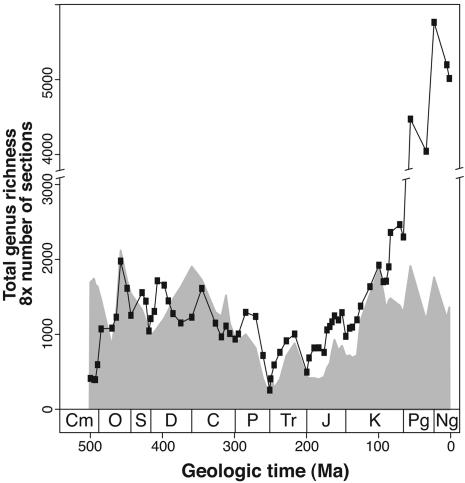
Global genus richness is positively correlated with the total number of sedimentary rock sections in 65 time intervals (see Data and Methods) from the Cambrian to the Pliocene (Fig. 1). This characteristic is true for both the raw time series (Fig. 1; r = 0.41) and when the data are detrended by examining interval-to-interval changes (i.e., first differences; r = 0.66; P < 0.0001). The weaker correlation for the raw time series reflects the strong divergence between the number of sections and total genus richness that begins in the Late Cretaceous and that continues for the remainder of the Cenozoic (Fig. 1).

Fig. 1.

Global genus richness (black line) and rock quantity (shaded area) plotted at age of interval base. Genus data are from Sepkoski's global compendium (24). Rock quantity is measured as the total number of sedimentary rock sections. Ordinate corresponds to eight times the number of sections. Note break in ordinate to accommodate Cenozoic increase in genus richness. See text for discussion.

The causes of the Late Cretaceous divergence between the amount of rock and global genus richness (Fig. 1) and the degree to which the so-called “Pull of the Recent” (28) has contributed to this effect has been discussed elsewhere (5–7, 29). Addressing this problem is beyond the scope of the present analysis, but it is clear that the number of marine animal genera in Sepkoski's compendium and the number of sedimentary sections are remarkably congruent on both short and long time-scales for much of the Phanerozoic. Because it has been suggested that rock quantity and diversity correlations might hold only at relatively coarse temporal resolution (15), these results are noteworthy.

Although rock quantity and genus diversity address essential questions that deserve more attention, the unique contribution of this work is that it allows the temporal continuity of the geologic record to be measured and compared directly with the temporal continuity of fossil data. The simplest way of doing this comparison is to count the total number of first and last occurrences observed in each time interval.

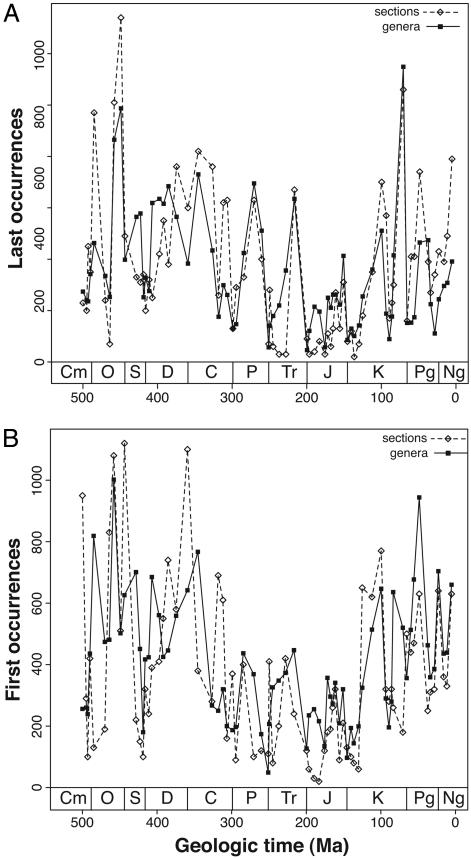
Fig. 2 shows time series for the total number of last occurrences (Fig. 2 A) and first occurrences (Fig. 2B) for both genera and sections in 71 time intervals (see Data and Methods) from the Dresbachian to the Pliocene. The total number of genus first and last occurrences is closely mirrored by analogous parameters in the sedimentary rock record (for last occurrences, r = 0.75; for first occurrences, r = 0.54). That is, intervals preserving few section terminations also preserve few genus last occurrences, and intervals in which many sections first appear after a hiatus also tend to preserve many genus first occurrences.

Fig. 2.

Time series of first and last occurrences for genera and sedimentary rock sections. (A) Last occurrences. (B) First occurrences. Ordinate corresponds to 10 times the number of section first and last occurrences.

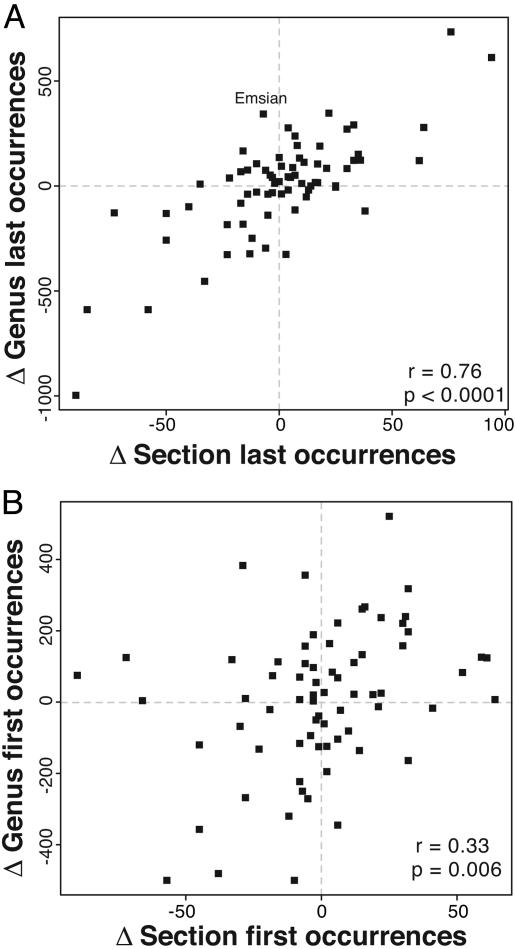
As is visually evident in the raw time series of first and last occurrences (Fig. 2), the detrended time series, which relate to short-term changes, are also positively correlated (Fig. 3). The detrended time series of genus and section last occurrences (Fig 3A). have no prominent outliers and are more strongly correlated than the detrended time series of genus and section first occurrences (Fig. 3B). The correlation between first differences in genus and section last occurrences is not driven by shared interval duration (partial correlation with changes in interval duration held constant is 0.75). For first occurrences, however, variable interval durations have contributed substantially to the correlation shown in Fig. 3B (partial correlation with changes in interval duration held constant is 0.22).

Fig. 3.

Scatterplots of first differences (value for an interval minus value for previous interval) for first and last occurrences of genera and sedimentary rock sections from Fig. 2. (A) Last occurrences. (B) First occurrences. Linear product–moment correlation coefficients and P values are shown. Correlations are also significant according to nonparametric tests (P < 0.002). Positive last occurrence outlier is labeled with stage name.

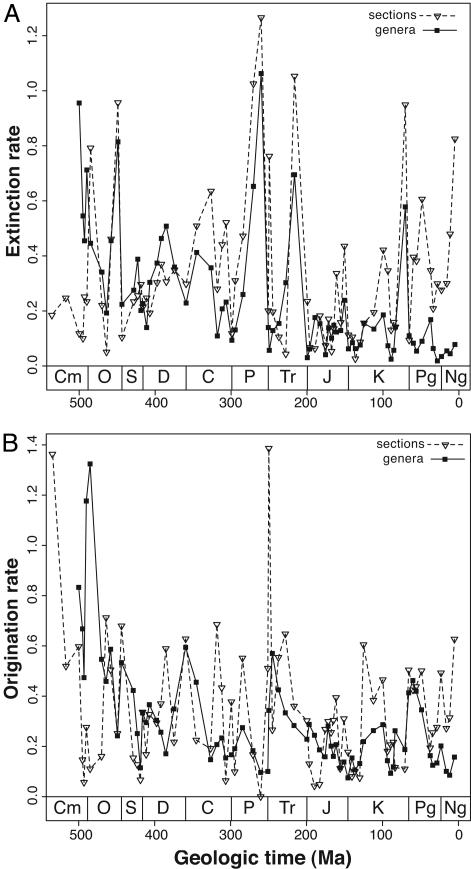
The number of first and last occurrences is related to underlying rates of origination and extinction, but counting these quantities is not a direct or appropriate measure of turnover because the total numbers of genus first and last occurrences are expected to be very sensitive to rates of fossil recovery (30) and, therefore, to the amount of preserved rock. Nevertheless, when the time series of per-interval rates of extinction and origination for genera and sections are calculated by using identical survivorship-based rate metrics (30) and are plotted on identical axes, it is apparent that rates of turnover among genera and sections are remarkably similar in many respects (Fig. 4).

Fig. 4.

Time series of genus and section turnover rates. (A) Extinction. (B) Origination. All rates are calculated on a per-interval basis by using identical survivorship-based rate metrics (30) and are plotted on identical axes.

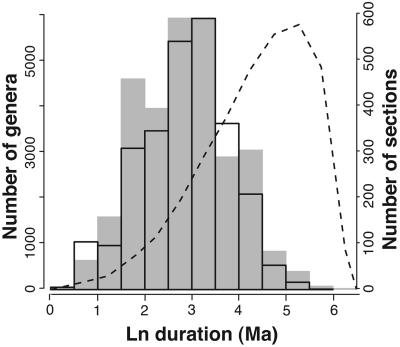
Perhaps the most striking aspect of the section and genus turnover histories is that the absolute values of the rates are very similar (Fig. 4). This finding means that the average longevity of a genus in the fossil record is comparable with the average duration of a sedimentary section. In fact, the entire frequency distribution of genus longevities is remarkably similar to that of section durations (Fig. 5). The small difference between the means and medians of the genus and section duration distributions shown in Fig. 5 is primarily due to a minority of genera that range throughout much of the Phanerozoic and to high rates of fossil recovery in the geologic recent that artificially lower rates of genus extinction in the late Cenozoic (30).

Fig. 5.

Histograms of the durations of genera (shaded distribution) and sedimentary rock sections (open distribution) measured in millions of years (Ma). Dashed line shows distribution of durations derived by randomly generating times of first and last occurrence in Ma and then recalculating range based on the discrete timescale used here. Ln, natural log.

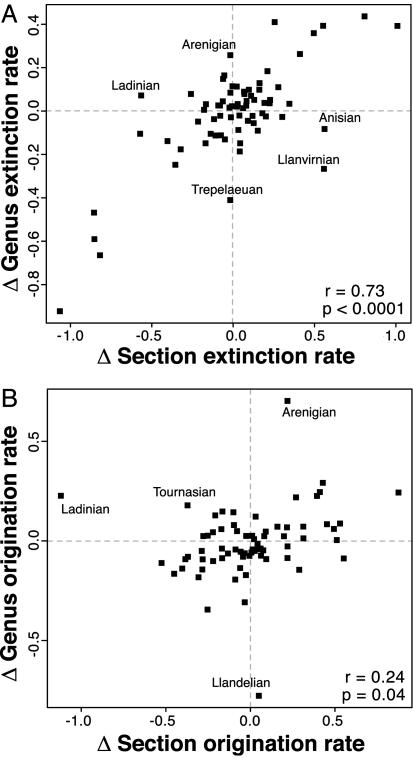
Similar average rates of turnover for genera and sections does not require that short-term variability in these rates also must be correlated. Nevertheless, the detrended time series of extinction and origination rates for genera and sections exhibit significant positive correlation (Fig. 6; partial correlations with changes in interval duration held constant are comparable with those shown). Similar to first and last occurrences (Fig. 3), the extinction rate correlation is substantially stronger (Fig. 6A) than that for origination (Fig. 6B). There are no prominent outliers in the genus–section extinction rate correlation, and those few potential outliers that are present are not the previously recognized major mass extinctions (13). By contrast, the genus–section origination rate correlation has several prominent outliers, one of which (Arenigian) may correspond to the previously recognized Ordovician radiation (31).

Fig. 6.

Scatterplots of first differences for genus and sedimentary rock section turnover rates from Fig. 4. (A) Extinction. (B) Origination. Linear product–moment correlation coefficients and P values are shown. Correlations also are significant according to nonparametric tests (P < 0.002). Several points that deviate from the overall relationships are labeled with stage names.

The detrended time series of section turnover rates also are correlated with Foote's rate-fitting optimization results (Table 1), which provide sampling-adjusted rate estimates for extinction and origination (12, 32). Rates of preservation derived from the total number of COSUNA sections also are correlated with Foote's estimated rates of preservation (r = 0.487; if Foote's very high fitted preservation rates in the Cambrian to Middle Ordovician are excluded, r = 0.576).

Table 1. Sampling-adjusted rate estimates and section rates.

	Origination		Extinction
Data source	r	ρ	r	ρ
Foote—COSUNA	0.502	0.325	0.756	0.704
Sepkoski—COSUNA	0.201	0.295	0.731	0.539
Foote—Sepkoski	0.328	0.274	0.703	0.545

Linear product—moment correlation coefficients (r) and Spearman rank-order correlation coefficients (ρ) between Paleozoic—Mesozoic first-differences in Foote's pulsed sampling-adjusted rate estimates (12), the COSUNA section results presented herein, and Sepkoski's face-value genus data (24). See text for discussion.

Discussion

These results demonstrate that the temporal distribution of genus first and last occurrences in the marine animal fossil record is intimately related to the temporal continuity and quantity of sedimentary rock. Determining why this result is the case is more challenging than demonstrating that it is so.

The quantitative relationships documented here are sufficiently strong and encompass so many freely varying parameters (i.e., diversity, numbers of first and last occurrences, absolute rates of turnover, short-term rates of turnover) that they are unlikely to be spurious. For example, comparing the geologic record of the USA with the global fossil record, as is done here, complicates the interpretation of residual variation (residuals could reflect anomalies in the USA sedimentary record relative to the global record rather than real biological effects), but doing so should be quantitatively conservative with respect to identifying any relationship in the first place.

Nevertheless, the shared geologic timescale and the limitations of biostratigraphic correlation must contribute to the strength of the positive correlations between geologic and fossil data. However, Sepkoski's genus compendium and the COSUNA correlation charts are as independent as two data sets that share the same timescale could possibly be. Thus, if stratigraphic correlation and the shared timescale are the only reasons for statistical similarity, then virtually all temporal patterns derived from the geologic record must be little more than methodological artifacts of binning and correlation. This possibility seems extremely unlikely (although quantifying the magnitudes of the statistical contributions of these factors is very important). Moreover, the effect of the shared timescale can be evaluated quantitatively by means of partial correlation, and these tests indicate that variable interval durations are not contributing substantially to most correlations, particularly with respect to last occurrences and rates of turnover (see Results).

Although it is unlikely that the shared timescale or errors in the data sets used here have unduly strengthened the section–genus correlations, one could argue that fossil animal genera are little more than arbitrarily chosen segments of evolutionary branches and that the temporal ranges of genera are therefore biologically meaningless (33). However, in order for taxonomic biases, such as the concentration of pseudoextinction at sequence boundaries (7), to explain all aspects of these results, taxonomists would have had to have unknowingly and consistently tied their definitions of genera to the temporal continuity of the sedimentary rock record. Taxonomic biases undoubtedly contribute to the strength of the genus–section correlations, but it seems unlikely that the work of hundreds of taxonomists has been so nonrandom (34) as to render the survivorship patterns of >32,000 genera from across the tree of life little more than a quantification of the structure of the sedimentary rock record. Nevertheless, testing, quantifying, and correcting taxonomic biases remains a critical component in interpreting many aspects of these results and in calibrating the true macroevolutionary history of marine animals.

Assuming that macroevolutionary patterns derived from genus first and last occurrences have the potential to be meaningful in a biological sense, the task then becomes to explain why patterns in the genus fossil record are closely duplicated by analogous patterns in the sedimentary rock record. As discussed above, there are two possibilities, (i) preservation bias and (ii) shared forcing mechanisms (common cause). Fortunately, these two alternatives make different predictions with respect to the specific relationships between geologic and biologic data and therefore can be preliminarily assessed with these data.

The bias hypothesis posits that the correlation between stratigraphic and fossil data are caused by preservation-induced truncation of genus ranges. This hypothesis therefore predicts a correlation between short-term variability in genus and section first and last and occurrences and rates of turnover. However, the preservation bias hypothesis makes no prediction about the long-term average rates of turnover (i.e., Phanerozoic mean values of data in Fig. 3) because these rates cannot be biased by interval-to-interval variation in rates of fossil recovery (30). The close agreement between the average duration of a genus and the average duration of a sedimentary section (Fig. 5) therefore must be explained as a coincidence or by unrealistically discontinuous sampling under the bias hypothesis.

In addition to failing to predict the average duration of a genus, which is arguably not a dramatic limitation because of the involved choice of taxonomic level, the preservation bias hypothesis also predicts that both genus extinction and genus origination should match equally well the short-term patterns predicted by the geologic record. However, the extinction correlation is consistently stronger than the origination correlation (Figs. 3 and 6). Nevertheless, because only unconformity and rock quantity biases (9, 20) are being measured here, it is possible that facies biases (9, 20, 35) and/or asymmetries in environmental preservation within sedimentary sequences are causing the stronger section–genus extinction correlation.

Under the common-cause hypothesis, however, genera are expected to originate early in a sedimentary basin's history as new habitats and environments expand and to go extinct abruptly when environmental changes eliminate the basin environments altogether. Thus, similar average durations for sections and genera as well as corresponding peaks and troughs in rates of origination and extinction are expected. Interestingly, the common-cause hypothesis also predicts that the genus–section extinction correlation should be stronger than the genus–section origination correlation because genus extinction can match the timing of rapid environmental shifts that result in section truncation, whereas genus origination may not be capable of responding instantly to the macroevolutionary opportunities afforded by basin expansion. This possibility is sensitive to choice of timescale, but it is supported by analyses that find less empirical support for pulsed genus origination than for pulsed genus extinction at the same level of temporal resolution in the Phanerozoic (36).

Although prima facie evidence for the common-cause hypothesis is found in such aspects of the section–genus relationship, corroborating evidence is afforded by Foote's preservation-adjusted rate estimates (12). If geologically mediated preservation biases were dominantly responsible for the results documented here, then Foote's rate-fitting procedure would have identified the variable sampling component in Sepkoski's data and fit constant or smoothly declining true rates of evolution (32). However, the survivorship structure of Sepkoski's data cannot be explained entirely by variable rates of fossil preservation. Instead, true variation in rates of extinction and origination are required (12).

Remarkably, Foote's preservation-adjusted rates of genus extinction and origination are generally more strongly correlated (albeit modestly so) with the corresponding section rates than either is with Sepkoski's original rates (Table 1). This result is expected under the common-cause hypothesis because Foote's procedure removes error due to the incomplete sampling of true turnover pulses (30). Although rate-fitting procedures do assume homogeneous sampling probabilities and therefore could be misled by geographic or facies biases (9, 20), convergence between sampling-corrected rate estimates and the structure of the geologic record refutes the notion that rock quantity and sequence biases are dominantly responsible for the section–genus correlations and supports the hypothesis that true variations in rates of evolution have occurred and that they have been driven by common-cause mechanisms.

Current predilections are challenged by the possibility that much of the macroevolutionary history of marine animals is driven by processes related to the formation and destruction of sedimentary basins, but this possibility is nothing new. Similar mechanisms that are related directly to sea-level variation and the common-cause hypothesis have been proposed for changes in biodiversity and several of the major extinctions (37–42). However, such explanations generally have been limited to specific time intervals and have been discounted in favor of unusual and abrupt forcing mechanisms, such as asteroid impacts (14, 43), large volcanic eruptions (44, 45), and other rapid or unusual environmental changes (45, 46). Nevertheless, because the geologic record is able to predict such a large component of the variability in the marine animal fossil record and because the mass extinctions do not appear to be prominent outliers, it would seem prudent to revisit some of the classic unifying hypotheses that are grounded in the effects of continually operating processes (37) and to reevaluate seriously the extent to which unusual or episodic events are required to explain the macroevolutionary history of marine animals.

Conclusions

Although variability in the sedimentary rock record, such as that documented here, has imposed a significant bias in fossil data that must be corrected quantitatively (12), and although taxonomic biases remain a potential obfuscator of macroevolutionary patterns in all global taxonomic databases (33), these results provide important constraints on the large-scale history of marine animal life. A combination of preservation bias and common-cause mechanisms must explain much of the observed macroevolutionary history of marine animals. Several aspects of the results presented here suggest that common-cause mechanisms may be more important than unconformity and rock quantity biases, but further tests are required to determine the specific quantitative contributions of each factor over the Phanerozoic.

With respect to short-term variation in rates of genus turnover, few major pulses of extinction, and none of the major mass extinctions (13), occur where the sedimentary rock record does not also record a similar increase in the rate of section truncation. This finding does not disprove the existence of true peaks in the intensity of biologic extinction, but it does indicate that no change in extinction rate, including the major mass extinctions, is particularly unusual in the context of the temporal continuity of the geologic record.

Although it is likely that some episodes of taxonomic turnover in the fossil record have been accentuated by processes that operate outside of those that normally cause the expansion and contraction of sedimentary basins, this analysis provides a substantial measure of support for the long-standing hypothesis (37) that a single suite of processes related to sea-level change and the formation and destruction of marine habitats within sedimentary basins have directly or indirectly controlled rates of taxonomic extinction as well as rates of taxonomic origination throughout the Phanerozoic. Further quantifying the relationships between the large-scale temporal and spatial structure of the geologic record and the distribution of fossil occurrences within this structure (47) will be important in overcoming persistent sampling biases and in testing the extent to which common-cause mechanisms have dominated the macroevolutionary history of marine animals.