Revealing a coherent cell state landscape across single cell datasets with CONCORD

Abstract

Batch integration, denoising, and dimensionality reduction remain fundamental challenges in single-cell data analysis. While many machine learning tools aim to overcome these challenges by engineering model architectures, we use a different strategy, building on the insight that optimized mini-batch sampling during training can profoundly influence learning outcomes. We present CONCORD, a self-supervised learning approach that implements a unified, probabilistic data sampling scheme combining neighborhood-aware and dataset-aware sampling: the former enhancing resolution while the latter removing batch effects. Using only a minimalist one-hidden-layer neural network and contrastive learning, CONCORD achieves state-of-the-art performance without relying on deep architectures, auxiliary losses, or supervision. It generates high-resolution cell atlases that seamlessly integrate data across batches, technologies, and species, without relying on prior assumptions about data structure. The resulting latent representations are denoised, interpretable, and biologically meaningful—capturing gene co-expression programs, resolving subtle cellular states, and preserving both local geometric relationships and global topological organization. We demonstrate CONCORD’s broad applicability across diverse datasets, establishing it as a general-purpose framework for learning unified, high-fidelity representations of cellular identity and dynamics.

Introduction

Cells express thousands of genes to perform specialized functions and maintain homeostasis. Gene expression is highly correlated, orchestrated by intricate gene regulatory networks and cell-cell interactions that constrain cells to a structured, low-dimensional “state landscape” within the high-dimensional gene expression space^1,2. Advances in single-cell technologies, particularly single-cell RNA sequencing (scRNA-seq), enable empirical mapping of this landscape. Emerging evidence suggests that such landscapes may contain diverse features—including discrete clusters, continuous trajectories, branching trees, and cyclic transitions—reflecting the underlying organization of cellular states^3,4. However, the presence and arrangement of these features are typically unknown a priori, underscoring the need for computational methods that can robustly and accurately capture their topology and geometry to illuminate the principles of development, homeostasis, and disease progression.

Dimensionality reduction, a form of representation learning, is commonly employed to uncover the structure of the cell state landscape. By projecting high-dimensional data into a lower-dimensional space, key structural patterns become more tractable to visualize and analyze. However, conventional methods—such as principal component analysis (PCA), non-negative matrix factorization (NMF)⁵, and factor analysis⁶—often overemphasize broad cell type distinctions, overlook subtle states, and can confound processes like differentiation with cell cycle progression. These challenges are exacerbated by batch effects, poorly understood sources of technical variation that obscure or skew genuine biological signals. Although an array of batch-correction tools—such as Harmony⁷, Scanorama⁸, Seurat⁹, scVI¹⁰, LIGER¹¹ and MNN¹² —have been developed, they frequently assume an underlying structure to technical variation and therefore can distort features by over- or under-correcting batch effects¹³, and many face scalability issues when applied to massive atlas-level datasets.

Among the growing number of representation learning approaches useful in single cell analysis, contrastive learning has recently shown promise^14–20. Initially developed for domains such as image and natural language processing^21–23, these methods learn informative cell representations by comparing similar (“positive”) cells against dissimilar (“negative”) ones within mini-batches - small subsets of cells iteratively sampled during training. However, current contrastive methods face fundamental limitations: supervised approaches require extensive manual annotation and struggle to generalize to novel states or continuous trajectories^19,20, whereas unsupervised methods form mini-batches through uniform sampling, emphasizing coarse cell-type differences while overlooking subtle biological variation^14–17. When applied across datasets, contrasting cells randomly sampled from different datasets can amplify dataset-specific artifacts rather than isolating true biological signals. While strategies involving generative adversarial networks (GANs)^17,24,25, unsupervised domain adaptation via backpropagation²⁶, and conditional variational autoencoders (CVAEs)²⁷ attempt to mitigate batch effects, their objective of minimizing dataset-specific differences inherently conflicts with contrastive learning’s goal of maximizing differences between dissimilar cells, frequently leading to incomplete batch-effect correction and potentially introducing distortions to the latent space. This dilemma raises a critical question: can contrastive learning fully capture cellular diversity while minimizing batch effects?

Here, we address this open question by transforming a core limitation of contrastive learning—its sensitivity to mini-batch composition—into a strength. The central insight is that mini-batch composition fundamentally determines the outcome of contrastive learning. We introduce CONCORD (COntrastive learNing for Cross-dOmain Reconciliation and Discovery), a framework that redefines the contrastive learning process through a probabilistic, neighborhood- and dataset-aware mini-batch sampling strategy. By enriching each mini-batch with biologically informative contrasts drawn from within datasets, CONCORD simultaneously enhances embedding resolution and mitigates batch-specific artifacts. In contrast to prior methods that rely on complex architectures or auxiliary losses for batch correction, CONCORD achieves dimensionality reduction, denoising, and data integration solely through principled sampling. We demonstrate its effectiveness using a minimalist, single-hidden-layer neural network across simulated and real datasets spanning a range of biological and technical complexity. CONCORD consistently outperforms state-of-the-art methods, producing high-resolution, denoised encodings that robustly capture diverse structures—including loops, trajectories, trees, and specialized cell states—reflecting bona fide biological processes even when the data originate from multiple technologies, time points, or species. This minimalistic, highly extensible framework scales from small to large datasets, generalizes to modalities beyond scRNA-seq, and establishes a rigorous foundation for next-generation single-cell machine learning models to power diverse downstream biological discoveries.

Results

The CONCORD framework

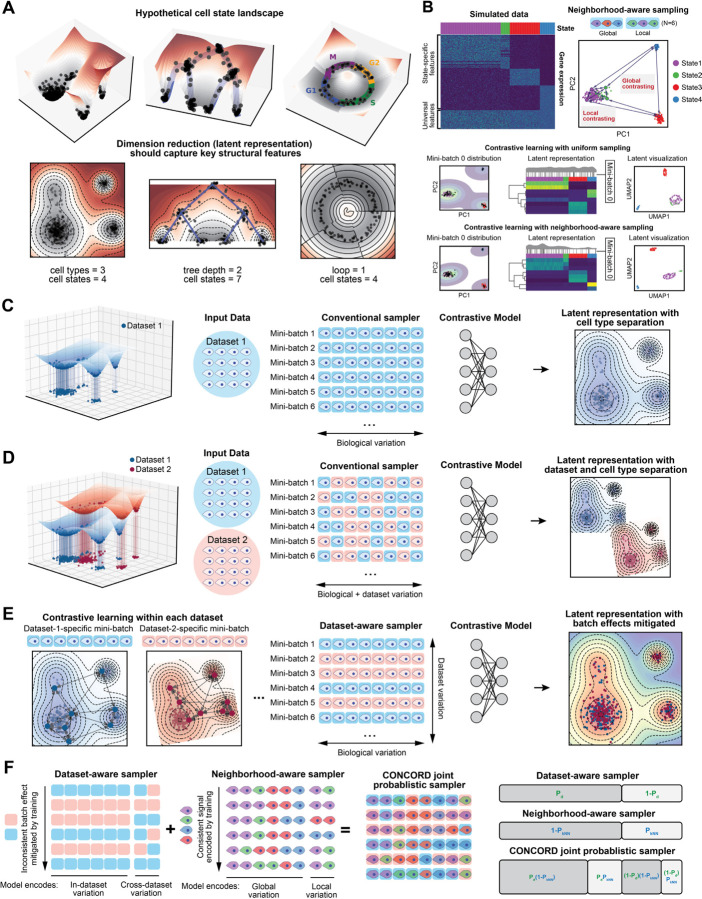
Analysis of single-cell sequencing data suggest that gene expression is not randomly sampled; rather, the mechanism of gene regulation imposes strong constraints, producing dynamically changing gene co-expression patterns reflected as intricate structures in the low dimensional embedding of cells^1–3,28. For example, at homeostasis, cells typically form discrete clusters corresponding to stable types or states, with adjacent clusters representing closely related states (Figure 1A, left). In developmental or pathological contexts—such as early embryogenesis, tissue repair, or tumorigenesis— cells often follow branching trajectories from progenitors to terminal fates, with semi-stable intermediate states forming denser clusters (Figure 1A, middle). Cyclic gene expression programs, such as those regulating the cell cycle, give rise to loop-like structures^3,4 (Figure 1A, right). Despite these rich patterns, conventional dimensionality reduction methods like PCA or NMF capture only partial representations of the cell state landscape, either oversimplifying complex structures or disproportionately emphasizing certain features while obscuring others.

Figure 1. The CONCORD sampler enables high-resolution, batch-effect-mitigated latent representation of scRNA-seq data generated by contrastive learning.

(A) Illustration of hypothetical cell state landscapes and corresponding dimensionality-reduced representations that capture key structural features of the landscape. (B) Comparison of neighborhood-aware and uniform sampling and their impact on contrastive learning in a simulated four-cell-state dataset. The heatmap shows the actual simulated expression. For each sampling scheme, PCA plots are color-coded by cell state, with black points indicating cells selected in a representative mini-batch, accompanied by density curves illustrating their distribution. Latent heatmaps display the representations learned using uniform and neighborhood-aware sampling, with black lines marking cells included in the selected mini-batch and density plots depicting their distribution. The resulting UMAP embeddings computed from the latent representations for each sampling method are also shown. (C) Contrastive learning performed in a single batch with the conventional sampler, which draws cells uniformly from the entire dataset to form mini-batches. (D) When applying standard contrastive learning to multiple datasets (represented by the blue or pink background), contrasting cells from different datasets within the same mini-batch amplifies dataset-specific biases, which is manifested in the latent embeddings. (E) CONCORD mitigates these dataset-specific artifacts by predominantly contrasting cells within each dataset and randomly shuffling mini-batches for each training epoch. (F) The CONCORD sampling framework. A “leaky” dataset-aware sampler addresses minimal or absent overlap between datasets and can be combined with the neighborhood-aware sampler to support both data integration and enhanced resolution. This is achieved by a joint probabilistic sampling framework, where the likelihood of selecting a given cell reflects the combined probabilities of dataset-aware (P_d) and neighborhood-aware sampling (P_kNN).

We hypothesized that a representation learning approach capable of encoding cells based on gene co-expression programs would provide a more comprehensive view of the cell state landscape. Recent evidence suggests that self-supervised contrastive learning significantly improves clustering and cell-type classification performance^15–17, likely due to its ability to recover sparse, structured gene co-expression signals from high-dimensional data²⁹ (see Methods). Like many modern machine learning methods, contrastive learning relies on mini-batches— small subsets of data sampled iteratively during stochastic gradient descent—as the basic unit of training. However, contrastive learning is uniquely sensitive to how mini-batches are composed: each cell is contrasted against every other cell within the same mini-batch, making the mini-batch itself the universe over which learning is defined. By differentiating each cell from others in the mini-batch, the model learns features that distinguish distinct cellular states. Simultaneously, aligning augmented versions of the same cell (typically generated through random masking) encourages the model to capture robust gene co-expression patterns, rather than relying on the expression of individual genes²⁹. As a result, the learned representations are inherently more robust to technical noise and dropout—pervasive artifacts in single-cell RNA-seq³⁰.

This reliance on within–mini-batch comparisons makes the sampling strategy—which dictates mini-batch composition—a critical determinant of the learned representation³¹. Existing methods adopt uniform sampling across the entire single cell datasets, leading to two key limitations. First, uniform sampling emphasizes broad differences, such as major cell types, while underrepresenting rare subpopulations or subtle distinctions, leading to poor resolution of fine-scale cellular states (Figure 1B). Second, mixing cells from different datasets within the same mini-batch can amplify dataset-specific differences, inadvertently encoding batch effects rather than isolating biologically meaningful variation.

To address the first issue, we developed a neighborhood-aware sampler, inspired by k-nearest-neighbor (kNN) based sampling³¹. In this approach, cells are sampled probabilistically from both the global distribution and local neighborhoods (Figure 1B). Local sampling, guided by a coarse graph approximation of the cellular state landscape, compels the model to contrast cells against their neighbors, allowing it to capture subtle differences between closely related states. Meanwhile, global sampling preserves a broad perspective of major cell types, ensuring the model robustly encodes large-scale distinctions. By iteratively presenting the model with local neighborhoods (e.g., T cells in one mini-batch, epithelial cells in another) alongside the global distribution, the model allocates capacity to represent both large-scale distinctions and nuanced local details, leading to improved resolution in the learned latent space (Figure 1B).

When applied to a single dataset, contrastive learning effectively captures biological variation in the latent space (Figure 1C). However, with uniform sampling across multiple datasets, both biological and dataset-specific variations are encoded, leading to latent spaces that separate by dataset as well as cell type (Figure 1D). To address this, we also introduce a dataset-aware sampler that restricts mini-batches to a single dataset, ensuring contrasts reflect only biological differences, as in the single-dataset setting (Figure 1E). Dataset-specific biases are further diminished through random mini-batch shuffling: if such signals are encoded in one batch, they are disrupted and overwritten by subsequent mini-batches from other datasets. Consequently, only biologically meaningful signals, such as gene co-expression patterns, persist throughout training, resulting in a latent space that reflects biological variation with minimal batch effects (Figure 1E). Importantly, this strategy of removing batch effect imposes no assumptions on the structure of the data beyond the existence of shared biological programs across datasets. In cases where datasets have minimal or no overlap, a “leaky” dataset-aware sampler enables soft alignment without imposing artificial harmonization, supporting flexible integration across both fully and partially overlapping datasets (Figure 1F). Unlike prior batch-correction strategies that struggle in contrastive learning due to competing objectives, CONCORD integrates batch correction directly into the contrastive learning process via its sampling design, resulting in latent representations inherently robust to batch effects.

Both the neighborhood-aware and dataset-aware samplers follow a unified principle: probabilistically structuring mini-batches to balance global biological diversity with local and dataset-specific variation. We integrate both samplers into a joint sampling framework, where the likelihood of selecting a cell satisfies both sampling schemes (Figure 1F). This generalized sampling scheme fundamentally reconfigures contrastive learning, enabling both high-resolution representation learning and robust dataset integration within a single contrastive objective, and forms the core of the CONCORD framework (Supplemental Figure 1). With this simple innovation to contrastive learning, CONCORD achieves state-of-the-art performance using only a minimalist encoder with a single hidden layer, demonstrating that the sampling framework alone can transform contrastive learning performance—even without deep or complex architectures. This simplicity reduces training data requirements, enhances robustness, and increases interpretability by efficiently compressing heterogeneous cell states into a compact latent space.

CONCORD learns denoised latent representations that preserve underlying structures

Recovering biologically meaningful insights from single-cell data requires preserving both the geometric organization and topological structure of the gene expression space. To evaluate whether CONCORD meets this criterion, we benchmarked its performance on both simulated and real-world datasets. Existing simulators (e.g., splatter³²) produce discrete clusters but fail to capture complex biological structures such as branching, loops, and multi-scale hierarchies. We therefore developed a custom simulation workflow that generates a wide range of realistic structures with flexible control over noise and batch effects (Figure 2A).

Figure 2. Benchmarking CONCORD and other dimensionality reduction methods across diverse structures.

(A) Simulation pipeline for generating data structures. The pipeline first produces a noise-free gene expression matrix based on a user-defined structure, then introduces noise following a specified noise model, and finally applies batch effects in various forms. (B) Evaluation pipeline. Using the simulated datasets, the latent representations produced by each method was compared with the noise-free ground truth to assess how well topological and geometric features are preserved. For cluster simulations, we further evaluate the correlation of cluster-specific variances in the noisy data versus the latent space. Metrics from the scIB³³ package were incorporated for evaluating conservation of biological labels and harmonization of batch effects. (C) Performance on simulated clusters, highlighting the resulting UMAP visualization, cosine distance matrices, persistence diagrams, and Betti curves for CONCORD and other methods. In the persistent homology analysis, the H₀ point representing infinity was excluded from the persistence diagram and curve. (D) Performance on a complex trajectory with 3 loops, highlighting the same diagnostic plots as C. (E) Summary table for the three-cluster simulation, listing key topological and geometric evaluation metrics. (F) Table summarizing the methods’ performance on the complex trajectory-loop simulation. (G) KNN graph visualization of latent embeddings from each method on a complex tree simulation, with zoomed-in views of the darkened region highlighting detail on one of the branches.

To assess the quality of learned representations, we implemented an evaluation pipeline combining geometric and topological metrics (Figure 2B.). Traditional benchmarking pipelines like scIB³³ focus on label preservation and batch correction but overlook structural fidelity. We addressed this by incorporating geometric metrics such as trustworthiness and distance correlation, along with topological data analysis (TDA) based on persistent homology and Betti numbers (Figure 2B). Trustworthiness quantifies local neighborhood preservation, while persistent homology captures global topological features—like clusters (Betti-0), loops (Betti-1), and voids (Betti-2)—across scales. These features are visualized in persistence diagrams and Betti curves, where stable structures appear as long-lived features in the persistence diagram and extended plateaus in the Betti curve, whereas transient, noise-induced features vanish quickly.

We first evaluated CONCORD on a simple simulation of three well-separated clusters corrupted by cluster-specific Gaussian noise (Figure 2C, Supplemental Figure 2A). Compared to a broad set of dimensionality reduction methods—including diffusion map, NMF, Factor Analysis, FastICA, Latent Dirichlet Allocation (LDA), ZIFA, scVI, and PHATE —CONCORD cleanly separated clusters and closely matched the ground truth in both the latent space and pairwise distance matrix. In contrast, many methods failed to fully resolve the clusters or introduced spurious structures, such as trajectory-like artifacts (Figure 2C). Persistent homology confirmed these observations: CONCORD’s Betti-0 plateau accurately reflected the expected three-cluster topology and closely matched the noise-free reference, highlighting its combined strength in denoising and structure preservation.

For more complex structures, such as a self-connecting trajectory with three loops and multiple branching points (Figure 2D, Supplemental Fig. 2B), CONCORD was the only method that accurately recovered the full topology. Other methods either collapsed the structure into discrete clusters or failed to detect multiple loops in Betti analysis, likely due to excessive noise retention. Although PHATE produced a visually smooth embedding, its Betti curve revealed only a single persistent loop, missing key topological features of the underlying structure.

We evaluated performance across simulated structures using geometric and topological metrics, finding that CONCORD consistently outperformed alternative methods (Figure 2E, 2F). Notably, despite its denoising capabilities, CONCORD preserved relative noise levels in the latent space, evidenced by the strong correlation between input and latent variance—critical for retaining biologically meaningful variability such as transcriptional noise. It also maintained high trustworthiness across a wide range of neighborhood sizes, underscoring its ability to preserve local geometry at multiple scales (Supplemental Figure 2C, 2D). In contrast, other methods exhibit sharp declines in trustworthiness, indicating a loss of fine-scale geometric relationships in the latent space.

To assess the impact of neighborhood-aware sampling, we simulated a hierarchical branching tree mimicking a hypothetical differentiation trajectory (Figure 2G, Supplemental Figure 2E). Without local sampling, sub-branches were unresolved. Moderate enrichment improved resolution, while excessive local focus (>0.6 intra-kNN probability) suppressed global distinctions (Supplemental Figure 2E–F). These results support using intra-kNN sampling probabilities below 0.5 to balance fine-grained resolution with global structure preservation.

CONCORD learns a coherent, batch-effect-mitigated latent representation

Batch effects often appear as dataset-specific global signals that can obscure biological variation. In CONCORD, these signals rapidly diminish during training when mini-batches are restricted to single datasets (Figure 1E, Figure 3A). Unlike conventional batch-correction methods that rely on explicit alignment models, CONCORD makes minimal assumptions about the source or form of batch effects and instead prioritizes learning coherent, biologically meaningful gene covariation patterns. This leads to more accurate preservation of biological structure while mitigating technical artifacts.

Figure 3. Benchmarking CONCORD and other data integration methods across diverse structures.

(A) Two-batch, five-cluster simulation. For ground truth, we show kNN graphs (k=15 by default, with edges omitted) of both the noise-free and noise-added data (no batch effect). Latent spaces from each integration method are visualized by kNN graphs, colored by batch (top) and cluster (bottom). (B) Trajectory simulation with varying batch overlap. The ground truth is shown with PCA and a kNN graph. For each method, the resulting latent space is depicted with a kNN graph (k = 15) to assess how well cells are integrated across batches along the trajectory. In the gap simulation, an additional kNN graph (k = 30), colored by simulated time, demonstrates that CONCORD accurately captures the correct orientation of the trajectories along time despite the gap. (C) Loop simulation with varying batch overlap. Shown here are kNN graphs of the ground truth (with edges omitted) and the CONCORD latent space. Full results for other methods are provided in Supplementary Figure 3D. (D) Tree simulation with varying batch overlap. kNN graphs for the ground truth and the CONCORD latent space are shown. Full results for other methods are provided in Supplementary Figure 3E. (E) scIB benchmarking on the two-batch, five-cluster simulation. Integration performance was evaluated using metrics from the scIB-metrics package³³. (F) Ranking of integration methods. Each method’s performance is scored across topological, geometric, and scIB metrics. The overall rank is based on the average ranking across all metrics.

We tested CONCORD on a simulated dataset with five clusters corrupted by batch effects and noise. CONCORD was the only method to accurately recover all clusters; others either failed to resolve closely related states or introduced artifacts - such as the ring-like structure produced by Scanorama⁸. Notably, using a conventional uniform sampler without dataset-aware sampling resulted in pronounced batch effects (Figure 3A). While effectively denoising, CONCORD preserved cluster-specific variance rather than over-smoothing (Supplemental Figure 3A), and its performance was consistent across various noise models (e.g. Gaussian, Poisson) and batch-effect types, underscoring its flexibility and generalizability (see Methods; data not shown).

Beyond clustering, a key challenge in integration is aligning datasets representing related but distinct conditions - such as developmental stages, perturbations, or species - with partial or no overlap in cell states. Methods relying on matched clusters or mutual nearest neighbors often fail under such conditions, producing distorted or fragmented embeddings, especially when the number of datasets increases. To systematically assess this, we simulated batch effects across clusters, trajectories, loops, and trees (Figure 3B–D, Supplemental Figure 3B–E). On a trajectory simulation where batches were fully overlapping, most methods achieved some degree of alignment, though several exhibited suboptimal corrections (e.g., scVI, LIGER) (Figure 3B). As overlap decreased, performance deteriorated: some methods failed to align batches (e.g., LIGER, Harmony), while others introduced artifacts, such as artificial loops (Scanorama) or merged clusters (scVI). In contrast, CONCORD consistently recovered the correct structure with reduced noise, even when shared cell states were sparse or absent (Figure 3A–D, Supplemental Figure 3B–E, Supplemental Table 1).

CONCORD’s robustness arises from its focus on learning gene co-expression programs (see Methods, Figure 1B, Supplemental Figure 2A, 2B, 2E), which naturally group transcriptomically similar cells without requiring explicit reference anchors - a key distinction from many batch-correction approaches. As a result, CONCORD achieves high biological label conservation in scIB benchmarks (Figure 3E, 3F), though its batch-correction score is slightly lower because it does not explicitly merge batches. It also excels at preserving local geometry, as indicated by high trustworthiness scores, but shows lower global distance correlation - a common trade-off in manifold learning^34,35 (Figure 3F, Supplemental Table 1). Nonetheless, CONCORD consistently ranks among the top methods for topological preservation, label conservation, and overall performance (Figure 3F). These results demonstrate that CONCORD provides a reliable and generalizable framework for dimensionality reduction and batch correction, even in scenarios with unknown structure or limited batch overlap.

CONCORD aligns whole-organism developmental atlases and resolves high-resolution lineage trajectories

To assess whether CONCORD captures biologically meaningful structures across technologies, we first benchmarked it against popular integration methods on lung and pancreas atlases³³ (Supplemental Figure 4A, B). While CONCORD effectively identified discrete cell types, these datasets lack continuous or hierarchical structure, limiting their utility for evaluating performance in common yet complex scenarios such as development and disease progression. To address this, we turned to C. elegans embryogenesis—a well-characterized system with a nearly invariant lineage tree³⁶, conserved in the related species C. briggsae³⁷. Packer et al. initially generated a lineage-resolved atlas of C. elegans³⁸, which was recently expanded by Large et al. to include over 200,000 C. elegans cells and 190,000 C. briggsae cells³⁷. With expert-curated annotations generated through iterative, labor-intensive zoom-in analyses and validated by fluorescent imaging, these datasets provide an ideal benchmark for evaluating whether integration methods can accurately reconstruct and align developmental trajectories across species.

Running CONCORD on the C. elegans dataset³⁸ produced UMAP embeddings that recapitulated known developmental trajectories (Supplemental Figure 5A). The effect of neighborhood-aware sampling mirrored trends observed in simulations: moderate local enrichment improved resolution of subtle differences among neurons, while excessive local sampling disrupted the global structure (Supplemental Fig. 5A–C).

Applied to the larger, cross-species dataset, CONCORD generated a unified developmental atlas closely aligned with original cell-type and lineage annotations (Figure 4A), clearly separating broad cell classes (Supplemental Figure 6A) and capturing smooth developmental transitions (Figure 4B). The complexity of the learned structure exceeded the capacity of 2D UMAP, necessitating 3D visualization to resolve trajectory crossovers (Figure 4A). Running CONCORD with or without a decoder yielded similar UMAP embeddings (Figure 4B), and we present the with-decoder version due to slightly less entangled trajectories. To fully explore the intricate structures captured by CONCORD, we highly encourage readers to view the interactive 3D visualizations (https://qinzhu.github.io/Concord_documentation/galleries/cbce_show/#tabbed_1_1).

Figure 4. Benchmarking CONCORD on C. elegans/C.briggsae embryogenesis atlas.

(A) Global 2D and 3D UMAPs of CONCORD (with decoder) colored by cell type and estimated embryo time. (B) UMAP of CONCORD and other integration methods colored by estimated embryo time and species. (C) Boxplots show the fraction of C. elegans cells within randomly sampled 100-nearest-neighbor (100-NN) neighborhoods, stratified by embryo time bins. The red horizontal line represents the expected species fraction based on the global composition of each time bin. Well-integrated datasets should show species fractions closely matching this expected value with minimal variation. (D) Global 3D UMAPs of CONCORD (with decoder), Seurat and scVI, highlighting cells mapped to the lineage sub-tree that give rise to ASE, ASJ and AUA neurons. For each method, the most representative view was selected. (E) Heatmap showing the top 50 most variable latent dimensions in the ASE, ASJ, and AUA neuron subset for scVI, Seurat, and CONCORD (with decoder). Expression of gcy-5 and gcy-14 were plotted on the CONCORD (with decoder) UMAP. (F) Latent space distance between medoids of ectodermal cells (AB lineage), stratified by cell generation and lineage relationship. AB5 refers to cells derived after five successive divisions of the AB founder cell, with AB6 to AB9 representing progressively later generations. (G) Spearman correlation between lineage distance and latent space distance across integration methods for AB lineages from generations 5 to 9. Statistical significance of differences in correlations was assessed using a two-sided Mann-Whitney U test, with asterisks indicating significance levels (**p < 0.01, ***p < 0.001, ****p < 0.0001). (H) Zoom-in UMAPs for mesoderm cells excluding pharynx. Major input lineages and cell types were highlighted. Each lineage was represented by its cluster medoid on the UMAP, and lines connect each parental lineage to its daughter lineages following the lineage tree. (I) Zoom-in UMAPs for pharynx, annotated with cell types and broad input lineages. Selected lineage paths that give rise to pm1/2, pm3–5, and pm6 are highlighted. (J) Run time comparison of different integration methods. *Harmony was run using a 300-dimensional PCA input, whereas all other methods were applied to the gene expression matrix containing 10,000 variably expressed genes.

To quantitatively evaluate integration, we analyzed each method’s latent space. As standard benchmarking tools (e.g., scIB³³) could not scale to this dataset, we adapted a neighborhood-based species mixing analysis - similar to kBET³⁹ - stratified by developmental time (Figure 4C). CONCORD maintained expected species fractions within local neighborhoods, while methods such as Scanorama, scVI, and LIGER showed poor mixing or high variability. Harmony and scVI achieved species alignment but at the cost of resolution, obscuring subtypes and trajectories (Figure 4B–C). Seurat and CONCORD recovered divergent terminal fates, but only CONCORD preserved continuous, fine-grained trajectories from progenitors to terminal cell types.

Projecting the lineage tree onto CONCORD’s embedding revealed strong concordance with known lineage and fate relationships (Supplemental Figure 6B, C). For example, the ASE, ASJ, and AUA neurons—derived from AB progenitors—formed branching trajectories that mirrored their true lineage structure (Figure 4D). In contrast, scVI and Seurat introduced large discontinuities between parent and daughter lineages, failed to resolve key bifurcation points, and generated artificial trajectory distortions. CONCORD’s latent space also distinguished functional subtypes, such as ASE-left (ASEL) and ASE-right (ASER) neurons, characterized by differential expression of GCY receptors (Figure 4E). Although morphologically symmetric, these neurons exhibit functional asymmetry in salt-sensing responses^40,41.

To systematically assess the preservation of lineage structure, we replicated the analysis from Packer et al.³⁸ by correlating latent distances with lineage distances for AB-derived cells, which produce ~70% of terminal embryonic cells (Figure 4F). Consistent with the original study - where transcriptome distances correlated with lineage distances - CONCORD’s latent distances showed strong correlation with lineage distances, even in early generations where transcriptomic differences were minimal. This highlights CONCORD’s ability to capture subtle, progressive molecular changes. Notably, it outperformed all other methods in overall correlation (Figure 4G), underscoring its potential for trajectory inference in developmental studies^42,43.

The advantage of CONCORD in resolving fine-scale structure became even more evident when zooming into specific cell subsets. In early embryonic cells, Scanorama, Harmony, and scVI failed to fully align species or lost resolution, whereas CONCORD revealed extensive lineage bifurcations (Supplemental Figure 6D). On muscle formation, CONCORD showed the MS, C, and D lineages converge into sub-branches of body wall muscle, positioned from the head (anterior) to the tail (posterior) in an orientation reflecting genuine spatial gene expression gradients (Figure 4H, Supplemental Figure 6E). CONCORD also resolved rare lineage convergence events, such as the integration of ABplp/ABprp- and MS-derived cells into intestinal muscle (mu_int). Pharyngeal development, involving complex branching and convergence of AB- and MS-derived cells, was likewise resolved by CONCORD (e.g., pm3–5 deriving from both AB and MS lineages, and pm1–2, 6–8 specific to AB/MS lineage), whereas scVI and Seurat recovered fewer fine-grained details (Figure 4I, Supplemental Figure 6F). Crucially, all analyses were performed directly on CONCORD’s global latent space, without the need for subset-specific variable gene selection or re-alignment – steps that are often recommended for other methods.

Finally, CONCORD showed superior scalability, integrating the 400,000-cell, 20-batch dataset in ~30 minutes on an NVIDIA A100 GPU - significantly faster and more memory-efficient than LIGER, Seurat, and scVI (Figure 4J). These results establish CONCORD as a powerful and scalable tool for aligning and reconstructing complex developmental trajectories.

CONCORD captures cell cycle and differentiation trajectories in mammalian intestinal development

Unlike C. elegans, where early divisions are largely driven by maternal transcripts⁴⁴, mammalian development involves extensive proliferation coupled with ongoing differentiation. To assess whether CONCORD can resolve these intertwined processes, we applied it to a single-cell atlas of embryonic mouse intestinal development⁴⁵, which spans multiple developmental stages, batches, spatial segments, and enriched cell populations—posing a challenging integration task due to incomplete batch coverage (Figure 5A).

Figure 5. Benchmarking CONCORD on mammalian intestine development.

(A) 2D and 3D UMAP visualizations of CONCORD latent space, colored by cell type and cell cycle phase, with cell-type-colored UMAPs from scVI and Seurat shown for comparison. (B) Zoom-in views of epithelial cells in the 3D global UMAP, colored by cell subtype, zonation, and expression of zonation-specific markers (Bex4, Onecut2). A red marker and arrow indicate the viewing angle within the 3D global UMAP. (C) Zoom-in view of enteric nervous system (ENS) cells, colored by cell cycle phase and cell state/branch annotations, based on Morarach et al⁴⁷, along with state-specific gene expression. A red marker and arrow indicate the viewing angle. (D) Zoom-in view of Pdgfra- mesenchymal cells and smooth muscle cells, colored by cell cycle phase, subtype annotation, and selected subtype-specific markers. A red marker and arrow indicate the viewing angle. (E) Heatmap of all latent encodings generated by CONCORD, Seurat, and scVI. (F) Interpretation of CONCORD latent space using gradient-based attribution techniques. Activation of Neuron 46 (Z46) in epithelial and ENS cells is attributed to the co-expression of epithelial- and neuron-specific gene sets in their respective contexts. GO enrichment analysis of these gene sets is shown.

CONCORD efficiently integrated the data and resolved fine-grained substructures across diverse cell types (Figure 5A, Supplemental Fig. 7A, 8). It uniquely revealed loop-like patterns within many cell types—often missed by other methods—corresponding to cell cycle progression. Erythrocytes, which lack proliferative capacity, appropriately showed no such loop (Supplemental Figure 8). Given the complexity of these structures, 3D UMAP visualizations better preserved trajectory continuity than 2D projections (Supplemental Figure 7B), and we strongly encourage readers to explore the interactive embedding: (https://qinzhu.github.io/Concord_documentation/galleries/huycke_show/).

In intestinal epithelial cells, CONCORD not only resolved rare subtypes such as enteroendocrine cells (EECs), but also revealed two parallel differentiation trajectories, each forming its own cell cycle loop corresponding to spatially distinct regions (Figure 5B). These structures were not captured by other methods and were supported by adult zonation markers such as Bex4 and Onecut2⁴⁶, suggesting that CONCORD can detect epithelial zonation as early as embryonic day 13.5.

In the enteric nervous system (ENS), CONCORD captured cell cycle of Sox10⁺ progenitor cells and identified a Cck⁺ neuroblast population as the branch point leading to two purported differentiation trajectories marked by Etv1 and Bnc2⁴⁷ (Figure 5C). These trajectories appear to converge through shared expression of neuronal maturation genes broadly active at late stage of both branches (Supplemental Figure 7C). Notably, CONCORD was the only method that preserved both the cell cycle loop and the bifurcation, whereas other methods introduced discontinuities or misplaced the branching point (Supplemental Figure 8).

For mesenchymal cells, which comprise a major fraction of this dataset, CONCORD recovered the previously studied Pdgfra⁺ trajectory involved in villus formation⁴⁵ (Supplemental Figure 8) and uncovered extensive heterogeneity within the Pdgfra⁻ and smooth muscle populations (Figure 5D). These included four consecutive cell cycle loops marked by expression of Ebf1, Slit2, Kit, and Acta2, with gradual transitions between the loops (Figure 5D). Interestingly, Ebf1 and Slit2 have been linked to mesenchymal multipotency^48,49, while Kit marks interstitial cells of Cajal (ICC) and their progenitors^50,51. Unlike traditional approaches where cell cycle often confounds cell type annotation, CONCORD preserves both proliferation and differentiation structures, enabling the identification of previously uncharacterized subpopulations.

Unlike Seurat and scVI, which left many latent dimensions underutilized, CONCORD produced a dense and interpretable latent space that reflects rich biological structure and makes full use of its representational capacity (Figure 5E). As such, Each latent dimension in CONCORD typically encapsulates multiple gene co-expression programs and can be interpreted at single-cell or cell-state resolution using gradient-based attribution methods⁵² in a context-dependent manner (Figure 5F). For instance, latent neuron 46 (N46) was activated in both epithelial cells and the ENS cells but driven by two distinct sets of highly co-expressed genes in each context (Figure 5F, Supplemental Figure 7C). In epithelial cells, N46 activation was linked to goblet cell–specific genes enriched in glycosylation pathways, while in ENS cells, it reflected neuronal maturation genes expressed in late-stage neurons. Neither gene set shows strong expression outside its respective context, indicating that CONCORD latent captures biologically meaningful, context-specific gene co-expression programs.

Discussion

Mini-batch gradient descent underpins modern machine learning—including large language models, foundation models, and diffusion models. Growing evidence suggests that the composition of these mini-batches can influence model performance^31,53. In contrastive learning, where each sample is contrasted against others within a mini-batch, this influence is amplified—especially in biological datasets spanning multiple batches, where naive sampling can exacerbate batch effects and distort learned representations. Yet in contrastive learning for single cell data, uniform random sampling remains the norm, limiting the method’s ability to capture biological meaningful structure.

Our central insight is that, in contrastive learning, mini-batch composition not only influences, but fundamentally shapes the outcome. By rethinking how mini-batches are assembled, we turn contrastive learning’s sensitivity to mini-batch composition into a strength - transforming a conventional self-supervised framework into a powerful, generalizable approach for denoising, dimensionality reduction, and batch integration.

At the core of CONCORD is a unified, probabilistic sampler that integrates neighborhood-aware and dataset-aware strategies. The neighborhood-aware sampler balances global diversity with local variation, enabling the model to resolve both broad and fine-grained biological structures—as validated by geometric and topological benchmarks. The dataset-aware sampler ensures that each mini-batch is enriched with cells from a single dataset, allowing the model to learn biological variation without entangling batch effects. Unlike traditional methods that rely on overlapping states or explicit batch-distortion models, CONCORD mitigates batch effects solely through principled sampling and training. As a result, it implicitly aligns cells based on shared gene co-expression programs—a hallmark of transcriptomic data^6,54,55—making it especially robust when datasets have minimal or no overlap.

Importantly, CONCORD achieves state-of-the-art performance using a minimalistic architecture—just a single hidden layer—demonstrating that substantial gains can be achieved through rational sampling and training alone, without relying on deep architectures, complex objectives, or supervision. Across both simulated and real datasets, CONCORD consistently learns latent spaces that are denoised, interpretable, and topologically faithful. In whole-organism embryogenesis atlases, it accurately reconstructs fate bifurcations and lineage convergences, enabling detailed tracing from progenitor cells to terminal states. In contrast, existing methods often misalign these datasets, lose resolution, or fragment continuous trajectories. In mammalian intestinal development, CONCORD captures complex hierarchies, spatial zonation, and cell cycle loops—all within a single integrated analysis. Unlike traditional workflows that regress out cell cycle effects, CONCORD preserves and resolves both proliferative and differentiation programs, facilitating investigations into their interplay. Its interpretable latent space further enables gradient-based attribution analyses, allowing gene-level mechanistic insights at single-cell or cell-type resolution.

The current implementation of CONCORD emphasizes simplicity to enhance robustness and scalability, but the framework is fully extensible to more complex architectures—such as transformers⁵⁶—to support more intricate data modalities or biological contexts. This minimalist design reduces the number of tunable parameters, though several hyperparameters remain critical for optimal performance, including neighborhood size, enrichment probability, masking fraction, and contrastive temperature. To support users, we provide a set of default parameters validated across diverse datasets, along with detailed tutorials and insights from prior studies⁵⁷ to guide effective parameter optimization. Future improvements may include adaptive neighborhood sampling that scales with distance or density, removing the need for manually defined radii and enrichment probabilities.

In addition to the core contrastive encoder, CONCORD supports an optional decoder and classifier modules for gene-level batch correction, label transfer, and annotation-guided learning. Preliminary results suggest these tasks benefit from the model’s robust latent space, though further validation is ongoing. While the current benchmarks focused on single-cell RNA-seq, we have observed promising outcomes across other modalities, including spatial transcriptomics and scATAC-seq. Owing to its domain-agnostic design and generalized sampling framework, CONCORD holds potential beyond single-cell biology, offering a flexible and powerful approach for representation learning across a wide range of domains.

Methods

Self-supervised contrastive learning and sparse coding

We implemented CONCORD in PyTorch, building on a self-supervised contrastive learning approach inspired by SimCLR²¹ and SimCSE²², but with a unique dataset- and neighborhood-aware sampler design. The core loss function is the Normalized Temperature-scaled Cross Entropy Loss (NT-Xent loss)^21,22,58 applied to cell representations generated via random masking - following the design principles of unsupervised SimCSE²².

Theoretically, it has been shown²⁹ that if input data $x$ can be approximated as:

$$x=Mz+\epsilon$$

where $Mz$ represents the sparse signal with ${‖z‖}_0=\tilde{O}\left(1\right)$, and $\epsilon$ denotes noise, contrastive learning can provably recover the underlying sparse features when trained with ReLU networks and random masking augmentation. CONCORD adopts similar conditions: we apply LeakyReLU activations and independent random masking to each augmented view, which enhances the model’s ability to capture correlated gene co-expression patterns while suppressing spurious noise.

This sparse coding formulation provides a generalizable framework for modeling gene expression, extending beyond traditional methods such as non-negative matrix factorization (NMF), principal component analysis (PCA), factor analysis, and variational autoencoders (VAEs). Unlike these methods, sparse coding:

• Does not enforce orthogonality on $M$ (as in PCA),

• Does not require non-negativity constraints (as in NMF),

• Does not assume a probabilistic generative model (as in factor analysis and VAEs),

• Does not enforce Gaussian priors on the latent space (as in VAEs).

Instead, it assumes an intrinsic low-rank structure shaped by gene co-expression programs—an assumption widely supported by single-cell transcriptomic studies^6,54,55. By relaxing constraints on orthogonality, non-negativity, and Gaussian priors, the contrastive learning framework is better positioned to capture diverse gene regulatory programs that deviate from conventional assumptions. Finally, the use of random masking improves robustness to dropout—a pervasive artifact in scRNA-seq—and enhances biological interpretability, enabling the latent space to more faithfully represent gene programs underlying both discrete cell types and continuous trajectories.

Dataset and neighborhood-aware probabilistic sampler

At the heart of CONCORD is a probabilistic mini-batch sampler that determines how cells are grouped and contrasted during training. Unlike conventional contrastive learning frameworks that rely on uniform random sampling, CONCORD introduces a unified, generalizable sampling strategy that simultaneously (i) enriches for local neighborhoods and (ii) restricts each mini-batch primarily to a single dataset. This principled design reshapes the outcome of contrastive learning, enabling the model to produce a coherent, high-resolution, and batch-effect-mitigated representation of the cell state landscape.

We begin by coarsely approximating the global data manifold using a k-nearest neighbors (kNN) graph, where k is a user-defined parameter (typically moderately large). The graph can be constructed from normalized gene expression values, PCA projections, or a preliminary CONCORD batch-corrected embedding generated with the dataset-aware sampler. For scalability, we leverage the Faiss library⁵⁹ for efficient neighbor retrieval in large datasets. This kNN graph then guides neighborhood-aware sampling, modulated by a user-defined neighborhood enrichment probability, $p_{kNN}$.

To construct mini-batches that are both dataset- and neighborhood-enriched, we partition each mini-batch into four subsets—in-dataset neighbors, in-dataset global samples, out-of-dataset neighbors, and out-of-dataset global samples (Figure 1F). A “core sample” is randomly selected from one dataset to anchor both neighborhood and dataset-aware sampling. The four subsets are then sampled based on P_d (the probability of sampling from the same dataset, default 0.95) and P_kNN (the probability of sampling from the local kNN neighborhood, default 0.3) as follows:

• In-dataset neighbors: $P_d\times P_{kNN}$

  Cells from the same dataset and within the core cell’s kNN neighborhood.

• In-dataset global samples: $P_d\times \left(1-P_{kNN}\right)$

  Uniformly sampled cells from the same dataset, outside the neighborhood.

• Out-of-dataset neighbors: $\left(\left.1-P_d\right)\times P_{kNN}\right)$

  Cells from other datasets that fall within the core cell’s kNN neighborhood.

• Out-of-dataset global samples: $\left(1-P_d\right)\times \left(1-P_{kNN}\right)$

  Uniformly sampled cells from all other datasets.

The sampler is implemented using vectorized operations in PyTorch and NumPy to optimize memory efficiency and minimize computational overhead, ensuring scalability across large datasets and enabling rapid training.

Model architecture

A key advantage of CONCORD lies in its architectural flexibility. In this study, we implement a minimalist encoder with a single hidden layer, demonstrating that significant performance gains can be achieved through principled sampling and training alone, without the need for deep or complex neural networks. However, the architecture is fully extensible: users may substitute the encoder with more advanced models - such as transformers - to accommodate different data modalities or capture higher-order biological structures.

1. Encoder:

   The encoder receives randomly masked gene expression vectors and produces low-dimensional latent representations. By default, it consists of a fully connected network with a single hidden layer, although users can modify the number of layers and neurons as needed. An optional learnable feature masking module can be added before the encoder to differentially weight input genes, encouraging sparse and interpretable feature usage.

   Input gene-expression values are typically normalized by total count and log-transformed, though CONCORD remains robust to various normalization schemes provided they are applied consistently and avoid introducing negative or zero values. During training, each cell is augmented by randomly masking a subset of genes (recommended dropout probability: 0.3–0.6), and two independently masked versions are encoded to generate embeddings used in contrastive learning.

2. Layer normalization and activation:

   Each linear layer is followed by layer normalization and a user-configurable activation function (default: Leaky ReLU). Layer normalization operates across features within each sample, offering robustness to batch-specific variation—making it preferable to batch normalization⁶⁰, though the latter is also supported.

3. Contrastive objective:

   CONCORD employs the NT-Xent loss^21,22,58 operating on mini-batches of N cells. Each cell is randomly masked and encoded twice, yielding two different latent representations: $z_i$ and $z_j$, then the contrastive loss is:

   $$l_{i,j}=-\log \left(\frac{\exp \left(sim\left(z_i,z_i^{\prime }\right)/\tau \right)}{{\sum }_{k=1}^{2N}{1}_{\left[k\ne i\right]}\exp \left(sim\left(z_i,z_k\right)/\tau \right)}\right)$$

   where $sim\left(z_i,z_i^{\prime }\right)=\frac{z_i^T{z}_j}{‖z_i‖‖z_j‖}$ is the cosine similarity, and $\tau$ (default 0.5) is a customizable temperature hyperparameter that controls the extent of local separation and global uniformity of the embeddings⁵⁷.

4. Optional decoder and classifier:

   For applications requiring reconstruction of gene expression profiles, a decoder can be attached to the latent embeddings. To prevent the decoder from reintroducing batch-specific variation, a separate, learnable dataset embedding is appended only at decoding time—keeping the core latent space batch-effect-free.

   A classification head (i.e., a multi-layer perceptron trained with cross-entropy loss) can be appended to the encoder for downstream tasks such as cell-type annotation or doublet detection. The classifier can be trained on top of a pre-trained encoder or jointly with the encoder to actively guide cell-type separation in the latent space. While joint training can enhance class distinction, it may also impose a strong prior on the latent structure, potentially disrupting the continuity of trajectories. To mitigate overfitting, we recommend a train–validation split with early stopping during classifier training.

Model training

During each training epoch, CONCORD constructs mini-batches using its dataset- and neighborhood-aware sampler, followed by random mini-batch shuffling. The core contrastive objective—NT-Xent loss—is optimized using the Adam optimizer⁶¹. Optional loss terms, including mean squared error (MSE) for the decoder, cross-entropy loss for classification, and L1/L2 regularization for feature-masking modules, can be incorporated as needed. By default, all loss components are weighted equally, but users may adjust these weights to suit specific tasks. A learning rate scheduler is employed to gradually reduce the learning rate over time, promoting stable convergence.

Simulation pipeline

We developed a versatile simulation pipeline to generate synthetic single-cell gene expression data with diverse underlying structures. Unlike conventional simulators that predominantly produce discrete clusters, our pipeline accommodates a broad range of topologies, including linear trajectories, branching trees, loops, and intersecting paths frequently observed in real single-cell datasets.

In the first stage the state simulator constructs data according to a user-defined structure:

• Clusters: Cells form discrete groups characterized by unique gene programs, optionally including shared or ubiquitously expressed genes.

• Trajectories: Cells exhibit gradual shifts in gene expression, emulating cell differentiation processes.

• Loops and intersecting paths: Continuous trajectories that close into loops or intersect, representing cyclic biological processes.

• Trees: Hierarchical, branching lineages representing progenitor-to-terminal fate differentiation, configurable by branching factor and tree depth.

With the chosen structure, the pipeline first generates a noise-free data matrix with customizable cell and gene numbers. Expression values are then sampled from selected distributions (e.g., Normal, Poisson, Negative Binomial), introducing realistic variability and dropout patterns. Users can precisely control parameters including mean baseline expression, dispersion (noise level), dropout probability, and can enforce non-negativity or integer rounding of the generated values.

In the second step, an optional batch simulator introduces dataset-specific technical variability. This stage enables simulation of batch effects through scaling factors, differential sampling rates, batch-specific gene subsets, and expression-dependent dropout mechanisms. Multiple simulated batches are then concatenated into a single dataset, with customizable proportions and varying degrees of batch overlap to mimic real-world sampling scenarios.

By combining diverse gene expression structures with realistic noise models and customizable batch effects, this simulation pipeline can approximate a broad spectrum of biological and technical scenarios. As such, it provides a powerful testbed for benchmarking data-integration techniques, trajectory-inference algorithms, and manifold-learning methods under controlled yet biologically realistic conditions.

Benchmarking pipeline

To comprehensively evaluate the performance of CONCORD and other dimensionality reduction or data integration methods, we designed a robust benchmarking pipeline that integrates geometric, topological, biological, and batch-mixing metrics. This multifaceted assessment framework consists of the following components:

1. Topological assessments:

   To quantify the preservation of intrinsic topological features, we employed persistent homology analysis implemented via Giotto-TDA⁶². Persistent homology captures structural properties of the data across multiple scales, using Vietoris-Rips complexes constructed over increasing radii to generate persistence diagrams and Betti curves. Persistence diagrams reveal the lifespan of topological features such as connected components (Betti-0), loops (Betti-1), and voids (Betti-2). We summarized these diagrams through Betti curves and compared their mode—representing the most persistent Betti number across all scales—to the known topological ground truths. Additionally, we computed the entropy of Betti curves to quantify the stability and complexity of the inferred topology, with lower entropy reflecting stable and distinct structures, and higher entropy indicating noisy or unstable topologies. These metrics were scaled between 0 and 1 using min-max normalization to facilitate comparisons among methods.

2. Geometric assessments:

   We evaluated the preservation of geometric relationships by calculating distance correlations between embeddings and the corresponding noise-free reference data, averaging Pearson, Spearman, and Kendall’s tau correlations to robustly quantify global geometric similarity. For local neighborhood preservation, we employed trustworthiness⁶³, a metric assessing how faithfully high-dimensional neighborhood structures are maintained in lower-dimensional embeddings. Trustworthiness scores range from 0 (poor preservation) to 1 (perfect preservation), and we computed average trustworthiness scores across neighborhood sizes (k-values) from 10 to 100 in increments of 10. Additionally, we visualized trustworthiness as a function of k to reveal how each method performs at different local scales. In cluster simulations with cluster-specific noise, we further assessed the correlation of variance between the latent embedding and the noisy input data, quantifying how accurately each method preserves relative noise levels.

3. Batch mixing and biological label conservation:

   We adopt established metrics from the scIB-metrics package³³ to systematically evaluate biological label conservation and batch mixing. Biological label conservation was quantified using metrics such as Normalized Mutual Information (NMI) and Adjusted Rand Index (ARI), which measure the correspondence between known biological labels and inferred clusters. Batch mixing quality was assessed using silhouette scores and graph metrics to determine how effectively embeddings integrate cells from different batches or datasets.

   A key limitation of the scIB pipeline is that the pipeline does not fully accommodate the hierarchical and continuous nature of many biological systems. Consequently, for simulations with continuous trajectories or loops, we first apply Leiden clustering to noise-free data to define “clusters” as ground truth, or use “branch” labels as a proxy for cell states in tree simulations. Under these conditions, the scIB metrics are applied in a more coarse-grained manner, offering an approximate assessment in these more complex scenarios.

Data Availability

The human lung and pancreas datasets were compiled by Luecken et al.³³, and obtained from the scIB-metrics website (https://scib-metrics.readthedocs.io/en/stable/notebooks/lung_example.html) and the Open Problems in Single-Cell Analysis website (https://openproblems.bio/datasets/openproblems_v1/pancreas), respectively. The C. elegans embryogenesis atlas was downloaded from the Gene Expression Omnibus (GEO) (www.ncbi.nlm.nih.gov/geo) under accession code GSE126954. The joint C. elegans and C. briggsae dataset was obtained via email request from the authors of Large et al³⁷. The mouse intestinal developmental atlas was acquired from GEO under accession code GSE233407.