Abstract
Slope fractures play an important role in slope destabilization accidents induced by rainfall, but its influence on seepage field and slope stability is not fully studied, especially under the conditions of soil permeability anisotropy. This study aims to investigate the influence of anisotropic permeability property of soil and fractures on the seepage field and slope stability under rainfall conditions. The surface cracks of the slope are regarded as continuous medium, and the saturated-unsaturated seepage theory is applied to the numerical simulation of the fractured soil slopes with different anisotropic permeability ratios by Geo-studio software. The evolution of seepage field and slope stability under the rainfall conditions are investigated using finite element simulation tool. The simulation results reveal that fractures mainly impact the pressure distribution in the seepage field of the shallow layer of slope, and have little effect on the deep layer. Furthermore, the anisotropic permeability of the soil has a significant effect on the seepage field, safety factor, and fracture action of the slope under rainfall conditions. These findings provide critical insights into slope engineering and management under anisotropic soil conditions.
Keywords: Anisotropic seepage, Fracture, Rainfall infiltration, Slope stability, Finite element analysis
Subject terms: Civil engineering, Natural hazards
Introduction
Landslides constitute a significant proportion of geological disasters in China, and rainfall infiltration is one of the crucial factors contributing to slope instability and damage1–3. Especially, the impact of unsaturated slopes on stability and safety is particularly noteworthy, and the existence of cracks further exacerbates the situation of rainfall infiltration4. Consequently, numerous scholars have conducted comprehensive investigations into slope stability under rainfall conditions. Li et al.5 developed an indoor rainfall system, which can accurately regulate both the flow rate and intensity of rainfall, and conducted experiments to analyze the break-up and instability rule of high and steep slopes under unsaturated conditions. Based on the Xinjiang Bazhizui Hydroelectric Hub project in Jiangxi Province, Luo et al.6 revealed the hysteresis situation of pore pressure changes under different rainfall pattern and their impact on slope stability rankings. Hermawan et al.7 utilized the TRIGRS model to study rainfall data and other factors, and the model results showed the slope stability in the study area was related to the pre-rainfall precipitation intensity. Wu et al.8 used Geo-Studio software to analyze the impact of rainfall duration, intensity and other factors on slope stability, and obtained that short-term heavy rainfall could seriously threaten the slope safety. Zhang et al.9 used the finite element strength reduction method to analyze the influence rule of rainfall on the slope stability. Xu et al.10 employed the upper bound theorem of limit analysis to establish an analytical assessment framework that incorporates three-dimensional characteristics of slope, and investigated the impact of different rainfall and three-dimensional slope characteristics on the slope instability mode and the stability. Deliveris et al.11 carried out deep excavation of slope by empirical methods and employed parametric analysis method to investigate the importance of the relevant parameters. The parameters that have the greatest impact on slopes were rainfall intensity, soil permeability. Tan and Xu12 utilized Midas GTS to simulate the variation in seepage field under rainfall conditions and evaluated slope stability using the intensity discount method, and indicated the rate and magnitude of the decrease in slope safety factor with cracks, as well as the range of influence on the matric suction of the slope body, are greater than those without fractures under rainfall conditions. Hou et al.13 conducted simulations on the transient seepage field and stability evolution characteristics of slope under rainfall conditions with different depths of fractures, indicating that fractures are significant factors affecting slope seepage and stability. Yuan et al.14 found that soil with a high volume of pores had a high risk of disintegration under impact loading. Cao15 established a theoretical model of the dynamic soil-water characteristic curve and permeability coefficient equations of the fractures through laboratory tests and numerical analysis methods, and introduced a dual medium model that incorporates both fracture and pore properties to analyze the effects of fractures on seepage field and stability of expansive soil slopes. Jamalinia et al.16 considered the effect of natural conditions, and employed a FEM model to simulate slope stability, and the simulation results revealed that fracturing had a significant effect on the slope safety factor. Considering the spatial distribution and strength of filling cracks in slope, Dai et al.17 adopted the method of layered filling—bevel cutting—refilling to analyze the stability of an expansive soil slope, and found that filling fissures can attenuate strength of the expansive soil. Yuan et al.18 found the waterproofing coating had good waterproofing effects on the small cracks by the seepage quantity test. Wang et al.19 used the discrete element method (DEM) to study the influence of drying/wetting cycles on the stability of an expansive soil slope and showed that cracks played an essential role in the stability of expansive soil slope. Yuan et al.20 studied the permeability characteristics of Engineering Muck and found that the porosity and permeability channel could be optimized by adjusting the liquid-solid ratio, effectively reducing the landslide risk of landfill slope. It can be seen from the above research that the seepage characteristics and pore structure of materials play a crucial role in engineering. The above literature generally assumes soil properties are isotropic for research convenience, whereas natural soils are inherently anisotropic due to variations of the soil particles arrangement and structure21, and some scholars have acknowledged that anisotropy significantly influences slope stability22–24. Foroutan et al.25 investigated the impact of soil strength anisotropy on the bearing capacity of foundations facing slope, and provided a three-dimensional application chart. Through numerical simulation, Yuan et al.26 elucidated the influence law of fracture-induced anisotropy on slope rainfall infiltration, considering factors such as the direction, degree, and distribution area of fracture anisotropy, respectively. Aamodt et al.27 employed the NGI-ADP model provided by PLAXIS software to consider the strength anisotropy of soils, which demonstrated a higher safety coefficient compared to isotropic scenarios. Luo and Agarwal28 selected several slope angles and soil properties of gentle and steep slopes with low failure probability to study the effects of soil rotation anisotropy and spatial variability on slope failure under seismic conditions, and the results emphasized the importance of considering the combined effects of soil anisotropy and major principal fluctuation scale direction when designing gentle and steep slopes under seismic conditions. Shuhaib and Khassa29 investigated the effects of anisotropic permeability on seepage mode and slope stability of earth dam under fast and slow depth reduction by using a small-scale dam model, and showed that anisotropic permeability increased the seepage rate by more than 75% and decreased the slope stability by more than 55% compared to the isotropic case. Cao et al.30 proposed a coupled method to characterize the formation uncertainty and the rotational anisotropy of soil properties, and studied the stability of unsaturated soil slope considering the two uncertainties, and discovered that the rotational anisotropy of soil had an important effect on the slope stability and groundwater level. Based on the limit analysis and strength reduction method, Qin31 calculated the stability factor of a stepped slope in heterogeneous anisotropic soils, and found that the stability of step slope decreased with the increase of anisotropic parameters. Gu et al.32 established various infiltration coefficient ratios utilizing a rainfall infiltration model and Geo-Studio software to investigate the impact of anisotropic infiltration characteristics of soil slopes on the seepage field and stability under rainfall conditions.
While the above have studied the soil anisotropy and its influence on slope stability, there remains a paucity of studies addressing the effects of soil anisotropic seepage on stability of fractured soil slopes under rainfall conditions. This study aims to further investigate the influence of anisotropic permeability property of soil and fractures on the seepage field and slope stability using finite element simulations, providing actionable insights for slope design and management in rainfall-prone regions. Based on the saturated-unsaturated seepage theory, a finite element model of a fractured slope is established using Geo-studio software. In the SEEP/W module, the seepage field changes of slopes with fractures under different anisotropic permeability are mainly studied, and the safety stability of slopes is analyzed through the SLOPE/W module on the basis of seepage.
Methods
Basic theory
Saturated-unsaturated seepage differential equation
In slope seepage analysis, rainfall may induce changes in surface runoff, rainwater infiltration, and groundwater level, thus forming saturated zone and unsaturated zone. The water movement between these zones is interrelated, so this situation can be regarded as a saturated-unsaturated flow problem. The traditional Darcy’s law is typically applied to address the saturated seepage issues. Richards33 then integrated fundamental principles of soil water movement to derive the control equation for unsaturated seepage:
 |
1 |
Where h is the total head,  and
and  are the permeability coefficients in the x-axial and y-axial directions, respectively, and Q is the flow boundary, and
are the permeability coefficients in the x-axial and y-axial directions, respectively, and Q is the flow boundary, and 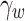 is the water weight, and t is the time, and
is the water weight, and t is the time, and  is the slope of the soil-water characteristic curve. The SEEP/W module employs of this governing Eq. (1) to analyze and calculate the saturated-unsaturated seepage problem.
is the slope of the soil-water characteristic curve. The SEEP/W module employs of this governing Eq. (1) to analyze and calculate the saturated-unsaturated seepage problem.
In numerical simulations, the horizontal and vertical directions are typically designated as the coordinate axes, but the primary seepage direction of slope soil often differs from this standard orientation in the actual projects. As illustrated in Fig. 1, a local coordinate system 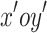 is employed where its axes align with the main seepage direction of the soil, and the coordinate system after the clockwise rotation angle
is employed where its axes align with the main seepage direction of the soil, and the coordinate system after the clockwise rotation angle  is the global coordinate system
is the global coordinate system 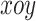 . Figure 1 illustrates the transformation from local to global coordinate systems, which aligns the axes with the main seepage direction for more accurate analysis.
. Figure 1 illustrates the transformation from local to global coordinate systems, which aligns the axes with the main seepage direction for more accurate analysis.
Fig. 1.

Global coordinate system and local coordinate system.
Fractures
In numerical simulation, the equivalent medium method is one of the most widely employed techniques for addressing fractures. This method simplifies the complex geometry and distribution characteristics of fractures, and fully considers the influence of fractures. The literature26 results indicated that when the saturated permeability coefficient along the fracture direction exceeded the rainfall intensity, fracture anisotropy had a minimal impact on the permeability field. Since the saturated permeability coefficient exceeds the rainfall intensity in this study, the fracture seepage anisotropy is not considered.
Rainfall mode
Calculation model
In this study, an unsaturated soil slope is selected as the research object, and fractures are uniformly distributed across the slope surface. A two-dimensional numerical calculation model is established using Geo-Studio software. The dimensions of the model are illustrated in Fig. 2. The SEEP/W module is used to conduct transient seepage analysis of the slope under rainfall conditions. The module can simulate the evolution of the seepage field in the slope, and determine the pressure distribution and provide key data on the water pressure distribution. The soil-water characteristic curve and hydraulic conductivity function of the material need to be set in the analysis process, so as to describe the moisture retention effect of the unsaturated soil. The heaviness of water 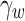 is
is  . The soil-water characteristic curve of the material is derived from measurements taken from an unsaturated soil sample by Wu34, which have been smoothed. The slope of this curve is
. The soil-water characteristic curve of the material is derived from measurements taken from an unsaturated soil sample by Wu34, which have been smoothed. The slope of this curve is 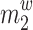 , as shown in Fig. 3. The hydraulic conductivity function was determined by derivation using Gardner function35 based on Van Genuchten model36 as depicted in Fig. 4.
, as shown in Fig. 3. The hydraulic conductivity function was determined by derivation using Gardner function35 based on Van Genuchten model36 as depicted in Fig. 4.
Fig. 2.
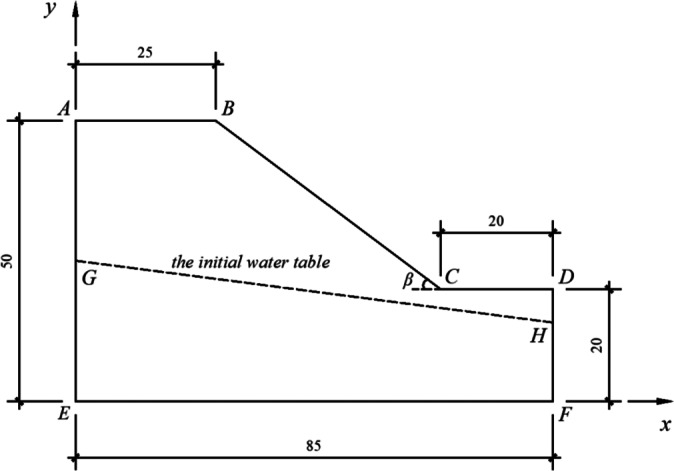
Slope model (unit: m).
Fig. 3.

The soil-water characteristic curve.
Fig. 4.

The direction x hydraulic conductivity function.
Based on the seepage analysis results obtained from the SEEP/W module, which provide critical information about pore water pressures and hydraulic conditions within the slope, the SLOPE/W module is subsequently used to calculate the safety factor of the slope and assess its stability. The analysis utilizes the Mohr-Coulomb model, with the physical and mechanical parameters of the soil are presented in Table 1. According to findings in literature37, it is assumed that the permeability coefficient of fractures is 2 to 4 orders of magnitude greater than that of the undisturbed soil. Consequently, the saturated permeability coefficient of fractures is set at 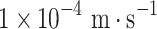 , reflecting this substantial disparity and its implications for slope stability assessments.
, reflecting this substantial disparity and its implications for slope stability assessments.
Table 1.
Physical and mechanical parameters of soil.
Horizontal saturated Permeability coefficient 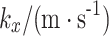
|
Internal friction Angle 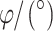
|
Cohesion 
|
Heavy 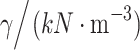
|
|---|---|---|---|
1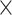 10−6 10−6
|
24 | 20 | 18 |
Boundary conditions and mesh
GH represents the initial water level of the slope, and the following areas GE and FH are designated as the constant head boundary conditions, with the head values set to 25 m and 14 m, respectively. Because the pressure head is zero, the head value at these constant head boundaries is the total head value h, and the above regions AG, DH and EF located at the bottom of the slope are set as no-flow boundary conditions. The slope surface areas AB, BC and CD are set as rainfall boundary conditions, which is the flow boundary Q, where the rainfall intensity of AB and CD is 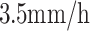 , and the rainfall intensity of the slope surface BC needs to be discounted, which is
, and the rainfall intensity of the slope surface BC needs to be discounted, which is  (where
(where  is the edge slope Angle). The rainfall time is set to be t = 48 h, and the total calculation time extends to 120 h. It is crucial to note that when rainfall intensity exceeds the permeability coefficient of the slope soil, the rainwater cannot completely infiltrate into the slope. In this scenarios, the water head of the slop surface will not change during the infiltration process. The rainfall boundary should be changed to a fixed head boundary to more accurately analyze the stability of the slope, with the head value equal to the elevation value.
is the edge slope Angle). The rainfall time is set to be t = 48 h, and the total calculation time extends to 120 h. It is crucial to note that when rainfall intensity exceeds the permeability coefficient of the slope soil, the rainwater cannot completely infiltrate into the slope. In this scenarios, the water head of the slop surface will not change during the infiltration process. The rainfall boundary should be changed to a fixed head boundary to more accurately analyze the stability of the slope, with the head value equal to the elevation value.
To enhance the accuracy of the numerical simulations, the grid refinement is applied specifically to the fracture regions within the slope. The calculation model grid is divided into 6311 nodes and 6166 units, as shown in Fig. 5. The black areas on the slope surface represent fissure units, which are critical for capturing the localized effects of fractures on seepage and stability.
Fig. 5.

Mesh division and locations of monitoring points.
Result and analysis
Slope stability analysis under rainfall conditions
Changes of seepage field in slope under rainfall conditions
In anisotropic soil, water flows preferentially in the direction of higher permeability, resulting in non-uniformity of flow path. This non-uniform flow will cause water accumulation in local areas or faster drainage speed, resulting in different water content in the slope, which affects shear strength and slope stability. In order to investigate the influence of soil anisotropic permeability on the slope, monitoring points R, S and T are established at coordinates (5, 10), (5, 30) and (5, 50), respectively, and the locations of these monitoring points are illustrated in Fig. 5. This study initially focuses on  , and studies the soil permeability anisotropy by considering horizontal and vertical directions. The anisotropy ratio of permeability coefficient
, and studies the soil permeability anisotropy by considering horizontal and vertical directions. The anisotropy ratio of permeability coefficient  is set to values of 0.1, 0.5, 1, 2, and 10, respectively. When the value of
is set to values of 0.1, 0.5, 1, 2, and 10, respectively. When the value of 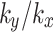 is 1, it indicates that the permeability of soil is isotropic. The variations of pore water pressure with time at each monitoring point for different values of
is 1, it indicates that the permeability of soil is isotropic. The variations of pore water pressure with time at each monitoring point for different values of 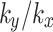 are presented in Fig. 6. It can be observed that pore water pressure of the slope has changed throughout the entire process, and the influence of different values of
are presented in Fig. 6. It can be observed that pore water pressure of the slope has changed throughout the entire process, and the influence of different values of  on the pore water pressure of the monitoring point is also different. The effects of rainfall on the pore water pressure at the monitoring point R for different values of
on the pore water pressure of the monitoring point is also different. The effects of rainfall on the pore water pressure at the monitoring point R for different values of  are illustrated in Fig. 6(a). When the values of
are illustrated in Fig. 6(a). When the values of 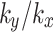 are 0.1 and 0.5, there exists a situation during which the water pressure remains at zero for a period of time. This is because the seepage coefficient in the vertical direction is smaller than the rainfall intensity, resulting in rainwater accumulation on slope surface, which increases the water content within the surface soil layer and decreases the negative pore water pressure values until they reach zero. With the increase of rainfall time, the rainfall can’t infiltration further into the soil. Before the end of the rainfall, the pore water pressure at monitoring point R remains at zero. When the value of
are 0.1 and 0.5, there exists a situation during which the water pressure remains at zero for a period of time. This is because the seepage coefficient in the vertical direction is smaller than the rainfall intensity, resulting in rainwater accumulation on slope surface, which increases the water content within the surface soil layer and decreases the negative pore water pressure values until they reach zero. With the increase of rainfall time, the rainfall can’t infiltration further into the soil. Before the end of the rainfall, the pore water pressure at monitoring point R remains at zero. When the value of  is 0.1, saturation of the slope surface is achieved more rapidly and persists for a longer duration. In contrast, when the value of
is 0.1, saturation of the slope surface is achieved more rapidly and persists for a longer duration. In contrast, when the value of 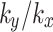 is 2, the vertical seepage coefficient exceeds that of the rainfall intensity, and the rainwater infiltrates into the soil promptly while maintaining an unsaturated state on the slope surface, and the pore water pressure is still negative. It is particularly noteworthy that when the value of
is 2, the vertical seepage coefficient exceeds that of the rainfall intensity, and the rainwater infiltrates into the soil promptly while maintaining an unsaturated state on the slope surface, and the pore water pressure is still negative. It is particularly noteworthy that when the value of  is 10, there is a significant difference compared to other cases, which is because the vertical permeability coefficient is much higher than the rainfall intensity, and the rainwater infiltrates into the slope more quickly, and the upper part of the water supply is insufficient, so the upper negative pore water pressure value continues to increase.
is 10, there is a significant difference compared to other cases, which is because the vertical permeability coefficient is much higher than the rainfall intensity, and the rainwater infiltrates into the slope more quickly, and the upper part of the water supply is insufficient, so the upper negative pore water pressure value continues to increase.
Fig. 6.
Changes of pore water pressure under different values of 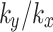 (Unit: kPa): (a) Monitoring point R, (b) Monitoring point S, (c) Monitoring point T.
(Unit: kPa): (a) Monitoring point R, (b) Monitoring point S, (c) Monitoring point T.
The effects of rainfall on pore water pressure at monitoring point S for different values of 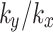 are shown in Fig. 6(b). As the value of
are shown in Fig. 6(b). As the value of 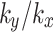 increases, the variation of pore water pressure becomes more pronounced. Notably, when the value of
increases, the variation of pore water pressure becomes more pronounced. Notably, when the value of 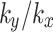 is 10, there is a sudden increase in the hydraulic gradient. This phenomenon can be attributed to an increase in the vertical permeability coefficient, which enhances the drainage rate of pore water within the slope and consequently results in an increase in pore water pressure inside the slope. For monitoring point T, the influence rule depicted in Fig. 6(c) aligns with that observed at monitoring point S. But any value of
is 10, there is a sudden increase in the hydraulic gradient. This phenomenon can be attributed to an increase in the vertical permeability coefficient, which enhances the drainage rate of pore water within the slope and consequently results in an increase in pore water pressure inside the slope. For monitoring point T, the influence rule depicted in Fig. 6(c) aligns with that observed at monitoring point S. But any value of 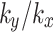 , it is important to note that the magnitude of the change in pore water pressure consistently is smaller than that at monitoring point S. Thus, the variation degree of pore water pressure inside the slope decreases as the depth of the monitoring point location increases.
, it is important to note that the magnitude of the change in pore water pressure consistently is smaller than that at monitoring point S. Thus, the variation degree of pore water pressure inside the slope decreases as the depth of the monitoring point location increases.
By comparison, it can be concluded that during the rainfall phase, the greater the value of  , the deeper the impact of rainfall on the pore water pressure of the slope. As the value of
, the deeper the impact of rainfall on the pore water pressure of the slope. As the value of 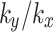 increases, rainwater infiltration is accelerated, and the soil infiltration front to descend downward until it connects with groundwater. This process results in significant changes in pore water pressure inside the slope, and the change of pore pressure at monitoring points S and T is more obvious. When the value of
increases, rainwater infiltration is accelerated, and the soil infiltration front to descend downward until it connects with groundwater. This process results in significant changes in pore water pressure inside the slope, and the change of pore pressure at monitoring points S and T is more obvious. When the value of  is less than 1, the changes of pore water pressure caused by rainfall are primarily concentrated near the surface of the slope, with notable variations of pore water pressure curve mainly occurs at the monitoring point R. After rainfall ceases, the rainwater inside the slope gradually dissipates and drains outward, which causes further changes in pore water pressure until the equilibrium is reached. The water pressure value that tends to equilibrate at the monitoring point R decreases as the increase of the value of
is less than 1, the changes of pore water pressure caused by rainfall are primarily concentrated near the surface of the slope, with notable variations of pore water pressure curve mainly occurs at the monitoring point R. After rainfall ceases, the rainwater inside the slope gradually dissipates and drains outward, which causes further changes in pore water pressure until the equilibrium is reached. The water pressure value that tends to equilibrate at the monitoring point R decreases as the increase of the value of 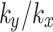 . Conversely, at monitoring points S and T, the water pressure value rises with the increase of the value of
. Conversely, at monitoring points S and T, the water pressure value rises with the increase of the value of 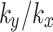 .
.
In order to investigate the pore water pressure near the fracture, monitoring lines a, b, d and g were set up at distances of 2 m, 3 m, 4 m and 5 m from the vertical slope surface, respectively, and the schematic positions of these four monitoring lines are illustrated in Fig. 4. The effects of different values of  on the pore water pressure near the fracture under the case of
on the pore water pressure near the fracture under the case of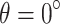 are investigated as follows. Additionally, changes in pore water pressure of the different monitoring lines for the 24 h moments of rainfall with
are investigated as follows. Additionally, changes in pore water pressure of the different monitoring lines for the 24 h moments of rainfall with 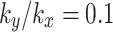 and 2 are presented in Fig. 7. In Fig. 7(a), it is evident that the curvature of pore water pressure at monitoring line a exhibits the most significant; conversely, the curve of pore water pressure at monitoring line g shows minimal floating, which indicates that the influence of fractures on the pore water pressure at monitoring line a is strongest while being weakest at monitoring line g. The change in pore water pressure depicted in Fig. 7(b) is the same as that observed in Fig. 7(a). However, the pore water pressure in monitoring line g increases significantly. This is attributed to the rise of groundwater level, and the infiltration of rainwater increases the saturation in the soil and the pressure within the slope. Overall, it is evident that the closer the distance to fractures, the greater variations in the distribution of pore water pressure. The influence of fractures on pore water pressure in the slope is negatively correlated with the distance from the fracture. This is consistent with the principle that the influence depth of features is limited. The monitoring line a has been selected to study the effect of 24-hour rainfall on the pore water pressure around fractures under different values of
and 2 are presented in Fig. 7. In Fig. 7(a), it is evident that the curvature of pore water pressure at monitoring line a exhibits the most significant; conversely, the curve of pore water pressure at monitoring line g shows minimal floating, which indicates that the influence of fractures on the pore water pressure at monitoring line a is strongest while being weakest at monitoring line g. The change in pore water pressure depicted in Fig. 7(b) is the same as that observed in Fig. 7(a). However, the pore water pressure in monitoring line g increases significantly. This is attributed to the rise of groundwater level, and the infiltration of rainwater increases the saturation in the soil and the pressure within the slope. Overall, it is evident that the closer the distance to fractures, the greater variations in the distribution of pore water pressure. The influence of fractures on pore water pressure in the slope is negatively correlated with the distance from the fracture. This is consistent with the principle that the influence depth of features is limited. The monitoring line a has been selected to study the effect of 24-hour rainfall on the pore water pressure around fractures under different values of 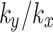 shown in Fig. 8. Within a distance in the horizontal direction, an increase in value of
shown in Fig. 8. Within a distance in the horizontal direction, an increase in value of  corresponds to a decrease in pore water pressure along monitoring line a; conversely, beyond this distance, an opposite phenomenon occurs due to the rise of the groundwater level caused by rainfall. As the value of
corresponds to a decrease in pore water pressure along monitoring line a; conversely, beyond this distance, an opposite phenomenon occurs due to the rise of the groundwater level caused by rainfall. As the value of 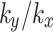 increases further, both the groundwater level and affected area expand, leading to more pronounced changes in pore water pressure. Due to the effect of fractures, the distribution pattern of pore water pressure in monitoring line a exhibits curvature resembling the shape of the fracture. When the value of
increases further, both the groundwater level and affected area expand, leading to more pronounced changes in pore water pressure. Due to the effect of fractures, the distribution pattern of pore water pressure in monitoring line a exhibits curvature resembling the shape of the fracture. When the value of 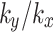 is 0.1 and 0.5, fluctuation degree is greater compared to the value of
is 0.1 and 0.5, fluctuation degree is greater compared to the value of 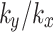 is 1, while the opposite is the case when values of
is 1, while the opposite is the case when values of  is 2 and 10. This phenomenon indicates that the impact of fractures on the pore water pressure distribution in the surrounding soil diminishes as the value of
is 2 and 10. This phenomenon indicates that the impact of fractures on the pore water pressure distribution in the surrounding soil diminishes as the value of  increases, which is due to the fact that the vertical permeability of the soil increases which reduces reliance on fractures as the preferential channel for rainwater infiltration when the value of
increases, which is due to the fact that the vertical permeability of the soil increases which reduces reliance on fractures as the preferential channel for rainwater infiltration when the value of 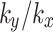 increases.
increases.
Fig. 7.
Pore water pressure diagram of different monitoring lines (Unit: kPa): (a)
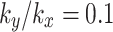 , (b)
, (b)
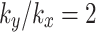 .
.
Fig. 8.

Pore water pressure of monitoring line a under different values of  (unit: kPa).
(unit: kPa).
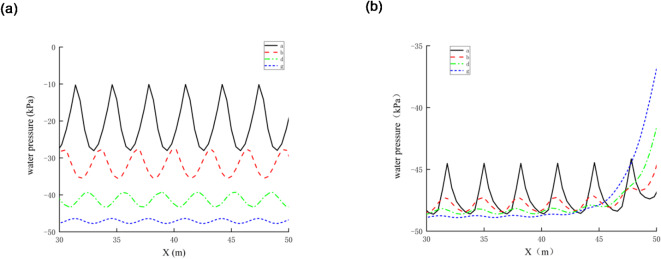
The variations of pore water pressure near the fractures under different the value of 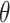 are further investigated. Figure 9 illustrates the variations of pore water pressure of the monitoring line a under different the value of
are further investigated. Figure 9 illustrates the variations of pore water pressure of the monitoring line a under different the value of  at 24-hour of rainfall when the value of
at 24-hour of rainfall when the value of 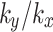 is 0.1 and 2, respectively. It is evident that the pore water pressure of soil surrounding fractures varies with different values of
is 0.1 and 2, respectively. It is evident that the pore water pressure of soil surrounding fractures varies with different values of 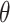 . The variations of pore water pressure at the value of
. The variations of pore water pressure at the value of  is 0.1 are depicted in Fig. 9(a). When
is 0.1 are depicted in Fig. 9(a). When 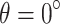 , the peak pore water pressures are − 10.3 kPa and − 28.1 kPa. When the value of
, the peak pore water pressures are − 10.3 kPa and − 28.1 kPa. When the value of 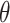 is -30° and − 60°, the peaks of pore water pressure are − 6.3 kPa, -15.3 kPa and − 15.6 kPa, -27.5 kPa, respectively, changing by 38.8%, 44.6% and 51.5%, 2.1%, respectively compared to the value of
is -30° and − 60°, the peaks of pore water pressure are − 6.3 kPa, -15.3 kPa and − 15.6 kPa, -27.5 kPa, respectively, changing by 38.8%, 44.6% and 51.5%, 2.1%, respectively compared to the value of 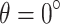 . When the value of
. When the value of  is 30° and 60°, the peaks pore water pressures are − 24.3 kPa, -41.3 kPa and − 45.6 kPa, -31.6 kPa, respectively, with changes of 135.9%, 47.0%, and 342.7%, 12.5%, respectively compared with the value of
is 30° and 60°, the peaks pore water pressures are − 24.3 kPa, -41.3 kPa and − 45.6 kPa, -31.6 kPa, respectively, with changes of 135.9%, 47.0%, and 342.7%, 12.5%, respectively compared with the value of 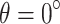 . Figure 9(b) shows the changes in pore water pressure when the value of
. Figure 9(b) shows the changes in pore water pressure when the value of 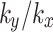 is 2, and the trend remains consistent with that observed at the value of
is 2, and the trend remains consistent with that observed at the value of  is 0.1, that is, the influence on the pore water pressure is greater when it is a positive value than negative one.
is 0.1, that is, the influence on the pore water pressure is greater when it is a positive value than negative one.
Fig. 9.
Pore water pressure of monitoring line a under different values of 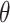 (unit: kPa): (a)
(unit: kPa): (a)
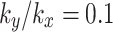 , (b)
, (b)
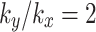 .
.
Changes of slope safety factor
Rainfall changes the original pore water pressure inside a slope, which directly affect the effective stress of the soil inside the slope, and further change the slope stability. On the basis of seepage calculations, a slope stability analysis module SLOPE/W based on Morgenstern-Price method, is employed to further investigate and elucidate the variations of the slope safety factor under different conditions. Additionally, it is essential to consider the effect of shear strength in the unsaturated zone on the slope stability, and this shear strength is calculated using the unsaturated soil shear strength formula (2) proposed by Fredlund38. Where, 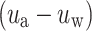 refers to the matrix suction of unsaturated soil, and the strength caused by it is related to the suction internal friction angle
refers to the matrix suction of unsaturated soil, and the strength caused by it is related to the suction internal friction angle  . In order to simplify the calculation, it is assumed that the suction internal friction angle
. In order to simplify the calculation, it is assumed that the suction internal friction angle  above the water level is equal everywhere, taking
above the water level is equal everywhere, taking  .
.
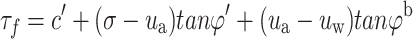 |
2 |
The variation curve of the safety factor of slope over time under different values of 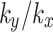 is illustrated in Fig. 10. At 120 h, the safety factors for values of
is illustrated in Fig. 10. At 120 h, the safety factors for values of  0.1, 0.5, 1, 2, and 10 are 1.2216, 1.1547, 1.0993, 1.0390, and 0.9792, respectively. When compared to the isotropic case, the safety factors for values of
0.1, 0.5, 1, 2, and 10 are 1.2216, 1.1547, 1.0993, 1.0390, and 0.9792, respectively. When compared to the isotropic case, the safety factors for values of  0.1, 0.5, 2, and 10 change by 11.13%, 5.04%, 5.49% and 10.93%, respectively. Thus, the anisotropic seepage has a significant influence on the slope safety factor. It can be generally observed from Fig. 10 that under identical rainfall conditions, a higher value of
0.1, 0.5, 2, and 10 change by 11.13%, 5.04%, 5.49% and 10.93%, respectively. Thus, the anisotropic seepage has a significant influence on the slope safety factor. It can be generally observed from Fig. 10 that under identical rainfall conditions, a higher value of 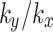 corresponds to a lower safety factor of the slope and consequently worse stability of slope. During the 0 ~ 48 h rainfall stage, as rainfall duration increases continuously leads to a decline in the slope safety factor which reaches its minimum at the end of the 48 h rainfall. Compared with its initial value, it decreases by 4.0%, 8.3%, 11.6%, 16.6%, and 27.8%, respectively. In the entire rainfall stage, the rate of decrease in the safety factor is negatively correlated with the value of
corresponds to a lower safety factor of the slope and consequently worse stability of slope. During the 0 ~ 48 h rainfall stage, as rainfall duration increases continuously leads to a decline in the slope safety factor which reaches its minimum at the end of the 48 h rainfall. Compared with its initial value, it decreases by 4.0%, 8.3%, 11.6%, 16.6%, and 27.8%, respectively. In the entire rainfall stage, the rate of decrease in the safety factor is negatively correlated with the value of 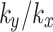 , indicating that at any given moment, a higher value of
, indicating that at any given moment, a higher value of  corresponds to a lower safety factor of the slope, thereby reflecting an increasingly unstable state. In the 48 h ~ 120 h rain cessation stage, with the completion of rainfall, the pore water pressure in the soil requires time to gradually release, and the slope safety factor rises slightly and then gradually tends to stabilize. With rising values of
corresponds to a lower safety factor of the slope, thereby reflecting an increasingly unstable state. In the 48 h ~ 120 h rain cessation stage, with the completion of rainfall, the pore water pressure in the soil requires time to gradually release, and the slope safety factor rises slightly and then gradually tends to stabilize. With rising values of 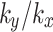 , the value of the safety factor that finally tends to stable is lower. Compared to its initial safety factor, it decreases by 5.0%, 10.5%, 14.8%, 19.4%, and 24.13%, respectively. Notably, when the value of
, the value of the safety factor that finally tends to stable is lower. Compared to its initial safety factor, it decreases by 5.0%, 10.5%, 14.8%, 19.4%, and 24.13%, respectively. Notably, when the value of 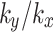 is 10, there is a marked difference in changes observed in the safety factor of the slope-demonstrating a continuous rebound phenomenon attributed to both high vertical seepage coefficient and fractures effect, which causes the rainwater to penetrate into the deeper soil layer, so that the saturation of the soil in the upper part of the slope continues to slowly decrease, and the stability of the slope slowly increases.
is 10, there is a marked difference in changes observed in the safety factor of the slope-demonstrating a continuous rebound phenomenon attributed to both high vertical seepage coefficient and fractures effect, which causes the rainwater to penetrate into the deeper soil layer, so that the saturation of the soil in the upper part of the slope continues to slowly decrease, and the stability of the slope slowly increases.
Fig. 10.

Slope safety factor curves under different values of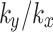 .
.
Since the soil permeability in all directions is equal when the value of 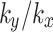 is 1, variations in the value of
is 1, variations in the value of 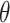 do not significantly affect the permeability properties of the slope. Figure 11 shows the curves of the change in the slope safety factor with time under different values of
do not significantly affect the permeability properties of the slope. Figure 11 shows the curves of the change in the slope safety factor with time under different values of 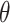 when the values of
when the values of 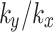 are 0.1 and 2. Under identical rainfall conditions, it is evident that the alterations in value of
are 0.1 and 2. Under identical rainfall conditions, it is evident that the alterations in value of 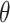 lead to differing safety factor of the slope. In Fig. 11(a), when the value of
lead to differing safety factor of the slope. In Fig. 11(a), when the value of  is 0.1, the slope stability factor decrease no matter how the value of
is 0.1, the slope stability factor decrease no matter how the value of 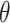 changes, and higher values of
changes, and higher values of  correspond to smaller the slope safety factors and consequently worse the slope stability. When the value of
correspond to smaller the slope safety factors and consequently worse the slope stability. When the value of 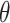 is 60°, the slope safety factor continues to decline during the rain cessation phase without exhibiting any convergence behavior. Conversely, the situation of
is 60°, the slope safety factor continues to decline during the rain cessation phase without exhibiting any convergence behavior. Conversely, the situation of 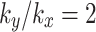 is shown in Fig. 11(b), the slope safety factor increases irrespective of changes in the value of
is shown in Fig. 11(b), the slope safety factor increases irrespective of changes in the value of 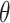 changes, and larger the value of
changes, and larger the value of 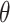 yield higher slope safety factor and improved slope stability. In this case, no matter how the value of
yield higher slope safety factor and improved slope stability. In this case, no matter how the value of  is taken, the slope safety factor curve tends to converge in the rain stop phase. The comparison shows that more attention should be directed towards the influence of the value of
is taken, the slope safety factor curve tends to converge in the rain stop phase. The comparison shows that more attention should be directed towards the influence of the value of  change on the slope stability when the values of
change on the slope stability when the values of 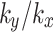 less than 1.
less than 1.
Fig. 11.
Slope safety factor curves under different values of : (a)
: (a)
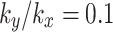 , (b)
, (b)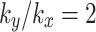 .
.
Conclusions
The seepage and stability of the slope with fractures under rainfall conditions are studied by numerical simulation, and the influence of anisotropic permeability ratio 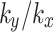 on fractured slope is emphasized. By analyzing the variations in pore water pressure distribution and slope safety factors under different anisotropic conditions, the influence laws of rainfall on both seepage and stability of the slope are studied under different anisotropic permeability coefficient ratios
on fractured slope is emphasized. By analyzing the variations in pore water pressure distribution and slope safety factors under different anisotropic conditions, the influence laws of rainfall on both seepage and stability of the slope are studied under different anisotropic permeability coefficient ratios  . The simulation results indicate that:
. The simulation results indicate that:
Rainfall significantly affects the pore water pressure distribution of the slope. The greater the value of
 , the greater the depth of rainfall influence on pore water pressure.
, the greater the depth of rainfall influence on pore water pressure.The impact of fractures on surrounding pore water pressure decreases as the value of
 increases. Notably, fractures exert a more pronounced influence on surrounding pore water pressure in scenarios with positive
increases. Notably, fractures exert a more pronounced influence on surrounding pore water pressure in scenarios with positive 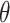 compared to negative ones.
compared to negative ones.The slope safety factor decreases with prolonged rainfall duration, but tends to stable gradually after the rain stops. A higher the value of
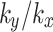 correlates with a lower the slope safety factor, resulting in an increased rate of decline and variation in magnitude concerning the safety factor.
correlates with a lower the slope safety factor, resulting in an increased rate of decline and variation in magnitude concerning the safety factor.Compared with the isotropic case, the slope safety factor changes to a greater or lesser extent when considering the anisotropy of soil seepage under rainfall conditions. And when the value of
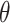 changes, the slope safety factor will be lower when the value of
changes, the slope safety factor will be lower when the value of 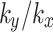 is less than 1, resulting in increased slope instability.
is less than 1, resulting in increased slope instability.
Acknowledgements
The research described in this paper was financially supported by the Foundation for University Key Teacher by the Ministry of Education of Henan Province (2015GGJS-277) and Educational Commission of Henan Province (21A560017).
Author contributions
C. Z.: Conceptualization, Writing-review, Editing, Funding Acquisition. M.Q.: Writing, Software, Investigation, Editing, Resources, Formal analysis. L. H.: Supervision, Validation. Y. Q.: Investigation, Resources. All authors have read and agreed to the published version of the manuscript.
Data availability
The datasets in the current study are available from the corresponding author upon reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Long Hong and Yunfei Qi contributed equally to this work.
References
- 1.Wu, L., He, B. & Peng, J. Analysis of rainfall-caused seepage into underlying bedrock slope based on seepage deformation coupling. Int. J. Geomech.24 (5), 04024076. 10.1061/IJGNAI.GMENG-9175 (2024). [Google Scholar]
- 2.Lian, J. et al. Shallow stability analysis for unsaturated clay slope of subgrade under rainwater infiltration. Journal of the China Railway Society. 43(09): 109–117. (2021). 10.3969/j.issn.1001-8360. 09. 015 (2021).
- 3.Khan, K. U. J. et al. Influence of rainfall infiltration on the stability of unsaturated coal gangue accumulated slope. J. Mt. Sci.18 (6), 1696–1709. 10.1007/s11629-020-6567-4 (2021). [Google Scholar]
- 4.Nian, G., Chen, Z., Bao, M., Zhang, L. & Zhu, T. Rainfall infiltration & three-dimensional stability analyses of fractured rock slopes considering Preferential flow. Nat. Hazards. 118 (3), 2629–2656. 10.1007/s11069-023-06112-9 (2023). [Google Scholar]
- 5.Li, X. et al. Experimental study on instability mechanism and critical intensity of rainfall of high-steep rock slopes under unsaturated conditions. Int. J. Min. Sci. Technol.33 (10), 1243–1260. 10.1016/j.ijmst.2023.07.009 (2023). [Google Scholar]
- 6.Luo, W. et al. Seepage field & stability analysis of slope under different rain type circulation. Sci. Technol. Eng.23 (25), 10918–10925 (2023). [Google Scholar]
- 7.Hermawan, K., Sugianti, K., Martireni, A. & Satrio, N. A. Spatial and temporal analysis prediction of landslide susceptibility using rainfall infiltration and grid-based slope stability methods in west bandung area of west Java-indonesia. IOP Conference Series: Earth and Environmental Science. 1173(1): 012031. (2023). 10.1088/1755-1315/1173/1/012031
- 8.Wu, X., Yang, Y. & Ye, Z. Stability of rock-soil slopes under rainfall infiltration and its influencing factors. J. Water Resour. Water Eng.33 (05), 189–199. 10.11705/j.issn.1672-643X.2022.05.24 (2022). [Google Scholar]
- 9.Zhang, C. et al. Stability analysis of slip resistant piles and 3-D Geonet Mats for grassed slope retaining slopes under rainfall effects. J. Henan Univ. Urban Constr.33 (03), 23–28. 10.14140/j.cnki.hncjxb.2024.03.004 (2024). [Google Scholar]
- 10.Xu, J., Du, X., Zhao, X. & Li, L. Analytical stability analysis of rainfall-infiltrated slopes based on the Green–Ampt model. Int. J. Geomech.23 (2), 04022277. 10.1061/(ASCE)GM.1943-5622.0002647 (2023). [Google Scholar]
- 11.Deliveris, A. V., Theocharis, A. I., Koukouzas, N. C. & Zevgolis, I. E. Numerical slope stability analysis of deep excavations under rainfall infiltration. Geotech. Geol. Eng.40 (8), 4023–4039 (2022). [Google Scholar]
- 12.Tan, Y. & Xu, W. Analysis of the influence of rainfall infiltration on the stability of fractured rock slopes. J. Geol. Hazards Environ. Preservation. 33 (02), 78–85 (2022). [Google Scholar]
- 13.Hou, D., Zhou, Y. & Zheng, X. Seepage and stability analysis of fissured expansive soil slope under rainfall. Indian Geotech. J.53 (1), 180–195. 10.1007/s40098-022-00667-3 (2023). [Google Scholar]
- 14.Yuan, B. et al. Sustainability of the polymer SH reinforced recycled granite residual soil: properties, physicochemical mechanism and applications. J. Soils Sediments. 23 (1), 246–262. 10.1007/s11368-022-03294-w (2023). [Google Scholar]
- 15.Cao, L. Evolution law of cracks & slope stability analysis of expansive soil. Shanghai Jiao Tong University. 001452. (2016). 10.27307/d.cnki.gsjtu.2016.001452
- 16.Jamalinia, E., Vardon, P. J. & Steele-Dunne, S. C. The impact of evaporation induced cracks and precipitation on Temporal slope stability. Comput. Geotech.122, 103506. 10.1016/j.compgeo.2020.103506 (2020). [Google Scholar]
- 17.Dai, Z. et al. Strength characteristics and slope stability analysis of expansive soil with filled fissures. Appl. Sci.10 (13), 4616. 10.3390/app10134616 (2020). [Google Scholar]
- 18.Yuan, B., Liang, J., Lin, H., Wang, W. & Xiao, Y. Experimental study on influencing factors associated with a new tunnel waterproofing for improved impermeability. J. Test. Eval.52 (1), 344–363. 10.1520/JTE20230417 (2024). [Google Scholar]
- 19.Wang, H., Wang, Y. & Jin, F. Stability of expansive soil slopes under Wetting–Drying cycles based on the discrete element method. Water16 (6), 861. 10.3390/W16060861 (2024). [Google Scholar]
- 20.Yuan, B. et al. Eco-efficient recycling of engineering muck for manufacturing low-carbon geopolymers assessed through LCA: exploring the impact of synthesis conditions on performance. Acta Geotech.10.1007/s11440-024-02395-9 (2024). [Google Scholar]
- 21.Zhang, C., Zhu, Y. & Wang, B. Research on Two-dimensional dynamic response of orthotropic medium. Chin. Q. Mech.37 (4), 648–657. 10.15959/j.cnki.0254-0053.2016.04.004 (2016). [Google Scholar]
- 22.Ng, C. W., Qu, C., Ni, J. & Guo, H. Three-dimensional reliability analysis of unsaturated soil slope considering permeability rotated anisotropy random fields. Comput. Geotech.151, 104944. 10.1016/j.compgeo.2022.104944 (2022). [Google Scholar]
- 23.Tang, H. & Wei, W. Finite element analysis of slope stability by coupling of strength anisotropy and strain softening of soil. Rock. Soil. Mech.40 (10), 4092–4100. 10.16285/j.rsm.2019.0164 (2019). [Google Scholar]
- 24.Ng, C. W. et al. Risk assessment of soil slope failure considering copula-based rotated anisotropy random fields. Comput. Geotech.136, 104252. 10.1016/j.compgeo.2021.104252 (2021). [Google Scholar]
- 25.Foroutan Kalourazi, A., Jamshidi Chenari, R. & Veiskarami, M. Bearing capacity of strip footings adjacent to anisotropic slopes using the lower bound finite element method. Int. J. Geomech.20 (11), 04020213. 10.1061/(ASCE)GM.1943-5622.0001858 (2020). [Google Scholar]
- 26.Yuan, L., Lin, Y., Ding, P. & Han, C. Influence of anisotropy induced by fissures on rainfall infiltration of slopes. Chin. J. Geotech. Eng.38 (01), 76–82. 10.11779/CJGE201601007 (2016). [Google Scholar]
- 27.Aamodt, M. T., Grimstad, G. & Nordal, S. Effect of strength anisotropy on the stability of natural slopes. IOP conference series: earth and environmental science. 710(1): 012025. (2021). 10.1088/1755-1315/710/1/012025
- 28.Luo, N. & Agarwal, E. Seismic stability and failure mechanisms of gentle and steep slopes considering soil rotated anisotropy and Spatial variability. Soil Dyn. Earthq. Eng.183, 108821–108821. 10.1016/J.SOILDYN.2024.108821 (2024). [Google Scholar]
- 29.Shuhaib, K. Z. & Khassa, I. S. Influence of permeability anisotropy on seepage and slope stability of an earthen dam during rapid and slow drawdown. Math. Modelling Eng. Probl.11 (5). 10.18280/MMEP.110527 (2024).
- 30.Cao, W., Zhou, A. & Shen, S. Stability of unsaturated soil slope considering stratigraphic uncertainty and rotated anisotropy of soil properties. Int. J. Numer. Anal. Meth. Geomech.48 (2), 359–376. 10.1002/NAG.3642 (2023). [Google Scholar]
- 31.Qin, G. Stability analysis of nonhomogeneous and anisotropic stepped slopes under the influence of earthquakes. Heliyon9 (4), e15057–e15057. 10.1016/J.HELIYON.2023.E15057 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gu, Y., Yuan, Y. & Li, X. Influence of soil anisotropic infiltration on slope stability under rainfall conditions. J. Saf. Sci. Technol.19 (S1), 43–49. 10.11731/j.issn.1673-193x.2023.S1.007 (2023). [Google Scholar]
- 33.Richards, L. A. Capillary conduction of liquids through porous mediums. Physics1 (5), 318–333. 10.1063/1.1745010 (1931). [Google Scholar]
- 34.Wu, J., Yuan, L. & Lu, T. Stability analysis of unsaturated expansive soil slope. Rock. Soil. Mech.29 (S1), 363–367. 10.16285/j.rsm.2008.s1.114 (2008). [Google Scholar]
- 35.Gardner, W. R., Hillel, D. & Benyamini, Y. Post-irrigation movement of soil water: 1. Redistribution. Water Resour. Res.6 (3), 851–861. 10.1029/WR006i003p00851 (1970). [Google Scholar]
- 36.Van Genuchten, M. T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J.44 (5), 892–898. 10.2136/sssaj1980.03615995004400050002x (1980). [Google Scholar]
- 37.Zhang, J. Study of the fissures, volume change and permeability of expansive soil under wetting and drying cycles. South. China Univ. Technol. 84 (3), (2010).
- 38.Fredlund, D. G. & Rahardjo, H. Soil Mechanics for Unsaturated Soils. John Wiley & Sons. (1993). 10.1002/9780470172759
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets in the current study are available from the corresponding author upon reasonable request.