Linkage Disequilibrium Patterns and tagSNP Transferability among European Populations

Abstract

The pattern of linkage disequilibrium (LD) is critical for association studies, in which disease-causing variants are identified by allelic association with adjacent markers. The aim of this study is to compare the LD patterns in several distinct European populations. We analyzed four genomic regions (in total, 749 kb) containing candidate genes for complex traits. Individuals were genotyped for markers that are evenly distributed at an average spacing of ∼2–4 kb in eight population-based samples from ongoing epidemiological studies across Europe. The Centre d'Etude du Polymorphisme Humain (CEPH) trios of the HapMap project were included and were used as a reference population. In general, we observed a conservation of the LD patterns across European samples. Nevertheless, shifts in the positions of the boundaries of high-LD regions can be demonstrated between populations, when assessed by a novel procedure based on bootstrapping. Transferability of LD information among populations was also tested. In two of the analyzed gene regions, sets of tagging single-nucleotide polymorphisms (tagSNPs) selected from the HapMap CEPH trios performed surprisingly well in all local European samples. However, significant variation in the other two gene regions predicts a restricted applicability of CEPH-derived tagging markers. Simulations based on our data set show the extent to which further gain in tagSNP efficiency and transferability can be achieved by increased SNP density.

Introduction

The efficiency of both candidate-gene and whole-genome approaches to identifying genetic loci associated with disease phenotypes relies on the minimization of SNP markers genotyped in a given population. For such a mapping approach, the selection process of markers to be genotyped is crucial (Chapman et al. 2003; Wang and Todd 2003). The observation that a significant fraction of the human genome is organized into a series of high–linkage disequilibrium (LD) regions that are separated by short segments in very low LD has led to the development of a number of algorithms that can be used to select informative markers for association studies (Cardon and Abecasis 2003). In Caucasians, approximately one-third to one-half of chromosomes are structured as high-LD regions, varying in length from a few kb to >300 kb (Gabriel et al. 2002; Phillips et al. 2003; Wall and Pritchard 2003; Ke et al. 2004). All marker-selection algorithms are based on the assumption that the complete set of sequence variants within a region of high background LD bears redundant information and can be significantly reduced to a selected subset of tagging markers. These markers can tag either neighboring markers or a set of common haplotypes within an LD block. There is an ongoing debate as to which tagging algorithm should be used, but little is known about the choice of reference populations to which such algorithms should be applied.

It has been suggested that the populations genotyped in the HapMap project may serve as reference populations for the selection of tagging markers in association studies (International HapMap Consortium 2003). In its first round, the HapMap project aims to genotype 600,000 SNPs at an average distance of 5 kb across the whole genome in four populations with African, Asian, and European ancestry (see HapMap Homepage). The European patterns are represented by 30 trios from a U.S. (Utah) population of northern and western European ancestry (CEPH sample [Dausset et al. 1990]).

As stated by the International HapMap Consortium (2003), the general applicability of the HapMap data has to be confirmed by samples from several local populations. Our study aims to describe the SNP allelic variation within candidate-gene regions in eight local European populations selected along a line from north to south. All samples represent population-based samples of ongoing epidemiological collections. The dense marker spacing of 2–4 kb over four autosomal regions (total size 749 kb) and a novel robust method to assess the reliability of LD block boundaries enables us to compare LD block boundaries and LD block content among these European populations. Although there was general agreement in the majority of LD patterns, detectable differences among study populations were found. In the context of association studies, we tested the performance of tagging SNPs (tagSNPs) that were defined in local population samples in comparison with tagSNPs that were defined in the HapMap sample, and we simulated the effect of an increased marker density.

Subjects and Methods

Population Samples

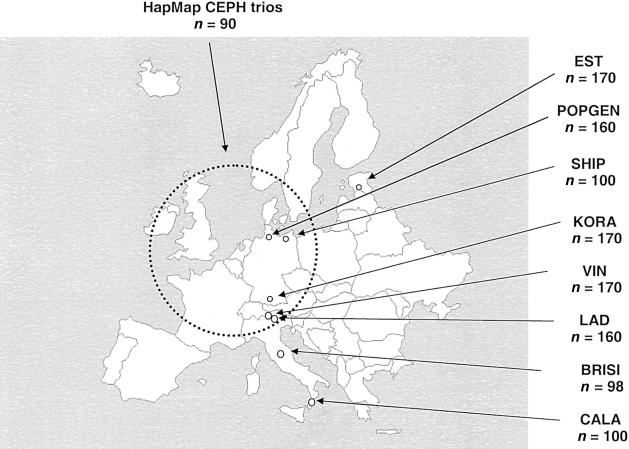
All population samples came from ongoing cross-sectional epidemiological surveys. Figure 1 shows the locations and sample sizes of eight regional population surveys. Samples were chosen randomly from the entire population. A ninth sample, 30 CEPH trios (Coriell Cell Repositories) used in the HapMap project, represents an emigrant population of northern and western European origin. The 170 individuals of Estonian ethnicity (EST) represent a random selection from ∼1.3 million Estonian inhabitants, excluding Russians. Randomly selected samples for the northern German population came from two epidemiological surveys, Study on Health in Pomerania (SHIP) (regional population size 212,000) and POPGEN (collected in Schleswig-Holstein [population size 1.15 million]) (see popgen Web site). The KORA samples were collected as part of a population-based, epidemiological project, KORA S2000 (Cooperative Health Research in the Region of Augsburg), and represent an urban region in the southern part of Germany with 610,000 inhabitants. Two Alpine populations were sampled: inhabitants of Vinschgau (VIN) in south Tyrol (population size 34,300), and members of the Ladin-speaking community (LAD) of Grödnertal and Gadertal (population size 16,800). The Brisighella sample (BRISI) represents a small town with 9,000 inhabitants from the region of Emilia-Romagna, Italy. A sample from Calabria (CALA) was sampled from a catchment area with 560,000 inhabitants. The sex ratio of all samples was ∼0.5, except for that of CALA, with 70 males and 30 females. Mean age was 55 years for all population samples except CALA and EST (mean 30 years). Prior to collection, we obtained approval from the relevant ethical committees/institutional review boards and informed consent from all participating subjects. When necessary, approval from data privacy oversight committees was obtained.

Figure 1.

Study populations and sample sizes (n)

SNP Selection and Genotyping

We selected four genomic regions, all containing candidate genes for different complex diseases. For each region, SNPs were evenly selected, covering the candidate gene and 76–174 kb of the upstream and downstream flanking regions (table 1). All information about the selected SNPs was extracted from the public dbSNP database. Genotyping of SNPs was achieved by primer extension of multiplex PCR products, with detection of the allele-specific extension products by matrix-assisted laser desorption/ionization time-of-flight (MALDI-TOF [Sequenom]) mass spectroscopy. The frequencies of genotypes from successfully typed SNPs (average call rate, 98%) were in Hardy-Weinberg equilibrium. The genotype data can be downloaded from our project Web site (see GSF European LD Pattern Project Web site).

Table 1.

Selected Gene Regions and SNPs

			Size(in kb) of		No. of SNPs					Median Spacing(in kb) of
Gene	Disease	Chromosome Region	Gene	Region	Selecteda	Validatedb	Commonc	For HapMapComparisond	PopulationDifferentiatinge (%)	ValidatedSNPs	HapMapSNPs
SNCA	Parkinson	4q21	112	188	97	78	73	33	5 (6)	2.1	4.5
LMNA	Cardiomyopathy	1q21.2	23	177	37	29	27	17	4 (14)	4.4	6.7
FKBP5	Depression	6p21.31	115	289	76	44	37	37	10 (23)	6.2f	6.3
PLAU	Alzheimer	10q22.2	6.3	95	53	34	32	13	27 (79)	2.2	6.0

^aSelected from public SNP databases.

^bPolymorphic in our sample set and in Hardy-Weinberg equilibrium.

^cMinor-allele frequency >5%.

^dFor comparison, we selected a set of SNPs similar to the currently available set in the International HapMap Project (April 2004).

^eP<.001.

^fSNP spacing within the gene is 3.7 kb.

Statistics and LD-Pattern Analyses

Population differentiation was tested by permutation tests (10,000 permutations) based on F statistics, by use of the software package ARLEQUIN. F_ST values were calculated on three levels: for each marker separately, for each gene region separately, and for all four gene regions combined. F_ST values based on haplotype frequencies in each block were also tested. The standard expectation-maximization algorithm was used to estimate the haplotype frequencies.

To compare haplotype block boundaries among populations, it is critical to apply a relatively robust method for the definition of haplotype blocks on a constant set of common markers (Cardon and Abecasis 2003; Schwartz et al. 2003). We developed a simple bootstrap approach based on the standard algorithm of Gabriel et al. (2002), which invokes confidence bounds of pairwise D′ to define sequences of markers with little evidence of historical recombination. Bootstrapping, in the present context, means resampling the individual multilocus genotypes of a given population with replacement. The frequencies of block boundary positions across all 100 bootstrap runs represent confidence estimates for block borders. We plot boundary frequencies for the start and end of blocks separately, to be able to track individual blocks. In addition, we allowed blocks to overlap each other, which gives a more natural framework. Because most block definitions define haplotype blocks by block-internal characteristics, neighboring blocks may compete for the same intermediary markers, and there is no reason why one of the blocks (e.g., the larger of the two in a greedy algorithm) should win. Each block with at least one private marker is considered to be a block. Blocks completely nested within a larger block are not considered. An overall measure of similarity between two populations was calculated as the sum of cross-products of bootstrap frequencies, standardized by the sums of within-products of bootstrap frequencies, similar to the genetic identity of Nei (1972). An appropriate distance was given by the negative logarithm of this measure and was used in a multidimensional scaling algorithm to map the overall block similarity.

Selection and Efficiency Testing of tagSNPs

Either the CEPH trios or the local European populations, with varying numbers of randomly selected subsamples (100 replicates), were used as reference samples. For these reference samples, two different tagSNP selection algorithms were applied. The first algorithm finds SNPs that best tag other typed SNPs (i.e., tagSNPs); the second algorithm finds SNPs that represent common haplotypes within predefined blocks (i.e., haplotype-tagging SNPs [htSNPs]).

A greedy algorithm for the selection of tagSNPs (Carlson et al. 2004) was employed. In the first step, a SNP exceeding an r² threshold of 0.8 with the maximum number of other SNP sites is identified. This SNP and all associated SNPs are grouped in one bin. A bin does not have to be a group of neighboring SNPs but rather can be split up in several regions. Any SNP exceeding the threshold r² with all other sites in the bin is specified as a tagSNP. There may be more than one tagSNP, and we used only the one with the maximum average r². This binning process is iterated, and all as-yet-unbinned SNPs are analyzed at each round, until all sites are binned or characterized as singleton bins. The efficiency of a given tagSNP set in other population samples is tested by the following criteria: an average r² among all typed SNPs and the best SNP-specific tagSNP, a minimal r² among all typed SNPs and the best SNP-specific tagSNP, and a ratio of SNPs above the threshold r² to any tagSNP.

The htSNP selection method started with the definition of blocks, in accordance with the standard method of Gabriel et al. (2002). Because we wanted to compare the efficiency of htSNPs across several populations, we always used the block structure of the CEPH trios as the reference and forced the block structure of other populations to this reference structure. A single optimal set of htSNPs within each block was identified by sequential steps (Zhang and Jin 2003); these steps account for haplotype coverage (80% and 90% thresholds), optimal r² among SNPs, and even spacing. To evaluate the selected htSNP set in any population and to compare between populations, we defined two statistics (chromosomal coverage of tagged haplotypes and ratio of nontagged common haplotypes), whereby common haplotypes are defined by a frequency >5%.

Results

Single SNPs

Allele frequencies of most single markers did not differ significantly among population samples. In three gene regions, the proportion of population-differentiating markers (defined by signficance level P<.001) varied between 6% and 23% (table 1). An exception was PLAU, with 79% population-differentiating SNPs. Maximum values for allele-frequency differences were ∼20% and were mostly seen between EST and CALA, thus indicating a geographical gradient between the northern and southern populations (table A1 [online only]). The pattern of population differentiation for each gene region is shown in table A2 (online only). Significant population differences in allele frequencies appeared mostly for the gene PLAU but also for FKBP5 and LMNA. The CEPH founders were significantly different from the southern Italian populations BRISI and CALA. EST and the northern German collections SHIP and POPGEN showed significant differences from all Italian populations. The Alpine populations of VIN and LAD differed both from the southern Italian populations and from the northern European populations. The overall pattern of genetic differentiation reflects well the geographical localization of the population samples (table A3 and fig. A1 [online only]).

LD Structure

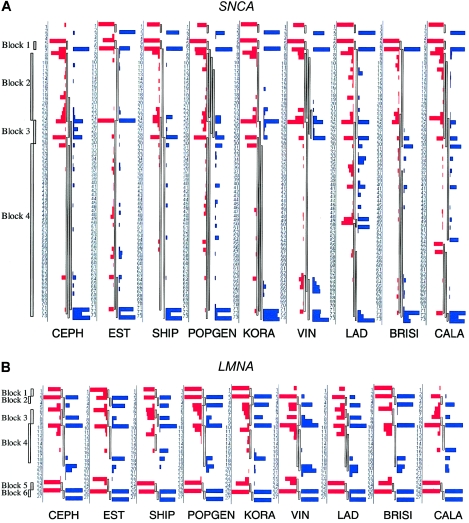
Standard plots of pairwise LD revealed similar patterns across samples (fig. A2 [online only]). To compare the LD structure across populations in a detailed and robust probability-based assessment, block overlaps were allowed and bootstrap frequencies of specific boundary positions were evaluated. The observed LD block structure and the bootstrap frequencies for each block start and block end are shown in figure 2. The calculations are based on a sample size of 100 individuals per population, to exclude variation in sample size as a potential confounder.

Figure 2.

Bootstrap frequencies of block starts and block ends in all population samples. All samples have an equal population size of 100 individuals (except BRISI, with 98 individuals). SNP markers are ordered vertically by their physical sequence. The length of red or blue bars indicates the bootstrap frequency of block starts or block ends, respectively, at the given position. Between the bars, the observed block structure is shown, with blocks allowed to overlap. To the left of each CEPH graph, the block structure of CEPH is shown, in accordance with the standard algorithm of Gabriel et al. (2002), without allowance for overlapping blocks . An example of a boundary shift can be seen at the end of block 4 in LMNA, which shows clear differences between the populations tested.

The general patterns of block structures are similar across samples, which is most prominent in the LMNA gene. Five of the six blocks in LMNA have nearly conserved block starts and ends across all study populations. Only the end of the largest block varied between positions 15 and 21, depending on the population studied. This represents a shift in the block extension in the range of 7–15 kb. Another example of differences in block boundaries is obvious for the SNCA region, where the largest block (between marker positions 30 and 73) has a tendency to break up into two pieces at different positions in the VIN (positions 63–67), LAD (positions 48–51), and CALA (positions 53–57) samples. Individual breakpoints of LD blocks for the Alpine populations VIN and LAD were also detected in the FKBP5 region between positions 14 and 18. PLAU also exhibited variable block structure.

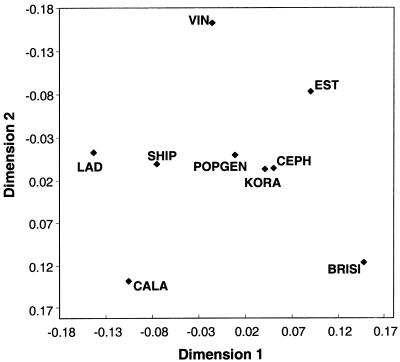
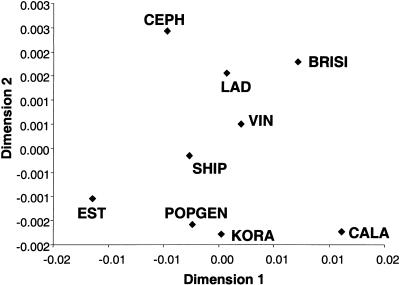
The overall variability in block structure among the populations is shown in figure 3. In a combined multidimensional scaling for all four gene regions, the most extreme and individual block structures were indicated for EST, LAD, VIN, BRISI, and CALA. The German populations, SHIP, POPGEN, and KORA, and the reference population CEPH appear in the center, indicating an intermediate block structure. Similar patterns were found when each gene was analyzed separately.

Figure 3.

Overall similarity of block boundaries across all four gene regions. The first two dimensions, after a multidimensional scaling of the dissimilarity measure of block boundaries, are shown. Sample sizes are adjusted to a size of 100 individuals. The Alpine and geographically peripheral populations (EST, LAD, VIN, BRISI, and CALA) differ the most from all other population samples.

Haplotypes

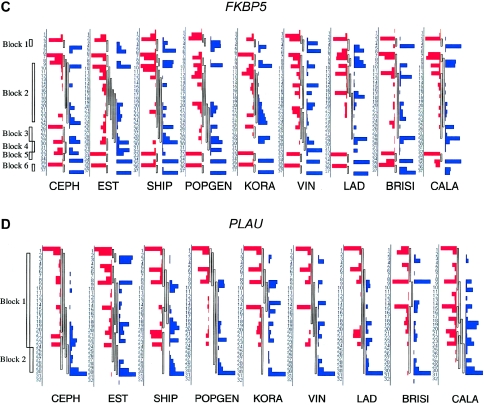
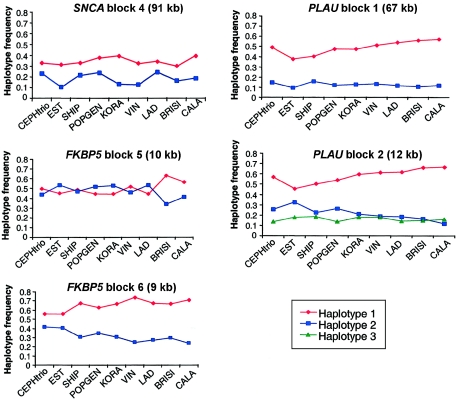
The standard algorithm of Gabriel et al. (2002), applied to the CEPH trios, allowed us to define four blocks in SNCA, six blocks in LMNA, six blocks in FKBP5, and two blocks in PLAU (see fig. 2, for reference of block positions, and fig. A3 [online only], for haplotype estimations). Significant haplotype frequency differences among populations were found only in block 4 of SNCA (P=.001), blocks 5 and 6 of FKBP5 (P=.03 and P=.02, respectively), and blocks 1 and 2 of PLAU (P=.001 and P=.01, respectively). Figure 4 shows the frequencies of all common haplotypes (frequency >10%) within the blocks that showed significant differences between populations. After Bonferroni correction for multiple testing, only the haplotype distributions of SNCA block 4 and PLAU block 1 remained significant. A clear geographic variation was evident with FKBP5 and PLAU but not with SNCA. In the PLAU gene region, haplotype 1 in block 1 showed the most extreme frequency values in EST (40%) and CALA (57%) and showed a gradient in between these two values in the remaining six populations. CEPH trios showed intermediate frequencies. A similar pattern was found for the haplotypes in block 2 of PLAU. There was also a gradient between EST and CALA in block 6 of FKBP5, but here CEPH trios are most similar to the EST sample. In block 5 of FKBP5, BRISI and CALA diverge from all other samples.

Figure 4.

Frequencies of common haplotypes (>10%) in all populations for the five haplotype blocks with significant population differentiation. For block numbers, see figure 2. Populations are arranged on the X-axis in a north-to-south localization. Geographical frequency gradients are prominent in blocks 1 and 2 of PLAU and in block 6 of FKBP5.

tagSNPs

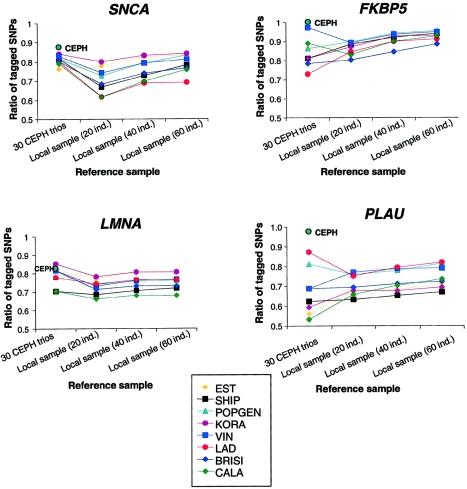
We first tested the efficiency of tagSNPs, which were defined to represent untagged SNPs with a high correlation coefficient (r² > 0.8 [Carlson et al. 2004]). Figure 5 shows the performance of CEPH trios, as a reference for this tagSNP selection, in comparison with local population samples of different sizes. For each sample size, average values across 100 replicates are given. Only the criterion of a ratio of tagged SNPs above the threshold, which is the relative portion of SNPs correlated with any tagSNP by an r² value >0.8, is shown. Other evaluation criteria (see the “Subjects and Methods” section) gave similar results (see table A4 [online only]). A reduced SNP set, which is comparable to the HapMap set, was used for the tagSNP selection (table 1). This reduced SNP set comprised ∼40% of SNPs identical to HapMap data. The selected tag SNPs were then tested on the full SNP set in all populations. The LD patterns appeared to be similar across all different SNP sets (see fig. A4 [online only]). There was no difference between the tagSNP set defined from CEPH trios and the tagSNP set defined from CEPH founders only, indicating that the additional phase information does not change the outcome.

Figure 5.

Performance of CEPH trios and local samples with different sample sizes used as references for tagSNP definition (by use of the method of Carlson et al. [2004]). The performance criterion shown is the ratio of tagged SNPs above the r² threshold of 0.8. The tagSNP sets that were defined in the CEPH trios were tested on all populations, whereas the tagSNP sets of local samples were tested only on the same local population. CEPH trios performed relatively well as reference (ratio of tagged SNPs >0.7), except for the PLAU gene region.

The tagSNPs identified in the CEPH trios performed well for the genes SNCA, FKBP5, and LMNA. For >70% of typed SNPs, the r² value was >0.8 with the best tagSNP. SNP allelic variation in KORA, for example, is well represented by CEPH tagSNPs for the genes SNCA and LMNA. In LMNA and SNCA, a local sample size of 20 individuals as a reference performs mostly worse than the 30 CEPH trios. Only a sample size of 40 or 60 individuals is comparable to CEPH trios. In FKBP5, most local samples of 20 individuals performed better as a reference than the CEPH sample, except for VIN and CALA. A different situation was seen in PLAU, where six populations showed a ratio of tagged SNPs of <70%, when the CEPH sample was used as reference—the worst ratio was from the CALA sample, with only 53%. For the same gene, data from 20 random individuals of most populations performed better as a reference than CEPH trios.

With the current HapMap SNP density as a reference, minimal r² values between tagged and tagSNPs were as low as 0.036, even for the most conserved gene regions around SNCA and LMNA. We therefore tested the performance of tagSNP sets, when selected from the full SNP set in SNCA and PLAU, for which we had a >2-fold SNP density compared with that of the HapMap. The general pattern—a local sample with 20 individuals performs mostly better as a reference than the CEPH sample in PLAU, and CEPH performs better than local samples in SNCA—did not change, but the differences were less pronounced, and, even for PLAU, the ratio of tagged SNPs was >70% in all tested populations (table A4 [online only]).

Performance patterns were similar when the haplotype-based tagSNP selection method (i.e., the htSNP selection method) was used (Zhang and Jin 2003), but differences between CEPH and local references were weaker than those measured by the r² method (table A5 [online only]). When CEPH trios were used as reference, chromosomal coverage of tagged haplotypes was below the intended threshold (80% and 90%, respectively) only for the PLAU gene (see population samples EST, SHIP, and KORA).

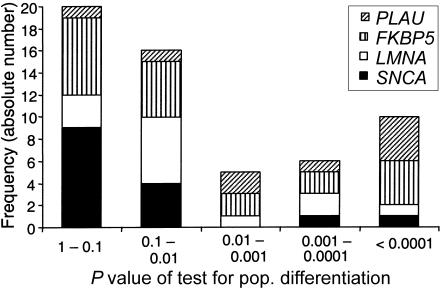
tagSNPs may also be seen as a set of relatively independent markers. To assess the probability of recruiting population-differentiating SNPs in a genomic approach, we plotted a histogram of the P values of tests for population differentiation for all tagSNPs defined by the method of Carlson et al. (2004) in CEPH trios (fig. 6). The majority of tagSNPs did not show strong population differences, underlining their universality. Most highly significant markers were found in the gene regions PLAU and FKBP5.

Figure 6.

Histogram of P values of tests for population differentiation, on the basis of 57 tagSNPs from all gene regions in the CEPH trios. The allele frequencies of most tagSNPs were similar across populations (P>.01). Exceptions were the tagSNPs of the PLAU gene.

Discussion

Individual population history and geographic variation may challenge the usefulness of a single European reference population for the selection of tagSNPs in association studies. Allele and haplotype frequencies show a clear geographic variation. Most dramatic frequency shifts lie in the upper range of values found in the survey of random loci done by Cavalli-Sforza et al. (1994), but these are still low compared with the values in strongly selected loci (e.g., cystic fibrosis variants [Lao et al. 2003]). The pattern of genetic differentiation corresponds relatively well to the European genetic variation described by Barbujani and Sokal (1990) and Cavalli-Sforza et al. (1994). The relatively strong genetic divergence of the Italian populations, CALA and BRISI, and the Alpine populations, LAD and VIN, from all other populations can be attributed to isolation resulting from linguistic differences (Germanic-Romance) and physical boundaries (the Alps). The two Italian populations, BRISI and CALA, also show significant differences from the CEPH sample and are therefore less well represented by this reference population.

Large-scale association studies—probably across different ethnic groups—are needed to detect small genetic effects on complex traits, and it is well known that even small amounts of cryptic population stratification can undermine such association studies (Marchini et al. 2004). However, high numbers of markers—in the range of several hundred microsatellite loci or a multitude of SNP loci—are required to detect genetic clusters of different ethnic origins in Europe (Rosenberg et al. 2002). Our results indicate that, in our total region of 749 kb, ∼28% (16/57) of the tagSNPs showed highly significant differences (P<.001) among our set of study populations. This rate indicates that the recruitment of population-differentiating SNPs for the purpose of genetic matching strategies in case-control studies is feasible (Hoggart et al. 2004).

Comparative analyses of the haplotype block structure revealed a high degree of concordance among European populations (Nejentsev et al. 2004; Ng et al. 2004; Stenzel et al. 2004), as well as among populations from different continents, such as Asia, Africa, and Europe (Gabriel et al. 2002; Wall and Pritchard 2003). This presumably reflects, in part, the shared ancestry of human populations or common variation patterns of recombination rates, but, to some extent, it also reflects the effect of uneven marker spacing in these studies. However, small, well-defined differences for block boundaries have been reported among Finnish subpopulations (Mannila et al. 2003). All the above-mentioned studies (except Mannila et al. 2003) compare the positions of LD block boundaries by use of a greedy algorithm—or just by inspection of pairwise LD measures—but do not account for the relative probabilities of specific boundary positions. With our method of evaluating the strength of block boundaries, which was applied to exactly the same set of common markers in each population, we were able to show clear examples of block boundary shifts and block fragmentation among European samples. The values of our similarity measure for block structure, which estimate the average probability that boundaries coincide, ranged from 0.72 among LAD and BRISI to 0.87 among SHIP and POPGEN. With the exception of the Alpine populations, the overall variation appeared in a pattern that was concordant with geography, indicating the usefulness of our similarity measure for population-genetic comparisons. The observed pattern suggests that demographic and/or biological factors shaping block boundaries vary in a geographical sense and differentiate in accordance with the level of presumed genetic isolation of populations.

The observed population differences in haplotype frequencies and LD structure may affect the power to detect phenotype-genotype associations. Association signals at markers, which are correlated with a true causal variant, may appear at different positions in populations with an individual LD structure, such as the VIN, LAD, and CALA populations. Repeated studies among such populations are likely to present different results and are problematic for finding positive replications. In contrast, population-specific fragmented LD blocks are useful for the fine-mapping of causal variants within the region.

We also tested the transferability of tagSNP sets among populations. It is often stated that tagSNPs are population specific and should be newly assessed in each local population or geographic area in which an association study is planned (Thompson et al. 2003; Weale et al. 2003; Carlson et al. 2004). On the other hand, the HapMap project claims that its data may be able to be used to define tagSNPs for related populations (International HapMap Consortium 2003). It has also been reported that tagSNPs can be effectively transferred among British, Norwegian, Finnish, and Romanian populations (Nejentsev et al. 2004). It is, however, not clear to what level of population differentiation tagSNPs are transferable between the HapMap data and local European populations. Our results indicate that tagSNPs defined in the HapMap CEPH trios perform relatively well for two of four candidate-gene regions, particularly in central European populations. For SNCA and LMNA, the data from CEPH trios perform even better as a reference than data from 20 local individuals. For two of the tested candidate genes (PLAU and FKBP5), CEPH is not such a good reference. A local sample size of only 20 individuals in most populations is more appropriate for determination of tagSNPs than the standard sample of 30 CEPH trios. By genotyping larger sample sizes (>20 individuals) in the population being studied, the advantage of a local reference will be stronger, but it appears that an increase in sample size beyond 40 individuals is not very effective. A substantial increase in tagSNP efficiency and transferability, however, is achieved by increasing the density of genotyped SNPs in the reference sample.

The surprisingly high performance of CEPH as a reference for tagSNP design in two gene regions was not due to an increased number of selected tagSNPs in CEPH or the additional phase information available from the trios (see table A4 [online only]). The special characteristic of CEPH being a multilocalized but panmictic European population probably confers the advantage to this sample collection. Our results suggest that future HapMap releases with a denser genotype data set will allow the sufficient selection of tagSNPs in the majority of gene regions in central European populations. However, for an as-yet-unknown proportion of genes, and especially for isolated and peripheral populations within Europe, the HapMap reference may not perform optimally, making it necessary to establish the LD pattern from a local sample.

Appendix A: Supplemental Material

Figure A1.

Multidimensional scaling plot based on Reynold distances (transformed F_ST values, linearized to population-divergence time). The F_ST values were calculated from allele frequencies of all four gene regions.

Figure A2.

LD structure (pairwise D′ values) across all nine population samples, with a minor-allele frequency (MAF) >5%.

Figure A3.

Estimated haplotypes with frequency >1% within each block of the four genomic regions for the CEPH trios. Blocks are defined by the standard Gabriel et al. (2002) algorithm (software used was Haploview).

Figure A4.

LD structure in CEPH trios for all four gene regions. For each gene, comparisons of different SNP sets are shown. 1, Original HapMap SNP set. 2, Our SNP set for HapMap comparison. 3, Our full SNP set (minor-allele frequency [MAF] >5%).

Table A1.

Minor-Allele Frequency for All Four Gene Regions

				Minor-Allele Frequency for
Gene Region and SNP	NCBI Build 34 (hg16)	Major Allele	Minor Allele	CEPH Trio Founders	EST	SHIP	POPGEN	KORA	VIN	LAD	BRISI	CALA
SNCA:
rs4122859	91054570	A	G	.042	.121	.05	.075	.08	.091	.081	.092	.09
rs3857046	91059165	G	A	.042	.089	.05	.066	.068	.077	.081	.031	.076
rs3857047	91064912	T	G	.058	.156	.14	.145	.176	.138	.128	.138	.21
rs356229	91064991	A	G	.45	.379	.419	.359	.396	.385	.4	.378	.328
rs3857048	91067353	C	T	.1	.109	.08	.116	.136	.106	.11	.117	.143
rs3906628	91076920	C	T	.1	.109	.081	.116	.136	.112	.111	.117	.143
rs356183	91084492	G	C	.467	.485	.434	.44	.435	.422	.439	.44	.422
rs356180	91086521	C	T	.35	.324	.354	.3	.349	.339	.347	.322	.27
rs356169	91091162	A	C	.342	.362	.345	.334	.376	.355	.394	.335	.345
rs2572323	91092946	G	A	.325	.323	.35	.3	.339	.338	.352	.299	.305
rs356215	91094955	A	G	.466	.449	.442	.545	.398	.399	.436	.387	.47
rs356219	91095995	A	G	.425	.407	.404	.375	.353	.377	.368	.347	.343
rs356220	91099734	C	T	.433	.413	.308	.373	.35	.371	.296	.353	.259
rs356222	91101517	T	C	.322	.312	.308	.294	.325	.321	.336	.293	.253
rs356165	91105280	A	G	.433	.41	.399	.375	.35	.371	.355	.358	.34
rs3775422	91113058	G	A	.1	.072	.062	.075	.021	.033	.019	.048	.078
rs356205	91115580	A	G	.336	.29	.32	.303	.318	.321	.34	.301	.245
rs3822086	91123188	C	T	.1	.093	.065	.075	.021	.042	.019	.059	.086
rs356203	91124435	A	G	.441	.414	.394	.375	.385	.393	.355	.35	.34
rs356202	91124685	A	G	.342	.321	.328	.3	.327	.334	.336	.289	.25
rs356200	91127008	G	A	.481	.518	.455	.482	.457	.454	.453	.432	.445
rs2736991	91130064	A	T	.312	.352	.33	.294	.339	.356	.334	.306	.237
rs356167	91132164	G	A	.298	.296	.273	.28	.269	.307	.263	.265	.209
rs356168	91132825	A	G	.483	.515	.45	.475	.45	.459	.453	.426	.445
rs2736990	91136935	T	C	.483	.506	.449	.472	.436	.443	.453	.418	.439
rs2572324	91137192	T	C	.333	.315	.32	.299	.33	.329	.334	.292	.253
rs356199	91140721	T	C	.322	.293	.293	.304	.306	.308	.334	.301	.258
rs356195	91141562	G	A	.34	.295	.298	.309	.313	.298	.334	.305	.25
rs356192	91146321	T	C	.325	.295	.3	.3	.301	.31	.334	.304	.25
rs356189	91149526	G	A	.331	.29	.295	.304	.296	.314	.333	.301	.25
rs356188	91149931	A	G	.158	.197	.215	.166	.21	.219	.216	.214	.175
rs356187	91150862	G	A	.339	.289	.295	.299	.304	.317	.334	.301	.25
rs356164	91151870	G	C	.117	.185	.146	.103	.14	.141	.154	.156	.066
rs356162	91155551	A	G	.158	.203	.217	.166	.207	.216	.216	.222	.175
rs4031753	91158555	G	C	.1	.087	.066	.081	.021	.046	.019	.056	.085
rs356184	91161627	G	A	.322	.297	.295	.3	.296	.31	.334	.307	.255
rs356186	91163758	C	T	.136	.173	.2	.152	.189	.195	.216	.196	.17
rs2737033	91166341	A	G	.325	.292	.295	.297	.313	.315	.341	.299	.255
rs2737029	91170164	A	G	.45	.449	.39	.428	.38	.405	.394	.399	.38
rs2737028	91175410	C	T	.149	.203	.217	.161	.205	.211	.216	.213	.175
rs2737025	91177586	C	T	.118	.219	.018	.028	.213	.217	.048	.212	.011
rs2737024	91179954	T	C	.317	.282	.282	.287	.304	.31	.337	.304	.237
rs2583959	91180031	C	G	.328	.284	.295	.297	.302	.308	.334	.301	.25
rs2619373	91180827	G	A	.317	.285	.308	.3	.303	.312	.321	.301	.234
rs2197120	91187996	G	A	.161	.203	.215	.166	.206	.214	.216	.224	.175
rs2619368	91188141	G	T	.15	.175	.212	.167	.18	.183	.214	.194	.173
rs2619369	91192063	A	G	.042	.04	.02	.034	.027	.024	.019	.036	.01
rs748849	91193355	A	G	.147	.155	.214	.154	.193	.191	.212	.198	.177
rs1837890	91194400	C	A	.192	.29	.255	.23	.249	.269	.266	.258	.235
rs2619370	91194979	C	T	.325	.279	.291	.276	.298	.314	.32	.312	.253
rs1442145	91195317	A	G	.173	.303	.25	.216	.217	.259	.252	.273	.239
rs972880	91197649	G	A	.164	.207	.203	.174	.219	.233	.217	.223	.159
rs1812923	91197933	C	A	.492	.429	.421	.474	.446	.428	.389	.422	.495
rs2737021	91198386	T	A	.153	.205	.217	.166	.212	.211	.253	.224	.192
rs2619341	91200167	G	A	.147	.204	.22	.166	.205	.214	.214	.224	.175
rs2737014	91203850	T	G	.316	.281	.29	.297	.311	.304	.333	.302	.255
rs2737012	91204101	C	T	.33	.284	.298	.296	.301	.301	.333	.305	.255
rs2583969	91204527	T	C	.325	.28	.288	.294	.277	.298	.331	.292	.258
rs2737010	91204860	T	C	.164	.208	.188	.16	.218	.236	.213	.23	.151
rs2737009	91205230	T	C	.322	.298	.29	.297	.293	.316	.331	.324	.255
rs2737008	91205577	C	T	.325	.274	.29	.297	.289	.299	.331	.293	.255
rs1811442	91206145	T	C	.147	.202	.22	.166	.213	.223	.217	.224	.175
rs920624	91206589	A	T	.483	.486	.531	.472	.517	.544	.56	.575	.432
rs1442146	91207040	C	G	.325	.284	.288	.299	.295	.31	.329	.301	.253
rs1442149	91207526	A	T	.322	.287	.29	.296	.301	.304	.331	.3	.255
rs2737001	91211871	C	T	.325	.282	.293	.3	.288	.298	.331	.3	.255
rs1372516	91214124	G	A	.328	.283	.29	.303	.291	.308	.331	.301	.255
rs2028535	91214815	G	C	.319	.218	.286	.289	.261	.258	.326	.294	.25
rs2301135	91216783	C	G	.483	.506	.49	.525	.471	.462	.447	.443	.555
rs2301134	91217339	T	C	.483	.509	.495	.525	.47	.471	.446	.438	.56
rs2619364	91218281	A	G	.317	.284	.283	.297	.291	.308	.33	.294	.265
rs2583988	91219222	C	T	.258	.132	.242	.278	.145	.15	.287	.172	.217
rs2619366	91221654	A	G	.317	.284	.288	.297	.298	.304	.328	.291	.265
rs2619367	91225489	A	C	.317	.285	.293	.302	.298	.312	.326	.291	.27
rs2583989	91227816	A	G	.317	.278	.286	.296	.298	.308	.326	.28	.263
rs2736993	91231245	T	G	.317	.283	.288	.299	.294	.312	.328	.291	.27
rs2737026	91238217	C	T	.186	.177	.22	.186	.225	.227	.225	.239	.205
rs2736994	91242922	C	T	.183	.207	.2	.163	.208	.205	.216	.26	.19
LMNA:
rs3820592_2	153222805	T	C	.23	.24	.21	.17	.23	.18	.18	.22	.12
rs2297792	153228236	C	T	.4	.34	.31	.32	.41	.35	.33	.41	.35
rs2275073	153247612	A	C	.2	.16	.2	.19	.22	.19	.13	.26	.2
rs2275075	153257102	G	A	.19	.14	.18	.17	.19	.15	.12	.23	.18
rs3814314	153261975	T	A	.21	.21	.21	.27	.23	.24	.25	.23	.14
rs6691151	153266330	C	T	.15	.1	.13	.13	.13	.14	.09	.23	.19
rs4661146	153276942	G	C	.16	.1	.13	.13	.13	.14	.09	.24	.19
rs6661281	153291637	T	C	.36	.32	.35	.4	.37	.41	.33	.46	.34
rs915180	153295875	C	T	.36	.33	.37	.4	.38	.39	.35	.46	.34
rs2485662	153300260	C	T	.26	.27	.25	.28	.28	.34	.3	.29	.24
LMNA_S17S	153301572	C	T	.01	0	.01	.01	.01	.01	0	.03	.01
rs547915	153302167	C	T	.08	.09	.04	.05	.09	.12	.04	.07	.08
rs503815	153306401	T	C	.05	.04	.04	.04	.07	.1	.05	.06	.1
rs501791	153306665	C	T	.05	.04	.04	.05	.06	.1	.05	.06	.09
rs593987	153313179	G	A	.05	.04	.03	.05	.07	.1	.04	.06	.09
LMNAR119R	153317223	C	T	0	.01	0	0	.01	.01	0	0	0
rs2485668	153318341	T	C	.05	.04	.04	.05	.07	.1	.05	.06	.1
rs538089	153321820	T	C	.08	.09	.05	.04	.09	.12	.05	.08	.06
rs553016	153323655	C	T	.08	.09	.07	.05	.08	.12	.06	.08	.11
rs4641	153324326	C	T	.28	.17	.25	.26	.24	.24	.25	.27	.25
rs520973	153324811	G	A	0	.04	.03	0	.08	.09	.01	.06	.05
rs6669212	153327105	G	A	.13	.16	.17	.18	.15	.18	.23	.16	.11
rs545731	153328082	G	A	.06	.04	.06	.07	.06	.1	.07	.09	.08
rs1468772_2	153333280	T	G	.28	.33	.35	.26	.26	.27	.26	.3	.29
rs3738582	153340022	C	G	.22	.18	.17	.19	.25	.26	.17	.24	.25
rs510441	153346760	A	G	.22	.25	.31	.21	.25	.27	.31	.24	.31
rs7695_2	153364118	T	C	.38	.39	.4	.37	.37	.42	.43	.39	.36
rs3738581	153364350	C	T	.44	.44	.44	.38	.4	.45	.47	.41	.43
rs2241109	153389874	C	T	.3	.34	.22	.3	.33	.21	.22	.26	.29
rs2241107	153399502	A	G	.37	.46	.32	.36	.41	.28	.32	.34	.38
FKBP5:
rs1051952	35467201	A	C	.45	.44	.49	.48	.43	.41	.4	.34	.38
rs1883636	35470074	A	G	.12	.11	.17	.15	.13	.13	.11	.08	.11
rs2273000	35479883	G	A	.27	.29	.32	.33	.32	.29	.24	.33	.37
rs1540910	35481677	G	A	.24	.26	.28	.28	.3	.26	.2	.29	.33
rs1883637	35496014	C	T	.08	.08	.11	.09	.08	.09	.06	.03	.04
rs3807050	35514341	C	T	.34	.25	.25	.21	.19	.23	.29	.12	.11
rs873941	35526292	A	T	.26	.31	.26	.33	.34	.27	.34	.36	.42
rs4713897	35529985	G	A	.17	.2	.18	.21	.2	.17	.15	.22	.26
rs3800374	35538821	C	T	.17	.18	.2	.21	.18	.17	.18	.22	.3
rs3800373	35543891	A	C	.23	.22	.29	.28	.28	.25	.25	.27	.31
rs755658	35551085	G	A	.05	.08	.11	.09	.09	.08	.06	.04	.04
rs992105	35556598	A	C	.14	.14	.16	.18	.16	.15	.16	.23	.25
rs7753746	35566837	A	G	.15	.14	.14	.16	.19	.15	.18	.28	.28
rs4713899	35570696	G	A	.15	.14	.14	.16	.19	.14	.17	.26	.27
rs737054	35576902	C	T	.23	.3	.27	.27	.3	.32	.3	.32	.29
rs3777747	35580417	A	G	.42	.49	.46	.47	.45	.49	.42	.53	.52
rs6457836	35581713	C	T	.15	.15	.14	.16	.2	.14	.18	.29	.28
rs7747121	35595398	A	G	.01	.01	.01	.01	.03	.01	.01	.03	.02
rs1591365	35605522	A	G	.25	.25	.29	.29	.3	.24	.28	.34	.34
rs1360780	35608986	C	T	.24	.25	.28	.29	.3	.24	.28	.33	.33
rs2143404	35612096	C	T	.15	.14	.13	.15	.18	.14	.2	.24	.27
rs4713902	35615441	T	C	.21	.29	.26	.28	.29	.32	.27	.31	.31
rs1334894	35616545	C	T	.06	.09	.11	.09	.08	.08	.06	.03	.04
rs6912833	35619000	T	A	.25	.27	.27	.28	.31	.27	.29	.34	.32
rs1475774	35620969	G	A	.01	.01	.02	.02	.02	.01	.02	.02	.02
rs2092427	35623622	G	A	.01	.01	.02	.02	.02	.01	.02	.02	.02
rs7747647	35630615	A	C	0	.03	.05	.06	.09	.03	.05	.06	.1
rs4713907	35644490	G	A	0	0	.01	.02	.01	0	.01	.02	.01
rs4713908	35648725	A	G	.01	.01	.02	.02	.02	.01	.02	.02	.02
rs6457839	35650245	T	C	.31	.34	.29	.31	.34	.33	.29	.41	.32
rs3800372	35656660	T	C	.22	.26	.31	.32	.18	.23	.3	.36	.34
rs7759392	35663234	T	C	.24	.28	.29	.29	.3	.27	.29	.32	.31
rs943297	35669275	C	T	.24	.29	.27	.28	.3	.27	.28	.33	.31
rs4713916	35671398	G	A	.25	.28	.28	.28	.29	.27	.28	.32	.31
rs4713921	35683192	C	T	.23	.31	.29	.28	.31	.28	.29	.34	.32
rs2766534	35687129	T	G	.24	.21	.22	.21	.19	.16	.13	.21	.2
rs2817035	35697778	G	A	.26	.28	.29	.28	.3	.28	.28	.32	.32
rs2817041	35707307	C	T	.23	.2	.19	.21	.15	.15	.11	.24	.19
rs2766543	35710049	T	G	.51	.45	.49	.45	.45	.52	.44	.64	.57
rs2766554	35720742	C	T	.45	.53	.49	.52	.53	.47	.53	.36	.41
rs2817054	35735114	G	A	.5	.44	.39	.44	.39	.27	.36	.31	.22
rs2296662	35746184	G	C	.43	.44	.32	.37	.32	.25	.32	.34	.27
rs2817010	35755964	G	A	.42	.41	.31	.35	.31	.25	.28	.3	.26
rs2766597	35766458	A	G	.03	.01	.02	.01	.01	.01	.01	.02	.01
PLAU:
rs2688626	74955693	A	G	.25	.27	.2	.27	.19	.15	.18	.12	.12
rs2250140	74957484	C	T	.43	.51	.51	.46	.42	.39	.39	.33	.35
rs2664282	74965360	G	A	.43	.44	.51	.46	.39	.33	.38	.28	.32
rs2664283	74970976	C	T	.08	.07	.06	.06	.04	.03	.03	.02	.02
rs4746154	74973999	G	A	.18	.2	.3	.18	.21	.22	.19	.18	.22
rs2688625	74976151	C	T	.43	.51	.51	.46	.42	.37	.4	.33	.35
rs2633312	74976358	A	T	.43	.47	.5	.46	.45	.39	.4	.32	.35
rs2675671	74977363	A	G	.43	.51	.52	.46	.43	.38	.39	.33	.36
rs2633303	74990485	T	G	.26	.33	.25	.28	.21	.17	.19	.15	.11
rs2688617	74990750	A	T	.26	.33	.24	.28	.21	.17	.19	.15	.11
rs2675677	74992852	T	G	.27	.33	.26	.3	.21	.17	.2	.17	.13
rs2675675	74993651	T	C	.26	.33	.24	.24	.2	.17	.18	.16	.11
rs2633306	74997050	G	T	.26	.34	.26	.29	.22	.17	.21	.16	.12
rs2688611	74997975	A	C	.27	.37	.25	.28	.28	.22	.19	.19	.11
rs2688610	74999534	T	C	.46	.54	.49	.45	.45	.41	.39	.38	.36
rs2675679	75003184	A	G	.47	.55	.49	.47	.43	.38	.39	.34	.4
rs2675680	75003467	G	A	.43	.52	.49	.45	.43	.38	.39	.32	.35
rs2675663	75004873	G	T	.46	.54	.51	.47	.44	.39	.4	.35	.4
rs2688607	75008339	C	T	.24	.32	.27	.26	.2	.2	.22	.18	.14
rs2633298	75010942	C	G	.26	.37	.3	.32	.25	.21	.23	.2	.19
rs2459449	75013616	C	T	.26	.32	.29	.31	.22	.2	.23	.19	.14
rs2227553	75014546	T	G	0	.02	.01	.01	.02	.01	.02	.01	.02
rs2227564	75017704	G	A	.21	.3	.24	.26	.2	.19	.21	.17	.13
rs2227568	75018482	C	T	.15	.16	.18	.14	.11	.15	.13	.14	.13
rs2227583	75019822	T	C	.02	.01	.01	.02	.01	0	.01	.02	.03
rs2461863	75024839	A	G	.4	.51	.45	.43	.38	.38	.35	.33	.28
rs2633314	75028193	A	G	.42	.54	.47	.46	.4	.38	.37	.33	.31
rs2633313	75028468	A	G	.41	.52	.47	.44	.39	.37	.36	.34	.29
rs2633317	75034871	G	A	.4	.52	.46	.42	.39	.37	.37	.33	.29
rs2633322	75038535	C	T	.26	.34	.26	.28	.21	.19	.21	.17	.13
rs2633323	75039429	A	G	.42	.54	.46	.45	.4	.38	.36	.33	.33
rs2688624	75040327	C	A	.25	.33	.24	.28	.21	.19	.19	.17	.12
rs4746158	75046458	A	G	.23	.33	.29	.27	.28	.25	.28	.36	.39
rs2675661	75050580	A	C	.04	.11	.08	.08	.06	.05	.06	.09	.14

Table A2.

Symmetric Matrix of Significant Population Pairwise F_ST Values for Each Gene Region^[Note]

Population	CEPH	EST	SHIP	POPGEN	KORA	VIN	LAD	BRISI	CALA
CEPH								F, P	F, P
EST					P	L, P	P	F, L, P	F, P
SHIP						P	P	P	P
POPGEN						P		F, P	P
KORA		P
VIN		L, P	P	P				F
LAD		P	P					F, L	L
BRISI	F, P	F, L, P	P	F, P		F	F, L
CALA	F, P	F, P	P	P			L

Note.— The gene regions with the significant (P<.01 [permutation tests]) differentiations are indicated as follows: P = PLAU; F = FKBP5; L = LMNA; and S = SNCA.

Table A3.

Population Pairwise F_ST Values, on the Basis of All Four Gene Regions

Population	CEPH	EST	SHIP	POPGEN	KORA	VIN	LAD	BRISI	CALA
CEPH	.0000
EST	.0022	.0000
SHIP	−.0011	.0000	.0000
POPGEN	−.0007	.0008	−.0019	.0000
KORA	.0017	.0048	−.0010	.0001	.0000
VIN	.0039	.0107	.0017	.0040	−.0003	.0000
LAD	.0024	.0095	.0023	.0030	−.0006	−.0007	.0000
BRISI	.0101	.0180	.0080	.0083	.0026	.0018	.0037	.0000
CALA	.0156	.0219	.0120	.0109	.0053	.0053	.0084	.0000	.0000

Table A4.

Performance of tagSNPs in All Four Gene Regions^[Note]

	Results for
	SNP Set Similar to HapMap				Full SNP Set, Using
		Local Sample					Local Population
Region, Tested Sample, and Evaluation criterion	CEPH Trios	n=20	n=40	n=60	CEPH Trios Phased	CEPH Founders (n=60)	n=20	n=60
SNCAa:
EST:
No. of tagSNPs	9	10.48	10.76	10.85	15	15	18.12	18.78
Ratio of tagged SNPsb	.763	.777	.827	.831	.921	.921	.823	.836
Mean r2c	.874	.872	.889	.891	.918	.920	.894	.900
Minimal r2d	.145	.145	.145	.145	.660	.660	.345	.339
SHIP:
No. of tagSNPs	9	9.09	9.15	9.47	15	15	15.45	16.25
Ratio of tagged SNPs	.816	.669	.728	.781	.934	.947	.838	.861
Mean r2	.896	.847	.867	.884	.939	.951	.909	.917
Minimal r2	.064	.064	.064	.064	.651	.740	.364	.382
POPGEN:
No. of tagSNPs	9	9.6	9.74	9.93	15	15	15.98	16.57
Ratio of tagged SNPs	.816	.727	.793	.831	.934	.934	.822	.857
Mean r2	.895	.857	.883	.894	.945	.947	.902	.922
Minimal r2	.096	.095	.096	.096	.444	.444	.399	.418
KORA:
No. of tagSNPs	9	10.95	10.43	10.34	15	15	17.56	17.58
Ratio of tagged SNPs	.842	.798	.833	.841	.895	.895	.800	.758
Mean r2	.867	.871	.883	.886	.929	.930	.875	.838
Minimal r2	.125	.124	.125	.125	.700	.700	.343	.282
VIN:
No. of tagSNPs	9	10.21	10.05	9.9	15	15	18	17.61
Ratio of tagged SNPs	.829	.743	.793	.812	.961	.974	.825	.822
Mean r2	.871	.852	.869	.874	.915	.918	.884	.884
Minimal r2	.101	.099	.101	.101	.740	.740	.342	.339
LAD:
No. of tagSNPs	9	9.78	9.91	9.71	15	15	16.02	17.83
Ratio of tagged SNPs	.803	.618	.689	.691	.855	.855	.788	.830
Mean r2	.904	.850	.872	.874	.932	.935	.894	.913
Minimal r2	.160	.160	.160	.160	.651	.651	.383	.414
BRISI:
No. of tagSNPs	9	10.31	10.73	10.76	15	15	17.92	18.68
Ratio of tagged SNPs	.803	.682	.740	.767	.908	.908	.805	.808
Mean r2	.870	.842	.864	.872	.908	.906	.897	.894
Minimal r2	.036	.034	.035	.035	.201	.201	.348	.345
CALA:
No. of tagSNPs	9	9.75	10.31	10.41	15	15	17.87	19.63
Ratio of tagged SNPs	.789	.616	.698	.756	.882	.895	.799	.842
Mean r2	.872	.812	.836	.855	.921	.923	.887	.912
Minimal r2	.075	.074	.074	.075	.584	.584	.296	.325
CEPH founders:
No. of tagSNPs	9	10.7	10.1
Ratio of tagged SNPs	.87	.82	.87
Mean r2	.9	.88	.9
Minimal r2	.08	.08	.08
LMNAe:
EST:
No. of tagSNPs	13	13.22	13.5	13.47
Ratio of tagged SNPs	.815	.769	.808	.806
Mean r2	.871	.851	.871	.870
Minimal r2	.185	.187	.188	.189
SHIP:
No. of tagSNPs	13	13.25	13.48	13.44
Ratio of tagged SNPs	.704	.684	.707	.718
Mean r2	.836	.818	.829	.835
Minimal r2	.188	.186	.186	.188
POPGEN:
No. of tagSNPs	13	12.7	12.68	12.73
Ratio of tagged SNPs	.778	.743	.756	.762
Mean r2	.846	.832	.836	.840
Minimal r2	.148	.146	.146	.148
KORA:
No. of tagSNPs	13	12.75	12.93	12.77
Ratio of tagged SNPs	.852	.781	.807	.805
Mean r2	.873	.853	.862	.861
Minimal r2	.159	.158	.159	.159
VIN:
No. of tagSNPs	13	12.51	12.77	12.92
Ratio of tagged SNPs	.815	.73	.760	.767
Mean r2	.867	.845	.852	.855
Minimal r2	.153	.146	.149	.150
LAD:
No. of tagSNPs	13	12.37	12.53	12.51
Ratio of tagged SNPs	.778	.742	.763	.765
Mean r2	.865	.841	.850	.850
Minimal r2	.156	.155	.155	.156
BRISI:
No. of tagSNPs	13	12.14	12.19	12.22
Ratio of tagged SNPs	.815	.713	.729	.729
Mean r2	.870	.848	.852	.853
Minimal r2	.264	.262	.260	.262
CALA:
No. of tagSNPs	13	11.9	12.34	12.36
Ratio of tagged SNPs	.704	.661	.679	.68
Mean r2	.859	.831	.840	.841
Minimal r2	.253	.231	.242	.247
CEPH founders:
No. of tagSNPs	13	12.2	12.5
Ratio of tagged SNPs	.81	.77	.77
Mean r2	.88	.87	.87
Minimal r2	.23	.23	.23
FKBP5f:
EST:
No. of tagSNPs	20	19.21	19.72	19.81
Ratio of tagged SNPs	.865	.875	.934	.938
Mean r2	.928	.929	.889	.950
Minimal r2	.536	.620	.713	.746
SHIP:
No. of tagSNPs	20	18.95	19.16	19.24
Ratio of tagged SNPs	.811	.886	.92	.939
Mean r2	.936	.934	.944	.949
Minimal r2	.607	.649	.712	.753
POPGEN:
No. of tagSNPs	20	18.55	18.9	19.26
Ratio of tagged SNPs	.865	.896	.942	.956
Mean r2	.936	.929	.942	.947
Minimal r2	.607	.622	.711	.749
KORA:
No. of tagSNPs	20	20.12	20.79	20.66
Ratio of tagged SNPs	.811	.870	.928	.931
Mean r2	.923	.930	.953	.954
Minimal r2	.513	.586	.703	.721
VIN:
No. of tagSNPs	20	18.96	19.27	19.32
Ratio of tagged SNPs	.973	.894	.936	.949
Mean r2	.948	.930	.943	.949
Minimal r2	.541	.609	.695	.726
LAD:
No. of tagSNPs	20	20.7	21.23	21.34
Ratio of tagged SNPs	.730	.845	.901	.913
Mean r2	.904	.930	.950	.953
Minimal r2	.499	.577	.700	.725
BRISI:
No. of tagSNPs	20	20.38	20.85	21.07
Ratio of tagged SNPs	.784	.803	.846	.884
Mean r2	.917	.921	.935	.944
Minimal r2	.408	.609	.676	.721
CALA:
No. of tagSNPs	20	18.76	19.06	19.55
Ratio of tagged SNPs	.892	.831	.901	.928
Mean r2	.934	.912	.937	.945
Minimal r2	.539	.591	.689	.738
CEPH founders
No. of tagSNPs	20	19.9	20.3
Ratio of tagged SNPs	1	.88	.94
Mean r2	.96	.95	.96
Minimal r2	.82	.65	.77
PLAUg:
EST:
No. of tagSNPs	8	8.29	8.25	8.76	9	9	12.04	12.31
Ratio of tagged SNPs	.563	.673	.682	.713	.844	.844	.803	.858
Mean r2	.827	.844	.845	.855	.904	.903	.909	.922
Minimal r2	.24	.24	.24	.24	.457	.457	.670	.726
SHIP:
No. of tagSNPs	8	8.14	8.34	8.58	9	9	11.61	12.27
Ratio of tagged SNPs	.625	.633	.652	.672	.750	.750	.792	.881
Mean r2	.830	.839	.845	.850	.896	.897	.910	.930
Minimal r2	.074	.07	.07	.07	.511	.511	.681	.739
POPGEN:
No. of tagSNPs	8	7.11	7.09	7.35	9	9	10.29	10.07
Ratio of tagged SNPs	.813	.758	.780	.814	.844	.844	.845	.900
Mean r2	.870	.856	.860	.867	.896	.896	.903	.914
Minimal r2	.130	.130	.130	.130	.528	.528	.689	.759
KORA:
No. of tagSNPs	8	8.41	8.34	8.44	9	9	11.03	11.77
Ratio of tagged SNPs	.594	.678	.676	.694	.875	.875	.812	.904
Mean r2	.831	.854	.854	.857	.918	.918	.906	.932
Minimal r2	.165	.165	.165	.165	.563	.563	.623	.738
VIN:
No. of tagSNPs	8	8.1	8.14	8.23	9	9	10.89	10.8
Ratio of tagged SNPs	.688	.771	.788	.792	.906	.938	.846	.911
Mean r2	.848	.867	.872	.873	.926	.921	.909	.928
Minimal r2	.184	.184	.184	.184	.604	.604	.660	.734
LAD:
No. of tagSNPs	8	6.74	6.88	6.77	9	9	9.98	9.77
Ratio of tagged SNPs	.875	.754	.793	.821	.969	.969	.886	.919
Mean r2	.879	.861	.866	.868	.933	.933	.920	.928
Minimal r2	.091	.091	.091	.091	.624	.624	.707	.763
BRISI:
No. of tagSNPs	8	7.98	8.26	8.39	9	9	11.43	12
Ratio of tagged SNPs	.688	.695	.711	.724	.750	.750	.838	.903
Mean r2	.833	.841	.845	.849	.897	.897	.904	.920
Minimal r2	.197	.197	.197	.197	.464	.464	.610	.715
CALA:
No. of tagSNPs	8	8.2	8.78	9.16	9	9	12.44	12.64
Ratio of tagged SNPs	.531	.659	.703	.734	.813	.813	.822	.913
Mean r2	.791	.824	.840	.851	.903	.901	.902	.926
Minimal r2	.113	.113	.113	.113	.504	.509	.628	.724
CEPH founders:
No. of tagSNPs	8	7	7.2
Ratio of tagged SNPs	.97	.78	.82
Mean r2	.93	.89	.89
Minimal r2	.26	.26	.26

Note.— tagSNPs were defined in accordance with the r² method of Carlson et al. (2004).

^atagSNPs defined in CEPH trios (HapMap comparison SNP set) for SNCA are rs2583969, rs2572323, rs356188, rs356200, rs4031753, rs3857048, rs2736994, rs356229, and rs1812923.

^bRatio of SNPs above the r² threshold of 0.8 to any tagSNP.

^cMean r² among all typed SNPs and the best SNP-specific tagSNP.

^dMinimal r² among all typed SNPs and the best SNP-specific tagSNP.

^etagSNPs defined in CEPH trios (HapMap comparison SNP set) for LMNA are rs501791, rs2275073, rs6661281, rs510441, rs7695_2, rs2241109, rs2241107, rs2485662, rs553016, rs1468772_2, rs4661146, rs3814314, and rs3738582.

^ftagSNPs defined in CEPH trios (HapMap comparison SNP set) for FKBP5 are rs992105, rs943297, rs1591365, rs2273000, rs1334894, rs4713902, rs2296662, rs2766534, rs1051952, rs2766554, rs2766543, rs3800372, rs2817054, rs3777747, rs873941, rs3807050, rs1883637, rs6457839, rs2817035, and rs1883636.

^gtagSNPs defined in CEPH trios (HapMap comparison SNP set) for PLAU are rs2688607, rs2633313, rs2664282, rs2227568, rs2227564, rs2633322, rs4746158, and rs2664283.

Table A5.

Performance of htSNPs in Four Gene Regions^[Note]

	Performance of htSNPs Defined in
	CEPH Trios		Local Population
			n=20		n=40		n=60
Region, Tested Sample, and Evaluation Criterion	90%	80%	90%	80%	90%	80%	90%	80%
SNCA:
CEPH:
No. of htSNPs	6	5
Coverage of tagged haplotypes	.952	.906
Ratio of nontagged haplotypes (>5%)	0	.182
EST:
No. of htSNPs	6	5	8.3	6.3	8.2	6.2	7.7	5.7
Coverage of tagged haplotypes	.923	.887	.946	.904	.956	.915	.943	.900
Ratio of nontagged haplotypes (>5%)	.154	.308	.092	.223	.046	.192	.077	.262
SHIP:
No. of htSNPs	6	5	7.5	5.5	8	5.6	6.7	5.2
Coverage of tagged haplotypes	.938	.907	.934	.911	.953	.918	.938	.910
Ratio of nontagged haplotypes (>5%)	0	.182	.073	.127	.027	.118	.036	.164
POPGEN:
No. of htSNPs	6	5	8	5.6	7.4	5.4	7.2	5.2
Coverage of tagged haplotypes	.941	.905	.942	.911	.953	.915	.957	.908
Ratio of nontagged haplotypes (>5%)	.083	.25	.075	.2	.04	.2	.025	.225
KORA:
No. of htSNPs	6	5	7	5.4	7.3	5.2	6.6	5.1
Coverage of tagged haplotypes	.921	.913	.932	.917	.937	.913	.932	.914
Ratio of nontagged haplotypes (>5%)	.1	.1	.03	.08	.02	.09	.02	.09
VIN:
No. of htSNPs	6	5	7	5.2	7.2	5.2	6.7	5
Coverage of tagged haplotypes	.935	.918	.937	.916	.942	.921	.938	.918
Ratio of nontagged haplotypes (>5%)	.1	.1	.03	.1	.03	.08	.04	. 1
LAD:
No. of htSNPs	6	5	7.1	4.9	6.7	4.9	7	5.3
Coverage of tagged haplotypes	.934	.926	.948	.912	.946	.916	.951	.929
Ratio of nontagged haplotypes (>5%)	.1	.1	.03	.11	.02	.11	.02	.08
BRISI:
No. of htSNPs	6	5	7.9	5.6	7.3	5.2	7	5.1
Coverage of tagged haplotypes	.930	.909	.941	.913	.936	.912	.931	.910
Ratio of nontagged haplotypes (>5%)	0	0	0	0	0	0	0	0
CALA:
No. of htSNPs	6	5	7.5	5.9	7.6	5.6	7.2	4.3
Coverage of tagged haplotypes	.921	.899	.918	.901	.940	.910	.937	.859
Ratio of nontagged haplotypes (>5%)	.167	.25	.133	.208	.058	.192	.075	.292
LMNA:
CEPH:
No. of htSNPs	5	4
Coverage of tagged haplotypes	.977	.938
Ratio of nontagged haplotypes (>5%)	.1	.2
EST:
No. of htSNPs	5	4	5.2	4.1	5.3	4	5.2	4
Coverage of tagged haplotypes	.963	.937	.969	.938	.971	.936	.969	.935
Ratio of nontagged haplotypes (>5%)	.11	.22	.09	.211	.08	.22	.09	.22
SHIP:
No. of htSNPs	5	4	5.6	4.3	5.3	4	5.3	4
Coverage of tagged haplotypes	.965	.934	.971	.937	.971	.934	.969	.933
Ratio of nontagged haplotypes (>5%)	.11	.22	.044	.189	.08	.22	.078	.22
POPGEN:
No. of htSNPs	5	4	4.6	4.2	4.9	4	4.9	4
Coverage of tagged haplotypes	.97	.938	.954	.941	.967	.938	.965	.938
Ratio of nontagged haplotypes (>5%)	.11	.22	.156	.2	.122	.22	.122	.22
KORA:
No. of htSNPs	5	4	5	4	4.1	4	5.2	4
Coverage of tagged haplotypes	.969	.937	.965	.937	.971	.937	.972	.937
Ratio of nontagged haplotypes (>5%)	.1	.2	.1	.2	.09	.2	.08	.2
VIN:
No. of htSNPs	5	4	5	4.3	5.3	4	5	4.1
Coverage of tagged haplotypes	.965	.932	.964	.941	.970	.932	.966	.935
Ratio of nontagged haplotypes (>5%)	.1	.2	.1	.17	.08	.2	.1	.19
LAD:
No. of htSNPs	5	4	5	4.1	5.1	4.1	5.4	4
Coverage of tagged haplotypes	.964	.943	.966	.945	.971	.946	.977	.942
Ratio of nontagged haplotypes (>5%)	.11	.22	.122	.211	.1	.211	.067	.22
BRISI:
No. of htSNPs	5	4	5.1	4.4	5.1	4.3	5.3	4.6
Coverage of tagged haplotypes	.972	.912	.967	.939	.974	.934	.978	.950
Ratio of nontagged haplotypes (>5%)	.1	.2	.09	.16	.09	.17	.07	.14
CALA:
No. of htSNPs	5	4	5.3	4.4	5	4	5.2	4.1
Coverage of tagged haplotypes	.969	.926	.970	.946	.971	.929	.974	.933
Ratio of nontagged haplotypes (>5%)	.1	.2	.09	.16	.1	.2	.08	.19
FKBP5:
CEPH:
No. of htSNPs	12	10
Coverage of tagged haplotypes	.967	.948
Ratio of nontagged haplotypes (>5%)	.059	.059
FKBP5:
EST:
No. of htSNPs	12	10	11.9	10.3	11.7	10	11.4	9.9
Coverage of tagged haplotypes	.958	.937	.935	.915	.948	.931	.951	.932
Ratio of nontagged haplotypes (>5%)	0	0	.04	.075	.006	.038	0	.019
SHIP:
No. of htSNPs	12	10	11.7	9.2	10.9	9.4	10.4	9.2
Coverage of tagged haplotypes	.953	.942	.944	.919	.948	.926	.944	.923
Ratio of nontagged haplotypes (>5%)	.059	.059	.065	.118	.047	.1	.053	.106
POPGEN:
No. of htSNPs	12	10	10.9	9.3	11	9.6	10.8	9.2
Coverage of tagged haplotypes	.954	.939	.942	.919	.947	.929	.945	.922
Ratio of nontagged haplotypes (>5%)	.059	.059	.071	.118	.065	.088	.059	.106
KORA:
No. of htSNPs	12	10	11.8	9.6	11.6	9.9	10.9	9.2
Coverage of tagged haplotypes	.943	.932	.933	.911	.943	.921	.938	.916
Ratio of nontagged haplotypes (>5%)	0	0	.019	.069	0	.031	0	.05
Tested samples:
VIN:
No. of htSNPs	12	10	11.3	9.7	11.5	9.6	11.3	9.4
Coverage of tagged haplotypes	.959	.940	.939	.924	.951	.930	.950	.929
Ratio of nontagged haplotypes (>5%)	0	0	.031	.056	.006	.044	0	.038
LAD:
No. of htSNPs	12	10	11.9	9	11.9	9.1	11.3	8.8
Coverage of tagged haplotypes	.931	.927	.924	.899	.937	.902	.932	.908
Ratio of nontagged haplotypes (>5%)	.059	.059	.106	.165	.047	.147	.059	.135
BRISI:
No. of htSNPs	12	10	12.1	9.6	12.7	9.9	11.9	10
Coverage of tagged haplotypes	.918	.913	.933	.895	.940	.911	.940	.913
Ratio of nontagged haplotypes (>5%)	.167	.111	.056	.156	.05	.144	.039	.144
CALA:
No. of htSNPs	12	10	11.6	8.7	11.2	9.4	10.7	8.9
Coverage of tagged haplotypes	.935	.932	.935	.907	.939	.926	.935	.923
Ratio of nontagged haplotypes (>5%)	0	0	.013	.047	0	0	0	.007
PLAU:
CEPH:
No. of htSNPs	6	4
Coverage of tagged haplotypes	.965	.857
Ratio of nontagged haplotypes (>5%)	0	.25
EST:
No. of htSNPs	6	4	7.4	5	6.6	4.8	6.4	3.7
Coverage of tagged haplotypes	.872	.756	.899	.855	.905	.833	.905	.786
Ratio of nontagged haplotypes (>5%)	0	.167	0	.03	.017	.117	0	.167
SHIP:
No. of htSNPs	6	4	6.7	4.9	6.7	4.6	6.7	4.5
Coverage of tagged haplotypes	.876	.769	.898	.838	.909	.826	.912	.828
Ratio of nontagged haplotypes (>5%)	.143	.286	.029	.1	.014	.114	0	.129
POPGEN:
No. of htSNPs	6	4	6.1	4.1	6.7	4.1	6.1	3.5
Coverage of tagged haplotypes	.913	.827	.894	.825	.923	.839	.924	.817
Ratio of nontagged haplotypes (>5%)	0	.167	.033	.167	.017	.15	0	.167
KORA:
No. of htSNPs	6	4	5.5	3.8	6.4	3.4	5.5	4
Coverage of tagged haplotypes	.891	.794	.883	.817	.910	.788	.901	.823
Ratio of nontagged haplotypes (>5%)	0	.167	.033	.133	.033	.2	.017	.117
VIN:
No. of htSNPs	6	4	5.4	3.4	5.6	3.4	5.2	3.5
Coverage of tagged haplotypes	.918	.810	.915	.819	.925	.813	.919	.829
Ratio of nontagged haplotypes (>5%)	0	.167	.017	.167	0	.167	0	.133
LAD:
No. of htSNPs	6	4	5.1	3.1	4.9	3.1	5.1	3.3
Coverage of tagged haplotypes	.921	.844	.903	.844	.923	.847	.924	.857
Ratio of nontagged haplotypes (>5%)	0	.167	.05	.15	0	.15	0	.117
BRISI:
No. of htSNPs	6	4	6	3.6	6.3	3.7	5.3	3.1
Coverage of tagged haplotypes	.915	.817	.908	.824	.936	.854	.921	.824
Ratio of nontagged haplotypes (>5%)	0	.167	.067	.217	.017	.117	.017	.167
CALA:
No. of htSNPs	6	4	4.9	3.3	5.5	3.6	5	3.1
Coverage of tagged haplotypes	.907	.825	.897	.845	.915	.852	.910	.842
Ratio of nontagged haplotypes (>5%)	.143	.286	.114	.243	.057	.229	.057	.271

Note.— Zhang and Jin's (2003) htSNP selection method was used; htSNPs were selected by use of two different thresholds (80% and 90%) for coverage of common haplotypes.