Robust Multipoint Identical-by-Descent Mapping for Affected Relative Pairs

Abstract

The genetic mapping of complex traits has been challenging and has required new statistical methods that are robust to misspecified models. Liang et al. proposed a robust multipoint method that can be used to simultaneously estimate, on the basis of sib-pair linkage data, both the position of a trait locus on a chromosome and its effect on disease status. The advantage of their method is that it does not require specification of an underlying genetic model, so estimation of the position of a trait locus on a specified chromosome and of its standard error is robust to a wide variety of genetic mechanisms. If multiple loci influence the trait, the method models the marginal effect of a locus on a specified chromosome. The main critical assumption is that there is only one trait locus on the chromosome of interest. We extend this method to different types of affected relative pairs (ARPs) by two approaches. One approach is to estimate the position of a trait locus yet allow unconstrained trait-locus effects across different types of ARPs. This robust approach allows for differences in sharing alleles identical-by-descent across different types of ARPs. Some examples for which an unconstrained model would apply are differences due to secular changes in diagnostic methods that can change the frequency of phenocopies among different types of relative pairs, environmental factors that modify the genetic effect, epistasis, and variation in marker-information content. However, this unconstrained model requires a parameter for each type of relative pair. To reduce the number of parameters, we propose a second approach that models the marginal effect of a susceptibility locus. This constrained model is robust for a trait caused by either a single locus or by multiple loci without epistasis. To evaluate the adequacy of the constrained model, we developed a robust score statistic. These methods are applied to a prostate cancer–linkage study, which emphasizes their potential advantages and limitations.

Introduction

Mapping susceptibility loci for complex traits by linkage analysis has been exceptionally challenging, although new genomic technologies and new statistical methods offer hope that the challenges will diminish. Despite the maturation of research on complex genetic models and their corresponding likelihood methods, model misspecification still occurs and can dramatically bias parameter estimates. To overcome this bias when estimating the position of a trait locus on a chromosome, Liang et al. (2001a) proposed a novel robust multipoint method to simultaneously estimate both the position of a trait locus and its effect on disease status and standard errors for these estimates. The advantage of their method is that it does not require specification of an underlying genetic model, so estimation of the position of a trait locus on a specified chromosome and of its standard error is robust to a wide variety of genetic mechanisms. This robust procedure avoids specification of the number of trait loci, the number of trait-locus alleles, allele frequencies, and penetrance. If multiple loci influence the trait, the method models the marginal effect of a locus on a specified chromosome. The main critical assumption is that there is only one trait locus on the chromosome of interest. Although this approach offers appeal, its limitation to affected sib pairs (ASPs) only can be too restrictive. For this reason, we extend the methods of Liang et al. (2001a) so that they can be used with a variety of affected relative pairs (ARPs).

There are many factors that make it difficult to map complex traits. One critical factor is the influence of phenocopies—these pedigree members dramatically weaken the linkage signal. For some diseases, phenocopies can be distinguished, to some degree, from genetically caused cases by measurable features, as exemplified by age at diagnosis for breast cancer. Unfortunately, many common diseases do not have such distinguishing features. However, if the frequency of phenocopies in a pedigree differs according to degree of relationship from the primary sampling unit (e.g., a proband—or perhaps a nuclear family with multiple affected members—could be a sampling unit), then it might be possible to use this information when evaluating linkage results. Hence, another aspect of our motivation was to develop new statistical methods to measure the linkage evidence for different types of ARPs and to test whether there is significant heterogeneity of linkage information across the different types of ARPs. Other causes of differences in sharing of alleles identical by descent (IBD) include gene-environment interaction, epistasis, and varying marker information content.

Before we discuss the background of statistical methods that form the basis of our approach, it is helpful to consider the linkage information provided by different pedigree structures. For common diseases, phenocopies are frequent, and it is difficult to define appropriate pedigree-sampling criteria that reduce the impact of phenocopies on linkage studies. For example, there has been extensive discussion in the literature about the advantages and disadvantages of sampling large pedigrees versus sampling ASPs (see McCarthy et al. [1998] and Schaid et al. [1999]). Risch (1990b) evaluated the power of different types of ARPs for linkage studies, on the basis of the risk ratio for relatives of an affected person compared with the population prevalence of disease. For a single-locus model, the power of a linkage study depends on the risk ratio λ, which is interpreted as the ratio of risk for a relative who shares one allele IBD with an affected person to the risk for a random subject who shares no alleles IBD. Risch showed that when λ is large, relatives more distantly related offer greater power, which suggests that larger extended pedigrees should be sampled. In contrast, when λ is small, ASPs offer greater power. In practice, linkage studies of complex traits that have an older age at diagnosis are often based on collections of pedigrees with as many affected members as possible, typically resulting in pedigrees of small-to-moderate size, with a mixture of different types of ARPs. A question faced by these types of studies is whether the evidence for linkage is the same for different types of ARPs.

A good example that illustrates these issues is the study of linkage for hereditary prostate cancer. Many such studies have collected information on pedigrees of small-to-moderate size (see Easton et al. [2003] and other articles in the same journal issue). These studies are complicated by the fact that prostate cancer is quite common; the current lifetime probability that a man will have the disease is ∼17%. A further complication is that the methods used to diagnose prostate cancer have changed over time, with the advent of prostate-specific-antigen testing in the late 1980s. A critical question is whether the linkage evidence is the same for ASPs versus affected cousin pairs, when it is possible that some cousins could be phenocopies (and, of course, some siblings could be phenocopies as well). Similarly, one might ask whether affected pairs from different generations, such as uncle-nephew pairs, are enriched for phenocopies, because of secular changes in methods of diagnosis.

To estimate the position of a trait locus on a chromosome (and its standard error) from different types of ARPs, we propose robust methods. We base our methods on the robust multipoint-linkage method for ASPs that was proposed by Liang et al. (2001a), and we extended it to multiple types of ARPs and provided ways to evaluate whether there is heterogeneity of the effect of a trait locus across different types of ARPs. In the “Methods” section, we first reviewed the necessary details of the approach by Liang et al. (2001a) and then derived extensions that allow estimation of the position of a trait locus, while allowing for different effects across different types of ARPs. We then developed a way to model the marginal effect of a trait locus by use of different types of ARPs, under the assumption of homogeneity of effects across the different types of ARPs, and then derived a score statistic to formally test homogeneity. We applied these new methods to a linkage study of hereditary prostate cancer, which facilitated discussion of the interpretation of our proposed methods.

Methods

We first describe the approach that Liang et al. (2001a) derived for ASPs, which will introduce the basic ideas and notation needed for our extensions to other types of ARPs. For N ASPs, let Y_i denote a vector of the marker information for the ith ASP; Y_i=(Y_i[t₁],…,Y_i[t_M]), where Y_i(t_M) is the data for the marker at position t_M. Conditional on all marker data and by use of marker-allele frequencies when parental marker data is not available, one can estimate the probability of sharing j alleles IBD for the ith ASP and at each marker position t_M. Let f_ji(t_M) denote this conditional probability, which is computed by popular linkage software, such as S.A.G.E., Genehunter (Kruglyak et al. 1996), Allegro (Gudbjartsson et al. 2000), or Merlin (Abecasis et al. 2002). By use of these probabilities, the estimated number of alleles shared IBD at chromosome position t can be calculated as

Note that the estimated fraction of alleles shared IBD, commonly used for creating linkage statistics, is simply π_i(t)=S_i(t)/2. Assuming the Haldane mapping function to convert recombination fractions to genetic distances in centimorgans, Liang et al. (2001a) showed that the expected value of S_i(t) depends on both the genetic distance from the position t to the trait-locus position, τ, and the effect of the trait locus on disease status. The effect of the trait locus can be measured by C=E[S(τ)]-1, the expected departure from random sharing at the trait locus. The expected value of S_i(t), conditional on both sibs affected, is

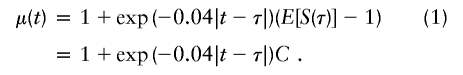Although the coefficient C depends on the underlying genetic mechanisms, this approach obtains its robustness by allowing C to be freely estimated. To provide insights, however, Liang et al. (2001a) discuss the dependence of C on a variety of single- and two-locus models. For example, for a single-locus model with no genetic dominance, the parent-offspring recurrence risk ratio, λ^(O), and the sibling recurrence risk ratio, λ^(S), are equal; let λ denote this common risk ratio. Under these assumptions, the C coefficient depends on λ, according to C=(λ-1)/(2λ).

After using all the marker data to calculate the multipoint IBD probabilities, and in turn using these to calculate S_i(t), Liang et al. (2001a) estimate τ and C and their standard errors by using an estimating equation that models the relationship of the expected values of S(t) and S(τ), as illustrated in equation (1). An intuitive way to see this is to recognize that if τ were known, then the linear regression of S(t)-1 on exp(-0.04|t-τ|) would provide an unbiased estimate of C. However, because the amount of information can vary from marker to marker and because the influence of τ is nonlinear, a more efficient estimation is provided by an estimating equation. Let γ denote the vector of the two unknown parameters, γ=(τ,C). Furthermore, let μ_γ denote the vector of expectations given in equation (1), evaluated at all M marker loci with the parameters in γ. Similarly, let S_i denote the vector of estimated IBD sharing counts at all M marker loci. Let ∂μ_γ/∂γ be an M×2 matrix of partial derivatives of μ_γ with respect to each of the parameters in γ, and let V_γ be an M×M covariance matrix for the vector S_i, which depends on γ, as we shall discuss below. Then, solving the following estimating equation provides unbiased estimates for γ:

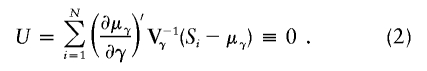We later refer to U, or the terms being summed over, as “score vectors.” When this estimating equation is used, a modification of μ_γ(t) is required, because, as t→τ, the derivative of μ_γ(t) with respect to τ is not defined. Liang et al. (2001a) approximate |t-τ| with a differentiable function; details are provided in appendix A.

The variance matrix V_γ has the following elements for positions t_i and t_j:

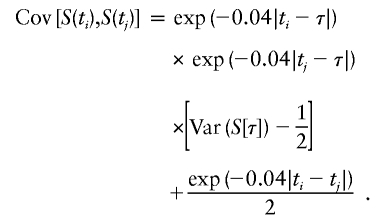For the marginal effect of a locus without dominance, -C² can be substituted for [Var(S[τ])-1/2] in the above expression (Liang et al. 2001a). This covariance expression emphasizes the fact that the covariance of the number of alleles shared IBD along a chromosome depends on the genetic distance of each of the markers to the trait locus, the distance between the genetic markers and the magnitude of the genetic effect at the trait locus.

In practice, the solution to the estimating equation (2) is iterative, and a Newton-Raphson method can speed convergence. Because of the iterative method, repeated inversion of V_γ can take too much time, and an approximation that uses a simpler “working” covariance matrix will usually suffice. The working covariance matrix that Liang et al. use in their distributed Fortran “gee.f” source code assumes that all off-diagonal covariance terms are zero, so that V^-1_γ requires inversion of only the diagonal variance terms. Let W_γ be this working covariance matrix. Then, the working information matrix used for the Newton-Raphson step can be computed as

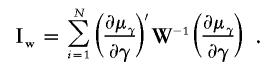The covariance matrix for the estimated parameters is based on the robust “sandwich” estimator (Zeger and Liang 1986). Let U_i denote the sum of vectors of scores for all pairs within the ith pedigree (i=1,…,P). A robust information matrix can be estimated according to

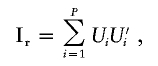and an estimate of the covariance matrix for γ is

This robust estimator accounts for misspecification of the working information matrix and accounts for any correlation among multiple ARPs from the same pedigree. On the basis of large-sample theory, the solutions to the estimating equations provide parameter estimates that are consistent and asymptotically normally distributed, which provides a means to construct confidence intervals for parameter estimates.

Extensions to ARPs

To extend Liang’s method to ARPs beyond siblings, we considered two approaches. The first approach was to estimate a single τ but an unconstrained C for each type of ARP. The second approach also estimated a single τ but constrained the C coefficients for different types of ARPs to depend on a parameter λ. This second approach reduces the number of unknown parameters, although potentially at the risk of a misspecified model. As we shall show, these two approaches complement each other.

Different C Coefficients for Each Type of ARP

For a variety of types of ARPs, Risch (1990b) derived the relationship between the probability of IBD sharing at a marker locus and the probability of IBD sharing at a trait locus and showed that this relationship depends on the recombination fraction between the two loci and the magnitude of genetic effect at the trait locus. By use of Risch’s results and under the assumption of the Haldane mapping function, the expected value of S_i(t) can be derived easily. These expectations, denoted μ_k(t) for an ARP of type k, are presented in table 1 for a variety of types of ARPs. The expressions in table 1 emphasize the fact that the rate of decrease of μ_k(t) as the marker moves away from the trait locus at τ depends on the type of relationship. In general, the expected number of alleles shared IBD for an ARP of type k can be expressed as

where a_k is the expected count for random sharing, b_k(d) controls the rate of decrease of expected sharing as the distance d from the trait locus increases, and C_k is E[S_k(τ)-a_k], the expected departure from random sharing at the trait locus for an ARP of type k. Allowing the C_k parameters to be unconstrained provides robust estimation of τ and the marginal effects of a trait locus on a specified chromosome.

Table 1.

Expected Value E[S(t)] for Different ARP Types

ARP	μk(t)a
Full siblings	1+exp(-.04d)C1
Half siblings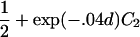
First cousins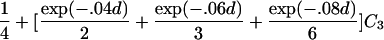
Grandparent-grandchild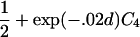
Avuncular pairs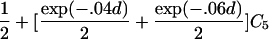

^aSee appendix A for definition of d.

To estimate τ and the C_k coefficients, we follow Liang’s approach and use the estimating equation in equation (2) but now keep track of the type of ARP in order to use the appropriate μ_k, as well as its partial derivatives, with respect to τ and the C_k coefficients. The partial derivatives with respect to τ are given in table 2. The partial derivative of μ_k(t) with respect to C_l is b_k(t) if l=k and =0 otherwise. The covariance matrix of γ can be estimated by the robust estimator in equation (3).

Table 2.

Partial Derivatives of μ_k(t), with Respect to τ for Different ARP Types

ARP	∂μk(t)/∂τa
Full siblings	C1fexp(-.04d)(-.04)
Half siblings	C2fexp(-.04d)(-.04)
First cousins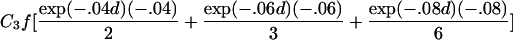
Grandparent-grandchild	C4fexp(-.02d)(-.02)
Avuncular pairs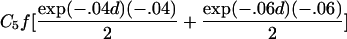

^aSee appendix A for definitions of d and f.

It is important to recognize that the interpretation of the C_k parameters depends on the underlying genetic mechanisms that lead to disease. If only sib pairs are available, then the single C coefficient cannot identify the underlying genetic model. However, different types of ARPs can have the potential to provide some insight to the underlying genetic model. First consider a single trait-locus model. Risch (1990a) showed that the risk ratios for different types of relative pairs follow a well-defined pattern. Using the offspring-risk ratio λ^(O) to represent first-degree relatives, Risch showed that λ^(O)-1 decreases by a factor of 2 for each increasing degree of unilineal relationship. Hence, λ^(O)-1=2[λ⁽²⁾-1]=4[λ⁽³⁾-1], where λ⁽²⁾ is the risk ratio for second-degree relatives (e.g., grandparent-grandchild and pairs of aunt/uncle with niece/nephew, which are referred to as “avuncular pairs”), and λ⁽³⁾ is the risk ratio for third-degree relatives (e.g., first cousins). Although a single trait locus is not likely for the setting of complex traits for which we wish to develop robust methods, this pattern of λ^(R)-1 decreasing by a factor of 2 with each degree of relationship also holds for some multilocus models. Specifically, Risch (1990a) showed that the marginal effect of a specific locus, out of multiple loci that influence disease penetrance, follows the above pattern for risk-ratio decrease if the loci act additive on penetrance or if there is genetic heterogeneity. In contrast, for a multiplicative-penetrance (epistatic) model, λ^(R)-1 decreases more rapidly than a factor of 2. By “epistasis,” we mean that the loci have multiplicative effects on the penetrance (see Risch [1990b] for further discussion of these models). The rate of decrease depends on the number of loci and the degree of epistasis. Now, if we model the marginal effect of a trait locus on a specified chromosome, with the assumption of no epistasis, we can translate each C_k coefficient to a corresponding λ_k, as long as there is no dominance (λ^(S)=λ^(O)). Dominance can be assessed by comparison of the risk ratio for siblings with that for offspring or parents, by use of epidemiological studies. Whether there is dominance depends on the trait of interest, but, for complex traits, additive effects of alleles may very well provide an adequate description of the recurrence risk to siblings. So, assuming no epistasis and no dominance, we can translate each C_k coefficient to a corresponding λ. This λ is scaled according to the degree of relationship. For example, for first-cousin pairs, λ_C-1=(λ-1)/4; instead of using λ_C, we use the scaled λ. By scaling according to degree of relationship, λ can be interpreted as λ^(O), the risk ratio for a pair of relatives sharing one allele IBD at the trait locus, compared with a pair of relatives not sharing alleles IBD. For our exposition, we let λ_k denote this risk ratio when translated from C_k.

We present in table 3 the function λ(C) that translates each C_k to a λ_k. To be clear about our notation, we use λ to denote a parameter and λ(C) to denote a function. The λ(C) functions in table 3 emphasize the fact that the C_k coefficients can differ across different types of ARPs, even if the corresponding λs are expected to be equal (e.g., either a single-trait locus or the marginal effect of a locus in a multilocus setting without epistasis). Hence, it is more informative to translate the C_k values to λ_k values to examine whether the λ_k values differ across different types of ARPs than to compare the C_k values. To place confidence intervals on the estimates of the λ_k parameters, we first calculate confidence intervals on the C_k parameters, then use the λ(C) functions shown in table 3 to translate these to confidence intervals for the λ_k parameters. Under our assumptions of no dominance and no epistasis, the estimated λs should be approximately equal, within the tolerance of sampling error. If there is epistasis, then λ is expected to decrease as the degree of relationship of an ARP increases. If there is no epistasis yet there is dominance but no inbreeding, then λ is expected to be similar among all types of relative pairs except sib pairs. Hence, examination of the λ_k estimates may provide additional insights. Because it is natural to ask whether the λ_k estimates are statistically different from each other, below we derive a method to formally test the null hypothesis of homogeneity of all λ_k values. However, before we present this method, we first present a method to estimate τ and a single underlying value of λ, because these estimates are needed for the test of homogeneity.

Table 3.

Functions to Map C to λ and Vice Versa and Derivatives^[Note]

ARP	C(λ)	∂C/∂λ	λ(C)	∂λ/∂C
Full siblings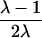
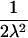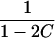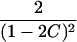Half siblings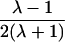
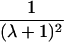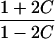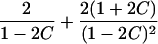First cousins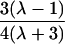
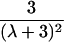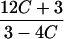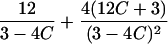Grandparent-grandchild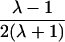
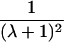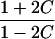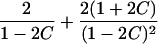Avuncular pairs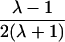

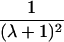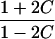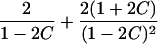Note.— Subscript k for ARP type is dropped to improve clarity of presentation.

Modeling C_k as Function of λ

For a single-trait–locus model—or a multilocus model without epistasis—and with the assumption of no dominance, the C_k coefficients depend on only a single parameter, λ. To emphasize this dependence, we use the function C_k(λ), which is illustrated in table 3 for a variety of types of ARPs. Note that C_k(λ) is the inverse of the function λ_k(C). To estimate τ and λ, the score equation (2) is modified by using C_k(λ) to calculate the C_k terms in γ and by calculating the derivative of μ_k(t) with respect to λ. By use of the chain rule, ∂μ_k(t)/∂λ=b_k(d)∂C_k/∂λ, where b_k(d) is the coefficient in front of C_k in table 1 and ∂C_k/∂λ is shown in table 3. Hence, only minor modifications to the score estimating equation (2) are required to estimate τ and a common λ.

Test of Homogeneity of λ_k

To test the null hypothesis that all values of λ_k are equal to a common value, say λ, we use robust score tests, as reviewed in Boos (1992) and originally derived by White (1982). First observe that the null hypothesis H_o:λ₁=λ₂=…=λ_K can be expressed in terms of the C_k coefficients by use of the λ(C) functions, H_o:λ₁(C₁)=λ₂(C₂)=…=λ_K(C_K). Then, to test H_o, we constructed contrasts of the λ(C) functions according to δ_i =λ₁(C₁)-λ_(i+1)[C_(i+1)] for i=1,2,…,(K-1). That is, for K types of ARPs, there are K-1 contrast functions, δ_i. To test the null hypothesis that the vector of these δ contrast functions is equal to zero, we need the matrix H with elements

There are K-1 rows in H for the contrasts, and there are K+1 columns in H, one for τ and K for the C coefficients in the parameter vector γ. This matrix is illustrated below for K=3.

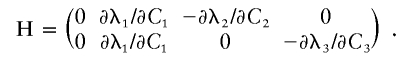Then, the score statistic to test H_o is

where the tilde means that a term is evaluated under the null hypothesis, 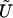is the score equation (2), 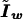is the working information matrix, and 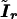is the robust information matrix. To evaluate these terms under H_o, we first use the methods in the “Modeling C_k as Function of λ” section to model all C_k coefficients as a function of a single λ, simultaneously estimating τ, (call these estimates 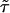and 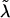); we then use the C_k(λ) functions, with the common 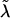, to determine the appropriate 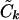terms in 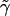; and, finally, we use the terms in 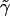to evaluate the terms in equation (5). The statistic T has an approximate χ² distribution, with K-1 df.

It is worthwhile to note that other hypotheses regarding the λ parameters can be constructed easily with slight extensions of the above score statistic. For example, if there is no epistasis yet there is dominance, the λ value for sib pairs (denoted as “λ₁”) is expected to differ from that for other types of relative pairs, yet λ is expected to be constant over all types of pairs that are not siblings (this common parameter is denoted as “λ₂”). One can then exclude sib pairs to estimate the common λ₂ in the constrained model of the “Modeling C_k as Function of λ” section and adapt the above robust score statistic to test H_o:λ₁=λ₂. For example, H is a vector with elements H=(0,∂λ₁/∂C₁,-∂λ₂/∂C₂,…,-∂λ₂/∂C_K), and the resultant score statistic has 1 df.

A caveat with the estimating equation methods, both those for the score statistics and those for placing confidence intervals on parameter estimates, is that the asymptotic distribution depends mainly on the number of independent pedigrees and less so on the number of ARPs. For a small number of pedigrees, or if the trait locus is estimated to be at the extreme end of a chromosome—where there is little information to bound the estimated location, and hence the estimated variance may not be precise—it may be worthwhile to use bootstrap methods (e.g., bootstrapping pedigrees) to calculate confidence intervals.

Application to Prostate Cancer Linkage

A genome linkage scan of 167 families with multiple cases of prostate cancer was conducted by investigators at the Mayo Clinic by use of SNP markers in the Early Access Affymetrix Mapping 10K array (Schaid et al. 2004). The strongest linkage signal was detected on chromosome 20. We reanalyzed this data from chromosome 20, restricted to ARPs, with our new methods. There were 303 full-sib pairs, 134 first-cousin pairs, and 30 avuncular pairs; other types of ARPs were excluded because there were so few. There were 124 SNP markers on chromosome 20, with median intermarker distance of 0.4 cM. For this data, we subset to each type of ARP, estimated both τ and C for each subset, and then translated the C coefficients to λs, to assist interpretation and comparisons. Furthermore, because the solution of the estimating equation depends on a set of starting values, we used different sets of starting values to determine whether we consistently found a single solution. These results are presented in table 4. For each estimated parameter, we also present 95% CIs, although these are only approximations, given the small number of ARPs in some of the subsets (particularly for avuncular pairs). For each of the subsets of full-sib and avuncular pairs, a single solution was found. In contrast, for first-cousin pairs, two different solutions were found. The estimated λs for all types of ARPs were remarkably similar, ∼1.4. However, the estimated τ differed across the different types of ARPs. For first cousins, there were two solutions, τ=24.1 and τ=92.3. It is not clear whether (1) there are two susceptibility loci on chromosome 20 or (2) our finding is due to large variation in the shape of the mean allele-sharing curve because of the small number of cousin pairs used in our study. The confidence intervals, however, on these estimates of τ are broad and overlap for all three types of ARPs (except for τ=24.1 for first cousins).

Table 4.

Parameter Estimates for Prostate Cancer Linkage

	Estimate (95% CI) for
Type of Analysis and ARP	τ	λ
Subsetsa:
Full siblings	73.0 (63.3–82.7)	1.4 (1.1–2.0)
First cousins:
Solution 1	24.1 (9.8–38.5)	1.4 (.8–2.3)
Solution 2	92.3 (77.2–107.3)	1.4 (.9–2.0)
Avuncular pairs	58.1 (25.0–91.2)	1.3 (.6–3.4)
Model Cb:
Full siblings		1.4 (1.1–2.0)
First cousins		1.3 (.8–1.9)
Avuncular pairs		1.2 (.8–2.1)
Common τ	72.9 (64.1–81.7)
Model λc	72.7 (64.2–81.1)	1.4 (1.1–1.7)

^aSeparate τ and C were fit for each different ARP subset.

^bA common τ with different C coefficients for the different ARP types.

^cThe C coefficients were modeled as dependent on a single common λ, simultaneously with a single τ.

We also fit the model from the “Different C Coefficients for Each Type of ARP” section, which allowed for different C coefficients for the different types of ARPs but a common τ. These results are presented in the “Model C” section of table 4. The estimated τ was 72.9 cM, with a confidence interval that was tighter, particularly compared with those for the small subsets. The estimated C coefficients were translated to λs; these did not differ much from those estimated by the separate subset analyses.

We then proceeded to model the C coefficients as a function of a single λ, and these results are presented in the “Model λ” section of table 4. The results from this model are remarkably consistent with those from the “Model C” analyses. The estimated common λ was 1.4, with a tighter confidence interval than for any of the above-mentioned models. The estimated τ is 72.7 cM, with a slightly narrower confidence interval than that for models in which the C coefficients were not constrained. If the model with a common λ fit well, we would expect the confidence interval for τ to be more narrow than for the model with unconstrained C parameters. By use of the methods described in the “Test of Homogeneity of λ_k” section, the λ parameters were not significantly different across the three types of ARPs; the resultant test statistic was T=0.22, with 2 df and a P value of .90.

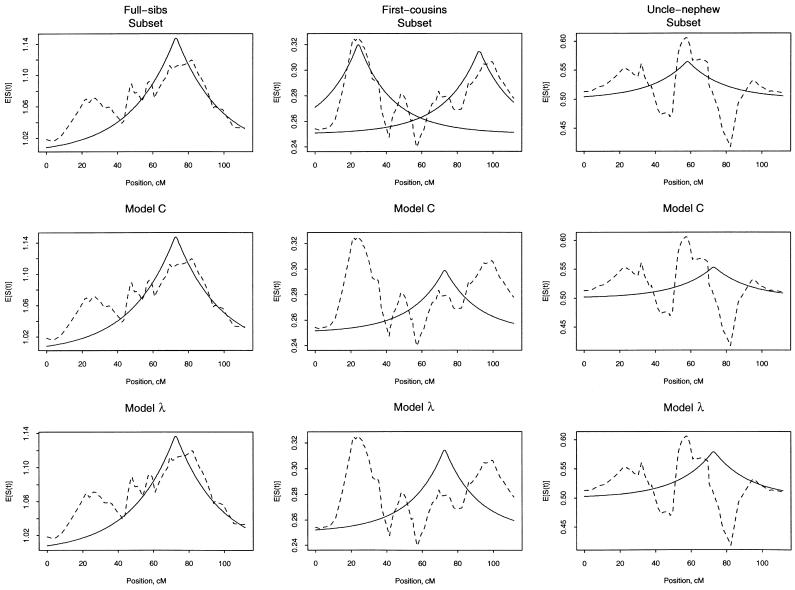
To view the fit of our models, we plot the mean estimated count of alleles shared IBD versus the fitted allele sharing (fig. 1). For each panel of this figure, we plot the observed mean sharing within each type of ARP and the fitted sharing, according to the type of analysis described in table 4. Note that the intercept (a_k in eq. [4]) for these plots represents the expected count for random sharing and differs across the different types of ARPs (see table 1). As expected, the subset analyses give observed and fitted lines that are close to each other. For first cousins, there are two fitted lines, because there were two solutions to the estimating equation. For the model C analyses, the observed and fitted lines match well for full sibs but not as well for first-cousin and avuncular pairs. For the model λ analyses, the fitted values for first-cousin pairs appear inflated around 70 cM. Although the plots in figure 1 do not illustrate the large statistical variation within subsets, they suggest that there may be systematic differences between the different types of ARPs in the data set.

Figure 1.

Average of the estimated number of alleles shared IBD (broken line) and fitted values (solid line) for the different types of ARPs (columns) and different types of analyses (rows). Analyses correspond to those in table 4. Top row, separate τ and C were fit for each different type of ARP subset. Middle row, we used a common τ with different C coefficients for the different types of ARPs. Bottom row, the C coefficients were modeled as dependent on a single common λ, simultaneously with a single τ.

Discussion

Given the difficulties of mapping genetically complex traits, particularly diseases of older onset, new statistical methods are needed to account for the many sources of heterogeneity. Liang et al. (2001a) developed robust multipoint methods to simultaneously estimate the trait-locus position and its effect size for ASP linkage data, along with standard errors and confidence intervals for those estimates. The gain in robustness comes from modeling the expected value of the number of alleles shared IBD, by use of estimating equations, without the need to specify a particular genetic model. The price of this robustness is potentially reduced efficiency compared with a full likelihood using the true underlying but unknown genetic model. However, misspecification of the genetic model can grossly bias the estimated position of the trait locus and, hence, the appeal of Liang’s robust methods. He and others have extended their approach for other types of analyses with sib-pair linkage data (Liang et al. 2000, 2001b; Glidden et al. 2003). They have emphasized that the parameter of most interest is the position of the trait locus τ and that their methods are useful to provide confidence intervals on regions worthy of further fine mapping.

We have extended the robust multipoint approach of Liang et al. (2001a) to account for different types of ARPs. Although the primary focus is on precise estimation of the position of a trait locus, use of a variety of types of ARPs allows richer modeling of the effect of a trait locus. Our first method estimates a separate parameter for the trait-locus effect for each type of ARP, whereas our second method constrains the C_k coefficients to depend on a single parameter, λ. This constrained model is appropriate for either a single causative locus or for multiple causative loci without epistasis. On the basis of published reports on the efficiency of modeling the C coefficients as functions of covariates (Liang et al. 2001b; Glidden et al. 2003), we speculate that if the constrained model is appropriate, there may be slight gains in efficiency for the τ parameter, but, if inappropriate, bias in τ and decreased efficiency can occur. Hence, one should be cautious when using the constrained model. To evaluate the fit of the constrained model, we derived a robust score statistic to test whether the λ parameters differ significantly over the different types of ARPs. In our application to a prostate cancer–linkage study, we found both models to give similar results. Although the details of the original genome linkage scan are presented elsewhere (Schaid et al. 2004), some points are worth noting. One of the largest linkage signals was on chromosome 20, with a model-free LOD score of 2.4. The position of this LOD score was at 76 cM, and a 1-unit decrease from the maximum LOD score had the range 65–87 cM. Application of our new methods gave an estimate of the position of a trait locus as 73 cM, with a 95% CI of 64–81 cM, which is 23% shorter than the 1-unit decrease from the maximum LOD score.

An advantage of our methods is that they can be used to evaluate the consistency of linkage evidence from different types of ARPs, which may help to understand the sources of linkage information and possibly sources of heterogeneity that weaken the linkage signal. For our prostate cancer example, the expected allele-sharing model fit well to the full-sib pairs but not as well to affected first-cousin and avuncular pairs. This could be due to phenocopies or to a complex genetic etiology, including epistasis. Unfortunately, the sizes of our subsets are not sufficient to resolve this issue. It is likely that large collaborative studies would be required to have sufficient power to detect at least moderate levels of heterogeneity.

A critical assumption made by Liang et al. (2001a) that we have followed is that only one trait locus exists on the chromosome of interest, although other causative loci could exist on other chromosomes. This assumption is required for correct specification of the mean function for the IBD sharing. If there are multiple loci linked to a chromosomal region, then the mean function would be misspecified. For example, between two causative loci, the mean IBD sharing would be greater than that predicted by a single causative locus. Hence, if multiple causative loci reside in a linked region, the parameter estimates will be biased. To overcome this, Biernacka et al. (2004) extended the estimating equations for ASPs to allow for two linked causative loci. Further work that combines their methods with ours would allow estimation of parameters for two causative loci for a variety of types of ARPs.

The main advantage of these methods is robust estimation of the position of a trait locus. If there is no predominant peak in the mean allele sharing, then the parameters will not be estimable. Hence, these methods are most useful for follow-up of a linkage signal to pursue further fine mapping. Our unconstrained model may provide guidance on which type of ARPs might be most informative for further fine mapping. Our unconstrained model may provide additional insights, through examination and modeling of the C_k (and hence λ_k) coefficients. However, it is wise to be cautious when interpreting the estimated λ parameters. Complex genetic mechanisms, environmental factors that modify causative loci, and varying linkage information content can all influence the λ parameters. Furthermore, if a genome scan suggests that a particular region of a chromosome is interesting because it has a high LOD score, then estimates of the genetic effect size for loci in the interesting region are biased upward (Göring et al. 2001). This occurs because the LOD score depends on the estimate of the locus-specific effect size, and so maximizing the LOD score over the genome implicitly maximizes the locus-specific effect size. This maximization process, essentially a multiple-testing process, biases the estimated effect size upward, but the estimated τ remains unbiased. This does not invalidate the use of our proposed methods to assess the consistency of the λ estimates across different types of ARPs, but it does emphasize the need for caution when interpreting the estimated λ parameters for regions of the genome that were detected by a genome-linkage screen. On the other hand, this type of bias does not occur with application of our proposed methods to independent data sets used to replicate an initial linkage report.

Appendix A :

With use of the Haldane mapping function, which depends on |t-τ|, μ(t) is not differentiable with respect to τ. To modify μ(t) so that it is differentiable, Liang et al. (2001a) replace |t-τ| with

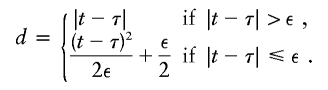Liang et al. (2001a) show that the choice of ε has little impact when ε⩽1. For ASPs, the resultant partial derivatives are

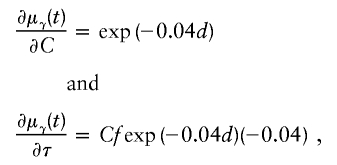where

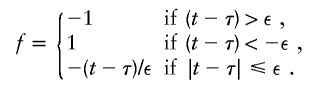Appendix B : Software Availability

Software that implements the methods outlined in this article is a combination of the S programming language and C (for more computationally intensive components). This is integrated into a package, called arp.gee, which runs in both S-PLUS and R computing environments. The package is available at the authors' Web site; for R users, the package is available at the Comprehensive R Archive Network site.