In Silico Analysis of Disease-Association Mapping Strategies Using the Coalescent Process and Incorporating Ascertainment and Selection

Abstract

We present a new method for simulating samples of marker haplotypes, genotypes, or diplotypes in case-control studies in which the markers are linked to a disease locus in any specified region of the genome. The method allows realistic features to be incorporated into the simulations, including selection acting on disease alleles, sample ascertainment of disease chromosomes and polymorphic markers, a genetic dominance model of disease expression that allows incomplete penetrance and phenocopies, and an accurate genetic map of recombination rates and hotspots for recombination in the human genome (or, alternatively, an improved method for simulating the distribution of hotspots). The new method uses an approach that combines simulation of the coalescent process for the sampled chromosomes with a diffusion process used to model the evolution of the disease-mutation frequency over time. Examples illustrate how the method may be used to study the expected power of a marker-disease association study.

Recent initiatives such as the International HapMap Project, as well as expanding databases of mapped SNPs (dbSNP) and microsatellite polymorphisms (Marshfield Center for Medical Genetics), have created opportunities for large-scale association studies to map human disease loci with the use of unrelated cases and controls. To examine the power of particular mapping strategies, a comprehensive simulation program is needed that allows samples of haplotypes, genotypes, or diplotypes to be generated under realistic conditions. Here, we present a new simulation methodology that has been developed for this purpose. The method combines a coalescent process (which is used for modeling the genealogy underlying a sample of chromosomes from cases and controls) and a diffusion process (which is used for modeling the evolutionary history of the frequency of a disease mutation), and it allows for the incorporation into simulation studies of additional features that are very important in human populations (and human disease studies) but that have been neglected by past simulation methodologies. New features include sample ascertainment of disease chromosomes and polymorphic markers, a genetic dominance model of disease expression that allows incomplete penetrance and phenocopies, and an accurate genetic map of recombination rates and hotspots for recombination in the human genome (or, alternatively, an improved method for simulating the distribution of hotspots).

Several programs have been developed recently to simulate samples of chromosomes under either a neutral Fisher-Wright model (Hudson 2002; Posada and Wiuf 2003) with recombination and genetic drift or a model with selection acting on a specified locus (Spencer and Coop 2004). These methods are perfectly adequate for simulating a random sample of chromosomes from a large population. However, in case-control association studies, linkage disequilibrium mapping studies, and other disease-gene mapping contexts, the sample is highly nonrandom. Ascertainment of individuals that exhibit a disease enriches the sample for an underlying disease mutation, increasing its frequency in the sample, relative either to that in the population or to that expected in a random sample. Zöllner and von Haeseler (2000) developed a method for simulating the joint coalescent structure for a neutral disease locus in cases and controls in which all cases have exclusively disease-mutation–bearing chromosomes and all controls have exclusively normal chromosomes. This is suitable for modeling a sample of cases and controls for a rare recessive disease, for example. One drawback to their approach is that it assumes that the population frequency of the disease mutation has remained constant since it arose. Wang and Rannala (2004) used a diffusion process to model the evolution of the disease-allele frequency over time, thus relaxing the assumption of a constant disease-mutation frequency but retaining the assumption of a simple Mendelian inheritance pattern and a neutral disease locus. The objective of the present study is to extend the model of Wang and Rannala (2004) to allow both for a complex model of inheritance for a disease locus and for natural selection acting on the locus. We also incorporate more-realistic models of recombination hotspots into our simulation procedure. Our approach builds on earlier work by Kaplan et al. (1988) and Hudson and Kaplan (1988), who focused primarily on modeling the effects of deterministic selection on summary statistics (such as the number of segregating sites) for a random sample of chromosomes by use of a coalescent theory framework.

A unique (nonrecurrent) mutation is assumed to arise as a single copy at generation T^′ in the past (fig. 1A). A present-day sample of chromosomes is generated by fixing the age of the mutation (T^′) and then simulating the frequency of the mutation forward through time, conditional on nonextinction, where p_t is the frequency at generation t in the past. Our method also allows one to condition on the present-day allele frequency, p₀, via rejection sampling. For a neutral allele, the process of random drift of the allele frequency can be simulated by use of a diffusion approximation (e.g., Kimura and Takahata 1983). Given the sample path of the frequency of the disease allele over time, p={p_t, p_t-1, …, p₀}, the coalescent process with recombination is simulated on the basis of an ancestral recombination graph with variable population size 2N_tp_t among chromosomes carrying the mutation and with variable population size 2N_t(1-p_t) among those not carrying the mutation (Wang and Rannala 2004). We assume a model of either constant population size or continuous exponential growth, but arbitrary population growth patterns can be readily incorporated.

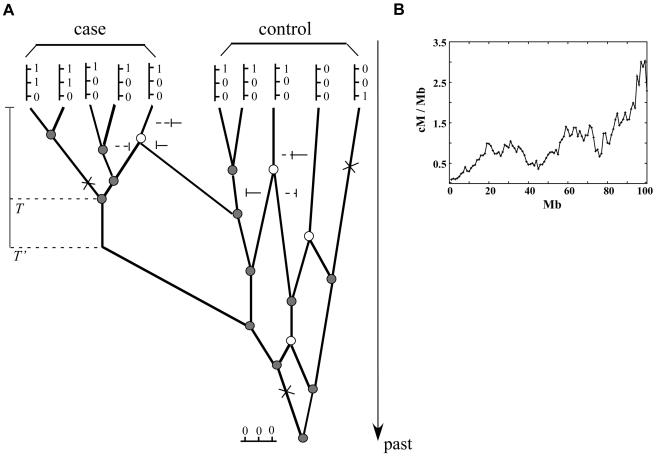
Figure 1.

A, The structure of a coalescent model with recombination, between a chromosomal segment descended from a disease mutation at a given locus (left) and a sample of chromosomes not descended from the mutant (right). The alleles present at three diallelic marker loci are indicated by “0” and “1” for the sampled chromosomes that are represented as vertical lines at the top of the figure. Ancestral chromosomes involved in coalescence and recombination events are indicated by shaded and unshaded circles, respectively, on the ancestral recombination graph, and mutation events are represented as crosses. Segments of chromosomes transmitted to descendent lineages from each of the two ancestral lineages following a recombination event are represented as solid and broken horizontal lines. B, The distribution of recombination rates over a chromosome, generated by one instance of a GBM simulation.

The waiting time until a coalescent event occurs in the gene tree of either mutation-bearing chromosomes or normal chromosomes is simulated using a discrete-time model (with time measured in units of generations), rather than the more usual continuous-time model. To efficiently simulate the waiting times on a discrete-time scale, a recursion strategy is used (Wang and Rannala 2004). At times after the origin of the mutation, mutant chromosomes only coalesce with one another, as do the normal chromosomes. Recombination can occur both within and between genealogies of the mutant and normal chromosomes. If a homogeneous recombination model is used, then the recombination breakpoints are uniformly distributed along the chromosomal region. Otherwise, recombination rates along the region either are simulated using a geometric Brownian motion (GBM) model (described below) or are extracted from the Icelandic recombination map data (Kong et al. 2002).

After the genealogy of the sample of the disease and normal chromosomes is generated, mutations are superimposed on it. Given the size of the chromosomal interval and the mutation rate either for SNPs under a Jukes-Cantor model or for STRP (microsatellite) markers under a stepwise mutation model (Ohta and Kimura 1973; Valdes et al. 1993), the number of mutations that occur in the history of the sample at each site follows a Poisson distribution. The numbers and the positions of markers are treated as random variables, and the distribution of the positions of mutations on branches of the genealogy is uniform under a Poisson process model of mutation (see Hudson 1990). Only polymorphic sites are retained as potential markers. The evolution of the polymorphic sites is simulated forward in time. Because of recombination or relatively younger mutations at marker loci, some markers may be monomorphic or may have a low polymorphism level. The markers that comprise the sample are randomly chosen in accordance with a predefined polymorphism cutoff level.

If a disease locus is under selection, the sample path of the population frequency of the disease mutation is instead generated by use of a diffusion model with selection. The Kimura and Takahata (1983) procedure for simulation of the sample path under neutral drift can be modified to incorporate selection. The allele frequency at the next generation, given the current frequency, is normally distributed, with expectation and variance determined by the diffusion model. The average change of allele frequency per generation under selection (with selection coefficient s >0) is M_δp=sp(1-p), in accordance with a diffusion approximation (with no dominance). If population size (N) is constant, the variance of the change in allele frequency (σ²_δp) that results from random drift is p(1-p)/(2N). If we assume that the population has grown exponentially with rate r to the current population size (N₀), then, at generation t in the past, σ²_δp=p(1-p)/(2N₀e^-rt). Given the age and initial frequency, 1/(2N₀e^-rT′), of the disease mutation, the change of frequency is simulated by generating a uniform random variable with mean M_δp and variance σ²_δp, conditional on nonextinction. If fewer than four copies of the disease allele are present in the population, the diffusion approximation is no longer accurate, and the number of alleles in the next generation is instead simulated as a Poisson random variable (with parameter pe^r) by use of the branching-process approximation for a rare allele (see Ewens 1979). The method can be extended to other selection models by simply replacing the average rate of change of allele frequency under a diffusion model.

Recent studies suggest that the human genome consists of haplotype blocks (Phillips et al. 2003). This haplotype-block structure is a consequence of population processes as well as recombination hotspots, and, to accurately model human haplotype structure, both processes should be incorporated into the model. Recent evidence suggests that recombination rates in humans are higher near the telomeres and lower near the centromeres. The Icelandic recombination map displays a large number of recombination rate peaks and valleys distributed along each chromosome, with an increasing trend in rates from centromere to telomere (Kong et al. 2002). We propose a new method that uses a GBM model, with the recombination rate evolving over the length of the chromosome, to simulate the distribution of nonhomogeneous recombination rates along a chromosomal region. The GBM process, also called “log-normal growth,” is a particularly attractive model of rate evolution because it assumes that changes of rate are random but that the magnitude of such changes is proportional to the current rate.

Under a GBM model, the log ratio of the recombination rate at one point on a chromosome, conditional on the rate at the preceding point, follows a normal distribution, with the mean and variance correlated with the physical distance between the two points. If a GBM model is used to simulate the distribution of recombination rates in this way, it implies that adjacent loci will tend to have similar crossover rates, yet there exists a stochastic deviation of rates between loci that depends on the diffusion coefficient (σ²) in the GBM process and the physical distance between the two sites. If a GBM process with drift (μ>0) is assumed, if the initial recombination rate is set to a relatively small value, and if recombination rates are always simulated from centromere to telomere, then the process mimics the tendency for recombination to be high near the telomere and low near the centromere. An example of a simulated GBM process of the evolution of recombination hotspots on a chromosome is given in figure 1B.

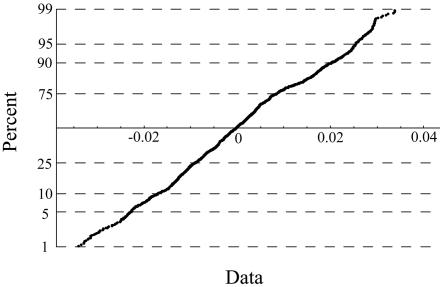
The validity of the GBM model for the distribution of recombination rates along a chromosome was examined by fitting the conditional distribution of the normalized log rates at adjacent sites to a standard normal distribution via a normal probability plot applied to the data of Kong et al. (2002) (fig. 2). In the simulation program, the default drift (μ) and diffusion (σ²) parameters are the average of the maximum-likelihood estimator (MLE) over all autosomal chromosomes (pooling females and males), calculated by using the data of Kong et al. (2002). The MLEs are μ=3.074×10^-8 and σ²=2.503×10^-8, respectively. Other options included in the program are uniform rates of recombination (e.g., 1 cM = 1 Mb) and rates of recombination for any specified chromosomal interval obtained directly from the Icelandic map (Kong et al. 2002).

Figure 2.

Normal probability plot, constructed by use of conditional distribution of normalized log recombination rates for the Icelandic map data of Kong et al. (2002). The plot is based on marker data obtained from the q arm of chromosome 2 in females. The more linear the appearance of the plot, the better the fit to the GBM model.

Phenocopies, low penetrance, and other factors may lead to a loss of power for identification of disease-mutation location by use of association methods. The effect of disease penetrance was incorporated into in our simulation procedure by using a standard three-parameter penetrance model. At the disease-mutation locus, the disease-causing allele is denoted by “D,” and the alternative allele is denoted by “N.” The probability that an individual has a certain genotype at the disease locus (e.g., genotype DN), given that the individual expresses the disease phenotype, is

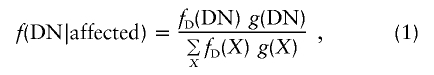where f_D(·) represents the penetrance of a genotype at the disease locus and g(·) denotes the frequency of a genotype. If we assume Hardy-Weinberg equilibrium at the disease locus and if the population frequency (p) of the disease mutation is known, equation (1) becomes

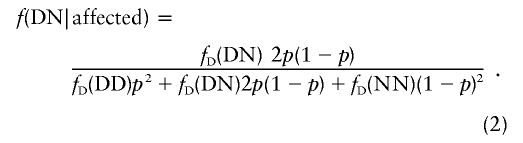Similarly, the probability that an individual has a certain genotype at the disease locus (e.g., genotype DN), given that the individual does not express the disease phenotype, denoted by “f(DN|unaffected),” can be obtained by replacing f_D(DN) in f(DN|affected) with 1-f_D(DN). Conditional probabilities for other genotypes can be calculated using the above equation, by substituting the corresponding penetrance and frequency terms.

Given the above conditional probabilities for two categories (cases and controls) and the number of individuals in these two categories, the distribution of the counts of individuals in a sample with each genotype at the disease locus will follow a multinomial distribution. The distribution of the number of disease and normal chromosomes in a sample is therefore completely specified by this sampling model. Genotypes are simulated from the multinomial distribution defined by this model. For example, the distribution of genotypes among n_A affected individuals is

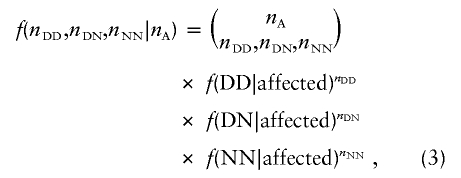where n_DD, for example, is the number of DD genotypes in a sample of n_A affected individuals. Given the numbers of disease-mutation–bearing chromosomes and normal chromosomes in the sample (a simple function of the genotype counts), the simulation methods discussed above are used to generate a sample of disease and normal chromosomes that have multiple linked markers.

Here, we provide several examples of how our program can be applied to examine the prospective power of association studies to detect a mutation that contributes to a disease. Power is measured as the proportion of replicate simulations for which the simulated case-control genotype data show a significant marker-disease association, as determined by a χ² test of association applied to genotypes, with the critical value set at P=.05. The parameters and variables used in the simulations are summarized in table 1.

Table 1.

Descriptions of Parameters and Variables Used in Simulation Studies

Parameter/Variable	Description
nD and nN	Numbers of affected and normal (control) individuals in the sample
N0	Current population size
r	Exponential population growth rate
T′	Age (in generations) of the disease-susceptibility allele
p	Population frequency of the disease-susceptibility allele
E(p)	Expected population frequency of the disease-susceptibility allele
θ(·)	Marker location (in Mb)
s	Selection coefficient
f(·)	Disease-penetrance parameter of a genotype
φ	Disease prevalence
R(·)	Genotype-specific disease risk relative to the homozygous (nonsusceptibility allele) genotype

Two penetrance models were considered in our simulation study: additive and multiplicative models. If, for convenience, we define ρ and α as two intermediate coefficients, then f_D(DD)=2ρ, f_D(DN)=ρ+α, and f_D(NN)=2α for the additive model and f_D(DD)=ρ², f_D(DN)=ρα, and f_D(NN)=α² for the multiplicative model. Given φ=f_D(DD)p²+f_D(DN)2p(1-p)+f_D(NN)(1-p)² and the relative disease risk for genotype DD (denoted as “R_DD” [we define the risk relative to genotype NN]), the parameters ρ and α in an additive penetrance model are

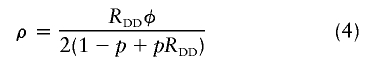and

and the parameters ρ and α in a multiplicative model are

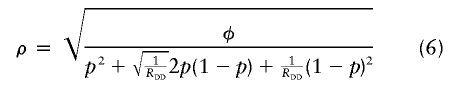and

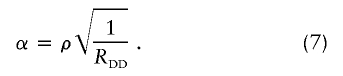The results of our simulations will be presented in terms of relative risk, etc., rather than in terms of the parameters of the penetrance model, to make the interpretation more straightforward.

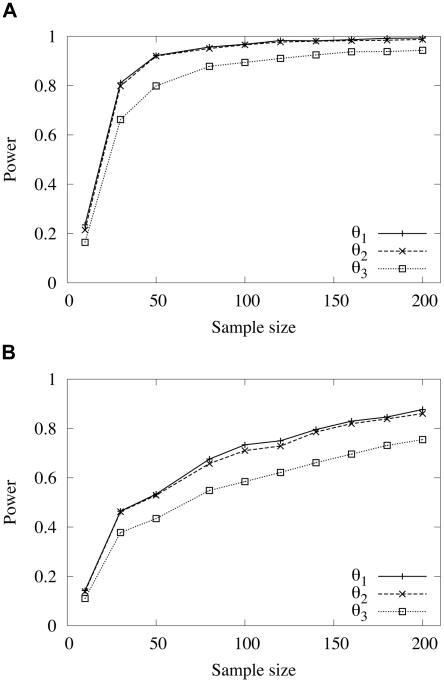
Simulation studies were performed to examine the power of marker-disease association studies for simple Mendelian disorders and for a range of more complex models of disease inheritance. In the case of a purely recessive disease (f_DD=1, f_DN=0, and f_NN=0), the power of association methods to detect a disease locus is high, as expected, and is >0.9 when the sample size exceeds 50 for both cases and controls (fig. 3). For a purely dominant disease (f_DD=1, f_DN=1, and f_NN=0), association studies are less powerful, but the power consistently increases with increasing sample sizes (fig. 3). For both sets of results shown in figure 3, the parameters N₀=10⁶, r=0.01, and s=0 were used to perform the simulations, and T^′=840 was chosen to satisfy E(p)=0.1. A total of 5,000 replicates were used to compute the expected power.

Figure 3.

Expected power, as a function of sample size, of an association study to detect a disease locus with either purely recessive (A) or purely dominant (B) inheritance for markers positioned in three different chromosomal intervals, with average distances of 1 kb (θ₁), 10 kb (θ₂), or 100 kb (θ₃) from the disease locus. The parameters N₀=10⁶, r=0.01, and s=0 were used for the simulations. The disease-mutation age T^′=840 was chosen to satisfy E(p)=0.1. A total of 5,000 replicate simulations were used to compute the expected power.

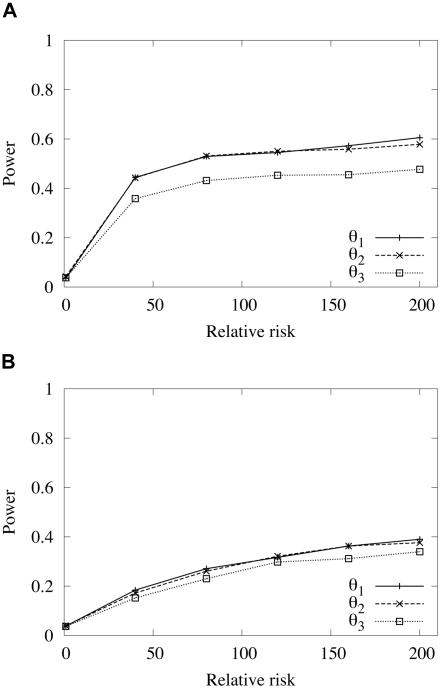
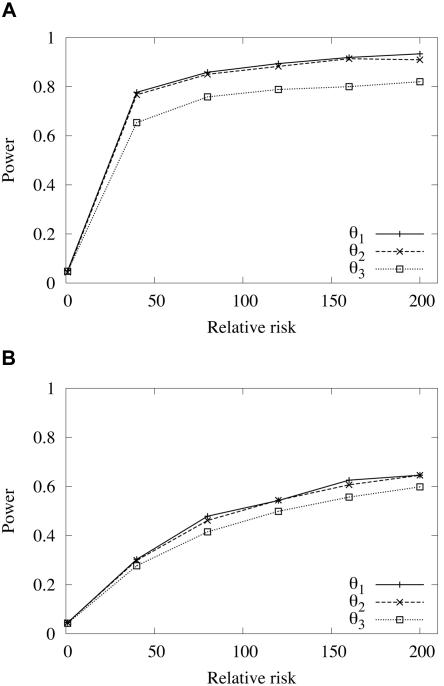
For more-general models of disease inheritance, given E(p), φ, and R_DD, an additive model is assumed, and penetrance parameters are calculated using equation (2). The power of association studies is plotted against the relative risk of a disease. The parameters N₀=10⁶, r=0.01, n_D=100, and n_N=100 were used for the simulations. Two different average present-day population frequencies of a disease mutation were considered: a relatively high frequency of 0.1 and a relatively low frequency of 0.01. The age of the disease mutation was chosen such that the mean frequency would be equal to the present-day population frequency—either 840 or 600 generations (for frequencies of 0.1 and 0.01, respectively) for a neutral disease mutation (fig. 4) or 780 or 560 generations (for frequencies of 0.1 and 0.01, respectively) for a disease mutation under selection with s=0.001 (results [not shown] are virtually identical to those shown in fig. 4). Figure 5 shows the results when the simulation parameters used to generate figure 4 are again used, but with a larger sample size (n_D=500 and n_N=500, instead of n_D=100 and n_N=100). For sample sizes of n_D=100 and n_N=100, the power to detect an association, computed by using the markers at three chromosomal intervals, is moderately higher for a more frequent disease than for a less frequent disease, and the power is similar, independent of whether markers in any of the three intervals are used, especially for a less frequent disease (fig. 4). Selection appeared to have little effect on the power. The results shown in figure 5 suggest that sample size can greatly affect the power of marker-disease association studies; much greater power is achieved if sample size is increased. This is true for both common and rare diseases.

Figure 4.

Expected power, as a function of genotype relative risk, of an association study to detect a neutral disease-associated mutation, computed by using markers positioned in three different chromosomal intervals, with average distances of 1 kb (θ₁), 10 kb (θ₂), or 100 kb (θ₃) from the disease locus. Power was estimated using simulated samples with n_D=100 and n_N=100. A, Expected power, with an average present-day population frequency of the disease mutation of p=0.1 and a mutation age of 840 generations. B, Expected power, with an average present-day population frequency of the disease mutation of p=0.01 and a mutation age of 600 generations.

Figure 5.

Expected power, as a function of genotype relative risk, of an association study to detect a neutral disease-associated mutation, computed by using markers positioned in three different chromosomal intervals, with average distances of 1 kb (θ₁), 10 kb (θ₂), or 100 kb (θ₃) from the disease locus. Power was estimated using simulated samples with n_D=500 and n_N=500. A, Expected power, with an average present-day population frequency of the disease mutation of p=0.1 and a mutation age of 840 generations. B, Expected power, with an average present-day population frequency of the disease mutation of p=0.01 and a mutation age of 600 generations.

The method we present focuses on a single disease locus. Allelic and locus heterogeneity are incorporated into the model in a vague manner through the phenocopy probability. It is straightforward to simulate two or more disease mutations of the same gene (allelic heterogeneity) with the use of our methodology by simulating multiple disease-locus genealogies. One could then use an expanded penetrance model (e.g., with six parameters for two disease-risk alleles). Similarly, one could model disease-locus heterogeneity (for unlinked loci) by using a quantitative genetic model that allows for epistasis among two or more disease loci to obtain the probability distribution of multilocus genotypes in cases and controls and then by independently simulating each locus in cases and controls.

Another way the model could be extended would be to allow population genotype frequencies to deviate from Hardy-Weinberg equilibrium proportions by incorporating an inbreeding coefficient. This would be useful for simulating small populations with high levels of consanguineous matings, for example. Our method conditions on the disease-mutation age and then simulates the present-day frequency. To condition on frequency and age, we use rejection sampling; the user specifies an interval for the population frequency of the disease mutation, and only those simulated data sets for which the frequency is in this interval are accepted. Although technically correct, this can be computationally inefficient, and alternative approaches might instead either condition on frequency and generate random ages via the simulation or condition on both frequency and age. The simulation method of Spencer and Coop (2004) conditions on the frequency of the disease mutation and samples from the distribution of mutation ages, taking advantage of the reversibility property of the diffusion process (Griffiths 2003). The method assumes that population size is constant, however, and it cannot be easily extended to model growing populations.

A final problem in simulating case-control studies is how to correct for marker ascertainment bias. In many instances, markers are prescreened for polymorphisms by using a sample of unrelated normal individuals; a subset of these prescreened polymorphic markers is then screened in cases and controls. We modeled ascertainment bias by assuming that a random subset of markers is chosen in an interval from the total set of polymorphic markers in the interval (in sampled cases and controls). One could make this procedure slightly more realistic by assuming that the markers are chosen from those sites that are polymorphic in an expanded sample of “normal” chromosomes (rather than from the present sample of normal and disease chromosomes). In our opinion, power analyses based on computer simulations of population samples, such as those proposed here, are more reliable for predicting when a particular study design will have low power than for predicting when the design will have high power. This is because we expect important (and perhaps unidentified) factors that have not been included in the model to be more likely, a priori, to reduce the power than to increase it.

The program GeneArtisan, written in the C++ language, is available as either a command-line program or a crossplatform graphical interface program for Linux, Windows, and Mac OS X. The program can be downloaded from authors' Web site.