Computational Micromechanics and Machine Learning-Informed Design of Composite Carbon Fiber-Based Structural Battery for Multifunctional Performance Prediction

Abstract

Integrating load-bearing and energy storage capabilities within a single material system, known as multifunctional structural batteries, holds immense promise for advancing structural energy storage technologies. These systems offer significant weight reduction and enhanced safety, but their commercialization is hindered by challenges due to vast unexplored design spaces and costly trial-and-error processes. In this work, we employ an experimentally validated computational framework to accelerate the design of carbon fiber (CF)-based structural batteries impregnated with solid polymer electrolyte (SPE). To analyze the mechanical behavior, a finite element analysis (FEA) model powered by computational micromechanics was used to investigate the CF/SPE interface and damage mechanisms to predict the macro-effective material properties. To preform accurate forecasts on energy storage, a data-driven machine learning approach based on artificial neural networks (ANN) was optimized via a Bayesian optimization algorithm to predict the structural battery’s future capacity. Furthermore, we validate the optimized ANN model in a rapid capacity degradation condition, showcasing the suitability of such algorithms for studying coupled multifunctional structures under mechanical and electrochemical loads, providing promising insights for optimizing the development of multifunctional composites.

1. Introduction

The global shift toward sustainability demands efficiency enhancement of engineered structures by prioritizing weight reduction, emission reduction, and cost-effectiveness. In this regard, the structural design of advanced engineering systems, an accurate understanding of the material’s functional limitations, such as moduli and failure stresses, is indispensable. Similarly, energy storage devices necessitate precise predictions of state of health (SOH) and energy retention to ensure reliability and efficiency.¹⁻⁶ Consequently, these systems must be meticulously engineered to perform under anticipated operating conditions.

One promising approach to enhancing efficiency in these systems is through multi-functionality, where a single material serves multiple roles. This concept has gained significant attention, particularly in applications like structural batteries and supercapacitors.⁷⁻¹³ Multi-functionality not only enhances efficiency but also reduces the overall weight and design complexity of the system, leading to greater design versatility.

Carbon fiber (CF)-based structural batteries exemplify such innovative technologies. Due to their similar microstructure to the anode materials in conventional lithium-ion batteries (LIBs), CFs can effectively function in energy storage. This concept offers a theoretical weight reduction of up to 62% when structural batteries are used to replace the roof of an electric vehicle, providing significant economic and efficiency benefits.¹⁴ These batteries are typically composed of CFs and a functional matrix, often referred to as a solid polymer electrolyte (SPE). In this configuration, CFs function as reinforcement, active anode material, and current collector. Simultaneously, the SPE acts as an adhesive matrix that binds the fibers, transfers loads, and facilitates ion conduction.¹⁵⁻¹⁸

To this extent, the real-life implementation of novel multifunctional structural batteries has been hindered by high uncertainty in performance, with specific capacity ranging widely from ∼30–360 mA h/g in the initial cycle to approximately 20–180 mA h/g by the 10th cycle, depending on the CF grade and properties.¹⁶ Additionally, significant drops in modulus occur as the electrolyte content in the SPE is introduced and increased incrementally.^17,19 This contrasts with the more predictable design of monofunctional devices using conventional materials like metals and composites, which offer narrow and well-defined design values as outlined by engineering guidelines i.e., Ashby Charts.²⁰ Thus, commercialization hurdles often stem from the costly, impractical, and cumbersome nature of conducting numerous trial-and-error experiments, which not only restricts the design space but also hampers efficiency. Moreover, conflicting design considerations further complicate the design and prediction process.^19,21−24 Consequently, computational methods such as finite-element analysis (FEA) and machine learning (ML) have been used in engineering as an indispensable tool for exploring design parameters, validating assumptions, and optimizing performance with great accuracy, customization, and computational efficiency.²⁵⁻²⁸ Yet, their potential remains largely unexplored in the literature of CF-based structural batteries.

Regarding the application of such computational methods in the scope of CF-based structural batteries, few researchers have reported such analyses. Most studies focus on characterizing the coupled multi-physics interactions between the constituents, such as diffusion stress, thermal expansion/shrinkage, electrochemical effects, etc.²⁹⁻³⁷ These studies predominantly address molecular, nano, or microscale phenomena, such as lithium-ion transport, electron mobility, and concentration of molecules, and their theoretical effect on the state of charge (SOC) and stress state in single/few circular fibers (i.e., radial, hoop), based on analytical or semi-analytical 2D problem definitions.^31,38,39

The complex nature of composite structural batteries, spanning advanced manufacturing (i.e., fiber packing, assembly attributes, interface considerations), material composition (e.g., matrix properties, electrolyte integration), mechanical behaviors (e.g., stress–strain response, fatigue), and environmental factors (i.e., temperature, humidity), mandates the development of an experimentally validated, accurate, and efficient computational framework for the design and characterization of these multifunctional structures. Most importantly, this computational framework must effectively correlate with key macroscopic and design properties, including multiaxial modulus and battery capacity, to ensure comprehensive structural battery design and optimization.

In this study, we introduce an experimentally validated computational framework for the design and performance prediction of SPE-impregnated CF-based structural batteries. Building on our previous work,^40,41 which primarily addressed experimental aspects, this work extends those findings into the computational domain. The objective of this study is to establish a foundational framework that integrates micromechanical modeling and data-driven machine learning methodologies to predict the performance of CF-based structural batteries. It lays the groundwork for future research aimed at coupling mechanical and electrochemical analyses to provide a more holistic understanding of the performance of multifunctional structural batteries.

The mechanical analysis employed computational micromechanics via FEA, focusing on fracture mechanics-inspired modeling of the CF/SPE interface using cohesive zone modeling (CZM). A 3D representative volume element (RVE) approach captured fiber volume fraction, matrix plasticity/damage, and interfacial damage propagation under multiaxial loading, predicting material moduli and failure. For electrochemical analysis, data-driven machine learning with artificial neural networks (ANN), Bayesian hyperparameter optimization, and K-fold cross-validation were integrated to optimize the neural network architecture and improve the prediction accuracy of CF-based battery cell capacity. Additionally, the trained and optimized neural network was successfully validated in an accelerated aging environment (∼5 °C), demonstrating its robust performance. Our results highlight the effectiveness of experimentally validated FEA combined with data-driven ML algorithms in designing multifunctional composites, demonstrating its promising potential as an efficient optimization technique for such coupled applications. Figure 1 illustrates the FEA/ML computational framework predicting the multifunctional performance of composite structural batteries. FEA was employed to study the mechanical problem i.e., CF/SPE interface and micromechanics RVE Modeling. ML was used to analyze the energy problem i.e., battery’s capacity prediction. The illustration includes a representative schematic of a car roof, showing the transition from steel to carbon fiber-reinforced plastic (CFRP) to structural battery.

Figure 1.

Schematic of FEA/ML computational framework for CF-based structural batteries performance prediction. The illustration includes a representative schematic of a car roof, showing the transition from steel to carbon fiber-reinforced plastic (CFRP) to structural battery.

2. Experimental Section

2.1. Materials

Carbon fiber spread tows (T700s CFSTs; length ∼100 mm and width ∼18 mm) were obtained from Toray Industries Inc., Japan. Bisphenol A diglycidyl ether epoxy resin (DGEBA) was purchased from KUKDO Chemical, Korea. Methylhexahydrophthalic anhydride (MHHPA), N,N-dimethylbenzylamine (BDMA), 1-ethyl-3-methylimidazoliumtetrafluoroborate (EMIMBF4), Whatman GF/A separators, ethylene carbonate (EC), and1,2-dimethoxyethane (DME) were purchased from Sigma-Aldrich, Korea. Lithium bis(trifluoromethanesulfonyl)imide (LiTFSI), CR2032 coin cells, and lithium metal chips (Dia. Sixteen mm, T. 0.45 mm) were purchased from MTI, Korea.

2.2. Preparation of Bifunctional SPE & CF-Based Structural Battery

To prepare the biphasic SPE, the structural phase (i.e., DGEBA/MHHPA/BDMA) was mixed at a stoichiometric mixing ratio of 100:90:1 parts per weight, respectively. For the liquid electrolyte phase, 1 mol of LiTFSI was dissolved in EMIMBF4 and then mixed with the structural epoxy phase based on specified weight percent ratios (i.e., 0%, 30%, 40%, 50%) until a homogeneous mixture was achieved, denoted as SPE X, where X represents the electrolyte weight percent.

Similar to our previous work,⁴⁰ a structural composite battery was fabricated by means of wet-layup and vacuum bagging, followed by vacuum-assisted compression molding (VACM). In which a robust cure cycle with high pressure (∼11 MPa) was employed to impregnate SPE inside CFST lamina, resulting in the formation of a lamina with a fully cross-linked epoxy-based functional polymer, and CF-based multifunctional lamina with uniform thickness and an enhanced fiber volume fraction (FVF). For ease of handling and impregnation, the SPE mixtures were partially cured according to the prescribed cure cycle (Supporting Information, Table S1) before being coated onto the CFST. More details on the fabrication process and material characteristics can be found in the reference provided.

2.3. Tensile Tests

Tensile tests were performed using a universal tensile testing machine (UTM Instron 5969; Instron, USA) equipped with a 50 kN load cell, while strain evolution was recorded using digital image correlation (DIC; GOM Correlate, Germany). Both dogbone SPE samples and multifunctional strip composite laminas were subjected to a cross-head speed of 0.5 mm/min to accurately capture and analyze the progression of damage.

2.4. Interfacial Shear Strength (IFSS)

Interfacial shear strength (IFSS) between the CF’s surface and the SPE was assessed using a single fiber microdroplet shearing test as shown in Figure 2a. A microdroplet of the polymer [embedded length: ∼80 μm to ∼160 μm] was deposited onto the carbon fiber surface using a needle tip, then droplets were cured using the designated cure cycle. The droplet underwent interfacial de-bonding initiated by a micrometer knife edge, with a cross-head speed of 0.1 mm/min (5 N load cell UTM Instron 5969; Instron, USA). The IFSS was determined from eq 1.

1

where F: maximum force, D: fiber diameter (7 μm), and l: embedded length.

Figure 2.

(a) Schematic of the experimental IFSS specimen setup. (b) Schematic of the axisymmetric FEM used in the simulation of microbond test.

2.5. Galvanostatic Charge/Discharge (GCD)

Electrochemical cells were assembled in an argon-filled glovebox with H₂O & O₂ ≤ 1 ppm. The voltage limits of the half-cell were cycled between 0.002 and 1.5 V under constant current constant voltage (CC–CV) charging protocol. The cells’ rated capacity was estimated based on the average of the initial 5 cycles of a pristine CF cell, and it was found to be approximately 105 mA h/g. Stable cycling tests was conducted at both ambient room temperature (25 °C), and cold temperature (5 °C), to stimulate accelerated aging. The temperature was controlled with a thermal chamber (±0.3 °C) from JEIO TECH, Korea.

3. Numerical Methods

3.1. Finite-Element Analysis

3.1.1. Computational Modeling of CF/SPE Interface

An axisymmetric finite element model (FEM) inspired by the experimental CF/SPE interfacial shear strength (IFSS) setup was developed using ABAQUS, Dassault Systèmes, 2021. This model, with geometry, boundary conditions, and loading conditions inspired by the experimental microbond test, was used to simulate and validate the interfacial behavior. The FEA-derived IFSS results were systematically compared with experimental values for validation. Figure 2a, shows a schematic of the IFSS microbond specimen arrangement. The axisymmetric model adaptation used in the simulation of the microbond test is schematically illustrated in Figure 2b, in which the interfacial contact between the fiber and droplet is represented by a cohesive zone model (CZM).⁴²⁻⁴⁶

A zero-thickness mixed-mode CZM^45,46 was used to simulate the CF/SPE interfacial bonding, closely replicating the conditions of the single fiber/microdroplet interfacial test. The CZM was based on a bilinear traction-separation constitutive law to simulate crack initiation and damage propagation with linear softening. A quadratic stress criterion is employed to model failure, while the Benzeggagh–Kenane (BK) law (see Supporting Information, Figure S1) is utilized to represent crack damage propagation. Initially, a baseline FE model was used to calibrate the interface model against a random specimen until the error is ≤5% as the prediction threshold for conditional setting used to terminate iterations against a randomly selected benchmark specimen. Subsequently, the interface model was validated against the averaged results of all experimental specimens using an iterative scheme (Supporting Information, Figure S2 and Table S2). The framework demonstrated strong generalizability by being validated against experimental values for various SPE formulations, accurately predicting IFSS, load–displacement curves, and de-bonding behavior. More elaborate information can be found elsewhere (Supporting Information IFSS CZM Modeling).

Both fiber and droplet are modeled using 4-node bilinear axisymmetric quadrilateral elements (CAX4R). The SPE material was assumed to be linear elastic, while the fiber was modeled as transversely isotropic. The material properties are shown in Table 1. The coefficient of thermal expansion (CTE) and glass transition temperature (T_g) were evaluated via thermomechanical analysis (TMA) (Supporting Information TMA Analysis of SPE and Figure S3).

Table 1. Thermomechanical Properties of the Carbon Fiber (CF) and the SPE Matrix.

property	fibera	matrixb [epoxy//SPE]
material type	carbon T700s		tensile modulus (MPa)	Poisson’s	CTE (10–6/°C)
axial modulus (GPa)	230	SPE 0	2691.6	0.38	85.7
transverse modulus (GPa)	15
shear modulus (GPa)	24 (axial)/5.03 (transverse)	SPE 30	1337.0	0.33	68.3
Poisson’s 1–2	0.20
Poisson’s 2–1	0.25
density (g/cm3)	1.80	SPE 40	1170.7	0.21	63.0
single fiber diameter (μm)	7.00
axial CTE (10–6/°C)	–0.54	SPE 50	782.7	0.20	56.33
radial CTE (10–6/°C)	10.10

^aThe material properties are based on the manufacturer’s specification.^47,48

^bModulus and Poisson’s ratio are obtained from tensile tests, and CTE is obtained from TMA.

To accurately simulate the interfacial characteristics, a thermal preload step was initially applied to account for the thermal residual stress prior to the de-bonding step. The compressive residual stresses in the fiber, induced by thermal shrinkage during cooling from the curing temperature to room temperature, were simulated by applying a thermal preload. The glass transition temperature (T_g) was used as the stress-free temperature, and the operating temperature was set to room temperature.^42,46 These compressive thermal residual stresses, due to the different orthotropic properties in the axial and transverse directions, contribute to progressive de-bonding during the loading process, the maximum de-bonding force (i.e., IFSS), and frictional sliding after de-bonding. Following the thermal step, a prescribed pulling load at a rate of 0.1 mm/min was applied, mirroring the experimental loading conditions.

3.1.2. Representative Volume Element (RVE) Modeling

To study the effect of the interface and estimate the macroscopic effective properties, a hexagonal representative volume element (RVE) unit cell was established via Python scripting. This unit cell, generated with and without interfaces, allowed for the analysis of the CF/SPE’s interface impact on the structural battery’s performance under multiaxial loadings. The fibers were generated based on the diameters obtained from the image processing (i.e., 7.10 μm ± 0.51). The hexagonal unit-cell RVE is shown in Figure 3.

Figure 3.

(a) Hexagonal fiber arrangement, and unit-cell. (b) Hexagonal RVE unit cell showing the three phases i.e., matrix, fiber, and interface.

Two models were developed based on the hexagonal RVE: the idealized RVE (FEA: IDL) and the realistic RVE (FEA: RE). The idealized model was created with no interface, assuming perfect bonding between the fibers and matrix, and thus includes only two phases: fibers and matrix. In contrast, the realistic RVE was developed with three phases: fibers, matrix, and interface, to more accurately represent the actual conditions.⁴⁹⁻⁵⁴ FEA models are created in ABAQUS/Explicit, and the interface thickness was specified as ∼0.1 μm. The meshing of fibers and matrix involves six-node linear triangular prism elements (C3D6) with hourglass control, while the interface is meshed using eight-node cohesive elements (COH3D8). Simulation results provide localized stress and strain details within the RVE, but the response of UD composites can be examined via the homogenized stress σ_ij and the homogenized strain ε_ij. The homogenized quantities can be calculated at each time step from eq 2.

2

where, ⟨ξ⟩; model variable, i.e., [stress ⟨σ⟩||strain ⟨ε⟩||deformation ⟨δ⟩].

Carbon fibers are modeled as linear, elastic, transversely isotropic solids, with their anisotropic properties accounted for through independent elastic constants. In contrast, the isotropic matrix is assumed to exhibit elastic perfectly plastic behavior.⁵³ Importantly, the analysis accounts for nonlinear displacements within the RVE, encompassing phenomena such as interface de-bonding, plasticity, progressive damage, and element deletion. The linear Drucker-Prager yield criterion, coupled with the ductile damage criterion, is employed to model plastic deformation and capture damage progression in the polymer matrix, respectively (Supporting Information, Figures S4 and S5). More elaborate information can be found elsewhere (Supporting Information Computational Micromechanics: RVE Modeling).

3.2. Machine Learning-Driven Design

3.2.1. Data Acquisition and Structuring

Enabled by data-driven methods, unlike traditional electrochemical or equivalent circuit modeling,^55,56 ML-based algorithms can predict battery capacity and SOH by reflecting inherent aging characteristics, deriving predictions solely from experimental data without the need to consider the electrochemical principles of the battery.⁵⁷⁻⁶⁰ Nevertheless, before using the experimental battery data obtained from the battery management system (BMS) in the machine learning pipeline to predict future battery capacity under aging, it is essential to preprocess the raw data. This preprocessing includes discretization, removing outliers, feature engineering, normalization, and subsampling.

Time, voltage, current, and discharge capacity, are acquired as raw data from the BMS and utilized to analyze the structural battery’s degradation behavior during the aging. The charging profile is commonly used to describe the battery’s behavior, as it can provide a more representative depiction of actual battery usage and internal battery parameters compared to the discharging and rest periods. Nevertheless, a significant number of data points (∼10,000,000) are obtained during the charging process, depending on the BMS frequency setting. Utilizing all this data in the ML model is inefficient due to data sensitivity, estimation complexity, and the risk of overfitting on nonrepresentative data. Thus, an initial data structuring process was implemented, systematically storing each battery cycle in a MATLAB structure array with separate fields for charging and discharging data. These fields contained arrays for key parameters: test time, voltage, current, and capacity. This organized approach ensured clear segregation of operational states and accurate capture of each cycle’s temporal progression, which was essential for efficient data analysis, manipulation, and processing in support of the machine learning-driven design process.

Then, uniform subsampling and pattern recognition were applied to preserve apparent changes during the charging interval and maintain relative intervals between measurements. This step was crucial for isolating significant trends and behaviors within the data, reducing noise, and focusing on the most relevant information from the raw data set. The input matrix is formed by concatenating the V, I charge profiles, each with 10 samples. The number of samples is chosen to consider the distinct changes in time and the model complexity. Additionally, to mitigate oscillations within short time intervals, the data was averaged over the sampling period.

To enhance training, min–max normalization is employed. This technique preserves the original data distribution while scaling it to the range of [0,1]. By doing so, it ensures that all features contribute equally to the training process and prevents features with larger scales from dominating the learning process. It is shown in eq 3.

3

where x is a collection of all charging cycles, i.e., [x^k_i] and n represents the number of samples per cycle. Eventually, a denormalization process is applied at the end for observing the final results.

3.2.2. Artificial Neural Network (ANN)-Based Capacity Prediction

The detailed procedure for the artificial neural network (ANN) building and training with Bayesian optimization is illustrated in (Figure 4 and Supporting Information, Table S3). Initially, Bayesian optimization is used to optimize the ANN architecture, also referred as hyper-parameters, including the number of hidden layers, the number of neurons in each layer, learning rate, dropout probability, and damping parameter. Then, the neural network is built based on the assigned hyper-parameters. The training-validation process continues until the model’s combined predictions for training and validation samples are within a 5% error margin. If not, hyperparameters are updated using Bayesian optimization by updating the Gaussian process model and sampling the hyperparameters using the acquisition function. The ANN building and training are iterated with the updated hyper-parameters until the accuracy is reached. Furthermore, K-fold cross-validation, shown in eq 4, was implemented prior to every iteration to increase the model’s robustness, improve generalization, reduce overfitting, and increase the data utilization efficiency.⁶¹

4

Figure 4.

Coupled automated process of ANN building and training with Bayesian optimization.

The models are evaluated with the standard metrics shown in eqs 5–7.

5

6

7

where, n is the number of observations, y_i is the actual value and 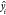is the predicted value.

Thus, in summary, a single iteration includes 50 objective function evaluations generated by a Bayesian algorithm, where each evaluation involves 5 formations of ANN structures (i.e., for a K-fold cross-validation of 5). During each evaluation, the neural network’s hyperparameters are optimized to minimize the combined loss metric across both training and validation data sets. The training-validation process continues until the model’s predictions achieve a combined RMSE of less than 0.05 (5%). This means that for each evaluation, the ANN is trained and validated using the provided data sets, and the RMSE is calculated for both the training and validation sets. If the combined RMSE exceeds 0.05, the Bayesian optimization algorithm continues to iterate, adjusting the hyperparameters in subsequent evaluations.

After completing the optimization, a new ANN is constructed with the optimized hyperparameters and used for training, validation, and testing of the experimental battery data. This optimized ANN then predicts the future capacity of the structural battery using only readily available voltage and current data.

4. Results and Discussion

4.1. Computational Micromechanics: Structural Battery Effective Moduli Prediction

To accurately predict the effective design moduli under various loading conditions, the computational modeling of the CF/SPE interface is first validated, as illustrated in Figure 5.

Figure 5.

(a) Effect of thermal residual stress on the CF/SPE interface. (b) IFSS load–displacement curves: FEA simulation (Navy) vs experimental results (SPE 0, SPE 30, SPE 40, SPE 50, from top to bottom, colored). (c) Von Mises stress (MPa; upper) and damage evolution along the CF/SPE40 interface (lower).

The difference between the CTEs of CF and SPE during the curing and cooling process subjects the interface to residual compressive radial forces, as illustrated in Figure 5a. The higher CTE of the SPE matrix, compared to the CF, results in volumetric shrinkage during cooling, leading to a net residual compressive stress exerted on the fiber along the embedded length of the interface. The trend in residual compressive stress along the interface can be attributed to the reduction in the CTE of the SPE as the electrolyte content increases (Supporting Information, Figure S3). Furthermore, Figure 5b compares the load–displacement curves of the validated IFSS FEA model with the experimental data for various SPE formulations. Notably, the model accurately simulates the frictional force even after complete interface failure. Additionally, as the electrolyte percentage in the SPE increases, frictional forces decrease. This reduction can be attributed to the lower compressive stress and the increased presence of the electrolyte phase, which may act as a friction-reducing agent. The damage evolution stages along the interface are captured in (Figure 5c and Supporting Information, Figure S6). The de-bonding stages can be illustrated as follows.

• (1)(Stage I) Linear load–displacement relationship up to the initiation of de-bonding. Shear stress arises at the interface and is transferred to the fiber. There is no crack nucleation at the interface (τ < τ_critical).
• (2)(Stage II) Stable crack propagation with friction between the crack faces. τ = τ_critical, hence damage is locally initiated near the blade location and progresses circumferentially. The micro-band test loading has reached around 22% of the peak levels of force.
• (3)(Stage III) Unstable crack growth with a sudden drop in the load. The load reaches the complete de-bonding limit at maximum force, stress is ultimately transferred to the matrix.
• (4)(Stage IV) Complete de-bonding of the interface. The interfacial energy is completely consumed, and sliding occurs between the fiber/matrix.

The IFSS and maximum force developed at the interface are compared between the FEA simulation and the experimental results for each CF/SPE formulation in Figure 6.

Figure 6.

Validation of IFSS and maximum force: FEA vs experimental results.

After successfully modeling and experimentally validating the CF/SPE interface, an RVE can be developed to accurately estimate the overall effective material moduli, as shown in Figure 7.

Figure 7.

(a) CFST/SPE lamina effective material moduli w.r.t FEA, analytical approximations, and experiments. (b) Predicted interface failure and matrix plasticity/damage for CF/SPE 40 lamina.

As illustrated in Figure 7a, the developed realistic RVE model (i.e., FEA: RE) accurately predicts the effective material moduli compared to experimental results and analytical models. In contrast, the idealized RVE model (i.e., FEA: IDL) shows considerable overestimation due to the absence of interfacial de-bonding, damage progression, and the assumption of perfect bonding between the constituents. The tensile modulus along the fibers predicted with FEA: RE shows excellent accuracy relative to both experimental and analytical results, with percentage errors of 0.357% and 0.0496% for SPE 0, 1.050% and 1.525% for SPE 30, 1.067% and 1.511% for SPE 40, and 0.0915% and 0.745% for SPE 50, respectively. The effect of interface modeling is more pronounced in estimating the major Poisson’s ratio, with the FEA: RE model aligning more closely with the experimental estimation standard deviation compared to the analytical and idealized models.

Furthermore, transverse and shear loadings (i.e., matrix/interface dominated) revealed significant discrepancies, resulting in much lower expectations in the FEA: RE models than those predicted by the analytical and idealized models. This difference can be attributed to factors such as increased reliance on the less stiff matrix system and interface failure, which leads to a loss of stiffness and a reduction in effective load transfer upon de-bonding. This difference can be attributed to phenomena such as the higher dependence on the less stiff matrix system and interface failure leading to loss of stiffness and depletion of effective load transfer upon de-bonding. Future work will focus on experimentally validating these results, as the thin lamina specimen shape poses challenges, necessitating further investigation. These effects are illustrated in Figure 7b and further detailed in Supporting Information, Movie S1. It is noted that element size analysis was conducted considering a balance between computational time and adequate accuracy (Supporting Information, Figure S7).

4.2. Machine-Learning: Structural Battery Capacity Prediction

The concept of utilizing the voltage and current profiles for predicting the CF-based structural battery’s capacity as it ages is illustrated in Figure 8. A battery based on CF impregnated with SPE 40 was fabricated and cycled for around 2800 h, at a specific current of 10.4 mA g^–1 (∼0.1C). The voltage and the current profiles are shown in Figure 8a, showing in the inset, as the battery ages (∼2500 h.) the voltage increases at a much faster rate, and the current begins to drop from constant current at an earlier stage than the initial state of the battery. This can be attributed to the increased internal resistance, decreased capacity, and charge transfer kinetics.⁶⁰ Different data segmentation ratios [train/validation/test] are used for predicting the battery’s future capacity.

Figure 8.

(a) Voltage and current profiles with magnification in the inset. (b) The battery’s capacity estimation based on the optimized ANN machine learning model compared to the experimental capacity for different training (yellow), validation (rose), and testing (navy) ratios. (c) The models’ performance evaluation metrics of training and testing stages for different data set segmentations.

Three simulations of the optimized ANN are averaged and used to predict the battery’s capacity for each data split, as shown in Figure 8b. The results show the predicted capacity is in well agreement with the experimental results. The evaluation metric graphs for a single iteration of each data split are presented in Figure 9. These graphs demonstrate consistent performance trends across different splits, even when the training data is reduced. The symmetry of the error distribution, with errors concentrated near zero and minimal outliers, further highlights the model’s accuracy and generalization capabilities. Additionally, the performance curve shows that the “best Epoch,” where the validation error is lowest, is found early on, before the training error decreases excessively. This indicates that the model avoids overfitting by generalizing well rather than memorizing the training data. Overall, these results emphasize the model’s robustness to noisy data, reduced dependency on large data sets, and ability to maintain consistent performance across varied data compositions.

Figure 9.

Error histogram, and performance graphs with “best Epoch” for one iteration for each data splits for the SPE40-based structural battery operated at room temperature.

The optimized neural networks’ performance evaluation metrics are shown in Figure 8c. The results show a promising and insightful future for the design and prediction of structural battery performance, as by training the model, the future capacity of approximately 250 cycles can be predicted with a RMSE less than 10 × 10^–6. This can be attributed to the robust ANN hyperparameters and architecture as it enables a more accurate learning to be achieved yielding a MSE in the ranges of (10^–5 to 10^–4). Such performance metrics are unique to the training data, the neural network architecture, and of course, the CF-based battery chemistry, etc. however, a simple comparison to different metrics achieved in the conventional battery’s research in which various input parameters were used (voltage, current, temperature, impedance) showcase the promising the significance of machine learning models for enabling and commercializing CF-based structural batteries^57,58 (Supporting Information, Table S4). Furthermore, the effect of sampling points was also analyzed (Supporting Information, Table S5). It was observed that increasing the ANN sampling size led to reduced prediction performance due to overfitting. Additionally, the computational time increased significantly, which aligns with findings from previous studies.^57,60 This highlights the critical importance of selecting an optimal sampling size to balance model accuracy, generalization, and computational efficiency.

Despite the columbic efficiency averaging to 100% (Supporting Information, Figure S8) for more than 800 cycles accounting to the reversibility of the reaction, the rated capacity degraded notably, particularly in the initial cycles due to the failed formation of the solid electrolyte interphase (SEI). Thus, future research will focus on optimizing the formation protocols to establish a stable SEI layer on the carbon fibers as anode materials. Nevertheless, the ML model demonstrated robustness even when applied to different material compositions, as shown in (Supporting Information, Figures S9 and S10). Specifically, for the SPE50-based sample, voltage/current data were fed into the optimized ANN model, yielding predicted capacity performances with MAPE values of 10.77 ± 0.4, 12.49 ± 0.59, and 14.040 ± 1.79 for each corresponding data split. Additionally, the error histogram, with errors concentrated near zero and minimal outliers, indicates the model predicts accurately and generalizes well across data sets. Furthermore, the “best Epoch,” where validation error is lowest, occurs before the training error begins to drop excessively, avoiding overfitting where the model would memorize instead of generalizing. These findings suggest that the model is robust to noise and data variations, maintaining consistent performance across different data splits and demonstrating insensitivity to changes in data composition.

In multifunctional application, there is an intimate coupling between the mechanical and the electrochemical problems, as the mechanical loading can rapidly decrease the battery’s capacity, leading to an increased rate of aging, evident by the change of the voltage/current profiles and affected SOH.^9,62,63 To simulate and check the validity of machine learning algorithms in predicting rapid CF-based battery aging, a test cell was cycled in a cold environment (∼5 °C) for around 500 cycles, showing excellent prediction accuracy by ANN. This demonstrates the suitability of the well-trained and optimized ANN in predicting capacity performance and health even during rapid battery degradation conditions, further enabling ML as a vital approach for structural batteries design (Supporting Information, Figure S11). As the optimized ML model has demonstrated its validity in accurately predicting structural battery performance under rapid degradation schemes, future analyses will focus on extending this approach to couple the mechanical response and its associated rapid degradation with corresponding capacity and health predictions.

5. Conclusions

In this study, we evaluated the mechanical properties and battery capacity of a carbon fiber-based structural battery, developing experimentally validated numerical methods to simulate behavior and predict performance. Computational micromechanics via FEA and machine learning-driven methods were employed to analyze mechanical and electrochemical performance, reaching the following.

• (1)The CF/SPE interface was successfully modeled using a cohesive zone model (CZM). Residual thermal stress and damage propagation, were simulated, resulting in an IFSS error of ≤5% compared to experiments.
• (2)An RVE model incorporating matrix plasticity/damage and interfacial de-bonding, based on experimental data, was developed. The effective elastic moduli properties obtained from the RVE for CFST/SPE laminas were validated against analytical theories and experiments, demonstrating excellent prediction accuracy. Specifically, the longitudinal tensile modulus showed a percentage error <2%.
• (3)A machine learning-driven capacity prediction scheme for CF-based structural batteries was developed using ANN. Hyperparameters and architecture optimization were achieved through Bayesian optimization and K-fold cross-validation.
• (4)After training the neural network, readily available voltage and current profiles were used to predict the battery’s future capacity, achieving MAPE prediction errors of approximately 5.76%, 11.011%, and 11.93% for 80, 160, and 250 cycles, respectively.
• (5)The error histograms and performance graphs validated the ML model’s robustness, demonstrating its ability to generalize well and handle noise without overfitting. The model’s prediction accuracy is on par with ML-based models in conventional battery research, despite using fewer input variables.
• (6)Machine learning was proven viability for predicting the battery’s capacity, even in harsh and rapid-aging environments, thus showing a promise in analyzing multifunctional mechano-electrochemical coupling in the future.

The results affirm that FEA and machine learning are effective tools for developing and optimizing structural batteries. Their integration promises to accelerate innovation, commercialization and enhance the performance and reliability of future advanced functional composite materials.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon request. Also, the data and associated codes will also be made publicly available on GitHub: https://github.com/MohamadA-RJ

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.4c19073.

• Cure cycle of the SPE; IFSS CZM Modeling; IFSS calibration/validation scheme; TMA Analysis of SPE; Computational Micromechanics: RVE Modeling; ANN Hyperparameters Optimization via Bayesian Optimization; Damage evolution along the CF/SPE interface; Schematic of various loading conditions: Comparison with ML-based models for commercial battery capacity prediction; Dependency on the sampling points for network performance; Cycling stability of CF|SPE 40; CF/SPE50 battery operated at room temperature; Error histogram, and performance graphs and CF/SPE40 battery operated in a cold environment (PDF)

• Predicted Interface Failure and Matrix Plasticity/Damage (MP4)

Author Contributions

M.A.R.: Conceptualization, Methodology, Data curation, Investigation, Visualization, Validation, Writing—Original draft, Writing—Reviewing and Editing; W.K.: Methodology, Reviewing and Editing; W.K.: Methodology, Reviewing and Editing; S.H.L.: Methodology, Reviewing and Editing; S.S.K.: Supervision, Writing—Reviewing and Editing.

The authors declare no competing financial interest.