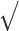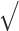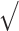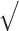Abstract
This study compared the performance of the Bayesian multivariate survival tree approach constructed from extended Cox proportional hazard with gamma frailty term, and two shared gamma frailty models with exponential and Weibull baseline hazard function, respectively. A simulation study was applied to evaluate the impact of the baseline hazard function, number of clusters (200, 500, 1000), cluster size (5, 10, 20), and right censoring rate (10%, 50%, 80%) on the performance of classification. We generated 90 clustered survival datasets having correlated failure times and 50 covariates at cluster level and at individual level. Each dataset was resampling 1000 times by selecting clusters at random 70% as training datasets and the rest 30% as the test datasets. The performance of a Bayesian multivariate survival tree approach based on shared gamma frailty models with Weibull distribution provided the highest accuracy. All three models, the accuracy tended to increase with an increase in the cluster size and the number of clusters. The accuracy decreased monotonically with increasing the percentage of censoring rate. In conclusion, the use of the Bayesian multivariate survival tree approach constructed from the shared gamma frailty with baseline hazard function as Weibull distribution was recommended.
Keywords: Frailty model, Bayesian survival trees, Classification accuracy, Tooth loss
Subject terms: Health care, Medical research, Risk factors, Mathematics and computing
Introduction
Correlated multivariate data frequently occur in medical studies. The correlations naturally appear, one the one hand, due to recurrence of events in the same individual and on the other hand, due to the fact that groups of patients typically share similar characteristics and, in doing so, form clusters. In general, the Cox proportional hazard model is popular model for analyzing univariate survival data1 such that subjects are assumed to be drawn from homogeneous population having the same risk (e.g., risk of disease recurrence or risk of death). It is a semi-parametric model since its baseline hazard function is not specified. In contrast, parametric proportional hazard models involve pre-defined hazard functions that come, for example, in terms of exponential or Weibull distribution functions2–4. Although the exponential model is a simple model with single parametric, it may not be useful in real life for studying the recurrence of events within a lifetime. The Weibull model (which includes the exponential model as a special case) is a more acceptable model because it allows for modeling various types of hazards varying with time such as increasing hazard, constant hazard, or decreasing hazard5.
However, the Cox proportional hazard models fail to account for the correlations in survival times6. Frailty models were introduced that can explain such correlations arising in clustered survival data and are also known as random effect models6–8. Frailty models can be considered as generalizations of the Cox proportional hazard model in which both the frailty term and the covariate effects are assumed to act multiplicative on the baseline hazard9,10. In particular, shared frailty models have been frequently used to describe multivariate survival times related to clusters, where every cluster has its own unique frailty and these frailties are independent of each other11. The frailty variable itself can be distributed in various ways such as a gamma, log-normal, or inverse gaussian distribution11,12.
In addition, the shared frailty model approach can generate the model for each cluster, which is designed for correlated data. In the medical area, patients exhibiting some kind of failure times need to be classified based on shared characteristics. In general, machine learning algorithms can solve various types of data analysis tasks13–16 and may outperform purely statistical models by exhibiting lower error rates for prediction17,18. In particular, machine learning approaches can address this classification problem by constructing appropriate survival trees, which are decision trees for survival data. Survival trees have the advantage of classification individuals in an unbiased way into groups such as risk or prognosis groups19–21. A benchmark machine learning algorithm in this regard is the CART (Classification and Regression Tree) algorithm19. Group specific survival curves and group’s median survival can be estimated from a non-parametric K-M approach22.
In general, tree-based analyses come with another useful feature: they determine which factors out of a set of candidate factors are the important ones that influence the outcome variable of interest. More precisely, during the construction of a tree, an algorithm typically determines which factors are suitable for outcome predictions and rank the suitable ones according to their importance in a semi-hierarchical order. This benefit will be demonstrated in Section “Results” for the data being considered in the present study. In addition, in the context of our tree-based analysis, variable importance can also be determined with a quantitative measure23,24 that again will be discussed in Section “Results”.
Ignoring limitations of proportional hazard models and frailty models, as such they are powerful tools to analyze survival data. That is, a given data set may be first analyzed using a proportional hazard (or frailty) model and subsequently using survival tree models25,26 or random survival forest models17,18. Recently, rather than exploiting these two approaches independently, attempts have been made to merge the two methods. In doing so, dual integrated approaches have been suggested in which hazard models are placed in the nodes which are parts of survival trees, see Table 1 and Fig. 1 (for reviews see11,20).
Table 1.
Dual and triple integrated approaches in previous studies and in the current study.
Fig. 1.
Dual and triple integrated approaches in previous studies and in the current study.
Accordingly, Gao et al.30 proposed a method to integrate a gamma frailty model within the CART survival analysis to analyze multivariate survival data and account for correlated events in studying the risk of catheter infections in dialysis patients. While for the data set at hand the standard frailty modeling analysis just showed an effect of gender, the integrated frailty survival tree model showed that there was an interaction effect between gender and age such that for females two prognostic groups based on age could be identified (while for males this was not the case). Not only the gamma frailty model was merged with survival tree analysis30,32,39 but also other hazard models such as the standard Cox model28 or the exponential frailty model29,31,39. In this context, Calhoun et al.39 presented the R package MST (Multivariate Survival Tree) that allows researchers to construct multivariate survival trees involving frailty models. Growing survival trees that involve hazard models as part of their structures requires to define appropriate splitting rules. A maximum likelihood method for building multivariate survival trees based on gamma frailty models was proposed by Su and Fan32. Fan et al.28 used a robust log-rank statistics as splitting rules for their approach to integrate the Cox model into the survival tree analysis. A test statistic based on the Fisher information matrix was also suggested by Fan et al.29. Several researchers suggested a different way to generalize the standard frailty modeling analysis by focusing on the parameter estimation part34,35. Instead of using standard maximum likelihood estimators in order to estimate the parameters of frailty models, they suggested to utilize a Bayesian framework involving Bayesian estimators as obtained for example by the MCMC approach. In general, the MCMC method is a powerful algorithm for Bayesian estimation40 In doing so, the benefit of frailty models to model random effects across clusters was merged with the flexibility of the Bayesian methodology.
Classical tree-based approach, in general, and survival trees, in particular, involve splitting rules (as mentioned above) that are based on fitting criteria that are maximized19,20,36. This classical approach relies only on observation for data analysis. In opposite, Bayesian tree approach overcomes limitations of the classical tree-based approach by fully exploring the tree space, avoiding bias towards predictor variables with many distinct values, and generating multiple unbiased trees41. This Bayesian approach integrates prior information with observations. In Bayesian tree approach, prior distributions are defined for the components of classical tree approaches. Stochastic search algorithms such as Markov chain Monte Carlo (MCMC) algorithms, or deterministic search algorithms are then used to explore the tree space. The Bayesian tree approach investigates different tree structures with different splitting variables, splitting rules, and tree sizes. Consequently, Bayesian approaches investigate tree spaces in more comprehensive ways as compared to non-Bayesian approaches41. In short, Bayesian tree models are dual approaches that merge the Bayesian approach with the classification and regression tree analysis23,36,37, see Table 1 again .
Finally, Levine et al.38 took a further step and suggested to merge the aforementioned (dual-integrated) frailty survival tree models with the Bayesian approach. By integrating frailty models into survival trees and using, in addition, the Bayesian perspective for tree construction, a triple-integrated approach is achieved that exploits the benefits of all three approaches, see Table 1. The current study contributes to this comprehensive, triple-integrated approach for survival times analysis.
Tooth loss data has served in previous studies as a useful example of multivariate failure time data that can be addressed from the dual frailty survival tree analysis. For example, the approach allowed to classify teeth into five prognostic groups ranging from good to hopeless28,29,31. Among other things, for the McGuire-1991 data set considered by Fan et al.28 teeth were classified as good if they had no furcation involvements and were from patients under the age of 40. The so-called DLS data set considered by Fan et al.29 out of all possible factors only five factors were identified as prognostic factors. Two of them were tooth type and bone loss. Accordingly, molars had a worse overall outlook than non-molars. Levine et al.38 used the aforementioned tripe-integrated approach to analyze the DLS data set as well. For molar teeth they found again that bone loss was the major predictor for tooth loss. Some subject-level variables such as a score for the healthiness of the gums (gingiva score) also played the role of potential predictors. For non-molar teeth bone loss again acted as key predictor. However, in contrast to molar teeth, for non-molar teeth the aforementioned gingiva score was found to be a predictor almost as important as bone loss. The current study will evaluate with the help of the triple-integrated survival analysis approach the Creighton University data set that Calhoun et al.39 made available in the aforementioned MST package.
Previous researches left several issues open. A simulation study that evaluates the performance of the triple-integrated Bayesian frailty survival tree approach for data with different censoring rates is missing. Moreover, as mentioned above and as it will be motivated in the methods section, the Weibull distribution as a hazard function exhibits certain advantages over the exponential distribution. Therefore, a comparison of the performance of both models in the context of the Bayesian frailty survival tree approach would be desirable. As far as the survival analysis of tooth loss data is concerned, it is important to note that problems with oral health, such as poor oral hygiene, tooth cavities, periodontal disease, gum disease, and tooth loss, are more common in elderly patients than in other age groups42. There are many risk factors assessed that could potentially affect tooth loss. The lifetime dental hygiene habits will play an important role in preventing tooth loss in elderly, but there are other causes of tooth loss than hygiene. Diabetes is one of the risk factors that cause tooth loss43. Furthermore, molars tend to have worse caries and periodontal attachment loss in general, and are usually the first causalities of para-functional habits such as grinding of teeth. Since tooth type may thus be instrumental in prediction of tooth loss. As a result, at issue is to study tooth loss in elderly people with an eye on the distinction between diabetic and non-diabetic individuals.
Accordingly, the objectives of our study are the following. Our first aim is to conduct a simulation study that allows to evaluate the performance of the triple-integrated Bayesian survival tree analysis for three specific hazard models: the extended Cox proportional hazard model, the shared gamma frailty model with exponential baseline hazard function and the shared gamma frailty model with a Weibull hazard function. To this end, simulated data sets will be used that exhibit the characteristics of the Creighton University data set (MST package data set). In this context, the objective is not only to study the impact of the model type but also to examine the impact of data features such as the censoring rate. The second aim is to analyze tooth loss in elderly individuals as reported in the Creighton University data set with the help of the aforementioned approach for all three types of hazard models. In particular, we are interested in studying two groups of elderly patients: elderly individuals with diabetes and non-diabetic elderly individuals. Insights from the thus obtained classifications and decision-trees will help to identify risk factors and help to improve the prognosis for tooth loss. In sum, the two objectives of our study were the following. Firstly, to evaluate the impact of right censoring rate, number of clusters, and number of observations in each cluster on the performance of Bayesian multivariate survival tree using extended Cox model with frailty term without specifying any distribution form, and shared gamma frailty survival models with baseline hazard function as exponential and Weibull distributions. Secondly, to apply the three candidate models to real data of tooth loss as observed in four elderly patient groups classified by diabetes status and type of tooth loss (molar and non-molar).
This study is organized as follows. Section “The Creighton university dental data set at the MST R package" briefly introduces into Creighton University dental data set. Section “Material and methods" provides the methods section and details of the Bayesian frailty survival tree analysis method. Section “Results” presents the results from the simulation study (Section “Simulation studies”) and subsequently from the application to the dental data (Sectioin "Application to tooth loss data'). The main findings are summarized and discussed in Section “Discussion”.
The Creighton university dental data set at the MST R package
We analyzed the data available in the open database in the MST R package39 as object Teeth. The data set contains data from 5,336 patients with periodontal diseases who were treated at the Creighton University School of Dentistry from August 2007 to March 2013. Risk factors associated with tooth loss consisted of 51 covariates including 2 demographics (gender, age); 2 health status (diabetes status, smoking); 25 clinical variables at the patient level; and 22 clinical variables at the tooth level. For the 5,336 patients the data set reports failure times in terms of tooth loss times (in years) for a total 65,228 teeth with 25,331 molar teeth and 39,897 non-molar teeth. The patients had an average age of 56 years. 49% of the patients were male, 9% had diabetes mellitus, and 23% were smokers. There are 2,533 elderly patients and 2,803 non-elderly patients, when using a cut-off age given by 60 years as recommended followed the age-group classification of Thailand44. Our study focused on the elderly patients as mentioned above. In the group of elderly patients, there were 395 elderly patients with diabetes and 2,138 elderly patients with non-diabetic. The dataset also reports from 10,824 molar teeth of the elderly patients and 22,559 non-molar teeth. The 395 elderly patients with diabetes had 4,867 teeth in total (1,494 molar teeth and 3,373 non-molar teeth), and the 2,138 elderly patients without diabetes had 28,516 teeth in total (9,330 molar teeth and 19,186 non-molar teeth). In addition, for each elderly patient had the number of molar teeth ranged from 1 to 12, while the number of non-molar teeth had a wider range from 1 to 20.
Material and methods
Study design and clustered survival data
A simulation study with a factorial designs that involved different number of clusters G, different cluster sizes n, and different right censoring rates RC was conducted to evaluate the impact of these three factors on the performance of Bayesian multivariate survival trees. The performance of these trees for the aforementioned different scenarios was furthermore investigated for three different multivariate survival model approaches: (1) an extended cox proportional hazard model with frailty term, (2) a shared gamma frailty survival model with baseline hazard function as exponential distribution, and (3) shared gamma frailty survival models with baseline hazard function as Weibull distribution. Each Dataset was created having fixed 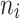 observations per cluster and fixed value of correlation among failure time observations in all clusters. Each of
observations per cluster and fixed value of correlation among failure time observations in all clusters. Each of  observations in each cluster was generated by the same structure of random triples (
observations in each cluster was generated by the same structure of random triples ( , where the (ij) subscript indicates the
, where the (ij) subscript indicates the 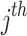 individual unit in the ith cluster,
individual unit in the ith cluster,  is the smallest time between
is the smallest time between  and
and  ,
, 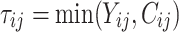 ,
,  is failure time and
is failure time and  is censoring time, the event status. Moreover,
is censoring time, the event status. Moreover, 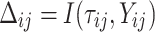 , is coded as 1 for event observation if
, is coded as 1 for event observation if 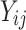 the true failure time is observed, and 0 if it is censored observation. The obtained times
the true failure time is observed, and 0 if it is censored observation. The obtained times 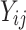 and
and 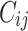 were independent by assumption. Finally,
were independent by assumption. Finally,  denotes a vector of p covariates, containing covariates at cluster level and individual level.
denotes a vector of p covariates, containing covariates at cluster level and individual level.
According to the characteristic of real data of tooth loss presented in Section “The Creighton university dental data set at the MST R package”, our work focused on four elderly patient groups with combination of diabetes status (DB = 1 if a patient has diabetes disease, DB = 0 if not), and type of tooth loss (1 = molar, 0 = non-molar). Each patient was considered as a cluster. Accordingly, in what follows G represents the number of patients and 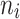 is the number of teeth of each patient i. Importantly, the simulation study mimicked the patterns of patient characteristics of each elderly patient group as observed in the real data described in Section “The Creighton university dental data set at the MST R package”. To this end, the datasets
is the number of teeth of each patient i. Importantly, the simulation study mimicked the patterns of patient characteristics of each elderly patient group as observed in the real data described in Section “The Creighton university dental data set at the MST R package”. To this end, the datasets  with p = 50 covariates were created on the basis of the real data set using a standard Monte Carlo technique. Moreover, failure time
with p = 50 covariates were created on the basis of the real data set using a standard Monte Carlo technique. Moreover, failure time  and censoring time
and censoring time 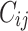 were also simulated by assuming known basic hazard function, such that for each observation in a given dataset the values
were also simulated by assuming known basic hazard function, such that for each observation in a given dataset the values  and
and 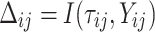 were given as well. For the number of clusters (i.e., the number of patients) the following three levels were used: G = 200, 500, 1000 patients. For the right censoring rate again three levels were used: RC = 10%, 50%, 80%. Note that in the real data set the observed number of molar teeth in elderly patients was no more than 12. Consequently, for molar teeth two levels of cluster sizes were used:
were given as well. For the number of clusters (i.e., the number of patients) the following three levels were used: G = 200, 500, 1000 patients. For the right censoring rate again three levels were used: RC = 10%, 50%, 80%. Note that in the real data set the observed number of molar teeth in elderly patients was no more than 12. Consequently, for molar teeth two levels of cluster sizes were used: 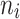 = 5, 10 teeth. In contrast, for non-molar teeth, 3 levels were used
= 5, 10 teeth. In contrast, for non-molar teeth, 3 levels were used 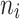 = 5, 10, 20. Possible scenarios for elderly patients with molar teeth consisted of
= 5, 10, 20. Possible scenarios for elderly patients with molar teeth consisted of  = 3 × 2 × 3 = 18 scenarios as presented in the diagram below. For elderly patients with non-molar teeth, there were 27 possible scenarios. Therefore, a total of 90 scenarios were considered. A schematic of a data set is presented in Table 2. refers to the scenario of G = 50 elderly patients with DB with each patient has n=5 molar teeth and data exhibiting a censoring rate = 10%.
= 3 × 2 × 3 = 18 scenarios as presented in the diagram below. For elderly patients with non-molar teeth, there were 27 possible scenarios. Therefore, a total of 90 scenarios were considered. A schematic of a data set is presented in Table 2. refers to the scenario of G = 50 elderly patients with DB with each patient has n=5 molar teeth and data exhibiting a censoring rate = 10%.
Table 2.
Clustered survival data structure from the scenario for which the number of patients is 50 and the number of considered molar teeth of each patient is 5.
| ID of patient (i) |
Teeth (j) |
Covariate 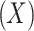
|
Failure time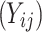
|
Censoring time
|
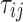
|
Event status 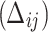
|
|---|---|---|---|---|---|---|
| 1 | 1 |
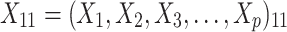
|
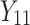
|
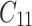
|
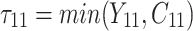
|
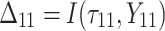
|
| 2 |

|
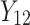
|

|
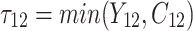
|
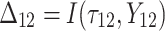
|
|
| 3 |
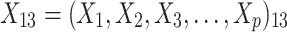
|
|
|
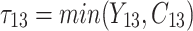
|
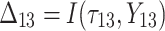
|
|
| 4 |

|
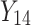
|
|

|
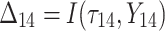
|
|
| 5 |

|

|

|

|

|
|
| 2 | 1 |

|
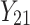
|
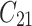
|

|
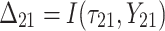
|
| 2 |

|
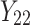
|
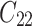
|
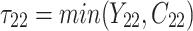
|

|
|
| 3 |

|
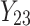
|
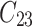
|

|
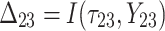
|
|
| 4 |
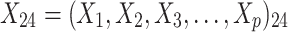
|
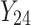
|
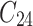
|
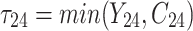
|

|
|
| 5 |

|

|
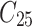
|
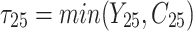
|
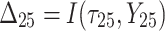
|
|
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 50 | 1 |

|

|
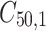
|

|

|
| 2 |

|
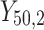
|
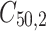
|
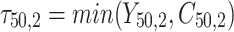
|
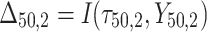
|
|
| 3 |

|
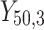
|
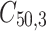
|
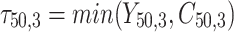
|

|
|
| 4 |
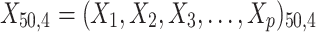
|
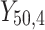
|

|
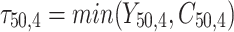
|

|
|
| 5 |
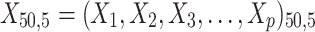
|
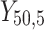
|
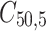
|
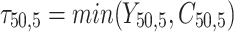
|
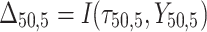
|
Frailty models
To account for correlations in failure times within cluster, every cluster should have its own unique frailty (random effects) and these frailties should be independent to each other. As mentioned in Section “Study design and clustered survival data” the following three models were used
 |
1 |
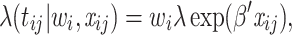 |
2 |
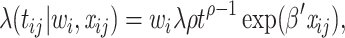 |
3 |
Models (1), (2), and (3) are the extended Cox model1, the shared frailty model with exponential distribution7,45, and the shared frailty model with Weibull distribution6,46. In all models 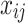 is the vector of covariates for the
is the vector of covariates for the  tooth in the
tooth in the  patient, and
patient, and 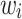 is the frailty term for the
is the frailty term for the  patient. Importantly,
patient. Importantly, 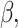 denotes a vector of regression coefficients. The frailty terms,
denotes a vector of regression coefficients. The frailty terms,  are assumed to be independent and identically distributed (iid) among patients. For the extended Cox model (1)
are assumed to be independent and identically distributed (iid) among patients. For the extended Cox model (1)  is an unspecified baseline hazard function. For the shared frailty model with exponential distribution (2) baseline hazard function,
is an unspecified baseline hazard function. For the shared frailty model with exponential distribution (2) baseline hazard function, 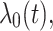 is constant like
is constant like 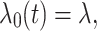 where
where  known as scale parameter. In contrast, for the shared frailty model with Weibull distribution (3) the function
known as scale parameter. In contrast, for the shared frailty model with Weibull distribution (3) the function  corresponds to
corresponds to  where
where  denotes the scale parameter and
denotes the scale parameter and 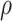 denotes the shape parameter for the baseline hazard. In this study, for all models it was assumed that the frailty terms are distributed like a gamma distribution with
denotes the shape parameter for the baseline hazard. In this study, for all models it was assumed that the frailty terms are distributed like a gamma distribution with
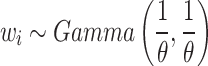 |
4 |
where 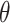 describes the variance of
describes the variance of 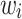 .
.
Survival tree construction and the Bayesian approach
A survival tree combines the technique of decision tree (DT) and survival analysis to analyze time to event data. The primary goal of a survival tree is to classify all observations into mutually groups based on important features in data that have distinct survival experiences. Each classified group exhibits its own survival curve known as Kaplan–Meier curve (K–M) and its own median survival time. The construction of survival trees in general is based on decision tree algorithms47. A dataset is broken down into smaller and smaller subsets using certain splitting rules. The current study will use a Bayesian approach to split tree nodes and construct survival trees. As mentioned in the introduction, such Bayesian approaches have certain advantages over non-Bayesian approaches. In particular, the current study will follow an earlier proposal by Levine et al.38, who presented a Bayesian multivariate survival tree method based on gamma frailty models with exponential baseline hazard function. In particular, the Bayesian survival tree approach takes into account the relationship between failure time 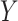 and covariates
and covariates 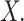 The binary tree partitions the domain of
The binary tree partitions the domain of  and the frailty model is applied for each subset of the partition of the total B terminal nodes of tree T. In the Bayesian tree framework, samples are drawn from the posterior distribution of trees, providing a set of multiple trees for decision-making. The posterior space of trees is explored using Markov chain Monte Carlo (MCMC) methods, defining prior distributions of the tree,
and the frailty model is applied for each subset of the partition of the total B terminal nodes of tree T. In the Bayesian tree framework, samples are drawn from the posterior distribution of trees, providing a set of multiple trees for decision-making. The posterior space of trees is explored using Markov chain Monte Carlo (MCMC) methods, defining prior distributions of the tree,  and survival model parameters (
and survival model parameters (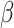 ). Let
). Let 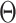 denote the parameter collection of all terminal node. Then the pair (
denote the parameter collection of all terminal node. Then the pair ( specifies the tree model. The tree prior distribution
specifies the tree model. The tree prior distribution  is specified in the Bayesian tree method and satisfies
is specified in the Bayesian tree method and satisfies 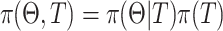 36. The prior distribution
36. The prior distribution 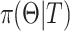 is given in the frailty model.
is given in the frailty model.
Let 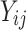 denote an observation for failure time
denote an observation for failure time  of cluster
of cluster 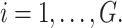 In an internal node, in line with the models listed in Eqs. (1), (2), and (3) the frailty model is expressed as
In an internal node, in line with the models listed in Eqs. (1), (2), and (3) the frailty model is expressed as
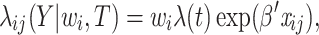 |
5 |
where
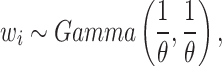 |
6 |
In Eq. (5) the term  corresponds to one of the three possibilities considered in the current study, see Eqs. (1), (2) or (3) again. That is, we have
corresponds to one of the three possibilities considered in the current study, see Eqs. (1), (2) or (3) again. That is, we have 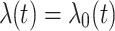 unspecified,
unspecified,  constant, or
constant, or  (for the Weibull case). In addition,
(for the Weibull case). In addition,
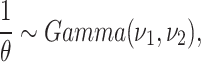 |
7 |
the frailty model prior distribution parameters  are assumed known.
are assumed known.
The parameters of regression coefficients  with different priors distribution was generated based on the type of variables in a Bayesian model. A beta prior is for binary variables, a Dirichlet prior is for multinomial variables, and a normal prior is assumed for continuous variables.
with different priors distribution was generated based on the type of variables in a Bayesian model. A beta prior is for binary variables, a Dirichlet prior is for multinomial variables, and a normal prior is assumed for continuous variables.
Following the general construction of decision trees, out of the set of covariates a splitting variable is randomly selected to obtain child nodes, and finally terminal nodes, with at least m observations per node. The probability of splitting for node  of tree depends on variable (var)
of tree depends on variable (var) 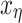 and its threshold (thresh)
and its threshold (thresh)  with
with  and
and  respectively.
respectively.
The probability that a given node is a terminal node or an internal node (split) also determined the prior choice of tree size and tree construction. The probability of splitting for node  is given by
is given by
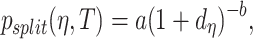 |
8 |
where  and
and 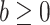 are known and
are known and 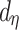 is the tree depth being the number of splits above node
is the tree depth being the number of splits above node 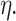 Monte Carlo investigations of the prior tree space specify a and b values, specifically focusing on the (prior) distribution of the number of terminal nodes, as simulating trees from the hierarchical tree prior distribution
Monte Carlo investigations of the prior tree space specify a and b values, specifically focusing on the (prior) distribution of the number of terminal nodes, as simulating trees from the hierarchical tree prior distribution 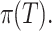
We start Bayesian tree analysis with sampling from the posterior distribution 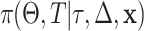 using the Monte-Carlo and Metropolis-Hastings (M-H) sampler. The Monte Carlo specifications of candidate trees are applied for binary search tree algorithms. The M-H is used for developing stochastic searches of tree space using the acceptance-rejection algorithm. At this stage, we borrowed the method described by Levine et al.38 in Section “Survival tree construction and the Bayesian approach” to apply for this study, as seen in our simulation steps.
using the Monte-Carlo and Metropolis-Hastings (M-H) sampler. The Monte Carlo specifications of candidate trees are applied for binary search tree algorithms. The M-H is used for developing stochastic searches of tree space using the acceptance-rejection algorithm. At this stage, we borrowed the method described by Levine et al.38 in Section “Survival tree construction and the Bayesian approach” to apply for this study, as seen in our simulation steps.
Simulation studies
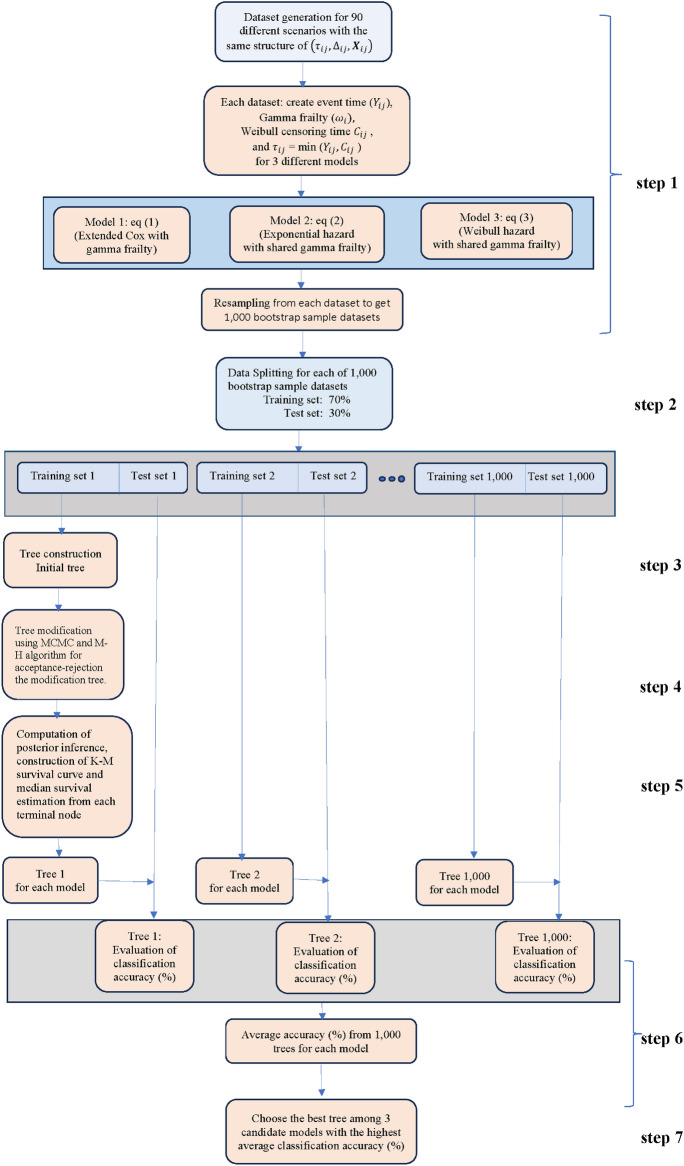
As mentioned in Section “Study design and clustered survival data” in the simulation part of our study 90 different scenarios as described in Fig. 2 were considered. Each of the 90 scenarios were studied in the context of the aforementioned three models which led to 270 cases. These cases were distinguished with the help of the independent variable vector IV=(DB, tooth type, G,  RC, model). For each specific case given by a specific IV the following procedure was conducted. The procedure is graphically presented in Fig. 3.
RC, model). For each specific case given by a specific IV the following procedure was conducted. The procedure is graphically presented in Fig. 3.
Fig. 2.
Diagram of possible scenarios for four elderly patient groups with a combination of diabetes status and type of tooth.
Fig. 3.
Flowchart of simulation study.
Dataset generation
A data set was created that described the teeth of the patients of interest (see Table 2 for cases referring to IV(DB, tooth type, G=50, 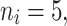 RC, model)). A graphical illustration of this step is shown in step 1 of Fig. 3. To this end, the 50 entries of the regression vector
RC, model)). A graphical illustration of this step is shown in step 1 of Fig. 3. To this end, the 50 entries of the regression vector 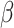 showing up in models (1), (2), (3) were estimated from the real data set. For data generating purposes,
showing up in models (1), (2), (3) were estimated from the real data set. For data generating purposes, 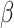 was estimated with the help a simple Cox proportional hazard model without frailty term. In this context, the baseline function was selected consistent with the respective model (1), (2) or (3). Second, for each tooth the 50 covariates were created such that the created entries followed the distribution as found in the real data set. In particular, the first 22 covariates describing properties on the tooth level differed from tooth to tooth of a given simulated patient. Third, for all models and all G patients frailty values
was estimated with the help a simple Cox proportional hazard model without frailty term. In this context, the baseline function was selected consistent with the respective model (1), (2) or (3). Second, for each tooth the 50 covariates were created such that the created entries followed the distribution as found in the real data set. In particular, the first 22 covariates describing properties on the tooth level differed from tooth to tooth of a given simulated patient. Third, for all models and all G patients frailty values 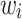 were taken from a gamma distribution with mean 1 and variance 2. With
were taken from a gamma distribution with mean 1 and variance 2. With 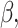 x,
x,  and
and  obtained from the previous steps, temporary failure times
obtained from the previous steps, temporary failure times  for all teeth j and all patients i were computed from
for all teeth j and all patients i were computed from 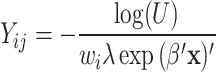 for models 1 and 2 and
for models 1 and 2 and 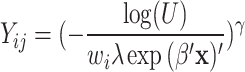 for model 3, where U was given by a random variable uniformly distributed between 0 and 1. The parameter
for model 3, where U was given by a random variable uniformly distributed between 0 and 1. The parameter  will be explained below.
will be explained below.
Censoring times  were obtained from a Weibull distribution like
were obtained from a Weibull distribution like 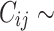 Wei
Wei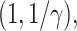 where the parameter
where the parameter 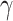 was adjusted such that the censoring rate RC of interest (i.e., as defined in IV) was obtained. Given the values
was adjusted such that the censoring rate RC of interest (i.e., as defined in IV) was obtained. Given the values 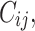 the final simulated failure time values
the final simulated failure time values  were computed from
were computed from 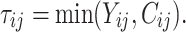 In doing so, a data set for the case specified by IV with properties similar to the real data set was created.
In doing so, a data set for the case specified by IV with properties similar to the real data set was created.
Dataset splitting
This data set specific for case IV was split at random into a training set with 70% of the data and a test set with the remaining 30% of the data and the model under consideration defined either by Eqs. (1), (2) or (3) was fitted to the training data, see also step 2 of Fig. 3.
Tree construction
Subsequently the classification tree for the data split and case IV was constructed, see step 3 of Fig. 3. The following steps were used. First, prior distributions for the model parameters were set up. In line with Eqs. (1), (2) and (3) priors the following priors for the baseline hazard functions were selected: a gamma prior for the hazard rates of model 1, and exponential model for the hazard function of model 2 with a gamma prior for the hazard rate constant  , and gamma priors for the scale parameter
, and gamma priors for the scale parameter 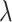 and the shape parameter
and the shape parameter 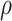 of model 3. Second, for all three models priors for the regression coefficients
of model 3. Second, for all three models priors for the regression coefficients 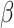 were given in terms of beta priors for binary variables, Dirichlet priors for multinomial variables, and normal priors for continuous variables. Third, for all three models gamma priors were assigned to frailty variance. Finally, for the tree structure the following two priors were set. On the one hand, the probability of splitting a node was set as
were given in terms of beta priors for binary variables, Dirichlet priors for multinomial variables, and normal priors for continuous variables. Third, for all three models gamma priors were assigned to frailty variance. Finally, for the tree structure the following two priors were set. On the one hand, the probability of splitting a node was set as 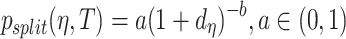 and
and 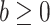 were hyperparameter controlling the splitting behavior and
were hyperparameter controlling the splitting behavior and 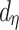 was the tree depth being the number of splits above node
was the tree depth being the number of splits above node 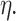 In this study, we followed Chipman et al.48 and set up
In this study, we followed Chipman et al.48 and set up 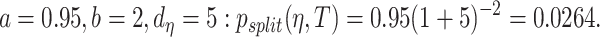 On the other hand, the prior for the splitting rule from internal node was that a variable was randomly selected and likewise its cut-point was randomly selected.
On the other hand, the prior for the splitting rule from internal node was that a variable was randomly selected and likewise its cut-point was randomly selected.
Tree modification
The initial tree structure  was initialized with the most significant variable. Subsequently, as indicated in Fig. 3 (see level 4), tree modifications to the current tree structure were proposed. One of the following four modification steps were selected at random with equally probability of 0.25: grow, prune, change, and swap. In case of the grow modification a terminal node was selected randomly, a splitting variable was chosen randomly, and two child nodes based on the splitting rule was created. In case of the prune modification an internal node having two child nodes was selected, then the child nodes were removed, and the internal node was treated as terminal node. In the case of a change modification, again an internal node was selected at random but then its existing splitting rule was changed to a new rule drawn from the prior. Finally, in the case of a swap modification, the splitting rules between a parent and a child node were swapped provided that the tree remained valid. Given the new tree structure, in the next step, posterior probabilities were calculated. To this end the prior probability of the tree structure was computed, the marginal likelihood of the data under the current tree was computed, and the marginal likelihood of the data under the new tree was computed. Subsequently, the posterior probabilities of the model parameters (e.g., baseline hazard, regression coefficients, frailty variance), and the current tree and the new tree were computed by combining the aforementioned marginal likelihoods with the prior probability. Next, the Metropolis-Hastings (M-H) acceptance algorithm was applied to evaluate the proposed tree modification. More precisely, the acceptance probability for the proposed tree modification was calculated. Following the standard M-H procedure, a uniformly distributed random number u in the interval 0,1 was generated and the proposed modification was accepted when u was smaller than the acceptance probability. Otherwise, it was rejected. If accepted, the proposed new tree became the current tree for the next iteration. If rejected, the current tree remained unchanged. Parameters were then updated. In particular, new values for the parameters (e.g., baseline hazard, regression coefficients, frailty variance) given the current tree structure were sampled using M-H steps.
was initialized with the most significant variable. Subsequently, as indicated in Fig. 3 (see level 4), tree modifications to the current tree structure were proposed. One of the following four modification steps were selected at random with equally probability of 0.25: grow, prune, change, and swap. In case of the grow modification a terminal node was selected randomly, a splitting variable was chosen randomly, and two child nodes based on the splitting rule was created. In case of the prune modification an internal node having two child nodes was selected, then the child nodes were removed, and the internal node was treated as terminal node. In the case of a change modification, again an internal node was selected at random but then its existing splitting rule was changed to a new rule drawn from the prior. Finally, in the case of a swap modification, the splitting rules between a parent and a child node were swapped provided that the tree remained valid. Given the new tree structure, in the next step, posterior probabilities were calculated. To this end the prior probability of the tree structure was computed, the marginal likelihood of the data under the current tree was computed, and the marginal likelihood of the data under the new tree was computed. Subsequently, the posterior probabilities of the model parameters (e.g., baseline hazard, regression coefficients, frailty variance), and the current tree and the new tree were computed by combining the aforementioned marginal likelihoods with the prior probability. Next, the Metropolis-Hastings (M-H) acceptance algorithm was applied to evaluate the proposed tree modification. More precisely, the acceptance probability for the proposed tree modification was calculated. Following the standard M-H procedure, a uniformly distributed random number u in the interval 0,1 was generated and the proposed modification was accepted when u was smaller than the acceptance probability. Otherwise, it was rejected. If accepted, the proposed new tree became the current tree for the next iteration. If rejected, the current tree remained unchanged. Parameters were then updated. In particular, new values for the parameters (e.g., baseline hazard, regression coefficients, frailty variance) given the current tree structure were sampled using M-H steps.
The tree modification and acceptance steps described above were repeated for 50,000 iterations. The first 10,000 iterations were considered as burn-in period. Samples of tree structures and model parameters for posterior inferences were collected after the burn-in period was completed.
Posterior inference
Posterior inference steps (Fig. 3 level 5) were conducted based on the samples obtained from the post-burn-in period. In these steps posterior mean values for inferences about the survival model and the tree structure and the posterior distribution of the tree structure were estimated. At the end of the 50,000 iterations the results were summarized for the obtained tree: for each terminal node the K-M survival curve and the median survival time were determined. Subsequently, the obtained tree model was evaluated. To this end, the survival tree obtained for the training data set under consideration was applied to its corresponding test set to evaluate the tree classification accuracy. The accuracy measures will be discussed in Section “Survival tree accuracy metrics” below.
Evaluation of accuracy
As mentioned above, the data set specific for a case IV was divided at random into a training and test set. To this end a 70–30% partitioning was used. The classification tree for the new partitioning was then constructed using the same steps as described above. In fact, a total of 1,000 trees were thus obtained from 1,000 different training and test sets partitions. In doing so, averages of classification accuracy were obtained for each of the 270 cases considered in the simulation study. The best tree was selected based on the highest classification accuracy to be representative for each scenario and applied to the real dataset.
Survival tree accuracy metrics
The performance of models was evaluated in terms of classification accuracy49. The accuracy of an empirical tree model for simulation (T) relative to the true tree for original data (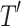 ) using the Node homogeneity (NH) statistic. It measures the proportion of the observations in each node
) using the Node homogeneity (NH) statistic. It measures the proportion of the observations in each node 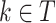 that were classified in the same true group (class) in
that were classified in the same true group (class) in 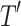 . Let
. Let  be the proportion of observations in node
be the proportion of observations in node 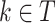 that came from class
that came from class  and let
and let 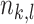 be the total number of observations at node
be the total number of observations at node 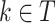 from class
from class  .
.
Then, the overall node homogeneity statistic was computed as suggested by Bertsimas et al.49:
 |
9 |
where n be the total number of observations at all node.
The higher percentage of classification accuracy of overall node homogeneity statistics indicates the better model for survival tree.
Results
To meet the objectives of study, this section has two parts. First, we present the results from the simulation study. Second, we summarize the results from the application to the real dental data.
Simulation studies
The simulation study compared the accuracy of a Bayesian multivariate survival tree based on three candidate models for predicting tooth prognosis in elderly patients, both diabetic and non-diabetic, and both molar and non-molar teeth. The results of the simulation study are summarized in Tables 3 and 4. More precisely, Tables 3 and 4 show the average accuracy as function of the 135 cases tested in the stimulation study in which simulated patients with diabetes were considered. Overall, it was found that the approach that was based on the shared frailty model with Weibull distribution (model 3) consistently provided the highest accuracy scores across all considered scenarios, including different numbers of teeth, different number of patients, and different censoring rates. The approach based on the shared frailty model with exponential distribution (model 2) generally followed in accuracy, while the approach involving the extended Cox proportional hazard model (model 1) often performed with lowest accuracy.
Table 3.
The average accuracy of the Bayesian multivariate survival tree approaches based on models 1, 2, and 3 for molar teeth in elderly patients with diabetes simulated in our simulation study.
| Number of teeth per patient | % of censoring rate | Number of patients = 200 | Number of patients = 500 | Number of patients = 1000 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | ||
 |
10 | 0.7932 | 0.8779 | 0.9277 | 0.8053 | 0.8808 | 0.9482 | 0.8351 | 0.8917 | 0.9591 |
| 50 | 0.7743 | 0.8691 | 0.9038 | 0.7964 | 0.8785 | 0.9139 | 0.8179 | 0.8894 | 0.9248 | |
| 80 | 0.7684 | 0.8656 | 0.8949 | 0.7782 | 0.8694 | 0.9017 | 0.7826 | 0.8802 | 0.9126 | |
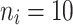 |
10 | 0.8147 | 0.8899 | 0.9303 | 0.8295 | 0.8961 | 0.9575 | 0.8463 | 0.9070 | 0.9684 |
| 50 | 0.7904 | 0.8797 | 0.9273 | 0.8076 | 0.8806 | 0.9346 | 0.8218 | 0.8915 | 0.9455 | |
| 80 | 0.7856 | 0.8764 | 0.9016 | 0.7921 | 0.8797 | 0.9136 | 0.8174 | 0.8906 | 0.9246 | |
Bold face numbers indicate the highest classification accuracy across the three models under each scenario.
Table 4.
The average accuracy of the Bayesian multivariate survival tree approaches based on models 1, 2, and 3 for non-molar teeth in elderly patients with diabetes simulated in our simulation study.
| Number of teeth per patient | % of censoring rate | Number of patients = 200 | Number of patients = 500 | Number of patients = 1000 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | ||
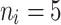 |
10 | 0.7935 | 0.8981 | 0.9326 | 0.8285 | 0.8934 | 0.9576 | 0.8363 | 0.9043 | 0.9685 |
| 50 | 0.7821 | 0.8713 | 0.9105 | 0.8159 | 0.8816 | 0.9289 | 0.8265 | 0.8925 | 0.9398 | |
| 80 | 0.7672 | 0.8756 | 0.9025 | 0.7743 | 0.8761 | 0.9152 | 0.7954 | 0.8870 | 0.9262 | |
 |
10 | 0.8156 | 0.8999 | 0.9403 | 0.8342 | 0.9061 | 0.9646 | 0.8512 | 0.9170 | 0.9756 |
| 50 | 0.8014 | 0.8873 | 0.9319 | 0.8262 | 0.8908 | 0.9457 | 0.8431 | 0.9017 | 0.9566 | |
| 80 | 0.7929 | 0.8732 | 0.9152 | 0.8164 | 0.8864 | 0.9264 | 0.8214 | 0.8973 | 0.9373 | |
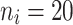 |
10 | 0.8313 | 0.9113 | 0.9571 | 0.8472 | 0.9246 | 0.9722 | 0.8596 | 0.9355 | 0.9832 |
| 50 | 0.8167 | 0.8996 | 0.9412 | 0.8378 | 0.9136 | 0.9634 | 0.8472 | 0.9245 | 0.9744 | |
| 80 | 0.8054 | 0.8737 | 0.9218 | 0.8257 | 0.9008 | 0.9559 | 0.8361 | 0.9118 | 0.9669 | |
Bold face numbers indicate the highest classification accuracy across the three models under each scenario.
Regarding the effects of cluster size (number of teeth per patient) on the performance accuracy, it was found that the accuracy improved with an increase in the cluster size (number of teeth per patient). This effect was independent of model type, censoring rate, the number of patients being considered, and simulated tooth type. Furthermore, it was found that the accuracy improved when the number of patients was increased. Again, this effect was independent of the other independent factors such as model type, censoring rate, the number of teeth, and simulated tooth type. Finally, accuracy decreased monotonically when censoring rate was increased irrespective of model type, cluster size, number of patients, and tooth type. In summary, as far as the simulated diabetic patients were concerned four main effects of model type, number of teeth (cluster size), number of patients and censoring rate were identified. Performance accuracy was not subjected to any qualitative interaction effect. Likewise, based on the results listed in Tables 3 and 4, we could not point out any obvious quantitative interaction effect.
Tables 5 and 6 present the average accuracy as function of the remaining 135 cases for simulated non-diabetic patients. Just as for the simulated diabetic patients, it was found that the approach involving model 3 outperformed the two alternative approaches based on models 1 and 2. Moreover, the survival tree analysis approach based on model 2 again performed better than the approach involving model 1. This effect of the model type was independent of the remaining factors. Regarding the three remaining factors, the effects of cluster size (number of teeth per patient), the number of patients, and the percentage of censoring rate, the same effects as for the diabetic patients were obtained. It was found that the accuracy improved with an increase in the cluster size (number of teeth per patient) and the number of patients, and it decreased when censoring rate was increased.
Table 5.
The average accuracy of the Bayesian multivariate survival tree approaches based on models 1, 2, and 3 for molar teeth in elderly patients with non-diabetic simulated in our simulation study.
| Number of teeth per patient | % of censoring rate | Number of patients = 200 | Number of patients = 500 | Number of patients = 1000 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | ||
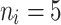
|
10 | 0.8032 | 0.8781 | 0.9256 | 0.8251 | 0.8934 | 0.9376 | 0.8368 | 0.9043 | 0.9485 |
| 50 | 0.7961 | 0.8603 | 0.9105 | 0.7974 | 0.8816 | 0.9230 | 0.8145 | 0.8925 | 0.9339 | |
| 80 | 0.7712 | 0.8523 | 0.8925 | 0.7842 | 0.8661 | 0.9052 | 0.7972 | 0.8770 | 0.9162 | |

|
10 | 0.8169 | 0.8866 | 0.9325 | 0.8256 | 0.9028 | 0.9463 | 0.8478 | 0.9137 | 0.9573 |
| 50 | 0.7924 | 0.8726 | 0.9219 | 0.8106 | 0.8908 | 0.9369 | 0.8216 | 0.9017 | 0.9479 | |
| 80 | 0.7871 | 0.8675 | 0.9025 | 0.7948 | 0.8764 | 0.9140 | 0.8183 | 0.8873 | 0.9250 | |
Bold face numbers indicate the highest classification accuracy across the three models under each scenario.
Table 6.
The average accuracy of the Bayesian multivariate survival tree approaches based on models 1, 2, and 3 for non-molar teeth in elderly patients with non-diabetic simulated in our simulation study.
| Number of teeth per patient | % of censoring rate | Number of patients = 200 | Number of patients = 500 | Number of patients = 1000 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | ||
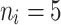
|
10 | 0.8097 | 0.8814 | 0.9357 | 0.8254 | 0.9037 | 0.9457 | 0.8386 | 0.9138 | 0.9558 |
| 50 | 0.7924 | 0.8729 | 0.9249 | 0.8167 | 0.8960 | 0.9399 | 0.8279 | 0.9061 | 0.9500 | |
| 80 | 0.7783 | 0.8629 | 0.9050 | 0.7832 | 0.8709 | 0.9124 | 0.8014 | 0.8810 | 0.9225 | |

|
10 | 0.8201 | 0.8963 | 0.9445 | 0.8321 | 0.9175 | 0.9530 | 0.8562 | 0.9276 | 0.9631 |
| 50 | 0.8016 | 0.8864 | 0.9387 | 0.8279 | 0.9082 | 0.9494 | 0.8473 | 0.9183 | 0.9595 | |
| 80 | 0.7971 | 0.8754 | 0.9125 | 0.8172 | 0.8841 | 0.9204 | 0.8316 | 0.8942 | 0.9305 | |
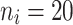
|
10 | 0.8354 | 0.9113 | 0.9571 | 0.8497 | 0.9246 | 0.9722 | 0.8624 | 0.9355 | 0.9832 |
| 50 | 0.8219 | 0.9036 | 0.9458 | 0.8371 | 0.9157 | 0.9513 | 0.8503 | 0.9258 | 0.9614 | |
| 80 | 0.8193 | 0.8969 | 0.9266 | 0.8313 | 0.9072 | 0.9584 | 0.8415 | 0.9173 | 0.9685 | |
Bold face numbers indicate the highest classification accuracy across the three models under each scenario.
As far as the two factors  and G were concerned, that is, the number of teeth and the number of patients, the two effects may be summarized to state that the performance accuracy of our triple-integrated Bayesian machine learning approach improved when larger data sets were considered. In our simulation study, these larger data sets were either obtained by increasing
and G were concerned, that is, the number of teeth and the number of patients, the two effects may be summarized to state that the performance accuracy of our triple-integrated Bayesian machine learning approach improved when larger data sets were considered. In our simulation study, these larger data sets were either obtained by increasing 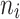 or G or by increasing both factors. While an interaction effect between the two factors
or G or by increasing both factors. While an interaction effect between the two factors  and G might be thinkable, based on the results presented in Tables 3, 4, 5 and 6, we could not identify such an effect.
and G might be thinkable, based on the results presented in Tables 3, 4, 5 and 6, we could not identify such an effect.
Application to tooth loss data
In the data set we distinguished between patients with 1–5 molar teeth and 6–12 molar teeth. Likewise, patients were put into three groups according to the number of non-molar teeth: 1–5, 6–10, and 11–20. Table 7 summarizes the characteristics of the groups thus obtained. We matched the characteristics to the scenarios considered in the simulation study, as shown in Table 8.
Table 7.
Number of teeth per patient, number of patient and percentage of censoring rate for 4 cases.
| Case | Real data | Corresponding scenario | ||||
|---|---|---|---|---|---|---|
| No. of teeth per patient | No. of patients | % of censoring rate |  |
G | % of censoring rate | |
| Diabetes and molar teeth | 1–5 | 219 | 78.07 |
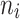 = 5 = 5 |
G = 200 | 80 |
| 6–12 | 115 | 89.64 |
 = 10 = 10 |
G = 200 | 80 | |
| Diabetes and non-molar teeth | 1–5 | 101 | 88.67 |
 = 5 = 5 |
G = 200 | 80 |
| 6–10 | 139 | 87.53 |
 = 10 = 10 |
G = 200 | 80 | |
| 11–20 | 142 | 89.93 |
 = 20 = 20 |
G = 200 | 80 | |
| Non-diabetic and molar teeth | 1–5 | 1074 | 92.45 |
 = 5 = 5 |
G = 1,000 | 80 |
| 6–12 | 837 | 94.78 |
 = 10 = 10 |
G = 1,000 | 80 | |
| Non-diabetic and non-molar teeth | 1–5 | 535 | 90.76 |
 = 5 = 5 |
G = 500 | 80 |
| 6–10 | 723 | 87.63 |
 = 10 = 10 |
G = 500 | 80 | |
| 11–20 | 828 | 92.44 |
 = 20 = 20 |
G = 1,000 | 80 | |
Table 8.
Comparison the result of the average classification accuracy over 1,000 test sets of Bayesian multivariate survival trees obtained from 3 candidate models between simulation data and real dental data.
| Case | No. of teeth per patient | Simulation data | Real dental data | ||||
|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | ||
| Diabetes and molar teeth | 1- | 0.7684 | 0.8656 | 0.8949 | 0.7764 | 0.8758 | 0.9051 |
| 6-2 | 0.7856 | 0.8764 | 0.9016 | 0.7935 | 0.8866 | 0.9118 | |
| Diabetes and non-molar teeth | 15 | 0.7672 | 0.8756 | 0.9025 | 0.7854 | 0.8863 | 0.9254 |
| 610 | 0.7929 | 0.8732 | 0.9152 | 0.8163 | 0.8966 | 0.9366 | |
| 11-0 | 0.8054 | 0.8737 | 0.9218 | 0.8176 | 0.8963 | 0.9354 | |
| Non-diabetic and molar teeth | 15 | 0.7972 | 0.8770 | 0.9162 | 0.7983 | 0.8872 | 0.9264 |
| 6-2 | 0.8183 | 0.8873 | 0.9250 | 0.8198 | 0.8975 | 0.9352 | |
| Non-diabetic and non-molar teeth | 15 | 0.7832 | 0.8709 | 0.9124 | 0.7961 | 0.8811 | 0.9226 |
| 610 | 0.8172 | 0.8841 | 0.9204 | 0.8283 | 0.8943 | 0.9306 | |
| 11–20 | 0.8415 | 0.9173 | 0.9685 | 0.8471 | 0.9275 | 0.9787 | |
Bold face numbers indicate the highest classification accuracy across the three models under each scenario.
Table 8 shows the average accuracy of the Bayesian multivariate survival tree approach when applied to the real tooth loss data. In all case, the shared frailty model with Weibull distribution (model 3) performed better than the other two models in terms of a classification accuracy. Similarly, model 2 performed better than model 1. This pattern of results was consistent with the results obtained from the simulation study. Interestingly, when comparing the explicit accuracy scores, we found that overall classification accuracy was slightly higher for the dental data set as compared to the corresponding simulated data sets.
Example of Bayesian multivariate survival tree for molar teeth in elderly patients
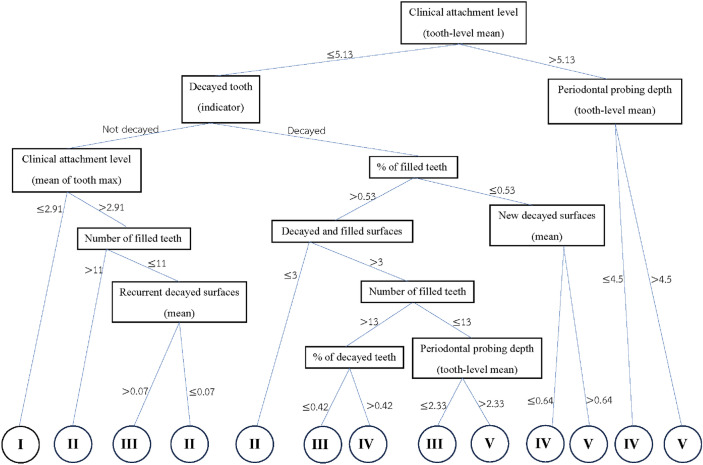
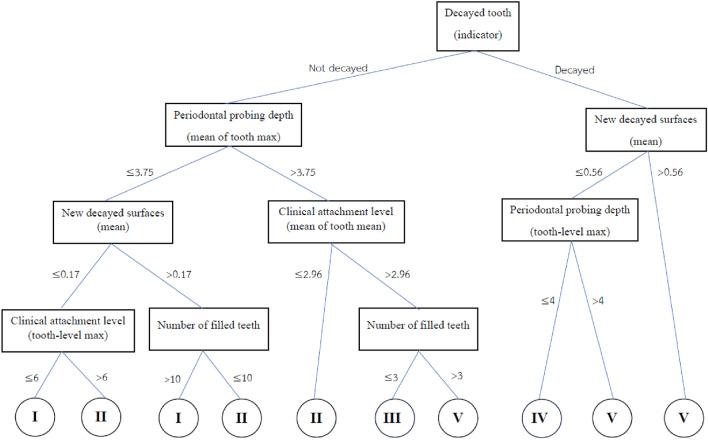
The best tree of Bayesian multivariate survival tree with shared frailty models with Weibull distribution for molar teeth in elderly diabetic and non-diabetic patients are shown in Figs. 4 and 5, respectively. The root and internal nodes are represented by rectangles and the splitting variables are listed there. The splitting rules are listed at the tree branches. The tree shown in Fig. 4 demonstrates the tree for diabetic patients, which splits the molar teeth into 13 terminal nodes, exceeding the 5 diagnostic groups (good, fair, poor, questionable, and hopeless) that are of clinical interest. To reduce the number of groups to five, log-rank statistics were employed. The Roman numeral I representing a prognosis group of “good”, II indicating a “fair” group, III is a “poor” group, IV is defined a “questionable” group, and V is group of “hopeless”. Similarly, Fig. 5 shows the survival tree for non-diabetic patients, but with different splitting variables and fewer terminal nodes, reflecting the relatively better prognosis for non-diabetic patients.
Fig. 4.
The best tree of Bayesian multivariate survival tree with shared frailty models with Weibull distribution for molar teeth in elderly patients with diabetes.
Fig. 5.
The best tree of Bayesian multivariate survival tree with shared frailty models with Weibull distribution for molar teeth in elderly patients with non-diabetic.
When comparing Fig. 4 (diabetic patients) with Fig. 5 (non-diabetic patients), the tree for diabetic patients shows a more complex structure, splitting molar teeth into more terminal nodes. This suggests that diabetic patients have more complex prognostic factors for tooth survival compared to non-diabetic patients. The other hand, the tree for non-diabetic patients tends to be less complex, indicating a more stable prognosis for tooth survival.
From the tree shown in Fig. 4 it follows that the decision rules for classifying molar teeth in elderly patients with diabetes into the five prognosis group under consideration are as follows:
Group I (good prognosis)
Mean of clinical attachment level less than 5.13, not decayed tooth, and mean of maximum clinical attachment level less than 2.91
Group II (Fair prognosis)
Mean of clinical attachment level less than 5.13, not decayed tooth, and mean of maximum clinical attachment level larger than 2.91, and number of filled teeth larger than 11 teeth or
Mean of clinical attachment level less than 5.13, not decayed tooth, and mean of maximum clinical attachment level larger than 2.91, number of filled teeth less than 11 teeth, and mean of recurrent decayed surfaces less than 0.07 or
Mean of clinical attachment level less than 5.13, decayed tooth, average filled teeth greater than 0.53%, and recurrent decayed surfaces less than 3.
Group III (Poor prognosis)
Mean of clinical attachment level less than 5.13, no decayed tooth, and mean of maximum clinical attachment level greater than 2.91, number of filled teeth less than 11 teeth, and mean of recurrent decayed surfaces greater than 0.07 or
Mean of clinical attachment less than 5.13, decayed tooth, average filled teeth greater than 0.53%, recurrent decayed surfaces greater than 3, number of filled teeth greater than 13 teeth, and average decayed teeth less than 0.42% or
Mean of clinical attachment level less than 5.13, decayed tooth, average filled teeth larger than 0.534%, recurrent decayed surfaces larger than 3, number of filled tooth less than 13 teeth, and average periodontal probing depth less than 2.33
Group IV (Questionable prognosis)
Mean of clinical attachment level less than 5.13, decayed tooth, average filled teeth larger than 0.53%, recurrent decayed surfaces larger than 3, number of filled tooth larger than 13 teeth, and average decayed teeth larger than 0.42% or
Mean of clinical attachment level less than 5.13, decayed tooth
Mean of clinical attachment level larger than 5.13, mean of periodontal probing depth less than 4.5
Group V (Hopeless prognosis)
Mean of clinical attachment level less than 5.13, decayed tooth, average filled teeth larger than 0.53%, recurrent decayed surfaces larger than 3, number of filled tooth less than 13 teeth, and average periodontal probing depth larger than 2.33
Mean of clinical attachment level less than 5.13, decayed tooth, average filled teeth less than 0.53%, average of new decayed surfaces larger than 0.64%
Mean of clinical attachment level larger than 5.13, mean of periodontal probing depth larger than 4.5
From the tree shown in Fig. 5 it follows that the decision rules for classifying molar teeth in elderly patients with non-diabetic into the five prognosis group under consideration are as follows:
Group I (good prognosis)
Not decayed tooth, mean of maximum periodontal probing depth less than 3.75, mean of new decayed surfaces less than 0.17, and maximum clinical attachment level less than 6 or
Not decayed tooth, mean of maximum periodontal probing depth less than 3.75, mean of new decayed surfaces larger than 0.17, and number of filled teeth larger than 10 teeth
Group II (Fair prognosis)
Not decayed tooth, mean of maximum periodontal probing depth less than 3.75, mean of new decayed surfaces less than 0.17, and maximum clinical attachment level larger than 6 or
Not decayed tooth, mean of maximum periodontal probing depth less than 3.75, mean of new decayed surfaces larger than 0.17, and number of filled teeth larger than 10 teeth or
Not decayed tooth, mean of maximum periodontal probing depth larger than 3.75, and mean of clinical attachment level less than 2.96
Group III (Poor prognosis)
Not decayed tooth, mean of maximum periodontal probing depth larger than 3.75, mean of clinical attachment level larger than 2.96, and number of filled teeth less than 3 teeth
Group IV (Questionable prognosis)
Decayed tooth, mean of new decayed surfaces less than 0.56, and maximum periodontal probing depth less than 4
Group V (Hopeless prognosis)
Not decayed tooth, mean of maximum periodontal probing depth larger than 3.75, mean of clinical attachment level larger than 2.96, and number of filled teeth less than 3 teeth
Decayed tooth, mean of new decayed surfaces less than 0.56, and maximum periodontal probing depth larger than 4
Decayed tooth, and mean of new decayed surfaces larger than 0.56
Example of survival curves from the five prognosis groups for molar teeth in elderly patients
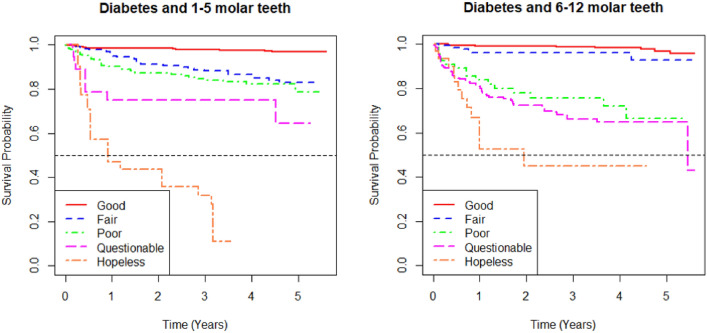
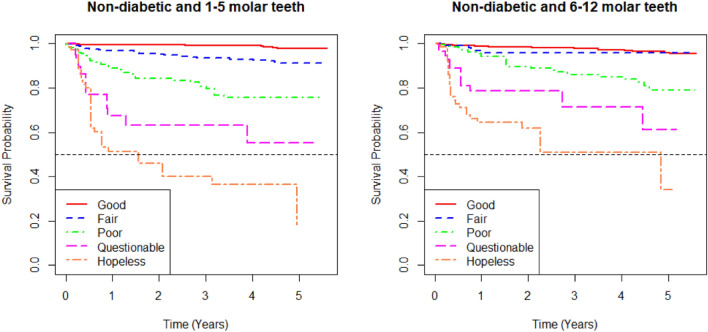
Figures 6 and 7 present the survival curves of the five prognosis groups of the best Bayesian multivariate survival tree shown in Figs. 4 and 5, respectively. The left panel shows the survival probability over time for 1–5 molar teeth, while the right panel shows the same for 6–12 molar teeth.
Fig. 6.
K-M survival curves from the five prognosis groups derived from best tree of Bayesian multivariate survival tree with shared frailty models with Weibull distribution for 1–5 molar teeth (left) and 6–12 molar teeth (right) in elderly patients with diabetes.
Fig. 7.
K-M survival curves from the five prognosis groups derived from best tree of Bayesian multivariate survival tree with shared frailty models with Weibull distribution for 1–5 molar teeth (left) and 6–12 molar teeth (right) in elderly patients with non-diabetic.
In both panels, the curves represent different prognosis groups: “good,” “fair,” “poor,” “questionable,” and “hopeless”. The survival probabilities decrease over time, with the “good” group having the highest survival probability and the “hopeless” group having the lowest. The differences in survival probability among the groups become more dramatic as time progresses, indicating the varying risks associated with each prognosis group.
When comparing the survival outcomes between the 1–5 molar teeth and the 6–12 molar teeth, the 1–5 molar teeth group shows a more distinct differentiation between prognosis groups, with a more rapid decline in survival probability, particularly in the “hopeless” group. In contrast, the 6–12 molar teeth group shows less variation in survival probabilities among the “fair,” “poor,” and “questionable” groups, with these curves being closer to each other. Overall, the survival outcomes suggest that the 1–5 molar teeth may be at a higher risk of earlier tooth loss compared to the 6–12 molar teeth in elderly patients.
In terms of survival curves, Figs. 6 (diabetic patients) and 7 (non-diabetic patients) display important differences. For diabetic patients (Fig. 6), the survival probabilities for each group decline rapidly, particularly in the “hopeless” group, with a clear distinction between prognosis groups. For non-diabetic patients (Fig. 7), survival probabilities are generally higher, and there is less variation between the “fair”, “poor”, and “questionable” groups. This indicates that diabetic patients are at higher risk of early tooth loss compared to non-diabetic patients, with the prognosis groups showing more distinct survival outcomes in diabetic patients.
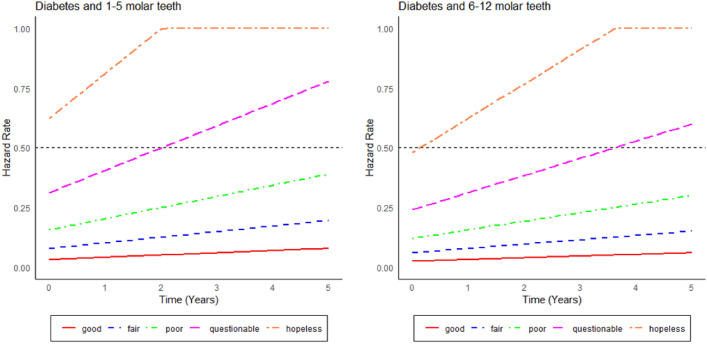
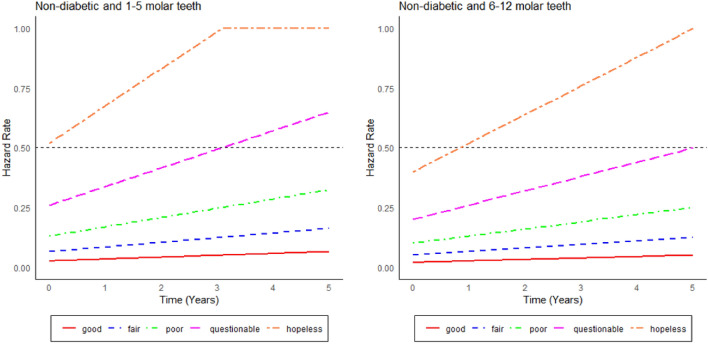
Hazard curves
Figures 8 and 9 show the hazard curves corresponding to the cases presented in Figs. 6 and 7. Accordingly, hazard curves are shown separated by diagnostic tooth groups (good, fair, poor, questionable, hopeless) and the number of teeth (1–5 teeth and 6–12 teeth). The curves are presented separately for the diabetes (Fig. 8) and non-diabetes group (Fig. 9). The hopeless and questionable teeth exhibit a noticeable increase in hazard rates over time, especially in the DB group. In contrast, the teeth considered to be good and fair exhibit consistently low hazard rates throughout the observation period. When comparing the diabetic and non-diabetic patient groups, the teeth of diabetic patients consistently demonstrate higher hazard rates, especially in the hopeless and questionable categories. This pattern aligns with clinical evidence suggesting that diabetes significantly increases the risk of tooth loss, particularly when teeth are in poor condition43. Conversely, the teeth of non-diabetic patients exhibit lower hazard rates across all diagnostic groups, indicating a slower progression toward tooth loss compared to the group of diabetic patients. When comparing Figs. 6, 7, 8 and 9, respectively, we see that the survival curves nicely match - at least qualitatively - with the hazard curves.
Fig. 8.
Hazard curves from the five prognosis groups derived from best tree of Bayesian multivariate survival tree with shared frailty models with Weibull distribution for 1–5 molar teeth (left) and 6–12 molar teeth (right) in elderly patients with diabetes.
Fig. 9.
Hazard curves from the five prognosis groups derived from best tree of Bayesian multivariate survival tree with shared frailty models with Weibull distribution for 1–5 molar teeth (left) and 6–12 molar teeth (right) in elderly patients with non-diabetic.
The core variables determining tooth survival and their relative importance
As mentioned in the introduction, tree-based approaches in general help to identify and rank the most important factors affecting an outcome of interest. In our context, the best trees presented in Figs. 4 and 5 reveal the core variables that determine according to our analysis tooth survival. These variables occur in the tree nodes and the related classification rules listed in Sections “Example of Bayesian multivariate survival tree for molar teeth in elderly patients” and “Example of survival curves from the five prognosis groups for molar teeth in elderly patients”. Accordingly, for elderly patients with diabetes there are 10 core variables, while for non-diabetic patients the set of core variables consists of 7 variables. That is, from the initial set of 50 covariates 40 covariates can be discarded as non-relevant for prognosis purposes for diabetic patients and, likewise, 43 covariates can be dropped for non-diabetic patients. This leads to an enormous reduction of complexity of the classification problem at hand. As far as the core variables are concerned, variables showing up at higher levels of a tree are generally considered to be more important. From Fig. 4 it follows that clinical attachment level, decayed tooth, and periodontal probing depth should be considered to represent the most important variables for predicting tooth survival in diabetic patients. In contrast, for non-diabetic patients, as can be seen in Fig. 5, the three most important predictor variables are decayed tooth, periodontal probing depth, and new decayed surfaces. Consequently, the two predictors “decayed tooth” and “periodontal probing depth” can be regarded as key predictors irrespective of the diabetic status of patients. This discussion illustrates that the data analysis approach proposed in the current study can yield insight into the prognostic role of covariates at hand. Let us supplement this qualitative discussion about variable importance by taking a more quantitative perspective. In line with previous work, variable weight may be determined by counting how frequently a variable occurs in the trees generated for testing23,24. Table 9 shows the variable weights thus obtained. For sake of brevity, only the variables occurring in the best trees were considered. That is, the occurrence frequencies of the variables are shown that occur in the best trees and are reported as probabilities. These probabilities represent the importance weight of each variable. In addition, based on the occurrence frequency each variable is ranked. As can be seen in Table 9, clinical attachment level, periodontal probing depth, and decayed tooth showed up in the generated trees for diabetic patients most frequently and, consequently, were the variables that had the largest weights (with occurrence probabilities of 76.5%, 71.4%, and 65.4%), respectively). This finding is consistent with the fact that the three aforementioned variables occur in the two top levels of the best-tree (see Fig. 4). For non-diabetic patients similar considerations on variable weight can be made (compare Table 9 with Fig. 5). In particular, the root node of the tree has the largest weight (with occurrence probability of 75.2%).
Table 9.
The importance weight of each variable in the trees.
| Variable | DB | Non-DB | |||
|---|---|---|---|---|---|
| Probability | Rank | Probability | Rank | ||
 |
Clinical attachment level (tooth-level mean) | 0.765 | 1 | 0.463 | 9 |
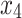 |
Periodontal probing depth (tooth-level mean) | 0.714 | 2 | 0.453 | 11 |
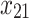 |
Decayed tooth (indicator) | 0.654 | 3 | 0.752 | 1 |
 |
Number of filled teeth | 0.464 | 4 | 0.493 | 8 |
 |
Decayed and filled surfaces | 0.438 | 5 | 0.217 | 23 |
 |
Clinical attachment level (mean of tooth max) | 0.437 | 6 | 0.496 | 7 |
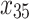 |
New decayed surfaces (mean) | 0.422 | 7 | 0.549 | 5 |
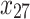 |
Clinical attachment level (mean of tooth mean) | 0.415 | 8 | 0.694 | 2 |
 |
% of decayed teeth | 0.403 | 9 | 0.197 | 24 |
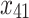 |
% of filled teeth | 0.365 | 10 | 0.134 | 27 |
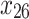 |
Periodontal probing depth (mean of tooth max) | 0.128 | 25 | 0.638 | 3 |
 |
Periodontal probing depth (tooth-level max) | 0.185 | 20 | 0.624 | 4 |
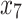 |
Clinical attachment level (tooth-level max) | 0.213 | 18 | 0.539 | 6 |
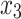 |
Plaque score (percentage) | 0.353 | 13 | 0.462 | 10 |
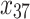 |
Recurrent decayed surfaces (mean) | 0.075 | 34 | 0.079 | 34 |
Bold face numbers indicate variables that actually occur in the respective trees
Plausibility of some decision rules
Let us briefly comment on the plausibility of some decision rules obtained by our machine learning approach. In general, increasing attachment loss over years leads eventually to tooth loss50. Not surprisingly, high attachment levels (indicating a high degree of attachment loss) are know to be risk factors for tooth loss51,52. In our study, for diabetic patients attachment level occurs in the root node (see Fig. 4) and, accordingly, is the most important predictive factor. It shows up in any decision rule (as listed in Section “Example of Bayesian multivariate survival tree for molar teeth in elderly patients”). This dominant role of consistent with the aforementioned literature from the field of dentistry research. In particular, according to two last-mentioned decision rules listed in Section “Example of Bayesian multivariate survival tree for molar teeth in elderly patients” for teeth with questionable and hopeless prognoses, if a tooth exhibits a high attachment level above 5.13, then this property sends the tooth directly to one of the two worst categories.
A measure frequently used by dentists to make decisions about the type of treatment administered to a given tooth is the periodontal probing depth53. In particular, clinical studies have shown that probing depth is a risk factor for tooth loss54. Our data-driven approach identified probing depth as a key variable determining the fate of a tooth. Both for diabetic and non-diabetic patients probing depth is used to distinguish whether a tooth is questionable (group IV) or hopeless (group V), see Figs. 4 and 5. Moreover, probing depth shows up both for diabetic and non-diabetic patients on the second levels of their respective decision trees, indicating that the variable exhibits relative high importance—as it should based on the aforementioned literature.
This brief discussion around the factors clinical attachment and probing depth illustrates that our approach is able to capture relationships that are known in the field of dentistry to play important roles.
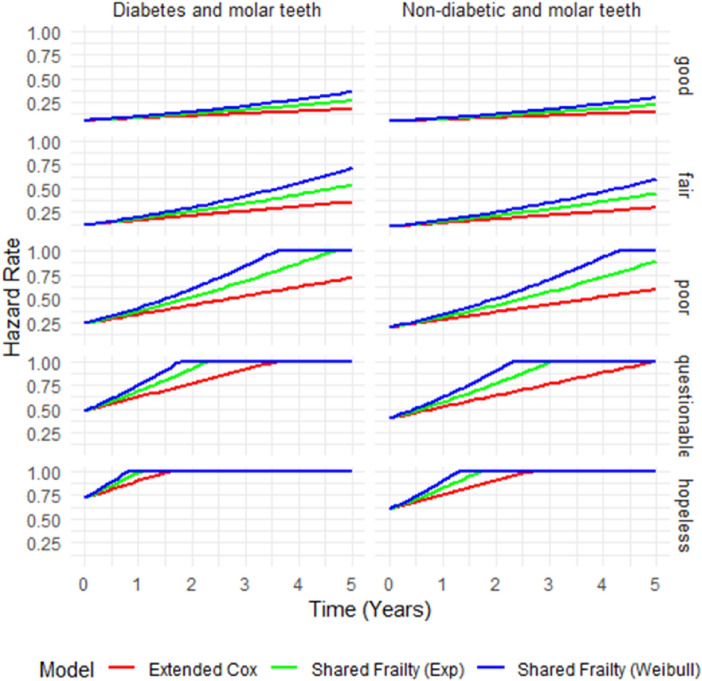
Performance comparison of the models with respect their hazard curves
As argued in Section “Simulation studies”, the models considered in the current study can be compared with the help of their average accuracy measures and the Weibull model performs best among all three models. In this section, we exemplify how the models differ with respect to their predicted hazard curves. Figure 10 present hazard curves obtained under the simulation scenario with n = 10 teeth per patient, G = 1,000 patients, and a 50% censoring rate. The hazard curves describe estimated hazard functions over time, reflecting the risk of tooth loss at each time point given that the tooth has survived up to that time. A comparison is made for the three statistical model studied in the current work: the extended Cox model, the shared frailty model with exponential distribution, and the shared frailty model with Weibull distribution. Furthermore, the analysis distinguishes between diabetic and non-diabetic patients and between the five diagnostic tooth groups: good, fair, poor, questionable, and hopeless. As can be seen in Fig. 10, in general all hazard rate curves are monotonically increasing or stay constant at the fatal 100% level that describes tooth loss. However, the Weibull frailty model exhibited the highest hazard at the initial stage. The exponential frailty model, on the other hand, predicted second largest hazard rates over time. The extended Cox model showed the lowest hazard rates—which makes it the most optimistic model. When stratified by diagnostic groups (good, fair, poor, questionable, and hopeless), the hazard rate increased progressively from good to hopeless, aligning well with clinical expectations—consistent with what we have found earlier for the real data set (see above). The teeth in the hopeless category exhibited the highest hazard, reflecting a greater likelihood of tooth loss, whereas the teeth in the good tooth group had the lowest hazard, indicating better tooth survival prospects. Additionally, a comparison between diabetic and non-diabetic patients revealed that hazard curves for diabetic patients were consistently higher across all diagnostic groups—just as in the abovementioned analysis of the real data set.
Fig. 10.
Hazard curves for three models across prognosis groups in diabetic (left) and non-diabetic (right) patients under the simulation scenario with 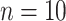 teeth per patient,
teeth per patient, 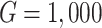 patients, and a 50% censoring rate in elderly patients.
patients, and a 50% censoring rate in elderly patients.
Discussion
Based on our study to compare the accuracy of Bayesian multivariate survival trees, shared gamma frailty models were emphasized in predicting tooth prognosis among elderly patients, both diabetic and non-diabetic and both molar and non-molar teeth. There are two parts of study, one is a simulation study and the other one in an application to a real dental dataset. The key findings and implications of these results are discussed below.
Simulation studies
One notable observation is that the accuracy of all models improved with an increase in the cluster size (number of teeth per patient) and the number of clusters (number of patients), highlighting the importance of larger sample sizes for model precision. Conversely, accuracy decreased monotonically with increasing percentages of censoring, indicating that higher censoring rates can significantly impact the performance of survival models. This finding aligns with previous studies, such as Bunyatisai35, who also observed that larger sample sizes lead to better predictive accuracy. The study highlights how increasing either the cluster size or the number of clusters leads to more precise survival estimates, validating our results. Additionally, models performed better with smaller percentages of right censoring. The negative impact of higher censoring rates on survival analysis has been discussed in several studies, including Bunyatisai35 and Lambert et al.55, which emphasize that higher censoring reduces model accuracy by limiting event observations.
Our findings are consistent with previous studies that have demonstrated the advantages of using frailty models for survival analysis in clustered data. For instance, studies by Lambert et al.55 and Rondeau et al.6 have shown that shared frailty models, particularly those with flexible baseline hazard functions like the Weibull distribution, provide more accurate predictions in the presence of unobserved heterogeneity. Eckel et al.27, Fan et al.28, Fan et al.29 and Rondeau et al.6 showed that flexible baseline hazards improve prediction accuracy in the presence of unobserved heterogeneity. Similar to these studies, our study highlights the superior performance of the Weibull-based frailty model compared to more traditional approaches, such as the Cox proportional hazards model.
In opposite, unlike some previous studies that found little difference in model performance between different baseline hazard functions when frailty terms were included, such as those by Therneau et al.56 and Rondeau et al.57, our study demonstrates a distinct advantage of using the Weibull baseline hazard in Bayesian multivariate survival trees. While Therneau et al.56 observed little influence on model outcomes when comparing different baseline hazards like the Weibull and exponential in the context of frailty models, our findings indicate that the Weibull-based model significantly outperforms others, particularly in terms of predictive accuracy and classification performance. As noted by Chipman et al.36 and Levine et al.38, Bayesian tree-based methods provide a flexible framework that allows for accurate model estimation, particularly when frailty terms and baseline hazard functions are integrated.
Application to tooth loss data
The application of Bayesian multivariate survival trees to real dental data correspond to the findings from the simulation study. The shared gamma frailty model with Weibull distribution (model 3) again showed superior performance in terms of classification accuracy compared to models 2 and 1. This consistency across simulated and real data sets reinforces the robustness and reliability of the Weibull-based Bayesian multivariate survival tree approach. This finding is in line with previous work by Clarke and West23 and Denison et al.37, who emphasized the robustness of Bayesian approaches for survival analysis in complex datasets.
Moreover, the real data analysis revealed that model 2 outperformed model 1 in all cases, which aligns with the simulation study outcomes. The slight increase in overall classification accuracy for the real dental dataset compared to the simulated data sets suggests that the models might be even more effective when applied to actual clinical data, possibly due to more complex real-world patterns that are better captured by the models. As noted by Hallett et al.31, real-world applications often demonstrate more nuanced behaviors, which can be better modeled by Bayesian methods that incorporate frailty.
Implications and future research
The findings of this work have important implications for the prognosis of tooth survival, especially in elderly populations. The superior performance of the Bayesian multivariate survival tree with Weibull distribution suggests that this model can be a valuable tool for clinicians in predicting tooth loss and making informed decisions about patient care.
Tentative future research may focus on further refining these models by incorporating additional patient-specific factors and exploring other types of frailty models such as spatial frailty models.
Overall, the study underline the potential of Bayesian methods in survival analysis and their application in dental prognosis, offering a more accurate and reliable approach compared to traditional methods.
Conclusion
The simulation study demonstrated that the Bayesian multivariate survival trees based on shared gamma frailty models with Weibull distribution (model 3) consistently provided the highest accuracy across various scenarios, including different numbers of patients, teeth per patient, and censoring rates. This model outperformed the shared gamma frailty model with an exponential distribution (model 2) and the extended Cox proportional hazards model with frailty term (model 1).
Acknowledgements
We would like to express appreciation to Department of Statistics, Faculty of Science, Kasetsart University, Bangkok, Thailand, and International SciKU branding (ISB), Faculty of Science, Kasetsart university.
Data availability
There is no direct link to the data set. The anonymised data collected are available as open data via the Creighton University School of Dentistry online data repository: https://www.rdocumentation.org/packages/MST/versions/2.2/topics/Teeth. The dataset can be accessed by installing the MST package in R and loading the dataset named “Teeth”. For further clarification contact corresponding author.
Declarations
Completing interests
All authors have no conflicts of interest to declare. They have read and agree with the work of the manuscript.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Cox, D. R. Regression models and life-tables. J. Roy. Stat. Soc.: Ser. B (Methodol.)34, 187–202 (1972). [Google Scholar]
- 2.Sahu, S. K., Dey, D. K., Aslanidou, H. & Sinha, D. A weibull regression model with gamma frailties for multivariate survival data. Lifetime Data Anal.3, 123–137 (1997). [DOI] [PubMed] [Google Scholar]
- 3.Royston, P. & Parmar, M. K. Flexible parametric proportional-hazards and proportional-odds models for censored survival data, with application to prognostic modelling and estimation of treatment effects. Stat. Med.21, 2175–2197 (2002). [DOI] [PubMed] [Google Scholar]
- 4.Santos, C. A. & Achcar, J. A. A bayesian analysis in the presence of covariates for multivariate survival data: an example of application. Revista Colombiana de Estadistica34, 111–131 (2011). [Google Scholar]
- 5.Vaupel, J. W. & Yashin, A. I. Heterogeneity’s ruses: Some surprising effects of selection on population dynamics. Am. Stat.39, 176–185 (1985). [PubMed] [Google Scholar]
- 6.Rondeau, V., Commenges, D. & Joly, P. Maximum penalized likelihood estimation in a gamma-frailty model. Lifetime Data Anal.9, 139–153 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Vaupel, J. W., Manton, K. G. & Stallard, E. The impact of heterogeneity in individual frailty on the dynamics of mortality. Demography16, 439–454 (1979). [PubMed] [Google Scholar]
- 8.Aalen, O. O. Survival and Event History Analysis: A Process Point of View (Springer, 2008).
- 9.Bunyatisai, W., Prasitwattanaseree, S. & Ingsrisawang, L. Assessing frailty survival models in describing variations caused by unobserved covariates. Chiang Mai J. Sci.44, 1191–1200 (2017). [Google Scholar]
- 10.Shoukri, M. M. Analysis of Correlated Data with SAS and R (CRC Press, 2018).
- 11.Gorfine, M. & Zucker, D. M. Shared frailty methods for complex survival data: A review of recent advances. Ann. Rev. Stat. Appl.10, 51–73 (2023). [Google Scholar]
- 12.Locatelli, I., Lichtenstein, P. & Yashin, A. I. The heritability of breast cancer: A Bayesian correlated frailty model applied to Swedish twins data. Twin Res. Hum. Genet.7, 182–191 (2004). [DOI] [PubMed] [Google Scholar]
- 13.Brownlee, J. Data Preparation for Machine Learning: Data Cleaning, Feature Selection, and Data Transforms in Python (Machine Learning Mastery, 2020).
- 14.Ingsrisawang, L., Ingsriswang, S., Somchit, S., Aungsuratana, P. & Khantiyanan, W. Machine learning techniques for short-term rain forecasting system in the northeastern part of Thailand. Int. J. Comput. Inf. Eng.2, 1422–1427 (2008). [Google Scholar]
- 15.Luenam, P., Ingsriswang, S., Ingsrisawang, L., Aungsuratana, P. & Khantiyanan, W. A neuro-fuzzy approach for daily rainfall prediction over the central region of Thailand. Proc. Int. Multiconfer. Eng. Comput. Sci.1, 17–19 (2010). [Google Scholar]
- 16.Mernngurn, J., Wongoutong, C., Frank, T. D. & Ingsrisawang, L. Predictors of pm2.5 concentrations in bangkok, thailand: obtaining novel insights for vertical measurements by combining feature selection and deep learning approach. Lobachevskii J. Math. ((in press)).
- 17.Zhang, Y.-F. et al. Predicting survival of advanced laryngeal squamous cell carcinoma: Comparison of machine learning models and cox regression models. Sci. Rep.13, 18498 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kolasseri, A. E. Comparative study of machine learning and statistical survival models for enhancing cervical cancer prognosis and risk factor assessment using seer data. Sci. Rep.14, 22203 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Breiman, L. & Ihaka, R. Nonlinear discriminant analysis via scaling and ACE (University of California Davis One Shields Avenue, Department of Statistics, 1984).
- 20.Bou-Hamad, I., Larocque, D. & Ben-Ameur, H. A Review of Survival Trees. (2011).
- 21.Linden, A. & Yarnold, P. R. Modeling time-to-event (survival) data using classification tree analysis. J. Eval. Clin. Pract.23, 1299–1308 (2017). [DOI] [PubMed] [Google Scholar]
- 22.Segal, M. R. Regression trees for censored data. Biometrics 35–47 (1988).
- 23.Clarke, J. & West, M. Bayesian Weibull tree models for survival analysis of Clinico-genomic data. Stat. Methodol.5, 238–262 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pittman, J., Huang, E., Nevins, J., Wang, Q. & West, M. Bayesian analysis of binary prediction tree models for retrospectively sampled outcomes. Biostatistics5, 587–601 (2004). [DOI] [PubMed] [Google Scholar]
- 25.Meira-Machado, L., Soutinho, G., Moreira, C. & Azevedo, M. Analysis of survival data with multiple events. (2022).
- 26.Ramezankhani, A., Tohidi, M., Azizi, F. & Hadaegh, F. Application of survival tree analysis for exploration of potential interactions between predictors of incident chronic kidney disease: a 15-year follow-up study. J. Transl. Med.15, 1–17 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Eckel, K. T., Pfahlberg, A., Gefeller, O. & Hothorn, T. Flexible modeling of malignant melanoma survival. Methods Inf. Med.47, 47–55 (2008). [DOI] [PubMed] [Google Scholar]
- 28.Fan, J., Su, X.-G., Levine, R. A., Nunn, M. E. & LeBlanc, M. Trees for correlated survival data by goodness of split, with applications to tooth prognosis. J. Am. Stat. Assoc.101, 959–967 (2006). [Google Scholar]
- 29.Fan, J., Nunn, M. E. & Su, X. Multivariate exponential survival trees and their application to tooth prognosis. Comput. Stat. Data Anal.53, 1110–1121 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gao, F., Manatunga, A. K. & Chen, S. Identification of prognostic factors with multivariate survival data. Comput. Stat. Data Anal.45, 813–824 (2004). [Google Scholar]
- 31.Hallett, M., Fan, J., Su, X., Levine, R. & Nunn, M. E. Random forest and variable importance rankings for correlated survival data, with applications to tooth loss. Stat. Model.14, 523–547 (2014). [Google Scholar]
- 32.Su, X. & Fan, J. Multivariate survival trees: A maximum likelihood approach based on frailty models. Biometrics60, 93–99 (2004). [DOI] [PubMed] [Google Scholar]
- 33.Jia, B. et al. Mixture survival trees for cancer risk classification. Lifetime Data Anal.28, 356–379 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Banerjee, S., Wall, M. M. & Carlin, B. P. Frailty modeling for spatially correlated survival data, with application to infant mortality in Minnesota. Biostatistics4, 123–142 (2003). [DOI] [PubMed] [Google Scholar]
- 35.Bunyatisai, W. A Bayesian Approach for Multivariate Frailty Models on Correlated Survival Data. PhD thesis, Kasetsart University, Bangkok, Thatiland (2016).
- 36.Chipman, H. A., George, E. I. & McCulloch, R. E. Bayesian cart model search. J. Am. Stat. Assoc.93, 935–948 (1998). [Google Scholar]
- 37.Denison, D. G., Mallick, B. K. & Smith, A. F. A bayesian cart algorithm. Biometrika85, 363–377 (1998). [Google Scholar]
- 38.Levine, R. A., Fan, J., Su, X. & Nunn, M. E. Bayesian survival trees for clustered observations, applied to tooth prognosis. Stat. Anal. Data Mining ASA Data Sci. J.7, 111–124 (2014). [Google Scholar]
- 39.Calhoun, P., Su, X., Nunn, M. & Fan, J. Constructing multivariate survival trees: the mst package for r. J. Stat. Softw.83 (2018).
- 40.Feroze, N. et al. Applicability of modified Weibull extension distribution in modeling censored medical datasets: A Bayesian perspective. Sci. Rep.12, 17157 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Malehi, A. S., Jahangiri, M. & Vizureanu, P. Classic and Bayesian tree-based methods. In Enhanced Expert Systems, 27–51 (IntechOpen, 2019).
- 42.Griffin, S. O., Jones, J. A., Brunson, D., Griffin, P. M. & Bailey, W. D. Burden of oral disease among older adults and implications for public health priorities. Am. J. Public Health102, 411–418 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Armitage, G. C. Periodontal diagnoses and classification of periodontal diseases. Periodontol.2000(34), 9–21 (2004). [DOI] [PubMed] [Google Scholar]
- 44.Bureau of Dental Health. Age-group classification of thailand,. Available from: Bureau of Dental Health (Ministry of Public Health, Thailand, 2017).
- 45.Clayton, D. G. A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence. Biometrika65, 141–151 (1978). [Google Scholar]
- 46.Duchateau, L. & Janssen, P. The Frailty Model (Springer, 2008).
- 47.Quinlan, J. R. C4. 5: programs for machine learning (Elsevier, 2014).
- 48.Chipman, H. A., George, E. I. & McCulloch, R. E. Bart: Bayesian additive regression trees. (2010).
- 49.Bertsimas, D., Dunn, J., Gibson, E. & Orfanoudaki, A. Mach. Learn.111, 2951–3023 (2022). [Google Scholar]
- 50.Needleman, I. et al. Mean annual attachment, bone level, and tooth loss: A systematic review. J. Clin. Periodontol.45, S112–S129 (2018). [DOI] [PubMed] [Google Scholar]
- 51.Halazonetis, T. D., Haffajee, A. D. & Socransky, S. S. Relationship of clinical parameters to attachment loss in subsets of subjects with destructive periodontal diseases. J. Clin. Periodontol.16, 563–568 (1989). [DOI] [PubMed] [Google Scholar]
- 52.Machtei, E. E. et al. Longitudinal study of predictive factors for periodontal disease and tooth loss. J. Clin. Periodontol.26, 374–380 (1999). [DOI] [PubMed] [Google Scholar]
- 53.Persson, R. & Svendsen, J. The role of periodontal probing depth in clinical decision-making. J. Clin. Periodontol.17, 96–101 (1990). [DOI] [PubMed] [Google Scholar]
- 54.Meisel, P., Völzke, H. & Kocher, T. Periodontal probing depth trajectory in 10 years of follow-up as associated with tooth loss. J. Clin. Periodontol. (2025). [DOI] [PMC free article] [PubMed]
- 55.Lambert, P., Collett, D., Kimber, A. & Johnson, R. Parametric accelerated failure time models with random effects and an application to kidney transplant survival. Stat. Med.23, 3177–3192 (2004). [DOI] [PubMed] [Google Scholar]
- 56.Therneau, T. M., Grambsch, P. M. & Pankratz, V. S. Penalized survival models and frailty. J. Comput. Graph. Stat.12, 156–175 (2003). [Google Scholar]
- 57.Rondeau, V., Marzroui, Y. & Gonzalez, J. R. frailtypack: An r package for the analysis of correlated survival data with frailty models using penalized likelihood estimation or parametrical estimation. J. Stat. Softw.47, 1–28 (2012). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
There is no direct link to the data set. The anonymised data collected are available as open data via the Creighton University School of Dentistry online data repository: https://www.rdocumentation.org/packages/MST/versions/2.2/topics/Teeth. The dataset can be accessed by installing the MST package in R and loading the dataset named “Teeth”. For further clarification contact corresponding author.