Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2025 Mar 24;10(13):13515–13528. doi: 10.1021/acsomega.5c00226

MoTe2 Polymorphs: A DFT Approach to Structural, Electronic, Mechanical and Vibrational Properties

Lathifa Banu S †, Kanimozhi Balakrishnan ‡, Vasu Veerapandy ‡, Nalini Vajeeston §, Ponniah Vajeeston §,*
PMCID: PMC11983220  PMID: 40224400

Abstract

graphic file with name ao5c00226_0015.jpg

Molybdenum ditelluride (MoTe2), a key member of the transition metal dichalcogenides (TMDCs) family, holds significant potential for applications in electronics, energy storage, and catalysis. Despite its importance, the range of MoTe2 structural forms that has been explored is still limited. The primary aim of this research is to identify new stable MoTe2 polymorphs that may exist under zero-temperature and zero-pressure conditions. This study offers an in-depth analysis of 11 different structural variations (polymorphs) of MoTe2 using advanced computational methods based on density functional theory (DFT). By employing the Heyd-Scuseria-Ernzerhof (HSE06) hybrid functional, accurate calculations of electronic properties, such as band structure, are achieved. Bonding analysis, including charge density and electron localization, reveals consistent covalent interactions across the hexagonal and trigonal forms of MoTe2. The study also assesses the mechanical stability of these polymorphs using elastic constants, identifying both stable and metastable forms. Additionally, phonon and thermal properties, including heat capacity and entropy, are calculated for all dynamically stable polymorphs. Raman and infrared spectra provide insights into their distinct vibrational modes. These findings help distinguish structural attributes relevant to layer-specific applications. This comprehensive investigation of MoTe2 polymorphs uncovers new stable structures and provides crucial insights for their potential use in technological applications.

1. Introduction

TMDCs are a significant type of materials characterized by unique properties such as ultrathin materials for electronics, high-performance semiconductors flexible and lightweight building materials sustainable building materials, functional materials for sensors, and so on.1 MoTe2 occurs in various polymorphs, mainly including the hexagonal 2H, monoclinic 1T’, and orthorhombic Td phases.2 Each polymorph displays unique electronic properties: the 2H phase is a semiconductor with a moderate bandgap, making it suitable for transistors and photodetectors, whereas the 1T’ and Td phases are metallic, offering potential for topological and quantum spin Hall applications.3 The polymorphic versatility of MoTe2 allows it to transition between various electronic states when subjected to external influences (such as temperature, strain, or chemical doping), creating opportunities for phase engineering in functional devices. A comprehensive investigation of MoTe2 polymorphs is still lacking, despite growing interest. Some researchers have experimentally studied MoTe2 and their findings are summarized in the literature review as follows: An experimental study by Zhou et al., reported the impact of defects on the phase stability of MoTe2. Defects can potentially drive phase transitions between the semiconducting 2H phase and the metallic 1T’ or Td phases, indicating their importance in phase engineering efforts to create functional devices.4 Keum et al., investigated the phase transition between 2H and 1T’ phases under controlled strain, revealing electronic band structure changes theoretically.5 Chen et al., describe how chemical functionalization stabilizes the metastable 1T’ phase of MoTe2, contributing to phase control for electronic applications.6

Song et al., analyzed an experimental study of semimetal MoTe2 as multimode transport behavior.7 Huang et al., used the first-principles method to explain the phase transition between 2H-MoTe2 and 1T-MoTe2 even if just a few polymorphs are explored in MoTe2.8 Furthermore, Duerloo et al., explained the structural phase change in the monolayer of electrostatically doped MoTe2.9 According to Cao. et al., based on the first principle calculation, hexagonal structures can be used as photocatalysts in water-splitting applications.10 Naturally, the environmental changes defect the activated molecular interaction changes in MoTe2 which were explained by Chen et al. using the DFT method.11 Additionally, Yuan et al., explained that the ferroelectricity in 1T-MoTe2 will be down to the atomic monolayer at room temperature experimentally and theoretically.12 Monolayer MoTe2–H exhibits ultrafast band gap renormalization and optical gain accumulation was reported by theoretically Meckbach et al.13 These studies have collectively contributed to understanding MoTe2 polymorph synthesis, stability, and electronic, optical, and mechanical properties, paving the way for their potential application in new material technologies. MoTe2 is used for a variety of purposes; however, there is still a lack of diverse polymorph utilization for a broad range of applications. Selecting input structures for MoTe2 from the ICSD and Materials Project databases for the AX2 composition requires significant effort and computational resources.8 By employing energy-volume curve fitting, low-energy polymorphs are effectively identified, ultimately selecting 11 distinct MoTe2 polymorphs from the available options. This work primarily focused on a few known phases and unreported phases of MoTe2, and the investigation delves into the relative stability, electronic structure, vibrational properties, thermal behavior, and the effective masses of electrons and holes in the semiconductive polymorphs. This study provides a detailed characterization of the bonding nature in hexagonal and trigonal polymorphs through charge density, charge transfer, and electron localization function (ELF) computations. The dynamical stability of the MoTe2 polymorphs was conducted from phonon analyses, which were subsequently used for vibrational studies through the computation of IR and Raman spectra. A key innovative aspect of this work is the evaluation of the thermal stability of dynamically stable polymorphs, which provides valuable insights into their potential practical applications. Through this systematic exploration, we have discovered novel stable polymorphs that have been previously unreported. These newly identified stable structures opened new opportunities for their use in various applications, such as energy storage, catalysis, optoelectronics, and microelectronics.

2. Result and Discussion

2.1. Structure and the Stability of MoTe2 Polymorphs

MoTe2 features a unique structure where a molybdenum (Mo) atom is nestled between two layers of tellurium (Te), creating a Te–Mo–Te sandwich-like configuration. The combination of strong intralayer covalent bonds and weak interlayer van der Waals forces gives MoTe2 its unique mechanical and electronic characteristics.14 Within the layer, MoTe2 will have either a trigonal prismatic phase with a hexagonal structure or an octahedral prismatic phase with a trigonal structure. Depending on the layer stacking, MoTe2 can create various numbers of polymorphs. Variations in the stacking order and registration of consecutive Se–Mo–Se sandwiches of the trigonal prismatic and octahedral prismatic forms 11 different polymorphs 1H-MoTe2, 2H-MoTe2, 3Ha-MoTe2, 3Hb-MoTe2, 2T-MoTe2, 4T-MoTe2, 2R1-MoTe2, 1T1-MoTe2, 1T2-MoTe2, 3T- MoTe2 and 2R2-MoTe2, are used as the base for this investigation. In this structure, the number of layers per unit cell along the c-axis is defined as an integer. The structural symmetries are indicated by the letters T, H, and R representing trigonal, hexagonal, and rhombohedral symmetries, respectively. The a and b suffixes of the 3Ha-MoTe2 and 3Hb-MoTe2 denote the stacking arrangement of layers.

The total energy is determined as a function of the volume for all of the polymorphs of MoTe2. In this study, the polymorphs are categorized into two distinct groups, group A and group B, based on their total energy. Group A consists of the polymorphs 1H-MoTe2, 2H-MoTe2, 3Ha-MoTe2, 3Hb-MoTe2, 2T-MoTe2, 4T-MoTe2, and 2R1-MoTe2 which exhibit hexagonal, trigonal, and rhombohedral structures, as illustrated in Figure 1. Group B, on the other hand, includes the polymorphs 1T1-MoTe2, 1T2-MoTe2, 3T-MoTe2, and 2R2-MoTe2 featuring octahedral prismatic phases as well as trigonal and rhombohedral structures, as shown in Figure 2.

Figure 1.

Figure 1

Open in a new tab

Structure and the top view of group A polymorphs are shown. 1H-MoTe2 in (a), 2H-MoTe2 in (b), 2T-MoTe2 in (c), 4T-MoTe2 in (d), 3Ha-MoTe2 in (e), 3Hb- MoTe2 in (f) and 2R1-MoTe2 in (g).

Figure 2.

Figure 2

Open in a new tab

Structure and top view of group B polymorphs. 1T1-MoTe2 in (a), 1T2-MoTe2 in (b), 3T- MoTe2 in (c), and 2R2-MoTe2 in (d).

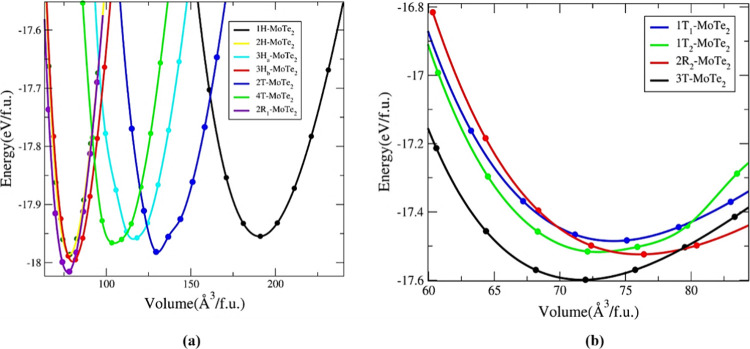
Figure 3a,b depicts the total energy of the group A and group B polymorphs as a function of volume. Group A exhibits relatively low energy values, ranging from −18.25 to −17.95 eV/f.u. Within this group, the 2R1-MoTe2 polymorph has the lowest total energy, indicating its high stability among the polymorphs studied. Interestingly, despite their differences in volume, the 1H-MoTe2, 3Ha-MoTe2, and 4T-MoTe2 polymorphs show closely aligned energy values, suggesting that their energy landscapes are quite similar. This proximity in energy indicates that these polymorphs can transition between phases with minimal energy barriers, highlighting their potential for phase flexibility and tunability in various applications. The group B polymorphs exhibit relatively low energy values, ranging from −17.6 to −17.5 eV/f.u. with the 3T-MoTe2 polymorph having the lowest total energy within this group. In comparison, the group A polymorphs have a lower total energy, indicating that they are more stable than those in group B. The minimum energy and corresponding volume of each polymorph are provided in Table S1 of the Supporting Information on page S1.

Figure 3.

Figure 3

Open in a new tab

Total energy vs volume curve for group A (a) and group B (b) MoTe2 polymorphs. All of the energy volumes are normalized to one formula unit (f.u.).

Initially, all of the polymorphs were optimized, and their positions along with lattice constants are summarized in Table 1. The lattice constant of the 2H-MoTe2 (a = 3.504 Å, c = 14.745 Å) and 1T1-MoTe2 (a = 3.479 Å, c = 7.164 Å) well coincided with the experimental and theoretical results which are shown in Table 1.8,15

Table 1. List of Calculated Unit Cell Constants and Coordinates for the Investigated MoTe2 Polymorphsa.

polymorph cell constants (Å) coordinates
1H-MoTe2 (P6̅m2; mp-1023924) a = 3.497, c = 18.033 Mo1 (1a) 0.000 0.000 0.000
Te1 (2h) 0.333 0.666 0.100
2H-MoTe2 (P63/mmc; mp-1018809) a = 3.504, c = 14.745 Mo1 (2b) 0.000 0.000 0.250
a = 3.590, c = 13.9669 Te1 (4f) 0.666 0.333 0.372
a = 3.519, c = 13.97015          
a = 3.517, c = 13.94916
3Ha-MoTe2 (P6̅m2; mp-1025874) a = 3.506, c = 33.297 Mo1 (2g) 0.000 0.000 0.721
Mo2 (1c) 0.333 0.666 0.000
Te1 (2g) 0.000 0.000 0.054
Te2 (2h) 0.333 0.666 0.333
Te3 (2h) 0.333 0.666 0.775
3Hb-MoTe2 (P63/mmc; mp-2815) a = 3.506, c = 15.361 Mo1 (2d) 0.666 0.333 0.250
Te1 (4f) 0.666 0.250 0.867
2T - MoTe2 (P3̅m1; mp-1023939) a = 3.445, c = 25.180 Mo1 (2d) 0.666 0.333 0.859
Te1 (2d) 0.666 0.333 0.212
Te2 (2d) 0.666 0.333 0.067
4T- MoTe2 (P3̅m1; mp-1027525) a = 3.269, c = 35.382 Mo1 (1a) 0.333 0.666 0.088
Mo2 (1a) 0.666 0.333 0.911
Mo3 (1a) 0.333 0.666 0.697
Mo4 (1a) 0.666 0.333 0.302
Te1 (1a) 0.333 0.666 0.347
Te2 (1a) 0.666 0.333 0.652
Te3 (1a) 0.333 0.666 0.957
Te4 (1a) 0.666 0.333 0.042
Te5 (1a) 0.333 0.666 0.743
Te6 (1a) 0.666 0.333 0.866
Te7 (1a) 0.333 0.666 0.133
Te8 (1a) 0.666 0.333 0.256
2R1-MoTe2 (R3̅m; ICSD_31067;1434) a = 3.501, c = 22.070 Mo1 (1a) 0.999 0.999 0.999
Te1 (1a) 0.415 0.415 0.415
Te2 (1a) 0.251 0.251 0.259
1T1-MoTe2 (P3̅m1; mp-147) a = 3.479, c = 7.164 Mo1 (1a) 0.000 0.000 0.000
a = 3.493, c = 6.0488 Te1 (2d) 0.666 0.333 0.258
1T2-MoTe2 (P3̅; mp-164) a = 3.494, c = 6.818 Mo1 (1a) 0.000 0.000 0.000
Te1 (2d) 0.666 0.333 0.267
3T-MoTe2 (R3̅m; mp-1558544) a = 3.442, c = 21.034 Mo1 (1b) 0.500 0.500 0.500
Te1 Te1 0.744 0.744 0.744
2R2-MoTe2 (P3m1; mp-11238797) a = 3.440, c = 7.415 Mo1 (1b) 0.000 0.000 0.500
Te1 (2d) 0.666 0.333 0.238
Open in a new tab
a

The space group and material project ID are given near the polymorphs.

2.2. Electronic Structure

The electronic structures of MoTe2 are highly dependent on its polymorphic form. In this study, a comprehensive exploration of the electronic structure of MoTe2 using DFT is presented. However, standard DFT calculations using the local density approximation (LDA) are known to underestimate the band gap of semiconducting materials due to the lack of accurate treatment of electronic correlation.17 To address this limitation, hybrid functionals such as the Heyd-Scuseria-Ernzerhof (HSE06) are employed in our calculations to provide more reliable bandgap predictions.18 The band structures of both group A and group B polymorphs are calculated at zero pressure, focusing on the high-symmetry points within the first Brillouin zone.19 Excluding the 4T-MoTe2 polymorph, all of the group A polymorphs show semiconducting properties. On the other hand, the electronic structure of all the polymorphs in group B shows metallic behavior. For monolayer 1H-MoTe2, DFT studies indicate a direct bandgap of 1.59 eV at the K-point of the Brillouin zone.

Similarly, the electronic band structure of 3Ha-MoTe2 exhibits a direct bandgap, with strong contributions from Mo d-orbitals and Te p-orbitals. Other polymorphs, such as 2H-MoTe2, 3Hb-MoTe2, 2T-MoTe2, and 2R1-MoTe2, exhibit an indirect band gap. This band gap is sensitive to factors such as strain, external electric fields, and the number of layers, offering tunability for specific applications.

The primary difference between 1H-MoTe2 and 3Ha-MoTe2 in terms of their electronic band structures lies in the presence of additional bands in 3Ha. The specific hybridization of these orbitals varies depending on the polymorph, resulting in unique band structures for each MoTe2. This difference arises due to its multilayer stacking and interlayer interactions. The other 2H-MoTe2, 3Hb-MoTe2, 2T-MoTe2, and 2R1-MoTe2 polymorphs have an indirect bandgap because their CBM is located at the K-point while the VBM lies along the K-Γ path in the Brillouin zone.20Figure 4 shows the band structure of 1H-MoTe2 and 2H-MoTe2 polymorphs. The other band structure of group A is given in Figure S1 of the Supporting Information. Except for 4T-MoTe2, group A polymorphs have band gaps between 1.01 and 1.5 eV, making them suitable for application in photovoltaic solar cells, photocatalysis, and water-splitting applications. The overlap of the conduction and valence bands of Group B polymorph band structures gives them a metallic nature since they are no longer separated by an energy gap, allowing electrons to travel freely. The band topologies demonstrate the absence of a bandgap, confirming the metallic character of these polymorphs. Figure 5 shows the band structure of 1T1-MoTe2 and 1T2-MoTe2, and the other band structure of group B is given in Figure S2 of the Supporting Information on page S2. However, the introduction of an additional layer into the 3T-MoTe2 polymorph led to an increase in the number of bands. This suggests that the layering in this polymorph modifies its electronic structure, resulting in a more complex distribution of energy bands while retaining the overall metallic behavior observed in the other group B polymorphs.

Figure 4.

Figure 4

Open in a new tab

HSE06 band structure for group A polymorphs 1H-MoTe2 in (a) and 2H-MoTe2 in (b) with direct band and indirect band gaps, respectively.

Figure 5.

Figure 5

Open in a new tab

HSE06 band structure of group B polymorphs 1T1-MoTe2 in (a) and 1T2-MoTe2 in (b) demonstrates a metallic nature.

In MoTe2 polymorphs, the band flatness between the Γ and A points could indeed be influenced by the interlayer spacing in the crystal structure. In materials such as MoTe2, the interlayer spacing influences the overlap of atomic orbitals between adjacent layers. If the interlayer distance is large, the wave functions of atoms in one layer have little overlap with those in neighboring layers, leading to flat bands, especially along certain directions in the Brillouin zone. In multilayer materials, the weak van der Waals forces holding the layers together can result in weak interlayer coupling, especially if the layers are not strongly bonded. This weak coupling contributes to the formation of flat bands because the electron hopping between layers is minimized. This flatness could affect the properties of the material in various ways, including the potential for unconventional superconductivity under certain conditions. The band flatness in the band structure may depend on the interlayer spacing of MoTe2 polymorphs.14,20

In monolayer 1H-MoTe2, the effective mass of electrons and holes has been reported as m*e = 0.56 m0 and m*h= 0.64 respectively, based on first-principles density functional theory calculations using the HSE06 hybrid functional study of Liu et al.22 In bulk 2H-MoTe2, the effective masses of electrons and holes are reported as m*e = 0.70 m0 and m*h= 0.76, respectively, based on density functional theory calculations with GGA and spin–orbit coupling effects.23 This study reports the effective mass of the electrons and holes for the semiconductor polymorphs 1H-MoTe2, 2H-MoTe2, 3Ha- MoTe2, 3Hb-MoTe2, 2T-MoTe2, and 2R1-MoTe2 which are listed in Table 2.

Table 2. Calculated HSE06 and GGA Band Gap Value, the Effective Mass of the Electron (me*), the Effective Mass of the Hole (mh*), and the Band Gap Type of Group-A MoTe2 Polymorphs.

polymorph bandgap value in GGA (eV) band gap value in HSE06 (eV) effective mass ofelectrons me* [me] (m0) effectivemass ofhole mh* [mh] bandgap type
1H-MoTe2 1.188 1.588 0.635 0.777 direct
1.18020
2H- MoTe2 1.007 1.076 0.858 0.826 indirect
1.0509
1.08021
2T-MoTe2 0.977 1.014 0.915 0.847 indirect
3Ha-MoTe2 1.163 1.498 0.632 0.771 direct
3Hb- MoTe2 1.0085 1.245 0.680 0.768 indirect
3R1- MoTe2 0.995 1.041 0.749 0.814 indirect
Open in a new tab

2.2.1. Density of State

The density of states (DOS) shows the number of available electronic states at each energy level, while the projected density of states (PDOS) breaks it down by the contribution of individual atomic orbitals to the total DOS.15,25 The Fermi level (EF) is set to zero in the DOS plot. Group A and group B polymorphs exhibit different electronic behaviors, and DOS calculations were performed for all polymorphs. The DOS for 2H-MoTe2 shows a semiconducting behavior with an indirect bandgap of approximately 1.07 eV (Figure 6). In 2H-MoTe2, the Mo-d orbitals contribute mainly to the states below the Fermi level, while the Te-p orbitals contribute to the states above the Fermi level. Roldán also analyzed the electronic structure of MoTe2 using PDOS and found that the conduction band is mainly composed of Mo-d orbitals, while the valence band is mainly composed of Te-p orbitals. They further found that the spin–orbit coupling (SOC) effect is significant in MoTe2 and leads to a splitting of the valence band maximum (VBM) and conduction band minimum (CBM).26,27 1T1-MoTe2 is a layered transition metal chalcogenide with a distorted octahedral coordination has a metallic character due to the overlap of the Te-p and Mo-d orbitals. The electronic structure of 1T1-MoTe2 can be analyzed using the DOS calculation as shown in Figure 7. The study by Dawson et al. provides a detailed analysis of the electronic and structural properties of MoTe2 and WTe2 monolayers using DFT calculations. The study finds that both monolayers exhibit metallic behavior with a strong anisotropy in the in-plane directions, and their stability is strongly dependent on the stacking order of the layers. The study also suggests that the stability of the 1T-MoTe2 phase is due to the strong hybridization between the metal d and chalcogen p orbitals.15,24

Figure 6.

Figure 6

Open in a new tab

Density of state for 2H- MoTe2 in (a), LDOS for 2H- MoTe2 in (b), PDOS of Mo in (c), and PDOS of Te in (d).

Figure 7.

Figure 7

Open in a new tab

Density of state for 1T1- MoTe2 in (a), LDOS for 1T1-MoTe2 in (b), PDOS of Mo in (c), and PDOS of Te in (d).

2.3. Bonding Nature of Polymorphs

Bonding interactions in polymorphs are described by the projected valence-charge-density distribution. Figure 8 shows the charge density, charge transfer, and electron localization function (ELF) plots for 1T1- MoTe2 and 2H- MoTe2 polymorphs.18,28

Figure 8.

Figure 8

Open in a new tab

Charge density (a), charge transfer (b), and ELF (c) of trigonal prismatic of MoTe2(1T1- MoTe2) and the charge density (d), charge transfer (e), and ELF (f) of octahedral prismatic of MoTe2 (2H- MoTe2).

The trigonal polymorphs of Mo–Te are arranged as shown in Figure 8a, demonstrating typical covalent bonding. In Figure 8d, the charge density of the hexagonal polymorph reveals that Te–Mo–Te bonds form a trigonal pattern, reflecting a similar covalent character. The yellow regions signify a more dispersed position of an anion, whereas the red regions show tightly constrained charge transfer between cations. This covalent nature is evidenced by electron sharing between cations and anions, as depicted in Figure 8b,e.21,29Figure 8c,f shows electron localization between Te (like a cap) and Mo atoms in both hexagonal and trigonal forms, where the electron localization is heightened when the ELF value exceeds 0.5, suggesting covalent bonding between Mo and Te.30−32 Thus, the charge density, charge transfer, and ELF analyses for both hexagonal and trigonal polymorphs consistently indicate the covalent nature of their bonds.33

2.4. Dynamical Properties

Lattice dynamic stability refers to the stability of a crystal structure under small atomic vibrations. It is an essential property that indicates whether a material will remain structurally intact or spontaneously distort. This stability is determined by analyzing phonon frequency vibrational modes within the crystal lattice. If all phonon frequencies are positive, the crystal structure is considered dynamically stable, and it can exist at equilibrium without collapsing or transforming. The lattice dynamical and vibration properties of all the polymorphs are computed by the pre/postprocessing tool of PHONOPY.34 The frozen phonon technique has been used to calculate the force constants.35−37 In this study, the total phonon density of states (PhDOS) and phonon dispersion curves of all the polymorphs are determined at the equilibrium volume, with the high symmetry direction of the Brillouin zone.28,38 In our study, we observed that all of the polymorphs in group A show positive frequencies except 2T-MoTe2. The result of this study exhibits the dynamic stability of the six group A polymorphs (1H-MoTe2, 2H-MoTe2, 3Ha-MoTe2, 4T-MoTe2, 3Hb-MoTe2, and 2R1-MoTe2). 2T-MoTe2 polymorph in group A was determined unstable dynamically due to the exhibit of a negative/soft mode of frequencies or a negative eigenvalue. Figure 9 shows the positive phonon frequency and phonon dispersion of 1H-MoTe2 and 2H-MoTe2. The phonon frequency and phonon dispersion of other polymorphs are given in Figure S3 of the Supporting Information.

Figure 9.

Figure 9

Open in a new tab

Positive phonon dispersion and phonon density of states for 1H-MoTe2 (a) and 2H-MoTe2 (b).

Phonon dispersions of the dynamically stable polymorphs have well-separated optical and acoustical phonons, which are well-suitable for optical properties like photonics, optoelectronics, and medical imaging.39 All the stable polymorphs in group A owned the same frequency range of optical modes in the region of 5 and 9 THz. In all the stable polymorphs in group A, the smaller Te atom dominates the lower frequencies, whereas the larger Mo atom dominates the higher frequencies (over 8.5 THz). The stable polymorphs in group A had similar wave vectors for phonon dispersion, demonstrating that temperature and pressure can affect the phase change. As potential energy levels drop close to the equilibrium atomic position, polymorphs become less stable. The soft/negative modes of frequency present in all group B polymorphs exhibit unstable dynamical characteristics for 1T1-MoTe2, 1T2-MoTe2, 3T-MoTe2, and 2R2-MoTe2 polymorphs.40 For the 1T1-MoTe2 and 1T2-MoTe2 polymorphs, Figure 10 displays the unstable phonon dispersion and phonon density of state.40Figure S4 of the Supporting Information on page S3 provides information on the other phonon dispersions and phonon densities of states for group B polymorphs.

Figure 10.

Figure 10

Open in a new tab

Phonon dispersion and phonon density of states for 1T1-MoTe2 (a) and 1T2-MoTe2 (b) polymorphs in group B.

2.5. Mechanical Stability

It is essential to emphasize a complete understanding of the mechanical properties to maximize the potential of polymorphs for a variety of applications. Here, using an elastic constant tool, we estimated the fundamental mechanical characteristics of all polymorphs.32,42 The VASPKIT program is used to determine elastic constants by using the “stress-strain” method. Under a small deformation, the linear dependence of the applied strain and the stress component is evaluated based on the tensorial form of the Hooks law. Each stress and strain consists of three tensile and three shears. This 6 × 6 symmetric matrix with 27 different components describes the elastic constant of the crystal. The number of pieces can be naturally decreased by selecting polymorphs with pre-existing symmetry, this stiffness constant Cij is used to calculate the mechanical properties of the polymorphs. There are six elastic constants for each hexagonal and trigonal polymorph (C11, C12, C13, C33, C44, and C66). The Rhombohedra structure consists of seven elastic constants (C11, C12, C13, C14,C33, C44, and C66).32,43,44

To examine the mechanical stability, the polymorphs have to satisfy the born stability criteria.44 In this work 2H-MoTe2, 3Hb-MoTe2, and 2R1-MoTe2 polymorphs satisfied the stability criteria of elastic constant for hexagonal as well as group B polymorphs satisfied the trigonal stability criteria of elastic constant.44 In this study, mechanical properties such as the bulk modulus B, sheared modulus G, Young’s modulus E and Poisson’s ratio ν are calculated for all the polymorphs using the Voigt(V)-Reuss(R)-Hill(H) approach.45Tables 3 and 4 show the bulk modulus B, sheared modulus G, Young’s modulus E, Poisson’s ratio ν, and Born stability criteria of the elastic constant for group A and group B respectively.

Table 3. Calculated Single-Crystal Elastic Constants Cij (in GPa), Born Criteria, the Bulk Modulus B (in GPa), Shear Modulus G (in GPa), Poisson’s Ratio Ν, Young’s Modulus E (in GPa), and Pugh Ratio (B/G) of the Group A Polymorph.

polymorph 1H -MoTe2 3Ha-MoTe2 3Hb-MoTe2 2H-MoTe2 4T-MoTe2 2T-MoTe2 2R1-MoTe2
crystal system hexagonal hexagonal hexagonal hexagonal trigonal trigonal rhombohedra
C11 51.02 81.58 117.91 123.43 101.73 80.84 125.07
1019
C12 11.65 18.97 27.33 32.32 20.50 16.39 29.95
329
C13 0.48 0.88 2.65 11.13 0.93 0.87 8.15
C14 0 0 0 0 - 0.01 0.05 1.76
C33 1.25 2.26 7.41 25.86 2.20 2.38 20.00
C44 –0.12 –0.07 4.06 3.49 –0.80 –0.54 7.80
C66 19.68 31.30 45.28 45.55 40.61 32.22 47.56
Born No No Yes Yes No No Yes
B 7.75 12.61 20.69 32.82 15.00 12.30 29.28
G 4.80 7.84 15.78 16.18 8.64 7.16 20.32
E 11.95 19.50 37.75 41.69 21.74 17.99 49.51
Ν 0.24 0.24 0.19 0.28 0.25 0.25 0.21
B/G 1.61 1.61 1.31 2.03 1.74 1.72 1.44
Open in a new tab

Table 4. Calculated Single-crystal Elastic Constants Cij (in GPa), Born Criteria the Bulk Modulus B (in GPa), Shear Modulus G (in GPa), Poisson’s Ratio Ν, Young’s Modulus E (in GPa), and Pugh Ratio (B/G) of the Group B Polymorphs.

polymorph 1T1-MoTe2 IT2- MoTe2 2R2-MoTe2 3T-MoTe2
crystal system trigonal trigonal rhombohedra trigonal
C11 132.39 141.13 135.24 150.66
C12 6.97 14.77 5.41 9.95
C13 26.95 42.12 17.68 19.03
C14 0 0 1.99 2.83
C33 38.23 52.16 30.49 56.79
C44 8.32 20.81 3.01 31.84
C66 62.71 63.18 64.91 70.35
Born Yes Yes Yes Yes
B 41.53 54.56 35.41 46.42
E 58.30 75.91 48.34 99.15
G 23.02 29.93 18.99 43.33
Ν 0.26 0.26 0.27 0.14
B/G 1.80 1.82 1.86 1.06
Open in a new tab

In Table 3, 2H -MoTe2, 3Hb-MoTe2, and 2R1-MoTe2 polymorphs from group A are identified as mechanically stable, satisfying the Born stability criteria. other polymorphs from group A failed to meet these criteria, indicating mechanical instability. In group A, 1H-MoTe2, 4T-MoTe2, and 3Ha-MoTe2 polymorphs have stable phonons, however, because of their unstable mechanical properties, these are classified as metastable polymorphs. The elastic constants, including bulk modulus B, shear modulus G, Young’s modulus E, Poisson’s ratio ν, and the Born stability criteria for Group B polymorphs, are detailed in Table 4. Although group B polymorphs meet the mechanical stability requirements, they are dynamically unstable, which poses a challenge for the experimental synthesis. In group A, the 2R1-MoTe2 polymorph exhibits the highest C11 value, while the 1H-MoTe2 polymorph has the lowest. As shown in Tables 3 and 4, all polymorphs display C11 values that exceed C33, indicating that the x–y plane is stiffer than the z-direction. Furthermore, each polymorph has a C12 value greater than C13, suggesting that tension is more effectively distributed along the x- and z-axes than along the y-axis. Due to their relatively low C44 values, the 1H-MoTe2, 4T-MoTe2, and 3Ha-MoTe2 polymorphs in Group A are more susceptible to shear deformation. Further, group B MoTe2 polymorphs exhibit higher bulk modulus and shear modulus values (Table 2), highlighting the increased hardness of the 2R1-MoTe2 and 3T-MoTe2 polymorphs. The Pugh’s ratio (B/G) provides additional insights, where a higher ratio (>1.75) suggests ductility, while a lower ratio (<1.75) indicates brittleness.41 In group A, the 2H-MoTe2 polymorph stands out with a high Pugh’s ratio, indicating ductile behavior. Except for 2H-MoTe2, the Pugh’s ratio for all other Group A polymorphs is below 1.75, classifying them as brittle in nature. Conversely, in group B, only the 3T-MoTe2 polymorph exhibits a Pugh’s ratio below 1.75, indicating brittleness, while all other group B polymorphs exceed this threshold, signifying ductility.

Poisson’s ratio (ν) is another criterion for distinguishing between brittle and ductile materials, with values greater than 0.26 indicating ductility. Among the studied polymorphs, the 2H-MoTe2 in group A and 2R2-MoTe2 in group B exhibit higher Poisson’s ratios, suggesting a more ductile nature compared to other polymorphs. With the exception of 2H-MoTe2, all group A polymorphs have Poisson’s ratios below 0.26, reflecting their inherent weakness. The presence of a positive Young’s modulus (E) indicates that atoms in stable polymorphs exhibit compressibility. In this study, all group A polymorphs display positive values for Young’s modulus, with the 2R1-MoTe2 polymorph showing a particularly high value, suggesting greater atomic compressibility compared to other polymorphs. By evaluation of the physical properties and anisotropy of E and ν, this investigation establishes the isotropic characteristics of mechanically stable polymorphs. Young’s modulus, derived from elastic compliance constants, also reveals the orientation-dependent behavior of the polymorphs.32,46 For isotropic materials, Young’s modulus surface should ideally exhibit a spherical shape. Figure 11 presents a 3D plot of Young’s modulus for the dynamically and mechanically stable polymorphs 2H-MoTe2, 3Hb-MoTe2, and 2R1-MoTe2. Among these, 2R1-MoTe2 shows the highest Young’s modulus, whereas 2H-MoTe2 exhibits the lowest within group A.38,43

Figure 11.

Figure 11

Open in a new tab

3D plot of Young’s modulus (E) for stable polymorphs 2H-MoTe2 in (a), 3Hb-MoTe2 in (b), and 2R1-MoTe2 in (c).

2.6. Thermodynamical Properties

The thermodynamic analysis is used to predict the temperature-dependent behavior of dynamically stable polymorphs.34 Thermodynamic parameters that vary with temperature, including specific heat at a constant volume (Cv), entropy (S), internal energy (E), and vibrational free energy (F), are presented in Figure 12. Figure 12a,b shows the exponential increase in vibrational energy and the exponential decrease in free energy.38,36Figure 12c shows that the specific heat at constant volume (Cv) increases linearly with temperature, indicating that all dynamically stable polymorphs follow the classical Dulong-Petit law at high temperatures, where the specific heat approaches a constant value. At lower temperatures, the behavior transitions to follow Debye’s T3 law, which describes the temperature dependence of specific heat in solids at low temperatures, reflecting the contribution of acoustic phonons to thermal properties.12 All of the dynamically stable polymorphs increase the entropy as the temperature rises by the third rule of thermodynamics. Energy as a function of temperature in Figure 12d shows the maximum value reaches 178 J/K/mol at 1000 K, for all dynamically stable polymorphs. Our observations for various temperatures follow the two key laws of thermodynamics, suggesting that all of the dynamic polymorphs under investigation are thermodynamically stable even for wider pressure ranges. Although no theoretical or experimental results have been found, it is challenging to compare the results.

Figure 12.

Figure 12

Open in a new tab

Vibrational free energy “F” (a) internal energy “E” (b), specific heat at constant volume “Cv” (c), and Entropy “S” (d) as a function of temperature for dynamic stable MoTe2 polymorphs.

2.7. IR and Raman Spectra

2.7.1. Raman Spectra

Raman spectroscopy is a powerful technique for characterizing phonon properties at the zone center in crystalline materials.6 Raman spectra are calculated for the dynamically stable polymorphs (1H-MoTe2, 2H-MoTe2, 3Ha-MoTe2, 4T-MoTe2, 3Hb-MoTe2, and 2R1-MoTe2) to understand the vibrational behavior. Table 5 shows the Raman active modes for the dynamically stable polymorphs. The 1H-MoTe2, polymorph shows that the A′1 mode involves out-of-plane vibrations where Mo and Te atoms oscillate perpendicularly to the basal plane of the layer. Zhang et al., discuss the E′ mode (in-plane) around 235 cm–1 and the A′1 mode (out-of-plane) near 170 cm–1.

Table 5. Raman Active Modes and IR Active Modes for the Dynamically Stable Polymorphs.
polymorph Raman activemode (cm–1) IR activemode (cm–1)
1H-MoTe2 E’: 233 A″2: 288
2E″: 117 2E’: 233
A′1: 171  
2H- MoTe2 2E2g: 233 A2u: 287
2E1g: 117 2E1u: 233
A1g: 171, 17148  
3Ha- MoTe2 2E’: 117, 233 2A″2: 288
2A′1: 3, 171, 288 4E’: 117, 233
2E″: 6, 117, 233  
3Hb- MoTe2 2E2g: 11, 233 A2u: 285
2E1g: 117 2E1u: 233
A1g: 171  
4T- MoTe2 2Eg: 117,233 A2u: 171,287,288
A1g: 171,287,288 2Eu: 117,233
2R1- MoTe2 2E: 171,233 A2u: 285
2A1: 117,288 2E1u: 233
Open in a new tab

These modes are typically used to characterize monolayer MoTe2 and confirm its structural and thickness attributes.6 In the 2H-MoTe2 polymorph, the A1g mode involves out-of-plane vibrations and is typically observed around 171 cm–1.E2g modes typically appear around 233 cm–1 for 2H-MoTe2. Its frequency and intensity provide insights into the structural integrity and layer interactions and can be used to detect strain effects. Particularly out of the plane mode for all polymorphs occur at 233 cm–1 (Figure 13) and in-plane modes occur at the same point, 171 cm–1, which is well coincides with the experimental value.48 This demonstrates that despite the differences in the polymorphs, the mode of vibration appears at the same distance for all the polymorphs.49 Low-frequency modes can arise in multilayer 3Ha-MoTe2 and 3Hb-MoTe2 due to interlayer shear and breathing vibrations. These modes occur below 50 cm–1 and are useful for determining the layer number and studying interlayer coupling.

Figure 13.

Figure 13

Open in a new tab

Raman intensity as a function of wavenumber for dynamically stable polymorphs.

2.7.2. IR Spectrum

The stable phonon polymorphs involved in the IR spectra are investigated and the corresponding modes of representation are evaluated in this paper.50Table 5 shows the IR active modes for the dynamically stable polymorphs. In our observation the phonon shows two IR modes are active, one is in the plane (E’) and another one is out of the plane for all stable polymorphs.51 All of the phonon-stable polymorphs in Figure 14 show the in-plane mode at the same wavenumber value of 233 cm–1. All polymorphs show the strong mode of the peak which dominates in plane mode.52 The A″2 IR mode of 1H-MoTe2 and 3Ha-MoTe2 involves out-of-plane vibrations of the Te atoms concerning the Mo layer. This mode results in perpendicular oscillations to the basal plane, which are typical for layered structures. The frequency varies from 285 to 288 cm–1 depending on the number of layers and different structures of MoTe2.48

Figure 14.

Figure 14

Open in a new tab

IR intensity as a function of wavenumber for dynamically stable MoTe2 polymorphs.

3. Conclusions

In conclusion, the stability analysis of MoTe2 polymorphs reveals that group A structures (1H-MoTe2, 2H-MoTe2, 3Ha-MoTe2, 3Hb-MoTe2, 2T-MoTe2, 4T-MoTe2, 2R1-MoTe2) exhibit lower total energies, indicating higher stability compared to group B (1T1-MoTe2, 1T2-MoTe2, 3T- MoTe2 and 2R2-MoTe2). The electronic structure analysis highlights the semiconducting nature of group A and the metallic behavior of group B MoTe2 polymorphs. The bandgap and effective mass values, particularly for 1H-MoTe2 and 2H-MoTe2, show promise for applications in photovoltaics and photocatalysis, while the metallic properties of group B polymorphs suggest potential in conductive applications. The DOS and PDOS analyses reveal that 2H-MoTe2 exhibits semiconducting behavior with distinct orbital contributions from Mo-d and Te-p states, while 1T1-MoTe2 displays metallic character due to the strong overlap of these orbitals. These findings underscore the influence of orbital hybridization and stacking on the electronic properties of the MoTe2 polymorphs. The charge density, charge transfer, and ELF analyses consistently confirm the covalent bonding character between the Mo and Te atoms in both hexagonal and trigonal MoTe2 polymorphs. The result of this study confirms the dynamic stability of the six polymorphs 1H-MoTe2, 2H-MoTe2, 3Ha-MoTe2, 4T-MoTe2, 3Hb-MoTe2, and 2R1-MoTe2. This study analyzes the mechanical properties of MoTe2 polymorphs, identifying stable and metastable forms. 2R1-MoTe2, 3Hb-MoTe2, and 2H-MoTe2 display ductility and exhibit strong mechanical properties. The Raman and IR spectral analyses of MoTe2 polymorphs highlight consistent vibrational modes across different structures. Phonon and elastic tensor studies reveal that the polymorphs 1H-MoTe2, 3Ha-MoTe2, and 4T-MoTe2 are metastable, while polymorphs 2H-MoTe2, 3Hb-MoTe2, and 2R1-MoTe2 exhibit dynamic and mechanical stability. This comprehensive study highlights the application potential of these stable MoTe2 polymorphs in the electronic, mechanical, and optoelectronic fields.

4. Method of Calculation

In the periodic density functional theory, the VASP (Vienna Ab Initio Simulation Package) code is used for the initial optimization.45,54 Generally, the interaction between the core and valence electrons is described by the projector-augmented wave (PAW) approach.47,55,56 In this study, with the use of the Pardew-Burke-Ernzerhof (PBE) exchange-correlation, the structure of each polymorph is initially optimized. To obtain PBE level optimal structure, the DFT/vdw-df2 approach is applied.57 From the optimized structure, an energy volume curve was computed to determine the lowest energy. Structure-related parameters can only be applied to forecast dependability for large E-cuts, we employed a 550 eV energy cutoff.58 The screened hybrid function, developed by Heyd, Scuseria, and Ernzerhof, was used to identify the electrical characteristics of polymorphs that are optimized at the PBE level (HSE06).59 The polymorphs employed a Monkhorst-pack 2 × 2 × 1 as k-mesh for structural optimization. By calculating the periodic Kohn–Sham equation on ten k-points along each direction of high symmetry of the irreducible part of the first Brillouin zone, bands of the polymorphs are calculated.60 Using the CASTEP (Cambridge Sequential Total Energy Package) program, investigations of charge density, charge transfer, and electron localization function (ELF) were carried out, which aided in understanding the nature of the bonds and interactions between the MoTe2 polymorphs.61 For the supercells of the polymorphs, a suitable supercell mode is performed, and the phonon dispersion and phonon density of the state are calculated using PHONOPY software.60 The VASP code is used to determine the supercell’s force constant. To get the matrices to create a force constant, each atom in the binary system is moved by a finite displacement of 0.007 in the x, y, and z directions. After determining the force constant, we build a dynamic matrix in the Brillouin zone for various q vectors. To obtain the phonon frequency eigenvalues and mode eigenvectors, the dynamic matrices are solved. Table S2 of the accompanying information on page S4 lists a suitable supercell mode and Monkhorst-pack gird. By comparing imaginary and real polymorphic modes, we examined the dynamical stability of each polymorph is examined. For the investigated polymorphs, thermal parameters, such as heat capacity, free energy, and system entropy, are derived. The dynamical stability of all polymorphs is checked by observing imaginary and real modes of polymorphs. Thermal properties are obtained for the studied polymorphs, including heat capacity, free energy, and entropy of the system. In this work, single crystal elastic constants are computed to understand the mechanical stability of all polymorphs. The stress tensor is generated after a series of strains (−0.015, −0.010, −0.005, 0.000, 0.005, 0.010, and 0.015) have been applied to each crystal system. By linear fitting of the stress–strain curve, VASPKIT is used to calculate the elastic constants. All of the polymorphs of MoTe2 have their Raman and IR spectra obtained using the CASTEP software.53 For the CASTEP computations, we used an optimized VASP structure to obtain a precise result.61

Acknowledgments

The authors gratefully acknowledge the Research Council of Norway for providing the computer time (under the project number NN2875k and NS2875k) at the Norwegian supercomputer facility.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.5c00226.

  • Minimum energy, electronic structure, phonon dispersion relation of polymorphs, k-grid, and supercell size of MoTe2 polymorphs (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao5c00226_si_001.pdf (743.9KB, pdf)

References

  1. Nafiujjaman M.; Nurunnab M.. Graphene and 2D Materials for Phototherapy. in Biomedical Applications of Graphene and 2D Nanomaterials; Elsevier, 2019, 105–117. [Google Scholar]
  2. Slušná L. P.; Vegso K.; Dobročka E.; Vojteková T.; Nádaždy P.; Halahovets Y.; Sojková M.; Hrdá J.; Precner M.; Šiffalovič P.; Chen Z.; Huang Y.; Ražnjević S.; Zhang Z.; Hulman M. Ordered growth of hexagonal and monoclinic phases of MoTe2 on a sapphire substrate. CrystEngComm 2023, 25, 5706–5713. 10.1039/D3CE00378G. [DOI] [Google Scholar]
  3. Qian X.; Liu J.; Fu L.; Li J. Quantum spin hall effect in two - dimensional transition metal dichalcogenides. Science 2014, 346, 1344–1347. 10.1126/science.1256815. [DOI] [PubMed] [Google Scholar]
  4. Zhou W.; Zou X.; Najmaei S.; Liu Z.; Shi Y.; Kong J.; Lou J.; Ajayan P. M.; Yakobson B. I.; Idrobo J. C. Intrinsic structural defects in monolayer molybdenum disulfide. Nano Lett. 2013, 13, 2615–2622. 10.1021/nl4007479. [DOI] [PubMed] [Google Scholar]
  5. Keum D. H.; Cho S.; Kim J. H.; Choe D. H.; Sung H. J.; Kan M.; Kang H.; Hwang J. Y.; Kim S. W.; Yang H.; Chang K. J. Bandgap opening in few-layered monoclinic MoTe2. Nat. Phys. 2015, 11, 482–486. 10.1038/nphys3314. [DOI] [Google Scholar]
  6. Chen J.; Li F.; Tang Y.; Tang Q. Tuning the phase stability and surface HER activity of 1T′-MoS 2 by covalent chemical functionalization. J. Mater. Chem. C Mater. 2020, 8, 15852–15859. 10.1039/D0TC03943H. [DOI] [Google Scholar]
  7. Song P.; Hsu C.; Zhao M.; Zhao X.; Chang T.-R.; Teng J.; Lin H.; Loh K. P. Few-layer 1T′ MoTe2 as gapless semimetal with thickness dependent carrier transport. 2D Mater. 2018, 5, 031010 10.1088/2053-1583/aac78d. [DOI] [Google Scholar]
  8. Huang H. H.; Fan X.; Singh D. J.; Chen H.; Jiang Q.; Zheng W. T. Controlling phase transition for single-layer MTe2 (M = Mo and W): Modulation of the potential barrier under strain. Phys. Chem. Chem. Phys. 2016, 18, 4086–4094. 10.1039/C5CP06706E. [DOI] [PubMed] [Google Scholar]
  9. Duerloo K. A. N.; Ong M. T.; Reed E. J. Intrinsic piezoelectricity in two-dimensional materials. J. Phys. Chem. Lett. 2012, 3, 2871–2876. 10.1021/jz3012436. [DOI] [Google Scholar]
  10. Cao M.; Ni L.; Wang Z.; Liu J.; Tian Y.; Zhang Y.; Wei X.; Guo T.; Fan J.; Duan L. DFT investigation on direct Z-scheme photocatalyst for overall water splitting: MoTe2/BAs van der Waals heterostructure. Appl. Surf. Sci. 2021, 551, 149364 10.1016/j.apsusc.2021.149364. [DOI] [Google Scholar]
  11. Chen B.; Sahin H.; Suslu A.; Ding L.; Bertoni M. I.; Peeters F. M.; Tongay S. Environmental changes in MoTe2 excitonic dynamics by defects-activated molecular interaction. ACS Nano 2015, 9, 5326–5332. 10.1021/acsnano.5b00985. [DOI] [PubMed] [Google Scholar]
  12. Yuan S.; Yin Y. X.; Guo Y. G. Room-temperature ferroelectricity in MoTe2 down to the atomic monolayer limit. Nat. Commun. 2019, 10, 1775. 10.1038/s41467-019-09669-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Meckbach L.; Hader J.; Huttner U.; Neuhaus J.; Steiner J. T.; Stroucken T.; Moloney J. V.; Koch S. W. Ultrafast band-gap renormalization and build-up of optical gain in monolayer MoTe2. Phys. Rev. B 2020, 101, 075401 10.1103/PhysRevB.101.075401. [DOI] [Google Scholar]
  14. Eidsvåg H.; Rasukkannu M.; Velauthapillai D.; Vajeeston P. In-depth first-principle study on novel MoS2polymorphs. RSC Adv. 2021, 11, 3759–3769. 10.1039/D0RA10443D. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Dawson W. G.; Bullett Electronic structure and crystallography of MoTe2 and WTe2. Phys. C: Solid State Phys. 1987, 20, 6159. 10.1088/0022-3719/20/36/017. [DOI] [Google Scholar]
  16. Brixner L. H. Preparation and properties of the single crystalline ab2-type selenides and tellurides of niobium, tantalum, molybdenum, and tungsten. J. Inorg. Nucl. Chem. 1962, 24, 257–263. 10.1016/0022-1902(62)80178-X. [DOI] [Google Scholar]
  17. Borlido P.; Aull T.; Huran A. W.; Tran F.; Marques M. A. L.; Botti S. ‘Large-Scale Benchmark of Exchange-Correlation Functionals for the Determination of Electronic Band Gaps of Solids. J. Chem. Theory Comput. 2019, 15, 5069–5079. 10.1021/acs.jctc.9b00322. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Heyd J.; Peralta J. E.; Scuseria G. E.; Martin R. L. Energy band gaps and lattice parameters evaluated with the Heyd-Scuseria-Ernzerhof screened hybrid functional. J. Chem. Phys. 2005, 123, 174101. 10.1063/1.2085170. [DOI] [PubMed] [Google Scholar]
  19. Conan A.; Bonnet A.; Amrouche A.; Spiesser M. Semiconducting properties and band structure of MoTe2 single crystals. J. Phys. France 1984, 45, 459–465. 10.1051/jphys:01984004503045900. [DOI] [Google Scholar]
  20. Vellinga M. B.; De Jonget R.; Haas C. Semiconductor to Metal Transition in MoTe. J. Solid State Chem. 1970, 2, 299–302. 10.1016/0022-4596(70)90085-X. [DOI] [Google Scholar]
  21. Liu J.; Ma Y.-Q.; Dai Y.-W.; Chen Y.; Li Y.; Tang Y.-N.; Dai X.-Q. Electronic properties of size-dependent MoTe2/WTe2 heterostructure. Chin. Phys. B 2019, 28, 107101. 10.1088/1674-1056/ab3b53. [DOI] [Google Scholar]
  22. Liu G.-B.; Shan W.-Y.; Yao Y.; Yao W.; Xiao D. Three-band tight-binding model for monolayers of group-VIB transition metal dichalcogenides. Phys. Rev. 2013, 88, 085433 10.1103/PhysRevB.88.085433. [DOI] [Google Scholar]
  23. Yadav M.; Sanyal B. First principles study of thermoelectric properties of Li-based half-Heusler alloys. J. Alloys Compd. 2015, 622, 388–393. 10.1016/j.jallcom.2014.10.025. [DOI] [Google Scholar]
  24. Popescu A.; Pertsova A.; Balatsky A. V.; Woods L. M. Optical Response of MoTe2 and WTe2 Weyl Semimetals: Distinguishing between Bulk and Surface Contributions. Adv. Theory Simul. 2020, 3, 1900247 10.1002/adts.201900247. [DOI] [Google Scholar]
  25. Roldán R.; Jose A.; Silva-Guillén M.; López-Sancho P.; Guinea F.; Cappelluti E.; Ordejón P. Electronic properties of single-layer and multilayer transition metal dichalcogenides MX2 (M = Mo, W and X = S, Se). Ann. Phys. 2014, 526, 347–357. 10.1002/andp.201400128. [DOI] [Google Scholar]
  26. Huang H. H.; Fan X.; Singh D. J.; Chen H.; Jiang Q.; Zheng W. T. Controlling phase transition for single-layer MTe2 (M = Mo and W): Modulation of the potential barrier under strain’. Phys. Chem. Chem. Phys. 2016, 18, 4086–4094. 10.1039/C5CP06706E. [DOI] [PubMed] [Google Scholar]
  27. Yilmaz T.; Tong X.; Dai Z.; Sadowski J.; Schwier E.; Shimada K.; Hwang S.; Kisslinger K.; Kaznatcheev K.; Vescov E.; Sinkovic B. Emergent flat band electronic structure in a VSe2/Bi2Se3 heterostructure. Commun. Mater. 2021, 2, 11. 10.1038/s43246-020-00115-w. [DOI] [Google Scholar]
  28. Yang L. M.; Ravindran P.; Vajeeston P.; Tilset M. Ab initio investigations on the crystal structure, formation enthalpy, electronic structure, chemical bonding, and optical properties of experimentally synthesized isoreticular metal-organic framework-10 and its analogues: M-IRMOF-10 (M = Zn, Cd, Be, Mg, Ca, Sr and Ba). RSC Adv. 2012, 2, 1618–1631. 10.1039/C1RA00187F. [DOI] [Google Scholar]
  29. Deng S.; Simon A.; Köhler J. The origin of a flat band. J. Solid State Chem. 2003, 176, 412–416. 10.1016/S0022-4596(03)00239-1. [DOI] [Google Scholar]
  30. Wang W.; Shi Y.; Zakharov A. A.; Syväjärvi M.; Yakimova R.; Uhrberg R. I. G.; Sun J. Flat-Band Electronic Structure and Interlayer Spacing Influence in Rhombohedral Four-Layer Graphene. Nano Lett. 2018, 18, 5862–5866. 10.1021/acs.nanolett.8b02530. [DOI] [PubMed] [Google Scholar]
  31. Kuklin A. V.; Ågren H. Quasiparticle electronic structure and optical spectra of single-layer and bilayer PdSe2: Proximity and defect-induced band gap renormalization. Phys. Rev. B 2019, 99, 245114 10.1103/PhysRevB.99.245114. [DOI] [Google Scholar]
  32. Balakrishnan K.; Veerapandy V.; Fjellvåg H.; Vajeeston P. First-Principles Exploration into the Physical and Chemical Properties of Certain Newly Identified SnO2Polymorphs. ACS Omega 2022, 7, 10382–10393. 10.1021/acsomega.1c07063. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Mimaki J.; Tsuchiya T.; Yamanaka T. The Bond Character of Rutile Type SiO2, GeO2 and SnO2 Investigated by Molecular Orbital Calculation. Z. Kristallogr. - Cryst. Mater. 2009, 215, 419–423. 10.1524/zkri.2000.215.7.419. [DOI] [Google Scholar]
  34. Togo A.; Tanaka I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. 10.1016/j.scriptamat.2015.07.021. [DOI] [Google Scholar]
  35. Bacic V.; Heine T.; Kuc A. Analytical Approach to Phonon Calculations in the SCC-DFTB Framework. J. Chem. Phys. 2020, 153, 144109. 10.1063/5.0023666. [DOI] [PubMed] [Google Scholar]
  36. Mann S.; Rani P.; Kumar R.; Jindal V. K. DFT study of phonon dispersion in pure graphene. AIP Conf. Proc. 2015, 1675, 030035 10.1063/1.4929251. [DOI] [Google Scholar]
  37. Qin G.; Qin Z.; Fang W.-Z.; Zhang L.-C.; Yue S.-Y.; Yan Q.-B.; Ming H.; Gang S. Diverse anisotropy of phonon transport in two-dimensional group IV-VI compounds: A comparative study. Nanoscale 2016, 8, 11306–11319. 10.1039/C6NR01349J. [DOI] [PubMed] [Google Scholar]
  38. Van De Walle A.; Ceder G. The Effect of Lattice Vibrations on Substitutional Alloy Thermodynamics. Rev. Mod. Phys. 2022, 74, 11. 10.1103/RevModPhys.74.11. [DOI] [Google Scholar]
  39. Wang R.; Zobeiri H.; Xie Y.; Wang X.; Zhang X.; Yue Y. Distinguishing Optical and Acoustic Phonon Temperatures and Their Energy Coupling Factor under Photon Excitation in nm 2D Materials. Adv. Sci. 2020, 7, 2000097 10.1002/advs.202000097. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Yu L.; Yan Q.; Ruzsinszky A. Negative Poisson’s ratio in 1T-type crystalline two-dimensional transition metal dichalcogenides. Nat. Commun. 2017, 8, 15224 10.1038/ncomms15224. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Zhang C.; Li L.; Yuan Z.; Xinyang X.; Song Z.; Zhang Y. R. Mechanical properties of siderite and hematite from DFT calculation. Miner. Eng. 2020, 146, 106107 10.1016/j.mineng.2019.106107. [DOI] [Google Scholar]
  42. Mehl M. J.; Singh D. J.; Papaconstantopoulos D. A. Properties of Ordered Intermetallic Alloys: First-Principles and Approximate Methods. Mater. Sci. Eng. 1993, 170, 49–57. 10.1016/0921-5093(93)90368-O. [DOI] [Google Scholar]
  43. Imani Yengejeh S.; Wen W.; Wang Y. Mechanical properties of lateral transition metal dichalcogenide heterostructures. Front. Phys. 2021, 16, 13502. 10.1007/s11467-020-1001-5. [DOI] [Google Scholar]
  44. Banu S. L.; Veerapandy V.; Fjellvåg H.; Vajeeston P. First-Principles Insights into the Relative Stability, Physical Properties, and Chemical Properties of MoSe2. ACS Omega 2023, 8, 13799–13812. 10.1021/acsomega.2c08217. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Pugh S. F. X. C. I. I. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 1954, 45, 823–843. 10.1080/14786440808520496. [DOI] [Google Scholar]
  46. Ranganathan S. I.; Ostoja-Starzewski M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 101, 055504 10.1103/PhysRevLett.101.055504. [DOI] [PubMed] [Google Scholar]
  47. Li R.; Shao Q.; Gao E.; Liu Z. Elastic anisotropy measure for two-dimensional crystals. Extreme Mech. Lett. 2020, 34, 100615 10.1016/j.eml.2019.100615. [DOI] [Google Scholar]
  48. Wang Y.; Xiao J.; Zhu H.; Li Y.; Alsaid Y.; Fong K. Y.; Zhou Y.; Wang S.; Shi W.; Wang Y.; Zettl A.; Reed E. J.; Zhang X. Structural phase transition in monolayer MoTe2 driven by electrostatic doping. Nature 2017, 550, 487–491. 10.1038/nature24043. [DOI] [PubMed] [Google Scholar]
  49. Grzeszczyk M.; Gołasa K.; Zinkiewicz M.; Nogajewski K.; Molas M. R.; Potemski M.; Wysmołek A.; Babiński A. Raman scattering of few-layers MoTe2. 2D Mater. 2016, 3, 025010 10.1088/2053-1583/3/2/025010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. David T.Practical Group Theory and Raman Spectroscopy, Part II: Application of Polarization. Spectroscopy 2014, 29. [Google Scholar]
  51. Joshi J.; Stone I. R.; Beams R.; Krylyuk S.; Kalish I.; Albert V.; Davydov; Vora P. M.; Lezama I. G.; Arora A.; Ubaldini A.; Barreteau C.; Giannini E.; Potemski M.; Morpurgo A. F. Indirect-to-Direct Band Gap Crossover in Few-Layer MoTe2. Nano Lett. 2015, 15, 2336–2342. 10.1021/nl5045007. [DOI] [PubMed] [Google Scholar]
  52. Pham T. T.; Castelino R.; Felten A.; Sporken R. Study of surface oxidation and recovery of clean MoTe2 films. Surf. Interfaces 2022, 28, 101681 10.1016/j.surfin.2021.101681. [DOI] [Google Scholar]
  53. Wang V.; Xu N.; Liu J. C.; Tang G.; Geng W.-T. VASPKIT: A User-friendly Interface Facilitating High-throughput Computing and Analysis Using VASP Code. Computer physics communication 2021, 267, 108033 10.1016/j.cpc.2021.108033. [DOI] [Google Scholar]
  54. Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
  55. Blöchl P. E. Projector Augmented-wave Method. Phys. Rev. B 1994, 50, 17953 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  56. Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  57. Kresse G.; Furthmü J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
  58. Kresse G.; Furthmiiller B. J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [Google Scholar]
  59. Heyd J.; Scuseria G. E.; Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. 10.1063/1.1564060. [DOI] [Google Scholar]
  60. Joshi J.; Stone I. R.; Beams R.; Krylyuk S.; Kalish I.; Albert V.; Davydov; Vora P. M. Phonon anharmonicity in bulk Td-MoTe2. Appl. Phys. Lett. 2016, 109, 031903 10.1063/1.4959099. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Refson K.; Tulip P. R.; Clark S. J. Variational density-functional perturbation theory for dielectrics and lattice dynamics. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 73, 155114 10.1103/PhysRevB.73.155114. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao5c00226_si_001.pdf (743.9KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES