Abstract
We introduce a novel concept of coarse extrinsic curvature for Riemannian submanifolds, inspired by Ollivier’s notion of coarse Ricci curvature. This curvature is derived from the Wasserstein 1-distance between probability measures supported in the tubular neighborhood of a submanifold, providing new insights into the extrinsic curvature of isometrically embedded manifolds in Euclidean spaces. The framework also offers a method to approximate the mean curvature from statistical data, such as point clouds generated by a Poisson point process. This approach has potential applications in manifold learning and the study of metric embeddings, enabling the inference of geometric information from empirical data.
Keywords: Coarse curvature, Extrinsic curvature, Optimal transport
Introduction
Synthetic lower bounds on Ricci curvature is a powerful tool in the study of classical geometric analysis and metric measure spaces. Ollivier’s notion of Coarse Ricci Curvature is distinct in that it approximates the curvature itself, rather than merely providing a lower bound. By selecting as test measures weighted localized volume measures, supported on a ball of radius , the Wasserstein 1-distance between two such measures reveals the generalized Ricci tensor; applying to random geometric graphs sampled from a Poisson point process with non-uniform intensity leads to similar conclusions [2].
Inspired by the concept of coarse Ricci curvature, in this article we seek a suitable notion of extrinsic curvature for embedded manifolds. With manifold learning applications in mind, we initially work with curves and surfaces and subsequently define a concept of coarse extrinsic curvature for general embedded manifolds. This notion captures the inner product between the mean curvature and the second fundamental form in a principal curvature direction. It may prove useful for studying embedded metric spaces and could be relevant in manifold learning contexts.
Let M be a smooth manifold isometrically embedded in another Riemannian manifold. We propose a family of test measures 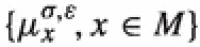 , where are small parameters, whose ‘derivative’ in the 1-Wasserstein distance with respect to variation of the point x describes some kind of curvature.
, where are small parameters, whose ‘derivative’ in the 1-Wasserstein distance with respect to variation of the point x describes some kind of curvature.
This consideration leads to a novel concept of coarse curvature in the setting of Riemannian submanifolds. Within the applicable range of the parameters, we have an approximation of the mean curvature and the second fundamental form, providing a valuable tool for evaluating these extrinsic curvatures. In more practical applications, we can take test measures built from statistical data and simulations; for instance through the empirical measures of point cloud samples. There is scope for extending to metric embeddings of metric spaces.
In contrast to the intrinsic Riemannian curvature, which characterizes the geometry of a manifold independently of its embedding, the second fundamental form of submanifolds is an extrinsic concept. It provides a means for describing the shape of a submanifold in relation to its ambient space, offering views into its bending properties. For instance, a surface embedded in is locally isometric to a plane if and only if its second fundamental form vanishes.
The extrinsic curvature of M, isometrically embedded in N, is expressed by the second fundamental form, which we recall to be defined as the bilinear form
| 1.1 |
where W is an arbitrary vector field on M with . Letting m denote the dimension of M, the mean curvature is defined as the vector field
Here is an arbitrary local orthonormal frame on a neighbourhood of x in M. Note that we omit the factor of 1/m that usually appears in this definition in the literature in order to simplify the statement of our results. It is a standard fact that both  and H(x) are vectors which are perpendicular to the submanifold M. We refer to e.g. [19, Chapter 5] for a detailed treatment of these objects. For instance, one of the examples we consider below is that of a planar curve with radius of osculating circle . A simple computation shows that in this case
and H(x) are vectors which are perpendicular to the submanifold M. We refer to e.g. [19, Chapter 5] for a detailed treatment of these objects. For instance, one of the examples we consider below is that of a planar curve with radius of osculating circle . A simple computation shows that in this case
where is the Euclidean magnitude.
There exists a considerable body of literature on description of submanifold properties by tubular volume, of which we name a few representatives. The early work of Weyl [32] proved the classical tube formula for submanifolds embedded in Euclidean spaces, which is an expansion with respect to the width of the tubular volume and its coefficients are geometric invariants of the submanifold. Federer [10] introduced the notion of boundary measures, which lead to generalization of the tube formula to compact subsets of Euclidean spaces. More recent works of Chazal et al. [5, 6] studied geometric inference via point cloud approximations to boundary measures using Monte Carlo methods. For a comprehensive treatment on properties of tubular neighbourhoods, we refer to the monograph [16]. The approach in our present work differs from the above in that it gives a local and directional information about the second fundamental form, and also the mean curvature.
Notions of synthetic Ricci curvature were motivated by the study of geometry of metric measure spaces and were pioneered by the seminal works [4, 23, 30], see also the survey [22]. In a metric measure space, a global lower bound on the synthetic Ricci curvature leads to properties of the metric measure space which are analogous to the Riemannian setting, such as the Poincaré and log-Sobolev inequalities, the concentration of measure phenomenon, and closure under measured Gromov–Hausdorff convergence [1, 8, 28]. We note also the related direction of the works [4, 31].
To our understanding, there has not been a notion of a synthetic extrinsic curvature. Our notion of coarse extrinsic curvature is inspired by coarse Ricci curvature of Ollivier [25], which is defined in the Riemannian setting through the expansion of the 1-Wasserstein distance of two uniform measures supported on geodesic balls of a small radius, the radius being the variable of expansion [25, Example 7], see also the survey [26]. This is different from the above mentioned synthetic Ricci curvature lower bounds in that it puts a precise number on the value of curvature at a point. Moreover, it can be applied to general metric spaces by choosing a family of measures indexed by points in the space for the evaluation of the 1-Wasserstein distance. Coarse Ricci curvature can be computed explicitly for a number of examples on graphs, where the measures are provided by a Markov chain. We adopt and modify Ollivier’s approach to the submanifold setting by choosing suitable measures for the expansion of the 1-Wasserstein distance, showing that this yields a geometrically meaningful information.
As an immediate application of our result, we venture into the setting of [2, 18] to explore retrieval of curvature information from point clouds generated by a Poisson point process. In the first of the mentioned works, Hoorn et al. proved that Ollivier’s coarse Ricci curvature of random geometric graphs sampled from a Poisson point process with increasing intensity on a Riemannian manifold converges in expectation at every point to the classical Ricci curvature of the manifold. This was extended in the second mentioned work to weighted Riemannian manifolds. In the present work, we show that coarse extrinsic curvature can recover the mean curvature in expectation at a point. In this case, it is not necessary to impose a graph structure to connect points of the sample.
In the context of deep learning, it is noteworthy that computational algorithms for effectively computing optimal transport maps have been proposed, as discussed in [17, 29]. Additionally, relevant work in the fields of manifold learning and inverse problems is worth mentioning. One particularly interesting inverse problem is whether an embedded manifold can be learned from a set of samples where belongs to a submanifold and are independent Gaussian random variables on . The reconstruction of embedded manifolds has been studied in [9, 11, 12, 27]. An algorithm for constructing an embedded submanifold is provided in [13]. Although manifold learning is still in its early stages, manifold approximation and reconstruction have a longer history, we point out some more recent publications on this topic [3, 7, 7, 14, 15].
Main results
In our setting, M is an m-dimensional compact Riemannian manifold embedded isometrically in a Euclidean space and is the local -tubular neighbourhood of M in , defined for sufficiently small as
For any compact subset , the projection mapping from its tubular neighbourhood
is well-defined for all sufficiently small, with the same notation for as above.
Denote by the exponential mapping in M with base point x. Fix a point , a unit tangent vector and denote for . Fix a constant smaller than the uniform injectivity radius of some fixed compact neighbourhood of in M. Assume so that lie within the uniform injectivity radius away from and assume is small enough so that the projection is well-defined on the -tubular neighbourhood of the -geodesic ball at in M. These requirements on the parameters will henceforth be encapsulated in the assumption that they are “sufficiently small”. This ensures that all locally defined maps are well-defined, in particular the projection map (smallness of ) and the Fermi coordinates (smallness of and ) used later on.
As our test measures, we choose the probability measures
where denotes the -geodesic ball at x in M. Note that these measures are supported on compact subsets of . We seek to obtain the expansion of with respect to the parameters and .
To relate the Wasserstein distance to the second fundamental form, we first localize to a tubular neighbourhood of a fixed open set on the submanifold. We expand the densities of the test measures in Fermi coordinates, and for the subsequent computations we rely on a crucial observation developed in Sect. 2.2: if T is an approximate transport map from to , in a sense defined later, then is close to . The remaining task involves proposing a concrete approximate transport map, which is at the same time close enough to optimal.
When dealing with test measures on an embedded manifold, accounting for the effect of the bending of the submanifold in the ambient space becomes crucial. The proposed transport map is thus formulated in terms of the Fermi frame along , adapted to the submanifold M in a way that separates tangent and normal coordinate directions at every point.
We give a rough outline of the proposed transport map, made precise in Sect. 2.4. In terms of Fermi coordinates, if represent submanifold tangent directions with being associated with the direction of , and if represent the normal directions, an initial proposal informed by the circle example (Sect. 3.1) was
This can be construed as translation by in the direction of the first coordinate, together with reflection in the first coordinate. From studying the planar curve example (Sect. 3.2), it turned out that an additional bending correction needs to be put on top of the components of the transport by adding terms involving the derivative of the mean curvature. Favourably, such a correction contributes to the final estimate of the Wasserstein distance only at the fourth order and higher, and hence does not interfere with the mean curvature term, which will appear at third order of the expansion. The test measures are first expressed in Fermi coordinates in Sect. 2.3. The proposed transport map is then presented in Sect. 2.4, where we prove that it is indeed an approximate transport map of degree 3, i.e.
This precision is sufficient for obtaining the 1-Wasserstein distance approximation (see Sect. 2.2):
From here the strategy is to construct a test function  with Lipschitz norm approximately 1 and satisfying the estimate
with Lipschitz norm approximately 1 and satisfying the estimate
which allows us to estimate the distance between the original measure and its transport by means of the relation
On the whole, we find that the Wasserstein distance between the initial measure and the target measure is approximated by up to (see Lemma 2.25), which is explicitly computable as an expansion in and with geometric quantities as coefficients.
Using the above tools, in Sect. 3 we thus compute the expansion of , beginning with the case of a planar curve:
Proposition 1.1
Let be a smooth unit speed curve in such that and . For all sufficiently small with , it holds that
where R is the radius of the osculating circle of the curve at .
This expansion can be rearranged as
We refer to the quantity on the left as the coarse extrinsic curvature of between and y at scales . A version of this result for spatial curves is presented in Theorem 3.10. In Theorem 3.16, we then proceed to study the case of coarse extrinsic curvature along a geodesic on a surface embedded in .
This work culminates with the most general form:
[Style2 Style3 Style3]Theorem 4.1
Let M be an isometrically embedded submanifold of , and a unit speed geodesic in M such that and . Let be an orthonormal basis of with and assume that 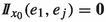 for all . Then for every sufficiently small with it holds that
for all . Then for every sufficiently small with it holds that
The assumption on the second fundamental form is necessary for optimality of our proposed transport map up to sufficient order and can always be satisfied for submanifolds of codimension 1, in particular surfaces embedded in , by choosing the basis of principal curvature directions. Further commentary is provided in Remark 4.2.
To interpret such expansions in terms of mean curvature, we can remove the directionality of the above result caused by transport in the direction of . Denoting the square norm of the mean curvature vector as
for an arbitrary orthonormal basis of the normal space , we deduce the following:
Corollary 1.2
Let be an orthonormal basis of , and for , let . Assume that  for . Then for all sufficiently small with it holds that
for . Then for all sufficiently small with it holds that
Observe that the left side of the equation is independent of the choice of orthonormal basis because the norm on the right side is basis-invariant. Moreover, the assumption on the second fundamental form always holds for submanifolds of codimension 1 (see Remark 4.2).
In Proposition 5.4, we deduce that the coarse extrinsic curvature of suitable test measures on Poisson point clouds sampled from the tubular neighbourhood retrieves the same extrinsic geometric information consistent with Theorem 4.1.
One key ingredient in the proofs of the above theorems is the geometric approximate transport map introduced in Definition 2.18, defined by means of Fermi coordinates (as per Definition 2.14) adapted to the submanifold. Test measures in these coordinates encode information about the second fundamental form of the submanifold. The proposed map is verified to be an approximate transport map between the test measures with sufficient order of accuracy, as specified and motivated in Sect. 2.2. The optimality up to fourth order is proved by choosing a concrete test function for the Wasserstein lower bound by the Kantorovich–Rubinstein duality.
In the resulting expansion of the Wasserstein distance, the second fundamental form at the fixed point appears at third order, and its derivatives appear at fourth and higher orders. As a consequence, information about the second fundamental form at a point can be retrieved in a suitably scaled limit of coarse curvature. Please see the discussion below for an example.
Discussion
We illustrate this work using the following prototypical example. Let be a smooth, unit speed planar curve, and a unit normal vector field along , unique up to sign. Denote by the radius of the osculating circle at the point . To detect the extrinsic curvature at , captured here by R(0), we define test probability measures centered at nearby points indexed by .
Denote the Lebesgue measure on , as the image of the curve, and as a small enough tubular neighbourhood of M so that the orthogonal projection is well-defined. Denote
where is the distance along . Define for with , the Borel measure on ,
We compare these in 1-Wasserstein distance to the initial measure, i.e. when and is denoted . The Wasserstein distance has the form:
Rearranging this expansion yields
| 1.2 |
From this point, depending on the application, we may consider three different regimes for the parameters and as y converges to . We recall the asymptotic notation means there exist such that for all ,
and means .
-
(i)for some known constant , i.e. the decay of both and is controlled. In this case,
-
(ii)and , i.e. the decay of is controlled, while the parameter of support size vanishes fast. In this case,
-
(iii)and , i.e. the decay of is controlled, while the size of the tubular neighbourhood vanishes fast. In this case,
The requirements and in the respective cases are in place to ensure the remainder term in (1.2) does not explode upon division by (resp. ) in the limit as .
In light of the above discussion, we may define the coarse extrinsic curvature between and y at scales as:
| 1.3 |
This quantity can be estimated from point cloud data and used for geometric inference.
In summary, this work focuses on Riemannian submanifolds embedded isometrically in Euclidean spaces with the aim of producing a reasonable measurement for the bending energy. This bending energy can also be estimated from point clouds obtained from sampling. One of the novel ingredients is the construction of a test function for using the Kantorovich–Rubinstein duality to obtain a lower bound for the Wasserstein distance in this setting.
The outline of this work is as follows. In Sect. 2, we establish geometric preliminaries pertaining to the volumes of tubular neighbourhoods and present approximate transport maps as a novel tool for approximating the 1-Wasserstein distance. In Sect. 3, we give description of coarse extrinsic curvature for a planar curve, space curve and a 2-surface embedded in . The coarse extrinsic curvature of a general submanifold of arbitrary codimension is studied in Sect. 4. We present several immediate corollaries to our results with practical applications in Sect. 5. Although the cases of curves and surfaces in Sect. 3 are just instances of the general result in Sect. 4, they provide value in understanding this general case. Sections 3 and 4 can be read separately after reading Sect. 2, which contains all preliminaries.
Preliminaries
We prove a formula for volume growth of tubular neighbourhoods of submanifolds, leading to a disintegration of the ambient volume measure adapted to the submanifold. This formula is subsequently utilized to derive explicit formulas for such disintegration in Fermi coordinates, considering cases such as a planar curve, space curve, and a surface in Sect. 3, and general Riemannian submanifolds in Sect. 4.
Following the geometric preliminaries, we introduce the notion of an approximate transport map, enabling the computation of Wasserstein distances up to a sufficiently high degree of error. Subsequently, we define the test measures to be transported and their representation in Fermi coordinates. Finally, we propose a transport map to evaluate the Wasserstein distance of these test measures.
Ambient volume disintegration
We begin with a simple lemma on evolution of probability densities. We denote 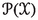 as the space of probability measures on a measurable space
as the space of probability measures on a measurable space  . The notation denotes the fact that the measure is absolutely continuous with respect to the measure .
. The notation denotes the fact that the measure is absolutely continuous with respect to the measure .
Lemma 2.1
Consider 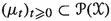 such that for all . Let
such that for all . Let  , be a family of functions with locally integrable, and such that for every . Then
, be a family of functions with locally integrable, and such that for every . Then
Proof
The change of density at any satisfies
implying
which has the unique solution by standard ODE theory.
Notation 2.2
Throughout this article, M is a compact Riemannian manifold of dimension m, isometrically immersed in a Riemannian manifold N of dimension n. Set . Let be a fixed number smaller than half the reach of M in N. The reach is defined as the maximal number r such that each point within a distance r from M has a unique orthogonal projection to M,  . The projection map is well-defined within the ‘reach’.
. The projection map is well-defined within the ‘reach’.
Let be a sufficiently small open neighbourhood such that there exists an orthonormal frame of unit normal vector fields on U and a one-parameter family of vector fields such that is an orthonormal frame on for every , and is smooth for every . The latter can be constructed by taking the pushforward of an arbitrary initial orthonormal frame by , denoted by , and applying the Gram–Schmidt orthonormalization procedure.
Definition 2.3
Let be a unit normal vector field, and define the normal flow by
where denotes the exponential mapping on N. Denote by  the parallel transport with respect to the Levi-Civita connection along for a fixed , and note that
the parallel transport with respect to the Levi-Civita connection along for a fixed , and note that  .
.
For every , is a diffeomorphism onto its image, and is smooth with non-vanishing derivative for every . Equip every with the Riemannian metric inherited from the ambient space. The mean curvature of the leaf is then given by
In particular, for any unit normal vector field on U,
The following lemma shows 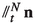 stays normal to the leaves as t changes.
stays normal to the leaves as t changes.
Lemma 2.4
The vector field 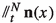 is normal to for every , i.e.
is normal to for every , i.e.  for any local tangent frame on M.
for any local tangent frame on M.
Proof
For every , being a diffeomorphism implies that if is a frame on U, then is a frame on , not necessarily orthonormal. Then
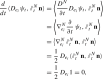 |
where on the second line we used that 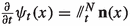 . The initial condition gives , so we may conclude that
. The initial condition gives , so we may conclude that 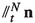 is normal to all tangent directions on for all t.
is normal to all tangent directions on for all t.
The action of push-forwards of volume forms on any orthonormal basis of tangent vectors is characterized by the determinant of the mapping which we make precise below. Let be Riemannian manifolds of the same dimension m, a diffeomorphism, an orthonormal frame on an open set and an orthonormal frame on an open set , and the corresponding coframes characterized by . Below, by the determinant of we mean that of the matrix representing the map in these bases:
By the rules of differential forms acting on tangent vectors, for all ,
Since linear maps are determined by their values on basis vectors, we may deduce
| 2.1 |
With the above notation we return to the exponential map .
Proposition 2.5
(Change of volume) For every ,
| 2.2 |
and hence the volume of the image of any Borel measurable can be expressed as
| 2.3 |
where is the Riemannian volume on .
Proof
First, we extend the map to by the flow condition
for all s and t in . This determines uniquely because is a foliation of the tubular neighbourhood . Then on every leaf of the foliation, we have . If and are orthonormal coframes on and respectively, the change of variable formula for volume forms (2.1) states that
Then for every Borel measurable and ,
using respectively the flow property, definition of the push-forward of a measure, and the change of variable formula with and .
Denoting by the covariant derivative along , the Jacobi formula for the derivative of determinants gives
 |
From the second to third line, the other term coming from the product rule applied on the bracket does not contribute to the trace, because for ,
using that so . From the fourth to fifth line, we used normality of the flow , and on the last line applied from definition of the extension , before pulling the integral from back to A.
Hence the evolved volume measure pulled back to U satisfies the dynamics
| 2.4 |
which together with the initial condition implies
by Lemma 2.1, setting to be the right-hand side of (2.4). Equation (2.3) is then simply the change of variable formula for the map .
Remark 2.6
The formula of Proposition 2.5 can be extended from the neighbourhood U to all of M by a partition of unity argument, nonetheless the local formulation is sufficient for our purpose.
We proceed to derive a disintegration of the ambient volume measure adapted to a submanifold of arbitrary codimension, at the cost of specialising to the case . Note that the covariant derivative then becomes the plain derivative denoted by D.
Notation 2.7
Let be a local orthonormal frame for on U and denote 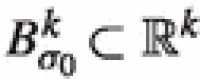 the centered Euclidean ball of radius . Define the map
the centered Euclidean ball of radius . Define the map
 |
2.5 |
which gives the k-dimensional foliation of with leaves of dimension m. Extend and smoothly to so that the restrictions to the submanifold are an orthonormal frame in the tangent space and the normal space, respectively, for every .
Denote which was shown in Lemma 2.4 to be normal to each leaf . Then the mean curvature of in the direction is
Denote also the components of mean curvature in each of the directions of the normal frame,
so that
Remark 2.8
The collection of submanifolds is indeed a foliation of (see e.g. the definition of foliation in [21]). The leaves are disjoint submanifolds of dimension m. Defining
where is an arbitrary chart on U, we have by definition that
so each leaf is a level set of F and thus F is a flat chart for the foliation.
Proposition 2.9
(Disintegration) The ambient volume measure on disintegrates with respect to the submanifold and the normal frame as
| 2.6 |
for any Borel measurable set 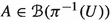 in the tubular neighbourhood.
in the tubular neighbourhood.
Proof
We apply the change of coordinates by the map defined by (2.5), which at every has block-triangular derivative with respect to the orthonormal bases
and
in the domain and codomain respectively, since
Hence the determinant can be computed as
for which we have the right-hand side of (2.2).
Denoting , the coframes characterized by and ,
 |
on the second line using the change of variable formula and on the third line plugging in the determinant expression (2.2) with and . The final expression is obtained by the substitution so that
Corollary 2.10
(Codimension 1) If M has codimension 1 then the ambient volume measure on can be written in terms of the disintegration
| 2.7 |
for all  , where is the volume measure of the submanifold M and is the mean curvature on the Riemannian submanifold .
, where is the volume measure of the submanifold M and is the mean curvature on the Riemannian submanifold .
Approximate transport maps
In the sequel, we work with transport maps which are only optimal up to sufficiently high degree for asymptotically small diameter of support of the test measures. We present a result which justifies the use of such transport maps.
Let  be a Polish space,
be a Polish space,  the set of probability measures, define
the set of probability measures, define
and consider two families of probability measures  ,
, 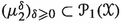 .
.
Lemma 2.11
( distance approximation) If and for every with the density satisfying , then
Proof
By the reverse triangle inequality and Kantorovich–Rubinstein duality, for all 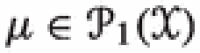 :
:
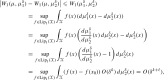 |
where is arbitrary. On the last line, we introduced the term
because is constant and the density integrates to 1, and then used the 1-Lipschitz property of f together with the bound on the diameter of the support of .
Let 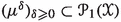 be another family of probability measures.
be another family of probability measures.
Definition 2.12
(Approximate transport map) A measurable map  is said to be an approximate transport from to with degree k if and the density satisfies
is said to be an approximate transport from to with degree k if and the density satisfies
Corollary 2.13
If 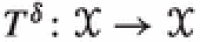 is an approximate transport map from to with degree k and then
is an approximate transport map from to with degree k and then
Proof
Set and apply the previous lemma.
Test measures in Fermi coordinates
Let (M, g) be a Riemannian submanifold of codimension k in and an open neighbourhood of a point as in Notation 2.2. The Fermi coordinates are a suitable tool for explicit computations and will be used throughout the rest of this work. The following is a modification of classical Fermi coordinates to the submanifold setting.
Definition 2.14
(Fermi coordinates) Let be a unit speed geodesic with small enough for to be contained in U, the uniform injectivity radius in M along and smaller than half the reach of U in . Let be an orthonormal frame for the fibres of TM along such that and for and every . Also let be a local orthonormal frame for fibres of the normal bundle along .
Denote by the centered ball of radius in and by the centered ball of radius in . Denote and define
which is a diffeomorphism provided that are sufficiently small. This is referred to as the Fermi chart along adapted to the submanifold M. See Fig. 3 for an illustration on a 2-surface in .
Fig. 3.
Fermi coordinates along adapted to the surface M embedded in
The Riemannian metric is expressed in the Fermi coordinates as
| 2.8 |
Remark 2.15
The advantage of over a generic as given in Notation 2.7 is that is adapted to the geodesic in a way that simplifies computations of distances relevant to our optimal transport problem. The chart yields again a foliation of .
Definition 2.16
(Test measures) Denote the cylinder-like segment in of height and radius centered at as
and let be the Lebesgue measure on . For any define the family of test probability measures
indexed by .
Denote so that . The main purpose of the expansion in the following lemma is twofold. First, we use it to design the third order corrections in the approximate transport map of Definition 2.18 so that density matching occurs in Proposition 2.23. Second, the first order term of the expansion interacts with first order term of pointwise distance when integrating to get the Wasserstein upper bound in the proofs of Sects. 3 and 4.
Lemma 2.17
(Test measures in Fermi coordinates) For any , the expansion of the density of test measures in Fermi coordinates is
| 2.9 |
where Z is the probability normalization constant and is the Riemannian metric of M in Fermi coordinates given by (2.8).
Proof
First, note the pull-back of the test measure to Fermi coordinates is
The Riemannian metric in Fermi coordinates expands as
| 2.10 |
Indeed, for all , and hence also . We show this by cases:
for all : because for every fixed , are normal coordinates within the injectivity radius of at (see e.g. [19, Section 1.4] for a proof),
for all : for any as the orthonormal frame along used to define the Fermi chart is parallel translated along ,
- for all and and any :
using that and . The latter vanishes for again by normality of the chart on , and for because is given by parallel translation along .
The Riemannian volume expanded in the Fermi coordinates then simplifies to
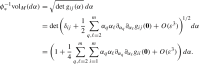 |
Moreover, expand the exponent in the normal part of the disintegration as
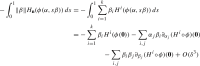 |
and apply the approximation up to second order to obtain
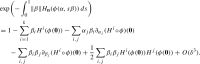 |
2.11 |
We conclude the result by taking the product of the two factors (2.10) and (2.11), merging third order terms in into by the assumption .
The probability normalization constant can be deduced by integration of (2.11) with respect to as
and so
Proposed transport map
As mentioned in the introduction, when considering an embedded manifold, it is crucial to include the mean curvature in the transport map. We will show that the transport map proposed below is an approximate transport map with degree 3. We then present a criterion for optimality of the proposed map in Lemma 2.25.
Definition 2.18
Define in Fermi coordinates as
Denote by and similarly for , and denote the input vector on the right in the above definition as 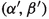 . Note that
. Note that
Remark 2.19
Observe that T is a local diffeomorphism and
and deduce
| 2.12 |
Remark 2.20
The third order terms in the definition of T are adjustments to cancel out second order terms in the proof of Proposition 2.23 below, obtaining an approximate transport of degree 3 as a result. In fact, the form of T is tailored precisely for this to occur. It turns out these third order adjustment terms do not influence the Wasserstein distance computation up to order 4.
We need two general lemmas to show that T is an approximate transport of degree 3.
Lemma 2.21
(Density under pushforward) Let 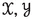 be measurable spaces,
be measurable spaces, 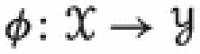 a measurable bijection with measurable inverse, and two measures on
a measurable bijection with measurable inverse, and two measures on 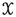 with . Then the push-forward measures are also absolutely continuous with density
with . Then the push-forward measures are also absolutely continuous with density
Proof
For all measurable sets 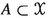 ,
,
Noting that the representations (2.6) and (2.7) are decompositions into skew-products of two measures, the following will be used for density comparisons.
Let 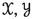 be measurable spaces. Given measures
be measurable spaces. Given measures 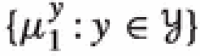 on
on  and a measure on
and a measure on  , the skew-product is defined as follows: For all bounded measurable real valued functions f on
, the skew-product is defined as follows: For all bounded measurable real valued functions f on 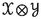 ,
,
Lemma 2.22
(Skew-product density factorization) Consider two families of measures  and
and  on
on  such that for every
such that for every  and the map is measurable. Furthermore, let and be measures on
and the map is measurable. Furthermore, let and be measures on 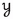 with . Consider the skew products of
with . Consider the skew products of  with and that of
with and that of  with . Then and
with . Then and
Proof
Plugging in the densities, for all 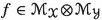 bounded:
bounded:
 |
We verify that the density of via T matches that of up to .
Proposition 2.23
The proposed map is an approximate transport map of degree 3, i.e.
Proof
First, combining the elementary change of variable formula with the Fermi coordinate representation of , with notation of Definition 2.18 we have
 |
2.13 |
using the expansions (2.12) for the determinant of and (2.9) for the coordinate representation of .
We use Lemma 2.21 to push the density into Fermi coordinates, and then Lemma 2.22 allows us to take the ratio of the densities of (2.13) and (2.9), obtaining
because the second order terms cancel out. Here we also used that T is a diffeomorphism from to , hence
Remark 2.24
Building upon the preceding proposition and leveraging Corollary 2.13, we readily deduce that the proposed transport map satisfies:
taking also into account that leading to when . Thus, when computing the coarse curvature, we may use . This is justified as terms involving the second fundamental form at the point emerge only at the third order in the expansion of , making precision up to sufficient.
The following will allow us to deduce a Wasserstein lower bound from an upper bound provided by an approximate transport map of degree 3, and merging these into a both-sided estimate up to .
Lemma 2.25
If 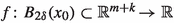 is smooth and takes the form
is smooth and takes the form
| 2.14 |
and the magnitude of its gradient satisfies
then for all sufficiently small with ,
Proof
Using the expansion , we deduce that
By the mean value theorem, a differentiable function divided by the supremum of its gradient is 1-Lipschitz. Then by Kantorovich–Rubinstein duality
 |
using the assumption (2.14) on the third and fourth line.
Finally, in order to integrate over the correct range of Fermi coordinates to cover precisely as the support of , we need to find the range parameter such that if
then
This is a necessary consideration, because in general non-flat spaces
The following is a classical result of Toponogov, which is a generalization of the Pythagoras theorem for Riemannian manifolds and gives a characterisation of sectional curvature. See e.g. [24] for a proof.
Lemma 2.26
For any point and any sufficiently small, the Riemannian distance between and has the expansion
As a consequence, we deduce that given a coordinate , the range parameter is characterized by the relation
where the coefficient in the remainder term only depends on a fixed neighbourhood of . This implies and
We shall label the remainder term for the purpose of the following proof. The next corollary will allow us to ignore the distinction between and up to whenever we integrate with respect to the test measure in Fermi coordinates.
Corollary 2.27
If 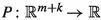 is a polynomial with no constant term and then
is a polynomial with no constant term and then
Proof
We split the domain of integral on the right so that one part matches the domain on the left and the integral of the other part is :
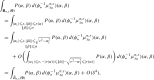 |
on the last line we using that has no constant term and .
Curves and surfaces
We establish explicit formulas for the coarse extrinsic curvature defined by (1.3) in four practically relevant cases: a circle, a planar curve, a space curve, and a surface. We begin by presenting the common setup shared among all these cases.
The circle example
Our motivating example is the circle with a fixed radius , which avoids technicalities arising from varying radius in the osculating circle, an issue that will be addressed in Sect. 3.2 in the case of planar curves.
Notation 3.1
Denote the polar coordinates
| 3.1 |
where parametrizes arc-length distance from the point (R, 0) along the circle and parametrizes the direction normal to the circle.
Denote and for every denote .
Lemma 3.2
The test measures in polar coordinates take the form
Proof
At any , the radial coordinate is , the radial length element is and the angular element is , giving the volume element , with as the probability normalization factor for the support .
This is consistent with the formula of Proposition 2.9, as the mean curvature at is , which gives the density
on .
The transport map of Definition 2.18 boils down to
| 3.2 |
and note that . See also Fig. 1 below.
Fig. 1.

Planar curve case: test measures in red with some transport pairs of T in blue (Color figure online)
Remark 3.3
In this case the transport map T is precise in the sense that . Indeed, for any Borel measurable,
 |
Proposition 3.4
For all sufficiently small with , it holds that
Proof
For every point ,
which is the Euclidean distance of two points on the circle at angle apart. Integrating with respect to the test measure yields
For the lower bound, we test against the 1-Lipschitz function
We have
and so , giving
| 3.3 |
Then we compute using (3.1), (3.2) and (3.3):
by trigonometric identities. Therefore
which shows the lower bound agrees exactly with the upper bound.
Planar curve
Let be a smooth unit speed curve. As before, let , where .
The normal vector field along is given by , the radius of the osculating circle is and we have the relationships
| 3.4 |
Let be given as follows:
This is the Fermi chart along . While we have the general Fermi coordinate representation in terms of the expansion in Lemma 2.17, in this case we arrive at a precise form:
Lemma 3.5
The test measures at are
Proof
To evaluate in applying Proposition 2.9, normalize the vector field tangent to the curve and compute the second derivative in as
The second term is tangential to the curve, so may be ignored for the computation of H. Moreover,
Note that is normal to for every since
therefore the mean curvature is
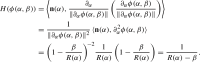 |
Finally,
and the Lebesgue measure of the support is the normalization factor because the term vanishes when integrating over .
In this case the proposed transport map of Definition 2.18 reduces to
As a consequence of Corollary 2.13,
Lemma 3.6
For all sufficiently small with , it holds that
For notational ease we shall from here onwards denote and .
Proposition 3.7
Let be a smooth unit speed curve in such that and . For all sufficiently small with , it holds that
where R is the radius of the osculating circle of the curve at .
Proof
Lemma 3.6 allows computing instead. Throughout the proof, terms of order and higher are absorbed into . For the upper bound, we compute by expansion with respect to the orthonormal basis at ,
having inserted for the derivatives at 0 using the list (3.4). Then the distance of the transport pairs up to order 4 is
| 3.5 |
having used the factorizations and . By orthonormality of , we compute this norm as
 |
3.6 |
by the expansion for the square root on the last line.
Moreover, expanding the volume distortion factor as
and multiplying the expression for by this factor, we integrate and note that only terms of even order in both and contribute, yielding
To obtain the factor on the last line, we applied that
which can be deduced by plugging in for in the previous computation of . The coefficient came from integrating the term of the integrand, . The terms with odd power in or such as vanished as they are mean zero.
We proceed with showing the lower bound, using again the 1-Lipschitz test function
Express the vector between the centres of the two test measures, recalling ,
This vector has magnitude
and so we deduce that
Then we compute, using the expression (3.5) for obtained above,
We see that this agrees with the pairwise transport distance (3.6) up to , hence Lemma 2.25 applies and the upper and lower bounds agree up to an term.
Space curve
Let be a smooth, unit speed curve with velocity . Define the unit normal and binormal vector fields along as
This yields the so-called Frenet–Serret frame of along . Writing for the radius of the osculating circle and for the torsion, the Frenet–Serret formulas give relationships between the vector fields of the frame,
| 3.7 |
From these, we deduce the higher order derivatives
| 3.8 |
We will employ the Frenet–Serret frame for explicit computations of distances between points in the tubular neighborhood of a space curve. Additionally, we will employ it in formulating a sufficiently accurate approximate transport map between test measures, represented through an expansion in Fermi coordinates.
Definition 2.14 for Fermi coordinates requires a choice of a local orthonormal frame of the normal bundle along . We choose as follows:
where come from the Frenet–Serret frame.
Definition 3.8
Define the Fermi coordinates , adapted to , by the formula:
Denote , , , .
Consider the family of curves Denote the particular unit normal vector fields
The mean curvature of each curve in the direction is expressed as
where the second equality holds because is normal to by Lemma 2.4.
Remark 3.9
We perform computations in terms of the Frenet–Serret frame as it can be interpreted in terms of the radius of the osculating circle and torsion of the curve.
- As a special case of Lemma 2.17, using that the mean curvature components are
the test measures at every in Fermi coordinates along are
where is the remainder.
Fig. 2.

Space curve case: test measures in red with some transport pairs of T in blue (Color figure online)
Theorem 3.10
Let be a space curve with and the test measures defined in Definition 2.16 with coordinate representation of Remark 3.9. For all sufficiently small and with , it holds that
where is the radius of the osculating circle.
Proof
Due to Lemma 3.6, it is sufficient to work with the distance as it approximates . The computation of the pairwise distances is similar to the planar curve case, (3.5), with additional terms due to the component . Concretely, since
and using the derivatives (3.7) and (3.8), compute
Then similarly to (3.5) we obtain
| 3.9 |
The Wasserstein distance upper bound is then computed by integration with respect to using the coordinate representation of Remark 3.9 as
applying on the last line that . In the integral on the first line, terms of odd order vanish upon integration, and the remaining terms amount to integration of quadratic polynomials.
We now address the lower bound. Analogously to the plane curve case, define the test function for the Kantorovich–Rubinstein duality as
which is again clearly 1-Lipschitz in . We wish to apply Lemma 2.25 to show the lower bound and upper bound coincide up to . Noting that , we deduce from (3.9) that
and so
Therefore
This is the same expression as for , hence Lemma 2.25 applies and the lower and upper bounds agree up to .
Surface
We now consider a smooth 2-surface and a unit speed geodesic in M, denoting again for sufficiently small. Let be the unit normal vector field and the unit vector field along orthogonal to the velocity . Both and are unique up to sign.
Definition 3.11
- Define the Fermi coordinates along in M as
- Define the Fermi coordinates along in adapted to the surface M as
See Fig. 3 for a graphical representation of and . - For denote the components of the second fundamental form in the Fermi coordinates
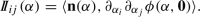
Remark 3.12
We point out that we overload the second fundamental form symbol 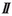 depending on the context of use. In the notation (1.1) and in the statements of Theorem 3.16 and Theorem 4.1, the subscript is the point on the manifold and the bracket arguments are tangent vectors. On the other hand, in coordinate computations taking place in the proofs, the subscripts will represent components with respect to the Fermi frame at Fermi coordinates in brackets.
depending on the context of use. In the notation (1.1) and in the statements of Theorem 3.16 and Theorem 4.1, the subscript is the point on the manifold and the bracket arguments are tangent vectors. On the other hand, in coordinate computations taking place in the proofs, the subscripts will represent components with respect to the Fermi frame at Fermi coordinates in brackets.
Similarly to the Frenet–Serret frame in the case of a planar curve, we now consider the orthonormal frame with the intent to expand at , i.e. .
Lemma 3.13
The first derivatives of the normal vector field at are
Hence the derivatives of at up to third order are
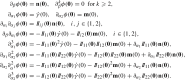 |
Proof
The derivatives involving are clear, recalling the definition
and the first derivatives in follow from the definition of .
For we check its components with respect to the frame ,
and similarly for .
For the second derivatives in at for any and ,
having introduced the term , which vanishes for , because is a geodesic on M and is the parallel translation of along . By the same argument, for any ,
because is a geodesic for every .
For the second derivatives in and one of and , deduce and plug in for .
For the third derivatives at , write by the chain rule
and plug in for in each.
Denote the plain derivative in the direction of a vector field V as a smooth map from an open subset of to .
Notation 3.14
Denote .
Consider the family of surfaces For any , we denote the unit normal vector field of the surface as , which is unique up to sign. The corresponding mean curvature is:
where is an orthonormal frame on each .
Remark 3.15
- As a special case of Lemma 2.17, the test measures at in these Fermi coordinates are
where is a second order remainder.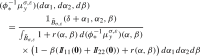
3.10
Fig. 4.
Test measures in red with some transport pairs of T in blue (Color figure online)
Fig. 5.
Top-down perspective for the transport map T
Fig. 6.
Cross-sectional perspective for the transport map T
Theorem 3.16
Let M be an isometrically embedded surface in , let be a point and an orthonormal basis of principal curvature directions at . Let be a unit speed geodesic in M with , and denote . For all sufficiently small with , it holds that
Remark 3.17
If we set , we note that the bracket on the right reduces to 1. This is due to the effects of second fundamental form and the curvature of the submanifold cancelling out, so it would appear in such special case that the coarse extrinsic curvature is flat, even though the second fundamental form may be non-vanishing. Such a special case is due to having an additional degree of freedom because of the additional parameter and the sign of the term happens to oppose that of the term. The extrinsic curvature should thus be seen as encapsulated by varying both and in .
Proof
The conclusion of Corollary 2.13 holds, so we may compute instead. For every point , expanding up to third order and using the list of derivatives of Lemma 3.13, we collect terms as components of the frame at ,
 |
3.11 |
While the terms are only of order 3, they are linear in , and hence will not influence the integral with respect to up to . In the same way an expression for the proposed transport
can be obtained by making corresponding substitutions for the components in the above expression for . Then the pointwise transport vector is
 |
3.12 |
and its magnitude is
| 3.13 |
Using the density of the test measure in Fermi coordinates given by (3.10), the upper bound is
 |
In the third equality, we plugged in for as computed above and used that terms of odd order in one of integrate to 0 and again absorbed higher order terms into . On the last line, we used that
We proceed with showing the lower bound. Define
and the test function
| 3.14 |
for the Kantorovich–Rubinstein duality, with the intention of applying Lemma 2.25 to conclude. We first expand
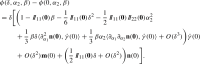 |
Deduce
and therefore
| 3.15 |
Then it can be verified using expansions (3.12) and (3.15) to compute the inner product that
by comparison with (3.13).
It remains to show that the magnitude of the gradient of f satisfies
For this we need to expand the inverse matrix of the metric in Fermi coordinates. Using the expansion (3.11), compute
 |
We shall label the term
Then the metric matrix has the shape
with
Note that the matrix is of the form
with , which means the expansion of its inverse is
We compute
and thus
From (3.15) we deduce the derivatives of the projection vector field in coordinates are
Then the first derivatives of the test function defined in (3.14) are
 |
Then the magnitude of the gradient is
and we find the individual summands
 |
which indeed gives
as the first and second order terms cancel out. Hence Lemma 2.25 applies and we conclude the lower bound coincides up to with the upper bound.
General Riemannian submanifolds
We now consider a Riemannian submanifold M of arbitrary dimension m and codimension k embedded isometrically in . Theorems 3.10 and 3.16 are thus special cases of Theorem 4.1 below. We begin by defining an orthonormal frame of -valued vector fields on a sufficiently small open domain U in the submanifold M, which is used to define the Fermi coordinates on U in this general setting.
Frame extension
We take the ambient manifold to be . Recall the second fundamental form at a point is
where W is an arbitrary local vector field on M with . The mean curvature at x is
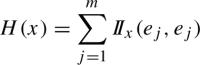 |
for an arbitrary orthonormal basis of . Both  and H(x) are normal to the submanifold, i.e.
and H(x) are normal to the submanifold, i.e.
Recall from Definition 2.14 that the Fermi coordinates in M along are given by
where is the parallel transport along of an orthonormal basis of with . We refer back to Sect. 2 for properties of the Fermi chart.
Denote so that . Extend the frame defined along to by imposing
i.e. by parallel translating in M along the geodesic .
Given an initial orthonormal basis of , first extend it to a frame along by requiring that
The first requirement implies
which together with the second requirement implies the first order ODE
 |
4.1 |
The solution exists and is unique by standard ODE theory. Having defined the frame along the geodesic , we may also extend it to the submanifold by requiring that for every and ,
Similarly to the above, the first requirement implies that for all ,
and from the second requirement we conclude the frame satisfies the first order ODE
along each geodesic in M.
With these concrete vector fields, recall the Fermi coordinates in along adapted to the submanifold M were defined in Definition 2.14 as
and note that .
For every , the map is the exponential chart on its image. It is known that the Christoffel symbols vanish at the centre for such charts, i.e.
Moreover, since for is parallel transport of along , also
noting that .
Denote the components of the second fundamental form with respect to the Fermi coordinates as
Note that the first index represents the normal direction and the latter two represent manifold directions. Then we can write for every ,
| 4.2 |
In addition, (4.1) can be written as
Thus the third derivatives with at least one in are
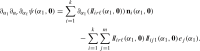 |
4.3 |
Main theorem
In the statement of the theorem,  is the vector of second fundamental form. In the proof exclusively,
is the vector of second fundamental form. In the proof exclusively,  denotes the ij-component of the second fundamental form with respect to the Fermi frame at Fermi coordinates .
denotes the ij-component of the second fundamental form with respect to the Fermi frame at Fermi coordinates .
[Style2 Style3 Style3]Theorem 4.1
Let M be an isometrically embedded submanifold of , and a unit speed geodesic in M such that and . Let be an orthonormal basis of with and assume that  for all . Then for every sufficiently small with it holds that
for all . Then for every sufficiently small with it holds that
Remark 4.2
We point out two special cases:
- If the submanifold has dimension 1 then the condition on the second fundamental form is trivially satisfied as there are no submanifold directions other than that of the curve itself. In this case
and hence
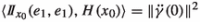 . This is the square curvature of the curve and for , agrees with Theorem 3.10.
. This is the square curvature of the curve and for , agrees with Theorem 3.10. If the submanifold has codimension 1 with a normal vector field on the submanifold, then the orthonormal eigenbasis of
 satisfies the condition
satisfies the condition 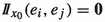 for . Such a basis always exists as
for . Such a basis always exists as 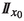 is symmetric and consists of the so-called principal curvature directions. Thus for , , we obtain Theorem 3.16 as a special case.
is symmetric and consists of the so-called principal curvature directions. Thus for , , we obtain Theorem 3.16 as a special case.In general codimension, however, such a basis may not exist for a general submanifold, hence the assumption on the second fundamental form needs to be made and is highly restrictive. If this assumption was dropped, the upper bound for the Wasserstein distance via the proposed transport map would still apply. However, the computation of the lower bound using a projection plane, as done in the proof of Theorem 3.16 and applied again in the proof below, would yield additional lower order terms not agreeing with the upper bound. This is symptomatic of the non-optimality of the transport map up to third order. The more general computation including the off-diagonal terms to show this is straightforward but rather lengthy and is thus omitted. Qualitatively, the issue is that the off-diagonal terms of the second fundamental form introduce a deformation of the supports of the test measures which is not easily remedied and leaves the fully general case open. The deformation arises because the principal curvature directions above the reference point for each leaf of the foliation of the tubular neighbourhood change their vertical alignment as we consider leaves further away from the base submanifold M. On the other hand, the diagonal assumption on the second fundamental form ensures an aligned stacking of principal curvature directions of leaves above , leading to the favourable cylinder-like support of the test measures.
For the interpretation of the special case of the parameters , we refer back to Remark 3.17.
Proof of Theorem 4.1
Expand the Fermi chart up to and including third order as
 |
From the definition of the Fermi chart and (4.2), (4.3), we have the derivatives at the origin on the right-hand side:
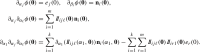 |
With these we obtain:
 |
In the above, the sum of third derivative terms in was split into those that involve at least one power in , for which we have a formula, and those that don’t. The other third derivatives for are not easily written in Fermi coordinates, but will not be needed for our computations. Rearranging the terms, we write in terms of the basis , and apply the assumption  :
:
 |
4.4 |
We will henceforth denote
Let T be the transport map defined in Definition 2.18. With asymptotic notation for the third order terms,
In the expansion of above, from the third derivatives in we only needed to specify those involving , because the transport map T changes only the first coordinate up to . These derivatives were given by (4.3). Then the pointwise transport vector is
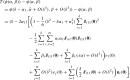 |
4.5 |
Therefore, using the expansion , the pointwise transport distance is
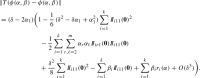 |
4.6 |
Lemma 2.17 expressed the density of the test measure in Fermi coordinates up to second order. Denoting the second order remainder of the density as , the density simplifies to give
 |
4.7 |
where the form of the normalizing factor in the denominator is deduced from the two facts
We deduce the upper bound in the statement of Theorem 4.1 by computing the integral on the right side of the inequality
up to and including third order terms. Using the product of expressions (4.7) and (4.6), this amounts to integrating a quadratic polynomial in . First, as terms with odd power in one of the coordinates vanish, we simplify the integral to
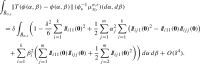 |
We now use the fact that the average integral of the square of any coordinate over a d-dimensional ball of arbitrary radius is
where  denotes the integral normalised by the volume of the ball and using that
denotes the integral normalised by the volume of the ball and using that
This in particular gives
Then
 |
Furthermore, from (4.6) for we deduce
Therefore, we can rewrite in terms of the Euclidean distance:
We now address the lower bound. Denoting
emphasizing that this vector does not depend on , we propose
as the test function for Kantorovich–Rubinstein duality, with the intention of applying Lemma 2.25 to conclude the upper bound is also a lower bound up to . We deduce from (4.5) that
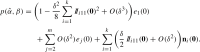 |
4.8 |
Then it can be verified, using the expansions (4.5) and (4.8) to compute the inner product up to and including third order terms, that
by comparison with (4.6).
Finally, we wish to compute the square magnitude of the gradient of the test function in order to verify that its supremum over is for Lemma 2.25 to apply. For this we need to establish the Riemannian metric in Fermi coordinates The first derivatives of the Fermi chart are deduced by differentiating (4.4) as
 |
Then the entries of the inverse metric matrix are computed from these to be
 |
Note that and needed to be expanded up to second order due to the particular role of the first coordinate. For the rest, expansion up to first order is sufficient. The above means the metric matrix has the block structure
In particular, denoting
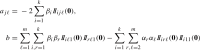 |
and the matrix
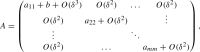 |
having used that for as 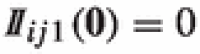 by assumption, we can write
by assumption, we can write
Noting that the second matrix is , the expansion of its inverse is
due to the block structure. Computing
we deduce
 |
by plugging in for and b, and also
We remark that for the expansion of up to the linear term suffices for the computations to follow, while the expansion of up to second order is necessary.
We now compute the expansions of the derivatives of the test function. The first derivatives of the projection vector field in coordinates can be computed from (4.8) as
Then computing the inner products, using (4.4) for the derivatives of the chart,
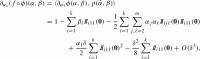 |
and for ,
and for ,
We wish to compute
The individual summands are
 |
All first and second order terms vanish upon summation, hence we may conclude that as required.
Applications
Poisson point processes on manifolds
In applications one may wish to recover curvature information from coarse curvature of a random point cloud represented by a Poisson point process. Such an approach has already been investigated in [18] and [2] for the Ricci curvature and generalised Ricci curvature, respectively.
We first recall the definition of a Poisson point process. Let  be a -finite measure space,
be a -finite measure space, 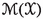 the set of measures on
the set of measures on  and
and 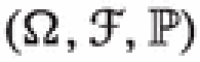 a probability space.
a probability space.
Definition 5.1
A Poisson point process on 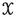 with intensity measure is a random measure
with intensity measure is a random measure  (equivalently
(equivalently  ) such that the following three properties hold:
) such that the following three properties hold:
For all -finite measurable sets
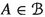 :
:  is a random variable.
is a random variable.For all disjoint, measurable -finite sets
 :
:  and
and  are independent random variables.
are independent random variables.For all :
 is a measure on
is a measure on  .
.
It turns out (see [20, Chapter 6]) that all Poisson point processes with a finite intensity measure take the form of a random empirical measure, i.e.
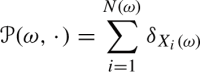 |
where N is a 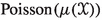 random variable, are independent -distributed random variables on
random variable, are independent -distributed random variables on  and are independent. Denote the random set of points thus generated by
and are independent. Denote the random set of points thus generated by  as
as
Notation 5.2
Let 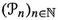 be a sequence of Poisson point processes on the ambient space with uniform intensity measure . Denote by
be a sequence of Poisson point processes on the ambient space with uniform intensity measure . Denote by 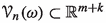 the discrete random set of points generated by
the discrete random set of points generated by 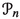 . Let , , sequences of positive reals and for a fixed unit vector . As the discrete counterpart to the test measures , for any point denote the random empirical measures adapted to the submanifold,
. Let , , sequences of positive reals and for a fixed unit vector . As the discrete counterpart to the test measures , for any point denote the random empirical measures adapted to the submanifold,
If then .
Using the following result proved in [18, Corollary 3], it is possible to quantify the approximation of the test measures by the empirical measures in the Wasserstein metric:
Lemma 5.3
For all , it holds that
| 5.1 |
We may then deduce that coarse curvature of point clouds with the empirical measures as test measures has the same limit as coarse extrinsic curvature if the intensity of the point process increases fast enough relative to the parameter . Denote
This leads immediately to a corollary of Theorem 4.1:
Proposition 5.4
Under the assumptions of Theorem 4.1, if the sequences , and satisfy and , then
Proof
By the triangle inequality and (5.1),
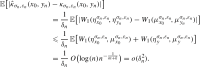 |
At the same time, from Theorem 4.1 we have
which gives the final result upon substitution and taking the limit as .
Retrieving mean curvature
Theorem 4.1 could in practice be exploited in the two settings already alluded to in the introduction, which considered the planar curve case for illustrative purposes. In the scope of generality of Theorem 4.1, we have
In particular, we may distinguish two limit regimes:
- Assuming and ,
This represents a situation where one can obtain a sample from the ambient measure in a tubular neighbourhood of the surface. Decreasing corresponds to localization of the geometric information thus retrieved.
- Assuming and ,
In this case, we have a noisy sample from the surface and obtain convergence of the coarse extrinsic curvature under attenuation of the noise as decreases.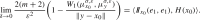
Note that these expressions depend on the vector v with . We can remove this directionality by adding up coarse curvatures in all directions of an orthonormal frame at , thus obtaining an expression involving the mean curvature.
Denote the square norm of the mean curvature vector as
for an arbitrary orthonormal basis of the normal space 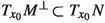 .
.
Corollary 5.5
Let be an orthonormal basis of , and for , let . Assume that 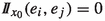 for . Then for all sufficiently small with it holds that
for . Then for all sufficiently small with it holds that
Proof
We express the coarse curvatures using the expansion of Theorem 4.1 and sum up, noting that indexing each direction plays the role of the first coordinate,
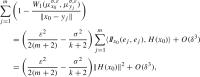 |
completing the proof.
This implies that given the family of coarse curvatures
one can retrieve the square magnitude of the mean curvature vector of the surface at as
In conclusion, we introduced the notion of coarse extrinsic curvature of Riemannian submanifolds embedded isometrically in a Euclidean space and verified that in a scaled limit of the parameters we retrieve meaningful geometric information about the submanifold. As illustrative examples, in the case of a curve we retrieve the inverse squared radius of the osculating circle at a given point, while in the case of a 2-surface we obtain an expression in terms of the second fundamental form and mean curvature. Such coarse extrinsic curvatures can be combined to yield the square magnitude of the mean curvature as a scaled limit.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Xue-Mei Li acknowledges support from Engineering and Physical Sciences Research Council grant EP/V026100/1. Benedikt Petko was supported by the Engineering and Physical Sciences Research Council Centre for Doctoral Training in Mathematics of Random Systems: Analysis, Modelling and Simulation (EP/S023925/1).
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Ambrosio, L., Gigli, N., Savaré, G.: Diffusion, optimal transport and Ricci curvature for metric measure spaces. Eur. Math. Soc. Newsl. 103, 19–28 (2017) [Google Scholar]
- 2.Arnaudon, M., Li, X.M., Petko, B.: Coarse Ricci curvature of weighted Riemannian manifolds (2023). arXiv:2303.04228
- 3.Boissonnat, J.-D., Guibas, L.J., Oudot, S.Y.: Manifold reconstruction in arbitrary dimensions using witness complexes. Discrete Comput. Geom. 42(1), 37–70 (2009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bonciocat, A.-I., Sturm, K.-T.: Mass transportation and rough curvature bounds for discrete spaces. J. Funct. Anal. 256(9), 2944–2966 (2009) [Google Scholar]
- 5.Chazal, F., Cohen-Steiner, D., Lieutier, A., Mérigot, Q., Thibert, B.: Inference of curvature using tubular neighborhoods. In: Najman, L., Romon, P. (eds.) Modern Approaches to Discrete Curvature. Lecture Notes in Mathematics, vol. 2184, pp. 133–158. Springer, Cham (2017) [Google Scholar]
- 6.Chazal, F., Cohen-Steiner, D., Mérigot, Q.: Boundary measures for geometric inference. Found. Comput. Math. 10(2), 221–240 (2010) [Google Scholar]
- 7.Eilat, M., Klartag, B.: Rigidity of Riemannian embeddings of discrete metric spaces. Invent. Math. 226(1), 349–391 (2021) [Google Scholar]
- 8.Erbar, M., Maas, J.: Ricci curvature of finite Markov chains via convexity of the entropy. Arch. Ration. Mech. Anal. 206(3), 997–1038 (2012) [Google Scholar]
- 9.Faigenbaum-Golovin, S., Levin, D.: Manifold reconstruction and denoising from scattered data in high dimension. J. Comput. Appl. Math. 421, Art. No. 114818 (2023)
- 10.Federer, H.: Curvature measures. Trans. Amer. Math. Soc. 93, 418–491 (1959) [Google Scholar]
- 11.Fefferman, C., Ivanov, S., Kurylev, Y., Lassas, M., Narayanan, H.: Reconstruction and interpolation of manifolds. I: the geometric Whitney problem. Found. Comput. Math. 20(5), 1035–1133 (2020)
- 12.Fefferman, C., Ivanov, S., Lassas, M., Lu, J., Narayanan, H.: Reconstruction and interpolation of manifolds II: inverse problems for Riemannian manifolds with partial distance data (2021). arXiv:2111.14528
- 13.Fefferman, C., Ivanov, S., Lassas, M., Narayanan, H.: Fitting a manifold of large reach to noisy data (2022). arXiv:1910.05084
- 14.Genovese, C.R., Perone-Pacifico, M., Verdinelli, I., Wasserman, L.: Manifold estimation and singular deconvolution under Hausdorff loss. Ann. Stat. 40(2), 941–963 (2012) [Google Scholar]
- 15.Gold, D., Rosenberg, S.: Discretized gradient flow for manifold learning. Int. J. Math. 35(11), Art. No. 2450040 (2024)
- 16.Gray, A.: Tubes. 2nd edn. Progress in Mathematics, vol. 221. Birkhäuser, Basel (2004)
- 17.Gu, X., Yau, S.-T.: Optimal transport for generative models. ICCM Not. 10(1), 1–27 (2022) [Google Scholar]
- 18.van der Hoorn, P., Lippner, G., Trugenberger, C., Krioukov, D.: Ollivier curvature of random geometric graphs converges to Ricci curvature of their Riemannian manifolds. Discrete Comput. Geom. 70(3), 671–712 (2023) [Google Scholar]
- 19.Jost, J.: Riemannian Geometry and Geometric Analysis, 7th edn. Universitext. Springer, Cham (2017)
- 20.Last, G., Penrose, M.: Lectures on the Poisson Process. Institute of Mathematical Statistics Textbooks, vol. 7. Cambridge University Press, Cambridge (2018)
- 21.Lee, J.M.: Introduction to Smooth Manifolds. Graduate Texts in Mathematics, vol. 218. 2nd edn. Springer, New York (2013)
- 22.Lott, J.: Optimal transport and Ricci curvature for metric-measure spaces. In: Cheeger, J., Grove, K. (eds.) Surveys in Differential Geometry. Vol. XI. Surv. Differ. Geom., vol. 11, pp. 229–257. International Press, Somerville (2007)
- 23.Lott, J., Villani, C.: Ricci curvature for metric-measure spaces via optimal transport. Ann. Math. 169(3), 903–991 (2009) [Google Scholar]
- 24.Meyer, W.: Toponogov’s theorem and applications (2004). https://www2.math.upenn.edu/~wziller/math660/TopogonovTheorem-Myer.pdf
- 25.Ollivier, Y.: Ricci curvature of Markov chains on metric spaces. J. Funct. Anal. 256(3), 810–864 (2009) [Google Scholar]
- 26.Ollivier, Y.: A visual introduction to Riemannian curvatures and some discrete generalizations. In: Dafni, G., et al. (eds.) Analysis and Geometry of Metric Measure Spaces. CRM Proceedings and Lecture Notes, vol. 56, pp. 197–220. American Mathematical Society, Providence (2013) [Google Scholar]
- 27.Puchkin, N., Spokoiny, V., Stepanov, E., Trevisan, D.: Reconstruction of manifold embeddings into Euclidean spaces via intrinsic distances. ESAIM Control Optim. Calc. Var. 30, 3 (2024)
- 28.von Renesse, M.-K., Sturm, K.-T.: Transport inequalities, gradient estimates, entropy, and Ricci curvature. Commun. Pure Appl. Math. 58(7), 923–940 (2005) [Google Scholar]
- 29.Rout, L., Korotin, A., Burnaev, E.: Generative modeling with optimal transport maps (2022). arXiv:2110.02999
- 30.Sturm, K.-T.: On the geometry of metric measure spaces. II. Acta Math. 196(1), 133–177 (2006) [Google Scholar]
- 31.Sturm, K.-T.: Remarks about synthetic upper Ricci bounds for metric measure spaces. Tohoku Math. J. 73(4), 539–564 (2021) [Google Scholar]
- 32.Weyl, H.: On the volume of tubes. Amer. J. Math. 61(2), 461–472 (1939) [Google Scholar]






