High-purity and stable single-photon emission in bilayer WSe₂ via phonon-assisted excitation

Abstract

The excitation scheme is essential for single-photon sources, as it governs exciton preparation, decay dynamics, and the spectral diffusion of emitted photons. While phonon-assisted excitation has shown promise in other quantum emitter platforms, its proper implementation and systematic comparison with alternative excitation schemes have not yet been demonstrated in transition metal dichalcogenide (TMD) quantum emitters. Here, we investigate the impact of various optical excitation strategies on the single-photon emission properties of bilayer WSe₂ quantum emitters. Based on our theoretical predictions for the exciton preparation fidelity, we compare the excitation via the longitudinal acoustic and breathing phonon modes to conventional above-band and near-resonance excitations. Under acoustic phonon-assisted excitation, we achieve narrow single-photon emission with a reduced spectral diffusion of 0.0129 nm, a 1.8-fold improvement over above-band excitation. Additionally, excitation through breathing-phonon mode yields a high purity of 0.947 ± 0.079  and reduces the decay time by over an order of magnitude, reaching (1.33 ± 0.04) ns. Our comprehensive study demonstrates the crucial role of phonon-assisted excitation in optimizing the performance of WSe₂-based quantum emitters, providing valuable insights for the development of single-photon sources for quantum photonics applications.

Phonon-assisted excitation has shown promise in quantum emitter platforms to control the emission properties, but it remains unexplored for transition metal dichalcogenide quantum emitters. This study reveals that phonon-assisted excitation significantly enhances the single-photon emission properties of bilayer WSe₂ quantum emitters, improving spectral diffusion and emission purity.

Introduction

A key component in optical quantum information technologies is an on-demand source of single photons encoding the quantum information¹. The fundamental requirement for a usable source is single-photon emission with near-unity purity, efficiency, and indistinguishability. Spontaneous parametric down-conversion² in a nonlinear material is a well-established method to generate highly indistinguishable photons³. However, its probabilistic nature limits the efficiency to merely a few percent. On the other hand, a two-level system⁴ allows for the deterministic emission of single photons through the spontaneous emission process. Recently, highly efficient emission of indistinguishable photons has been achieved from semiconductor quantum dots (QDs)^5–7 placed in carefully engineered microstructures. Nevertheless, epitaxial growth of high-quality QD material requires advanced and costly epitaxy tools. As an alternative, quantum emitters (QEs) in two-dimensional (2D) transition metal dichalcogenides (TMDs) materials have recently emerged as an attractive platform for deterministic single-photon emission^8–13. This platform provides several advantages, including accessible cost-effective materials, deterministic fabrication methods^14–16, and ease of integration with photonic¹⁷ and plasmonic systems^18,19. Additionally, the reduced dimensionality of TMDs facilitates efficient light extraction²⁰. Consequently, single-photon emission over a broad spectrum from visible²¹ to telecommunication ranges²² has been demonstrated from mono- and few-layer TMDs via strain- and defect engineering^15,23–26.

Despite significant efforts in developing high-quality quantum emitters in TMDs, the efficient generation of indistinguishable single photons from these platforms remains an open fundamental challenge. Spectral diffusion and phonon-induced dephasing are the primary obstacles that degrade the figures of merit for single-photon sources. Strategies to mitigate these effects include integrating emitters into high-Q resonant cavities, stabilizing the charge environment, and implementing advanced optical excitation schemes. Recently, a strategy of coupling such quantum emitters to a resonant open cavity has been successfully demonstrated, exhibiting state-of-the-art efficiency as high as 65% to the first lens, but limited indistinguishability of around 2%²⁷. The same strategy was later employed to engineer the coherence of the emitted photons by selectively boosting the emission of the zero-phonon line²⁸. Additionally, the spectral diffusion of the emitted photons has been improved via hBN encapsulation^15,29, substrate choice engineering³⁰ as well as with the implementation of electrical contacts³¹. The choice of excitation scheme also significantly impacts the figures of merit for single-photon sources³². While continuous-wave (CW) resonant and non-resonant excitations of TMD quantum emitters have been reported^33,34, on-demand generation of single-photon generation requires pulsed excitation with short laser pulses.

Above-band excitation, though widely used, introduces photo-induced charge carriers and complex exciton dynamics through higher-order states that limit photon indistinguishability³⁵. In contrast, resonant excitation achieves near-unity indistinguishability³⁶, but it is hindered by the reduced collection efficiency (maximum 50%) inherent to the cross-polarization setup. Pulsed phonon-assisted excitation offers a promising alternative, balancing efficient population inversion and high photon indistinguishability, previously demonstrated on semiconductor QDs^37,38. This method leverages phonon scattering to mediate rapid relaxation to the exciton state, enabling efficient photon collection above 50% while rejecting laser background. The feasibility of phonon-assisted excitation in TMD quantum emitters has been theoretically predicted³⁹, yet its experimental implementation remains unexplored.

In this work, we systematically implement and compare three pulsed optical excitation schemes, i.e., above-band, near-resonant, and phonon-assisted, to investigate their impacts on the single-photon properties of bilayer WSe₂ quantum emitters. We demonstrate high single-photon purity under pulsed excitation, reaching 0.921  ±  0.015 and 0.943  ±  0.018 for above-band and near-resonant excitation, respectively. Near-resonant excitation also yields shorter and simpler decay dynamics, with a decay constant of (12.62  ±  1.18) ns.

To explore phonon-assisted excitation, we first develop a theoretical model that describes a quantum emitter coupled to the phonon environment specific to bilayer WSe₂. Here, we consider both longitudinal acoustic (LA) phonon modes, which are present in both mono- and bilayer WSe₂, and interlayer shear modes (SMs) and breathing mode (BM), which are unique to bilayer structures and exhibit energy dependence on the interlayer distance. Due to the inherent strong coupling to LA phonons, our theoretical calculations predict an efficient exciton population above 80% under LA phonon-assisted excitation at a detuning of  −0.4 nm. We also predict a sizable population at a larger detuning of  −2.7 nm, dependent on the strength of the exciton-BM coupling. Guided by our theoretical predictions, we experimentally demonstrate LA phonon-assisted excitation in WSe₂, achieving a two-fold reduction in spectral diffusion of the emission line compared to above-band excitation. Finally, we perform phonon-assisted excitation through the interlayer breathing mode. Owing to the larger detuning between the laser and the emitter’s energy, we achieve full residual laser rejection and carry out single-photon characterization. We obtain a purity of 0.947  ±  0.079 and a much faster decay rate (τ₁ = (1.33  ±  0.04) ns) in contrast to above-band and near-resonance excitations.

Our work contributes to the fundamental understanding of WSe₂ quantum emitter platform and to its application in future quantum photonics.

Results

System under study: mono- and bilayer WSe₂ quantum emitters

We begin our study by preparing highly-polarized single-photon emitters out of WSe₂ flakes through a combination of deterministic strain and defect engineering as illustrated in Fig. 1(a). Based on the process presented in our previous work in Ref. ⁴⁰, mechanically exfoliated mono- and bilayer WSe₂ flakes were transferred onto a thermally oxidized silicon substrate (${\mathrm{d}}_{{\mathrm{SiO}}_{\mathrm{2}}}$ = 110 nm) featuring an array of star-shaped nanostructures (d_pillars = 150 nm). The long and sharp tips of the three-pointed star geometries induce strain on the material, generating spatially isolated nanowrinkles. Moreover, this type of geometry can host multiple nanowrinkles per site, increasing the number of available quantum emitters. The localized one-dimensional strain alters the energy bands leading to the efficient migration of free charge carriers to the area¹³, while the orientation of the strain dictates the directionality of the linear polarization. Subsequently, deterministically introducing defects to the sample via e-beam irradiation has previously been shown to increase the quantum emitter yield in this platform^15,40. The “Methods” section provides further details on the fabrication process. To investigate the optical properties of the fabricated samples, we mounted them in an optical cryostat operating at 4 K. The cryostat is equipped with nanopositioners and a low-temperature objective lens (NA = 0.81, 60×). Initially, a low-temperature photoluminescence (PL) image of the sample was acquired under 470 nm light-emitting diode (LED) excitation. A 700 nm long-pass optical filter was employed to eliminate reflected signals from the excitation. As depicted in the inset of Fig. 1(b), the PL image reveals bright spots originating from the nanowrinkles in mono- and bilayer WSe₂, which are distinctly contrasted against the emission signal from the planar, unstrained flakes.

Fig. 1. Quantum emitters in mono- and bilayer WSe₂.

a Sketch of mono- (1L) and bilayer (2L) flake deposited on top of star-shaped nanostructures leading to the formation of nanowrinkles nearby their vertex. The nanowrinkles host the quantum emitters. Inset: atomic force microscopy (AFM) image of a star-shaped nanostructure covered by a bilayer flake with the visible presence of a nanowrinkle originating from the top vertex. b μ PL spectra under 532 nm pulsed laser excitation of the two bright spots in 1L WSe₂ (gray) and 2L WSe₂ (red) encircled in the inset image, integrated over 1 s. They show typical emission imprints of the two different thicknesses' flakes. Inset: color-coded PL image of the sample taken at T = 4 K under CW LED excitation at 470 nm. The white dashed lines highlight the contours of the 1L and 2L flakes. The full widefield PL image of the sample is reported in Fig. S1. c Second-order correlation measurement of emitter Q1 from the bilayer spot (red dashed circle in inset in (b)). The fit reveals a g⁽²⁾(0) value of 0.098 ± 0.045.

For a quantitative comparison between the mono and bilayer emitters, we measured the PL spectra of the individual bright spot regions of each under a 532 nm pulsed excitation (pulse duration 150 fs, repetition rate 80 MHz) using a spectrometer (f = 550 mm, 1200 grooves/mm grating). Figure 1b shows the emission spectra obtained from two exemplary mono- and bilayer regions, circled with red and white lines in the inset, respectively, hosting strain-engineered quantum emitters (refer to Supplementary Fig. S1 for the full raw PL image in grayscale). The monolayer emission spectrum exhibits numerous intense and narrow emission lines spreading across a broad spectral range of 720–810 nm on top of a broad, weak emission background from the planar monolayer. The observed narrow lines are attributed to single-photon emission from several different emitters^8,9,12, while the broad background is ascribed to the emission from the planar monolayer region around the emitter, present in the measurement due to the diffraction-limited collection spot. On the other hand, the bilayer quantum emitter presents a single isolated narrow emission line (with a full-width half-maximum (FWHM) of 0.14 nm) without any noticeable background, due to the indirect nature of the bandgap in pristine bilayer⁴¹. Surprisingly, despite the bilayer WSe₂ host being an indirect bandgap, the intensities of the emission lines are comparable to those observed in the monolayer under identical experimental conditions (more exemplary spectra in Fig. S2 of the Supplementary Information). These considerations make WSe₂ bilayer a preferable platform over monolayer for our scopes. We will focus on bilayer QEs in the following.

We measured the single-photon purity of bilayer WSe₂ emitters by measuring the second-order correlation of a representative emission line (Q1) under CW excitation at 470 nm. A 750 nm long-pass filter helps suppress the emitted light from the laser light. The measurement is performed with a Hanbury Brown-Twiss (HBT) setup, which includes a 50:50 fiber beam splitter and a pair of superconducting nanowire single-photon detectors (SNSPDs). In Fig. 1c, we show the obtained correlation histogram as a function of delay, which exhibits a strong antibunching behavior. The suppressed coincidence counts at zero time delay establish the clear single-photon nature of the emission with extracted single-photon purity of g⁽²⁾(0) = 0.098 ± 0.045.

Above-band vs. near-resonant optical excitation

To systematically compare the effect of the above-band and the near-resonant excitation schemes on the bilayer quantum emitters, we conducted an investigation of the optical properties of two emitters (Q1 and Q2). Our study includes high-resolution emission spectra, lifetime, and purity. We analyze the differences to find the most effective approach for optimal performance.

Above-band optical excitation

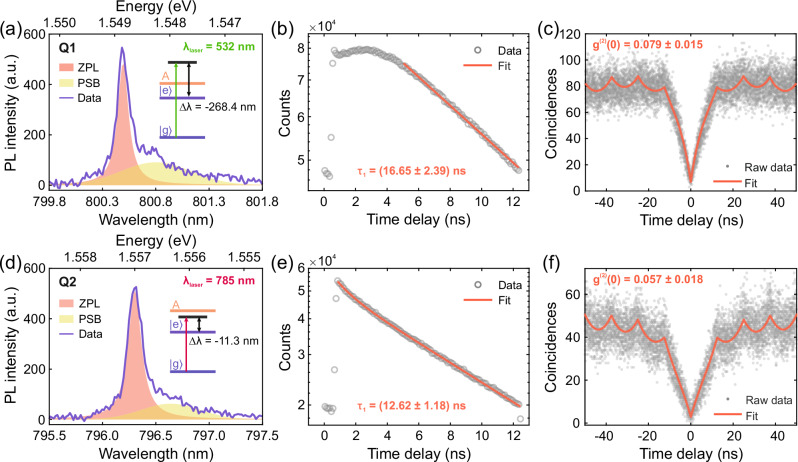
Here, we used a 532 nm pulsed laser excitation. Figure 2(a) shows the μ PL spectrum obtained from Q1 at 4 K (see Fig. S5 of the Supplementary Information for the temperature-dependent series up to 40 K), revealing a narrow zero-phonon line (ZPL) at 800.5 nm and a visible broad phonon side-band (PSB). By fitting the ZPL and to the PSB with a Lorentzian and a Gaussian function, respectively, we qualitatively extract a width of 0.108 nm (0.209 meV) for the ZPL and 0.782 nm (1.513 meV) for the PSB, and a Debye-Waller factor DWF = I_ZPL/(I_ZPL + I_PSB) of 0.551 (Fig. 2(a)). This suggests a strong exciton-phonon coupling, which is in good agreement with previous reports^39,42,43. The ZPL is orders of magnitude broader than its Fourier-limited value of 57.0 × 10⁻⁶ nm (0.11 μeV), considering the decay time of 16.65 ns (see next paragraph). This suggests that the pure dephasing and charge noise contributions to the total linewidth is substantial, consequently resulting in lower indistinguishability³¹. Additionally, we observe that the width of the emission line gets broader when increasing the laser excitation power, almost doubling its value at the saturation level, as shown in Fig. S3 of the Supplementary Information.

Fig. 2. Above-band and near-resonant excitations.

Emission spectra of emitter Q1 under pulsed above-band excitation at 532 nm (a) and emitter Q2 under near-resonant pulsed excitation at 785 nm (d). The graphs present fittings to the raw data (solid purple line) with a sum of a Lorentzian (red area) and a Gaussian (yellow area) accounting for the contribution from the ZPL and the PSB, respectively. The inset schemes on the right side show a simplified band diagram of the emitters as a two-level system ($\mid g\left(\right.⟩$ and $\mid e\left(\right.⟩$) with the respective pumping energy, while A represents the energy level of the planar WSe₂ A-exciton. b Semi-logarithmic plot of the time-resolved PL measurement from Q1 (grey circles) with relative single decay exponential fitting function (red line) with a constant τ₁ = (16.65 ± 2.39) ns. c Second-order intensity correlation measurement (g⁽²⁾(τ)) of Q1 under above-band pulsed excitation. From the double exponential fit (red line), we extract an antibunching value of g⁽²⁾(0) = 0.079 ± 0.015. e Semi-logarithmic plot of the time-resolved PL measurement from Q2 (grey circles) with relative double decay exponential fitting function (red line). The two extracted time constants are τ₁ = (12.62 ± 1.18) ns and τ₂ = (1.14 ± 0.21) ns, accounting for 96.5% and 3.5% of the fit curve, respectively. f Second-order intensity correlation measurement of Q2 under near-resonant excitation. The g⁽²⁾(0) value extracted is 0.057 ± 0.018. The measurements in b and e are integrated over 3 minutes, while those in c and f over 8 hours.

For the characterization of the dynamic behavior of an individual quantum emitter under above-band excitation, we carried out a time-resolved PL (TRPL) measurement. As shown in Fig. 2(b), we observe a relatively fast decay at shorter time delays (≤0.5 ns), after which the curve rises again and reaches its maximum at around 3 ns. We attribute this to trapped states involved in the population of the excited state^44,45. At longer delay times, the decay is fitted with a single exponential (red line), revealing a decay time of τ₁ = (16.65 ± 2.39) ns (uncertainty given as standard error). Such value is in good agreement with previous observations on TMD single-photon sources^40,46,47. The second-order correlation measurement under pulsed above-band excitation, shown in Fig. 2(c), reveals a g⁽²⁾(0) of 0.079 ± 0.015. The extracted value is consistent with the one in Fig. 1(c) under CW operation, indicating a good single-photon purity also under triggered excitation.

Near-resonant optical excitation

To perform near-resonant excitation, the wavelength of the pulsed laser was varied from 730 nm to 790 nm, corresponding to a detuning Δλ = λ_laser − λ_X from  −66.3 nm to  −6.3 nm with respect to the quantum emitter (λ_X = 796.3 nm), in steps of 10 nm. The energy corresponding to this pumping wavelength is below the energy of the A-exciton of planar WSe₂⁴⁸, but above the excitonic transition energy considered ($\mid g\left(\right.⟩\to \mid e\left(\right.⟩$) (cf. the band diagram scheme in the inset of Fig. 2d), thus, we refer to such a range of detuning as near-resonant. We observed that the quantum emitter could be excited over a large range of detunings (see Supplementary Note 4 for more details). This behavior has been previously reported in WSe₂^9,49 based on photoluminescence excitation spectroscopy measurement. In our case, the maximum emission intensity occurred when the laser was detuned Δλ = −11.3 nm (9.1 meV) from the emission line, with results reported in Fig. 2d–f. At this detuning, the zero-phonon line and phonon sideband linewidths corresponding to emitter Q2 are found to be 0.124 nm and 0.760 nm, respectively. From this we compute the Debye-Waller factor as DWF = 0.538. (Fig. 2d). Additionally, under near-resonant excitation, we achieved a g⁽²⁾(0) value of 0.057 ± 0.018 (Fig. 2f). These results are similar to those obtained under the above-band excitation and suggest that the emission spectrum and single-photon purity of these particular quantum emitters may not be heavily dependent on the excitation scheme.

However, an evident dissimilarity between the two excitation schemes arises from the time-resolved measurement. As shown in Fig. 2e, the lifetime histogram obtained under near-resonant excitation exhibits a predominant single exponential decay contribution with a time constant of τ₁ = (12.62 ± 1.18) ns. This particular contrast in decay dynamics under near-resonant excitation as compared to the above-band measurement presented in Fig. 2b can be attributed to the quantum emitter being optically excited near its bandgap. These experimental results suggest that directly populating a bilayer quantum emitter with a proper excitation scheme is essential to avoid unnecessary internal relaxation processes and the creation of additional unwanted photo-induced charge carriers, resulting in simpler dynamics and reduced lifetime.

Phonon-assisted excitation

Theory: signatures of exciton-phonon coupling in the population inversion of bilayer WSe₂ QEs

We now consider a laser excitation closer to resonance mediated by phonon-assisted relaxation, with a detuning of only a few nanometers or sub-nanometer. To support our experimental results, we first develop a theory of phonon-coupled QEs in bilayer WSe₂ and calculate the population inversion under pulsed laser excitation. Earlier experimental and theoretical reports have shown evidence of strong exciton-phonon coupling in WSe₂. While low-energy phonon coupling in monolayer WSe₂ is mainly due to 2D LA phonons^28,39,49, bilayer structures have a richer phonon landscape including interlayer vibrational modes^50,51.

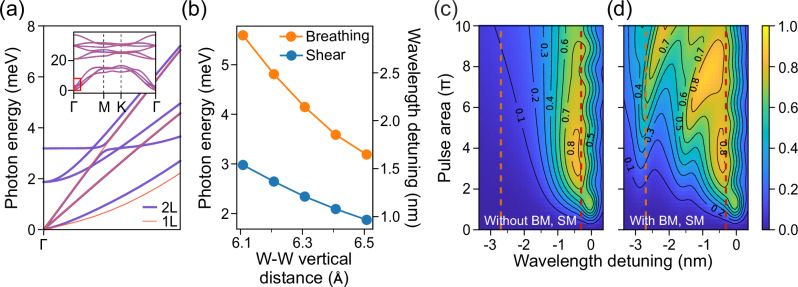
First, the phonon bandstructure of pristine mono- and bilayer WSe₂ is calculated with Density Functional Theory (DFT) and shown in Fig. 3a, see the “Methods” section for the details. In the low-energy sector around Γ, monolayer WSe₂ supports three acoustic phonon branches with vanishing energy at Γ, corresponding to out-of-plane, transverse, and longitudinal modes respectively. In contrast, bilayer WSe₂ has two additional shear modes (SMs), involving lateral sliding between layers, and one breathing mode (BM), characterized by the out-of-plane compression and expansion of layers. Their energies at the Γ point of the Brillouin zone are 1.9 meV and 3.2 meV, respectively. Both SMs and the BM are inherently absent in monolayers.

Fig. 3. DFT-based phonon signatures on the population inversion for mono- and bilayer WSe₂.

a Calculated phonon dispersion in mono- and bilayer WSe₂ around the Γ point. For the bilayer, the equilibrium value d_W-W = 6.5 Å is used for the vertical distance between W atoms in different layers. The inset shows the phonon dispersion across the full Brillouin zone. b Energy of interlayer SMs and BM at Γ as a function of the interlayer W-W distance d_W-W. c Calculated population inversion in the presence of LA phonon coupling, as a function of wavelength detuning λ_laser − λ_X from the exciton and pulse area Θ. The laser pulse has a FWHM of 0.30 nm (t_p = 2.65 ps in our notation). d Same as in (c), including also the coupling to SMs and BM. Here, we use d_W-W = 6.1 Å for the interlayer W-W distance, and the dimensionless BM coupling weight is set to ξ_BM = 5 (see the “Methods” section). Dashed orange and red lines are placed at detunings of  −2.7 nm and  −0.3 nm, respectively.

Additionally, SMs and BM are sensitive to the interlayer distance, which is likely modified in the strain-engineered nanowrinkle. As shown in Fig. 3b, the energy of SM and BM phonon modes increases to 3.0 meV and 5.6 meV, respectively, when the distance d_W-W between W atomic planes is compressed from the equilibrium value of 6.5 Å to 6.1 Å. This indicates that the optical signature of SM (BM) phonons moves from a detuning of  −0.97 nm (−1.65 nm) with respect to the emission line to  −1.54 nm (−2.89 nm) under a small relative compression of 6% in the out-of-plane direction. Larger compression shifts the SM and BM further towards higher energy.

Next, we calculate the population inversion under pulsed laser excitation for emitter Q1 and for wavelength detuning up to Δλ = −3.4 nm. We calculate the excited state population after a Gaussian electric field pulse $\mathrm{\Omega }\left(t\right)=\frac{\mathrm{\Theta }}{\sqrt{\pi }{t}_p}{e}^{-{\left(t/t_p\right)}^2}$, with $\mathrm{\Theta }={\int }_{-\infty }^{+\infty }\mathrm{d}t\mathrm{\Omega }\left(t\right)$ the pulse area. The model includes the influence of the phonon environment with a numerically exact process tensor formalism (see the “Methods” section). The calculation includes a suitable spectral broadening to reproduce the experimental spectrum. In Fig. 3c, we consider only the coupling to LA phonons, which occurs in both mono- and bilayer structures. A sizeable population  >0.8 is observed at detuning Δλ ≈ −0.4 nm and for a moderate pulse area of 3–5π (for the population inversion results at different laser parameters, see Supplementary Note 7). The signal decreases monotonically for larger detuning. We interpret these results as a signature of LA phonon-assisted excitation, where a laser pulse with a shorter wavelength than the exciton is able to populate the excited state by exciting additional phonon modes. The optimal detuning corresponds indeed to the maximum of the LA phonon spectral density. Closer to resonance (∣Δλ∣ < 0.3 nm), we observe the signature of Rabi oscillations as a function of the pulse area. We interpret these as resonant excitation of the emitter with the tail of the laser pulse, whose spectral width is FWHM = 0.30 nm. For narrower laser pulses, oscillations are confined to the strictly resonant condition Δλ ≈ 0 (see Supplementary Note 7).

The inclusion of SM and BM phonon coupling changes the scenario drastically. As seen in Fig. 3d, the exciton population after the laser pulse evolves non-monotonically as a function of the wavelength detuning. For Θ < 5π, a first peak is observed at Δλ ≈ −2.8 nm and corresponds to phonon-assisted pumping via the BM. A second peak occurs around Δλ≈−1.5 nm and is caused by coupling to SM phonons. Finally, LA phonon-assisted excitation emerges at a shorter detuning. For larger pulse areas, the signature of BM and SM phonons shifts closer to the exciton and tends to merge with the LA band.

It should be noted that the spectral density of SM and BM coupling has been calculated under the assumption that the emitter-phonon coupling mechanism is the same as for LA modes, however, the contribution of the BM coupling in Fig. 3d has been magnified by a factor ξ_BM = 5 to obtain qualitative agreement with the subsequent experiment. Optical signatures of BM phonons in the population inversion are also visible at ξ_BM = 1, as reported in Supplementary Note 7 and Figure S8. A detailed study of the BM and SM coupling mechanism deserves further investigation in a separate work.

Longitudinal acoustic modes and spectral diffusion

To experimentally demonstrate phonon-assisted excitation on bilayer WSe₂ quantum emitters, first, we identified a single isolated emission line (λ = 808.2 nm) under the above-band excitation of a 532 nm pulsed laser. Then we performed a photoluminescence excitation (PLE) measurement with smaller laser detuning to the emission line scanning a constant power pulsed laser, ranging from Δλ = −2.2 nm to Δλ = +0.5 nm (Fig. 4(a)). The obtained coarse PLE measurement reveals two maxima. Fitting the data points, the two maxima appear to be centered at Δλ = −1.7 nm and Δλ = −0.3 nm respectively, in qualitative agreement with the theoretical prediction for SM and LA modes. The signal goes down to negligibly small values at positive detuning, after crossing the ZPL. The power-series measurement in Fig. 4b at Δλ = −1.4 nm detuning shows a saturation behavior of the peak emission intensity, which could be interpreted as a signature of exciton preparation through incoherent processes^37,52. While carrying out the PLE measurement close to the resonance condition, the emission line under LA phonon-assisted excitation clearly appears to be more stable and narrower in contrast to the emitter excited under the above-band excitation.

Fig. 4. Longitudinal acoustic phonon-assisted excitation and spectral diffusion.

a Coarse PLE spectrum of the quantum emitter, showing two absorption maxima centered at detuning Δλ = −1.7 nm and Δλ = −0.3 nm, respectively. b Power dependence of the peak intensity evaluated at a detuning Δλ = −1.4 nm. High-resolution PL spectra at time 1 s (c) and (d) and their time evolution (e) and (f) for above-band excitation and phonon-assisted excitation, respectively. g, h show the statistical analysis of the central wavelength of the ZPL as extracted from the fitting of each line in the map. The red curves are Gaussian fittings of the obtained distributions. The mean value and the standard deviation in (g) are μ_ZPL = 800.49 nm and σ_ZPL = 0.0232 nm, respectively. At the same time, their values for (h) are μ_ZPL = 800.62 nm and σ_ZPL = 0.0129 nm.

To quantitatively evaluate and compare the line broadening and the spectral diffusion under different excitation schemes, we performed μ PL time evolution measurements from the same emitter Q1 under phonon-assisted and above-band excitation. For the phonon-assisted measurements, the excitation laser detuning was fixed at Δλ = −0.3 nm. On the other hand, for the above-band excitation measurement, a 532 nm pulsed laser (Δλ = −268.4 nm) was used to excite the emitter Q1, as in Fig. 2a–c. The emission line excited via the acoustic phonons (Fig. 4c) exhibits a FWHM of the fitted μ PL spectrum of 0.074 nm (151 μeV). This value is close to the nominal resolution of our spectrometer (0.05 nm), which might, thus, not allow us to resolve the true linewidth of the emission. Anyhow, the obtained value is 1.5 times narrower than the FWHM of 0.108 nm from the spectrum under the below-saturation above-band excitation (Fig. 4d).

The broadening of the peak’s linewidth provides an indication of energy shift of the quantum emitter energy in timescales faster than the experimental acquisition time, which is one of the main impediments to indistinguishable photon generation. On the other hand, spectral diffusion of the order of 1Hz can be traced over the measurement timescale. In this regard, we then recorded the emission signal as a function of time under both excitation schemes, as shown in Fig. 4e, f. The spectral diffusion at a timescale slower than the experimental acquisition time is also drastically reduced under acoustic phonon-assisted excitation. In both maps, each horizontal frame corresponds to 1 second of measurement, during which the PL emission is integrated over 0.7 s. By fitting each spectrum with a Lorentzian function, we can extract the resonance of the ZPL as a function of time. The histogram plots in Fig. 4g, h show the number of occurrences in the wavelength range of emission, grouped up in 0.005 nm-broad bins. Fitting the histograms with a Gaussian function allows us to extract a mean value of μ_ZPL = 800.49 nm and a standard deviation of σ_ZPL = 0.0232 nm for the distribution of the peaks’ central position under above-band excitation, with μ_ZPL  =  800.62 nm and σ_ZPL = 0.0129 nm under acoustic phonon-assisted excitation.

This suggests that a more stable charge environment is achieved under phonon-assisted excitation thanks to the reduced creation of additional photo-induced charges compared to above-band excitation, resulting in lower spectral diffusion. Both the inhomogeneous broadening of the ZPL and its spectral diffusion, here mitigated, are critical obstacles to single-photon indistinguishability, which requires a lifetime-limited linewidth, identical emission energy, and well-defined polarization. Improved reduction of inhomogeneous broadening and spectral wandering of the emission peak could be achieved by combining the current pulsed excitation scheme with a more beneficial substrate material choice³⁰.

Despite the efficacy of excitation via acoustic phonons, the laser leakage into the ZPL of the emission line under such a small detuning deteriorates the single-photon purity. Filtering out the laser leakage is a practical challenge that arises when the detuning is in the order of the sub-nanometer. As a consequence, in the following, we aim to perform excitation through BM absorption, as suggested from Fig. 3d. As mentioned before, the BM mode is a unique feature of bilayer structures, and its appearance at higher spectral detuning from the ZPL compared to the LA modes makes it more practically feasible to perform efficient excitation of bilayer QEs for high-purity single-photon generation with uncomplicated spectral filtering to suppress the pump laser.

Breathing mode and single-photon characterization

To exploit the BM phonon for the exciton preparation of bilayer quantum emitters, we tuned the laser at wavelength λ_laser = 805.5 nm, which corresponds to a detuning of Δλ ≈ 2.7 nm (5.1 meV) from the Q3 line, centered at 808.2 nm (Fig. 5a). By coarsely scanning the laser wavelength, we experimentally observed that the emission intensity is rather sensitive to laser spectral shift, completely disappearing for detunings deviating  ±0.2 nm from the optimal condition of Δλ = −2.7 nm. It is worth mentioning that such larger laser detuning (−2.7 nm) of the BM excitation compared to the excitation via LA phonons makes spectral filtering of the laser light from the single-photon emission more straightforward. The extracted FWHM with a Lorentzian fit is 0.174 nm (0.33 meV), approximately 40% larger compared to Q1 and Q2 under above-band and near-resonant excitation. Note that the Debye-Waller factor under this excitation has increased to 0.712. The broader ZPL compared to those in Fig. 2a, d under above-band and near-resonant excitations, respectively, can be attributed to the fact that pulsed excitation at a detuning of  −2.7 nm (5.1 meV) requires high excitation power, potentially resulting in additional line broadening. The second-order autocorrelation measurement (see Fig. 5b) shows a g⁽²⁾(0) of 0.053 ± 0.079, establishing highly pure single-photon emission similar to those under above-band and near-resonant excitations. This testifies to the success of using the BM to perform excitation of the bilayer quantum emitter and obtain high single photon purity thanks to easier spectral filtering.

Fig. 5. Phonon-assisted excitation.

a PL spectrum of emitter Q3 under pulsed excitation at detuning of  −2.7 nm from the quantum emitter. The fit function on the raw data (purple) is a sum of a Lorentzian (red area) and a Gaussian (yellow area) accounting for the contribution from the ZPL and the PSB, respectively. The inset shows a simplified band diagram of an emitter as a two-level system highlighting the pumping energy detuning. b Second-order autocorrelation measurement of Q3. From the double exponential fit (red line), we extract an antibunching value of g⁽²⁾(0) = 0.053 ± 0.079. c Time-resolved PL measurement from Q3 in a semilogarithmic plot with relative double exponential fitting function with extracted time constants of τ₁ = (1.33 ± 0.04) ns (80.4%) and τ₂ = (8.31 ± 6.29) ns (19.6%). d Zoom-in of g⁽²⁾(τ) in (c) for time delays up to  ±50 ns.

However, the most remarkable observation is the shortened decay time of the emission under phonon-assisted excitation. The double exponential fit on the time-resolved PL data presented in Fig. 5c suggests that 80.4% of the contribution to the emitted light has a decay time of (1.33 ± 0.04) ns. This is five times shorter than the minimum decay time recorded under above-band excitation in mono- and bilayer WSe₂ from the flake at issue, and among the shortest decay times reported in the literature of WSe₂-based quantum emitters on a dielectric substrate without any cavity (see Supplementary Note 8 and Fig. S11). Therefore, the lifetime measurement under phonon-assisted excitation can confidently be attributed to the employed excitation mechanism rather than to variability among different quantum emitters. We attribute this reduction of about one order of magnitude as compared to the above-band excitation to the fact that exciting near the resonance of the emitter via the efficient acoustic phonons avoids additional relaxation processes before populating the system. The relevance of this result lies in the fact that faster exciton recombination paves the way for a deterministically triggered source at a higher rate for future quantum computing devices based on WSe₂ quantum emitters. Besides that, the additional low contribution (below 20% of the total integrated counts) of longer decay time τ₂ = (8.31 ± 6.29) ns can be attributed to additional slow carrier recombination processes within the bilayer quantum emitter. A previous report on monolayer WSe₂ quantum emitter shows CW excitation at a detuning of 5.07 meV³³, corresponding to  − 2.5 nm, where coupling to a blue-shifted exciton (BS-X) resonance is identified. The energy detuning is very similar to the energy of the breathing mode here considered. However, the work in Ref. ³³ is fully conducted on monolayer WSe₂, which does not support interlayer SM and BM phonons. Even though we cannot rule out the possibility of absorption from an additional charged or dark exciton state, the predictions from our theoretical model in the presence of SM and BM coupling are consistent with our experimental observation.

Discussion

Our results demonstrate that the exciton preparation scheme substantially affects the characteristics of the emitted single photons. Employing a proper pumping strategy is necessary to achieve high purity, fast dynamics, and minimal spectral diffusion. All the excitation schemes presented in this work rely on incoherent processes. In particular, the phonon-assisted scheme provides efficient population inversion and improved spectral stability, inescapable premises for a future efficient and indistinguishable source of single photons from bilayer WSe₂. Our theoretical model of the exciton preparation, including the QE coupling to LA phonon modes, SMs, and BM, is in qualitative agreement with the experiments and provides a pathway towards optimization of the excitation strategy. However, the exact physical mechanism behind the SM and BM coupling is not fully understood and deserves further investigation. Moreover, the coupling to longitudinal optical (LO) phonon modes, higher-order dark states⁵³ and charged states³³ is necessary for an accurate and realistic representation of the physical platform under study, eventually providing a deeper understanding of the exciton preparation and recombination mechanisms.

Yet, coherent state preparation is essential to increase the coherence time and to generate superposition states⁵⁴, which are base requirements for quantum computing and quantum information processing. In this regard, the strictly resonant (in a cross-polarization configuration) and the Swing-UP of the quantum EmitteR population (SUPER) excitation^39,55–57 were pursued in this work. Preliminary investigations reveal that resonant excitation is achieved even though the high linear polarization of the emitter dipole does not allow for the complete rejection of the back-scattered laser (see Supplementary Note 9), making it challenging to proceed with more detailed optical characterization. On the other hand, no emission was observed under the SUPER excitation. The main obstacles encountered could be related to low- and high-frequency noise in the charge environment, as well as strictly practical complications, such as the rejection of the high laser power necessary to perform this scheme, which required both spectral and cross-polarization filtering.

Nonetheless, the outcomes from the acoustic phonon-assisted excitation measurements, combined with the knowledge acquired during the coherent and SUPER excitation attempts, suggest that charge stabilization is imperative for the advancement of the WSe₂ platform. This can be achieved by electrical control via the implementation of external electrical biasing. Having contacted devices will also provide control of the in-plane and out-of-plane electric fields, allowing spectral tuning of the emission by Stark shift. On the other hand, increasing the efficiency of WSe₂ quantum emitters by enhancing the spontaneous emission rate can be achieved through the implementation of the emitter in an optical cavity^58,59. Additionally, understanding the exciton fine structure splitting in this type of quantum emitters will enable its control⁶⁰ and the development of tailored coherent excitation strategies.

Despite the incoherent nature of phonon-assisted excitation scheme⁶¹, its exploitation in terms of exciton preparation fidelity, purity, and indistinguishability of the emitted photons is sufficient to demonstrate six-photon boson sampling and heralded three-photon entanglement with semiconductor QDs³⁸. Moreover, it offers improved stability and robustness against laser detunings and power levels, as well as the possibility of exciting and collecting the photons in all polarization directions.

Conclusion

We have systematically investigated the single-photon properties of bilayer WSe₂ quantum emitters under various optical excitation schemes, including above-band, near-resonant, and phonon-assisted excitation via longitudinal acoustic (LA) and breathing phonon (BM) modes. Our combined experimental and theoretical approach provides insights into exciton-phonon coupling and its role in efficient exciton preparation in the case of bilayer WSe₂ quantum emitters. Our theoretical calculations predict an efficient population above 80% under LA phonon-assisted excitation at a detuning of  −0.4 nm. Additionally, we anticipate a sizable population at larger detunings of  −2.7 nm, dependent on the strength of exciton-BM coupling. Experimentally, we demonstrated that phonon-assisted excitation via the BM mode resulted in a faster recombination time of (1.33 ± 0.04) ns—more than an order of magnitude shorter than above-band and near-resonant excitations—while maintaining a high single-photon purity of 0.947  ±  0.079. The consistently high purity across all excitation schemes suggests that the emission purity is not strongly excitation-dependent. However, LA phonon-assisted excitation achieved a near resolution-limited zero-phonon line width of 0.072 nm and a 1.8-fold reduction in spectral diffusion compared to above-band excitation, demonstrating its advantage in emitter stability. These findings highlight the critical role of the excitation scheme in achieving high-fidelity single-photon emission from bilayer WSe₂. In particular, phonon-assisted excitation offers a promising pathway to minimizing spectral diffusion and improving emitter stability, representing a significant step toward realizing transform-limited linewidths and enhancing the indistinguishability of emitted photons—key requirements for scalable quantum technologies. Understanding the non-trivial correlation between excitation schemes and single-photon emission characteristics provides valuable insights for the development of deterministic, high-quality quantum light sources based on the TMD platform.

Methods

Sample fabrication and preparation

The sample consists of a bilayer WSe₂ transferred on top of a 3-point star-shaped SiO₂ (HSQ) nanopillar on a Si/SiO₂ substrate. For the pillar fabrication, the sample was spin-coated with a negative electron-beam resist (Fox-06), and the star-shaped structures were patterned using a 100 kV electron beam lithography machine (JEOL 9500) with a dose of 11000 μC/cm² and an electric current of 6 nA. The exposed resist was then developed in a (1:3) solution of AZ400K:H₂O. The HSQ resist is known to chemically change to SiO₂ after e-beam exposure, resulting in SiO₂ nanostructures of the same height as the resist (≈150 nm). The WSe₂ flake was exfoliated from the bulk crystals using the conventional scotch-tape technique and subsequently transferred to the patterned substrate by deterministic dry-transfer procedure. Finally, defects were introduced in the flake lattice by electron-beam irradiation of the strained areas using the same 100 kV EBL machine with a dose of 1000 μC/cm² and a current of 6 nA.

Optical characterization

To perform photoluminescence measurements, we placed the WSe₂ mono and bilayer samples in a closed-cycle helium cryostat (attoDRY 800, attocube systems AG) with a base temperature of 4 K. The cryostat is equipped with a microscope objective to focus the laser light onto the sample (NA = 0.81, 60×, attocube systems AG). The setup is configured in a cross-polarized configuration. For photoluminescence imaging, we employ a cooled sCMOS camera (Dhyana 400D, 4MP, Tucsen). To enable various excitation schemes, we employed a tunable OPO module (Chameleon Compact OPO-Vis, Coherent Inc.) pumped by a Ti:Sapphire laser (Chameleon Ultra II, Coherent Inc.) producing 150 fs pulses at an 80 MHz repetition rate. To further optimize the laser spectral window for various excitation methods, we also employed a home-built 4f pulse shaper (f = 500 mm) equipped with an 1800 groove/mm diffraction grating and a programmable single-mask transmissive spatial light modulator (SLM-S320, Jenoptik) in the Fourier plane. The SLM consisting of 320 pixels, helps to carve a narrow spectral range (FWHM ≈ 0.21 nm). To acquire the emission spectra, we utilized a fiber-coupled spectrometer (Horiba iHR 550) using either a 600 groove/mm or a 1200 groove/mm grating. For second-order correlation measurements, we employed a fiber-based Hanbury Brown and Twiss (HBT) interferometer coupled to superconducting nanowire single-photon detectors (SNSPD, ID218, ID Quantique) and time taggers (ID900, ID Quantique).

Data analysis

All the PL emissions from quantum emitters presented in the manuscript were fitted with a function that is a sum of a Lorentzian and a Gaussian. The Lorentzian contribution accounts for the homogeneous broadening of the line, while the Gaussian distribution fits the phonon sideband. From the fitting, it is possible to extract the complete set of 6 parameters defining the distributions, together with the standard error for each one of them. The data obtained from time-resolved photoluminescence (TRPL) measurements was fitted with a sum of two uncorrelated exponentially decaying functions added to a constant background: $F_{\mathrm{TRPL}}\left(\tau \right)=F_0+A_1{e}^{-\left(\tau -{\tau }_{01}\right)/{\tau }_1}+A_2{e}^{-\left(\tau -{\tau }_{02}\right)/{\tau }_2}$, where F₀ accounts for the constant background, A₁ and A₂ are the amplitudes of the two exponential functions, τ₁ and τ₂ the two extracted decay constants, and τ₀₁ and τ₀₂ the decay offsets. The relative weights of the two are extracted as a percentage. In this way, we gain insight into the types of transitions that will contribute to the purity measurement. For the analysis of the second-order correlation measurements, the raw data is fitted with the following expression: $F_{\mathrm{SOC}}\left(\tau \right)=B_1\left[e^{-\mid \tau \mid /{\tau }_1}+e^{-\mid \tau \mid /{\tau }_2}\right]+B_2{\sum }_n\left[e^{-\mid \tau +n{\tau }_{\mathrm{rep}}\mid /{\tau }_1}+e^{-\mid \tau +n{\tau }_{\mathrm{rep}}\mid /{\tau }_2}\right]$, where B₁ denotes the central peak area, B₂ the side peak areas, τ₁ and τ₂ the two extracted decay time constants, τ_rep the laser pulse repetition time, and n the index of each peak (n = 0, ±1, ±2, …). The g⁽²⁾(0) value is then calculated as $g^{\left(2\right)}\left(0\right)=F_{\mathrm{SOC}}\left(0\right)/\max \left[F_{\mathrm{SOC}}\left(\tau \right)\right]$.

Theory—DFT calculations

Ab-initio DFT calculations were performed within the Atomic Simulation Recipes (ASR) Python framework⁶², using the electronic structure code GPAW⁶³ and the Atomic Simulation Environment (ASE) library⁶⁴, and managed with the MyQueue job scheduler⁶⁵. Monolayer and bilayer atomic structures were obtained from the C2DB⁶⁶ and BiDB⁶⁷ databases, respectively. We used a plane wave basis set with a cutoff energy of 800 eV, uniform k-point grid of density 6.0/Å⁻¹, and Fermi-Dirac smearing of 50 meV. The Perdew-Burke-Ernzerhof (PBE)⁶⁸ exchange functional was used, including the DFT-D3⁶⁹ dispersion correction to account for van der Waals interlayer interactions. Atomic forces for phonon calculations were converged to 10⁻⁴ eV/Å. The phonon dispersion was calculated with the Phonopy package^70,71.

Theory—Open quantum system dynamics

The predicted population inversion under near-resonant excitation is obtained from the theoretical modeling of a QE coupled to phonons and to a Gaussian laser pulse, and assuming that electron-phonon interaction occurs via the deformation potential mechanism. We consider a two-level system (ground state $\mid G\left(\right.⟩$, excited state $\mid X\left(\right.⟩$) with Hamiltonian $H_0=\hslash {\omega }_X^{\left(0\right)}\mid X\left(\right.⟩\left.⟨\right)X\mid$ coupled to a bath $H_{\mathrm{ph}}={\sum }_m{\sum }_{\mathbf{k}}\hslash {\omega }_{m,\mathbf{k}}{b}_{m,\mathbf{k}}^{†}{b}_{m,\mathbf{k}}$ via the interaction $H_{\mathrm{int}}={\sum }_m{\sum }_{\mathbf{k}}\hslash g_{m,\mathbf{k}}\left(b_{m,\mathbf{k}}^{†}+b_{m,\mathbf{k}}\right)\mid X\left(\right.⟩\left.⟨\right)X\mid$. Here, the label m runs over different phonon modes (LA, SM₁, SM₂, and BM).

The influence of the linear LA mode (dispersion ω_LA,k = c∣k∣, with c = 4.4 × 10³ m s⁻¹ obtained by fitting the DFT result) is summarized by the spectral density

$$J_{\mathrm{LA}}\left(\omega \right)=\alpha {\omega }^2\exp \left(-\frac{{\omega }^2}{{\omega }_{\mathrm{c}}^2}\right),$$ 1

with $\alpha ={\left(D_e-D_h\right)}^2/\left(4\pi \hslash \rho c^4\right)$ = 0.29 ps obtained from first principles as outlined in Ref. ³⁹. Here, D_e (D_h) is the deformation potential for electrons (holes), and ρ the area density of a single layer of WSe₂. The cutoff frequency is determined as ω_c = 2.03 THz from the measured LA sideband.

For the two SM modes (SM₁ and SM₂, with degenerate energy at Γ), we fit the DFT phonon dispersion to the relativistic-like formula ${\omega }_{{\mathrm{SM}}_i,\mathbf{k}}=\sqrt{c_i^2\mid \mathbf{k}{\mid }^2+M^2}$, which is approximately linear for ∣k∣ ≫ M/c_i but has nonzero frequency M at the Γ point. We obtain the spectral density

$$J_{{\mathrm{SM}}_i}\left(\omega \right)=\alpha \frac{{\omega }^2-M^2}{r_i^4}\exp \left(-\frac{{\omega }^2-M^2}{r_i^2{\omega }_{\mathrm{c}}^2}\right),$$ 2

with r_i = c_i/c, see details in Supplementary Note 6.

The BM is modeled as a dispersion-less mode with frequency ω_BM obtained from the DFT value at Γ, resulting in a delta-like spectral density $J\left(\omega \right)=\alpha {\omega }_{\mathrm{c}}^4{\left(2{\omega }_{\mathrm{BM}}\right)}^{-1}\delta \left(\omega -{\omega }_{\mathrm{BM}}\right)$. To circumvent the numerical singularity, we use instead a Gaussian spectral density centered around ω_BM,

$$J_{\mathrm{BM}}\left(\omega \right)={\xi }_{\mathrm{BM}}\frac{\alpha {\omega }_{\mathrm{c}}^4}{2{\omega }_{\mathrm{BM}}}\frac{1}{\sqrt{\pi }\epsilon }\exp \left[-{\left(\frac{\omega -{\omega }_{\mathrm{BM}}}{\epsilon }\right)}^2\right],$$ 3

with width ε = 0.2 THz accounting for a finite phonon lifetime. Additionally, we introduce a dimensionless weight ξ_BM to control the strength of the BM coupling.

To model the laser excitation, the system is also coupled to a pulsed laser at frequency ω_laser via $H_{\mathrm{laser}}=\frac{\hslash }{2}\mathrm{\Omega }\left(t\right)\left(e^{-i{\omega }_{\mathrm{laser}}t}\mid X\left(\right.⟩\left.⟨\right)G\mid +e^{i{\omega }_{\mathrm{laser}}t}\mid G\left(\right.⟩\left.⟨\right)X\mid \right)$, with a Gaussian pulse $\mathrm{\Omega }\left(t\right)=\frac{\mathrm{\Theta }}{\sqrt{\pi }{t}_p}{e}^{-{\left(t/t_p\right)}^2}$ and $\mathrm{\Theta }={\int }_{-\infty }^{+\infty }\mathrm{d}t\mathrm{\Omega }\left(t\right)$ the pulse area. The dynamics is obtained by solving the master equation for the reduced density operator ρ(t) with the formalism of time-evolving matrix product operators (TEMPO)⁷² as implemented in the OQUPY Python package⁷³, allowing to treat the phonon environment at a numerically-exact level. We use four separate process tensors, one per each phonon mode. From the phonon spectral density, we calculate the mode-dependent Huang-Rhys factor as $S_m={\int }_0^{+\infty }\mathrm{d}\omega {\omega }^{-2}{J}_m\left(\omega \right)$, and the total Huang-Rhys factor as S = ∑_mS_m. To account for spectral broadening beyond the transform limited value, we add to the master equation a Lindblad term $\gamma {\mathcal{L}}_{{\sigma }^{†}\sigma }\left[\rho \right]$, where ${\mathcal{L}}_A\left[\rho \right]=A\rho A^{†}-\frac{1}{2}\left\{A^{†}A,\rho \right\}$.

To calculate the $\mid X\left(\right.⟩$ state population P_X after the laser pulse, the system is initialized in $\mid G\left(\right.⟩$ at time t = −3t_p and P_X is calculated as $P_X=\text{Tr}\left[\mid X\left(\right.⟩\left.⟨\right)X\mid \rho \left(t\right)\right]{\mid }_{t=3t_p}$. The pulse detuning in frequency is defined as Δω = ω_laser − ω_X, where ${\omega }_X={\omega }_X^{\left(0\right)}-D$ is the exciton frequency shifted by the total polaron shift D = ∑_m D_m, and $D_m={\int }_0^{+\infty }\mathrm{d}\omega {\omega }^{-1}{J}_m\left(\omega \right)$. The corresponding wavelength detuning is $\mathrm{\Delta }\lambda ={\lambda }_{\mathrm{laser}}-{\lambda }_X=2\pi c\left({\omega }_{\mathrm{laser}}^{-1}-{\omega }_X^{-1}\right)$. For a given value of t_p, the pulse FWHM in wavelength is calculated from the squared amplitude of the Fourier-transformed signal, $\mid \widehat{\mathrm{\Omega }}\left(\omega \right){\mid }^2=\frac{{\mathrm{\Theta }}^2}{2\pi }\exp \left(-\frac{1}{2}{t}_p^2{\omega }^2\right)$, and is given by $\mathrm{\Delta }{\lambda }_{\mathrm{FWHM}}={\lambda }_X^2\sqrt{2ln2}/\left(\pi c{t}_p\right)$.

Author contributions

A.P. fabricated the final samples with support from C.P. and A.M. C.P. performed all the optical measurements from the fabricated samples. C.P. and V.R. assembled a home-built pulse-shaping setup using the SLM. C.P., P.W., and A.P. contributed to experimental data analysis and processing. L.V. performed DFT calculations, modeled the coupling to shear and breathing phonon modes, and calculated the exciton population. L.V. and J.N. modeled the coupling to longitudinal acoustic phonons and fitted the experimental data. B.M. conceived the idea, and L.V., N.G., and B.M. coordinated the project. C.P. took the lead in writing the manuscript. All authors discussed the results and contributed to the final manuscript.

Peer review

Peer review information

Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.

Data availability

The set of experimental optical data presented throughout the study is available through “figshare.com” with the permanent identifier 10.11583/DTU.28648697. Additional data are available from the corresponding author upon reasonable request.

Code availability

The fitting and simulation codes are available upon reasonable request and can be provided upon request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s42005-025-02080-7.