Highlights
-
•
A novel generation dense medium was proposed for beneficiation process intensification.
-
•
Flow regime was theoretical investigated to understand the transition point of homogeneous expansion.
-
•
Homogeneous fluidization characteristics were systematically studied using the novel composed dense medium.
Keywords: Homogeneous fluidization, Flow regime, Dense medium, Wave propagation, Gas-solid separation fluidized bed
Abstract
Gas-solid separation fluidized beds are important for coal cleaning through the removal of ash-forming impurities. Homogeneous fluidization is considered as an ideal separation method because it results in fewer pressure fluctuations and smaller bubbles. And Geldart C ultrafine powder could further intensify the fluidization stability of Geldart A particles. Thus, the present work provides a breakthrough in the density adjustment method in the gas-solid separation field, namely, combining Geldart A magnetite particles and Geldart C fine coal particles as a novel dense medium. The results showed that the addition of ultrafine coal effectively increased the overall expansion of the dense phase by the adhesion of the coal particles on the surfaces of the magnetite particles. To comprehensively understand the difference in the dense phase expansion ratio between the Geldart B/D and Geldart A particles, the flow regime was investigated to determine the transition point of homogeneous expansion using various dense media. The propagation velocities of the shock and continuity waves were analyzed using the theory of elastic systems. A quantitative criterion is proposed to identify the transition point. Based on the error analysis, the available data in the literature and the present work gave an overall in 5 × 10−5 error range compared to the prediction data. Overall, this research provides a comprehensive understanding of homogeneous fluidization characteristics using a novel dense medium and a reliable quantitative transition criterion of the flow regime for Geldart B/D and Geldart A particles in a gas-solid separation fluidized bed.
Graphical abstract
1. Introduction
Particle flowability is crucial for the processing of particles in many industries, especially in fluidized bed reactors [1,2]. At the initial fluidization state in a gas-solid fluidized bed, the stack particles are mainly suspended by the upward gas flow, and thus they show pseudo-fluid characteristics [3], [4], [5]. These suspended particles can provide a sufficient superficial area to promote the contact efficiency between the gas flow and particles. Fluidized beds have also been proven to be effective reactors owing to their excellent high mass and heat transfer rate [6], [7], [8]. Currently, gas-solid fluidized beds are widely applied in many industrial operations, such as drying, combustion, petroleum processing, adsorption, pneumatic conveying, and filtration [9], [10], [11], [12], [13], [14], [15], [16]. Gas-solid separation fluidized beds can be considered as an extended application of fluidized beds [17,18]. In a fluidized bed, the dense medium is suspended by gas flow, causing a pressure drop in the vertical direction. The bed can therefore be considered to have basic fluid properties, such as density and viscosity, which facilitates dry coal beneficiation [19], [20], [21], [22], [23]. Separation technology was first proposed approximately 100 years ago in the US [24]. It is considered one of the best dry coal beneficiation methods, and thus it is used for coal cleaning in China, India, South Africa, Japan, and Australia [25], [26], [27], [28], [29].
A gas-solid separation fluidized bed is considered as a complex system with multiscale dynamics [30,31]. Generally, the fluidization regime occurs in a bubbling fluidized bed with low gas velocities. The bed consists of two main phases, namely, the bubble phase and dense phase [32,33]. However, the presence and movement of bubbles always lead to pressure fluctuations and particle backmixing [34]. There is experimental evidence that the bubble phase has negative effect on separation efficiency [35]. Scholars have attempted to promote fluidization stability and minimize the effect of bubble phase on coal separation, and the utilization of fine dense medium is a possible method for increasing separation performance [36]. For Geldart A particles, the bed expands in an essentially homogeneous manner with increasing gas flow rate before bubbles start to appear. For Geldart B particles, beds are characterized by the presence of bubbles at the onset of incipient fluidization conditions [37]. Thus, Geldart A particles are considered as reliable fine dense medium for realizing homogeneous fluidization. Furthermore, related research indicates that the addition of Geldart C fine particles can further enhance the flowability and fluidization quality of Geldart A particles [38]. The resulting homogeneous expansion ratio can further improve the density regulation range. We therefore propose combining Geldart A magnetite particles and Geldart C fine coal particles as the novel dense medium to better regulate the density in a gas-solid separation fluidized bed.
In this study, we mainly focused on the effect of different factors on dense phase expansion, such as gas velocity, bed height, and ultrafine coal particle content. Furthermore, the mechanism of fluidization process intensification was investigated by analyzing powder adhesion behavior. In addition, the flow regime transition from non-bubbling fluidization to bubbling fluidization is very important for understanding the dense phase expansion in gas-solid fluidized beds [39], [40], [41], [42], [43], [44], [45]. However, analysis of the transition point for Geldart B/D particles and Geldart A particles in a gas-solid separation fluidized bed is still lacking. Therefore, the propagation velocities of the shock and continuity waves in a gas-solid separation fluidized bed were analyzed using the theory of elastic systems. The flow regime was then investigated in detail to determine the transition point of homogeneous expansion.
2. Experimental
2.1. Experimental system
All experiments were conducted in a cylindrical fluidized bed under ambient conditions, as shown in Fig. 1. After filtration and compression, the surrounding air was sent to fluidize the solid particles in the bed column through a gas distributor. The airflow rate was controlled by a valve and measured using a rotameter. The fluidization apparatus was a cylindrical fluidized bed 15.2 cm in diameter. The gas distributor was a plastic sintered board with holes 10 µm in diameter and a perforated plexiglass plate with holes 2 mm in diameter. A camera with two lights was used to capture the bed height expansion during the experiments. The fluidized bed system had a disengaging section with a dust-absorbing cover and a cyclone dust collector. The recycled powder was periodically blown back during fluidized bed operation.
Fig. 1.
Schematic diagram of fluidized bed system. 1. Air generator; 2. Air tank; 3. Flow meter; 3. Air valve; 4. Flowmeter; 5. Air distribution box; 6. Distributor; 7. Fluidized bed column; 8. Dust absorbing Cover; 9. Cyclone dust collector; 10. electric machinery; 11. Digital camera; 12. Lights.
2.2. Experimental materials
The dense medium composed of fine magnetite particles and ultrafine coal particles was selected to study the dense phase expansion, namely, homogeneous expansion. The properties of the solids are listed in Table 1. Magnetite particles belong to Geldart A particles and ultrafine coal particles belong to Geldart C particles. In this study, ultrafine coal particles were used as additives to improve the fluidization quality of the magnetite particles in the fluidized bed system. The volume fraction of the ultrafine coal particles was controlled in the range of 0–27%.
Table 1.
Composed dense medium and detailed properties.
| Material | Size distribution (µm) | Average size (µm) | True density (g/cm3) | Bulk density (g/cm3) | Particle classification |
|---|---|---|---|---|---|
|
74–150 |
|
|
|
|
|
|
|
|
|
|
In addition, different particles were selected to investigate the flow regime transition in the gas-solid separation fluidized bed. The selected particles were magnetite particles, sand particles, gangue particles, and glass beads. The particle properties of the experimental materials for each size fraction are presented in Table 2. The properties showed that magnetite particles, glass beads, gangue particles and sand particles were all in the size range of 45–590 µm. These samples were sieved into the following size fractions: 45–100, 74–150, 150–300, 300–425, and 425–590 µm.
Table 2.
Experimental materials for analysis of flow regime transition.
| Material | Size distribution (um) | Average size (um) | True density (g/cm3) | Bulk density (g/cm3) |
|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.3. Density adjustment methods
Geldart B/D particles are particles with a high density or large size. In the fluidization process, bubbles easily begin to form using this kind of particles. It appears that bed expansion is relatively low without the phenomenon of uniform particle homogeneous expansion. Thus, the separation density is mainly adjusted by promoting expansion of the bubble phase. However, most bubbles rise fast, and bubble coalescence is the predominant phenomenon [37]. Furthermore, the bubble size increases linearly with both bed height and excess gas velocity due to a high frequency of bubble coalescence. As a result, the bed density frequently fluctuates, which interferes with fine coal separation.
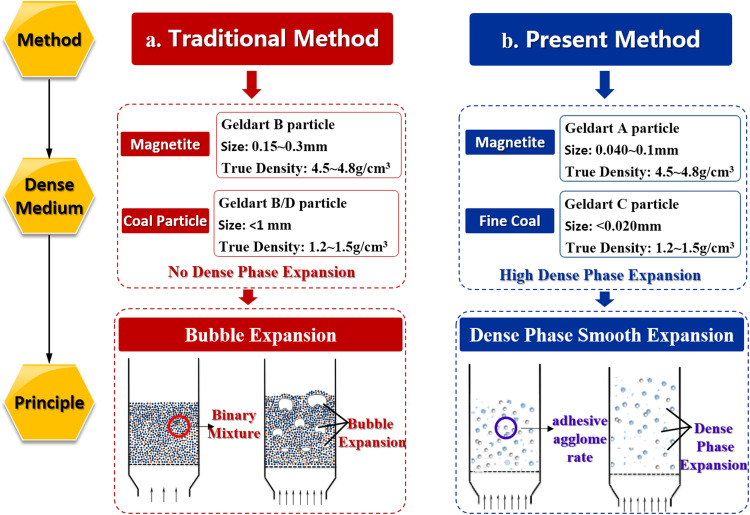
Geldart A particles are generally small and have low density. They also seem to exhibit uniform expansion under the action of interstitial gas. This uniform expansion characteristic is considered to be the dense phase. Furthermore, fluidized beds also expand considerably as small bubbles are generated. Thus, the bed stability is higher with Geldart A particles than that with Geldart B/D particles. Based on the above analysis, a comparison of the basic density adjustment principles is given in Fig. 2 using the two different types of dense medium. This figure shows that the separation density is mainly controlled by the dense phase and bubble phase in the two methods. In addition, the particle bulk density has an important effect on the separation density. Compared to Geldart B/D particles, Geldart A particles exhibit smooth fluidization behavior with high dense phase expansion. In addition, dense phase expansion can be further promoted by adding Geldart C fine coal particles. Thus, these findings provided inspiration for density adjustment by promoting dense phase expansion, as shown in Fig. 2b. It is also very important to master the variation tendency of dense phase expansion in subsequent studies.
Fig. 2.
Comparison of density adjustment methods.
3. Flow regime theoretical analysis
3.1. Dynamic wave propagation
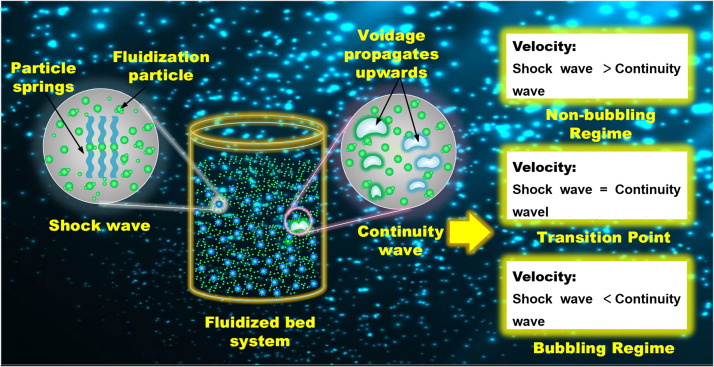
Davidson et al. [46] previously concluded that a fluidized bed is an elastic system, as demonstrated through observation. In this study, we therefore first assumed the separation fluidized system to comprise vertical chains of particles. The interaction forces between particles are considered as the “springs”. The vertically adjacent particles are buffered by balancing the drag and gravitational forces, as shown in Fig. 3. Compared to the concept of particle suspension in a bed, this assumption uses the expressions of particle and fluid interactions. To identify the transition from homogeneous to heterogeneous fluidization, we should first understand two concepts: continuity waves and shock waves.
Fig. 3.
Conceptions of shock wave and continuity wave.
First, shock waves can be explained by analogy to a string of floaters in a river. Initially, the particles are connected by springs and laid on the bed in several layers. When the gas flow is introduced, the external gas pressure first provides energy to the particles at the bottom, which is considered the first layer of particles. The particles then experience upward movement, which compresses the “springs” between the first- and second-layer particles. We can imagine that if an external force is applied to the first floater on the river, that external force can be transmitted to subsequent floaters. This mechanism is also suitable for the consequent increase in external pressure. Thus, the upward “pressure” can be considered as a shock wave transmitted longitudinally in the fluidized bed. Furthermore, we can assume that the fluidized bed has particulate expansion properties before a bubble exists. During the particulate expansion period, the gas flow has a direct effect on the voidage or solid holdup. Initially, the “sudden” change in voidage varies at the bottom. The voidage then propagates upward as a wave from the lower to upper zones. This phenomenon is considered as a continuity wave in the fluidized bed.
3.2. Propagation velocity of shock wave
As shown in Fig. 3, the fluidized bed can be assumed to consist of particle chain. For such a linked system, the velocity of the shock wave under isothermal conditions can be expressed as [39,40]:
| (1) |
where p* is the pressure intensity (Pa) and is the loose density of the dense phase that varies with gas flow (kg/m3).
According to the assumption of Foscolo et al. [40], the relation between the external pressure and compression net force on each particle with upward movement can be expressed as:
| (2) |
where A is the cross-sectional area (m2) and Ns is the number of particles in each layer. The relationship between the above parameters is given as follows:
| (3) |
or
| (4) |
Hence, the variation of external pressure intensity can be given as:
| (5) |
| (6) |
Although Foscolo et al. [40] proposed the correlation of effective weight on each particle, the net forceon each particle can be simply expressed as:
| (7) |
where is the gravity force of each particle (N), is the buoyancy force on each particle (N), and is the drag force on each particle (N). The correlations between the gravity force and buoyancy force are easily obtained. Therefore, it is important to propose a suitable correlation for the drag force on each particle.
For each particle, the drag force at infinite distance is given as:
| (8) |
where is the drag coefficient, is the particle size (m), is the fluid density (kg/m3), and is the terminal velocity for each particle (m/s). The relation between and is given as [40]:
| (9) |
where u is the gas velocity (m/s). Therefore, combining Eqs. 7, 8, and 9 yields:
| (10) |
In addition, the loose density of the dense phase varies with the gas flow and can be expressed as:
| (11) |
Combining Eqs. 6, 10, and 11 gives:
| (12) |
3.3. Propagation velocity of continuity wave
For the propagation velocity of continuity wave, it is reasonable to establish correlations according to research by Verloop et al. [39]. For a sudden disturbance from equilibrium conditions, the propagation velocity of a continuity wave can be expressed as:
| (13) |
Based on the R-Z equation for the relationship between the gas velocity and terminal velocity, we have:
| (14) |
Combining Eqs. 13 and 14 gives:
| (15) |
Generally, the drag coefficient varies with the Reynolds number (Re); the Re in the laminar regime is different from that in the turbulent regime. In the study, the particle size was relatively small and the operation velocity was relatively low. Thus, this regime was mainly the laminar regime. In the laminar regime:
| (16) |
| (17) |
Combining Eqs. 15 and 17 gives:
| (18) |
3.4. The transition from non-bubbling fluidization to bubbling fluidization
For the critical transition point from non-bubbling fluidization to bubbling fluidization, the propagation velocity of the shock wave is equal to that of the continuity wave. This can be expressed as:
| (19) |
Combining Eqs. 12 and 18 gives:
| (20) |
| (21) |
Because this research refers to gas–solid fluidization, , thus, Eq. 21 gives:
| (22) |
Thus, for the fine particles in this study, Eq. 22 was selected as the united correlation to confirm a quantitative criterion for non-bubbling fluidization to bubbling fluidization in a gas–solid separation fluidized bed. The constant number of flow regime transitions, Zd, yields:
| (23) |
where Re* is the quasi Reynolds number. It is noted that Eq. 23 is used to analyze flow regime transitions in gas-solid separation fluidized beds.
4. Results and discussion
4.1. Effect of air distributor on the bed expansion ratio
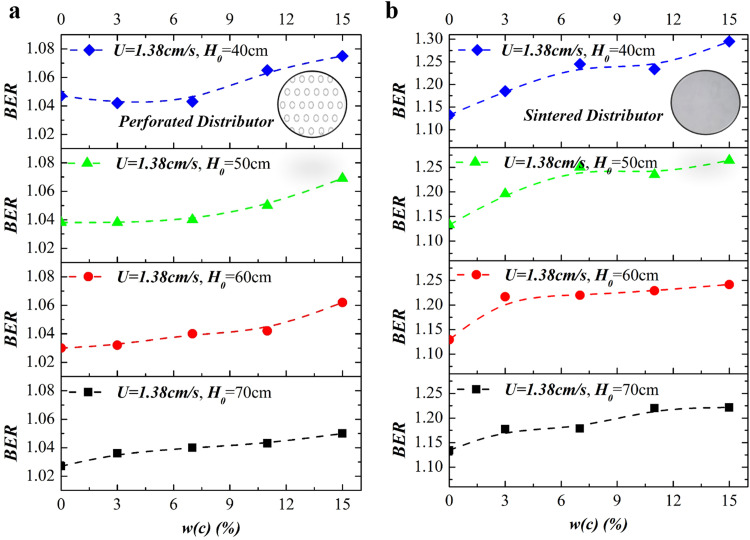
To select the optimal air distributor for promoting the fluidization quality, a perforated plate distributor and a sintered distributor were both tested in laboratory-scale columns. Fig. 4 shows the bed expansion ratios of the two distributors in a fluidized bed. When the perforated-plate distributor was used, the bed expansion ratio (BER) was approximately 1.027–1.05 at H0 = 70 cm. At H0 = 40 cm, the BER was approximately 1.047–1.075. Thus, the expansion at H0 = 70 was somewhat slower than that at H0 = 40 cm, indicating poor gas distribution and fluidization quality. Compared with the perforated-plate distributor, the BER was higher when the sintered distributor was used in the column. The BER was approximately 1.10–1.25 at H0 = 70 cm and approximately 1.10–1.35 at H0 = 40 cm. These differences can be attributed to the initial bubble generation. With the perforated-plate distributor, the initial bubble size generated at each distributor hole was relatively large. As a result, the gas preferentially flowed out through the bubble phase and thus less gas flow entered the dense phase for homogeneous expansion. Meanwhile, channeling was noticeable at the bottom of the bed, limiting the complete expansion of the dense medium. The sintered distributor, however, was conducive for generating microbubbles. In this case, the gas tended to enter the dense phase, thus promoting homogeneous fluidization as the dense phase expanded. Thus, a sintered distributor was selected for subsequent research.
Fig. 4.
Effect of distributor on the bed expansion ratio.
4.2. Effect of gas velocity on the dense phase expansion
To show the effect of gas velocity on the dense phase expansion, the dense phase expansion ratio (DER) is plotted against gas velocity in Fig. 5. As the gas velocity increases, the dense phase expansion initially increases, then gradually stabilizes, and then slightly decreases. When the gas velocity was maintained at 0–1.38 cm/s, the dense phase expansion continuously increased in the fluidized bed. When the gas velocity was gradually increased, the overall dense phase expansion showed a slight downward trend, but the degree of reduction was relatively low. This can be attributed to the fact that, as the gas velocity initially increased, the bed firstly showed uniform dense phase expansion. At this stage, there was a positive linear relationship between the dense phase expansion and gas velocity because the dense phase expansion ratio was low and thus the particles were not fully expanded. As the gas velocity continued to increase, the dense phase expansion reached its maximum value, with complete dense phase expansion before the appearance of bubbles. When the gas velocity was further increased, the fluidization stability was affected by the constant bubble generation in the fluidized bed. Owing to bubble movement, the gas exchange frequency between the bubble phase and dense phase was somewhat high, and the bubble phase ratio tended to increase. Consequently, the dense phase expansion tended to decrease at a high gas velocity.
Fig. 5.
Effect of gas velocity on the dense phase expansion.
4.3. Effect of bed height on the dense phase expansion
An investigation of the effect of bed height on the expansion ratio was carried out, and the results are shown in Fig. 6. The operating gas velocity was selected as U = 1.19–1.38 cm/s to ensure complete expansion of the dense phase in the bed. Generally, the dense phase expansion remained stable with the slight variation in bed height from 40 cm to 70 cm. For example, when the fine coal content was 0, the dense phase expansion remained 1.10–1.15 for magnetite powder only. When the fine coal content was gradually increased to 11%, the dense phase expansion stabilized at 1.20–1.25 because of the fluidization assistance of the fine coal. With gradually increasing bed height, the dense phase expansion also tended to decrease slightly. These results indicate that bed height also played an important role in the dense phase expansion using a dense medium. When the bed height was low, the bubble size was small and the bubble merger frequency was low, which could provide sufficient conditions for the expansion of the particles. When the bed height was gradually increased, the merger frequency gradually increased as the bubbles rose, the size of the bubbles increased, and the gas exchange rate between the dense phase and bubble phase increased, which also reduced the gas flow in the dense phase and inhibited the full expansion of the dense phase.
Fig. 6.
Effect of bed height on the dense phase expansion.
4.4. Effect of fine coal content on dense phase expansion
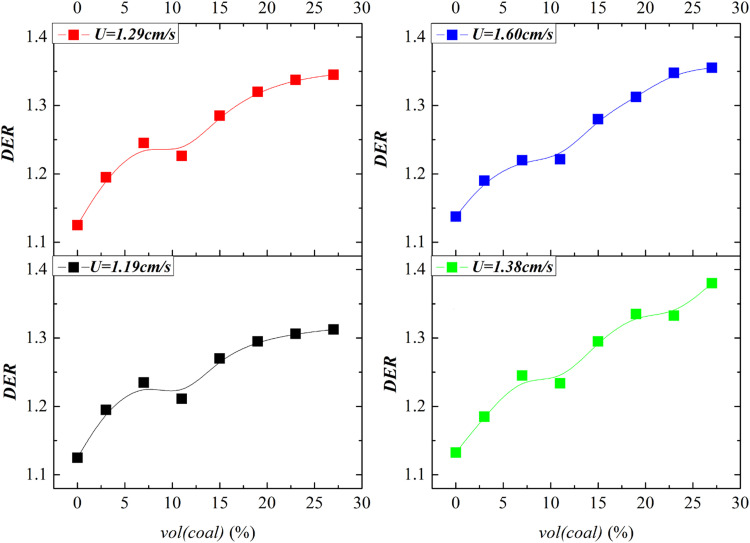
The effect of the fine coal content on the dense phase expansion was then investigated at U = 1.19–1.60 cm/s and H0 = 40 cm to ensure complete expansion of the bed. Fig. 7 shows the dense phase expansion with respect to fine coal content. The results show that a small amount of fine content had a significant impact on dense phase expansion. Furthermore, with increasing fine coal content, the overall DER tended to increase initially and then stabilize at the same superficial gas velocity. The dense phase expansion had an obvious initial upward tendency through the addition of ultrafine coal content from 0% to 19%. The results indicate that adding fine coal improves the fluidization quality of the dense medium in a gas–solid separation fluidized bed. As a result, the gas flows easily into the dense phase to loosen the particle layer uniformly. The resulting dense phase expansion can effectively adjust the separation density range and promote density stability. However, there is a limit to the modulation of fluidization quality by adding fine coal. As the content of fine coal was continuously increased, the further enhancement of DER was not obvious, and DER mainly stabilized at approximately 1.30–1.40. Thus, the fine coal content should be controlled within a reasonable range to ensure complete dense phase expansion.
Fig. 7.
Effect of fine coal content on dense phase expansion.
4.5. Mechanism of fluidization process intensification
To study the mechanism of fluidization process intensification, the effect of ultrafine coal on particle adhesion was investigated by scanning electron microscopy (SEM). As shown in Fig. 8a, magnetite particles (M1) had somewhat smooth surfaces rarely covered by the slight fine magnetite powder. With the addition of 7% ultrafine coal particles, the surfaces of the magnetite particles were covered by the fine coal particles, turning the surfaces rough. Using elemental analysis in surface scanning mode through energy dispersive X-ray spectroscopy (EDS), it was found that the covered particles were mainly ultrafine coal powder. These results indicate that the ultrafine coal particles and their aggregates were evenly distributed on the surfaces of the magnetite particles, which could promote the fluidization quality of magnetite particles with rough surfaces. In addition, considering the consumption of ultrafine coal particles during the process, particle adhesion was analyzed in detail for different fluidization times using SEM. The magnetite powder was modulated by 7% and 19% ultrafine coal particles for 0–24 h. The variations in particle adhesion were then compared in subsequent experiments. As shown in Fig. 8b, the surfaces of the magnetite particles were covered by the fine particles at different processing times. In addition, the content of covered particles remained stable, thus strengthening the fluidization expansion. Thus, the above results provide a detailed explanation of the process intensification of particle flow and homogenous fluidization through the adhesion of Geldart C ultrafine coal particles on Geldart A magnetite particles.
Fig. 8.
SEM images for analysis of mechanism of fluidization process intensification. (a) Analysis of particle adhesion of composed dense medium by SEM and EDS. (b) SEM images of Geldart A magnetite particles after modulation of Geldart ultra-fine coal.
4.6. Flow regime transition in gas solid fluidized bed
To obtain the quantitative transition criterion from the non-bubbling regime to the bubbling regime, data were collected for gas–solid separation fluidized bed and the Geldart B/D and Geldart A particles. The particle properties and operating conditions have a direct effect on the quantitative criterion. Hence, the index n is assumed to be closely related to Re and Ar. According to the comparison between the theoretical and experimental data, the optimal fitting value of index n yields:
| (24) |
And the Reynolds number can be expressed as:
| (25) |
The Archimedes number can be expressed as:
| (26) |
Hence, the constant number Zd gives for:
| (27) |
As shown in Fig. 9, the criterion provided an excellent prediction of the transition point from non-bubbling to bubbling fluidization in a gas–solid separation fluidized bed. In particular, the bed exhibits particulate fluidization for fine particles with a lower Re. The criterion also yielded a slight difference between the predicted and experimental data in the transition region. For the Geldart B/D particles, the value of Re was somewhat higher, and the bed had no particulate expansion period. Hence, the predicted data were far beyond the experimental data in the bubbling regime.
Fig. 9.
Analysis of fluidization transition in gas-solid separation fluidized bed.
Relevant data were collected to determine the feasibility of gas–solid fluidization for other applications. Table 3 provides the details of the transition point from non-bubbling to bubbling fluidization in a gas–solid fluidized bed, comparing the results of previous studies with those of the present research. The theoretical value of Zd is almost equal to the experimental value in both previous studies and this study. The error analysis of the proposed correlation for the quantitative criterion using the data available in the literature and in the present work is shown in Fig. 10. It can be seen that Eq. 27 gives an overall 5 × 10−5 error range compared to the experimental results, which shows agreement in the fluidization research field. Overall, the proposed correlation has the advantage of being considerably simpler with high accuracy for predicting the dense phase expansion in a gas–solid fluidized bed. Therefore, the proposed correlation can be used to accurately predict the quantitative criterion of homogenous fluidization expansion for Geldart B/D and Geldart A particles in a gas–solid separation fluidized bed.
Table 3.
Summary of transition point from Non-bubbling to Bubbling fluidization.
| References | Particle density, ρs (g/cm3) | Particle size, ds(µm) | Transition gas velocity (cm/s) | Voiadage at transition point |
|---|---|---|---|---|
| Geldart [37] | 1.18 | 78 | 0.85 | 0.542 |
| Geldart [37] | 1.18 | 118 | 1.17 | 0.496 |
| Geldart [37] | 1.18 | 141 | 1.34 | 0.481 |
| Geldart [37] | 1.18 | 155 | 1.60 | 0.465 |
| Geldart [37] | 1.18 | 190 | 1.76 | 0.452 |
| Geldart [37] | 1.18 | 263 | 3.11 | 0.444 |
| Geldart [37] | 1.18 | 318 | 4.11 | 0.444 |
| Geldart [37] | 1 | 25 | 0.25 | 0.645 |
| Geldart [37] | 1 | 39 | 0.35 | 0.629 |
| Geldart [37] | 1 | 55 | 0.59 | 0.645 |
| Geldart [37] | 1.5 | 45 | 0.51 | 0.675 |
| Geldart [37] | 1.5 | 87 | 0.73 | 0.600 |
| Geldart [37] | 1.5 | 95 | 0.82 | 0.610 |
| Geldart [37] | 1.5 | 115 | 0.84 | 0.610 |
| Foscolo, et al. [47] | 0.873 | 56 | 0.539 | 0.606 |
| Foscolo, et al. [47] | 0.873 | 56 | 0.49 | 0.601 |
| Foscolo, et al. [47] | 0.873 | 56 | 0.564 | 0.563 |
| Foscolo, et al. [47] | 1.054 | 62 | 0.756 | 0.573 |
| Foscolo, et al. [47] | 1.054 | 62 | 0.84 | 0.586 |
| Foscolo, et al. [47] | 1.054 | 62 | 0.774 | 0.552 |
| Foscolo, et al. [47] | 1.5 | 61 | 0.74 | 0.53 |
| Foscolo, et al. [47] | 1.5 | 61 | 0.64 | 0.538 |
| Foscolo, et al. [47] | 1.5 | 61 | 0.74 | 0.518 |
| Foscolo, et al. [47] | 1.65 | 69 | 0.759 | 0.49 |
| Foscolo, et al. [47] | 1.65 | 69 | 0.675 | 0.502 |
| Foscolo, et al. [47] | 1.65 | 69 | 0.836 | 0.467 |
| Grace, et al. [13] | 1.455 | 59 | 0.51 | 0.548 |
| Grace, et al. [13] | 1.44 | 60 | 0.57 | 0.529 |
| Grace, et al. [13] | 1.444 | 60 | 0.53 | 0.53 |
| Kono, et al. [48] | 1.4 | 70 | 0.7 | 0.559 |
| Kono, et al. [48] | 1.5 | 64.3 | 1.42 | 0.638 |
| Kono, et al. [48] | 1.395 | 68.3 | 0.7 | 0.562 |
| Kono, et al. [48] | 1.39 | 66.5 | 0.7 | 0.588 |
| Musmarra, et al. [49] | 2.6 | 75 | 0.77 | 0.469 |
| Musmarra, et al. [49] | 2.6 | 150 | 2.6 | 0.406 |
| Musmarra, et al. [49] | 2.6 | 500 | 20 | 0.447 |
| Musmarra, et al. [49] | 2.6 | 250 | 6.63 | 0.413 |
| Musmarra, et al. [49] | 2.1 | 75 | 0.64 | 0.462 |
| Musmarra, et al. [49] | 1.4 | 75 | 0.49 | 0.609 |
| Musmarra, et al. [49] | 0.675 | 75 | 0.28 | 0.695 |
Fig. 10.
Comparison ofZdwith all the available experimental data.
5. Conclusion
In the present work, we investigated the effects of different factors on the dense phase expansion of a novel dense medium. The results showed that the distributor played a critical role in the design of gas–solid fluidized beds using the novel dense medium. The sintered distributor exhibited satisfactory performance in terms of strengthening the dense phase expansion. The results also indicated that gas velocity and bed height had a significant effect on the dense phase expansion.
The research also proved that the addition of ultrafine coal effectively increased the overall dense phase expansion. The mechanism of the fluidization process intensification was then analyzed using SEM and EDS. The results showed that particle flow and fluidization were promoted by the adhesion of the ultrafine coal particles to the magnetite powder. Based on the above analysis, this study provides a comprehensive understanding of the homogeneous fluidization characteristics using a novel dense medium.
Based on the concept of a fluidized bed as an elastic system, the propagation velocity of the shock wave and continuity wave were theoretically analyzed by combining the operation factors and particle properties. A quantitative criterion was then proposed to identify the transition point from non-bubbling to bubbling fluidization. The criterion provided an excellent prediction of the maximum dense phase expansion, giving an overall in 5 × 10−5 error range compared to the prediction data. Overall, this research provides a reliable quantitative transition criterion of the flow regime for Geldart B/D and Geldart A particles in a gas–solid separation fluidized bed.
Declaration of competing interest
The authors declare that they have no conflicts of interest in this work.
Acknowledgments
The research work is financially supported by China National Funds for Distinguished Young Scientists (52125403), Natural Science Foundation of Jiangsu Province (BK20200651), National Natural Science Foundation of China (52104276, 52261135540, 52220105008), International Postdoctoral Exchange Fellowship Program (PC2021086).
Biographies
Chenyang Zhou received his Ph.D. from China University of Mining and Technology in 2019. His research focuses on the fundamental research on fluidization dynamics and dry coal beneficiation.
Chenlong Duan(BRID: 08379.00.88088) received his Ph.D. from China University of Mining and Technology in 2007, and currently is a professor and dean of Department of Postgraduate Administration in CUMT, Xuzhou, China. He has been granted the National Science Fund for Distinguished Young Scholars in 2021. Professor Duan has won the State Science and Technology Advancement Award (2nd Prize), the State Technological Innovation Award (2nd Prize), and the Science and Technology Advancement Award of Ministry of Education (Grand Prize).
Appendix
| A | Area of crossing section, m2 |
| Ar | Archimedes number |
| ds | Particle size, m. |
| Cd | Drag coefficient |
| Compression net force, N | |
| Buoyancy force on each particle, N | |
| Drag force on each particle, N | |
| Gravity force of each particle, N. | |
| Fr | Fred number |
| H0 | Initial bed height, m |
| m | Particle mass, kg |
| n | Coefficient |
| Ns | The number of particles in each layer |
| p* | Pressure intensity, Pa |
| Fluid density, kg/m3. | |
| Particle size, kg/m3. | |
| Loosen density of dense phase, kg/m3. | |
| Re | Reynolds number |
| Re* | Quasi Reynolds number |
| u | Gas velocity, m/s |
| ut | Terminal velocity for each particle, m/s |
| U | Operation gas velocity in gas solid separation fluidized bed, m/s |
| Velocity of shock wave, m/s. | |
| Propagation velocity of continuity wave, m/s. | |
| Zd | Quantitative criterion value |
| Voidage | |
| Fluid viscosity, Pa*s |
References
- 1.Yoshida M., Katayama T., Kikuchi R., et al. Influence of surface roughness created by admixing smaller particles on improving discharge particle flowability of main particles. Adv. Powder. Technol. 2019;30:156–163. [Google Scholar]
- 2.Han M., Zhou Y., Zhu J. Improvement on flowability and fluidization of Group C particles after nanoparticle modification. Powder. Technol. 2020;265:208–214. [Google Scholar]
- 3.Fu Z., Zhu J., Barghi S., et al. Minimum fluidization velocity of binary mixtures of medium particles in the air dense medium fluidized bed. Chem. Eng. Sci. 2019;207:194–201. [Google Scholar]
- 4.Fu Z., Zhu J., Barghi S., et al. Minimum fluidization velocity growth due to bed inventory increase in an air dense medium fluidized bed. Chem. Eng. J. 2019;359:1372–1378. [Google Scholar]
- 5.Zhu C., Yu Q., Dave R.N., et al. Gas fluidization characteristics of nanoparticle agglomerates. AIChE. J. 2005;51:426–439. [Google Scholar]
- 6.Wang Y., Wei F., Luo G., et al. The large-scale production of carbon nanotubes in a nano-agglomerate fluidized-bed reactor. Chem. Phys. Lett. 2002;364:568–572. [Google Scholar]
- 7.Kunii D., Levenspiel O. Circulating fluidized-bed reactors. Chem. Eng. Sci. 1997;52:2471–2482. [Google Scholar]
- 8.Rüdisüli M., Schildhauer T.J., Biollaz S.M., et al. Scale-up of bubbling fluidized bed reactors - a review. Powder. Technol. 2012;217:21–38. [Google Scholar]
- 9.Jia D., Bi X., Lim C.J., et al. Biomass drying in a pulsed fluidized bed without inert bed particles. Fuel. 2016;186:270–284. [Google Scholar]
- 10.Mathekga H.I., Oboirien B.O., North B.C. A review of oxy - fuel combustion in fluidized bed reactors. Int. J. Energ. Res. 2016;40:878–902. [Google Scholar]
- 11.Wang S., Lu H., Zhao F., et al. CFD studies of dual circulating fluidized bed reactors for chemical looping combustion processes. Chem. Eng. J. 2014;236:121–130. [Google Scholar]
- 12.Zimmermann S., Taghipour F. CFD modeling of the hydrodynamics and reaction kinetics of FCC fluidized-bed reactors. Ind. Eng. Chem. Res. 2005;44:9818–9827. [Google Scholar]
- 13.Grace J.R., Sun G. Influence of particle size distribution on the performance of fluidized bed reactors. Can. J. Chem. Eng. 1991;69:1126–1134. [Google Scholar]
- 14.Zhao X., Hickey R.F., Voice T.C. Long-term evaluation of adsorption capacity in a biological activated carbon fluidized bed reactor system. Water. Res. 1999;33:2983–2991. [Google Scholar]
- 15.Chen T., Wu C., Liu R., et al. Effect of hot vapor filtration on the characterization of bio-oil from rice husks with fast pyrolysis in a fluidized-bed reactor. Bioresource Technol. 2011;102:6178–6185. doi: 10.1016/j.biortech.2011.02.023. [DOI] [PubMed] [Google Scholar]
- 16.Zhu L.T., Ye M., Luo Z.H. Application of filtered model for reacting gas–solid flows and optimization in a large-scale methanol-to-olefin fluidized-bed reactor. Ind. Eng. Chem. Res. 2016;55:11887–11899. [Google Scholar]
- 17.Zhou C., Liu X., Zhao Y., et al. Recent progress and potential challenges in coal upgrading via gravity dry separation technologies. Fuel. 2021;305 [Google Scholar]
- 18.Zhou C., Fan X., Duan C., et al. A method to improve fluidization quality in gas–solid fluidized bed for fine coal beneficiation. Particuology. 2019;43:181–192. [Google Scholar]
- 19.Sahu A.K., Tripathy A., Biswal S.K., et al. Stability study of an air dense medium fluidized bed separator for beneficiation of high - ash Indian coal. Int. J. Coal. Prep. Util. 2011;31:127–148. [Google Scholar]
- 20.Oshitani J., Isei Y., Yoshida M. Influence of air bubble size on float–sink of spheres in a gas–solid fluidized bed. Adv. Powder. Technol. 2012;23:120–123. [Google Scholar]
- 21.Oshitani J., Kawahito T., Yoshida M., et al. Improvement of dry float–sink separation of smaller sized spheres by reducing the fluidized bed height. Adv. Powder. Technol. 2012;23:27–30. [Google Scholar]
- 22.Yoshida M., Oshitani J., Tani K., et al. Fluidized bed medium separation (FBMS) using the particles with different hydrophilic and hydrophobic properties. Adv. Powder. Technol. 2011;22:108–114. [Google Scholar]
- 23.Wang Q.G., Yang H.R., Feng Y.Q. Numerical study of the effect of operation parameters on particle segregation in a coal beneficiation fluidized bed by a TFM–DEM hybrid model. Chem. Eng. Sci. 2015;131:256–270. [Google Scholar]
- 24.T. Fraser, H.F. Yancey, Process of separating loosely mixed materials, U. S. Patent 1534846 [P]. 1925-4-21.
- 25.Azimi E., Karimipour S., Xu Z., et al. Statistical analysis of coal beneficiation performance in a continuous air dense medium fluidized bed separator. Int. J. Coal. Prep. Util. 2017;37:12–32. [Google Scholar]
- 26.Fu Z.J., Zhu J., Barghi S., et al. Dry coal beneficiation by the semi-industrial air dense medium fluidized bed with binary mixtures of magnetite and fine coal particles. Fuel. 2019;243:509–518. [Google Scholar]
- 27.Sahu A.K., Tripathy A., Biswal S.K. Study on particle dynamics in different cross-sectional shapes of air dense medium fluidized bed separator. Fuel. 2013;111:472–477. [Google Scholar]
- 28.Oshitani J., Kondo M., Nishi H., et al. Separation of silicastone and pyrophyllite by a gas-solid fluidized bed utilizing slight difference of density. Adv. Powder. Technol. 2003;14:247–258. [Google Scholar]
- 29.Chikerema P., Moys M. Effects of particle size, shape, and density on the performance of an air fluidized bed in dry coal beneficiation. Int. J. Coal. Prep. Util. 2012;32:80–94. [Google Scholar]
- 30.Musmarra D., Poletto M., Vaccaro S., et al. Dynamic waves in fluidized beds. Powder Technol. 1995;82:255–268. [Google Scholar]
- 31.Van Ommen J.R., Sasic S., Van der Schaaf J., et al. Time-series analysis of pressure fluctuations in gas–solid fluidized beds – a review. Int. J. Multiphas. Flow. 2011;37:403–428. [Google Scholar]
- 32.Zhou C., Dong L., Zhao Y., et al. Studies on bed density in a gas-vibro fluidized bed for coal cleaning. ACS Omega. 2019;4:12817–12826. doi: 10.1021/acsomega.9b01892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Li Y., Zhou C., Zhang G., et al. Gas–solid distribution theory in a pulsed fluidized bed based on the intermediate phase. Ind. Eng. Chem. Res. 2021;60:3228–3238. [Google Scholar]
- 34.Zhang Y., Zhang J., Zhao Y., et al. Investigations on dynamics of bubble in a 2D vibrated fluidized bed using pressure drop signal and high-speed image analysis. Chem. Eng. J. 2020;395 [Google Scholar]
- 35.Zhou E., Zhang Y., Zhao Y., et al. Influence of bubbles on the segregated stability of fine coal in a vibrated dense medium gas–solid fluidized bed. Particuology. 2021;58:259–267. [Google Scholar]
- 36.Prusti P., Sahu A., Biswal S.K. Prediction of the position of coal particles in an air dense medium fluidized bed system. Int. J. Min. Sci. Technol. 2015;25:421–427. [Google Scholar]
- 37.Geldart D. Types of gas fluidization. Powder. Technol. 1973;7:285–292. [Google Scholar]
- 38.Zhou C.Y. China University of Mining and Technology; 2019. Density Adjustment in Gas-Solid Fluidized Bed for Beneficiation Using Geldart A Dense Medium [D] [Google Scholar]
- 39.Verloop J., Heertjes P.M. Shock waves as a criterion for the transition from homogeneous to heterogeneous fluidization. Chem. Eng. Sci. 1970;25:825–832. [Google Scholar]
- 40.Foscolo P.U., Gibilaro L.G. A fully predictive criterion for the transition between particulate and aggregate fluidization. Chem. Eng. Sci. 1984;39:1667–1675. [Google Scholar]
- 41.Foscolo P.U., Gibilaro L.G. Fluid dynamic stability of fluidised suspensions: The particle bed model. Chem. Eng. Sci. 1987;42:1489–1500. [Google Scholar]
- 42.Buevich Y.A., Kapbasov S.K. Stability of finely dispersed vertical flows. Fluid. Dyn. 1993;28:796–802. [Google Scholar]
- 43.Sierra C., Tadrist L., Occelli R. Local and global dynamics of shallow gas-fluidized beds. Phys. Fluids. 2006;8 [Google Scholar]
- 44.Luo K., Tan J., Wang Z., et al. Particle-resolved direct numerical simulation of gas–solid dynamics in experimental fluidized beds. AIChE. J. 2016;62:1917–1932. [Google Scholar]
- 45.de Martín L. Influence of particle dynamics on the instability for pattern formation in shallow pulsed beds. Phys. Rev. Fluids. 2018;3 [Google Scholar]
- 46.Davidson J.F., Paul R.C., Smith M.J.S., et al. The rise of bubbles in a fluidised bed. Chem. Eng. Res. Des. 1959;37:323–328. [Google Scholar]
- 47.Gibilaro L.G., Di Felice R., Foscolo P.U. On the minimum bubbling voidage and the Geldart classification for gas-fluidised beds. Powder. Technol. 1988;56:21–29. [Google Scholar]
- 48.Kono H.O., Ells T.S., Chiba S., et al. E Morimoto. Quantitative criteria for emulsion phase characterization and for the transition between particulate and bubbling fluidization. Powder. Technol. 1987;52:69–76. [Google Scholar]
- 49.Musmarra D., Vaccaro S., Filla M., et al. Influence of particle properties on the propagation velocity of pressure disturbances in bubble-free fluidized beds. Int. J. Multiphas. Flow. 1993;19:705–710. [Google Scholar]