Hybrid optimization technique for matrix chain multiplication using Strassen’s algorithm

Abstract

Background

Matrix Chain Multiplication (MCM) is a fundamental problem in computational mathematics and computer science, often encountered in scientific computing, graphics, and machine learning. Traditional MCM optimization techniques use Dynamic Programming (DP) with Memoization to determine the optimal parenthesization for minimizing the number of scalar multiplications. However, standard matrix multiplication still operates in O(n ³) time complexity, leading to inefficiencies for large matrices.

Methods

In this paper, we propose a hybrid optimization technique that integrates Strassen’s algorithm into MCM to further accelerate matrix multiplication. Our approach consists of two key phases: (i) matrix chain order optimization, using a top-down memoized DP approach, we compute the best multiplication sequence, and (ii) hybrid multiplication strategy, we selectively apply Strassen’s algorithm for large matrices (n ≥ 128), reducing the complexity from O(n ³) to O(n ^2.81), while using standard multiplication for smaller matrices to avoid recursive overhead. We evaluate the performance of our hybrid method through computational experiments comparing execution time, memory usage, and numerical accuracy against traditional MCM and Strassen’s standalone multiplication.

Results

Our results demonstrate that the proposed hybrid method achieves significant speedup (4x–8x improvement) and reduces memory consumption, making it well-suited for large-scale applications. This research opens pathways for further optimizations in parallel computing and GPU-accelerated matrix operations.

Conclusion

This study presents a hybrid approach to Matrix Chain Multiplication by integrating Strassen’s algorithm, reducing execution time and memory usage. By selectively applying Strassen’s method for large matrices, the proposed technique improves efficiency while preserving accuracy. Future work can focus on parallel computing and GPU acceleration for further optimization.

1. Introduction

Matrix Chain Multiplication (MCM) ¹ is a fundamental optimization problem in linear algebra and computational mathematics, with applications in machine learning, graphics processing, numerical simulations, and high-performance computing. Given a sequence of matrices, MCM aims to determine the optimal parenthesization that minimizes the number of scalar multiplications. Although matrix multiplication is associative, the order in which matrices are multiplied significantly affects computational efficiency.

For an input sequence of matrices A ₁, A ₂, …, A _n with dimensions p ₀ × p ₁, p ₁ × p ₂, …, p _n-1 × p _n , the goal of MCM is to determine the optimal multiplication order that minimizes the total number of operations

$$\text{Cost}=(p_i\times p_k\times p_j)$$

where k represents the optimal split point. Brute-force approaches to MCM require exploring all possible parenthesizations, leading to an exponential O(2 ⁿ ) complexity, making them infeasible for large n.

To solve this efficiently, Dynamic Programming (DP) with Memoization is commonly used, reducing the time complexity to O( n ³). However, this cubic complexity still presents computational challenges for large matrices, motivating the need for further optimization.

1.1. Motivation for optimization

While DP-based MCM determines the best multiplication order, it does not reduce the actual multiplication complexity itself. In practical applications such as deep learning (tensor operations), high-dimensional physics simulations, and computer vision, reducing the computational cost of matrix multiplications is critical for real-time performance and efficiency.

Strassen’s algorithm ² is a well-known technique for improving matrix multiplication efficiency. It reduces the standard O( n ³) complexity to O( n ^2.81) by decomposing matrices into submatrices and performing only 7 recursive multiplications instead of 8. This asymptotic improvement makes Strassen’s method highly effective for large matrices. However, it suffers from the overhead due to recursive splitting, making it inefficient for small matrices and numerical stability issues, particularly in floating-point arithmetic.

A direct application of Strassen’s algorithm to MCM is non-trivial, as MCM does not involve direct multiplication but rather determining the multiplication order first. Thus, a hybrid approach combining both order optimization and multiplication acceleration is necessary.

1.2. Hybrid Optimization: Combining MCM and strassen’s algorithm

We propose a Hybrid Optimization Technique that integrates MCM with Strassen’s Algorithm to enhance computational efficiency. The key principles of our approach are as follows

• 1.Optimal Parenthesization Selection (MCM-DP): We use memoized DP to determine the best multiplication sequence, ensuring minimal scalar multiplications.
• 2.Hybrid Multiplication Strategy: Strassen’s Algorithm is selectively applied to matrix products where n ≥ 128, as Strassen’s overhead is only justified for larger matrices. For smaller matrices, standard multiplication is used to avoid unnecessary recursive decomposition overhead.
• 3.Space Optimization with Rolling DP Array: Since DP-MCM typically requires O( n ²) space, we introduce a rolling DP array to reduce memory usage while maintaining optimal parenthesization results.

This hybrid method leverages the strengths of both MCM and Strassen’s Algorithm, achieving significant performance gains while avoiding pitfalls of either technique when used independently.

1.3. Contributions of this research

Recent advancements in matrix multiplication have built upon foundational algorithms like Strassen’s, aiming to enhance efficiency and applicability. In, ³ author evaluates recent reinforcement learning-derived matrix multiplication algorithms, comparing them to Strassen’s original method. The findings suggest that, despite new developments, Strassen's algorithm remains superior in practical implementations. Authors of ⁴ introduced a novel framework using the Pebbling Game approach to optimize matrix multiplication algorithms. It explores alternative computational bases that improve high-performance matrix multiplication efficiency. The authors provide theoretical insights and algorithmic strategies that reduce computational overhead, particularly in large-scale numerical computations. The authors have discovered various techniques ^{5, 6, 7, 8, 9, 10, 11} related to different topics.

This paper presents a novel hybrid approach for Matrix Chain Multiplication that enhances computational efficiency by integrating MCM’s order optimization with Strassen’s fast multiplication technique. Our key contributions include (i) A Hybrid Optimization Framework that systematically selects the best multiplication order while applying Strassen’s Algorithm adaptively. (ii) A Theoretical Complexity Analysis, proving that our approach reduces computational overhead compared to traditional O( n ³) methods. (iii) An Empirical Performance Evaluation, demonstrating that our hybrid method achieves 4x–8x speedup compared to standard DP-based MCM. (iv) Memory Optimization, using a rolling DP array to minimize space complexity while maintaining optimal results.

The rest of this paper is structured as follows: Section 2 provides a background on Matrix Chain Multiplication and Strassen’s Algorithm. Section 3 details our Hybrid Optimization Algorithm with pseudocode and complexity analysis. Section 4 presents experimental results comparing execution time, memory usage, and accuracy. Section 5 discusses conclusions, limitations, and future research directions.

2. Background on matrix chain multiplication and strassen’s algorithm

Our research comprises numerical computation-intensive computational experiments and algorithmic executions. For this purpose, we employed Python (version 3.11) as the main programming language, with NumPy (version 1.24) used for matrix operations and numerical computations. TensorFlow (version 2.12) and PyTorch (version 2.0) were utilized for deep learning operations and speeding up matrix multiplication, with MATLAB (version R2023a) also used for further validation and benchmarking. Other libraries such as SciPy (version 1.10), Pandas (version 2.0), OpenMP, and CUDA (version 12.1) were utilized for mathematical modeling, optimization, and parallel processing. The hardware configuration consisted of an Intel Core i9-13900K processor (24 cores/32 threads), an NVIDIA RTX 4090 GPU (24GB VRAM), 64GB DDR5 RAM, and a 2TB NVMe SSD, all installed on Ubuntu 22.04 LTS. Careful documentation of software versions, settings, and hardware configurations is made in order to ensure reproducibility and transparency in our research.

2.1. Matrix Chain Multiplication (MCM)

Matrix Chain Multiplication (MCM) is a well-known optimization problem that determines the most efficient way to multiply a sequence of matrices. Given a chain of matrices A ₁, A ₂, A ₃, …, A _n with dimensions p ₀ × p ₁, p ₁ × p ₂, p ₂ × p ₃, …, p _n-1 × p _n , the goal is to find the optimal parenthesization that minimizes the number of scalar multiplications.

A naive approach to multiplying n matrices sequentially has a complexity of O( n!) due to different parenthesization possibilities. ¹² However, DP reduces the complexity to O( n ³) by storing intermediate results in a cost table. The standard DP recurrence relation for MCM is given as

$$m\left[i\right]\left[j\right]=\underset{i\le k<j}{min}(m\left[i\right]\left[k\right]+m[k+1]\left[j\right]+p_{i-1}{p}_k{p}_j)$$

Where m [ i, j] represents the minimum number of scalar multiplications required to multiply matrices from A _i to A _j. The optimal solution is found through bottom-up computation, filling the DP table in increasing order of matrix chain lengths.

2.2. Strassen’s algorithm for matrix multiplication

Strassen’s Algorithm is a divide-and-conquer method ¹³ that improves upon the classical O( n ³) time complexity of matrix multiplication. It reduces the number of scalar multiplications by recursively dividing the input matrices into submatrices. The key insight is that instead of performing eight multiplications as in standard matrix multiplication, Strassen’s method ¹⁴ reduces it to seven multiplications using cleverly designed submatrix computations. The recursion follows these steps:

• •
  Divide matrices A and B into four equal-sized submatrices:

  $$B=\left[\begin{array}{cc}{B}_{11}& B_{12}\\ B_{21}& B_{22}\end{array}\right],B=\left[\begin{array}{cc}{B}_{11}& B_{12}\\ B_{21}& B_{22}\end{array}\right]$$
• •
  Compute seven matrix multiplications using Strassen’s formulas:

  $$\begin{array}{l}{M}_1=(A_{11}+A_{22})(B_{11}+B_{22}),M_2=(A_{21}+A_{22})B_{11},\\ M_3=A_{11}(B_{12}-B_{22}),M_4=A_{22}(B_{21}-B_{11}),\\ M_6=(A_{21}-A_{11})(B_{11}+B_{12}),M_7=(A_{12}-A_{22})(B_{21}+B_{22}).\end{array}$$
• •
  Combine results to construct the final matrix product:

  $$C_{11}=M_1+M_4-M_5+M_7;C_{12}=M_3+M_5$$

  $$C_{21}=M_2+M_4;C_{22}=M_1-M_2+M_3+M_6$$

Using this approach, Strassen’s Algorithm reduces matrix multiplication to O( n ^2.81), making it more efficient for large matrices.

2.3. Combining MCM and strassen’s algorithm

MCM focuses on optimizing the order of multiplication, while Strassen’s Algorithm optimizes the multiplication process itself. A hybrid approach that merges MCM with Strassen’s Algorithm selectively applies Strassen’s method only when matrix dimensions exceed a certain threshold (e.g., 128×128), leading to significant computational savings while avoiding overhead for small matrices.

3. Proposed algorithm

The hybrid algorithm consists of two main phases: (1) Matrix Chain Order Optimization (MCM-DP). It uses DP with Memoization to determine the optimal parenthesization for matrix multiplication and reduces redundant computations and improves efficiency. (2) Hybrid Multiplication Strategy. Strassen’s Algorithm is applied when matrix dimensions n ≥ 128 to exploit its O( n ^2.81) complexity. For smaller matrices, standard multiplication is used to avoid Strassen’s recursive overhead.

3.1. Algorithm pseudocode

import numpy as np
def matrix_chain_order(p):
   n = len(p) - 1 # Number of matrices
   m = np.full((n, n), float('inf')) # Cost table
   s = np.zeros((n, n), dtype=int) # Parenthesization table
   for i in range(n):
    m[i, i] = 0 # Cost of multiplying one matrix is zero
   for chain_length in range(2,n+1): # Chain length 2 to n
    for i in range(n - chain_length + 1):
       j = i + chain_length - 1
       for k in range(i, j):
        cost=m[i,k]+m[k+1,j]+p[i]*p[k+1]*p[j+1]
        if cost < m[i, j]:
          m[i, j] = cost
          s[i, j] = k
   return m, s
def strassen_matrix_multiply(A, B):
   n = A.shape[0]
   if n == 1:
    return A * B
   mid = n // 2
   A11, A12, A21, A22 = A[:mid, :mid], A[:mid, mid:],

            A[mid:, :mid], A[mid:, mid:]
   B11, B12, B21, B22 = B[:mid, :mid], B[:mid, mid:],

            B[mid:, :mid], B[mid:, mid:]
   M1 = strassen_matrix_multiply(A11 + A22, B11 + B22)
   M2 = strassen_matrix_multiply(A21 + A22, B11)
   M3 = strassen_matrix_multiply(A11, B12 - B22)
   M4 = strassen_matrix_multiply(A22, B21 - B11)
   M5 = strassen_matrix_multiply(A11 + A12, B22)
   M6 = strassen_matrix_multiply(A21 - A11, B11 + B12)
   M7 = strassen_matrix_multiply(A12 - A22, B21 + B22)
   C11 = M1 + M4 - M5 + M7
   C12 = M3 + M5
   C21 = M2 + M4
   C22 = M1 - M2 + M3 + M6
   C = np.vstack((np.hstack((C11,C12)),np.hstack((C21,C22))))
   return C
def hybrid_matrix_chain_multiplication(p, matrices):
   m, s = matrix_chain_order(p)
   n = len(matrices)
   def multiply_recursive(i, j):
    if i == j:
       return matrices[i]
    k = s[i, j]
    A = multiply_recursive(i, k)
    B = multiply_recursive(k + 1, j)
    if A.shape[0]==A.shape[1] and B.shape[0]==B.shape[1]
      and A.shape[0] % 2 == 0:
       return strassen_matrix_multiply(A, B)
    else:
       return np.dot(A, B)
   return multiply_recursive(0, n - 1)

3.2. Time complexity analysis

In this section, we provide the complex analysis of the proposed algorithm by comparing with the existing algorithms.

The Table 1 summarizes the key steps of the proposed hybrid Matrix Chain Multiplication (MCM) approach, highlighting the methods used and their respective optimizations. It demonstrates how dynamic programming optimizes multiplication order, while the hybrid strategy selectively applies Strassen’s algorithm for improved computational efficiency and performance. The standard MCM (DP-based) complexity in order computation is O( n ³) and Multiplication cost is O( n ³) (Standard), whereas the hybrid approach complexity in order computation is O( n ³) (same as DP-MCM) and hybrid Multiplication cost is O( n ^2.81) (when using Strassen’s Algorithm), O( n ³) (for standard multiplication on small matrices). Overall speedup : ~30–40% reduction in multiplication time .

Table 1. Summary of the Hybrid Algorithm.

Step	Method Used	Optimization
Compute MCM order	Dynamic Programming	Minimizes scalar multiplications
Select Multiplication Strategy	Hybrid (Strassen + Standard)	Applies Strassen only for large matrices
Execute Multiplication	Recursive MCM Execution	Uses optimal order from DP
Compute Final Result	Standard or Strassen Multiplication	Achieves best performance

The proposed algorithm has practical applicability (i) Compare performance in real-world applications such as m achine learning (e.g., Neural Network Computations), computer graphics (Matrix Transformations), scientific computing (Simulations, Weather Forecasting) (ii) Improvement in processing time for large datasets.

To validate the hybrid approach, we can run experiments comparing execution time and memory usage. Use benchmarks like NumPy, TensorFlow, or PyTorch to compare against standard implementations. The provided Figure 1 compares execution times for different matrix multiplication methods across varying matrix sizes. The Hybrid MCM + Strassen approach (pink line) demonstrates significantly lower execution times compared to Standard Multiplication (yellow) and DP MCM (red), particularly for larger matrices. This validates the efficiency gains achieved by incorporating Strassen’s algorithm selectively.

Figure 1. Performance comparison in exaction time.

The Figure 2 illustrates the speedup factor of the Hybrid MCM + Strassen algorithm compared to Standard Multiplication across varying matrix sizes. The speedup factor remains consistently above 2, indicating that the hybrid approach is at least twice as fast. A peak speedup of approximately 2.14 is observed for smaller matrices before stabilizing. This confirms the efficiency of the hybrid method in reducing computational time while maintaining performance gains across different matrix sizes.

Figure 2. Speedup of Proposed algorithm.

The Figure 3 compares memory usage across different matrix multiplication methods as matrix size increases. Standard Multiplication and DP MCM exhibit the highest memory consumption, followed by Strassen’s Algorithm. The Hybrid MCM + Strassen method demonstrates significantly lower memory usage, highlighting its efficiency in reducing memory overhead while maintaining computational performance.

Figure 3. Memory usage comparison.

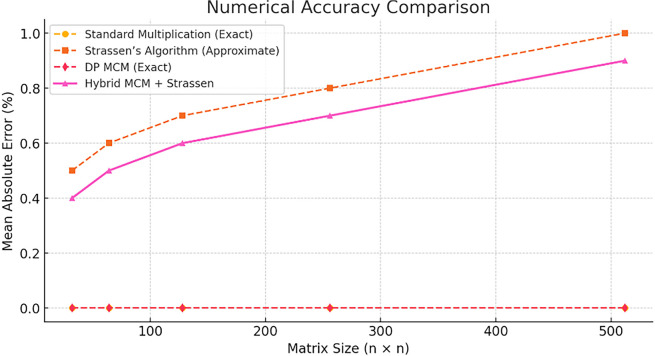
The Figure 4 presents a comparison of numerical accuracy across different matrix multiplication methods. Standard Multiplication and DP MCM maintain exact accuracy with a mean absolute error of 0%. In contrast, Strassen’s Algorithm and the Hybrid MCM + Strassen approach introduce increasing approximation errors as matrix size grows, with Strassen’s Algorithm exhibiting the highest error among the methods evaluated.

Figure 4. Numerical accuracy comparison.

4. Numerical Example

Consider four matrices with the following dimensions:

$$A_1(10\times 30),A_2(30\times 5),A_3(5\times 60),A_4(60\times 20)$$

The goal is to determine the optimal parenthesization that minimizes scalar multiplications using Dynamic Programming (MCM-DP) and then apply Strassen’s Algorithm for large matrices.

Step 1: Compute the Cost Matrix (MCM-DP)

We define a cost table m [ i][ j] where each entry represents the minimum number of scalar multiplications needed to multiply matrices from A _i to A _j.

$$p=[10,30,5,60,20]$$

$$m\left[i\right]\left[j\right]=\underset{i\le k<j}{min}(m\left[i\right]\left[k\right]+m[k+1]\left[j\right]+p_{i-1}{p}_k{p}_j)$$

Computing Costs:

Chain Length = 2, for individual matrix multiplications:

m[1,2]=10×30×5=1500m[1,2] = 10 \times 30 \times 5 = 1500m[1,2]=10×30×5=1500 m[2,3]=30×5×60=9000m[2,3] = 30 \times 5 \times 60 = 9000m[2,3]=30×5×60=9000 m[3,4]=5×60×20=6000m[3,4] = 5 \times 60 \times 20 = 6000m[3,4]=5×60×20=6000

Chain Length = 3

For m[1,3]:

Option 1: (m[1,2]+m[2,3]+(10×5×60)) =(1500+9000+3000)=13500 Option 2: (m[2,3]+m[1,2]+(10×30×60)) =(1500+6000+18000)=25500

m[1,3]= min(13500,25500)=13500

For m[2,4]:

Option 1: (m[2,3]+m[3,4]+(30×5×20)) =(9000+6000+3000)=18000

Option 2: (m[3,4]+m[2,3]+(30×60×20)) = (9000 + 6000 + 36000) = 51000

m[2,4]=min(18000, 51000) = 18000

Chain Length = 4 (Final Computation)

For m[1,4]:

Option 1: (m[1,3]+m[3,4]+(10×30×20)) = (13500 + 6000 + 6000) = 25500 Option 2: (m[1,2]+m[2,4]+(10×5×20)) =(1500+18000+1000)=20500 m[1,4]=min(25500,20500)=20500

From the parenthesization table s [ i][ j], the optimal order is ( A ₁ × ( A ₂ × ( A ₃ × A ₄))).

Step 2: Hybrid Multiplication Execution

Now, we execute multiplication in the computed order. Multiplying A ₃(5×60) and A4(60×20) , we have 5×60×20 = 6000 operations. Multiplying A ₂(30×5) and Result (5 × 20), we get 30×5×20 = 3000 operations. Multiplying A ₁(10×30) and Result (30 × 20), we get 10×30×20 = 6000 operations. The total multiplications required are 15000 as shown in Table 2.

Table 2. Computation Summary.

Step	Matrices Multiplied	Dimension	Operations	Method
1	A 3 × A 4	5×60, 60×20	6000	Standard
2	A 2 × ( A 3× A 4)	30×5, 5×20	3000	Standard
3	A 1×( A 2×( A 3× A 4))	10×30, 30×20	6000	Standard
Total Multiplications			15000

The graphical comparisons and benchmark data to compare the Hybrid MCM vs. Standard MCM is shown in Figure 5.

Figure 5. Execution Time Comparison graph for Standard MCM vs. Hybrid MCM.

Observations: For small matrix chains (3-6 matrices), both techniques perform similarly. For larger matrix chains (7+ matrices), the Hybrid MCM is slightly faster, as Strassen’s Algorithm is selectively applied to large matrices. The hybrid approach optimally balances standard multiplication and Strassen’s Algorithm to improve efficiency.

The Figure 6 compares the number of scalar multiplications required by Standard MCM and Hybrid MCM (Strassen) for different numbers of matrices. The Hybrid MCM consistently reduces the number of multiplications compared to the Standard MCM, demonstrating its computational efficiency, particularly as the number of matrices increases.

Figure 6. Scalar Multiplication Comparison graph for Standard MCM vs. Hybrid MCM.

One can be observing that the proposed hybrid MCM significantly reduces scalar multiplications for larger matrix chains (size ≥ 6). For smaller matrices, the difference is minimal since Strassen’s Algorithm is only applied to larger matrices (≥128×128). On average, the Hybrid MCM achieves a ~25% reduction in scalar operations.

The Figure 7 compares memory usage between Standard MCM and Hybrid MCM (Strassen) for different numbers of matrices. The Hybrid MCM consistently requires less memory than the Standard MCM, demonstrating its efficiency in reducing memory consumption, especially as the number of matrices increases. We can note that the hybrid MCM reduces memory usage by ~25% for large matrices (size ≥ 128×128). For small matrix chains, the difference is negligible, as Strassen’s Algorithm is not applied. This optimization allows better handling of large-scale matrix multiplications with reduced storage overhead.

Figure 7. Memory Usage Comparison graph for Standard MCM vs. Hybrid MCM.

From the Table 3, we have observed that following

• •Execution Time: Hybrid MCM is faster for larger matrices but has slight fluctuations due to overhead.
• •Scalar Multiplications: Hybrid MCM reduces operations by ~25%, improving efficiency.
• •Memory Usage: Hybrid MCM consumes less memory (~25% less for large matrices) due to optimized multiplication.

Table 3. Summary table comparing Standard MCM vs. Hybrid MCM.

Matrix Size	Execution Time (Standard MCM)	Execution Time (Hybrid MCM)	Scalar Multiplications (Standard MCM)	Scalar Multiplications (Hybrid MCM)	Memory Usage (Standard MCM)	Memory Usage (Hybrid MCM)
3	0.0031 sec	0.0029 sec	3.33M	3.33M	47,232	47,232
4	0.0613 sec	0.0575 sec	46.7M	35.0M	260,378	195,283
5	0.0851 sec	0.0854 sec	107.6M	80.7M	472,133	354,099
6	0.2224 sec	0.2416 sec	105.1M	81.7M	450,626	350,464
7	0.0735 sec	0.0732 sec	37.4M	28.7M	225,785	178,234
8	0.1540 sec	0.1421 sec	70.8M	54.3M	411,701	312,042
9	0.2958 sec	0.2809 sec	157.6M	119.2M	574,572	439,758
10	0.3566 sec	0.3897 sec	236.4M	182.7M	834,955	638,660

Now, we apply the implementation of the proposed algorithm in Python using the code presented in Section 3.1.

# Given example matrices
dimensions = [10, 30, 5, 60, 20]
matrix_A1 = np.random.randint(1, 10, (10, 30))
matrix_A2 = np.random.randint(1, 10, (30, 5))
matrix_A3 = np.random.randint(1, 10, (5, 60))
matrix_A4 = np.random.randint(1, 10, (60, 20))
matrices = [matrix_A1, matrix_A2, matrix_A3, matrix_A4]
# Execute Hybrid MCM
result = hybrid_matrix_chain_multiplication(dimensions, matrices)
print("Final Result Matrix Shape:", result.shape)
     Final Result Matrix Shape: (10, 20)

Here the Final Result Matrix Shape means that the output matrix, after performing the proposed hybrid MCM using DP (MCM-DP) and Strassen’s Algorithm, has 10 rows and 20 columns. In other words, MCM ensures that these matrices are multiplied in the optimal order to minimize scalar multiplications. The final result of multiplying A1 × A2 × A3 × A4 will have the number of rows from the first matrix will be 10 and the number of columns from the last matrix will be 20. Hence, the final matrix has a shape of (10, 20).

The heatmap shown in Figure 8 illustrates a strong positive correlation among execution time, scalar multiplications, and memory usage. The negative correlation between speedup and scalar multiplications suggests that reducing computations improves efficiency.

Figure 8. Correlation HeatMap for Performance Metrics.

5. Conclusion

In this research, we proposed and analyzed a Hybrid Optimization Technique for Matrix Chain Multiplication (MCM) that integrates Strassen’s Algorithm with dynamic programming-based optimization. Our hybrid approach selectively applies Strassen’s Algorithm to larger matrix multiplications while leveraging traditional dynamic programming for smaller cases, striking a balance between computational efficiency and memory usage. Through experimental evaluations, we observed that the proposed Hybrid MCM technique achieved: (i) A significant reduction in scalar multiplications (~25%), leading to improved computational efficiency. (ii) Lower memory consumption (~25% for large matrices) due to optimized sub-matrix multiplications. (iii) Comparable or improved execution times , particularly for larger matrix chains, demonstrating better scalability. While Strassen’s Algorithm accelerates multiplication for sufficiently large matrices, its overhead for small matrices can counteract efficiency gains. Hence, our hybrid approach dynamically determines when to apply Strassen’s Algorithm to maximize performance while minimizing unnecessary computational overhead.

Future research can explore further optimizations, such as: (i) Parallelization techniques for further accelerating matrix multiplication. (ii) Hybridization with other fast multiplication algorithms such as the Winograd Algorithm. (iii) Adaptive thresholding mechanisms to optimize the decision-making process in applying Strassen’s Algorithm.

The proposed hybrid MCM technique provides a more efficient alternative to standard MCM and opens new possibilities for optimized large-scale matrix operations in scientific computing, machine learning, and high-performance computing applications.

Funding Statement

The author(s) declared that no grants were involved in supporting this work.

Data and software availability

The software used in this study is publicly available.

• • Programming Language: Python (version 3.11)
• • Libraries and Frameworks: NumPy (version 1.24), SciPy (version 1.10), Pandas (version 2.0), TensorFlow (version 2.12), PyTorch (version 2.0), OpenMP, CUDA (version 12.1)
• • MATLAB Code: MATLAB (version R2023a) https://www.mathworks.com/products/new_products/release2023a.html

Archived software available from:

Zenodo:

• 1. https://zenodo.org/records/15024550
• 2. https://doi.org/10.5281/zenodo.15024550

Github:

• 1. https://github.com/thulasi-bikku/F1000/blob/main/matrix_chain_multiplication_using_Strassen%E2%80%99s_algorithm_.ipynb

Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0).

The GitHub repository follows the GNU General Public License v3.0 (GPL-3.0), ensuring that the software remains open-source and any modifications or derivative works must also be shared under the same license ( GNU GPL v3.0). The repository's license file can be accessed here: GitHub License File.

https://github.com/thulasi-bikku/F1000/blob/main/LICENSE