Estimation of parameters and hypothesis testing of multivariate spatial autoregressive model

Abstract

Spatial dependence plays a critical role in modeling multivariate response variables, particularly in fields such as epidemiology and environmental studies. However, existing spatial regression models, such as the Spatial Autoregressive (SAR) model, are designed for univariate responses and are insufficient when multiple response variables are influenced by spatial location. To address this gap, we introduce a Multivariate Spatial Autoregressive (MSAR) model. While previous research has focused primarily on parameter estimation for the proposed model, limited attention has been given to the statistical significance of these parameters. Moreover, existing estimation methods often rely on pseudo-distributions, which may not accurately reflect the underlying data characteristics. This study employs Maximum Likelihood Estimation (MLE), optimized using a concentrated log-likelihood approach, under the assumption of normally distributed data. To assess parameter significance, we apply both the Maximum Likelihood Ratio Test (MLRT) for joint hypotheses and the Wald Test for individual parameters. The findings confirm that the proposed model yields unbiased and consistent parameter estimates. Furthermore, the significance tests reveal key predictor variables associated with pneumonia and diarrhea cases among toddlers. The proposed model achieves a Root Mean Square Error of 5 and an R-squared value of 60 %, demonstrating its effectiveness in capturing spatial dependence in multivariate settings. The main contributions of this study include:

• •Development of a MSAR model estimated using MLE to capture spatial dependencies among multiple response variables.
• •Implementation of formal hypothesis testing procedures for model parameters using the Likelihood Ratio and Wald tests.
• •Application of the proposed model to spatial health data at the village level in Tuban District, East Java, Indonesia, focusing on health problems among children under five.

Graphical abstract

Specifications table

Subject area:	Mathematics and Statistics
More specific subject area:	Spatial Statistics, Spatial dependency, Multivariate Spatial Linear Models
Name of your method:	Multivariate Spatial Autoregressive Model
Name and reference of original method:	Original method: Multivariate Linear Regression. References: •Christensen, R.: Linear Models for Multivariate, Time Series, and Spatial Data. New York: Springer Science+Business Media (1991). •Johnson, R.A., & Wichern, D.W.: Applied Multivariate Statistical Analysis. New Jersey: Pearson Education, Inc (2007).
Resource availability:	None

Background

Spatial analysis has become a fundamental methodology in scientific research, particularly when the data exhibits a strong geographical component [1,2]. One widely used technique for addressing spatial dependence is the SAR model [[3], [4], [5]], which incorporates spatially lagged dependent variables to account for spatial autocorrelation. SAR models have been extensively studied with regard to parameter estimation and hypothesis testing. Among the available techniques, MLE is the most commonly used and yields consistent estimates [[6], [7], [8]]. However, a key challenge in estimating SAR model parameters is that the spatial effect parameters do not have closed-form solutions, so numerical iteration is required. In addition to estimation, hypothesis testing is typically conducted using the Likelihood Ratio Test (LRT) for joint significance and the Wald Test for individual parameters [[9], [10], [11]].

The SAR model has evolved into the MSAR model in econometric applications, with estimation methods including Quasi-Maximum Likelihood Estimation (QMLE) [12,13], Two-Stage Least Squares (2SLS) [14,15], and Three-Stage Least Squares (3SLS) [16,17]. However, when identification conditions are not met in complex spatial models, parameter estimates may become invalid, affecting the reliability of QMLE. Additionally, QMLE generally provides less efficient estimates than fully specified MLE, assuming the model is correctly specified [18]. More recent work has incorporated MSAR within simultaneous equation models, using the FGLS-3SLS estimation approach and numerical approximation via the average concentrated log-likelihood [16]. While that approach allows spatial effects to be estimated, it is still limited to univariate optimization. Thus, In this study, we extend this approach by applying multivariate optimization to the concentrated log-likelihood using the L-BFGS-B algorithm [[19], [20], [21]]. MSAR models have also been extended to network data. For example, Zhu and Huang (2020) compared QMLE and Least Squares Estimation (LSE) methods [22,23], but LSE remains less effective in handling parameter estimation in complex models, thus highlighting the need for a better methodology in this area using MLE methods that are able to provide accurate and consistent estimates. In addition, most existing studies have focused on parameter estimation without addressing hypothesis testing, which is essential for improving the accuracy and reliability of model predictions and evaluating regression parameters that can vary geographically.

This study proposes an area-based MSAR model for multivariate responses, designed to capture the spatial interaction between more than one correlated response variables, while considering the spatial dependence across regions Parameter estimation is carried out using MLE for the regression coefficients and the covariance matrix, with spatial parameters estimated via the concentrated log-likelihood function optimized using the L-BFGS-B algorithm [24]. In addition to estimation, hypothesis testing is performed using both the LRT and the Wald Test to evaluate spatially varying regression parameters.

Method details

The MSAR model is an extension of the SAR model that incorporates spatial dependencies into the analysis. In this model, the global structure is modeled using multivariate normal linear regression. Therefore, before discussing the MSAR model in detail, this section introduces the foundational concept of multivariate linear regression.

Multivariate normal linear regression

A multivariate linear regression model describes the relationship among multiple response variables and their corresponding predictors. This model is used to determine the relationship between the response variables $Y_1,Y_2,...,Y_p$ and the predictor variables $A_1,A_2,...,A_q$. Given a sample of n observations and suppose $j=1,2,...,p$, the multivariate normal linear regression model for the i-th observation, $i=1,2,...,n$, is represented in Eq. (1).

$$\begin{array}{ccc}\hfill Y_{1i}& =& {\beta }_{01}+{\beta }_{11}{A}_{1i}+...+{\beta }_{q1}{A}_{qi}+{\epsilon }_{1i}\hfill \\ \hfill Y_{2i}& =& {\beta }_{02}+{\beta }_{12}{A}_{1i}+...+{\beta }_{q2}{A}_{qi}+{\epsilon }_{2i}\hfill \\ & & ⋮\hfill \\ \hfill Y_{ji}& =& {\beta }_{0j}+{\beta }_{1j}{A}_{1i}+...+{\beta }_{qj}{A}_{qi}+{\epsilon }_{ji}\hfill \end{array}$$ (1)

The multivariate linear regression model can be expressed in matrix form as illustrated in Eq. (2).

$${\mathbf{Y}}_{(n\times p)}={\mathbf{A}}_{n\times (q+1)}{\mathbf{B}}_{(q+1)\times p}+{\mathit{\Xi }}_{(n\times p)}$$ (2)

With

$$\mathbf{Y}=\left[\begin{array}{cc}{\mathbf{y}}_1& {\mathbf{y}}_2\cdots {\mathbf{y}}_p\end{array}\right],\mathbf{A}=\left[\begin{array}{ccccc}1& A{}_{11}& A{}_{21}& \cdots & A{}_{q1}\\ 1& A{}_{12}& A{}_{22}& \cdots & A{}_{q2}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& A{}_{1n}& A{}_{2n}& \cdots & A{}_{qn}\end{array}\right],\mathbf{B}=\left[\begin{array}{cc}{\mathit{\beta }}_1& {\mathit{\beta }}_2\cdots {\mathit{\beta }}_p\end{array}\right],\mathit{\Xi }=\left[\begin{array}{cc}{\mathit{\varepsilon }}_1& {\mathit{\varepsilon }}_2\cdots {\mathit{\varepsilon }}_p\end{array}\right]$$

where ${\mathbf{y}}_j={\left[Y_{j1}{Y}_{j2}\dots Y_{jn}\right]}^T;j=1,2,...,p$; ${\mathit{\beta }}_j={\left[{\beta }_{0j}{\beta }_{1j}\dots {\beta }_{qj}\right]}^T;j=1,2,...,p$ and ${\mathit{\varepsilon }}_j={\left[{\epsilon }_{j1}{\epsilon }_{j2}\dots {\epsilon }_{jn}\right]}^T;j=1,2,...,p$. Furthermore, the multivariate linear regression model can be expressed in the form of a Vec operator and Kronecker product, as demonstrated in Eq. (3).

$$Vec{\left(\mathbf{Y}\right)}_{pn\times 1}={({\mathbf{I}}_p\otimes \mathbf{A})}_{pn\times p(q+1)}Vec{\left(\mathbf{B}\right)}_{p(q+1)\times 1}+Vec{\left(\mathit{\Xi }\right)}_{pn\times 1}$$ (3)

In Eq. (3), an assumption was made that $Vec\left(\mathit{\Xi }\right)\sim \mathbf{N}\left(\mathbf{0},{\mathbf{\Sigma }}_{p\times p}\otimes {\mathbf{I}}_{n\times n}\right)$ with$E\left(Vec\right(\mathit{\Xi }\left)\right)=0$and $Cov\left(Vec\left(\mathit{\Xi }\right)\right)={\mathbf{\Sigma }}_{p\times p}\otimes {\mathbf{I}}_{n\times n}$. Based on this assumption, $Vec\left(\mathbf{Y}\right)$ has a distribution of $Vec\left(\mathbf{Y}\right)\sim N_{pn}(({\mathbf{I}}_p\otimes \mathbf{A})Vec\left(\mathbf{B}\right),\mathbf{\Sigma }\otimes {\mathbf{I}}_n)$. The probability density function of $Vec\left(\mathbf{Y}\right)$ is therefore given by the following expression.

$$f\left(Vec\left(\mathbf{Y}\right)\right)={\left(2\pi \right)}^{-pn/2}{\left|\Sigma \right|}^{-n/2}\exp \left(-\frac{1}{2}{\left(Vec\left(\mathbf{Y}\right)-\left(\left({\mathbf{I}}_p\otimes \mathbf{A}\right)Vec\left(\mathbf{B}\right)\right)\right)}^T{\left(\mathbf{\Sigma }\otimes {\mathbf{I}}_n\right)}^{-1}\left(Vec\left(\mathbf{Y}\right)-\left(\left({\mathbf{I}}_p\otimes \mathbf{A}\right)Vec\left(\mathbf{B}\right)\right)\right)\right)$$

Further parameter estimation can be carried out using the MLE method, resulting in the following parameter estimators [25].

$$Vec\left(\widehat{\mathbf{B}}\right)=\left(\mathbf{I}\otimes {\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T\right)\left(Vec\left(\mathbf{Y}\right)\right)$$

$$\widehat{\Sigma }=\frac{\left({\mathbf{Y}}^T(\mathbf{I}-\mathbf{A}{\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T)\mathbf{Y}\right)}{n}$$

Multivariate spatial autoregressive

The MSAR model is a further development of the SAR model. Consequently, the analogy of the MSAR model can be traced back to the univariate SAR model. The MSAR model is used to determine the relationship between the response variables and the predictor variables by considering the spatial effect of the lag of the response variables symbolized by ρ and the spatial weight symbolized by W. The MSAR model is mathematically illustrated by Eq. (4):

$$\begin{array}{ccc}\hfill Y_{1i}& =& {\rho }_1{\mathbf{w}}_i{Y}_{1i}+{\mathbf{a}}^T{\mathit{\beta }}_1+{\epsilon }_{1i}\hfill \\ \hfill Y_{2i}& =& {\rho }_2{\mathbf{w}}_i{Y}_{2i}+{\mathbf{a}}^T{\mathit{\beta }}_2+{\epsilon }_{2i}\hfill \\ & & ⋮\hfill \\ \hfill Y_{pi}& =& {\rho }_p{\mathbf{w}}_i{Y}_{pi}+{\mathbf{a}}^T{\mathit{\beta }}_p+{\epsilon }_{pi}\hfill \end{array}$$ (4)

Eq. (4) can be decomposed into the following equation:

$$\left[\begin{array}{c}{Y}_{1i}\\ \begin{array}{c}{Y}_{2i}\hfill \\ ⋮\hfill \\ Y_{pi}\hfill \end{array}\end{array}\right]=\left[\begin{array}{c}{\mathit{\beta }}_{01}+{\rho }_1\sum _{i*=1,i\ne i*}^n{w}_{ii*}{\mathbf{y}}_{1i*}+{\mathbf{a}}^T{\mathit{\beta }}_1+{\epsilon }_{1i}\\ \begin{array}{c}{\mathit{\beta }}_{02}+{\rho }_2\sum _{i*=1,i\ne i*}^n{w}_{ii*}{\mathbf{y}}_{2i*}+{\mathbf{a}}^T{\mathit{\beta }}_2+{\epsilon }_{2i}\hfill \\ ⋮\hfill \\ {\mathit{\beta }}_{0p}+{\rho }_p\sum _{i*=1,i\ne i*}^n{w}_{ii*}{\mathbf{y}}_{pi*}+{\mathbf{a}}^T{\mathit{\beta }}_p+{\epsilon }_{pi}\hfill \end{array}\end{array}\right]$$

The MSAR model in matrix form can be written as Eq. (5), with ρ is diagonal in form, with the elements ${\rho }_1,{\rho }_2,...,{\rho }_p$ representing the spatial effects on each of the response variables.

$${\mathbf{Y}}_{n\times p}={\mathbf{W}}_{n\times n}{\mathbf{Y}}_{n\times p}{\mathit{\rho }}_{p\times p}+{\mathbf{A}}_{n\times (q+1)}{\mathbf{B}}_{(q+1)\times p}+{\mathit{\Xi }}_{n\times p}$$ (5)

If the MSAR model is written in the form of a Vec operator and using a Kronecker product, the resulting equation is given by Eq. (6).

$$Vec\left(\mathbf{Y}\right)=\left({\mathit{\rho }}^T\otimes \mathbf{W}\right)Vec\left(\mathbf{Y}\right)+\left({\mathbf{I}}_2\otimes \mathbf{A}\right)Vec\left(\mathbf{B}\right)+Vec\left(\mathit{\Xi }\right)$$

$$Vec\left(\mathbf{Y}\right)={\left(\mathbf{I}-\left({\mathit{\rho }}^T\otimes \mathbf{W}\right)\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{A}\right)Vec\left(\mathbf{B}\right)+{\left(\mathbf{I}-\left({\mathit{\rho }}^T\otimes \mathbf{W}\right)\right)}^{-1}Vec\left(\mathit{\Xi }\right)$$ (6)

The MSAR model assumes that the error term follows a bivariate normal distribution with mean $E\left(Vec\right(\mathit{\Xi }\left)\right)=\mathbf{0}$ and covariance matrix $Var\left(Vec\left(\mathit{\Xi }\right)\right)=\mathbf{\Sigma }\otimes {\mathbf{I}}_n$ [16]. The expectation and variance of $Vec\left(\mathbf{Y}\right)$are shown in the following equation:

$$E\left(Vec\left(\mathbf{Y}\right)\right)={\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{A}\right)Vec\left(\mathbf{B}\right)$$

$$Var\left(Vec\left(\mathbf{Y}\right)\right)={\left({\mathbf{I}}_{pn}-\left({\mathit{\rho }}^T\otimes \mathbf{W}\right)\right)}^{-1}(\mathbf{\Sigma }\otimes {\mathbf{I}}_n){\left({\mathbf{I}}_{pn}-\left(\mathit{\rho }\otimes {\mathbf{W}}^T\right)\right)}^{-1}$$

Once the expectation and variance of $Vec\left(\mathbf{Y}\right)$are established, the distribution of $Vec\left(\mathbf{Y}\right)$ is given by:

$$Vec\left(\mathbf{Y}\right)\sim N_{pn}\left({\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{A}\right)Vec\left(\mathbf{B}\right),{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left(\mathbf{\Sigma }\otimes {\mathbf{I}}_n\right){\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right)}^{-1}\right).$$

Parameter estimation of MSAR model

The MSAR parameters were estimated using the MLE estimation method combined with the numerical approximation of the concentrated log-likelihood using the L-BFGS-B optimization method. The MLE method is applied to estimate the regression coefficients and the variance-covariance matrix. The spatial effects were estimated by maximizing the concentrated log-likelihood function using the L-BFGS-B optimization method. The first step is to determine the likelihood function of the model in question. The likelihood function of the MSAR model is presented in Eq. (7).

$$\begin{array}{ccc}\hfill L\left(Vec\left(\mathbf{B}\right),\mathbf{\Sigma },\mathit{\rho }\right)& =& \prod _{i=1}^{n}f(Y_{1i},Y_{2i},...,Y_{pi})=f\left(Vec\left(\mathbf{Y}\right)\right)\hfill \\ & =& {\left(2\pi \right)}^{-pn/2}{\left|{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left(\mathbf{\Sigma }\otimes {\mathbf{I}}_n\right){\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right)}^{-1}\right|}^{-1/2}\hfill \\ & & \exp (-\frac{1}{2}{\left(Vec\left(\mathbf{Y}\right)-\left({\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{A}\right)Vec\left(\mathbf{B}\right)\right)\right)}^T\hfill \\ & & {\left({\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left(\mathbf{\Sigma }\otimes {\mathbf{I}}_n\right){\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right)}^{-1}\right)}^{-1}\hfill \\ & & \left(Vec\left(\mathbf{Y}\right)-\left({\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{A}\right)Vec\left(\mathbf{B}\right)\right)\right))\hfill \end{array}$$ (7)

Furthermore, the likelihood function is formulated in the form of a natural logarithm likelihood, as illustrated in Eq. (8).

$$\begin{array}{ccc}\hfill \ln L\left(Vec\left(\mathbf{B}\right),\mathbf{\Sigma },\mathit{\rho }\right)& =& \ln \left(\prod _{i=1}^{n}f(Y_{1i},Y_{2i},...,Y_{pi})\right)=\ln f\left(Vec\left(\mathbf{Y}\right)\right)\hfill \\ & =& -\frac{pn}{2}\ln (2\pi )-\frac{1}{2}\ln \left(\left|{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left(\mathbf{\Sigma }\otimes {\mathbf{I}}_n\right){\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right)}^{-1}\right|\right)\hfill \\ & & -\frac{1}{2}{\left(Vec\left(\mathbf{Y}\right)-\left({\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{A}\right)Vec\left(\mathbf{B}\right)\right)\right)}^T\hfill \\ & & \left(\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right){\left(\mathbf{\Sigma }\otimes {\mathbf{I}}_n\right)}^{-1}\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\right)\hfill \\ & & \left(Vec\left(\mathbf{Y}\right)-\left({\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{A}\right)Vec\left(\mathbf{B}\right)\right)\right)\hfill \end{array}$$ (8)

The subsequent stage in parameter estimation is to differentiate Eq. (8) with respect to the $Vec\left(\mathbf{B}\right)$ parameter and set it equal to zero, thereby obtaining an estimator for the $Vec\left(\mathbf{B}\right)$ parameter.

$$\begin{array}{ccc}\hfill \frac{\partial \ln L\left(Vec\left(\mathbf{B}\right),\mathbf{\Sigma },\mathit{\rho }\right)}{\partial Vec\left(\mathbf{B}\right)}& =& -2(\left({\mathbf{I}}_p\otimes {\mathbf{A}}^T\right){\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right)}^{-1}\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right)\left({\mathbf{\Sigma }}^{-1}\otimes {\mathbf{I}}_n\right)\hfill \\ & & \times \left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right))+2\left({\mathbf{I}}_p\otimes {\mathbf{A}}^T\right){\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right)}^{-1}\hfill \\ & & \times \left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right)\left({\mathbf{\Sigma }}^{-1}\otimes {\mathbf{I}}_n\right)\left(\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\right)\hfill \\ & & \left({\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{A}\right)Vec\left(\mathbf{B}\right)\right)=\mathbf{0}\hfill \end{array}$$

The result of the first derivative of $Vec\left(\mathbf{B}\right)$, which is equated to zero, is simplified to yield the $Vec\left(\mathbf{B}\right)$ estimator, symbolized by $Vec\left(\widehat{\mathbf{B}}\right)$, which is shown in Eq. (9).

$$Vec{\left(\widehat{\mathbf{B}}\right)}_{initial}=\left({\mathbf{I}}_p\otimes {\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right)$$ (9)

Once the $Vec\left(\mathbf{B}\right)$ parameter estimator has been obtained, the $\mathbf{\Sigma }$ parameter estimator can then be calculated. The steps involved in obtaining the$\mathbf{\Sigma }$parameter estimator is identical to those used for the $Vec\left(\mathbf{B}\right)$ parameter estimator. The initial step is to substitute $Vec\left(\mathbf{B}\right)$ into the ln-likelihood function in Eq. (8), with the estimated value given by Eq. (10).

$$\begin{array}{ccc}\hfill \ln L\left(Vec{\left(\widehat{\mathbf{B}}\right)}_{initial},\mathbf{\Sigma },\mathit{\rho }\right)& =& -\frac{pn}{2}\ln (2\pi )-\frac{1}{2}\ln \left(\left|{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left(\mathbf{\Sigma }\otimes {\mathbf{I}}_n\right){\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right)}^{-1}\right|\right)\hfill \\ & & -\frac{1}{2}(Vec\left(\mathbf{Y}\right)-{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{A}{\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T\right)\times \hfill \\ & & {\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right))}^T(\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right){\left(\mathbf{\Sigma }\otimes {\mathbf{I}}_n\right)}^{-1}\times \hfill \\ & & \left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right))(Vec\left(\mathbf{Y}\right)-{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\times \hfill \\ & & \left({\mathbf{I}}_p\otimes \mathbf{A}{\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right)).\hfill \end{array}$$ (10)

If we assume that $\mathbf{M}=\mathbf{A}{\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T$, then Eq. (10) can be rewritten as Eq. (11).

$$\begin{array}{ccc}\hfill \ln L\left(Vec{\left(\widehat{\mathbf{B}}\right)}_{initial},\mathbf{\Sigma },\mathit{\rho }\right)& =& -\frac{pn}{2}\ln (2\pi )-\frac{1}{2}\ln \left(\left|{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left(\mathbf{\Sigma }\otimes {\mathbf{I}}_n\right){\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right)}^{-1}\right|\right)\hfill \\ & & -\frac{1}{2}{\left(Vec\left(\mathbf{Y}\right)-{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{M}\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right)\right)}^T\hfill \\ & & \left(\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right){\left(\mathbf{\Sigma }\otimes {\mathbf{I}}_n\right)}^{-1}\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\right)\hfill \\ & & \left(Vec\left(\mathbf{Y}\right)-{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{M}\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right)\right).\hfill \end{array}$$ (11)

In Eq. (11), the final element in the quadratic form will yield a real number or a scalar, which is regarded as a $(1\times 1)$matrix [24]. Consequently, the trace of the element is the element itself. Hence, Eq. (11) can be rewritten as Eq. (12) and simplified through the utilization of the cyclic nature of the trace matrix.

$$\begin{array}{ccc}\hfill \ln L\left(\mathbf{\Sigma },\mathit{\rho }\right)& =& -\frac{pn}{2}\ln (2\pi )-\frac{1}{2}\ln \left(\left|{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left(\mathbf{\Sigma }\otimes {\mathbf{I}}_n\right){\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right)}^{-1}\right|\right)\hfill \\ & & -\frac{1}{2}tr[\left(\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right){\left(\mathbf{\Sigma }\otimes {\mathbf{I}}_n\right)}^{-1}\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\right)\times \hfill \\ & & \left(Vec\left(\mathbf{Y}\right)-{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{M}\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right)\right)\hfill \\ & & \times {\left(Vec\left(\mathbf{Y}\right)-{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{M}\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right)\right)}^T]\hfill \end{array}$$ (12)

Subsequently, the ln-likelihood function in Eq. (12) is derived from ${\sigma }_{jj*}$, which is illustrated in the following equation where ${\mathbf{T}}_{jj*}$ is a $\left(p\times p\right)$symmetrical matrix comprising element 1 in positions $\left(j,j^{*}\right)$and $\left(j^{*},j\right)$, and element 0 in all other row and column positions.

$$\begin{array}{ccc}\hfill \frac{\partial \ln \left(L\left(\mathbf{\Sigma },\mathit{\rho }\right)\right)}{\partial {\sigma }_{jj*}}& =& -\frac{1}{2}tr\left[\left({\mathbf{\Sigma }}^{-1}{\mathbf{T}}_{jj*}\otimes {\mathbf{I}}_n\right)\right]\hfill \\ & & +\frac{1}{2}tr[\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right)\left({\mathbf{\Sigma }}^{-1}{\mathbf{T}}_{jj*}{\mathbf{\Sigma }}^{-1}\otimes {\mathbf{I}}_n\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\times \hfill \\ & & \left(Vec\left(\mathbf{Y}\right)-{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{M}\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right)\right)\hfill \\ & & \times {\left(Vec\left(\mathbf{Y}\right)-{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{M}\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right)\right)}^T]=\mathbf{0}\hfill \end{array}$$

The partial derivative equal to zero is then solved by equalizing the form of the left equation with that of the right equation, thereby obtaining the estimator for the sigma parameter $\mathbf{\Sigma }$.

$$\begin{array}{ccc}\hfill \frac{1}{2}tr\left[\left({\mathbf{\Sigma }}^{-1}{\mathbf{T}}_{jj*}\otimes {\mathbf{I}}_n\right)\right]& =& \frac{1}{2}tr[\left({\mathbf{\Sigma }}^{-1}{\mathbf{T}}_{jj*}{\mathbf{\Sigma }}^{-1}\otimes {\mathbf{I}}_n\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)(Vec\left(\mathbf{Y}\right)-{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\hfill \\ & & \times \left({\mathbf{I}}_p\otimes \mathbf{M}\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right))(Vec\left(\mathbf{Y}\right)-{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\hfill \\ & & \times {\left({\mathbf{I}}_p\otimes \mathbf{M}\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right))}^T\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right)]\hfill \end{array}$$ (13)

If ${\mathbf{\Phi }}_{initial}$is the following equation.

$$\begin{array}{ccc}\hfill {\mathbf{\Phi }}_{initial}& =& \left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)(Vec\left(\mathbf{Y}\right)-{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{M}\right)\hfill \\ & & \times \left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right))(Vec\left(\mathbf{Y}\right)-{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{M}\right)\hfill \\ & & \times {\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right))}^T\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right)\hfill \end{array}$$

Given that ${\mathbf{\Phi }}_{initial}$ is a $(pn\times pn)$ matrix, the subsequent step is to transform it into a $(p\times p)$ matrix, which is represented by a symbolized matrix, and then to correlate it with an $(n\times n)$ identity matrix through the use of the Kronecker product.

$$\underset{pn\times pn}{{\widehat{\Phi }}_{initial}}=\underset{p\times p}{{\widehat{\Sigma }}_{initial}}\otimes \underset{n\times n}{{\mathbf{I}}_n}$$ (14)

The equation below is obtained from substituting Eq. (14) into Eq. (13)

$$\begin{array}{ccc}& & \frac{1}{2}tr\left[\left({\widehat{\Sigma }}^{-1}{\mathbf{T}}_{jj*}\otimes {\mathbf{I}}_n\right)\right]=\frac{1}{2}tr\left[\left({\widehat{\Sigma }}^{-1}{\mathbf{T}}_{jj*}{\widehat{\Sigma }}^{-1}\otimes {\mathbf{I}}_n\right)\left({\widehat{\Sigma }}_{initial}\otimes {\mathbf{I}}_n\right)\right]\hfill \\ & & tr\left[\left({\widehat{\Sigma }}^{-1}{\mathbf{T}}_{jj*}\otimes {\mathbf{I}}_n\right)\right]=tr\left[\left({\widehat{\Sigma }}^{-1}{\mathbf{T}}_{jj*}\otimes {\mathbf{I}}_n\right)\right]\hfill \end{array}$$

Based on the previous evidence, the$\mathbf{\Sigma }$parameter estimator can be approximated by Eq. (14). The $\widehat{\Sigma }$matrix can be formed from $(n\times n)$ block elements of ${\widehat{\Phi }}_{initial}$. Suppose ${\widehat{\Phi }}_{initial}$ has the following block structure where each ${\widehat{\Phi }}_{jj*}$is a $(n\times n)$ matrix.

$${\widehat{\Phi }}_{initial}=\left[\begin{array}{cccc}{\widehat{\Phi }}_{initial11}& {\widehat{\Phi }}_{initial12}& \cdots & {\widehat{\Phi }}_{initial1p}\\ {\widehat{\Phi }}_{initial21}& {\widehat{\Phi }}_{initial22}& \cdots & {\widehat{\Phi }}_{initial2p}\\ ⋮& ⋮& \ddots & ⋮\\ {\widehat{\Phi }}_{initialp1}& {\widehat{\Phi }}_{initialp2}& \cdots & {\widehat{\Phi }}_{initialpp}\end{array}\right]$$

The $\widehat{\Sigma }$ matrix can be taken from the main diagonal elements of the ${\widehat{\Phi }}_{jj*}$block. Thus, the parameter estimator is given by Eq. (15).

$${\widehat{\Sigma }}_{initial}=\left[\begin{array}{cccc}tr\left({\widehat{\Phi }}_{initial11}\right)/n& tr\left({\widehat{\Phi }}_{initial12}\right)/n& \cdots & tr\left({\widehat{\Phi }}_{initial1p}\right)/n\\ tr\left({\widehat{\Phi }}_{initial21}\right)/n& tr\left({\widehat{\Phi }}_{initial22}\right)/n& \cdots & tr\left({\widehat{\Phi }}_{initial2p}\right)/n\\ ⋮& ⋮& \ddots & ⋮\\ tr\left({\widehat{\Phi }}_{initialp1}\right)/n& tr\left({\widehat{\Phi }}_{initialp2}\right)/n& \cdots & tr\left({\widehat{\Phi }}_{initialpp}\right)/n\end{array}\right]$$ (15)

(9), (15) demonstrate that the equation is not in closed form, necessitating the utilization of a numerical approach for its resolution. The numerical approach to estimating $\mathit{\rho }$ is the concentrated log-likelihood with the L-BFGS-B optimization method. The concentrated log-likelihood function for $\mathit{\rho }$ is the likelihood function obtained from the substitution of the $Vec{\left(\widehat{\mathbf{B}}\right)}_{initial}$ and ${\widehat{\Sigma }}_{initial}$ estimates shown in Eq. (16).

$$\begin{array}{ccc}\hfill \ln L^{con}\left(\mathit{\rho }\right)& =& \ln L\left(Vec{\left(\widehat{\mathbf{B}}\right)}_{M\text{Re}g},{\widehat{\mathbf{B}}}_{WY},{\widehat{\Sigma }}_{con},\mathit{\rho }\right)\hfill \\ & =& -\frac{pn}{2}\ln (2\pi )-\frac{1}{2}\ln \left(\left|{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\widehat{\Sigma }}_{con}\otimes {\mathbf{I}}_n\right){\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right)}^{-1}\right|\right)\hfill \\ & & -\frac{1}{2}{\left(Vec\left(\mathbf{Y}\right)-\left({\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{A}\right)(Vec{\left(\widehat{\mathbf{B}}\right)}_{M\text{Re}g}-\left({\mathbf{I}}_p\otimes {\widehat{\mathbf{B}}}_{WY}\right)Vec\left(\mathit{\rho }\right))\right)\right)}^T\hfill \\ & & \left(\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right){\left({\widehat{\Sigma }}_{con}\otimes {\mathbf{I}}_n\right)}^{-1}\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\right)\hfill \end{array}$$

$$\left(Vec\left(\mathbf{Y}\right)-\left({\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{A}\right)\left(Vec{\left(\widehat{\mathbf{B}}\right)}_{M\text{Re}g}-\left({\mathbf{I}}_p\otimes {\widehat{\mathbf{B}}}_{WY}\right)Vec\left(\mathit{\rho }\right)\right)\right)\right)$$ (16)

where ${\widehat{\Sigma }}_{con}=\left[\begin{array}{cccc}tr\left({\widehat{\Phi }}_{con11}\right)/n& tr\left({\widehat{\Phi }}_{con12}\right)/n& \cdots & tr\left({\widehat{\Phi }}_{con1p}\right)/n\\ tr\left({\widehat{\Phi }}_{con21}\right)/n& tr\left({\widehat{\Phi }}_{con22}\right)/n& \cdots & tr\left({\widehat{\Phi }}_{con2p}\right)/n\\ ⋮& ⋮& \ddots & ⋮\\ tr\left({\widehat{\Phi }}_{conp1}\right)/n& tr\left({\widehat{\Phi }}_{conp2}\right)/n& \cdots & tr\left({\widehat{\Phi }}_{conpp}\right)/n\end{array}\right]$ with

$$\begin{array}{ccc}\hfill {\widehat{\Phi }}_{con}& =& \left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)-{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{A}\right)\left(Vec{\left(\widehat{\mathbf{B}}\right)}_{M\text{Re}g}-\left({\mathbf{I}}_p\otimes {\widehat{\mathbf{B}}}_{WY}\right)Vec\left(\mathit{\rho }\right)\right)\right)\hfill \\ & & {\left(Vec\left(\mathbf{Y}\right)-{\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{A}\right)\left(Vec{\left(\widehat{\mathbf{B}}\right)}_{M\text{Re}g}-\left({\mathbf{I}}_p\otimes {\widehat{\mathbf{B}}}_{WY}\right)Vec\left(\mathit{\rho }\right)\right)\right)}^T\left({\mathbf{I}}_{pn}-\mathit{\rho }\otimes {\mathbf{W}}^T\right).\hfill \end{array}$$

Eq. (16) represents the concentrated log-likelihood function. This equation cannot be maximized statistically so a numerical approach is needed with the L-BFGS-B optimization method. The following steps outline the numerical procedure for maximizing the concentrated log-likelihood, thereby obtaining the value of $\widehat{\rho }$:

• a. Generated a sequence of values for ${\rho }_j;j=1,2,..,p$ where ${\rho }_j=$seq(start value, end value, increasing) and substituted each into the rho matrix where $\mathit{\rho }=diag({\rho }_{1k},{\rho }_{2k},...,{\rho }_{pk});k=1,2,...,n\left(seq\left({\rho }_j\right)\right)$

• b. Performed bivariate regression of $Vec\left(\mathbf{Y}\right)$ with $\left({\mathbf{I}}_p\otimes \mathbf{A}\right)$ and obtained $Vec{\left(\widehat{\mathbf{B}}\right)}_{M\text{Re}g}$

• c. Regressed WY with A and obtained ${\widehat{\mathbf{B}}}_{WY}$which is a$(q+1)\times p$ matrix.

• d. Substituted $Vec{\left(\widehat{\mathbf{B}}\right)}_{M\text{Re}g}$and ${\widehat{\mathbf{B}}}_{WY}$ into concentrated log-likelihood function.

• e. Identified the value of $\mathit{\rho }$that gave the maximum $\ln L^{con}$ and then became $\widehat{\rho }$.

Properties of estimator

The coefficients parameter in the MSAR model are estimated using Eq. (9). $Vec\left(\widehat{\mathbf{B}}\right)$ is shown to be both unbiased and consistent. An estimator is considered unbiased if its expected value equals the true parameter, and consistent if it converges to the true parameter as the sample size increases. The proof is presented as follows.

$$\begin{array}{c}E\left(Vec\left(\widehat{\mathbf{B}}\right)\right)=E\left(\left({\mathbf{I}}_p\otimes {\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right)\right)\hfill \\ =\left({\mathbf{I}}_p\otimes {\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)E\left(Vec\left(\mathbf{Y}\right)\right)\hfill \\ =\left({\mathbf{I}}_p\otimes {\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right){\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)}^{-1}\left({\mathbf{I}}_p\otimes \mathbf{A}\right)Vec\left(\mathbf{B}\right)\hfill \\ =\left({\mathbf{I}}_p\otimes {\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T\right)\left({\mathbf{I}}_p\otimes \mathbf{A}\right)Vec\left(\mathbf{B}\right)\hfill \\ =\left({\mathbf{I}}_p\otimes {\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T\mathbf{A}\right)Vec\left(\mathbf{B}\right)\hfill \\ =Vec\left(\mathbf{B}\right)\hfill \end{array}$$

Since the expectation of $Vec\left(\widehat{\mathbf{B}}\right)$equals $Vec\left(\mathbf{B}\right)$, it follows that $Vec\left(\widehat{\mathbf{B}}\right)$ is an unbiased estimator of $Vec\left(\mathbf{B}\right)$.

Next, $Vec\left(\widehat{\mathbf{B}}\right)$ consistency is shown below.

$$\begin{array}{ccc}\hfill Var\left(Vec\left(\widehat{\mathbf{B}}\right)\right)& =& Var\left(\left({\mathbf{I}}_p\otimes {\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T\right)\left({\mathbf{I}}_{pn}-{\mathit{\rho }}^T\otimes \mathbf{W}\right)\left(Vec\left(\mathbf{Y}\right)\right)\right)\hfill \\ & =& \left[\begin{array}{cccc}tr\left({\widehat{\Phi }}_{11}\right)/n& tr\left({\widehat{\Phi }}_{12}\right)/n& \cdots & tr\left({\widehat{\Phi }}_{1p}\right)/n\\ tr\left({\widehat{\Phi }}_{21}\right)/n& tr\left({\widehat{\Phi }}_{22}\right)/n& \cdots & tr\left({\widehat{\Phi }}_{2p}\right)/n\\ ⋮& ⋮& \ddots & ⋮\\ tr\left({\widehat{\Phi }}_{p1}\right)/n& tr\left({\widehat{\Phi }}_{p2}\right)/n& \cdots & tr\left({\widehat{\Phi }}_{pp}\right)/n\end{array}\right]\otimes {\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}Var\left(Vec\left(\widehat{\mathbf{B}}\right)\right)& =& \underset{n\to \infty }{lim}\left[\begin{array}{cccc}tr\left({\widehat{\Phi }}_{11}\right)/n& tr\left({\widehat{\Phi }}_{12}\right)/n& \cdots & tr\left({\widehat{\Phi }}_{1p}\right)/n\\ tr\left({\widehat{\Phi }}_{21}\right)/n& tr\left({\widehat{\Phi }}_{22}\right)/n& \cdots & tr\left({\widehat{\Phi }}_{2p}\right)/n\\ ⋮& ⋮& \ddots & ⋮\\ tr\left({\widehat{\Phi }}_{p1}\right)/n& tr\left({\widehat{\Phi }}_{p2}\right)/n& \cdots & tr\left({\widehat{\Phi }}_{pp}\right)/n\end{array}\right]\otimes \underset{n\to \infty }{lim}{\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}\hfill \\ & =& \mathbf{0}\otimes {\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}\hfill \\ & =& \mathbf{0}\hfill \end{array}$$

It can be concluded that $Vec\left(\widehat{\mathbf{B}}\right)$ is an unbiased and consistent estimator.

Hypothesis testing of MSAR model

Hypothesis testing of the MSAR model parameters is conducted both simultaneously and partially. The MLRT is applied for simultaneous testing, while the Wald test is used for partial parameter testing [26,27]. The hypothesis for simultaneous testing of the model parameters is formulated as follows:

$$\begin{array}{c}{H}_0:{\beta }_{1j}={\beta }_{2j}=\dots ={\beta }_{qj}=0,j=1,2,...,p\hfill \\ H_1:\text{at}\text{least}\text{one}\text{of}{\beta }_{kj}\ne 0,k=1,2,\dots ,q,j=1,2,...,p\hfill \end{array}$$

The set of parameters under population, denoted by ${\mathit{\Omega }}_{MSAR}$, is given by ${\mathit{\Omega }}_{MSAR}=\left\{Vec\left(\mathbf{B}\right),Vec\left(\mathbf{\Sigma }\right),\mathit{\rho }\right\}$,while the set of parameters under H₀, denoted by ${\mathit{\omega }}_{MSAR}$, is given by ${\mathit{\omega }}_{MSAR}=\left\{{\mathit{\beta }}_{0\omega },\left(Vec\left({\mathbf{\Sigma }}_{\omega }\right)\right),{\mathit{\rho }}_{0\omega }\right\}$. The parameter estimators for the two sets, ${\widehat{\Omega }}_{MSAR}$ and ${\widehat{\omega }}_{MSAR}$, are obtained from parameter estimation using the MLE method described in the previous section. The LRT is calculated in consideration of the formula presented in Eq. (17).

$$LR=\frac{L\left({\widehat{\omega }}_{MSAR}\right)}{L\left({\widehat{\Omega }}_{MSAR}\right)}<L{R}_0$$ (17)

Where $L\left({\widehat{\omega }}_{MSAR}\right)$ is the likelihood value of MSAR model using the estimated parameters under H₀ and $L\left({\widehat{\Omega }}_{MSAR}\right)$ is the likelihood value of MSAR model using the estimated parameters under population. Consequently, the test statistics for testing the parameters simultaneously using the MLRT is presented in Eq. (18).

$$G_{MSAR}^2=-2\left(\ln \left(L\left({\widehat{\omega }}_{MSAR}\right)\right)-\ln \left(L\left({\widehat{\Omega }}_{MSAR}\right)\right)\right)$$ (18)

The critical regions for hypothesis testing are as follows:

$$\begin{array}{ccc}\hfill \alpha & =& P(LR<L{R}_0),0<L{R}_0\le 1\hfill \\ & =& P\left(\ln L{R}^2<L{R}_0^2\right)\hfill \\ & =& P(\ln L{R}^2<\ln L{R}_0^2)\hfill \\ & =& P(G_{MSAR}^2>{\chi }_{(\alpha ,df)}^2)\hfill \end{array}$$

$G_{MSAR}^2$ is distributed according to the chi-square distribution for $n\to \infty$, whereby the H₀ rejection region is $G_{MSAR}^2>{\chi }_{(\alpha ,df)}^2$or $p-value<\alpha$with degree of freedom (df), which is the number of parameters under the population minus the number of parameters under H₀.

$$\begin{array}{ccc}\hfill df& =& n(L\left({\widehat{\Omega }}_{MSAR}\right)-n\left(L\left({\widehat{\omega }}_{MSAR}\right)\right)\hfill \\ & =& \left(p\right(q+1)+2p+p)-(p+2p+p)=pq\hfill \end{array}$$

Once the null hypothesis (H₀) is rejected in the simultaneous test, partial hypothesis testing is conducted to identify which predictor variables exert a statistically significant influence on the response variable. The first partial test focuses on the spatial autoregressive parameter ρ, formulated under the following hypothesis framework:

$$\begin{array}{c}{H}_0:{\rho }_j=0\hfill \\ H_1:{\rho }_j\ne 0;j=1,2,...,p\hfill \end{array}$$

The test statistics used for testing the above hypothesis with the Wald test is shown in Eq. (19).

$$Wal{d}_{{\rho }_j}={\left(\frac{{\widehat{\rho }}_j}{\widehat{se}\left({\widehat{\rho }}_j\right)}\right)}^2\sim {\chi }_1^2$$ (19)

where $\widehat{se}\left(\widehat{{\rho }_j}\right)$ is obtained from the $\widehat{Var}\left(\widehat{{\rho }_j}\right)$ root. The$\widehat{Var}\left(\widehat{{\rho }_j}\right)$ value represents the main diagonal element of the Hessian matrix which is represented by $-{\left(\mathbf{H}\left(\widehat{\rho }\right)\right)}^{-1}$ and corresponds to $\widehat{{\rho }_j}$ . The Wald test statistics in Eq. (19) is deemed to be statistically significant if $Wal{d}_{{\rho }_j}>{\chi }_{\alpha ,1}^2$, thereby rejecting the null hypothesis (H₀).

Moreover, the partial testing of ${\beta }_{kj}$ parameters is conducted with the objective of identifying the parameters that exert a significant influence on the model. The following hypothesis is employed to test the partial ${\beta }_{kj}$ parameters:

$$\begin{array}{c}{H}_0:{\beta }_{kj}=0\hfill \\ H_1:{\beta }_{kj}\ne 0,k=1,2,\dots ,q,j=1,2,...,p\hfill \end{array}$$

The test statistics used for testing the partial ${\beta }_{kj}$ parameters with the Wald test is shown in Eq. (20).

$$Wal{d}_{{\beta }_j}={\left(\frac{{\widehat{\beta }}_{kj}}{\widehat{se}\left({\widehat{\beta }}_{kj}\right)}\right)}^2\sim {\chi }_1^2$$ (20)

In this context, the term $\widehat{se}\left(\widehat{{\beta }_{kj}}\right)$ represents the standard error of ${\widehat{\beta }}_{kj}$obtained from $\widehat{Var}\left(\widehat{{\beta }_{kj}}\right)$. $\widehat{Var}\left(\widehat{{\beta }_{kj}}\right)$ is the main diagonal element of the variance-covariance matrix $\widehat{Var}\left(Vec\left(\widehat{\mathbf{B}}\right)\right)$. The null hypothesis (H₀) is rejected if $Wal{d}_{{\beta }_j}>{\chi }_{\alpha ,1}^2$.

Measures of model fits

To select the most suitable regression model, two commonly used evaluation metrics are the Root Mean Square Error (RMSE) and the coefficient of determination (R²). RMSE represents the average prediction error of the model, expressed in the same unit as the response variable. Models with lower RMSE values are preferred, as they indicate predictions that are closer to the observed values, reflecting a better model fit. Meanwhile, R² measures the proportion of variance in the response variable that can be explained by the predictor variables [[28], [29], [30]]. A higher R² value signifies greater explanatory power and stronger predictive performance of the model. The formulas for RMSE and R² are provided in Eqs. (21) and (22) [[31], [32], [33]].

$$RMSE=RMS{E}_1+RMS{E}_2=\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(Y_{1i}-{\widehat{Y}}_{1i}\right)}^2}+\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(Y_{2i}-{\widehat{Y}}_{2i}\right)}^2}$$ (21)

$$R^2=1-\frac{SSE}{SST}=1-\frac{{\sum }_{i=1}^n{\left(Y_{1i}-{\widehat{Y}}_{1i}\right)}^2+{\sum }_{i=1}^n{\left(Y_{2i}-{\widehat{Y}}_{2i}\right)}^2}{{\sum }_{i=1}^n{\left(Y_{1i}-{\overline{Y}}_1\right)}^2+{\sum }_{i=1}^n{\left(Y_{2i}-{\overline{Y}}_2\right)}^2}$$ (22)

Data analysis procedure

The analysis was conducted through the following steps:

• 1.Check the correlation between response variables.
• 2.Test for multivariate normal distribution.
• 3.Model the data using multivariate normal linear regression.
• 4.Perform spatial weighting.
• 5.Perform spatial dependency testing.
• 6.Estimate the parameters of MSAR model.
• 7.Conduct simultaneous hypothesis testing using the test statistic in Eq. (18).
• 8.Conduct partial hypothesis testing using the test statistics in Eqs. (19) and (20).
• 9.Evaluate model fit using Eqs. (21) and (22).
• 10.Interpret the results and draw conclusions.

Method validation

To validate the application of the MSAR method, we used a real-world dataset on health issues in children under five years old.

Data set

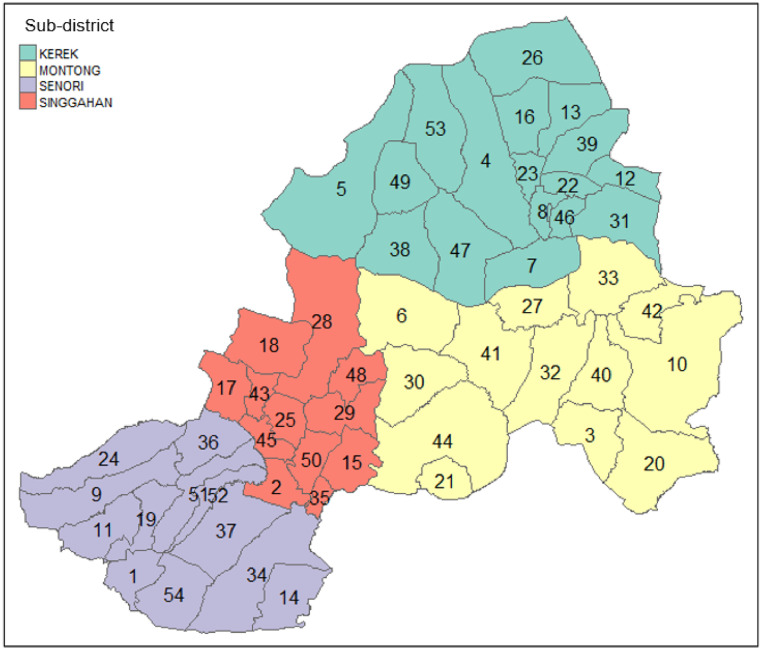
The dataset used in this study was obtained from the Center for the Study of Regional Resources and Community Empowerment at Institut Teknologi Sepuluh Nopember, Surabaya, Indonesia. The data are secondary in nature and pertain to the year 2023. Observations were collected from 54 villages located across four sub-districts in Tuban Regency, East Java—namely Singgahan, Kerek, Montong, and Senori—as illustrated in Fig. 1.

Fig. 1.

Administrative map of 54 villages (note: colored pink) in Tuban District.

The response variables selected for analysis are the percentage of cases of pneumonia and diarrhea in children under five years old. These two response variables were found to have a correlation coefficient of 0.585. The predictor variables used in this study include the percentage of infants who received exclusive breastfeeding, the percentage of children under five who received complete basic immunization, the percentage who received vitamin A supplementation, the percentage of pregnant women who attended government-sponsored prenatal classes, and the percentage of households with access to clean water. A summary of the research data is presented in Table 1.

Table 1.

Descriptive statistics of research data.

Variable	Description	Mean	SD	Min	Max
Response	Pneumonia in toddler (Y1) ( %)	4.82	4.91	0.00	16.68
	Diarrhea in toddler (Y2) ( %)	12.99	8.10	0.83	30.61
Predictor	Exclusive breastfeeding (X1) (10 %)	2.53	2.40	0.00	12.22
	Complete basic immunization (X2) ( %)	22.56	6.70	6.12	50.00
	Toddlers who received vit. A (X3) (10 %)	13.04	10.80	1.40	81.30
	Pregnant women who attended pregnancy classes (X4) (10 %)	5.09	5.99	0.00	33.33
	Households with clean water (X5) coverage ( %)	98.35	4.22	79.94	100.00

Modelling child health problems using multivariate normal linear regression

Before conducting multivariate linear regression analysis, the distribution of the response variables was assessed for multivariate normality using a quantile-quantile (Q-Q) plot. The results indicated that the Mahalanobis distance exceeded 50 %, with a proportion of 53.70 %, suggesting that the two response variables follow a bivariate normal distribution Subsequently, the parameters of the multivariate normal linear regression model were estimated, and the results are shown in Table 2. The table reveals that the predictor variables significantly influencing the prevalence of pneumonia (Y₁) in children under five are the percentage of infants who were exclusively breastfed (X₁) and the percentage of children who received complete basic immunization (X₂). Meanwhile, the variables influencing the prevalence of diarrhea (Y₂) include exclusive breastfeeding (X₁), complete basic immunization (X₂), and access to clean water (X₅).

Table 2.

Estimated values of multivariate normal linear regression parameters.

Parameters	Estimated Value	Standard Error	T	p-value
${\beta }_{01}$	16.6738	19.5660	0.8522	0.3961
${\beta }_{11}$	0.7882	0.3516	2.2416	0.0272*
${\beta }_{21}$	0.3373	0.1099	3.0685	0.0027*
${\beta }_{31}$	−0.0013	0.0669	−0.0206	0.9835
${\beta }_{41}$	−0.1088	0.1251	−0.8700	0.3863
${\beta }_{51}$	−0.2123	0.1954	−1.0867	0.2797
${\beta }_{02}$	67.2771	19.5660	3.4383	0.0008*
${\beta }_{12}$	0.7053	0.3516	2.0061	0.0475*
${\beta }_{22}$	0.5214	0.1099	4.7431	6.85 × 10–6*
${\beta }_{32}$	−0.0748	0.0669	−1.1187	0.2658
${\beta }_{42}$	0.0664	0.1251	0.5311	0.5965
${\beta }_{52}$	−0.6832	0.1953	−3.4966	0.0007*

^⁎: significant at 5 % alpha.

The multivariate normal linear regression model can be shown in the following equation.

$$\left[\begin{array}{c}{\widehat{Y}}_1\\ {\widehat{Y}}_2\end{array}\right]=\left[\begin{array}{c}16.6738+0.7882X_1+0.3373X_2-0.0013X_3-0.1088X_4-0.2123X_5\\ 67.2771+0.7053X_1+0.5214X_2-0.0748X_3+0.0664X_4-0.6832X_5\end{array}\right]$$

Spatial weighting and testing for spatial dependence

The MSAR model was used to estimate the prevalence of pneumonia and diarrhea among children under five in southwestern Tuban Regency. This analysis employed a queen contiguity spatial weighting matrix, which accounts for the asymmetrical geographical layout of the region. The matrix was constructed based on shared boundaries between villages.

Following the construction of the spatial weighting matrix, spatial dependence was assessed using the residuals from the multivariate normal linear regression model. The spatial dependence test was conducted in R using the Bivariate Moran's I statistic [[34], [35], [36]], which yielded a Moran's I value of 0.1101, with an expected value of –0.0073 and a variance of 0.0051. The resulting Z-score was 1.6513, which exceeds the critical value of Z₀.₀₅ = 1.64. Therefore, the null hypothesis (H₀) of no spatial dependence is rejected. This result indicates the presence of bivariate spatial dependence in the regression residuals, justifying further spatial analysis.

Modelling child health data using the MSAR model

In MSAR modelling, the regression coefficients include a spatial effect parameter, denoted as ρ. Therefore, estimating this parameter is the first step, conducted using a numerical approximation method based on the concentrated log-likelihood function. Once the $\widehat{\rho }$ parameter estimation has been obtained, $Vec\left(\widehat{\mathbf{B}}\right)$ and $\widehat{\Sigma }$ can be estimated. The results of the $Vec\left(\widehat{\mathbf{B}}\right)$ estimation is presented in Table 3, while the $\widehat{\Sigma }$ value is as follows.

$$\widehat{\Sigma }=\left[\begin{array}{cc}11.82& 6.36\\ 5.30& 33.48\end{array}\right]$$

Table 3.

Estimated values of multivariate spatial autoregressive parameters.

Parameters	Estimated Value	Standard Error	Wald Statistic	P-value
${\rho }_1$	0.42	0.01	2895.30	0.00*
${\beta }_{01}$	15.76	12.90	1.49	0.22
${\beta }_{11}$	0.59	0.23	6.59	0.01*
${\beta }_{21}$	0.25	0.07	11.98	0.00*
${\beta }_{31}$	0.02	0.04	0.21	0.65
${\beta }_{41}$	−0.10	0.08	1.46	0.23
${\beta }_{51}$	−0.20	0.13	2.46	0.12
${\rho }_2$	0.38	0.01	14,786.09	0.00*
${\beta }_{02}$	62.92	21.71	8.40	0.00*
${\beta }_{12}$	0.41	0.39	1.13	0.29
${\beta }_{22}$	0.40	0.12	10.95	0.00*
${\beta }_{32}$	−0.03	0.07	0.17	0.68
${\beta }_{42}$	0.05	0.14	0.14	0.71
${\beta }_{52}$	−0.66	0.22	9.25	0.00*

^⁎: significant at 5 % alpha.

The initial step involves simultaneous hypothesis testing of all model parameters to determine whether they collectively wield a significant influence. The value of the $G^2$test statistics was 43,240.59, which is greater than the ${\chi }_{(0,05;10)}^2=18.307$. Accordingly, the null hypothesis (H₀) is rejected, indicating that at least one parameter significantly contributes to the model. This justifies proceeding with partial (individual) hypothesis tests to identify which specific parameters are influential in the MSAR model.

Table 3 indicates that the parameters ${\rho }_1$ and ${\rho }_2$ are significant to the model, thereby suggesting that spatial dependencies in the rates of pneumonia and diarrhea must be considered in the model. The MSAR model for the percentage of pneumonia cases (Y₁) identifies two significant predictor variables: the percentage of infants exclusively breastfed (X₁) and the percentage of children under five who received complete basic immunization (X₂). Meanwhile, for the percentage of diarrhea cases (Y₂), the significant predictors are X₂ (complete basic immunization) and X₅ (households with access to clean water).

As shown in Table 4, the MSAR model better captures the relationship between predictor variables and child health outcomes than the standard multivariate normal linear regression model. This is demonstrated by its lower Root Mean Square Error (RMSE) of 4.97 and a higher R-squared value of approximately 60 %. These findings support the conclusion that, when multivariate data exhibit spatial autocorrelation, the MSAR model provides a more accurate and reliable estimation framework.

Table 4.

Model comparison.

Model	RMSE	R-square
Multivariate Normal Linear Regression	5.22	55.21 %
Model MSAR	4.97	59.98 %

In total, 54 distinct MSAR models were developed—one for each village. The model estimates for both pneumonia (Y₁) and diarrhea (Y₂) are summarized as ${\left[\begin{array}{cc}{\widehat{Y}}_{1i}& {\widehat{Y}}_{2i}\end{array}\right]}^T$ where:

$${\widehat{Y}}_{1i}=15.76+0.42\sum _{i*=1,i\ne i*}^{54}{w}_{ii*}{\mathbf{y}}_{1i*}+0.59X_{1i}+0.25X_{2i}+0.02X_{3i}-0.10X_{4i}-0.20X_{5i}$$

$${\widehat{Y}}_{2i}=62.92+0.38\sum _{i*=1,i\ne i*}^{54}{w}_{ii*}{\mathbf{y}}_{2i*}+0.41X_{1i}+0.41X_{2i}-0.03X_{3i}+0.05X_{4i}-0.66X_{5i}$$

Taking Gemulung village as an example, the MSAR model for Gemulung village (code number 5) is ${\left[\begin{array}{cc}{\widehat{Y}}_{15}& {\widehat{Y}}_{25}\end{array}\right]}^T$ where:

$$\begin{array}{ccc}\hfill {\widehat{Y}}_{15}& =& 15.76+0.11Y_{128}+0.11Y_{138}+0.11Y_{149}+0.11Y_{153}\hfill \\ & & +0.59X_{15}+0.25X_{25}+0.02X_{35}-0.10X_{45}-0.20X_{55}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\widehat{Y}}_{25}& =& 62.92+0.09Y_{228}+0.09Y_{238}+0.09Y_{249}+0.09Y_{253}\hfill \\ & & +0.41X_{15}+0.40X_{25}-0.03X_{35}+0.05X_{45}-0.66X_{55}\hfill \end{array}$$

The above MSAR model of Gemulung Village can be interpreted as follows:

• 1.For every 100 children under five, approximately 10 to 11 are affected by pneumonia, and 9 to 10 by diarrhea in Gemulung Village. Similar patterns are likely present in neighboring villages—Mulyoagung, Sidonganti, Trantang, and Wolutengah—due to spatial dependence.
• 2.A 1 % increase in the proportion of exclusively breastfed infants is associated with a rise in pneumonia cases, which contradicts theoretical expectations. This may be due to the lagging effect of exclusive breastfeeding on pneumonia incidence. Additionally, pneumonia cases in Gemulung appear to influence similar increases in the four neighboring villages. No significant relationship was found between exclusive breastfeeding and diarrhea prevalence.
• 3.A 1 % increase in the percentage of children receiving complete basic immunization is linked to higher pneumonia and diarrhea rates. This finding contradicts existing theory, likely due to temporal lag in the variable's impact. Increases in pneumonia and diarrhea in Gemulung are associated with corresponding rises (10–11 and 9–10 cases per 100 children, respectively) in neighboring villages.
• 4.The percentage of children under five who received vitamin A supplementation showed no significant effect on pneumonia or diarrhea incidence.
• 5.The proportion of pregnant women attending pregnancy classes did not significantly influence pneumonia or diarrhea rates among children under five.
• 6.A 1 % increase in household clean water coverage is associated with a decrease of approximately one diarrhea case per 100 children under five, but has no significant effect on pneumonia rates. Diarrhea cases in Gemulung also appear to influence similar increases (9–10 per 100) in the neighboring villages.

Conclusions

This study focused on area-based spatial modeling in the context of multivariate response regression, introducing the MSAR model as an extension of the conventional SAR model. The MSAR approach incorporates geographic weighting to account for spatial dependencies between neighboring regions. Parameter estimation was carried out using MLE via concentrated log-likelihood, which resulted in unbiased and consistent estimates. The significance of model parameters was tested both simultaneously using the LRT and partially using the Wald Test, which enabled the identification of influential predictor variables. The application of the MSAR model to data on pneumonia and diarrhea cases among children under five in Tuban Regency, East Java, demonstrated its effectiveness in handling spatial autocorrelation. Compared to the standard multivariate normal linear regression, the MSAR model showed better accuracy. The variables that affect the incidence of pneumonia and diarrhea were the percentage of infants who receive exclusive breastfeeding, the percentage of toddlers who receive complete basic immunization, and the percentage of households which have access clean water. However, the current model is limited to multivariate normal data distributions. Future research should explore extensions of the MSAR framework that can accommodate non-normal data.

Limitations

Assumption of error distribution is normal distribution.

Ethics statements

The data used in this research has been approved by the Center for the Study of Regional Resources and Community Empowerment Institut Teknologi Sepuluh Nopember Surabaya, Indonesia.

Supplementary material and/or additional information [Optional]

None

CRediT authorship contribution statement

Sutikno: Conceptualization, Methodology, Writing – original draft, Writing – review & editing, Validation. Purhadi: Methodology, Conceptualization. Fachrunisah: Visualization, Writing – review & editing, Software. Fajar Dwi Cahyoko: Writing – review & editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A

Fig. A1 and Table A1.

Table A1.

Village and neighbor codes.

Village Codes	Village	Sub-district	Count	Neighbor
1	Banyuurip	Senori	3	19	51	54
2	Binangun	Singgahan	6	34	37	45	50	51	52
3	Bringin	Montong	3	20	32	40
4	Gaji	Kerek	7	7	8	16	23	26	47	53
5	Gemulung	Kerek	4	28	38	49	53
6	Guwoterus	Montong	6	28	30	38	41	47	48
7	Hargoretno	Kerek	8	4	8	27	31	33	41	46	47
8	Jarorejo	Kerek	5	4	7	22	23	46
9	Jatisari	Senori	5	11	19	24	36	51
10	Jetakss	Montong	4	20	33	40	42
11	Kaligede	Senori	2	9	19
12	Karanglo	Kerek	3	22	31	39
13	Kasiman	Kerek	4	16	23	26	39
14	Katerban	Senori	1	34
15	Kedungjambe	Singgahan	4	29	35	44	50
16	Kedungrejo	Kerek	4	4	13	23	26
17	Lajo Kidul	Singgahan	4	18	36	43	45
18	Lajo Lor	Singgahan	3	17	28	43
19	Leran	Senori	4	1	9	11	51
20	Maindu	Montong	3	3	10	40
21	Manjung	Montong	1	44
22	Margomulyo	Kerek	6	8	12	23	31	39	46
23	Margorejo	Kerek	6	4	8	13	16	22	39
24	Medalem	Senori	2	9	36
25	Mergosari	Singgahan	5	28	29	43	45	50
26	Mliwang	Kerek	3	4	13	16
27	Montongsekar	Montong	4	7	32	33	41
28	Mulyoagung	Singgahan	8	5	6	18	25	29	38	43	48
29	Mulyorejo	Singgahan	7	15	25	28	30	44	48	50
30	Nguluhan	Montong	5	6	29	41	44	48
31	Padasan	Kerek	5	7	12	22	33	46
32	Pakel	Montong	6	3	27	33	40	41	44
33	Pucangan	Montong	7	7	10	27	31	32	40	42
34	Rayung	Senori	6	2	14	35	37	50	54
35	Saringembat	Singgahan	3	15	34	50
36	Sendang	Senori	5	9	17	24	45	51
37	Sidoharjo	Senori	4	2	34	52	54
38	Sidonganti	Kerek	5	5	6	28	47	49
39	Sumberarum	Kerek	4	12	13	22	23
40	Sumurgung	Montong	5	3	10	20	32	33
41	Talangkembar	Montong	7	6	7	27	30	32	44	47
42	Talun	Montong	2	10	33
43	Tanggir	Singgahan	5	17	18	25	28	45
44	Tanggulangin	Montong	6	15	21	29	30	32	41
45	Tanjungrejo	Singgahan	7	2	17	25	36	43	50	51
46	Temayang	Kerek	4	7	8	22	31
47	Tengger Wetan	Kerek	7	4	6	7	38	41	49	53
48	Tingkis	Singgahan	4	6	28	29	30
49	Trantang	Kerek	4	5	38	47	53
50	Tunggulrejo	Singgahan	7	2	15	25	29	34	35	45
51	Wanglu Kulon	Senori	8	1	2	9	19	36	45	52	54
52	Wanglu Wetan	Senori	4	2	37	51	54
53	Wolutengah	Kerek	4	4	5	47	49
54	Wonosari	Senori	5	1	34	37	51	52

Fig. A1.

Map of tuban regency village codes.

Data availability

Data will be made available on request.