Condensed complexes in vesicles containing cholesterol and phospholipids

Abstract

Animal cell membranes pose conceptual problems related to the physical chemistry of liquids. An avenue to the solution of some of these problems has been opened by the discovery of liquid–liquid immiscibility in synthetic membranes composed of cholesterol and phospholipids. This discovery has led to the development of a thermodynamic model involving condensed complexes. In this model, the phospholipids with longer fatty-acid chains react reversibly with cholesterol to form complexes. The complexes themselves can have a repulsive interaction with other phospholipids, leading to immiscibility. A striking example of this effect is revealed in the phase diagrams of ternary mixtures of cholesterol, a saturated phosphatidylcholine (or sphingomyelin), and an unsaturated phosphatidylcholine. As found by a number of investigators, all binary pairs are miscible in bilayers, whereas the ternary mixture can form two liquid phases. The model of condensed complexes accounts for this effect. Condensed complexes also have a major effect on the chemical activity of cholesterol and on the ordering of phospholipid acyl chains both in the presence and absence of phase separations. Model calculations of phospholipid order parameters account for several features of the deuterium NMR spectra of labeled phospholipid molecules in bilayer mixtures with cholesterol.

A number of early investigators have interpreted various physical chemical effects of cholesterol on phospholipids in membranes in terms of the formation of cholesterol–phospholipid complexes (1–5). The use of complexes to account for the properties of nonideal liquids has a long history (6, 7). Even so, this chemical picture of cholesterol–phospholipid interactions has been criticized in later work, because such complexes have never been isolated, and molecular dynamics calculations have not suggested specific molecular structures (8–11). Nonetheless, more recent studies have demonstrated the utility of a quantitative thermodynamic model for the formation of complexes between cholesterol and the more saturated phospholipids. In this model, the complexes were referred to as “condensed complexes” in recognition of the well-known effect of cholesterol in ordering the fatty-acid chains of phospholipids (12, 13). This thermodynamic model implies short-range order, but there is no requirement that the complexes have highly specific, static molecular structures. That is, the complexes may have structures that fluctuate rapidly over a range of conformations.

A striking example of the utility of the condensed complex model is provided by recent determinations of the ternary phase diagrams of lipid mixtures (14, 15). These diagrams describe mixtures of cholesterol and two phospholipids, one phospholipid with a relatively high melting temperature and the other with a low melting temperature. For these lipids, no binary pair shows liquid–liquid immiscibility, whereas some ternary mixtures form two liquid phases (14–17). That is, the isothermal three-component phase diagram shows a closed loop at a given temperature. We suggest that the explanation of this phenomenon is that cholesterol forms a complex with one of the phospholipids and that this complex is only partially miscible with the second phospholipid. In the present work, a “reactive phospholipid” is denoted R and refers to the phospholipid that preferentially forms a complex with cholesterol. These reactive components are the higher melting phospholipids such as dipalmitoylphosphatidylcholine (DPPC) or long-chain sphingomyelins. The complex is formed in a reversible reaction, C + R ⇆ X, where C is cholesterol, and X is the complex. In the experiments to be discussed, a low melting unsaturated phospholipid such as dioleoylphosphatidylcholine (DOPC) is considered to be an unreactive phospholipid and is denoted U. [Such ternary C, R, U mixtures are sometimes referred to as raft mixtures (16).] The immiscibility is attributed to a mean field thermodynamic repulsion between U and the complex X. The strength of this repulsion is measured by the critical temperature T⁰_c of a hypothetical binary mixture of U and X. A preliminary report has been given in ref. 18.

As discussed later, there are a few early reports of unexpected closed loops describing liquid–liquid immiscibility in ternary alloys as well as ternary mixtures of familiar chemical substances, such as phenol, acetone, and water (19). Our thermodynamic model of complexes may be appropriate to these systems as well.

The recent phase diagrams of Veatch and Keller (14, 15) and deuterium NMR data of Veatch et al. (20) stimulated the calculations in this work. Their data provide a significant challenge for any theoretical model of these mixtures. For a review of their work, together with an introduction to thermodynamic phase diagrams, see ref. 21.

Methods

In the thermodynamic model, a liquid bilayer mixture of cholesterol, reactive phospholipid, and unreactive phospholipid is assumed to contain four molecular species at equilibrium, the three starting components plus the complex. For simplicity the complex is assumed to be 1:1. The Gibbs free energy is

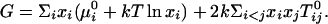[1]

Here μ⁰_i is the chemical potential of pure component i, and x_i is its equilibrium mole fraction. The T⁰_ij are the critical temperatures of the six binary pairs in the four-component mixture. These temperatures are measures of the mean-field repulsions between the various components. In our simple model, all of the chemical potentials are constant and can be set equal to zero except the chemical potential of the complex, –kT ln K. All of the critical temperatures are assumed to be well below 298 K, except the critical temperature of the binary U–X pair, hereafter denoted simply T⁰_c. There are then only two parameters, the equilibrium constant K and the critical temperature T⁰_c. The Gibbs free energy in Eq. 1 conforms to regular solution theory except for the introduction of the fourth component, the complex.

The calculations seek values of the two model parameters so as to mimic two experimental results in the ternary phase diagram for mixtures of cholesterol, palmitoyl sphingomyelin, and DOPC (15). One experimental result is the ternary critical temperature, T_c = 323 K. The second experimental result is the minimum separation of the miscibility loop boundary and the R–C axis at 298 K. That is, in the triangular phase diagram, the liquid–liquid miscibility closed loop approaches the reactive phospholipid-cholesterol axis to within ≈5 mol % but does not touch it (15). The mathematical aspects of the calculations were carried out as described in ref. 13.

Results

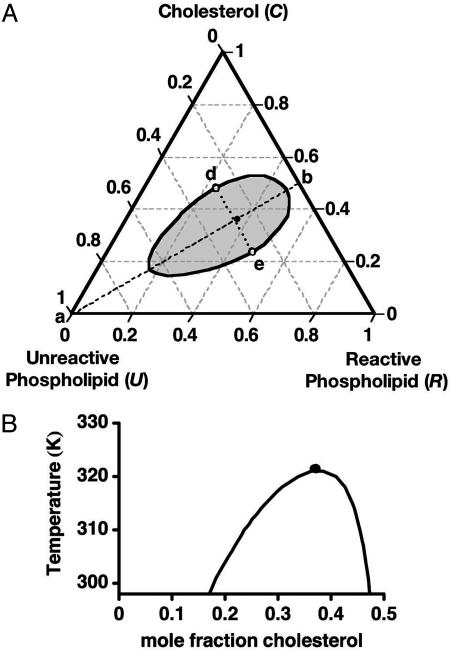
Phase Diagram and Critical Points. Fig. 1A shows a calculated ternary phase diagram for mixtures of cholesterol (C), reactive phospholipids (R), and unreactive phospholipids (U) at 298 K. The open circles at d and e are critical points. As the temperature is increased, these points move toward one another, and coincide at the ternary critical temperature, T_c, denoted by the black circle. For the parameters used, this ternary critical point almost lies on the line d–e connecting the two critical points. The assumed 1:1 stoichiometry of the complex simplifies the calculations and leads to symmetry in the ternary phase diagram about the line a–b. Along this line the initial concentrations of C and R are equal.

Fig. 1.

Calculated phase diagrams for a ternary mixture of cholesterol and two phospholipids. One phospholipid (R) reacts with cholesterol to form a 1:1 complex. The complex (X) is only partially miscible with the second phospholipid (U). (A) Isothermal ternary diagram at 298 K for equilibrium constant K = 142 and binary U–X critical temperature T⁰_c = 484 K. Along the stoichiometric line a–b the initial concentrations of the reactants are equal. The open circles at d and e are critical points at this temperature. The filled circle close to the line d–e gives the ternary critical composition at 323 K. (B) Pseudobinary phase diagram for compositions along the line a–b in A. The heat of reaction is taken to be –9.6 kcal/mol. The filled circle again denotes the ternary critical point.

Some of the important physical results of the calculations can be seen most easily by reference to a phase diagram that is similar to the phase diagram of a binary mixture. The portion of the line a–b that lies within the two-phase region is a tie line. Thus, mixtures of U together with 1:1 mixtures of cholesterol and R form pseudobinary mixtures. A calculated pseudobinary phase diagram for compositions along the line a–b is given in Fig. 1B. Here, 0% cholesterol corresponds to point a, and 50% cholesterol corresponds to point b. In this diagram, the black circle is at the ternary critical point. The two parameters that determine this pseudobinary phase diagram also fix the complete ternary diagram. These parameters were chosen to mimic two data of Veatch and Keller (15) for mixtures of cholesterol, palmitoyl sphingomyelin (R), and DOPC (U), as noted earlier. The values for the two model parameters are K = 142 at 298 K and 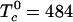K. This critical temperature parameter refers to the binar y pair, U–X. The heat of reaction was taken to be ΔH =–9.6 kcal/mol, in line with previous estimates (12, 22). For these parameters, the dissociation of the complex has a significant effect on the critical temperature, .

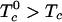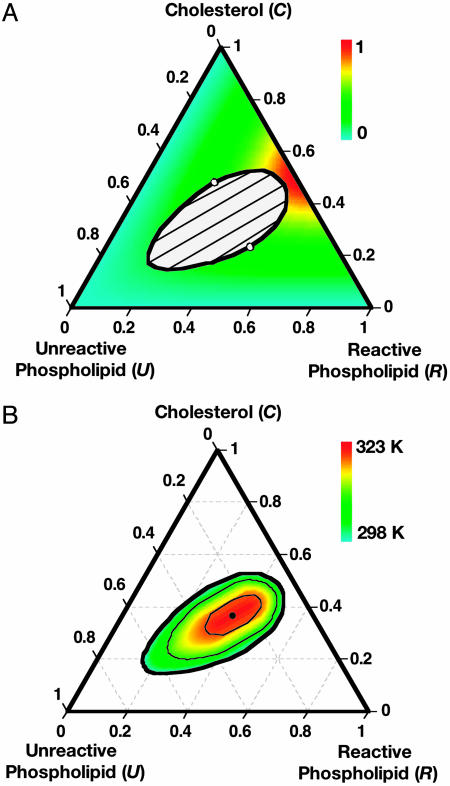
Tie Lines and Complex Concentrations. The calculated tie lines are given in Fig. 2A. The overall shape of the phase diagram and the direction of the tie lines are similar to the diagrams of Veatch and Keller (14, 15). In the phase diagram in Fig. 1A, the line a–b intersects the R–C axis at 50 mol % C, corresponding to the assumed 1:1 stoichiometry. The calculated tie lines are nearly parallel to the line a–b. Fig. 2A also shows a color-coded representation of the concentration of complex. As expected, this concentration is highest near the 1:1 R:C composition. Note that whereas the concentration of complex is much higher near this composition, the chemical activity of the complex in coexisting phases is the same. The chemical activity of the complex in the U-rich phase is large because of the U–X repulsion that is responsible for the immiscibility. In calculations not shown here, we have found that the temperature derivative of the concentration of complex shows a discontinuous increase at the ternary critical point.

Fig. 2.

Calculated ternary phase diagrams at various temperatures with tie lines and complex concentrations. Parameters used are the same as in Fig. 1. (A) Isothermal phase diagram at 298 K (same as Fig. 1 A). Tie lines are shown in the two-phase region. Outside the two-phase region, the mole-fraction concentration of complex is shown according to the indicated color code. (B) Ternary phase diagram as a function of temperature (see color code bar). The isothermal binodal curves are at 298, 308, and 318 K, and the ternary critical point is at 323 K. The minimum separation of the 298 K binodal curve and the R–C axis is ≈5 mol %.

Ternary Temperature–Composition Phase Diagram. A color-coded temperature composition phase diagram is given in Fig. 2B. The various isotherms given in dark lines correspond to 298, 308, and 318 K together with the critical point at 323 K. This diagram is qualitatively similar to that observed by Veatch and Keller (15) for the cholesterol–sphingomyelin–DOPC mixture.

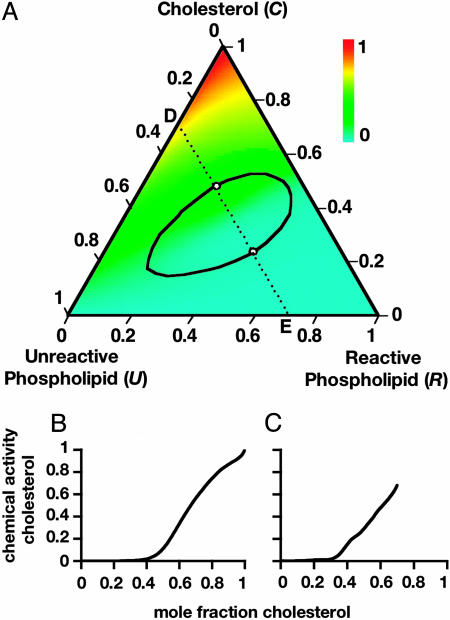
Chemical Activity Diagram. A color-coded plot of the chemical activity of cholesterol is given in Fig. 3A. This activity increases above the stoichiometric composition (given by the line a–b in Fig. 1A), because this region is where cholesterol is in excess. The equality of the chemical activities in coexisting phases is achieved by balancing complex formation against free cholesterol concentration. In our calculations, we do not include the possibility of formation of solid solutions of cholesterol, or phospholipid. Solid-solution phases in ternary phospholipid–cholesterol mixtures are described by Veatch and Keller (15). Solid solutions rich in cholesterol may be responsible for the β two-phase region found in the phase diagrams of corresponding binary mixtures in monolayers (12, 23). Solid phase formation does not in any way invalidate our calculations concerning the compositions of coexisting liquids. Experimentally, solid phase formation can obscure parts of the calculated liquid–liquid two-phase regions. The likelihood of this possibility can be understood by reference to Fig. 3. The chemical activity of cholesterol increases rapidly above the stoichiometric line a–b. When this activity reaches the activity of cholesterol in some other phase, a three-phase region is formed (partly inside the loop) or a two-phase region is formed (outside the loop). Similarly, below line a–b the activity of the phospholipid R increases rapidly and may then equal that of a solid solution of R, giving rise to new two- or three-phase equilibria. Plots of the chemical activity of cholesterol along the lines R–C and E–D are given in Fig. 3 B and C.

Fig. 3.

Calculated chemical activity of cholesterol at 298 K for the same parameters as in Fig. 1. (A) Color-coded chemical activity. Note that other two-phase or three-phase regions will appear in this diagram if at some point the activity of cholesterol is equal to the activity of cholesterol solid or solid solution. The same holds for the activity of the phospholipid R and its solid or solid solution. (B and C) Plots of chemical activity of cholesterol along directions R–C (B) and E–D (C). The chemical activity increases most rapidly around the 1:1 stoichiometric composition, in both the one-phase and the two-phase regions.

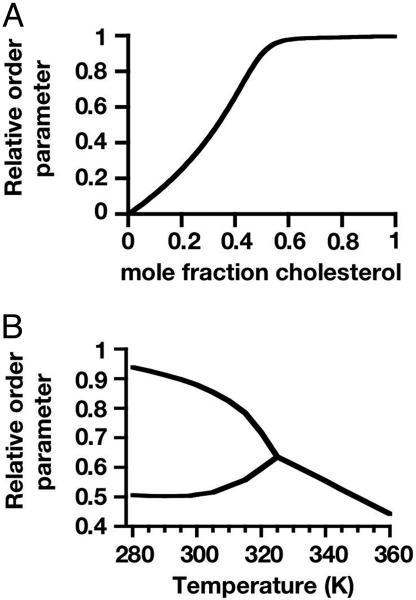
Order Parameters. Fig. 4 gives calculated average relative order parameters for the reactive phospholipid. The relative order parameter for the reactive phospholipid molecule is defined so that the order parameter equals one when the phospholipid is in a complex and is zero when the phospholipid molecule is free, not in a complex. The average is taken over the complexed and free phospholipid molecules in a single phase. In our simplified modeling, these order parameters are proportional to NMR quadrupole splittings of deuterated reactive phospholipids undergoing rapid chemical exchange. Fig. 4A gives order parameters calculated for compositions along the R–C axis in a single phase.

Fig. 4.

Average relative phospholipid order parameters calculated by using the same parameters as in Fig. 1. The relative order parameters are scaled so that a phospholipid molecule in a complex has an order parameter of one, and zero otherwise. (A) Average phospholipid order parameters at 298 K in the homogeneous binary mixture of cholesterol and the reactive phospholipid along the R–C axis in Fig. 1 A. (B) Average order parameters as a function of temperature at the critical composition. Below the ternary critical temperature there are two average order parameters, one for each phase. The order parameters in A and B should be a measure of deuterium quadrupole NMR splittings of deuterated phospholipids in a single lipid phase.

Fig. 4B shows calculated order parameters for the reactive phospholipid as a function of temperature for the ternary mixture at the critical composition (black dots in Figs. 1 A and 2B). As shown in this figure, above the critical temperature the order parameter increases with decreasing temperature due to the increasing concentration of complex. Below the critical temperature, there are two order parameters, one for each phase. The deuterium NMR spectra reported by Veatch et al. (20) show this qualitative behavior.

Discussion

Other Examples of Ternary Miscibility Loops. There are previous examples of experimental and theoretical phase diagrams with ternary critical temperatures that exceed the critical temperatures of the corresponding binary pairs. That is, the ternary phase diagrams show closed miscibility loops. Early experimental examples include familiar substances such as a mixture of phenol, acetone, and water (19, 24). Closed-loop liquid–liquid miscibility gaps also are found in alloys, such as Bi–Sb–Cu (25). In these cases, the model used here for cholesterol–phospholipid mixtures also might be applied, assuming a complex between phenol and acetone in the first case and a complex Cu₃Sb in the second. In a related phenomenon, the alloy Cu–Au–Ni mixture shows a closed loop miscibility gap of their solid solutions (25–27). Similar phase behavior has been found in a polymer blend for which there is spectroscopic evidence for a pairwise binding of two components (28).

Other Theoretical Models. Unlike our model, phase diagrams with ternary critical temperatures above binary critical temperatures (i.e., closed miscibility loops) can be modeled theoretically by using only a regular solution free energy. In this case, one of the mean field interaction parameters must be chosen to be large and negative (24, 29). For our problem, this requirement would correspond to omitting the terms for the complex in Eq. 1 and using a large negative absolute critical temperature for the R–C pair. Alternatively, one might use cubic and higher terms in the mole fractions of the components but with diminishing evident physical significance. Although such modeling may be appropriate for alloys with long-range order, it does not appear useful for molecular liquids where short-range order is of greatest interest. Moreover, this mean-field modeling does not lead in a natural way to calculating molecular-chain order parameters that are relevant to deuterium NMR splittings.

Background for This Model. The model used in the present work was used previously in connection with cholesterol–phospholipid mixtures in monolayers. The model is based on earlier general theoretical studies by Corrales and Wheeler (30), Talanquer (31), and Hueda et al. (32). In the monolayer work, the theoretical critical temperature parameters T⁰_ij in Eq. 1 are strongly pressure-dependent, generally changing from below to above room temperature as the monolayer pressure is changed. It is difficult to compare the monolayer and bilayer phase diagrams quantitatively because the parameters T⁰_ij are all likely to have different pressure dependences (33). Even so, evidence for complex formation in monolayers is compelling. The analysis of monolayer phase diagrams in terms of complexes yields a sphingomyelin–cholesterol complex with stoichiometry of 2:1 (34). Using this stoichiometry in the present study would improve somewhat the agreement between the observed and calculated phase diagrams and NMR order parameters. The monolayer work generally shows miscibility gaps in binary cholesterol–phospholipid mixtures at lower monolayer pressures. The immiscibility described by the so-called α two-phase regions has been attributed to repulsions between phospholipid and complex (12). It is generally found that the critical pressures for this α region decrease with increasing length of the saturated fatty acid chains in phosphatidylcholines as well as in sphingomyelins (34). Thus, it is perhaps not surprising that there is no immiscibility found along the R–C axis in the bilayer mixtures studied by Veatch and Keller (14, 15).

Phospholipid Chain Order and NMR Order Parameters. Our calculations emphasize the point that cholesterol-mediated phospholipid chain ordering can be, but need not be, associated with phase separation. That is, phase separation along the line a–b in Fig. 1 involves a separation into relatively ordered and disordered phases. However, for other composition ranges, for example along the binary cholesterol–phospholipid axis R–C, the chain ordering is not associated with phase separation. This result is of course a consequence of the assumptions used to model the reported experimental data.

In this connection it is important to note that Vist and Davis (35) interpreted their deuterium NMR spectra of binary mixtures of cholesterol and DPPC in terms of a phase separation into ordered and less-ordered domains. They proposed that there was rapid exchange of phospholipid molecules between the different phases. Given known diffusion coefficients, this hypothesis requires that the domains be small. Conversely, mixtures of these two lipids and DOPC have been found by Veatch and Keller (14, 15) to have phase diagrams closely similar to those calculated in the present work. Accordingly, our model of this phase behavior stipulates that binary mixtures of DPPC and cholesterol form a homogeneous phase. This subject is topical inasmuch as there is much uncertainty as to the size of lipid domains (sometimes termed lipid rafts) in cell membranes (16, 36, 37).

The deuterium NMR spectra of phospholipid molecules in these binary mixtures show composition-dependent quadrupole splittings and line broadening. In the simplest possible general model, the molecules exist in one of two states, with rapid exchange between these states on this NMR time scale (35, 38). The relative population of the putative two-state systems depends on membrane composition. We suggest that the deuterium NMR data be understood not in terms of a phase separation in this mixture but in terms of the two states corresponding to phospholipid molecules in complexes and those not in complexes. Thus, the relative order parameters in the R–C binary mixture in Fig. 4A qualitatively mimic the observed cholesterol concentration dependence of the deuterium quadrupole splittings. Moreover, one expects maximal line broadening due to this exchange to occur when the phospholipids are 50% in complex form, a result also compatible with the experiments. Thus, the deuterium line width should pass through a maximum as cholesterol is increased from zero to the putative stoichiometric composition, as observed (35, 38). For a related analysis involving spin labels, see ref. 39. The recent NMR studies of Hsueh et al. (40) for DPPC mixtures with ergosterol also appear to conform qualitatively to these expectations for a homogeneous phase with complexes (see Fig. 4A).

As noted earlier, the deuterium NMR spectra of labeled components of the C, R, U ternary mixtures appear to conform at least qualitatively to the relative order parameter plots given in Fig. 4B, at least for temperatures not close to the critical temperature. Interpretation of the NMR data close to the critical temperature may prove difficult because of the interplay of critical fluctuations, diffusion, and chemical exchange.

Chemical Activity of Cholesterol. It has been shown that the chemical activity of cholesterol in monolayers can be related to its rate of capture by β-cyclodextrin in aqueous solution (12, 41). The same principle applies to the loss from bilayers (42). A reversible specific binding of cholesterol to membrane proteins also should depend on the chemical activity of cholesterol, leading to membrane responses sharply dependent on cholesterol concentration. As shown in Fig. 3, a sharp dependence of activity on lipid composition can occur in a homogeneous membrane, as well as one with coexisting liquid phases. Just as in the case of pH, the chemical activity of cholesterol may be approximately constant throughout a cell, except for transient cellular activation and specialized compartments.

Because the cholesterol flip rate across bilayers is likely to be high (43), a model for asymmetric bilayers will require equality of the chemical potentials of cholesterol on the two sides of the bilayer. In monolayers, even a short saturated chain phosphatidylserine was found to form complexes with cholesterol, so bilayer mimics of cell membranes should include complex formation on both sides of the membrane (12, 44).