Abstract
Motorcyclists face an increased risk of injury severity at curved roadway segments due to a wide range of factors. Given the complex and evolving nature of factors influencing motorcyclist injury severity on curved roadway segments, there is a need for research that not only captures these contributing factors dynamics but also considers temporal variations and unobserved heterogeneity. The study used mixed logit models to analyze 8815 motorcycle crashes that occurred on curved segments in Texas between 2017 and 2022. Several normally distributed random parameters were identified, including clear weather, fixed objects, a 40–60 mph speed limit, White ethnicity, and riders aged 25–54 years old. Average marginal effects indicated increased fatal injury likelihood during cloudy weather, on marked lanes, roads without median, and collisions with fixed objects. Consistent factors affecting fatal injury severity across yearly models included cloudy weather and fixed-object collisions (increasing), daylight (decreasing), and riders aged 15–24 (decreasing). Interestingly, darkness in 2020 showed reduced fatal injury likelihood, likely due to lower traffic volumes and increased rider caution during the COVID-19 pandemic, contributing to less severe crash outcomes. These findings emphasize the need to consider temporal variations to understand changing risk factors and dynamics in motorcycle injury severity on curved road segments.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-025-97972-7.
Keywords: Motorcycle, Curved segments, Temporal variations, Cloudy, Fixed object, Darkness
Subject terms: Civil engineering, Energy infrastructure, Mechanical engineering
Introduction
According to the Fatality Analysis Reporting System (FARS), an estimated 5968 motorcyclists were killed in crashes in 2022, accounting for 22% of all driver fatalities in the U.S., the highest recorded number since 1975. Meanwhile, an estimated 80,910 motorcyclists were injured in traffic crashes in 2022, highlighting the ongoing safety challenges motorcyclists face on U.S. roadways. Despite advancements in safety gear, regulations, and road infrastructure, motorcycle fatalities remain disproportionately higher compared to other vehicle types. The fatality rate for motorcyclists per vehicle miles traveled (VMT) was approximately 24 times higher than that for passenger car occupants in 20211. A few other critical safety concerns with these specific road users are the lack of valid driving license, alcohol impairment, and helmet use. According to the National Highway Traffic Safety Administration (NHTSA) data, around 36% of the motorcycle riders in fatal crashes lacked valid driving licenses, and 43% of those in single-vehicle crashes were alcohol-impaired2. In states without universal helmet laws, 55% of motorcyclists killed were not wearing helmets, compared to 9% in states with such laws.
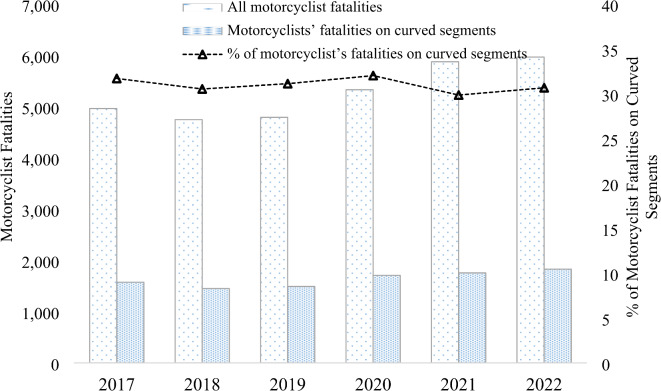
Curved roadway segments pose a greater challenge to motorcycle riders due to the need for precise handling and control, which is often compromised by factors like excessive operating speed, poor roadway conditions, adverse weather conditions, and limited visibility. This risk is exacerbated by less experienced motorcycle riders, making curved segments particularly dangerous and contributing to the overall vulnerability of motorcyclists on the road. The latest data collected from FARS illustrates a complete scenario of motorcyclists’ vulnerability on curved segments (details in Fig. 1).
Fig. 1.
Motorcyclists Fatal Crash Statistics in the US (2017–2022).
On average, around 31% of motorcyclists were killed in fatal crashes on curved segments during the 2017–2022 period, thus making it a serious traffic safety concern. In addition, the number of motorcyclist fatalities on the curved segment in 2022 was a 22.7% increase compared to 2019. This statistic underscores the need for an in-depth exploration of crash contributing factors and targeted safety measures on curved roadway segments specifically for motorcycle riders.
Motorcycle crashes have attracted extensive research attention during the last few decades. Most of the previous research focused on analyzing injury severity focusing on top crash contributing factors. Major predictors of fatal or severe crashes included higher posted speed limits, poor lighting conditions3,4, darkness during weekends3,5, specific road traffic controls6–8, older age of the crash victim6,9,10, and lack of helmet use3,4,11,12. Motorcycle collisions were found to be more concentrated in urban centers, whereas severe crash clusters were more common on road segments outside city limits13. Additionally, the strongest predictor of crash frequency was found to be curve radius, with smaller radii significantly increasing the crash likelihood14. Some studies focused on the specific spatial context. The primary types of motorcycle crashes included left-turn across paths, following too closely, and run-off-road crashes, with young male riders and impaired driving being significant contributing factors15. Some other studies focused on motorcyclists’ driving behavior on rural roads with horizontal curves, revealing riders’ tendencies to maintain consistent speed and trajectory, often positioning closer to the centerline irrespective of curve direction. Despite increased crash risk during nighttime travel, riders refrained from reducing speed, potentially due to perceived benefits such as enhanced perception of oncoming traffic16. Additionally, increased crash risk was observed during peak morning hours (7 am–8 am) and under low-light conditions, as well as on curved roads and within maintenance zones17.
Most previous studies have examined factors influencing motorcyclist injury severity, focusing on demographics, environmental conditions, helmet use, and risky behaviors like speeding and impaired riding. However, limited research has explored injury severity specifically on curved roadway segments while accounting for unobserved heterogeneity and temporal variation. To address this gap, the current study analyzes 8815 motorcycle crashes on curved segments in Texas using mixed logit models. The analysis considers a broad set of factors, including weather (clear, cloudy), lighting (daylight, darkness), roadway characteristics (two-lane roads), crash context (traffic control, intersections), and rider attributes (age, ethnicity). Additional variables such as traffic volume, shoulder width, and posted speed limits are also included to support a comprehensive assessment and inform targeted safety measures.
Literature review
This literature review section aims to provide a comprehensive understanding of the risk factors influencing motorcycle-involved crash severity from a general context, and then with a focus on methodological advancement.
Factors influencing motorcycle involved crashes
Most of the previous research on motorcycle crashes has predominantly examined the risk factors influencing the severity of crashes involving motorcyclists. These studies have investigated various factors, including the demographics of motorcyclist riders such as age, gender3, spatial elements, for example, roadway curvature8,9,18–20, posted speed limit, lighting conditions3,19, road surface3, temporal factors such as time of the day, day of the week, seasonal effects3,5, and weather conditions3. Research indicated that older motorcycle riders are more vulnerable to severe injuries in crashes9. In contrast, younger riders generally experience lower levels of injury severity; however, those under 26 years may have a higher likelihood of serious injuries while being less prone to fatal outcomes10. Rider behavior, particularly speeding, significantly contributes to the severity of motorcycle crashes, with research indicating that higher speeds increase the likelihood of fatal and severe injuries12,21. A study found that speeding, along with alcohol use and lack of helmets, increased injury severity3, while excessive speeding exacerbated fatal outcomes, especially for female riders12. Furthermore, motorcycle crashes pose significant public health challenges, as evidence shows that helmet use is associated with fewer severe head injuries and lower mortality rates11. On the other hand, non-helmeted riders demonstrated higher rates of severe head trauma and mortality compared to helmeted riders.
Motorcycle crashes, particularly on horizontally curved segments8,9,18–20,22 of rural two-lane highways5,8,23, are significantly influenced by roadway design features. A previous study found that crash frequency is strongly correlated with curve radius, indicating that sharper curves increase the likelihood of motorcycle-to-barrier crashes, especially when the radius is 820 feet or less14. Furthermore, research indicated that horizontal alignment plays a more critical role in single motorcycle crashes compared to lane and shoulder widths. Specifically, segments with adjacent reverse curves present a higher crash risk due to the added complexity of navigating these road features18. Supporting this, a previous study highlighted that sharp non-reverse curves pose the highest risk for motorcycle crashes19,23. In addition to roadway design, recent studies have demonstrated that motorcycle lean angles vary significantly based on the rider’s chosen travel path, even at the same speed on a constant radius curve24,25. The manner of collision plays a crucial role in motorcycle crashes, particularly concerning speed and the nature of the impact. For example, riding under the influence and navigating horizontal curves was found to increase the likelihood of severe injuries, while divided highways and intersections were found to be safer than undivided highways and roadway segments for single motorcycle crashes9. Moreover, single motorcycle crashes involving animals or barriers, as well as those on horizontal curves, are associated with a higher likelihood of severe injuries4,9,18,20,23,26. Research has demonstrated a strong association between relative speed and injury severity; for instance, at 70 km/h, the risk of serious injuries was 20% for collisions with wide objects, 51% for crash barriers, and 64% for narrow objects4,27. Additionally, head-on collisions between motorcycles and cars, both traveling at 60 km/h (resulting in a relative speed of 120 km/h), posed a 55% risk of serious injury to the rider27. Factors such as rider ejection significantly increase the risk of serious injuries, particularly in crashes on two-way roads without physical separation, where the dynamics of the crash can exacerbate injuries5. Adverse weather conditions significantly impact motorcycle safety and can lead to varying levels of crash severity. Crashes occurring during the summer and on weekends were associated with increased injury severity, indicating heightened risks during these periods3,5. In contrast, winter conditions and wet surfaces were correlated with lower injury severities3. In Table 1, contributing factors that influence the motorcycle involved crashes are listed below.
Table 1.
Top contributing factors affecting motorcycle involved crashes.
| Focus area | Contributing factors | Studies |
|---|---|---|
| Rider demographic | Rider age | (Farid and Ksaibati, 2021; Pour-Rouholamin et al., 2017; Seyfi et al., 2023) |
| Motorcyclists’ behavior | Excessive entry speed, combined with inattention and poor cornering skills, helmet use, alcohol use | (Brockhus et al., 2024; Eustace et al., 2011; Pour-Rouholamin et al., 2017; Rangaswamy et al., 2022; Wang et al., 2014) |
| Curve features | Curve radius | (Gabauer and Li, 2015; Wang et al., 2014; Xin et al., 2017) |
| Horizontal curves | (Farid and Ksaibati, 2021; Kvasnes et al., 2021; Rangaswamy et al., 2022; Z. Wang et al., 2019; Xin et al., 2017; Alnawmasi and Mannering, 2019) | |
| Reverse curves | (Kvasnes et al., 2021; Xin et al., 2017) | |
| Sharp non reverse curve | (Xin et al., 2019, 2018) | |
| Wider lanes and shoulder | (Kvasnes et al., 2021) | |
| Lean angle | (Rose et al., 2018; Wahba et al., 2019) | |
| Manner of collision | Single motorcycle crash | (Farid and Ksaibati, 2021; Kvasnes et al., 2021; Wang et al., 2014; Xin et al., 2017, 2018, 2019) |
| Multiple vehicle crashes | (Farid and Ksaibati, 2021) | |
| Collision with fixed objects (e.g., trees, utility poles) | (Ding et al., 2019; Wang et al., 2014) | |
| Head on collision | (Ding et al., 2019) | |
| Rider ejection | (Das et al., 2018) | |
| Roadway characteristics | Wet surface | (Pour-Rouholamin et al., 2017) |
| Rural two-lane curves | (Das et al., 2018; Rangaswamy et al., 2022; Xin et al., 2019) | |
| Environmental condition | Adverse weather, lighting conditions (dark) | (Pour-Rouholamin et al., 2017; Wang et al., 2014) |
| Temporal factors | Weekend, winter, and summer season | (Das et al., 2018; Pour-Rouholamin et al., 2017) |
| Other factors | Motorcycle Curve Assist (MCA), flashing beacons, signage and marking | (Brumec et al., 2019; Lucci et al., 2022; Rangaswamy et al., 2022) |
Methodological approaches in motorcycle crash investigation
Various studies have utilized statistical models to investigate factors contributing to motorcycle crash severity and frequency from a general perspective. Several analyses employed regression models like the multinomial logit model28, partial proportional odds3,29, Ordered Probit4,30, Logistic Regression9,26,27, and Negative Binomial Regression14 to assess how variables such as road curvature, traffic volume, rider behavior, and environmental conditions impact crash outcomes. Few other modeling techniques have also been employed including spatiotemporal analysis31,32, log-linear model33, latent class analysis34, Bayesian multivariate crash frequency model35, Bayesian Network36, multiple correspondence analysis37, taxicab correspondence analysis38, machine learning28,39, and data mining40,41. Studies involving deep learning5, computer simulations, and full-scale crash testing42 focused on innovative approaches to motorcycle crash analysis and safety interventions. A deep learning framework, DeepScooter, was developed to predict crash severities with high accuracy, revealing that rider ejection, curved roadways, and weekend crashes are associated with higher injury risks5.
Addressing unobserved heterogeneity in motorcycle crash data, few of the previous investigations utilized a random parameter modeling approach for analysis purposes9,10,17,40,43–53. While these studies provided valuable insights, they often approached motorcycle crashes from a generalized viewpoint, lacking a focused analysis of the distinctive characteristics of curved roadway segments. Although some investigations explored specific curve-related crash factors using models like negative binomial model14, ordered probit regression4, and matched case–control analysis18,23, these studies were limited by their narrow methodological scope and did not comprehensively address the multifaceted temporal nature of motorcycle crashes on curves. Moreover, previous research employing a mixed-effects logistic model on 11 years of motorcycle crash data from Florida20, failed to account for the temporal variation of influential factors, which is critical in understanding the evolving nature of crash risks over time.
Research gap and study objectives
The literature review focuses on the various factors influencing the severity of motorcycle crashes, particularly emphasizing helmet usage, demographic variables, road and environmental conditions, as well as socio-economic factors. Notably, a significant gap exists in the research concerning the analysis of motorcyclists’ injury severity at curved segments, especially when considering unobserved heterogeneity and temporal variations. This study aims to address this gap by utilizing a mixed logit model to account for unobserved heterogeneity in both means and variance, specifically concentrating on motorcycle crashes that occur on curved road segments. By developing temporal models for each year, this research captures annual variations in contributing factors that influence motorcyclist injury severities, thereby providing a dynamic perspective on how risks evolve over time. Furthermore, the integration of unobserved heterogeneity in both means and variances allows for a more nuanced understanding of the fundamental mechanisms underlying motorcycle crashes.
Data
The crash data analyzed in this study were sourced from the Crash Records Information System (CRIS), administered by the Texas Department of Transportation (TxDOT). Motorcycle-involved crashes occurring on curved roadway segments were identified through criteria based on vehicle type and roadway geometry, yielding a final dataset of 8815 incidents recorded in Texas between 2017 and 2022. To focus on crashes occurring on horizontal curves, the dataset was filtered using the Road Alignment variable provided in the CRIS database, retaining only records labeled as “Curve, level” and “Curve, grade.” As the dataset does not include continuous curvature measurements (e.g., curve radius), these predefined categorical classifications were used to capture the presence and nature of roadway curvature based on geometric conditions observed at the crash scene.
Crash severity was initially documented using the KABCO injury classification scale, which categorizes outcomes into five levels: fatal injury, incapacitating injury, non-incapacitating injury, possible injury, and no injury. For analytical clarity, these categories were consolidated into three groups: fatal injuries, moderate injuries (encompassing incapacitating, non-incapacitating, and possible injuries), and no injury. This reclassification aligns with methodologies employed in prior traffic safety research19,54–57, where simplifying multi-tier severity scales enhances model interpretability and statistical efficiency. By distinguishing between fatal, injury-related, and non-injury outcomes, the analysis prioritizes identifying risk factors associated with severe crashes and informs targeted safety interventions. A summary of the crash severity distribution within the dataset is presented in Table 2.
Table 2.
Motorcyclist crash frequency at curved segments in Texas (2017–2022).
| Year | K | ABC | O | Grand total |
|---|---|---|---|---|
| 2017 | 188 (12%) | 1230 (78.2%) | 155 (9.9%) | 1573 (100%) |
| 2018 | 197 (13.9%) | 1098 (77.4%) | 123 (8.7%) | 1418 (100%) |
| 2019 | 179 (12.7%) | 1115 (78.8%) | 121 (8.6%) | 1415 (100%) |
| 2020 | 167 (11.4%) | 1138 (78%) | 154 (10.6%) | 1459 (100%) |
| 2021 | 167 (11.3%) | 1169 (79%) | 144 (9.7%) | 1480 (100%) |
| 2022 | 144 (9.8%) | 1166 (79.3%) | 160 (10.9%) | 1470 (100%) |
| Grand total | 1042 (11.8%) | 6916 (78.5%) | 857 (9.7%) | 8815 (100%) |
The overall distribution of crashes according to severity levels is provided in the following Fig. 2. From 2017 to 2022, there were notable changes in the severity of motorcyclist crash outcomes on curved road segments in Texas. The data shows that no injury (O) crashes increased by 10.10%, indicating a positive trend where more crashes resulted in no injury to the motorcyclists involved. On the other hand, there was a significant decrease in fatal injuries (K) of 18.33%, reflecting a substantial reduction in the most severe crash outcomes. However, the ‘ABC’ category, which includes incapacitating, non-incapacitating, and possible injuries, experienced a slight increase of 1.41%.
Fig. 2.
Yearly injury class distribution of motorcyclists involved in crashes at curved segments.
In this study, a variety of variables (i.e., crash contributing factors) were selected to analyze motorcyclist crash outcomes based on diverse conditions and characteristics as seen in Table 3. Note that the variables are coded in binary format (1 for the presence of a specific factor, and 0 for the absence of that factor). In assessing the impact of visibility conditions (1 if the crash happened in clear weather conditions, 0 otherwise) on crashes, the mean values for clear weather increased from 0.818 in 2017 to 0.841 in 2022 and attained the maximum in the year 2020 (0.853), suggesting a notable change in weather conditions. In contrast, crashes during cloudy weather have decreased significantly from 0.152 in 2017 to 0.135 in 2022. For lighting conditions, there has been a slight decrease in crashes occurring in darkness over the years, with the mean from 0.186 in 2017 to 0.182 in 2022. Crashes occurring in the daylight, on the other hand, exhibited more consistency with a mean throughout the years peaking in 2020 (0.684), indicating persistent visibility challenges in darker conditions. Roadway characteristics observed a gradual decrease in crashes on two-lane, two-way roads, from a mean of 0.300 in 2017 to 0.297 in 2022. Crash characteristics showed an increase in means in the presence of traffic control (from 0.377 in 2017 to 0.430 in 2022) and collisions with fixed objects (from 0.311 in 2017 to 0.334 in 2022). The road class analysis showed little fluctuation, with city streets and farm-to-market roads both maintaining steady means near 0.265 and 0.273 respectively in 2022. Traffic characteristics, including the Annual Average Daily Traffic (AADT) volume, displayed a slight downward trend from 0.193 in 2017 to 0.188 in 2022, while the absence of median resulted in a slight increase from 0.344 in 2017 to 0.346 in 2022. Crashes within specified speed limits highlighted risks, particularly in the 40 to 60 mph range with the highest mean of 0.488 in 2021. Contributing factors such as the motorcyclist’s failure to control speed and riding at an unsafe speed reported means of 0.165 and 0.243 respectively in 2022, pointing to ongoing behavioral and safety challenges. Lastly, motorcyclists’ characteristics showed that younger motorcyclists (aged 16 to 24 years) consistently represented a significant portion of crash involvement with a mean of 0.196 in 2022. The 25 to 54 years age group showed a higher mean of 0.598 in 2022, indicating a broader vulnerability across age groups involved in motorcycle crashes during the specified period.
Table 3.
Descriptive statistics of the key selected variables.
| Variable | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | Total | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | |
| Weather condition | ||||||||||||||
| Clear weather (1 if crash happened weather was clear, 0 if no) | 0.818 | 0.386 | 0.815 | 0.389 | 0.820 | 0.384 | 0.853 | 0.355 | 0.818 | 0.386 | 0.841 | 0.366 | 0.827 | 0.378 |
| Cloudy weather (1 if crash happened when weather was cloudy, 0 if no) | 0.152 | 0.359 | 0.147 | 0.354 | 0.144 | 0.351 | 0.126 | 0.332 | 0.146 | 0.353 | 0.135 | 0.341 | 0.142 | 0.349 |
| Lighting condition | ||||||||||||||
| Darkness (1 if crash happened in dark, 0 if no) | 0.186 | 0.389 | 0.164 | 0.370 | 0.170 | 0.376 | 0.147 | 0.354 | 0.168 | 0.374 | 0.182 | 0.386 | 0.170 | 0.375 |
| Daylight (1 if crash happened in daylight, 0 if no) | 0.640 | 0.480 | 0.651 | 0.477 | 0.648 | 0.478 | 0.684 | 0.465 | 0.644 | 0.479 | 0.639 | 0.480 | 0.651 | 0.477 |
| Roadway characteristics | ||||||||||||||
| Two-lane, two-way road (1 if yes, 0 if no) | 0.300 | 0.458 | 0.289 | 0.453 | 0.300 | 0.458 | 0.332 | 0.471 | 0.320 | 0.467 | 0.297 | 0.457 | 0.307 | 0.461 |
| Crash characteristics | ||||||||||||||
| Traffic control (1 if crash happened in a marked lane with traffic control, 0 if no) | 0.377 | 0.485 | 0.391 | 0.488 | 0.392 | 0.488 | 0.382 | 0.486 | 0.403 | 0.491 | 0.430 | 0.495 | 0.396 | 0.489 |
| Collision with fixed object (1 if yes, 0 if no) | 0.311 | 0.463 | 0.303 | 0.459 | 0.317 | 0.465 | 0.308 | 0.462 | 0.337 | 0.473 | 0.334 | 0.472 | 0.318 | 0.466 |
| Overturn (1 if yes, 0 if no) | 0.449 | 0.497 | 0.467 | 0.499 | 0.431 | 0.495 | 0.454 | 0.498 | 0.416 | 0.493 | 0.410 | 0.492 | 0.438 | 0.496 |
| Intersection (1 if crash happened at intersection, 0 if no) | 0.086 | 0.280 | 0.069 | 0.254 | 0.073 | 0.261 | 0.069 | 0.254 | 0.103 | 0.304 | 0.080 | 0.272 | 0.080 | 0.272 |
| First harmful event (1 when one motor vehicle is going straight, 0 if no) | 0.772 | 0.420 | 0.793 | 0.405 | 0.770 | 0.421 | 0.788 | 0.409 | 0.760 | 0.427 | 0.753 | 0.431 | 0.772 | 0.419 |
| Attention diverted from driving (1 if yes, 0 if no) | 0.086 | 0.281 | 0.088 | 0.284 | 0.086 | 0.281 | 0.086 | 0.281 | 0.075 | 0.263 | 0.080 | 0.271 | 0.084 | 0.277 |
| Road Class | ||||||||||||||
| City Street (1 if crash happened in city streets, 0 if no) | 0.234 | 0.423 | 0.251 | 0.434 | 0.269 | 0.444 | 0.258 | 0.437 | 0.279 | 0.449 | 0.265 | 0.442 | 0.259 | 0.438 |
| Farm to market road (1 if crash happened in farm to market road, 0 if no) | 0.287 | 0.452 | 0.279 | 0.448 | 0.261 | 0.439 | 0.296 | 0.457 | 0.289 | 0.453 | 0.273 | 0.446 | 0.281 | 0.449 |
| Traffic characteristics | ||||||||||||||
| Annual average daily traffic between 401 and 4000 VPD* (1 if yes, 0 if no) | 0.193 | 0.395 | 0.175 | 0.380 | 0.170 | 0.376 | 0.217 | 0.412 | 0.200 | 0.400 | 0.188 | 0.391 | 0.191 | 0.393 |
| No median (1 if yes, 0 if no) | 0.344 | 0.475 | 0.331 | 0.471 | 0.344 | 0.475 | 0.376 | 0.485 | 0.359 | 0.480 | 0.346 | 0.476 | 0.350 | 0.477 |
| Right shoulder width of 5 to 20 ft (1 if yes, 0 if no) | 0.266 | 0.442 | 0.249 | 0.432 | 0.259 | 0.438 | 0.258 | 0.437 | 0.276 | 0.447 | 0.280 | 0.449 | 0.265 | 0.441 |
| Left shoulder width of 5 to 20 ft (1 if yes, 0 if no) | 0.247 | 0.431 | 0.230 | 0.421 | 0.244 | 0.429 | 0.241 | 0.428 | 0.253 | 0.435 | 0.261 | 0.439 | 0.246 | 0.431 |
| Two lanes (1 if yes, 0 if no) | 0.294 | 0.456 | 0.283 | 0.451 | 0.295 | 0.456 | 0.330 | 0.470 | 0.318 | 0.466 | 0.298 | 0.457 | 0.303 | 0.460 |
| Posted speed limit | ||||||||||||||
| PSL [30 to 40 mph] (1 if speed was between 30 and 40 mph, 0 if no) | 0.331 | 0.471 | 0.319 | 0.466 | 0.316 | 0.465 | 0.314 | 0.464 | 0.324 | 0.468 | 0.310 | 0.463 | 0.319 | 0.466 |
| PSL [40 to 60 mph] (1 if speed was between 40 and 60 mph, 0 if no) | 0.465 | 0.499 | 0.472 | 0.499 | 0.478 | 0.500 | 0.485 | 0.500 | 0.488 | 0.500 | 0.481 | 0.500 | 0.478 | 0.500 |
| Contributing factor | ||||||||||||||
| Motorcyclist failed to control speed (1 if yes, 0 if no) | 0.156 | 0.363 | 0.149 | 0.356 | 0.167 | 0.373 | 0.162 | 0.368 | 0.171 | 0.377 | 0.165 | 0.371 | 0.162 | 0.368 |
| Motorcyclist riding at an unsafe speed (1 if yes, 0 if no) | 0.266 | 0.442 | 0.246 | 0.431 | 0.240 | 0.427 | 0.275 | 0.446 | 0.245 | 0.430 | 0.243 | 0.429 | 0.253 | 0.435 |
| Motorcyclist’s characteristics | ||||||||||||||
| Hispanic (1 if yes, 0 if no) | 0.154 | 0.361 | 0.142 | 0.350 | 0.141 | 0.348 | 0.178 | 0.382 | 0.166 | 0.372 | 0.193 | 0.394 | 0.162 | 0.369 |
| White (1 if yes, 0 otherwise) | 0.704 | 0.457 | 0.688 | 0.463 | 0.719 | 0.450 | 0.670 | 0.470 | 0.690 | 0.463 | 0.693 | 0.462 | 0.694 | 0.461 |
| Motorcyclist aged 15 to 24 years old (1 if yes, 0 if no) | 0.205 | 0.404 | 0.192 | 0.394 | 0.190 | 0.392 | 0.183 | 0.387 | 0.184 | 0.388 | 0.196 | 0.397 | 0.192 | 0.394 |
| Motorcyclist aged 25 to 54 years old (1 if yes, 0 if no) | 0.589 | 0.492 | 0.605 | 0.489 | 0.601 | 0.490 | 0.609 | 0.488 | 0.612 | 0.487 | 0.598 | 0.490 | 0.602 | 0.489 |
VPD vehicle per day.
Methodology
Details of modeling framework
In this study, the injury severity is categorized into three discrete levels: K (fatal injury), ABC injuries (combining incapacitating injury, non-incapacitating injury, and possible injury), and O (no injury). Given the categorical nature of the dependent variable, a multinomial logit (MNL) modeling framework was employed initially to analyze these outcomes. Additionally, models were developed based on yearly data segments to investigate how the influence of factors on injury severity outcomes changes over time. The details of this are explained in the transferability tests. Initially, the MNL model was applied to both the complete dataset and the yearly subsets to gain deeper insights into the factors affecting severe motorcycle crash outcomes on curves. The base model included all 26 variables in the dataset, and backward elimination was used to remove insignificant variables (p-value > 10%). A 90% confidence level was used for all model comparisons and variable inclusion decisions. Including an intercept term in logit modeling allows for a more realistic representation of utility when all independent variables are zero. Therefore, a constant term as an intercept was initially included in the models and assessed for statistical significance. As the intercept term was found to be insignificant, it was excluded from the final model specification.
Following the MNL model, which is simple and computationally efficient but relies on a strict assumption that choices are independent of each other, limiting its ability to capture unobserved heterogeneity. The Mixed Logit model (also called Random Parameters Logit, or RPL) model addresses this by allowing individual-specific variations, improving flexibility but ignoring potential correlations between parameters. This involved testing the randomness of all model parameters and evaluating models where parameters had significant random means and standard deviations. Various metrics, including the likelihood ratio test, AIC, AIC/N, and McFadden Pseudo R-squared, were used to compare models and determine the best fit. The Correlated Random Parameters Logit (CRPL) model accounts for these correlations, enhancing accuracy but increasing computational complexity. After developing the optimal RPL models for each year and the entire dataset, the Random Parameters Logit with Heterogeneity in Means (RPLHM) model was conducted further to improve interpretability by incorporating systematic variations in random parameters. During the development of the RPLHM model, each variable in the dataset was assessed to determine its influence on the average of the random parameters. The Correlated Random Parameters Logit with Heterogeneity in Means (CRPLHM) model extends this by considering correlations between the random parameters, offering a more refined analysis but at the cost of increased model estimation difficulty. Finally, the Random Parameters Logit with Heterogeneity in Means and Variances (RPLHMV) model captures both mean and variance heterogeneity, providing the most comprehensive approach to examining each variable’s impact on the variability of the random parameters.
Mixed logit modeling framework
Police-reported crash data, collected at the scene, may omit key variables influencing injury severity, and the effects of observed factors can vary across individuals. This introduces unobserved heterogeneity, variation arising from factors not captured in the dataset, which can lead to biased parameter estimates and misleading conclusions if ignored58. Advanced mixed logit models address this limitation by allowing the effects of explanatory variables to vary across observations, thereby capturing individual-level heterogeneity. While the MNL model is commonly used for analyzing discrete outcomes, it assumes independently and identically distributed error terms and adheres to the independence of irrelevant alternatives (IIA) property, limiting its flexibility. The mixed logit model overcomes these restrictions by incorporating random parameters, enabling more realistic substitution patterns and accommodating panel structures with correlated choices over time.
The goal of this study is to investigate injury severity probability with a logit model with random parameters that can accommodate varying degrees of variability. This method, which is being used more often in empirical research, takes into consideration variances of random factors in addition to mean fluctuations59. This study specifically investigates three possible outcomes when analyzing injury severity in crashes: fatal (K), severe/non-severe/possible (ABC), and no injury (O). The modeling technique, which builds on previous research, starts by creating a function to determine the degree of injury59 as outlined by the following equation:
 |
1 |
The probability that a motorcycle with the label j will sustain an injury with level i is represented by 
in the equation. On the other hand, 
stands for the variables affecting this degree of severity. These factors are associated with the estimable 
parameters, and the error term is represented by 
. The typical multinomial logit model is based on this residual term when it follows an extreme value distribution.
 |
2 |
is the likelihood that a motorcycle j will experience a certain injury severity level, represented by i, in a set of three possible severity outcomes. Equation (2) can be written as follows to enable flexible estimate of one or more parameters within the set 
across various crash scenarios60.
 |
3 |
The probability density function connected to 
in this case is represented by the function 
, where 
is a set of parameters that define this function. The variances and the mean value are two examples of these factors. The meanings of all other terms stay the same. To allow parameters to vary across observations, 
represents a set of quantifiable parameters that may differ between crash scenarios due to the possibility of differences in the means and variances of random parameters61,62.
 |
4 |
where, 
stands for the average mean parameter estimates over all crashes. 
represents a vector of attributes that captures heterogeneity in the mean of random parameters and 
denotes the corresponding vector of estimable parameters. With corresponding estimable parameters labeled as 
, 
represents an additional set of observation-specific variables that explain variations in the standard deviation 
which captures heterogeneity in variances. In addition, the residual term is represented by 
. This equation is used in models that account for unobserved heterogeneity in both means and variances (RPLHM, RPLHMV). Additionally, the possible association between random parameters is considered in this approach59,63.
As may be shown below64, the correlated random parameters models (CRPL, CRPLHM) was investigated in situations when two or more random parameters are identified:
 |
5 |
In this case, 
is the random parameter vector’s mean, 
is the vector of explanatory variables that affect the mean of 
, η is the vector of estimable parameters that correspond to 
, and 
is the Cholesky matrix that is used to calculate the random parameter vector’s standard deviation. Furthermore, the random distributed term with a zero mean and variance 
is shown by 
. Based on both diagonal and off-diagonal elements of the symmetric Cholesky matrix, the standard deviation 
of the correlated random parameter r is defined as follows:
 |
6 |
where the diagonal element of the Cholesky matrix is denoted by 
, and the off-diagonal lower triangular matrix components of the random parameter r are represented by 
, 
, 
. The mean standard error of the standard deviation, or 
, can be found if 
is the standard deviation of observation-specific 
and 
is the number of crash observations. According to Fountas et al.65, the correlation coefficient between any two random parameters, 
and 
, is expressed as follows:
 |
7 |
where, 
is the covariance between the two indicator variables, 
and 
, where 
and 
stand for the random parameters. It is crucial to remember that the correlation coefficient, not the linear relationship between risk factors, indicates the correlation between the unobserved components recorded by the random parameters65.
In line with earlier studies58,60, the analysis’s methodology involved estimating models using simulated maximum likelihood with 1000 Halton draws. The normal distribution was selected for the random parameters since numerous studies have demonstrated that it offers a better fit than alternative distributions31,66. The study calculated marginal effects to assess the influence of a one-unit change in a particular explanatory variable on the likelihood of an outcome related to injury severity in order to aid in interpretation59. To provide thorough insights, these unique marginal effects were calculated for every observation and then averaged throughout the whole dataset.
Marginal effects
The influence of explanatory variables on the probabilities of injury severity outcomes is evaluated using marginal effects. A marginal effect represents the change in the probability of a specific injury severity level resulting from a change in a binary explanatory variable from 0 to 1. It is calculated as follows:59:
 |
8 |
All models are estimated using simulated maximum likelihood with 1000 Halton draws to ensure greater result stability67,68. A normal distribution is assumed for the random parameters, as previous studies have demonstrated that it often provides a better fit compared to alternative distributions31,66. Marginal effects were calculated for the best-fitting model in each year as well as for the full dataset. The likelihood ratio test was used to determine the overall optimal model, and marginal effects were subsequently derived from this selected model for both individual years and the combined dataset.
Transferability test
A crucial component of this research is the utilization of statistical analysis (transferability test) to examine if there are noteworthy variations among motorcycle crashes across the following years: 2017, 2018, 2019, 2020, 2021, and 2022. To investigate the null hypothesis, which states that parameters within individual models are similar and that the parameters derived from estimating various models using data from different time segments are stable and transferable, we performed two likelihood ratio tests. For the transferability tests, a general comparison is made between the models from the six different time segments and the model for the complete dataset. The test statistic used in this preliminary analysis is explained as follows59,
 |
9 |
The whole model, represented as T, is used to calculate the log-likelihood at convergence, 
, using data that includes all subgroups in consideration. Moreover, the log-likelihoods that are produced when the model converges using data especially from motorcycle crashes that happened in 2017, 2018, 2019, 2020, 2021, and 2022 are represented by 
, 
, 
, 
, 
, and 
, respectively. The 
statistic that is produced as a consequence has a chi-squared distribution, and the difference in the total number of estimated parameters between the segmented models and those in model T determines the degrees of freedom59.
To evaluate transferability, standard logit models were applied to a variety of datasets. Regarding the global test, the model estimate produced an 
value of 92.24 in the transferability test using Eq. (9), with a 
distribution with 115 degrees of freedom as shown in Table 4. With a confidence level higher than 92.24%, these results point to the rejection of the null hypothesis that all parameters in the individual models are the same. Therefore, developing separate models for each data segment or year is recommended.
Table 4.
Details of transferability test.
| Modeling framework | Degree of freedom | Likelihood ratio | Test statistics  [Eq. 9] |
Degree of freedom |
|---|---|---|---|---|
| Full model (2017–2022) | 23 | LL(full) = − 5689.11 | 92.24 | 115 |
| 2017 model | 23 | LL(2017) = − 998.43 | ||
| 2018 model | 23 | LL(2018) = − 933.59 | ||
| 2019 model | 23 | LL(2019) = − 883.85 | ||
| 2020 model | 23 | LL(2020) = − 944.91 | ||
| 2021 model | 23 | LL(2021) = − 946.42 | ||
| 2022 model | 23 | LL(2022) = − 913.32 |
The second test was a pairwise test designed to further investigate the transferability of factors determining motorcycle crash severities across different data frames, namely 2017, 2018, 2019, 2020, 2021, and 2022. The test statistics for the likelihood ratio analysis are displayed below:
 |
10 |
Log-likelihood comparison is performed between two different data subgroups, 
and 
. The log-likelihood at the convergence of a model fitted with significant parameters from subgroup m2 using m1’s data is represented by 
. The log-likelihood at the convergence of a model run with data from m1 is represented by 
, which may be used to determine the converged parameters of m2 without any parameter limits. To replicate this assessment, flip 
and 
. With degrees of freedom equal to the parameters in 
, which implies that the parameters between years m1 and m2 suggest that the parameters between data periods m1 and m2 are identical, the 
statistic evaluates the degree of confidence in rejecting or failing to reject the null hypothesis59.
Table 5 displays the outcomes of the pairwise likelihood ratio tests, which were calculated using Eq. (10). All thirty tests performed yielded confidence levels exceeding 99%. Consequently, the null hypothesis was rejected for all cases, indicating significant differences in the impacts of indicator variables on motorcycle crash severity outcomes across the designated data group pairings. These results suggest that none of the data groups share stable factors influencing motorcycle crash severities, as all tests revealed variability. Given these findings, it would be more appropriate to estimate individual models for each segment rather than relying on a comprehensive model based on the entire undivided dataset69.
Table 5.
Results of the likelihood ratio test for comparing motorcyclist injury severity in crashes at curved segments across 2017–2022.
| m1 | m2 | |||||
|---|---|---|---|---|---|---|
| 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | |
| 2017 | – | 55.87 [17] (> 99.99%) | 59.69 [17] (> 99.99%) | 245.59 [17] (> 99.99%) | 42.73 [15] (99.98%) | 69.12 [15] (> 99.99%) |
| 2018 | 69.77 [18] (> 99.99%) | – | 45.75 [17] (99.98%) | 323.32 [17] (> 99.99%) | 32.09 [15] (99.37%) | 55.12 [15] (> 99.99%) |
| 2019 | 55.40 [18] (> 99.99%) | 34.07 [17] (99.17%) | – | 251.96 [17] (> 99.99%) | 42.30 [15] (99.97%) | 63.19 [15] (> 99.99%) |
| 2020 | 38.42 [18] (99.65%) | 51.39 [17] (> 99.99%) | 44.88 [17] (99.97%) | – | 37.55 [15] (99.89%) | 39.39 [15] (99.94%) |
| 2021 | 62.16 [18] (> 99.99%) | 29.90 [17] (97.29%) | 62.88 [17] (> 99.99%) | 248.95 [17] (> 99.99%) | – | 45.34 [15] (> 99.99%) |
| 2022 | 79.02 [18] (> 99.99%) | 61.62 [17] (> 99.99%) | 75.10 [17] (> 99.99%) | 152.95 [17] (> 99.99%) | 51.22 [15] (> 99.99%) | – |
The table includes chi-square values (with degrees of freedom in brackets) and confidence levels (in parentheses).
Results
Since the crash dataset includes information from 2017 to 2022, it is still unclear whether the impact of variables on crash injury severity holds steady over time. Transferability tests suggested developing a model for each year separately. The results of likelihood ratio tests for transferability tests are represented in Table 5. As a result, the dataset was divided into individual years. For each of these six datasets, a thorough analysis and model selection procedure was carried out, which was similar to the procedure used for the overall dataset (see Table A1–A7). The results of the optimal models for each year, as well as the overall model, are presented in Table 6. The analysis revealed that the RPLHMV model was optimal for the entire dataset, 2017 and 2019 data segments. However, for the years 2020, 2021, and 2022 data segments, no parameters significantly affected the variance of random parameters, and thus, no RPLHMV model was established for that period, instead RPLHM is considered to be the optimal model. Furthermore, in the 2018 data segment, no parameter was found to be significant as a random parameter and improved the model compared to the MNL model, thus MNL was considered as the optimal model for 2018. Additionally, marginal effects for these optimal models are presented in Table 7.
Table 6.
Estimate results of optimal yearly and overall models on factors influencing motorcyclist injury severity in crashes at curved segments.
| Variables | 2017 RPLHMV | 2018 MNL | 2019 RPLHMV | 2020 RPLHM | 2021 RPLHM | 2022 RPLHM | Overall RPLHMV | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coeff | t-stat | Coeff | t-stat | Coeff | t-stat | Coeff | t-stat | Coeff | t-stat | Coeff | t-stat | Coeff | t-stat | |
| Weather condition | ||||||||||||||
| Clear weather (1 if crash happened weather was clear, 0 if no) [O] | − 3.10 | − 2.32 | − 0.68 | − 4.22 | − 1.63 | − 1.73 | − 2.14 | − 1.75 | − 1.13 | − 7.73 | − 3.26 | − 2.18 | − 2.71 | − 5.05 |
| St. dev. of clear weather | 3.29 | 2.28 | – | – | 3.72 | 2.94 | 2.62 | 1.79 | – | – | 2.65 | 1.86 | 3.17 | 5.12 |
| Cloudy weather (1 if crash happened when weather was cloudy, 0 if no) [O] | − 0.74 | − 2.94 | − 0.57 | − 2.36 | – | – | − 0.92 | − 2.84 | − 1.48 | − 5.52 | − 1.02 | − 3.36 | − 0.85 | − 6.72 |
| Lighting condition | ||||||||||||||
| Darkness (1 if crash happened in dark, 0 if no) [ABC] | – | – | – | – | – | – | 0.54 | 2.06 | – | – | – | – | – | – |
| Daylight (1 if crash happened in daylight, 0 if no) [K] | − 0.99 | − 3.45 | − 0.72 | − 4.06 | − 1.01 | − 5.30 | − 1.36 | − 6.54 | − 1.11 | − 4.82 | − 1.04 | − 6.39 | − 1.16 | − 8.31 |
| Crash characteristics | ||||||||||||||
| Traffic control (1 if crash happened in a marked lane with traffic control, 0 if no) [O] | – | – | − 0.28 | − 1.76 | − 0.95 | − 3.24 | – | – | – | – | – | – | − 0.33 | − 3.27 |
| Collision with fixed object (1 if yes, 0 if no) [K] | 0.67 | 2.40 | 0.75 | 3.99 | – | – | 0.62 | 2.76 | 0.39 | 1.77 | 0.44 | 2.34 | − 2.78 | − 1.83 |
| St. dev. of collision with fixed object | – | – | – | – | – | – | – | – | – | – | – | 7.01 | 3.25 | |
| Overturn (1 if yes, 0 if no) [ABC] | 0.99 | 3.87 | 0.57 | 4.17 | 0.52 | 2.76 | 0.46 | 2.21 | 0.36 | 2.20 | 0.42 | 2.30 | 0.36 | 3.87 |
| Intersection (1 if crash happened at intersection, 0 if no) [K] | − 2.08 | − 2.37 | – | – | – | – | − 1.00 | − 1.88 | – | – | – | – | − 1.13 | − 3.56 |
| First harmful event (1 when one motor vehicle is going straight, 0 if no) [O] | − 0.54 | − 1.99 | – | – | − 1.18 | − 4.53 | − 0.86 | − 2.85 | − 0.64 | − 3.64 | − 0.85 | − 3.05 | − 0.80 | − 6.50 |
| Attention diverted from driving (1 if yes, 0 if no) [ABC] | – | – | 0.47 | 1.91 | – | – | – | – | – | – | – | – | – | – |
| Road class | ||||||||||||||
| City street (1 if crash happened in city streets, 0 if no) [ABC] | – | – | 0.51 | 2.80 | – | – | – | – | 0.42 | 2.57 | – | – | 0.21 | 2.13 |
| Farm to market road (1 if crash happened in farm to market road, 0 if no) [ABC] | – | – | 0.47 | 2.67 | – | – | – | – | – | – | – | – | 0.22 | 1.98 |
| Traffic characteristics | ||||||||||||||
| No median (1 if yes, 0 if no) [K] | – | – | – | – | – | – | 0.43 | 1.85 | – | – | – | – | 0.57 | 3.43 |
| Right shoulder width of 5 to 20 ft (1 if yes, 0 if no) [ABC] | – | – | 0.35 | 2.23 | – | – | – | – | – | – | – | – | – | – |
| Left shoulder width of 5 to 20 ft (1 if yes, 0 if no) [K] | – | – | – | – | – | – | – | – | – | – | 0.37 | 2.05 | – | – |
| Posted speed limit | ||||||||||||||
| PSL [30 to 40 mph] (1 if speed was between 30 and 40 mph, 0 if no) [ABC] | – | – | 0.50 | 2.81 | 0.42 | 2.19 | – | – | – | – | 0.68 | 3.43 | – | – |
| PSL [40 to 60 mph] (1 if speed was between 40 and 60 mph, 0 if no) [ABC] | 0.82 | 3.39 | 0.41 | 2.58 | 0.36 | 2.04 | 1.83 | 2.51 | – | – | – | – | – | – |
| St. dev. of PSL [40 to 60 mph] | – | – | – | – | – | – | 2.24 | 2.14 | – | – | – | – | – | – |
| Contributing factor | ||||||||||||||
| Motorcyclist failed to control speed (1 if yes, 0 if no) [ABC] | – | – | – | – | – | – | – | – | 0.63 | 2.74 | 0.54 | 2.39 | 0.29 | 2.34 |
| Motorcyclist riding at an unsafe speed (1 if yes, 0 if no) [ABC] | – | – | – | – | – | – | – | – | – | – | – | – | 0.25 | 2.33 |
| Motorcyclist’s characteristics | ||||||||||||||
| Hispanic (1 if yes, 0 if no) [K] | – | – | – | – | − 0.70 | − 2.18 | – | – | − 0.75 | − 2.04 | − 0.54 | − 2.10 | − 0.47 | − 2.51 |
| White (1 if yes, 0 otherwise) [K] | − 4.35 | − 2.09 | − 0.45 | − 2.49 | − 0.74 | − 3.37 | – | – | − 0.65 | − 2.88 | − 0.80 | − 4.26 | − 2.91 | − 4.72 |
| St. dev. of white ethnicity | 4.74 | 2.35 | – | – | – | – | – | – | – | – | – | – | 2.59 | 4.86 |
| Motorcyclist aged 15 to 24 years old (1 if yes, 0 if no) [K] | − 1.87 | − 4.22 | − 1.14 | − 4.12 | − 1.28 | − 3.80 | − 1.85 | − 5.81 | − 1.29 | − 4.34 | − 0.54 | − 2.27 | − 1.78 | − 7.57 |
| Motorcyclist aged 25 to 54 years old (1 if yes, 0 if no) [K] | − 0.93 | − 3.49 | − 0.97 | − 5.34 | − 0.57 | − 2.71 | − 1.53 | − 7.17 | − 2.70 | − 2.16 | − 0.85 | − 4.63 | − 1.44 | − 8.68 |
| St. dev. of motorcyclist aged 25 to 54 years old | – | – | – | – | – | – | – | – | 2.18 | 1.97 | – | – | – | – |
| Heterogeneity in mean, Parameter: Variable | ||||||||||||||
| Effect of daylight on the mean of random parameter collision with fixed object | – | – | – | – | – | – | – | – | – | – | – | – | − 1.89 | − 2.14 |
| Effect of left shoulder width on the mean of random parameter white motorcyclists | – | – | – | – | – | – | – | – | – | – | – | – | 0.92 | 3.59 |
| Effect of intersection on the mean of random parameter clear weather | – | – | – | – | 1.92 | 2.43 | – | – | – | – | – | – | – | – |
| Effect of the collision with fixed object on the mean of random parameter clear weather | – | – | – | – | − 1.38 | 0.63 | – | – | – | – | – | – | – | – |
| Effect of white ethnicity on the mean of random parameter clear weather | – | – | – | – | − 1.04 | − 2.24 | – | – | – | – | – | – | – | – |
| Effect of 25–54 years old motorcyclist on the mean of random parameter clear weather | – | – | – | – | – | – | − 1.03 | − 2.49 | – | – | – | – | – | – |
| Effect of attention diverted from driving on the mean of random parameter clear weather | – | – | – | – | – | – | 1.15 | 1.91 | – | – | – | – | – | – |
| Effect of 25–54 years old motorcyclist on the mean of random parameter PSL [40–60 mph] | – | – | – | – | – | – | − 1.14 | − 2.90 | – | – | – | – | – | – |
| Effect of PSL [40 to 60 mph] on the mean of random parameter white | 1.02 | 1.75 | – | – | – | – | – | – | – | – | – | – | – | – |
| Effect of PSL [40 to 60 mph] on the mean of random parameter clear weather | 0.85 | 2.00 | – | – | – | – | – | – | – | – | – | – | – | – |
| Effect of motorcyclist’s aged 25 to 54 years old on the mean of random parameter clear weather | − 0.93 | − 2.06 | – | – | – | – | – | – | – | – | – | – | – | – |
| Effect of motorcyclist failed to control speed on the mean of random parameter motorcyclist’s aged 25 to 54 years old | – | – | – | – | – | – | – | – | 1.53 | 2.75 | – | – | – | – |
| Effect of cloudy weather on the mean of random parameter motorcyclist’s aged 25 to 54 years old | – | – | – | – | – | – | – | – | − 1.29 | − 1.86 | – | – | – | – |
| Effect of motorcyclist riding at an unsafe speed on the mean of random parameter motorcyclist’s aged 25 to 54 years old | – | – | – | – | – | – | – | – | 1.37 | 2.56 | – | – | – | – |
| Effect of PSL [30 to 40 mph] on the mean of random parameter clear weather | – | – | – | – | – | – | – | – | – | – | 0.77 | 1.95 | – | – |
| Heteroscedasticity in random parameters | ||||||||||||||
| Effect of 25–54 years old motorcyclist on the variance of clear weather | – | – | – | – | – | – | – | – | – | – | – | – | − 0.24 | − 4.16 |
| Effect of 25–54 years old motorcyclist on the variance of white ethnicity | – | – | – | – | – | – | – | – | – | – | – | – | 0.16 | 1.71 |
| Effect of motorcyclist age (25 to 54 years old) on the variance of clear weather | – | – | – | – | − 0.32 | − 2.51 | – | – | – | – | – | – | – | – |
| Effect of annual average daily traffic between 401 and 4000 VPD on the variance of clear weather | – | – | – | – | 0.26 | 1.75 | – | – | – | – | – | – | – | – |
| Effect of left shoulder width of 5 to 20 ft on the variance of white | 0.33 | 2.68 | – | – | – | – | – | – | – | – | – | – | – | – |
| Effect of daylight on the variance of white | − 0.30 | − 2.42 | – | – | – | – | – | – | – | – | – | – | – | – |
| Statistics | ||||||||||||||
| Number of observations | 1573 | 1418 | 1415 | 1459 | 1,480 | 1,470 | 8,815 | |||||||
| K | 18 | 15 | 17 | 17 | 16 | 15 | 23 | |||||||
| Log-likelihood at convergence | − 984.41 | − 937.47 | − 869.80 | − 937.59 | -941.02 | -918.28 | -5630.13 | |||||||
| Restricted log-likelihood | − 1728.12 | − 1557.83 | − 1554.54 | − 1601.88 | -1625.95 | -1614.96 | -9684.27 | |||||||
| McFadden Pseudo R-squared | 0.4304 | 0.3982 | 0.4405 | 0.4151 | 0.4212 | 0.4314 | 0.4186 | |||||||
| AIC | 2004.80 | 1904.90 | 1773.60 | 1909.20 | 1914.00 | 1866.60 | 11308.30 | |||||||
| AIC/N | 1.275 | 1.34 | 1.253 | 1.309 | 1.290 | 1.27 | 1.283 | |||||||
Table 7.
Marginal effect estimates for the optimal models.
| Variable | Injury Severity | 2017 RPLHMV | 2018 MNL | 2019 RPLHMV | 2020 RPLHM | 2021 RPLHM | 2022 RPLHM | Overall RPLHMV |
|---|---|---|---|---|---|---|---|---|
| Weather condition | ||||||||
| Clear weather (1 if crash happened weather was clear, 0 if no) [O] | O | 0.0106 | − 0.0797 | 0.0309 | − 0.0061 | − 0.0914 | − 0.0053 | 0.0009 |
| ABC | − 0.0089 | 0.0702 | − 0.0278 | 0.0024 | 0.0823 | 0.0043 | 0.0004 | |
| K | − 0.0017 | 0.0095 | − 0.0031 | 0.0037 | 0.0091 | 0.0010 | − 0.0013 | |
| Cloudy weather (1 if crash happened when weather was cloudy, 0 if no) [O] | O | − 0.0117 | − 0.0675 | – | − 0.0107 | − 0.0169 | − 0.0121 | − 0.0120 |
| ABC | 0.0108 | 0.0594 | – | 0.0085 | 0.0157 | 0.0105 | 0.0113 | |
| K | 0.0009 | 0.0081 | – | 0.0022 | 0.0012 | 0.0016 | 0.0007 | |
| Lighting condition | ||||||||
| Darkness (1 if crash happened in dark, 0 if no) [ABC] | O | – | – | – | − 0.0027 | – | – | – |
| ABC | – | – | – | 0.0095 | – | – | – | |
| K | – | – | – | − 0.0068 | – | – | – | |
| Daylight (1 if crash happened in daylight, 0 if no) [K] | O | 0.0024 | 0.0102 | 0.0032 | 0.0086 | 0.0055 | 0.0036 | 0.0026 |
| ABC | 0.0224 | 0.0474 | 0.0316 | 0.0488 | 0.0351 | 0.0428 | 0.0226 | |
| K | − 0.0248 | − 0.0576 | − 0.0348 | − 0.0574 | − 0.0406 | − 0.0464 | − 0.0252 | |
| Crash characteristics | ||||||||
| Traffic control (1 if crash happened in a marked lane with traffic control, 0 if no) [O] | O | – | − 0.0333 | − 0.0177 | – | – | – | − 0.0079 |
| ABC | – | 0.0293 | 0.0158 | – | – | – | 0.0074 | |
| K | – | 0.0040 | 0.0019 | – | – | – | 0.0005 | |
| Collision with fixed object (1 if yes, 0 if no) [K] | O | − 0.0016 | − 0.0106 | – | − 0.0028 | − 0.0015 | − 0.0015 | − 0.0034 |
| ABC | − 0.0139 | − 0.0492 | – | − 0.0184 | − 0.0105 | − 0.0172 | − 0.0226 | |
| K | 0.0155 | 0.0598 | – | 0.0212 | 0.0120 | 0.0187 | 0.0260 | |
| Overturn (1 if yes, 0 if no) [ABC] | O | − 0.0193 | − 0.0586 | − 0.0115 | − 0.0089 | − 0.0112 | − 0.0077 | − 0.0086 |
| ABC | 0.0325 | 0.0958 | 0.0237 | 0.0197 | 0.0187 | 0.0191 | 0.0149 | |
| K | − 0.0132 | − 0.0372 | − 0.0122 | − 0.0108 | − 0.0075 | − 0.0114 | − 0.0063 | |
| Intersection (1 if crash happened at intersection, 0 if no) [K] | O | 0.0004 | – | – | 0.0005 | – | – | 0.0003 |
| ABC | 0.0027 | – | – | 0.0023 | – | – | 0.0020 | |
| K | − 0.0031 | – | – | − 0.0028 | – | – | − 0.0023 | |
| First harmful event (1 when one motor vehicle is going straight, 0 if no) [O] | O | − 0.0223 | – | − 0.0461 | − 0.0367 | − 0.0409 | − 0.0330 | − 0.0359 |
| ABC | 0.0204 | – | 0.0416 | 0.0296 | 0.0369 | 0.0286 | 0.0337 | |
| K | 0.0019 | – | 0.0045 | 0.0071 | 0.0040 | 0.0044 | 0.0022 | |
| Attention diverted from driving (1 if yes, 0 if no) [ABC] | O | – | − 0.0485 | – | – | – | – | – |
| ABC | – | 0.0792 | – | – | – | – | – | |
| K | – | − 0.0307 | – | – | – | – | – | |
| Road class | ||||||||
| City street (1 if crash happened in city streets, 0 if no) [ABC] | O | – | − 0.0523 | – | – | − 0.0087 | – | − 0.0034 |
| ABC | – | 0.0855 | – | – | 0.0152 | – | 0.0053 | |
| K | – | − 0.0332 | – | – | − 0.0065 | – | − 0.0019 | |
| Farm to market road (1 if crash happened in farm to market road, 0 if no) [ABC] | O | – | − 0.0488 | – | – | – | – | − 0.0035 |
| ABC | – | 0.0798 | – | – | – | – | 0.0057 | |
| K | – | − 0.0308 | – | – | – | – | − 0.0022 | |
| Traffic characteristics | ||||||||
| No median (1 if yes, 0 if no) [K] | O | – | – | – | − 0.0020 | – | – | − 0.0009 |
| ABC | – | – | – | − 0.0105 | – | – | − 0.0078 | |
| K | – | – | – | 0.0125 | – | – | 0.0087 | |
| Right shoulder width of 5 to 20 ft (1 if yes, 0 if no) [ABC] | O | – | − 0.0357 | – | – | – | – | – |
| ABC | – | 0.0584 | – | – | – | – | – | |
| K | – | − 0.0227 | – | – | – | – | – | |
| Left shoulder width of 5 to 20 ft (1 if yes, 0 if no) [K] | O | – | – | – | – | – | − 0.0011 | – |
| ABC | – | – | – | – | – | − 0.0112 | – | |
| K | – | – | – | – | – | 0.0123 | – | |
| Posted speed limit | ||||||||
| PSL [30 to 40 mph] (1 if speed was between 30 and 40 mph, 0 if no) [ABC] | O | – | − 0.0521 | − 0.0075 | – | – | − 0.0110 | – |
| ABC | – | 0.0851 | 0.0165 | – | – | 0.0239 | – | |
| K | – | − 0.0330 | − 0.009 | – | – | − 0.0129 | – | |
| PSL [40 to 60 mph] (1 if speed was between 40 and 60 mph, 0 if no) [ABC] | O | − 0.0201 | − 0.0429 | − 0.0093 | − 0.0009 | – | – | – |
| ABC | 0.0351 | 0.0701 | 0.0205 | − 0.0138 | – | – | – | |
| K | − 0.0150 | − 0.0272 | − 0.0112 | 0.0147 | – | – | – | |
| Contributing factor | ||||||||
| Motorcyclist failed to control speed (1 if yes, 0 if no) [ABC] | O | – | – | – | – | − 0.0063 | − 0.0037 | − 0.0026 |
| ABC | – | – | – | – | 0.0128 | 0.0101 | 0.0042 | |
| K | – | – | – | – | − 0.0065 | − 0.0064 | − 0.0016 | |
| Motorcyclist riding at an unsafe speed (1 if yes, 0 if no) [ABC] | O | – | – | – | – | – | – | − 0.0035 |
| ABC | – | – | – | – | – | – | 0.0056 | |
| K | – | – | – | – | – | – | − 0.0021 | |
| Motorcyclist’s characteristics | ||||||||
| Hispanic (1 if yes, 0 if no) [K] | O | – | – | 0.0006 | – | 0.0009 | 0.0008 | 0.0003 |
| ABC | – | – | 0.0062 | – | 0.0059 | 0.0091 | 0.0032 | |
| K | – | – | − 0.0068 | – | − 0.0068 | − 0.0099 | − 0.0035 | |
| White (1 if yes, 0 otherwise) [K] | O | − 0.0036 | 0.0063 | 0.0027 | – | 0.0040 | 0.0038 | − 0.0008 |
| ABC | − 0.0241 | 0.0293 | 0.0340 | – | 0.0260 | 0.0443 | − 0.0038 | |
| K | 0.0277 | − 0.0356 | − 0.0367 | – | − 0.0300 | − 0.0481 | 0.0046 | |
| Motorcyclist aged 15 to 24 years old (1 if yes, 0 if no) [K] | O | 0.0014 | 0.0160 | 0.0008 | 0.0024 | 0.0018 | 0.0008 | 0.0011 |
| ABC | 0.0114 | 0.0747 | 0.0091 | 0.0143 | 0.0116 | 0.0093 | 0.0088 | |
| K | − 0.0128 | − 0.0907 | − 0.0099 | − 0.0167 | − 0.0134 | − 0.0101 | − 0.0099 | |
| Motorcyclist aged 25 to 54 years old (1 if yes, 0 if no) [K] | O | 0.0023 | 0.0138 | 0.0020 | 0.0093 | − 0.0001 | 0.0034 | 0.0032 |
| ABC | 0.0246 | 0.0639 | 0.0247 | 0.0584 | − 0.0036 | 0.0385 | 0.0298 | |
| K | − 0.0269 | − 0.0777 | − 0.0267 | − 0.0677 | 0.0037 | − 0.0419 | − 0.0330 | |
Findings from the estimated models
Weather condition
Analysis of the weather condition (clear weather) was found to significantly impact the severity of motorcycle crashes across every model that was studied as shown in Fig. 3. For the overall dataset, this variable has a negative coefficient of − 2.71 indicating a decreased likelihood of crash severity, particularly concerning no injury crashes as seen in Table 6. When weather conditions are optimal, not only is more traffic on the roads likely to be present, but motorcyclists might also have a false sense of security in their ability to control their vehicle. It is noted in another study that motorcyclists might be more inclined to drive recklessly in clear weather conditions, which may lead to an increased crash severity70. This finding can be generalized for other countries like United Kingdom, where an increased likelihood of fatal/severe injuries was observed in clear weather conditions71.
Fig. 3.
Marginal effect estimates for the indicator “Clear Weather”.
The marginal effects results from Table 7 for clear weather vary across models indicating the instability of this variable. For the overall dataset, there is a decreased likelihood of fatal injuries by 0.0013 and an increased likelihood of severe, moderate, or possible injuries and no injuries by 0.0004 and 0.0009. Concerning the 2017 model, the results indicate a decreased likelihood of fatal injuries and severe, moderate, or possible injuries by 0.0017 and 0.0089, while an increased likelihood of no injuries by 0.0106 is shown. In the 2018 model, an increased likelihood of fatal injuries and severe, moderate, or possible injuries by 0.0095 and 0.0702 is seen as well as a decreased likelihood of no injuries by 0.0797. The results for the 2019 model show a decrease in the likelihood of fatal injuries and severe, moderate, or possible injuries by 0.0031 and 0.0024 and an increase in the likelihood of no injuries by 0.0309. The marginal effects results show an increased likelihood of fatal injuries and severe, moderate, or possible injuries by 0.0037 and 0.0024 and a decreased likelihood of no injuries by 0.0061 for the 2020 dataset. When looking at the results for the 2021 model, an increased likelihood of fatal injuries and severe, moderate, or possible injuries by 0.0091 and 0.0826 and a decreased likelihood of no injuries by 0.0914 is seen. For the 2022 model, the results indicate an increase in the likelihood of fatal injuries and severe, moderate, or possible injuries by 0.0010 and 0.0043 as well as a decrease in likelihood of no injuries by 0.0053.
The variable ‘clear weather’ was also found to be a random parameter in the overall, 2017, 2019, 2020, and 2022 models (see Table 6). In the overall model, this random parameter has a mean (standard deviation) of − 2.711 (3.167) indicating that 80.4% of crashes occurring in clear weather conditions had a decreased likelihood of crash severity. Analysis showed for the 2017 model, the mean (standard deviation) of − 3.099 (3.294) of these parameters results in 82.66% of crashes sustaining reduced crash severity. For the 2019 model, this random parameter had a mean (standard deviation) of − 1.626 (3.716) suggesting a decreased likelihood of crash severity in 66.92% of crashes. The distributional characteristics of this random parameter in the 2020 model reveal that 79.31% of crashes will have lower severity based on the mean (standard deviation) of − 2.143 (2.622). In the 2022 model, the random parameter has a mean (standard deviation) of − 3.285 (2.650) indicating a decrease in likelihood of crash severity.
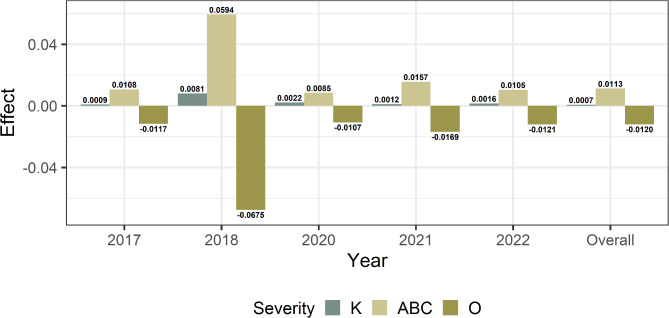
Cloudy weather is another variable found to affect motorcycle crash severity and was found to be significant in all models except for 2019 as shown in Fig. 4. A negative coefficient of − 0.85 in the overall dataset reveals a decrease in likelihood of crash severity when considering no injury crashes (see Table 6). Adverse weather conditions can decrease visibility, making motorcyclists more difficult for motorcyclists to see traffic, as well as creating road conditions that are not ideal for riding motorcycles. The stability of this indicator throughout all significant time periods is shown by the marginal effects results in Table 7. When assessing fatal injuries, the results indicate an increased likelihood of such by 0.0007, 0.0009, 0.0081, 0.0022, 0.0012, and 0.0016 for the overall, 2017, 2018, 2020, 2021, and 2022 models, respectively. These results also indicate an increased likelihood of severe, moderate, or possible injuries by 0.0113, 0.0108, 0.0594, 0.0085, 0.0157, and 0.0105 for the overall, 2017, 2018, 2020, 2021, and 2022 models. Finally, analysis reveals a decreased likelihood of no injuries by 0.0120, 0.0117, 0.0675, 0.0107, 0.0169, and 0.0121 for the overall, 2017, 2018, 2020, 2021, and 2022 datasets. These findings are supported by a study which is discovered that adverse weather conditions resulted in higher than average fatality rates12.
Fig. 4.
Marginal effect estimates for the indicator “Cloudy Weather”.
Lighting condition
Inadequate lighting can make curved segments difficult to see where motorcyclists cannot accurately judge an appropriate entry speed into the curve. Motorcycle crashes occurring in dark lighting conditions were found to be statistically significant in the 2020 model. An increased likelihood of severe, moderate, or possible injuries is indicated by the positive coefficient of 0.54 in Table 6 for this dataset. Previous studies by Seyfi et al.10 and Robbins and Fotios71 revealed similar results that insufficient lighting (dark and dusk/dawn) increased the probability of crash severity. The marginal effects results show an increased likelihood of severe, moderate, or possible injuries by 0.0095, while a decreased likelihood of fatal injuries or no injuries by 0.0068 and 0.0027 is seen for motorcycle crashes occurring in darkness (see Table 7). This decline may be attributed to travel restrictions resulting in lower traffic volumes during the COVID-19 period, potentially reducing crash exposure and high-risk interactions.
Analysis shows that motorcycle crashes occurring in daylight conditions significantly impact crash severity throughout all models as shown in Fig. 5. The negative coefficient of − 1.16 is seen in Table 6 for the entire dataset connotes a decrease in the likelihood of fatal injuries. With enhanced visibility due to favorable lighting conditions, motorcyclists will have more time to react to approaching curves or other dangers in the roadway. The stability of this variable is conveyed by the consistency of the marginal effects results in Table 7. The results show a decrease in the likelihood of fatal injuries by 0.0252, 0.0248, 0.0576, 0.0348, 0.0574, 0.0406, and 0.0464 for the entire, 2017, 2018, 2019, 2020, 2021, and 2022 models. Concerning crashes with severe, moderate, or possible injuries, an increased likelihood of these injuries is seen by 0.0226, 0.0224, 0.0474, 0.0316, 0.0488, 0.0351, and 0.0428 for the entire, 2017, 2018, 2019, 2020, 2021, and 2022 models. Also, there is an increased likelihood of no injuries by 0.0026, 0.0024, 0.0102, 0.0032, 0.0086, 0.0055, and 0.0036 for the entire, 2017, 2018, 2019, 2020, 2021, and 2022 datasets. A similar study reinforces these findings in that crashes tend to have lower injury severities when it is daylight72.
Fig. 5.
Marginal effect estimates for the indicator “Daylight”.
Crash characteristics
Motorcycle crashes on curved segments in a marked lane with traffic control was found to be significant in 2018, 2019 and in the entire dataset model. It was associated with a decreased likelihood of higher injury severity outcomes with a negative estimated coefficient of 0.33 for the entire dataset model (see Table 6). According to the marginal effect results from the entire dataset model, the likelihood of no injury decreased by 0.0079, while the likelihood of severe, moderate, and possible injuries increased by 0.0074, and the likelihood of fatal injury increased by 0.0005 (see Table 7). In 2018, these results were consistent, showing a decrease in the likelihood of no injury by 0.0333, an increase in the likelihood of severe, moderate, and possible injuries by 0.0293, and an increase in the likelihood of fatal injury by 0.0040. Similarly, the 2019 model exhibited a decreased likelihood of no injury by 0.0177, while the likelihood of severe, moderate, and possible injuries increased by 0.0158, and the likelihood of fatal injury increased by 0.0019. Traffic control points, such as those with signs or signals, present higher risks for fatal and severe crashes. Crashes at these locations have a higher likelihood of resulting in fatal injuries compared to crashes causing only injuries or property damage. Specifically, crashes at traffic control points increase the probability of fatal injuries by several percentages. Conversely, these crashes decrease the likelihood of no injury or property damage-only incidents28.
Motorcycle collisions with fixed objects were observed to be significant throughout the study period, except in 2019. While this variable was associated with a negative estimated coefficient of 2.78 in the overall dataset model, it reversed in the yearly-based models, exhibiting positive estimated coefficients (see Table 6). Additionally, this variable was identified as a random parameter with an estimated mean (standard deviation) of 7.008 (3.25). The distributional characteristics of this parameter indicated that for 98.45% of the crashes, the likelihood of high severity outcomes increased. Figure 6 illustrates the marginal effect estimates for the variable “Collision with Fixed Object” across different years, showing a consistent pattern where the probability of no injury and severe, moderate, and possible injuries generally decreased, while the likelihood of fatal injuries increased. Specifically, the overall dataset model indicates a decrease in the likelihood of no injury by 0.0034 and severe, moderate, and possible injuries by 0.0226, alongside an increase in the likelihood of fatal injuries by 0.0260. Year-by-year analysis in Table 7 reveals that in 2017, the likelihood of no injury decreased by 0.0016, severe, moderate, and possible injuries decreased by 0.0139, and fatal injuries increased by 0.0155. In 2018, the trends were more pronounced, with no injury likelihood decreasing by 0.0106, severe, moderate, and possible injuries by 0.0492, and fatal injuries increasing significantly by 0.0598. The years 2020, 2021, and 2022 followed similar patterns, with decreases in no injury and severe, moderate, and possible injuries, and increases in fatal injuries, confirming the overall trend observed in the dataset. This finding is consistent with previous studies of Xin et al.20 where collisions with fixed objects during single-motorcycle crashes on curves significantly increase the risk of severe injuries. The likelihood of severe injuries can increase by substantial percentages depending on the type of object involved. The reason for this increased risk is that fixed objects, due to their immobility and solidity, are likely to transfer more kinetic energy to the motorcyclist upon impact, exacerbating the severity of injuries.
Fig. 6.
Marginal effect estimates for the indicator “Collision with Fixed Object”.
Table 6 indicates that the variable “Overturn,” associated with motorcycle crashes on curves, has a positive estimated coefficient of 0.36, highlighting its significant impact on increasing injury severity outcomes. Figure 7 further illustrates the marginal effect estimates for this variable across different years, showing a consistent pattern where the likelihood of severe, moderate, and possible injuries increased, while the probabilities of fatal injuries and no injuries decreased. In the overall dataset model, the likelihood of severe, moderate, and possible injuries increased by 0.0149, whereas the probabilities of no injuries and fatal injuries decreased by 0.0086 and 0.0063, respectively (see Table 7). In 2017, the likelihood of severe, moderate, and possible injuries increased by 0.0325, while the probabilities of no injuries and fatal injuries decreased by 0.0193 and 0.0132. Notably, in 2018, the likelihood of severe, moderate, and possible injuries escalated by 0.0958, with significant declines in the probabilities of no injuries and fatal injuries, decreasing by 0.0586 and 0.0372, respectively. This general trend of increased likelihood of severe, moderate, and possible injuries, along with decreased probabilities of no injuries and fatal injuries, continues consistently in the subsequent years, affirming the heightened risk associated with overturning during motorcycle crashes. Similar results are seen in a study that found an increase of severe injuries by 17.1% in crashes that result in an overturned vehicle21.
Fig. 7.
Marginal effect estimates for the indicator “Overturn”.
Intersection-related motorcycle crashes on curves were only found to be significant in the 2017 and 2020 models, as well as in the model for the entire dataset. This variable is associated with a reduced likelihood of injury severity outcomes, especially for fatal injury outcome, as indicated by an estimated negative coefficient of 1.13 (see Table 6). The marginal effect result indicates that the likelihood of no injuries involved in an intersection related motorcycle crashes increased by 0.0004 in 2017, by 0.0005 in 2020 and by 0.0003 in the entire dataset model (see Table 7). Similarly, the likelihood of severe, moderate and possible injuries increased by 0.0027 in 2017, by 0.0023 in 2020 and by 0.0020 in the entire dataset model. Conversely, the likelihood of fatal injuries decreased by 0.0031 in 2017, by 0.0028 in 2020 and by 0.0023 in the entire dataset model. Prior research on roadway characteristics found that single motorcycle crashes at intersections were less likely to be severe compared to those on roadway segments. This was likely due to the lower speeds at intersections, where motorcyclists typically stopped and then accelerated from a stationary position9.
In Table 6, the variable ‘First Harmful Event,’ denoted when a motorcycle was going straight, exhibited a significant influence on injury severity with a negative estimated coefficient of 0.80 across the entire dataset. This suggests a reduced likelihood of injury severity outcomes, particularly for outcomes involving no injuries. Moving to Fig. 8, it illustrates an upward trend for fatal and severe, moderate or possible injuries, while showing a downward trend for no injuries over the years. This visual representation emphasizes how the severity of injuries tends to increase when motorcycles go straight during crash happened. The marginal effect results from Table 7 for the overall dataset and specific years, there is a noticeable decrease in the probability of no injuries, which decreased by 0.0359 in the entire dataset model and by 0.0223 in 2017. In contrast, the likelihood of severe, moderate, or possible injuries has increased, with increments such as 0.0337 in the entire dataset model and 0.0204 in 2017. Additionally, the data indicates a gradual increase in the probability of fatal injuries starting from a marginal effect of 0.0022 in the entire dataset model and of 0.0019 in 2017. The trend for other years follows a consistent trajectory where fatal and severe, moderate or possible injuries increase, and no injuries decrease, which underscores the growing impact of “First Harmful Event” on injury outcomes as the years progress.
Fig. 8.
Marginal effect estimates for the indicator “First Harmful Event”.
Motorcycle crashes occurring when the motorcyclist’s attention was diverted from driving were found significant only in the 2018 dataset model, with a positive estimated coefficient of 0.47. This suggests that this variable increases the likelihood of severe, moderate, and possible injury severity outcomes (see Table 6). According to the marginal effect estimates in Table 7, in 2018, the likelihood of no injuries decreased by 0.0485, fatal injuries decreased by 0.0307, while severe, moderate, and possible injuries increased by 0.0792. When rider’s inattention is identified as the primary cause of a motorcycle crash, it often indicates that speed played a less significant role. This type of inattention tends to lower the risk of fatal injuries but increases the likelihood of incapacitating injuries. The increase in less severe injuries is typically due to improper or insufficient evasive actions taken by the rider.
Roadway classification
Motorcycle crashes on curved city streets emerged as statistically significant occurrences in both 2018 and 2021, as well as across the entire dataset. Notably, the comprehensive dataset model revealed a positive estimated coefficient of 0.21, indicating the heightened likelihood of severe, moderate, and possible injury outcomes (see Table 6). The marginal effect result showed that the likelihood of no injuries decreased by 0.0523 in 2018, by 0.0087 in 2021 and by 0.0034 in the entire dataset model (see Table 7). In contrast, the likelihood of severe, moderate and possible injuries increased by 0.0855 in 2017, by 0.0152 in 2021 and by 0.0053 in the entire dataset. This indicator exhibits lower probability of fatal injuries by 0.0332 in 2018, by 0.0065 in 2021 and by 0.0019 in the overall dataset.
Crashes occurring on farm-to-market roads were found to be statistically significant incidents in both 2018 and across the entire dataset model. These crashes were associated with a heightened likelihood of injury severity, particularly severe, moderate, and possible injuries, as indicated by a positive estimated coefficient of 0.22 in the overall dataset model (see Table 6). From the marginal effect estimates the likelihood of no injuries decreased by 0.0488 in 2018 and by 0.0035 in the entire dataset model (see Table 7). Similarly, the likelihood of fatal injuries decreased by 0.0308 in 2017 and by 0.0022 in the entire dataset model while the likelihood of severe, moderate and possible injuries increased by 0.0798 in 2018 and by 0.0057 in the entire dataset model. According to the previous study of Wahab and Jiang28, motorcycle crashes on rural roads, particularly within village settlements, were more prone to result in fatal outcomes compared to crashes that lead to hospitalization or minor injuries. These rural areas experienced a significant increase in the likelihood of fatal crashes when compared to urban settings.
Traffic characteristics
Certain traffic characteristics such as having no median present were found to significantly impact the severity of motorcycle crashes. This indicator was found to be significant in the 2020 and overall model. With a positive coefficient of 0.57 in the overall dataset (see Table 6), an increased likelihood of injury severity for fatal injuries is signified. When no median is present in a motorcycle crash occurring in a curve, the motorcyclist has a greater chance of entering the lanes of oncoming traffic. The marginal effects results show the stability of this variable across both models (see Table 7). There is an increased likelihood of fatal injuries by 0.0087 and 0.0125 for the overall and 2020 datasets, respectively. Conversely, there is a decreased likelihood of severe, moderate, or possible injuries by 0.0078 and 0.0105 for the overall and 2020 datasets, while there is a decreased likelihood of no injury by 0.0009 and 0.0020 for the overall and 2020 datasets. Similar results are documented in previous study that found divided roads were inclined to see less severe crashes72.
Motorcycle crashes occurring when there is a right shoulder width of 5 to 20 ft were also determined to significantly impact crash severity, but only for the 2018 model. The positive coefficient of 0.35 for this year indicates an elevated likelihood of crash severity corresponding to severe, moderate, or possible injuries (see Table 6). The marginal effects results for this variable in 2018 reveal an increased likelihood of severe, moderate, or possible injuries by 0.0584 while there is a decreased likelihood of fatal injuries and no injuries by 0.0227 and 0.0357, respectively (see Table 7).
Another factor discovered to be statistically significant in impacting motorcycle crash severity is when there is a left shoulder width of 5 to 20 ft present. The presence and condition of road shoulders, as found in a previous study from Ghana, influence crash severity by increasing injury risk28. This indicator was only found to be significant in the 2022 dataset and with a positive coefficient of 0.35 it was found to increase the likelihood of crash severity when pertaining to fatal injuries (see Table 6). This relates to an increased likelihood of fatal injuries by 0.0123 as shown by the marginal effects results (see Table 7). On the other hand, there is a decreased likelihood of severe, moderate, or possible injuries and no injuries by 0.0112 and 0.0011, respectively. These results mimic another study in which it was found that motorcycle crashes were found to have higher probabilities of fatal injury where the shoulder width is between 9 and 12 ft73.
Posted speed limit
The speed at which motorcycle crashes occur can greatly affect the severity of the outcome. Such crashes transpiring where posted speed limits are between 30 and 40 mph were found to be significant in 2018, 2019, and 2022 datasets. A positive estimated coefficient is seen in all three of these models and is indicative of an increased likelihood of crash severity, particularly regarding severe, moderate, or possible injuries (see Table 6). The marginal effects results are consistent across these time periods which demonstrates the stability of this indicator (see Table 7). For the 2018 model, there is an increased likelihood of severe, moderate, or possible injuries by 0.0851 and a decreased likelihood of fatal injuries and no injuries by 0.0330 and 0.0521. In the 2019 model, the results indicate an increased likelihood of severe, moderate, or possible injuries by 0.0165 and a decreased likelihood of fatal injuries and no injuries by 0.0090 and 0.0075. Lastly, results for the 2022 model reveal an increase in likelihood of severe, moderate, or possible injuries by 0.0239 and a decrease in likelihood of fatal injuries and no injuries by 0.0129 and 0.0110. A decrease in fatal injuries by 7.59% was also seen in a similar analysis for crashes occurring where speed limits are less than 45 mph4.
Motorcycle crashes taking place where posted speed limits are between 40 and 60 mph were found to be significant in the 2017, 2018, 2019, and 2020 models. This variable had a positive coefficient in each of these models which shows an increased likelihood of crash severity for crashes that sustain severe, moderate, or possible injuries (see Table 6). The increased risk of road traffic collisions in darkness can be observed on roads with speed limits of 30 mph or below and 40–60 mph, similar to patterns seen in other countries like the UK71. Despite this, the marginal effects results are not consistent across these four years (see Table 7). In the 2017 model, these results show an increased likelihood of severe, moderate, or possible injury by 0.0351 and a decreased likelihood of fatal injuries and no injuries by 0.0150 and 0.0201. For motorcycle crashes occurring in 2018, there was an increase in likelihood of severe, moderate, or possible injuries by 0.0701 and a decrease in likelihood of fatal injuries and no injuries by 0.0272 and 0.0429. For the 2019 model, the results indicate an increased likelihood of severe, moderate, or possible injuries by 0.0205 and an increased likelihood of fatal injuries and no injuries by 0.0112 and 0.0093. However, the results for the 2020 model show an increased likelihood of fatal injuries by 0.0147 and a decreased likelihood of severe, moderate, or possible injuries and no injuries by 0.0138 and 0.0009. This variable was also found to be a random parameter in the 2020 model and has a mean (standard deviation) of 2.239 (2.14) (see Table 6). The distributional characteristics of this random parameter indicate that for 85.23% of motorcycle crashes, there was a greater chance of outcomes of high severity.
Most harmful factors
The impact on injuries sustained in crashes resulting when a motorcyclist failed to control speed was found to be statistically significant in the overall, 2021, and 2022 datasets. In the entire model, this variable has a positive coefficient of 0.29 which demonstrates an increased likelihood of crash severity corresponding to severe, moderate, or possible injuries (see Table 6). The ability for a motorcycle to turn is greatly hindered when applying the brakes. When a motorcyclist fails to control their speed navigating curves, the probability of running off the road or into oncoming traffic is increased. The stability of this variable is noted by the consistency of the marginal effects results in Table 7. These results show a decreased likelihood of fatal injuries by 0.0016, 0.0065, and 0.0064 for the entire, 2021, and 2022 datasets. For crashes sustaining severe, moderate, or possible injuries, the results show an increased likelihood of such injuries by 0.0042, 0.0128, and 0.0101 for the overall, 2021, and 2022 models. Similarly, a decrease in likelihood of no injuries is seen by 0.0026, 0.0063, and 0.0037 for the entire, 2021, and 2022 models. It was previously found that when the motorcyclist is classified as the offending driver, there tends to be a greater probability of more severe injuries30.
When the motorcyclist was riding at an unsafe speed, the impact of crash severity was found to be significant only in the overall model. With a positive coefficient of 0.25, an increased likelihood of crash severity is noted when dealing with severe, moderate, or possible injuries (see Table 6). Motorcyclists riding at unsafe speeds in China increased the likelihood of fatal crashes19. The power to weight ratio of motorcycles is generally much higher than that of passenger vehicles. This can allow for incredible acceleration and top speed, both of which present inherent danger for motorcyclists. A previous study analyzing motorcycle crashes in Calgary observed that injury severity tended to increase when unsafe speeds were a contributing factor74. The marginal effects results in Table 7 for this model reveal an increased likelihood of severe, moderate, or possible injuries by 0.0056 and a decreased likelihood of fatal injuries and no injuries by 0.0021 and 0.0035.
Motorcyclist’s characteristics
One motorcyclist characteristic found to significantly affect motorcycle crash severity is when the demographic characteristic of the motorcyclist being Hispanic. This variable was statistically significant in the overall, 2019, 2021, and 2022 models. In the overall model, this indicator revealed a decreased likelihood of crash severity pertaining to fatal injuries with a negative coefficient of − 0.47 in Table 6. The marginal effects results for this variable were consistent across these different models indicating its stability (see Table 7). For the entire dataset, the results show a decrease in likelihood of fatal injuries by 0.0035 and an increase in likelihood of severe, moderate, or possible injuries and no injuries by 0.0032 and 0.0003. The results for the 2019 model denote a decreased likelihood of fatal injuries by 0.0068 and an increased likelihood of severe, moderate, or possible injuries and no injuries by 0.0062 and 0.0006. In the 2021 model, there is a decreased likelihood of fatal injuries by 0.0068 and an increased likelihood of severe, moderate, or possible injuries and no injuries by 0.0059 and 0.0009. For the 2022 model, the results indicate a decreased likelihood of fatal injuries by 0.0099 and an increased likelihood of severe, moderate, or possible injuries and no injuries by 0.0091 and 0.0008.
Another factor contributing to the severity of motorcycle crashes is the demographic characteristic of being white as illustrated in Fig. 9. Analysis showed this variable to be significant in all models ran except for in 2020. A decreased likelihood of crash severity involving fatal injuries is noted by the negative coefficient of − 2.91 in the overall model as seen in Table 6. The instability of this indicator is also revealed by the inconsistent marginal effects results in Table 7. It is seen in the overall and 2017 models that there is an increased likelihood of fatal injuries and a decreased likelihood of severe, moderate, or possible injuries and no injuries. However, the results for the 2018, 2019, 2021, and 2022 models indicate a decrease in likelihood of fatal injuries and an increase in likelihood of severe, moderate, or possible injuries and no injuries. This variable was also identified as a random parameter with a mean (standard deviation) of − 2.911 (2.585) for the overall model and − 4.350 (4.741) for the 2017 model (see Table 6). The distributional characteristics of this random parameter indicate that for 86.99% of crashes in the entire dataset and 82.06% of crashes in the 2017 dataset there is a decreased likelihood of fatal injuries in motorcycle crashes.
Fig. 9.
Marginal effect estimates for the demographic characteristic of being white.
Analysis revealed that motorcyclists aged between 15 and 24 years old were found to significantly impact crash severity throughout all models that were investigated as illustrated in Fig. 10. The negative coefficient of − 1.78 in the overall model suggests a decrease in the likelihood of crash severity concerning fatal injuries (see Table 6). Sivasankaran et al.75 also reported that younger (18–25 years old) motorcyclists are less likely to be severely injured in crashes. Younger motorcyclists are likely to naturally have sharper reflexes and quicker reaction times allowing them more time to react in dangerous situations. The stability of this indicator is noted by the consistent marginal effects results (see Table 7). Throughout all models, the results indicate a decreased likelihood of fatal injuries and an increased likelihood of severe, moderate, or possible injuries. The most extreme of these marginal effects results occur in the 2018 model. In this model, the results show a decrease in likelihood of fatal injuries by 0.0907 and an increase in likelihood of severe, moderate, or possible injuries and no injuries by 0.0747 and 0.0160.
Fig. 10.
Marginal effect estimates of the indicator “Motorcyclist aged 15–24 years old”.
Collisions occurring with motorcyclists who are aged 25 to 54 years old were found to be significantly affecting crash severity in every yearly model that was analyzed as illustrated in Fig. 11. The overall model produced a negative coefficient of − 1.44 for this variable which relates to a decreased likelihood of crash severity when the motorcyclist suffers fatal injuries (see Table 6). Similar results are found in a study stating that working-age (25–64 years old) motorcyclists have a decreased likelihood of injury severity75. An older motorcyclist might not only have more experience riding motorcycles but also a greater level of maturity when making critical decisions on the road. The combination of these attributes can contribute to more responsible and safer motorcyclists. The marginal effects results for this variable were inconsistent across the different time periods indicating some temporal instability (see Table 7). In every model except for 2021, the results show a decrease in the likelihood of fatal injuries and an increase in the likelihood of severe, moderate, or possible injuries and no injuries. However, in the 2021 model, there is an increased likelihood of fatal injuries and a decreased likelihood of severe, moderate, or possible injuries and no injuries. In this same model, this indicator was identified as a random parameter. With a mean (standard deviation) of − 2.697 (2.182), the distributional characteristics of this random parameter indicate that 89.18% of motorcycle crashes will have a decreased likelihood of crash severity (see Table 6).
Fig. 11.
Marginal effect estimates of the indicator “Motorcyclist aged 25–54 years old”.
Heterogeneity in mean and variances
All independent variables were assessed for potential heterogeneity in the means and variances of random parameters across the mixed logit models. The variable clear weather was modeled as a random parameter in 2017, 2019, 2020, and 2022. In the 2017 and 2020 models, motorcyclists aged 25–54 years significantly reduced the mean of the clear weather parameter (− 0.93 in 2017; − 1.030 in 2020), possibly due to greater experience and caution. Conversely, speed limits of 40–60 mph and 30–40 mph were associated with increased crash likelihood in clear weather (0.85 in 2017; 0.77 in 2022), likely due to higher speeds increasing risk. In 2019, intersections were positively associated with clear weather crashes (1.92), suggesting increased traffic flow in good conditions may elevate crash risk. Negative associations were observed for collisions with fixed objects (− 1.38) and white motorcyclists (− 1.04), indicating lower crash risk in clear weather. However, attention diversion during clear weather in 2020 had a strong positive effect (1.15), highlighting the impact of relaxed driving behavior. In 2021, crashes involving motorcyclists aged 25–54 were positively influenced by failure to control speed (1.53) and riding at unsafe speeds (1.37), but negatively associated with cloudy weather (− 1.29), indicating increased caution in adverse conditions. White motorcyclists were modeled as random parameters in both the 2017 and full dataset models, where speed limits of 40–60 mph (1.02 in 2017) and wider left shoulders (0.92 in the full dataset) were positively associated with crash involvement.
Regarding heterogeneity in variances, motorcyclists aged 25–54 negatively affected the variance of clear weather (− 0.24) and positively affected the variance of white motorcyclists (0.16) in the full dataset, suggesting that the presence of this age group stabilizes crash behavior in clear conditions but increases variability across white motorcyclist cases. In 2017, wider left shoulders (5–20 ft) led to greater variance in crashes involving white motorcyclists (0.33), potentially reflecting more diverse roadway settings. Daylight reduced this variance (− 0.30), indicating more consistent behavior in well-lit conditions. In the 2019 model, the 25–54 age group again reduced variability in clear weather (− 0.32), while average annual daily traffic (AADT) between 401 and 4000 vehicles per day increased variance (0.26), possibly due to fluctuating traffic environments and localized roadway characteristics influencing crash patterns.
Policy recommendations
This study advocates the implementation of the Safe System Approach (SSA), a paradigm shifts of traffic safety philosophy of reactive to proactive countermeasures and policy-level implications. The context of motorcycle-involved crashes at curved segments is interconnected with the SSA elements including safer people (riders), safer roads (curved segments), safer vehicles (motorcycle), safer speed (speed management is a critical component for motorcycle riders at curved segments), and post-crash care. Based on the critical findings (factors increasing the likelihood of fatalities shown by positive marginal effects), the study identified that ‘collision with fixed object’ has a consistently positive effect on motorcycle riders’ fatal crash involvement at curved segments. Through the lens of SSA, several countermeasures can be recommended76. For example, infrastructure-based countermeasures such as enhanced roadside safety treatments, including barrier systems like motorcycle-friendly guardrails and impact attenuation devices, can help reduce the severity of fixed-object collisions. The implementation of forgiving roadsides, including wider clear zones and breakaway support structures, can also mitigate the consequences of run-off-road crashes. Additionally, improved roadway geometry design, such as increasing curve radii, implementing high-friction surface treatments, and adding advanced curve warning systems77, can assist riders in maintaining better control, especially in high-risk areas.
From a behavioral perspective, strategies aimed at safer people can include targeted motorcycle safety education programs focusing on curve negotiation techniques and hazard perception. Enforcing helmet laws and promoting high-visibility protective gear can also be instrumental in reducing injury severity in the event of a crash. Moreover, speed management strategies, such as dynamic curve speed warning systems, automated enforcement (e.g., speed cameras at high-risk curves), and stricter penalties for speeding violations, can effectively reduce excessive speeds, one of the key risk factors for motorcycle crashes on curved road segments.
The absence of a median on curved segments significantly increases the risk of fatal motorcycle crashes by exposing riders to head-on collisions, unintended lane departures, and loss of control. Several targeted countermeasures can help mitigate these risks. Wider lane widths and shoulder expansions can provide additional recovery space, reducing the likelihood of lane departures. Visual enhancements, such as contrasting centerline treatments and chevron alignment signs, can improve rider awareness and lane discipline. Additionally, intelligent lane departure warning systems using road-embedded sensors or connected vehicle alerts can notify riders when they drift toward opposing traffic. From a policy perspective, prioritizing motorcycle-specific design considerations in road safety audits can ensure that curved segments without medians receive appropriate countermeasures. Dynamic traffic management strategies, such as temporary median barriers or centerline rumble strips in high-risk locations, can act as an additional safeguard against cross-median crashes. Lastly, enhanced incident detection systems, including automated crash reporting and emergency response coordination, can improve post-crash care, reducing fatality risks involving motorcycle riders. Implementing these SSA-aligned strategies can significantly improve safety for motorcycle riders navigating curved road segments.
Conclusions
Motorcycle crashes on curved segments represent a unique and critical area of traffic safety research, largely due to the complex interplay of factors that increase the likelihood of incidents and the severity of injuries. Curved roadway segments introduce several challenges that exacerbate the risk for motorcyclists, including the need for precise vehicle control, the effects of road surface conditions, and the dynamics of speed and visibility. The dataset comprises 8815 records of motorcycle crashes that occurred on curved segments in Texas from 2017 to 2022. It progresses from basic Multinomial Logit Models to more complex Random Parameter Logit models that capture individual-specific variations and correlated parameters. The analysis also evaluates the stability of variables over time and computes marginal effects to understand the impact of changes in predictors on crash outcomes. The transferability tests using likelihood ratio tests revealed significant variations in the parameters across different yearly datasets of motorcycle crashes from 2017 to 2022. While the comprehensive model suggests parameter stability, individual yearly comparisons indicate substantial differences, with about half the dataset showing stable factors and the other half showing variations.
Key findings indicate that clear weather tends to decrease the likelihood of severe injuries due to possibly increased rider complacency and speed, while both cloudy and dark conditions increase injury risk due to reduced visibility and poorer road conditions. Specific road features like traffic control and the presence of fixed objects significantly influence outcomes, with fixed objects increasing the likelihood of fatal injuries. Additionally, personal characteristics of motorcyclists, such as age and ethnicity, were significant predictors of crash outcomes. Younger motorcyclists (aged 15–24 years) generally had a lower likelihood of fatal injuries, possibly due to better reflexes, while motorcyclists aged 25–54 showed varied results across the years, potentially reflecting differences in riding experience or behavioral changes over time. Analysis of the heterogeneity in motorcycle crash risks found that experienced riders aged 25–54 generally exhibit safer behaviors in clear weather, reducing crash likelihood. However, higher speed limits and distractions increase crash risks under the same conditions. Demographic traits affect outcomes differently; for instance, wider shoulders increase crashes among white motorcyclists. Variance analysis shows that traffic volume introduces more unpredictability to the conditions.
This study addressed the noted research gap by employing a mixed logit model to analyze motorcycle crash severity specifically on curved road segments, incorporating unobserved heterogeneity in both means and variance with temporal variations. This approach allowed for a comprehensive understanding of how various factors such as weather, lighting, and road characteristics uniquely affect the severity of injuries sustained in motorcycle crashes on curves. By focusing on individual-specific variations and the interplay between multiple variables, the study provides a deeper insight into the dynamics of motorcycle crashes that previous research has overlooked.
Despite its contributions, this study has several limitations. The use of historical data from 2017 to 2022 may not reflect recent changes in motorcycle safety regulations and technology. While the mixed logit model effectively accounts for unobserved heterogeneity, its accuracy depends on the completeness and quality of recorded data. Additionally, the study’s focus on Texas may limit the generalizability of findings to regions with different traffic laws, infrastructure, and riding behaviors. Nonetheless, the results offer valuable guidance for traffic safety initiatives, such as implementing dynamic speed limits, improving road design, enhancing signage on curves, and developing targeted rider training programs. Public awareness efforts can also address the heightened crash risk during clear weather conditions. Future research could explore crash dynamics by distinguishing between single- and multi-vehicle collisions, examine the influence of lighting conditions in greater detail, and assess the role of rider age in injury severity. Methodologically, future studies may also consider out-of-sample predictions, such as comparing pre- and post-COVID crash patterns.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgements
The authors would like to express their sincere gratitude to all those who contributed to this research. The authors extend their special appreciation to the Texas Department of Transportation for granting access to the Crash Records Information System (CRIS) data utilized in this study.
Author contributions
The contributions of the authors are as follows: M.J., as the first author, led conceptualization, formal analysis, and methodology. M.S. contributed to formal analysis, methodology, visualization, and drafting. Dr. A.H. supervised the analysis, validation, and editing processes. S.B. contributed to the formal analysis, validation, and drafting. Dr. N.A. revised the manuscript and validated the results. Dr. X.Y. provided revision on the final manuscript. Dr. S.D. conceptualized the research, managed resources, supervised the work, and contributed to the drafting and final review of the manuscript.
Data availability
The data supporting the findings of this study are available from the corresponding author upon reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.NHTSA. Motorcycle Safety | NHTSA. https://www.nhtsa.gov/book/countermeasures-that-work/motorcycle-safety (2023).
- 2.National Highway Traffic Safety Administration. Traffic Safety Facts, 2021 Data. https://crashstats.nhtsa.dot.gov/Api/Public/ViewPublication/813466 (2023).
- 3.Pour-Rouholamin, M., Jalayer, M. & Zhou, H. Modelling single-vehicle, single-rider motorcycle crash injury severity: An ordinal logistic regression approach. Int. J. Urban Sci.10.1080/12265934.2017.1311801 (2017). [Google Scholar]
- 4.Wang, Z., Lee, C. & Lin, P.-S. Modeling injury severity of single-motorcycle crashes on curved roadway segments. In 93rd Annual Meeting of the Transportation Research Board, Washington, DC (2014).
- 5.Das, S., Dutta, A., Dixon, K., Minjares-Kyle, L. & Gillette, G. Using deep learning in severity analysis of at-fault motorcycle rider crashes. Transp. Res. Record: J. Transp. Res. Board10.1177/0361198118797212 (2018). [Google Scholar]
- 6.Brumec, U., Hrabar, N. V., Strah, R., Matko, B. & Babić, D. Challenges to reduce speed of motorcycles in Stari log curves. In 26th World Road Congress (2019).
- 7.Lucci, C., Allen, T., Baldanzini, N. & Savino, G. Motorcycle curve assist: A novel approach based on active speed control for crash injury reduction. Traffic Inj. Prev.10.1080/15389588.2022.2106370 (2022). [DOI] [PubMed] [Google Scholar]
- 8.Rangaswamy, R., Kolla, R. D. T. N., Wang, Z., Lee, C. & Lin, P.-S. Evaluation of dynamic speed feedback signs to improve motorcycle safety on rural curves. ITE J. (2022).
- 9.Farid, A. & Ksaibati, K. Modeling severities of motorcycle crashes using random parameters. J. Traffic Transp. Eng. (English edition)10.1016/j.jtte.2020.01.001 (2021). [Google Scholar]
- 10.Seyfi, M. A., Aghabayk, K., Karimi Mamaghan, A. M. & Shiwakoti, N. Modeling the motorcycle crash severity on nonintersection urban roadways in the Australian state of victoria using a random parameters logit model. J. Adv. Transp.10.1155/2023/2250590 (2023). [Google Scholar]
- 11.Brockhus, L. A., Liasidis, P., Lewis, M., Jakob, D. A. & Demetriades, D. Injury patterns and outcomes in motorcycle driver crashes in the United States: The effect of helmet use. Injury10.1016/j.injury.2023.111196 (2024). [DOI] [PubMed] [Google Scholar]
- 12.Eustace, D., Indupuru, V. K. & Hovey, P. Identification of Risk Factors associated with motorcycle-related fatalities in Ohio. J. Transp. Eng.10.1061/(ASCE)TE.1943-5436.0000229 (2011). [Google Scholar]
- 13.Francis, F., Moshiro, C., Hans Yngve, B. & Hasselberg, M. Investigation of road infrastructure and traffic density attributes at high-risk locations for motorcycle-related injuries using multiple correspondence and cluster analysis in urban Tanzania. Int. J. Inj. Contr. Saf. Promot.10.1080/17457300.2021.1930060 (2021). [DOI] [PubMed] [Google Scholar]
- 14.Gabauer, D. & Li, X. Influence of horizontally curved roadway section characteristics on motorcycle-to-barrier crash frequency. Accid. Anal. Prev.10.1016/j.aap.2015.02.006 (2015). [DOI] [PubMed] [Google Scholar]
- 15.Lee, C., Wang, Z. & Yang, R. Understanding Florida Motorcycle Crashes and Injury Outcomes Using the Motorcycle Crash Causation Study (MCCS) Dataset. https://rosap.ntl.bts.gov/view/dot/62748 (2021).
- 16.Lemonakis, P., Eliou, N. & Karakasidis, T. Investigation of speed and trajectory of motorcycle riders at curved road sections of two-lane rural roads under diverse lighting conditions. J. Safety Res.10.1016/j.jsr.2021.05.009 (2021). [DOI] [PubMed] [Google Scholar]
- 17.Champahom, T. et al. Temporal instability of motorcycle crash fatalities on local roadways: A random parameters approach with heterogeneity in means and variances. Int. J. Environ. Res. Public Health10.3390/ijerph20053845 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kvasnes, S., Pokorny, P., Jensen, J. K. & Pitera, K. Safety effects of horizontal curve design and lane and shoulder width on single motorcycle accidents in Norway. J. Adv. Transp.10.1155/2021/6684334 (2021). [Google Scholar]
- 19.Wang, Y., Luo, Y. & Chen, F. Interpreting risk factors for truck crash severity on mountainous freeways in Jiangxi and Shaanxi, China. Eur. Transp. Res. Rev.10.1186/s12544-019-0366-4 (2019). [Google Scholar]
- 20.Xin, C., Wang, Z., Lee, C. & Lin, P.-S. Modeling safety effects of horizontal curve design on injury severity of single-motorcycle crashes with mixed-effects logistic model. Transp. Res. Record: J. Transp. Res. Board10.3141/2637-05 (2017). [Google Scholar]
- 21.Pour-Rouholamin, M. & Jalayer, M. Analyzing the severity of motorcycle crashes in North Carolina using highway safety information systems data. ITE J. (Institute of Transportation Engineers) (2016).
- 22.Alnawmasi, N. & Mannering, F. A statistical assessment of temporal instability in the factors determining motorcyclist injury severities. Anal. Methods Accid. Res.10.1016/j.amar.2019.100090 (2019). [Google Scholar]
- 23.Xin, C. et al. Development of crash modification factors of horizontal curve design features for single-motorcycle crashes on rural two-lane highways: A matched case-control study. Accid. Anal. Prev.10.1016/j.aap.2018.11.008 (2019). [DOI] [PubMed] [Google Scholar]
- 24.Rose, N. A., Carter, N. & Smith, C. Further validation of equations for motorcycle lean on a curve. SAE Int. J. Transp. Saf.10.4271/2018-01-0529 (2018). [Google Scholar]
- 25.Wahba, R. et al. Motorcycle lean angle variation around a constant radius curve at differing speeds and travel paths with an evaluation of data measurement systems. SAE Tech. Paper10.4271/2019-01-0437 (2019). [Google Scholar]
- 26.Xin, C., Wang, Z., Lee, C., Lin, P.-S., Chen, T., Guo, R. & Lu, Q. A matched case-control study on single-motorcycle crashes on rural, two-lane, undivided horizontal curves in Florida. In Transportation Research Board 97th Annual Meeting (2018).
- 27.Ding, C., Rizzi, M., Strandroth, J., Sander, U. & Lubbe, N. Motorcyclist injury risk as a function of real-life crash speed and other contributing factors. Accid. Anal. Prev.10.1016/j.aap.2018.12.010 (2019). [DOI] [PubMed] [Google Scholar]
- 28.Wahab, L. & Jiang, H. A multinomial logit analysis of factors associated with severity of motorcycle crashes in Ghana. Traffic Inj. Prev.10.1080/15389588.2019.1616699 (2019). [DOI] [PubMed] [Google Scholar]
- 29.Wang, S., Yu, J. & Ma, J. Identifying the heterogeneous effects of road characteristics on Motorcycle-Involved crash severities. Travel Behav. Soc.10.1016/j.tbs.2023.100636 (2023).36407119 [Google Scholar]
- 30.Quddus, M. A., Noland, R. B. & Chin, H. C. An analysis of motorcycle injury and vehicle damage severity using ordered probit models. J. Safety Res.10.1016/S0022-4375(02)00051-8 (2002). [DOI] [PubMed] [Google Scholar]
- 31.Li, X., Liu, J., Zhang, Z., Parrish, A. & Jones, S. A spatiotemporal analysis of motorcyclist injury severity: Findings from 20 years of crash data from Pennsylvania. Accid. Anal. Prevent. (2021). [DOI] [PubMed]
- 32.Li, Z., Chen, X., Ci, Y., Chen, C. & Zhang, G. A hierarchical Bayesian spatiotemporal random parameters approach for alcohol/drug impaired-driving crash frequency analysis. Anal. Methods Accid. Res.10.1016/j.amar.2019.01.002 (2019). [Google Scholar]
- 33.Haque, M. M., Chin, H. C. & Debnath, A. K. An investigation on multi-vehicle motorcycle crashes using log-linear models. Saf. Sci.10.1016/j.ssci.2011.09.015 (2012). [Google Scholar]
- 34.Shaheed, M. S. & Gkritza, K. A latent class analysis of single-vehicle motorcycle crash severity outcomes. Anal. Methods Accid. Res.10.1016/j.ssci.2011.09.015 (2014). [Google Scholar]
- 35.Cheng, W., Gill, G. S., Sakrani, T., Dasu, M. & Zhou, J. Predicting motorcycle crash injury severity using weather data and alternative Bayesian multivariate crash frequency models. Accid. Anal. Prevent. (2017) 10.1016/j.aap.2017.08.032 [DOI] [PubMed]
- 36.Das, S., Vierkant, V., Gonzalez, J. C., Kutela, B. & Sheykhfard, A. Bayesian network for motorcycle crash severity analysis. Transp. Res. Record: J. Transp. Res. Board10.1177/03611981231164386 (2023). [Google Scholar]
- 37.Jalayer, M. & Zhou, H. A multiple correspondence analysis of at-fault motorcycle-involved crashes in Alabama. J. Adv. Transp.10.1002/atr.1447 (2016). [Google Scholar]
- 38.Das, S. Identifying key patterns in motorcycle crashes: findings from taxicab correspondence analysis. Transp. A: Transp. Sci.10.1080/23249935.2020.1802362 (2021). [Google Scholar]
- 39.Wahab, L. & Jiang, H. Severity prediction of motorcycle crashes with machine learning methods. Int. J. Crashworthiness10.1080/13588265.2019.1616885 (2020). [Google Scholar]
- 40.Cunto, F. J. C. & Ferreira, S. An analysis of the injury severity of motorcycle crashes in Brazil using mixed ordered response models. J. Transp. Saf. Secur.10.1080/19439962.2016.1162891 (2017). [Google Scholar]
- 41.Kashani, A. T., Rabieyan, R. & Besharati, M. M. A data mining approach to investigate the factors influencing the crash severity of motorcycle pillion passengers. J. Saf. Res.10.1016/j.jsr.2014.09.004 (2014). [DOI] [PubMed] [Google Scholar]
- 42.Atahan, A. O., Hiekmann, J. M., Himpe, J. & Marra, J. Development of a continuous motorcycle protection barrier system using computer simulation and full-scale crash testing. Accid. Anal. Prev.10.1016/j.aap.2017.04.005 (2018). [DOI] [PubMed] [Google Scholar]
- 43.Chang, F., Yasmin, S., Huang, H., Chan, A. H. & Haque, M. M. Modeling endogeneity between motorcyclist injury severity and at-fault status by applying a Bayesian simultaneous random-parameters model with a recursive structure. Anal. Methods Accid. Res.10.1016/j.amar.2022.100245 (2022). [Google Scholar]
- 44.Chang, F., Xu, P., Zhou, H., Chan, A. H. & Huang, H. Investigating injury severities of motorcycle riders: A two-step method integrating latent class cluster analysis and random parameters logit model. Accid. Anal. Prev.10.1016/j.aap.2019.07.012 (2019). [DOI] [PubMed] [Google Scholar]
- 45.Flask, T., Schneider, W. H. IV. & Lord, D. A segment level analysis of multi-vehicle motorcycle crashes in Ohio using Bayesian multi-level mixed effects models. Saf. Sci.10.1016/j.ssci.2013.12.006 (2014). [Google Scholar]
- 46.Jomnonkwao, S., Champahom, T., Se, C., Hantanong, N. & Ratanavaraha, V. Contributing factors to near-miss experiences of motorcyclists in Thailand: A random parameter probit model approach. Heliyon9, e22625. 10.1016/j.heliyon.2023.e22625 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Se, C., Champahom, T., Jomnonkwao, S. & Ratanavaraha, V. Motorcyclist injury severity analysis: A comparison of Artificial Neural Networks and random parameter model with heterogeneity in means and variances. Int. J. Inj. Contr. Saf. Promot.10.1080/17457300.2022.2081985 (2022). [DOI] [PubMed] [Google Scholar]
- 48.Se, C., Champahom, T., Jomnonkwao, S., Chaimuang, P. & Ratanavaraha, V. Empirical comparison of the effects of urban and rural crashes on motorcyclist injury severities: A correlated random parameters ordered probit approach with heterogeneity in means. Accid. Anal. Prev.10.1016/j.aap.2021.106352 (2021). [DOI] [PubMed] [Google Scholar]
- 49.Shaheed, M. S. B., Gkritza, K., Zhang, W. & Hans, Z. A mixed logit analysis of two-vehicle crash severities involving a motorcycle. Accid. Anal. Prev.10.1016/j.aap.2013.05.028 (2013). [DOI] [PubMed] [Google Scholar]
- 50.Truong, L. T., Nguyen, H. T. & Tay, R. A random parameter logistic model of fatigue-related motorcycle crash involvement in Hanoi, Vietnam. Accid. Anal. Prevent.10.1016/j.aap.2020.105627 (2020). [DOI] [PubMed] [Google Scholar]
- 51.Wang, S., Li, F., Wang, Z. & Wang, J. A random parameter bivariate probit model for injury severities of riders and pillion passengers in motorcycle crashes. J. Transp. Saf. Secur.10.1080/19439962.2021.1916666 (2022). [Google Scholar]
- 52.Waseem, M., Ahmed, A. & Saeed, T. U. Factors affecting motorcyclists’ injury severities: An empirical assessment using random parameters logit model with heterogeneity in means and variances. Accid. Anal. Prev.10.1016/j.aap.2018.10.022 (2019). [DOI] [PubMed] [Google Scholar]
- 53.Zubaidi, H., Tamakloe, R., Al-Bdairi, N. S. S., Alnedawi, A. & Obaid, I. Exploring senior motorcyclist injury severity crashes: Random parameter model with heterogeneity in mean and variance. IATSS Res. (2023).
- 54.Aguero-Valverde, J. Multivariate spatial models of excess crash frequency at area level: Case of Costa Rica. Accid. Anal. Prev.59, 365–373 (2013). [DOI] [PubMed] [Google Scholar]
- 55.Kassu, A. & Hasan, M. Factors associated with traffic crashes on urban freeways. Transp. Eng.2, 100014 (2020). [Google Scholar]
- 56.Wang, Y., Wang, L. & Sun, L. What leads to severe multi-vehicle crashes on mountainous expressways in Western China?. J. South African Instit. Civil Eng.64, 63–70 (2022). [Google Scholar]
- 57.Yazdani, M. & Nassiri, H. The effect of weather on the severity of multi-vehicle crashes: a case study of Iran. Proc. Instit. Civil Eng. – Transp.174, 333–342 (2021). [Google Scholar]
- 58.Behnood, A. & Mannering, F. The effect of passengers on driver-injury severities in single-vehicle crashes: A random parameters heterogeneity-in-means approach. Anal. Methods Accid. Res.10.1016/j.amar.2017.04.001 (2017). [Google Scholar]
- 59.Washington, S., Karlaftis, M. G., Mannering, F. & Anastasopoulos, P. Statistical and econometric methods for transportation data analysis (CRC Press, 2020). [Google Scholar]
- 60.McFadden, D. & Train, K. Mixed MNL models for discrete response. J. Appl. Econ.15, 447–470 (2000). [Google Scholar]
- 61.Seraneeprakarn, P. et al. Occupant injury severities in hybrid-vehicle involved crashes: A random parameters approach with heterogeneity in means and variances. Anal. Methods Accid. Res.10.1016/j.amar.2017.05.003 (2017). [Google Scholar]
- 62.Yu, M., Zheng, C. & Ma, C. Analysis of injury severity of rear-end crashes in work zones: A random parameters approach with heterogeneity in means and variances. Anal. Methods Accid. Res.10.1016/j.amar.2020.100126 (2020). [Google Scholar]
- 63.Saeed, T. U., Hall, T., Baroud, H. & Volovski, M. J. Analyzing road crash frequencies with uncorrelated and correlated random-parameters count models: An empirical assessment of multilane highways. Anal. Methods Accid. Res.10.1016/j.amar.2019.100101 (2019). [Google Scholar]
- 64.Se, C., Champahom, T., Jomnonkwao, S., Karoonsoontawong, A. & Ratanavaraha, V. Temporal stability of factors influencing driver-injury severities in single-vehicle crashes: A correlated random parameters with heterogeneity in means and variances approach. Anal. Methods Accid. Res.32, 100179 (2021). [Google Scholar]
- 65.Fountas, G., Anastasopoulos, PCh. & Abdel-Aty, M. Analysis of accident injury-severities using a correlated random parameters ordered probit approach with time variant covariates. Anal. Methods Accid. Res.10.1016/j.amar.2018.04.003 (2018). [Google Scholar]
- 66.Damsere-Derry, J. et al. Evaluation of the effectiveness of traffic calming measures on vehicle speeds and pedestrian injury severity in Ghana. Traffic Inj. Prev.10.1080/15389588.2019.1581925 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Bhat, C. R. Quasi-random maximum simulated likelihood estimation of the mixed multinomial logit model. Transp. Res. Part B: Methodol.35, 677–693 (2001). [Google Scholar]
- 68.Train, K. E. Discrete choice methods with simulation, Second Edition. (2009).
- 69.Mannering, F. Temporal instability and the analysis of highway accident data. Anal. Methods Accid. Res.10.1016/j.amar.2017.10.002 (2018). [Google Scholar]
- 70.Lin, H.-Y. et al. Environmental factors associated with severe motorcycle crash injury in university neighborhoods: A multicenter study in Taiwan. Int. J. Environ. Res. Public Health10.3390/ijerph191610274 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Robbins, C. J. & Fotios, S. Motorcycle safety after-dark: The factors associated with greater risk of road-traffic collisions. Accid. Anal. Prev.10.1016/j.aap.2020.105731 (2020). [DOI] [PubMed] [Google Scholar]
- 72.Vahedi, M. & Singleton, P. A. Injury severity analysis of rural vehicle crashes involving familiar and unfamiliar drivers. Int. J. Transp. Sci. Technol.10.1016/j.ijtst.2023.11.002 (2024). [Google Scholar]
- 73.Islam, M. An analysis of motorcyclists’ injury severities in work-zone crashes with unobserved heterogeneity. IATSS Res.10.1016/j.iatssr.2022.01.003 (2022). [Google Scholar]
- 74.Rifaat, S., Tay, R. & De Barros, A. Severity of motorcycle crashes in Calgary. Accid. Anal. Prevent.10.1016/j.aap.2011.02.025 (2012). [DOI] [PubMed] [Google Scholar]
- 75.Sivasankaran, S., Rangam, H. & Balasubramanian, V. Investigation of factors contributing to injury severity in single vehicle motorcycle crashes in India. Int. J. Inj. Contr. Saf. Promot.10.1080/17457300.2021.1908367 (2021). [DOI] [PubMed] [Google Scholar]
- 76.Dumbaugh, E. & Khattak, A. A Safe Systems approach to motorcycle safety : CSCRS. https://www.roadsafety.unc.edu/research/projects/2021r40/ (2023).
- 77.Sangve, S. M., Kulkarni, M., Chawade, K., Marathe, G. & Pawar, P. Advanced driver assistance system (ADAS). In 2024 international conference on emerging smart computing and informatics (ESCI) (2024). 10.1109/ESCI59607.2024.10497387.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data supporting the findings of this study are available from the corresponding author upon reasonable request.