Data-driven discovery of biaxially strained single atoms array for hydrogen production

Abstract

The structure-performance relationship for single atom catalysts has remained unclear due to the averaged coordination information obtained from most single-atom catalysts. Periodic array of single atoms may provide a platform to tackle this inaccuracy. Here, we develop a data-driven approach by incorporating high-throughput density functional theory computations and machine learning to screen candidates based on a library of 1248 sites from single atoms array anchored on biaxial-strained transition metal dichalcogenides. Our screening results in Au atom anchored on biaxial-strained MoSe₂ surface via Au-Se₃ bonds. Machine learning analysis identifies four key structural features by classifying the ΔG_H* data. We show that the average band center of the adsorption sites can be a predictor for hydrogen adsorption energy. This prediction is validated by experiments which show single-atom Au array anchored on biaxial-strained MoSe₂ archives 1000 hour-stability at 800 mA cm^-2 towards acidic hydrogen evolution. Moreover, active hotspot consisting of Au atoms array and the neighboring Se atoms is unraveled for enhanced activity.

The structure-performance relationship of single-atom catalysts remains unclear. Here a data-driven approach with high-throughput DFT and machine learning is used to screen 1248 single atoms arrays, to provide a better understanding of the hydrogen evolution reaction mechanism.

Introduction

Green hydrogen production through electrochemical water splitting emerges as a promising technology due to its energy efficiency, high mass-energy density, and zero-carbon emission^1,2. Single-atom catalysts (SACs) are considered as ideal catalysts for hydrogen evolution reaction (HER), which exhibit high catalytic activity owing to unique coordination environments along with reduced material usage^3,4. Typically, atoms such as nitrogen, phosphorus, sulfur, carbon, and oxygen serve as coordination sites for anchoring single atoms on supports^5–10. However, under high current densities exceeding 500 mA cm⁻², isolated atoms are prone to migration and aggregation due to the relatively low formation energy of metal-metal (M-M), leading to structure degradation. Moreover, the coordination environment of SACs is a collective property typically inferred from synchrotron X-ray adsorption measurements. That means various types of coordination structures may co-exist, which creates the challenges of uncovering the true structure-property relationships. It has been found that well-ordered nanocrystal arrays with sub-nanometer distances can provide a precise unit arrangement in energy conversion and photoelectronic devices^11–15. Downsizing the unit of arrays to a single atom will open a window for SACs. Thus, single atoms array (SAA) with fine coordination environment could be an interesting system for exploring the structure-property correlation.

The strain effect has been a potential factor for tailoring the local electronic configuration and coordination environment of active sites for reactants^16–19. Very recently, supports with folded or uneven surfaces have been used to anchor single atoms^16,20–22. However, this approach often falls short in achieving sufficient modulation of the coordination environment and atom distribution due to the inhomogeneity of uniaxial strain. Biaxial strain in transition metal dichalcogenides (TMDs) with spherical surfaces leads to a uniform coordination environment due to the isotropic feature²³. In addition, the relatively high surface energy of a spherical surface is not conducive to the migration of atoms, which may improve structural stability. We propose that integrating single catalyst atoms array with biaxial-strained supports should pave an effective way to achieving both uniform coordination environment and atomic structural stability. To fabricate the biaxial-strained TMD, it is possible to apply gold (Au) nanospheres with ultra-smooth surfaces as both the template and source of single atoms^19,24. However, considering the massive diversity of combinations of the biaxial strain levels and TMDs substrates, it is experimentally tedious and unrealistic to identify the optimal SAA by trial-and-error method.

The high-throughput density functional theory (HT-DFT) calculations and machine learning (ML) have emerged in the exploration of high-dimensional and intricate systems in material science due to the extensive data generation and analysis ability^25–28. The data-driven strategy by the combination of HT-DFT and ML offers an efficient and accurate way to swiftly screen the most promising catalyst from the vast potential dataset, thereby accelerating the discovery of more efficient materials²⁹. Currently, ML operates primarily in two modes for catalytic structure design: the deductive and inductive mode³⁰. The deductive mode is focusing on predicting catalyst performance through trained models, where larger training datasets usually enhance the generalization of models. Inductive mode is used to identify pivotal features to elucidate catalytic properties, in which these interpretable and adjustable features are the key to effectively refining the direction of catalyst optimization. However, some potential key features may be masked in unclassified datasets by different features. Thus, we believe a proper pre-classification would determine the effectiveness of the dataset.

In this work, we predict and develop an Au single atoms array, assisted by HT-DFT calculations in combination with ML. Notably, Au atoms periodically anchored on biaxially strained MoSe₂ surface via three Se atoms coordinated Au-Se bond, namely SAA Au-bMoSe₂, represent an ideal system with uniform and accurate coordination conditions. Specifically, we first deploy HT-DFT to calculate the hydrogen adsorption energy of H (ΔG_H*, the key descriptor for HER) on biaxially strained TMDs to predict the most catalytically active sites (Fig. 1). The large datasets generated from HT-DFT are then applied to train machine learning models to extract top features and gain insight into the source of high active centers in SAAs. By this data-driven approach, we screen out of a family of 1248 hydrogen adsorption sites to pinpoint the optimal SAA Au-bMoSe₂ with charge accumulation around Au atoms (Fig. 1). It is found that the top four features, namely, d/p orbital center of adsorption site (ε_ads), lattice parameters (LP_a), bond length between the adsorbed H* and Au atom (L_Au-H), and difference between the z coordinate of adsorbed H* and the z coordinate of M atom (CA_Z-M), substantially influence the catalytic activity of adsorption sites. This guides us to fabricate the SAA Au-bMoSe₂ nanoshells via a template method, which exhibits high electrocatalytic activity for acidic HER (a low overpotential of 30 mV at 10 mA cm⁻² and low Tafel slope of 28.5 mV dec⁻¹). The data-driven results and in situ Raman analysis reveal the catalytic active hotspots array, each containing of one Au atom and the neighbor Se atoms. Compared to conventional transition metal single atoms anchored to carbon supports via bridge atoms (such as N, P, S), this hotspots array renders multiple hydrogen adsorption sites, leading to enhanced HER activity even at a high current of 800 mA cm⁻² over 1000 hours. This study provides the synthesis route for single-atom arrays, which could be an ideal system to understanding the intrinsic feature-activity relationship. It also illustrates the high potential of data-driven prediction in guiding the experimental exploration of multi-component electrocatalysts.

Fig. 1. Data-driven discovery of SAA Au-bMX₂ catalysts.

a Scheme of data-driven workflow developed by the combination of HT-DFT for calculating the ΔG_H* values and ML for predicting intrinsic structure-activity relationship. MX₂ (M = Mo and W, X = S, Se, and Te). b Pearson correlation plots of 17 features for the SAA Au-bMX₂ system. DFT calculated ΔG_H* versus ML predicted ΔG_H* for (c) model F (0.5–2.5 eV) and (d) model N (− 1 to − 0.5 eV). SHAP analysis for (e) model F and (f) model N. Each dot represents a hydrogen adsorption configuration in the SAA Au-bMX₂ system, with color intensity corresponding to the relative magnitude of the associated feature value. g Feature importance of the top four features for model F and model N. The solid dot signifies a positive correlation, while the hollow dot represents a negative correlation.

Results

HT-DFT calculations of SAA Au-bMX₂. The hydrogen adsorption free energy (ΔG_H*) of intermediate H on active sites, as a key descriptor, determines the HER activity. To predict the active surfaces, HT-DFT calculations were conducted to fabricate 72 kinds of potential SAA Au-bMX₂ slabs by considering two possible anchor sites of Au on 6 kinds of MX₂ (M = Mo and W, X = S, Se, and Te) under biaxial strain range of 0–2% (0, 0.5, 0.8, 1.2, 1.5, and 2%) (Supplementary Fig. 1). The Delaunay triangulation algorithm was then used to search for a family of 1248 hydrogen adsorption sites on the 72 kinds of SAA Au-bMX₂, with a collection of 1201 valid ΔG_H* values (Supplementary Fig. 2). As summarized in Supplementary Fig. 2, the calculated ΔG_H* values can be divided into two ranges of − 1–0.5 eV and 0.5–2.5 eV by a boundary of 0.5 eV, which shows two confusing partitions. To figure it out, the obtained H adsorption configurations on the family of SAA Au-bMX₂ surfaces were then mapped with the corresponding ΔG_H* values (Supplementary Figs. 3–8). The optimized H adsorption configurations close to the Au atom have more negative hydrogen adsorption-free energies, while those adsorbed at S/Se/Te sites (away from Au atoms) exhibit more positive ΔG_H*. This implies that the two groups of ΔG_H* data (− 1 ~ 0.5 eV and 0.5 ~ 2.5 eV) can be categorized into H adsorption near/on Au SAA and those away from Au SAA, respectively.

To obtain more accurate structure-activity relationships, we propose the applied biaxial strain could enlarge the lattice constant (LP_a) of the surface, which may be an undercover reason. The ΔG_H* results were thus plotted against the LP_a of MX₂ on different slabs, showing the gradual increase of ΔG_H* values with increasing lattice parameters, (Supplementary Fig. 9). Among the 72 optimized surfaces, the intrinsic activity of the SAA Au-bMX₂ system can be ranked in the order of MoSe₂ > WTe₂ > MoTe₂ > MoS₂ > WS₂ > WSe₂. Specifically, the H intermediates on the top of Au atoms on SAA Au-MoSe₂, SAA Au-MoTe₂, and SAA Au-WTe₂ structures exhibit much more optimized ΔG_H* near zero, signifying highly intrinsic active sites. Moreover, for the same type of structure, the larger biaxial strain will lead to higher ΔG_H* values (Supplementary Fig. 9). After the detailed analysis of HT-DFT data, the SAA Au-bMoSe₂ structure under 2% biaxial strain is selected as the optimal HER catalyst with a ΔG_H* value of − 0.013 eV. The charge density difference of SAA Au-bMoSe₂ indicates that the Se sites close to the Au atom show a dramatical drop in electron density (Supplementary Fig. 10). Bader charge analysis indicates that the Se atoms pump electrons to the adjacent Au atom, rendering the Au SAA an electron-rich nature (Supplementary Fig. 11). In addition, on the bare MoSe₂ under 0–2% biaxial stain (Supplementary Table 1), the Se sites on MoSe₂ exhibit rather weak hydrogen adsorption capabilities, underscoring the impact of the Au SAA. Hence, the HT-DFT has enabled us to screen structures with highly intrinsic activity based on ΔG_H* and emphasize the crucial role of Au SAA on biaxial strained MX₂ during HER. However, we believe ΔG_H* is only a superficial descriptor for the HER mechanism; what is the genuine and root structural factors of the library of SAA Au-bMX₂ that determine the ΔG_H* remain unclear.

To fill up the above gap, machine learning (ML) based on the HT-DFT dataset was conducted to identify the critical factors impacting the catalytic activity of the SAA Au-bMX₂ system. Considering the structural characteristics of the library of SAA Au-bMX₂, we divided the feature sets into three categories: adsorption site features, adsorbate features, and surface structure features. A feature set containing 17 features are then constructed from 1201 optimized structures. The classical random forest regression (RFR) algorithm is chosen as the ML training model for correlating ΔG_H*^31,32. To improve training efficiency and reduce prediction bias, a comprehensive analysis of feature correlations is carefully carried out (Fig. 1b). Features with a Pearson correlation coefficient (PCC) exceeding 0.93 and those that are computationally intensive were removed to reduce dimensionality and increase model accuracy, resulting in a critical dataset consisting of 13 features. The dataset comprising all 1201 hydrogen adsorption configurations was then used for training the RFR model. The test set shows a coefficient of determination (R²) of 0.992 and a root mean square error (RMSE) of 0.077 (Supplementary Fig. 12). We employed Recursive Feature Elimination (RFE) and Recursive Feature Elimination with Cross-Validation (RFECV) methods to guarantee proper feature selection (Supplementary Figs. 13, 14), then performed various proportional divisions and identical independent splits to the dataset to verify the reliability of the models (Supplementary Figs. 15–18). Feature importance analysis based on these models indicates that electron affinity (E_A) is considerably more significant than other features. SHapley Additive exPlanation (SHAP) analysis, together with the Permutation Feature Importance (PFI) method identifies the E_A has the most drastic influence on ΔG_H*, with a relationship of higher E_A value leading to a lower ΔG_H* (Supplementary Figs. 19, 20). This will enhance the surficial hydrogen adsorption capability^33,34. Among the examined elements, Au has the highest electron affinity (Supplementary Table 2), showing that the ΔG_H* values near the Au site are lower, aligning with HT-DFT results. However, as E_A is an intrinsic property of elements, it is difficult to derive the structure-activity relationship of catalytic structures from this feature alone.

Given the ΔG_H* data falling into two separated regions, the element differences of adsorption sites may cause the key features to be overshadowed by the E_A values. The ML model was thus trained on each of the two regions separately. The range from − 1 to −0.5 eV pertains to H adsorption sites close to Au SAA, consisting of 401 samples (model N), while the range from 0.5 to 2.5 eV corresponding to those far from Au SAA includes 800 samples (model F). As shown in Fig. 1c, d, the R² values for model N and model F are 0.953 and 0.972, respectively, achieving good training performance. The validity of the training results is also confirmed by performing various proportional divisions and identical independent splits to these two small datasets (Supplementary Figs. 21–24). For H adsorption structures near Au SAA, the importance of the four top features ranks in ε_ads > LP_a > L_Au-H > CA_Z-M, with a total contribution of about 70% (Fig. 1e). For H adsorption structures away from Au SAA, these four features predominantly influence the ΔG_H* values with an importance exceeding 76% (Fig. 1f and Supplementary Table 3). The ranking of the top four features is further affirmed by applying feature selection algorithms and the PEI method (Supplementary Figs. 25–30). In combination with the SHAP model, we further explore the specific effects of these four features on the SAA Au-bMX₂ system. For ε_ads, which denotes the average band center of the involved adsorption sites, the analyses from model N and model F both indicate that an increase in the ε_ads enhances H adsorption, in line with the trend of the classical d-band center theory. Considering that the ε_ads holds the highest importance (53.98%) in model N for favorable H* adsorption configurations, we propose that the ε_ads can be used to estimate the catalytic activity of SAA Au-bMX₂. The lattice constant (LP_a) of MX₂ structures is determined by the combined effects of strain and the atomic radius of the elements. As the LP_a increases, the hydrogen adsorption capacity of the MX₂ decreases, which aligns with the HT results. Given the importance of LPa, a dimensionless parameter LPa** (defined as the ratio of the 1T-phase lattice constant to the unstrained 2H-phase lattice constant) is further introduced (Supplementary Figs. 31–33). The results show that LPa** does not change the ranking of top important features, and thus the strong correlation between ΔG_H* and LPa is not influenced by other structural features. Regarding CA_Z-M and the L_Au-H, which represent the relative height of H* from the surface and the distance of H to Au SAA, respectively. The L_Au-H and the CA_Z-M exhibit opposite trends for the two types of hydrogen adsorption structures. For model F, as CA_Z-M and L_Au-H increase, the ΔG_H∗ value rises, leading to a reduced surface H adsorption. Regarding to model N, both features exhibit a negative impact on ΔG_H∗, demonstrating that an overly close distance between H and Au diminishes hydrogen adsorption capability. CA_Z-M and L_Au-H essentially describe how the geometric structure of SAA Au-bMX₂ affects ΔG_H*, emphasizing the crucial role of Au SAA in controlling the hydrogen adsorption capacity of the MX₂ surface. Overall, our ML results offer deeper insights into the structure-performance relationship of the SAA N-bMX₂ system, pointing out that ε_ads, LP_a, L_Au-H, and CA_Z-M extracted from SAA N-bMX₂ can substantially influence the catalytic activity of adsorption sites. As depicted in Fig. 1g, these features represent the collective contributions of SAA-N species, biaxial strain degree, and MX₂ structures. A larger ε_ads and smaller LP_a would enhance the interaction between H and bMX₂ slabs. Based on the combination of HT-DFT and ML, we have screened SAA Au-bMoSe₂ as the optimal HER catalyst and revealed the genuine structural factors of enhanced activity. This proposed features-activity principle will guide the design of high-performance electrocatalysts.

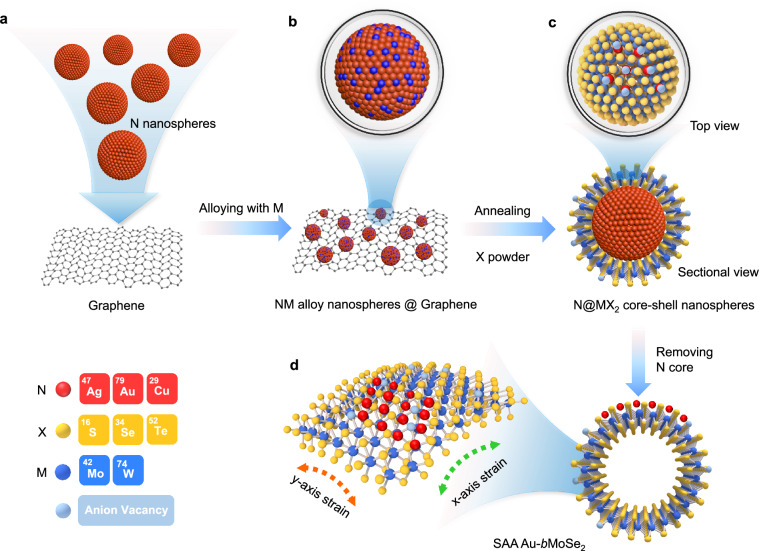
Guided by data-driven analysis, SAA N-bMX₂ nanoshells were designed and synthesized via in situ alloying and vulcanization process, followed by removing the metal N template (Fig. 2). We take SAA Au-bMoSe₂ as an example. First, single crystal Au NSs with ultrasmooth surfaces were synthesized by a polyol reduction method, serving as the template (Supplementary Fig. 34)²⁴. AuMo alloy NSs were then obtained by annealing treatment under argon protection with the molybdenum hexacarbonyl at the upstream. As shown in transmission electron microscopy (TEM) images, the AuMo alloy NSs uniformly dispersed on graphene without interparticle fusion, and the lattice distance of 0.23 nm can be indexed to the (111) planes of AuMo alloy (Supplementary Fig. 35). The uniform distribution of Au and Mo in the products and appearance of X-ray diffraction (XRD) peaks between those of Au and Mo references, implying the alloyed structure (Supplementary Fig. 35d). The energy-dispersive X-ray spectroscopy (EDS) mapping images illustrate the uniform distribution of elements, where the atomic percentages were calculated to be 96.5 and 3.5%, respectively (Supplementary Fig. 35e–h). Then, AuMo alloy NSs underwent an in situ sulfurization in the presence of selenium vapor to form Au@MoSe₂ NSs (Supplementary Fig. 36). It can be clearly observed that the inner spherical Au core is completely covered by a few layers of MoSe₂. The corresponding Au-Se and Mo-Se bonds indicate the existence of an Au-Se-Mo-Se interface (Supplementary Fig. 37). Finally, SAA Au-bMX₂ were obtained by chemically dissolving the Au templates via halogen-based solution (Fig. 3). However, the bMX₂ surface are anchored with randomly distributed Ag and Cu atoms due to the unsmooth surfaces of the metal template (Supplementary Fig. 38).

Fig. 2. Schematic of the synthesis process of SAA N-bMX₂ catalysts.

a N metal nanospheres (Ag, Au, or Cu) uniformly distributed on graphene via ultrasonic treatment. b, c N@MX₂ core-shell formed by two-step vapor deposition annealing treatment. d SAA Au-bMoSe₂ obtained by chemically dissolving the inner templates. The black circles in (b) and (c) highlight the magnified NM alloy and N@MX₂ core-shell nanospheres, respectively. The red and green arrows indicate the strain directions along the y and x-axis, respectively.

Fig. 3. Structural characterizations of SAA Au-bMoSe₂.

a, b TEM images. The inset in (a) shows the diameter distribution. c HAADF-STEM and elemental mapping images. d, e Spherical aberration-corrected HRTEM images. The yellow (blue) boxes correspond to 1 T (2H) phase MoSe₂. Au atoms exist only on 1 T phase (yellow box), as denoted by yellow balls in (e). f–h Local arrangement of one single Au atom (f), EDS line profile along the white arrow direction (g), and biaxial strain analysis via GPA (h). The blue and orange balls indicate the Mo and Se atoms, respectively. i Comparison of EXAFS spectra of Au in SAA Au-bMoSe₂, Au@bMoSe₂, and Au foil. j, k XPS spectra of Au (j) and Mo (k) in SAA Au-bMoSe₂. The orange and blue peaks in (k) indicate the 1 T and 2H phases of MoSe₂, respectively.

The obtained SAAAu-bMoSe₂ nanoshells exhibit an average diameter of 73.5 ± 4.5 nm (SAA Au-bMoSe₂ (M), M indicates the diameter) with a yield approaching 100% (Fig. 3a). TEM and high-angle annular darkfield scanning TEM (HAADF-STEM) images shows the uniform nanoshells with hollow and spherical morphology (Fig. 3b, c). The corresponding EDS elemental mapping images explicitly manifest the homogeneously distribution of the Se and Mo elements, along with a trace amount of Au (molar ratio, Se: 64.3%; Mo: 33.7%; Au: 2.1%). Aberration-corrected HAADF-STEM image shows that the isolated Au atoms (bright spots marked by the yellow frame) are dispersed on the 1 T MoSe₂ domains, while the bMoSe₂ without Au atoms maintains the 2H phase (Fig. 3d and Supplementary Figs. 39, 40). It should be noted that the arrangement of Au atoms clearly displays a z-like arrayed structure (Fig. 3e). Each Au atom is surrounded by six adjacent Mo and twelve spatial Se atoms (Fig. 3f). Moreover, the EDS line-scanning intensity profile indicates a single Au atom located on the top of Mo atom (Fig. 3g). The geometric phase analysis (GPA) indicates the SAA Au-bMX₂ were subjected to biaxial tensile strain (Fig. 3h and Supplementary Fig. 41). The extended X-ray absorption fine structure (EXAFS) spectra of Au for SAA Au-bMoSe₂ confirms the presence of Au-Se bonds, which is different from Au-Au bonds in Au@bMoSe₂ and Au foil (Fig. 3i). The X-ray photoelectron spectroscopy (XPS) spectra of Au and Mo in SAA Au-bMoSe₂ (Fig. 3j, k) and Raman results (Supplementary Fig. 42) illustrate the co-existence of 1 T and 2H phase of MoSe₂. These results imply that the biaxially strained MoSe₂ nanoshells could transit from 2H to 1 T phase after the anchoring of the arrayed Au atoms on Mo top sites. To obtain different strain levels, we synthesized SAA Au-bMoSe₂ with a smaller diameter of 35.1 ± 3.2 nm (S) and a larger diameter of 114.8 ± 4.7 nm (L). The corresponding biaxial tensile strain (ε) for SAA Au-bMoSe₂ (S), SAA Au-bMoSe₂ (M), and SAA Au-bMoSe₂ (L) are calculated to be 2%, 0.96%, and 0.6%, respectively (Supplementary Figs. 43–45).

X-ray adsorption spectroscopy (XAS) and XPS were conducted to gain insight into the local chemical states and electronic conditions of SAA Au-bMoSe₂ with controlled diameters. The Mo K-edge X-ray absorption near-edge spectroscopy (XANES) spectra show that the Mo absorption edges of SAA Au-bMoSe₂ (S), SAA Au-bMoSe₂ (M), and SAA Au-bMoSe₂ (L) locate between those of MoSe₂ and MoO₃ and gradually shifts toward higher energy, suggesting the decreased average electron densities on Mo sites (Fig. 4a). The white line peak analysis illustrates the oxidation states of Mo were calculated to be + 4.05, + 4.10, and + 4.77 for the S, M, and L sample, respectively, using Mo foil and MoO₃ as references (Fig. 4b). Furthermore, the d-band hole numbers for SAA Au-bMoSe₂ (S), SAA Au-bMoSe₂ (M), and SAA Au-bMoSe₂ (L) were estimated to be 8.38, 8.43, and 9.0 based on the Mo foil (4 d⁵) and MoO₃ (4 d⁰), indicating the presence of unoccupied Mo 4d-orbitals. These varied Mo 4d-orbitals would activate the surrounding Se atoms as active sites for HER. From the EXAFS spectra for the Mo K-edge, the coordination numbers of Mo-Se bonds at ~ 2.18 Å were calculated to be 5.0 for sample L, 4.6 for sample M, and 4.3 for sample S (Fig. 4c, Supplementary Figs. 46–49, and Supplementary Table 10). The electron paramagnetic resonance (EPR) signal intensity at g = 2.009 changes in a trend of SAA Au-bMoSe₂ (S) > for SAA Au-bMoSe₂ (M) > SAA Au-bMoSe₂ (L), indicating increased Se vacancy (Supplementary Fig. 50). The decreased Mo coordination and increased content of Se vacancy is mainly due to the enhanced curvature of SAA Au-bMoSe₂. Moreover, an obvious shift of Mo-Mo bonds to a longer location in R-space with the increased curvature deduce the enlarged distance of Mo-Mo bonds. FT k³-weighted EXAFS and the corresponding wavelet transform spectra of Au for three types of SAA Au-bMoSe₂ show the isolated Au single atoms are bonded to three Se atoms by forming Au-Se bonds (Fig. 4d–h and Supplementary Table 11).

Fig. 4. Structural and chemical states analysis.

a Mo K-edge EXAFS spectra. The inset in (a) is the magnified Mo absorption edges. b The corresponding Mo average oxidation states and d-band hole counts calculated by white line peaks. c R space profiles of controlled SAA Au-bMoSe₂ and commercial MoSe₂. d FT-EXAFS spectra of Au L₃-edge EXAFS spectra and corresponding fitting results (first coordination shell). e–h Wavelet transform of EXAFS data for Au foil, SAA Au-bMoSe₂ (S), SAA Au-bMoSe₂ (M), and SAA Au-bMoSe₂ (L). i–k XPS spectra of Se for (i) SAA Au-bMoSe₂ (S), (j) SAA Au-bMoSe₂ (M), and (k) SAA Au-bMoSe₂ (L). The orange and blue peaks in (i–k) indicate 1 T and 2H phases of MoSe₂, respectively.

From the XPS spectra of Se (Supplementary Fig. 51), the Au@MoSe₂ only shows two peaks located at 54.5 eV (Se 3d_5/2) and 55.4 eV (Se 3d_3/2) for 2H phase, while those peaks of SAA Au-bMoSe₂ can be split into two peaks at ~ 54.2 eV and ~ 55.1 eV for 2H phase and the other two peaks at ~ 53.2 eV and ~ 54.4 eV for 1 T phase (Fig. 4i–k). The Mo XPS spectra for three controlled SAA Au-bMoSe₂ also demonstrate the coexistence of 2H and 1 T phase of MoSe₂ (Supplementary Figs. 52–54). Taken together, the combined XAS and XPS results unambiguously confirm the Au single atoms array on biaxially strained MoSe₂.

The HER performance of SAA Au-bMoSe₂ electrocatalysts and reference samples were tested in a three-electrode cell in 0.5 H₂SO₄ electrolyte. The linear sweep voltammograms (LSV) show that the overpotentials of SAA Au-bMoSe₂ (S) electrode are 66, 116, and 143 mV at the currents of 100, 500, and 800 mA cm⁻², respectively, which are much smaller than those of SAA Au-bMoSe₂ (M) (162, 148, and 257 mV), SAA Au-bMoSe₂ (L) (217, 274, and 288 mV), and MoSe₂ reference (330, 476, and 570 mV) electrodes (Fig. 5a, b). The HER activities of atomic Au anchored bMoSe₂ follow a trend of Catalyst S > Catalyst M > Catalyst L, illustrating the positive effect of biaxial strain on activity. There is only a 27 mV increase in the overpotential when the current changes from 500 to 800 mA cm⁻², showing a negligible energy barrier for the SAA Au-bMoSe₂ (S) electrode at large current densities. The boosted reaction kinetics of SAA Au-bMoSe₂ (S) for HER is also verified by a much lower Tafel slope of 28.5 mV dec⁻¹ than SAA Au-bMoSe₂ (M) (97.6 mV dec⁻¹) and SAA Au-bMoSe₂ (L) (89.7 mV dec^-1), which is comparable to that of 20 wt% Pt/C (27.2 mV dec^-1) (Fig. 5c). In addition, the electrochemically active surface areas (ECSA), determined from electrochemical double-layer capacitance (C_dl) measurements, are 559.3, 519.4, and 365.6 cm^-2 for SAA Au-bMoSe₂ (S), SAA Au-bMoSe₂ (M), and SAA Au-bMoSe₂ (L), respectively (Supplementary Fig. 55 and Fig. 5d). Hence, ECSA increases with decreasing curvature of the nanoshells (Supplementary Fig. 56). When the LSV curves are normalized to the corresponding ECSA values, the SAA Au-bMoSe₂ (S) catalyst still displays the highest current of 0.28 mA cm⁻² at an overpotential of 100 mV (Supplementary Fig. 57). The turnover frequency (TOF) value for the SAA Au-bMoSe₂ (S) at the overpotential of 100 mV is calculated to be 0.04 s⁻¹, which is higher than those of the control catalysts (0.002 s⁻¹ for M and ~ 0.001 s⁻¹ for L). Furthermore, the charge transfer resistance (R_ct) obtained from the Nyquist plots (Fig. 5e) for the Catalyst S, M, and L are 20.2, 35.5, and 68.1 Ω, respectively. Hence, it is inferred that the larger biaxial strain could endow SAA Au-bMoSe₂ with high proton and electron transfer kinetics, corresponding to enhanced intrinsic HER activity.

Fig. 5. Electrochemical performance for acidic HER.

a HER polarization curves of SAA Au-bMoSe₂ (S), SAA Au-bMoSe₂ (M), SAA Au-bMoSe₂ (L), C-MoSe₂ reference, and 20 wt% Pt/C. b, c Comparison of overpotentials at 100, 500, and 800 mA cm⁻², respectively (b) and Tafel plots (c). d C_dl plots derived from CV curves at non-reactive regions. e Comprehensive comparisons of HER performance and stability of the SAA Au-bMoSe₂ (S) electrode with related electrocatalysts. f Durability test (V-t curves) of SAA Au-bMoSe₂ (S) electrode at 800 mA cm⁻² over 1000 h with 90% iR correction. The black dash circles indicate the replacement of electrolytes.

The operation stability is an important indicator in practical hydrogen production. The SAA Au-bMoSe₂ (S) electrode was tested by the chronopotentiometry method at an industrial-level current density of 800 mA cm⁻². The potential shows negligible degradation over 1000 hours, suggesting the stable function of the SAA Au-bMoSe₂ (Fig. 5f). To check the possible structure evolution, we examined the morphology, composition, and electronic structure of SAA Au-bMoSe₂ (S) after the durability test. The Raman peaks located at 232.1 and 352.4 cm⁻¹ indicate the co-existence of the 1 T and 2H phases (Supplementary Fig. 58). The unchanged hollow morphology is evidenced by the HAADF-STEM image. The corresponding EDS element mapping images show the uniform distribution of Au, Mo, and Se in the tested catalysts (Supplementary Fig. 59) with minor change in their molal ratios (Supplementary Tables 12, 13). Comparison to the literature shows that our SAA Au-bMoSe₂ (S) catalyst outperforms the reported 2D materials electrocatalysts for acidic HER in terms of reactivity, kinetics, and operation durability (Fig. 5g and Supplementary Table 14).

To gain insights to the reaction mechanism, we performed in situ Raman spectroscopy analysis by continuously changing the applied potential (Fig. 6a, b). The two peaks located at ~980 and 1052 cm⁻¹ can be ascribed to the symmetric stretching vibration of SO₄²⁻ and symmetric stretching of HSO₄^- ions, respectively, in the H₂SO₄ electrolyte. The other pair of peaks at ~1332 and 1600 cm⁻¹ are the characteristic D and G bands of graphene, respectively. When the applied potential increases from 0 to − 0.3 V vs. RHE, there is no obvious peak associated with the Se-H bond for the MoSe₂ sample, while the peak of the Se-H bond at ~2365 cm⁻¹ gradually intensifies for SAA Au-bMoSe₂ (S). This difference indicates more favored hydrogen adsorption on Se sites induced by the Au atoms. The crystal orbital Hamilton population (COHP) analysis reveals that the value of integrated COHP (iCOHP) for Se-H in Au atom anchored MoSe₂ is lower than that in MoSe₂ (Fig. 6c), indicating enhanced Se-H bond strength in the former. Hence, combining the HT-DFT, ML, and experimental results, we propose a catalytic active hotspot consisting of Au atoms and the neighboring Se atoms (Fig. 6d). This hotspot has a larger size than the active site (only single metal atoms) in the traditional SACs. Se atoms located away from the hotspot center (viz., Au atoms) will be less active. As a result, the large-sized active hotspot endows SAA Au-bMoSe₂ with multiple sites for hydrogen adsorption, accounting for higher overall HER activity.

Fig. 6. In situ Raman and DFT calculations for HER mechanism.

a, b In situ Raman spectra for bMoSe₂ and SAA Au-bMoSe₂ in 0.5 M H₂SO₄ with continuously changed potentials from 0 to − 0.3 V vs. RHE. The dash arrows in (a, b) show the increase in potential. D and G denote the disorder and graphitic bands, respectively. The blue, gray, and green shadings highlight the Raman peaks of SO₄^2-, D/G, and Se-H bonds, respectively. c Crystal orbital Hamilton population (COHP) analysis for Se-H bonds in MoSe₂ (left) and Au atom anchored MoSe₂ (right). d Scheme of SAA Au-bMoSe₂ structure (left) and an active hotspot for HER (right). The red, blue, yellow, and white balls in (d) illustrate the Au, Mo, Se, and H atoms, respectively. The gray arrows show the movement direction of H. The strain along the x and y-directions in (d) are indicated by the green and red dash arrows, respectively. The color bar in (d) changing from blue to red qualitatively indicates the enhancement in HER activity, and the large gradient-colored ball covering Mo and Se atoms presents the active hotspot.

Discussion

We have employed a data-driven approach by combining HT-DFT calculations and machine learning to screen the catalyst structure of SAA on TMDs and uncover the underlying critical feature-activity relationship. As the effectiveness of the dataset depends on not only its size but also the pre-classification, we classify the dataset by separating the ΔG_H* data. Four top features of ε_ads, LP_a, L_Au-H, and CA_Z-M have been extracted from 17 features to describe the HER activity. The optimal ΔG_H* of SAA Au-bMoSe₂ is pinpointed out of 1248 active sites. Following the theoretical guidance, SAA Au-bMoSe₂ is experimentally synthesized with a precise coordination environment and a tunable strain level. The catalyst with 2% tensile strain displays Pt-like HER activity and 1000 hour-stability at a high current of 800 mA cm⁻² under acidic conditions. The electron transfer from Se atoms to the adjacent Au atom renders the Au an electron-rich site for highly active HER. Based on the data-driven results and in situ Raman analysis, it is identified that the reaction center consists of Au atoms and the neighbor Se atoms. This active hotspot is larger compared to the active sites in traditional single-atom catalysts, contributing to the multiple active centers and increased HER activity. This work deepens our understanding of the root behind active descriptors.

For a broader perspective, the concept of biaxial strain can be extended to a diverse range of materials, including TMDs, fullerenes, Mxenes, etc., which would serve as potential candidates for constructing complex metal atoms arrays or atomic superstructures. The data-driven approach showcases a potent methodology to accelerate the discovery of superstructured atomic catalysts. Our results suggest that the compatibility of biaxial strained surface with 3d-5d transition metal atoms should be evaluated by considering various parameters, including types of metal atoms, strain dimension and degree, anion vacancies, and coordination environments. With the rapid advancement of artificial intelligence in chemistry, it is important, yet challenging, to develop feasible and scalable synthesis methods for atomic superstructures. Data-driven materials science is promising but has a long way to go.

Methods

Chemicals. Chloroauric acid (HAuCl₄, 99.9%), poly-(diallyldimethylammonium) chloride (PDDA, Mw = 100 000 − 200 000, 20 wt % in water), ethylene glycol (EG, ACS reagent), molybdenum hexacarbonyl (Mo(CO)₆, 98%), silver nitrate (AgNO₃, ≥ 99.8%), Selenium powder (Se, 99.95%), iodine (I, 99.8%), Nafion®117 solution (5%), and graphene were purchased from Sigma-Aldrich. Hydrochloric acid (HCl, 36% ∼ 38%), commercial Pt/C (20% wt%), potassium chloride (KCl, 99.8%,) and potassium iodide (KI, 99%) were obtained from Sinopharm Chemical Reagent Co., Ltd. The Carbon fiber paper (CFP, TGP-H-060) was purchased from Toray Industries, Inc. Deionized water (18.25 MΩ) was prepared with a UW-B10 water purification system. All chemicals were used without further purification.

Synthesis of Au nanospheres²⁴. A given amount of HAuCl₄, PDDA, and AgNO₃ were added into a 60 mL of EG solution to form a homogeneous solution with a concentration of 0.5 mM, 25 mM, and 0.01 mM, respectively. The obtained mixture was then reacted at 220 °C for 2 h in an oil bath. After cooling down to the room temperature, the final products an average diameter of 65 nm, were collected by centrifugation at 14,100 × ɡ for further use. Au nanospheres with a diameter of 31 nm) was synthesized by introducing saturated oxygen with the same method. Au nanospheres with an average diameter of 109 nm were reacted at 205 °C.

Synthesis of SAA Au-bMSe₂. 10 mg of Au NSs were homogeneously mixed with 50 mg of graphene via sonication for 60 min in 15 mL of deionized water. After drying in an oven, Au NSs/graphene were obtained. Then 10 mg of Au NSs/graphene was annealed at 550 °C in a tube furnace with 6 mg of Mo(CO)₆ at the upstream of nitrogen atmosphere, followed by selenization for another 0.5 hours. Au@MoSe₂/graphene were obtained. After carefully removing the Au core of Au@MoSe₂ by an etching agent of I/KI/HCl solution for 5-hour-treatment, SAA Au-bMoSe₂/graphene was obtained in high yield.

Characterization. Transmission electron microscopy (TEM), high-resolution TEM (HRTEM), and energy-dispersive X-ray spectroscopy (EDS) elemental mapping were conducted on a transmission electron microscope (FEI, Tecnai G2 F20) with an accelerating voltage of 200 kV. The powder X-ray diffraction (XRD) data were obtained by a Philips X’pert Pro X-ray diffractometer equipped with Cu Kα radiation. X-ray photoelectron spectroscopy (XPS) spectra were carried out with an ESCALAB MK II X-ray photoelectron spectrometer. X-ray absorption spectroscopy (XAS) results for the Mo K-edge and Au L-edge were obtained in fluorescence mode at beamline at BL14b2, SPring-8 Japan. Athena and Artemis software were used for XAS data analysis. The mass content of the samples was calculated by inductively coupled plasma mass spectrometry (ICP-MS). Electron spin resonance (ESR) spectra were measured on a Bruker EMX plus 10/12 instrument equipped with an Oxford ESR910 Liquid Helium cryostat at the Steady High Magnetic Field Facilities.

Electrochemical Measurements. All the electrochemical measurements were carried out using a CHI 760e electrochemical workstation (Shanghai Chenhua) with a standard three-electrode setup at ambient temperature. A catalyst ink was prepared by mixing 5 mg of SAA Au-bMoSe₂/graphene catalysts with 500 μL of deionized water, 480 μL of ethanol, and 20 μL of Nafion®117. The obtained ink was then drop onto a CFP working electrode (WE, 0.5 cm × 1 cm), while a graphite rod with a diameter of 6 mm and a saturated Ag/AgCl electrode with salt bridge served as a counter electrode (CE) and reference electrode (RE), respectively. The mass loading values of SAA Au-bMoSe₂/graphene on the WE were fixed to be 1 mg cm⁻². 26.65 mL of H₂SO₄ (98%) was added into a 1-liter volumetric flask and then fill DI water up to the 1-liter mark. The prepared 0.5 M H₂SO₄ electrolyte was transferred to the glass container for storing for further use. A nitrogen-saturated 0.5 M H₂SO₄ aqueous solution was used as the electrolyte. Linear sweep voltammetry (LSV) curves were obtained at a scan rate of 2 mV s⁻¹. The Nyquist plot was tested with a frequency range from 0.01 Hz to 100 kHz at an A.C. amplitude of 10 mV to evaluate the electrochemical impedance. The electrochemical double layer capacitance (C_dl) was conducted with a scan rate ranging from 20 to 200 mV s⁻¹ at an interval of 40 mV s⁻¹ in the non-Faraday current region (0.32– 0.42 V vs. RHE), in which the RHE is the reversible hydrogen electrode. All the polarization curves were converted to RHE. The durability was evaluated by the constant current chronopotentiometry.

The reference electrode against the reversible hydrogen electrode (RHE) was determined by using the following equation:

$$E\left(vsRHE\right)=E\left(vsAg/AgCl\right)+0.222V$$ 1

The electrochemical active surface area (ECSA) was calculated using the C_dl and a general surface specific capacitance (C_s) value of 0.040 mF cm⁻² in 0.5 M H₂SO₄ solution by the following equation:

$$ECSA=C_{dl}/C_s\times S$$ 2

where C_dl was calculated by the half slope of (Δj = j_anodic − j_cathodic) plotted against the scan rate, S is the geometric surface area of work electrode.

The turnover frequency (TOF) of the electrocatalytic reaction was calculated by the following equation:

$$TOF=\left(J\times A\right)/\left(2\times F\times n\right)$$ 3

where J represents the current density at a given overpotential, A is the geometric surface area of the working electrode (0.5 cm²), F is the Faraday constant (96485 C mol⁻¹), and n is the mole number of active atoms.

Computational Details. The Vienna Ab initio Simulation Package (VASP) were used to perform all the density functional theory (DFT)³⁵. We applied the projector augmented wave (PAW) basis set to compute the ion-electron interactions for all the theoretical structures³⁶. Moreover, the generalized gradient approximation (GGA) with the Perdew-Burke-Ernzerhof (PBE) function was deployed to collect the related exchange-correlation energies. The three important parameters, namely, cutoff energy, convergence criterion of energy, and force, were set to be 500 eV, 10⁻⁵eV, and 0.02 eV/Å, respectively. To optimize and calculate the electronic structures, we used the typical Monkhorst-Pack 3 × 3 × 1 k-point grids to simulate the Brillouin zones. Based on the experimental results, we applied a series of biaxial strains (0.5, 0.8, 1.2, 1.5, and 2%) along both x and y axes to different MX₂ (001) surfaces, followed by evaluating the lattice coefficients of MX₂ (001). To ensure an accurate expression of the long-range weak van der Waals (vdW) interaction, the DFT-D3 method was adopted for all DFT computations³⁷.

An open-source code Scikit-learn package in the Python3 environment was performed for All ML algorithms. The typical random forest regression (RFR) ML algorithm was used during the data-treatment process. Moreover, the root mean square error (RMSE) and coefficient of determination (R²) methods were selected to ensure the accuracy of this model. For obtaining all the hyperparameters from the RFR models, a comprehensive grid search was applied. All features during ML were collected from the Ptable database and the high-throughput DFT computations. The feature values of structures stabilized on the bridge and hollow sites were normalized via dividing by the corresponding coordination number. The processed dataset was then randomly divided into a training set and a test set, maintaining a ratio of 7:3.

The feature sets for the SAA Au-bMX₂ system were divided into three categories: surface structure, adsorption site features, and adsorbate features. The adsorption site features encompass the atomic characteristics and electronic structures of the adsorption sites. To maintain consistency across different hydrogen adsorption structures, we classified the optimized configurations based on the structural characteristics of three adsorption modes (top, bridge, and hollow site). Furthermore, we normalized the feature values of structures stabilized on the bridge and hollow sites via dividing by the corresponding coordination number (see Supplementary Table 4). Regarding adsorbate features, the characteristics of the H* intermediate are considered, including the Bond length between the Au atom and the adsorbed H* (L_Au-H) and the coordination number of H* (CN), etc. In addition, since we considered a range of strains in the high-throughput calculations, features related to strain were included in the surface structure features.

Author contributions

T.Z., Y.L., and H.J.F. supervised and conceived this project. T.Z. designed the experiments, conducted the synthesis, characterization, and electrical performance measurement, and analyzed the experimental and XAFS data. Z.T., Z.C., Z.H., and D.W. collected the XAFS data. T.Z., Q.Y., and Y.P.L. analyzed the theoretical calculations. Q.L. characterized the morphology of control samples. T.Z., Y.P.L., and H.J.F. wrote the manuscript.

Peer review

Peer review information

Nature Communications thanks Bolong Huang, Hong Seok Kang, and Tu Le for their contribution to the peer review of this work. A peer review file is available.

Data availability

Data supporting the findings of this work are available within the paper and its Supplementary Information files. The data generated in this study have been deposited in the figshare database under accession code 10.6084/m9.figshare.28280339.v4. The atomic coordinates of the optimized model for HT-DFT calculations are provided as a separate Supplementary Data 1. Source data are provided in this paper.

Code availability

The Python code written to train RFR models for identifying key features and the related source data has been open-sourced under the Apache 2.0 license and is accessible via 10.5281/zenodo.15093090.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-025-59053-1.