Abstract
For metaproteomics data derived from the collective protein composition of dynamic multi-organism systems, the proportion of missing values and dimensions of data exceeds that observed in single-organism experiments. Consequently, evaluations of differential analysis strategies in other mass spectrometry (MS) data (such as proteomics and metabolomics) may not be directly applicable to metaproteomics data. In this study, we systematically evaluated five imputation methods [sample minimum, quantile regression, k-nearest neighbors (KNN), Bayesian principal component analysis (bPCA), random forest (RF)] and six imputation-free methods (moderated t-test, two-part t-test, two-part Wilcoxon test, semiparametric differential abundance analysis, differential abundance analysis with Bayes shrinkage estimation of variance method, and Mixture) for differential analysis in simulated metaproteomic datasets based on both data-dependent acquisition MS experiments and emerging data-independent acquisition experiments. The simulation datasets comprised 588 scenarios by considering the impacts of sample size, fold change between case and control, and missing value ratio at random and nonrandom. Compared to imputation-free methods, KNN, bPCA, and RF imputation performed poorly in datasets with a high missingness ratio and large sample size and resulted in a high false-positive risk. We made empirical recommendations based on the balance of sensitivity in analysis and control of false positives. The moderated t-test was optimal in scenarios of large sample size with a low missingness ratio. The two-part Wilcoxon test was recommended in scenarios of small sample size with a low missingness ratio or large sample size with a high missingness ratio. The comprehensive evaluations in our study can provide guidance for the differential abundance analysis in metaproteomics.
Keywords: metaproteomics, differential abundance analysis, two-part statistics, missing value, imputation missing mechanism
Introduction
Metaproteomics has emerged as a robust strategy for analyzing the taxonomic structure and functional characteristics of microbial communities across diverse environments [1], including the gut [2], soil [3], wastewater [4], and deep sea [5]. Advances in liquid chromatography–tandem mass spectrometry (LC-MS/MS) technologies facilitate the comprehensive characterization of microbial proteins in a deep, broad, and high-throughput manner. The identification of key microorganisms or microbial proteins within communities is crucial for elucidating the metabolic activities and interactions of microorganisms in diverse environments. Consequently, a sensitive and precise differential abundance analysis strategy is imperative for metaproteomic data.
However, the analysis of LC-MS/MS data is compromised by its high missing value ratio [6]. The sparsity of metaproteomic data could be even higher due to the huge diversity and specificity both within and between samples [7, 8]. Metaproteomic data derived from label-free quantitative techniques coupled with data-dependent acquisition (DDA) mass spectrometry (MS) experiments may exhibit missingness ratios ranging from ~40% to ~90% [9–11] and, under certain extreme conditions, as high as 96% [12]. Although data-independent acquisition (DIA) strategies reduced the missingness ratio of MS data, current attempts of DIA metaproteomic analyses still yield data with ~30%–40% missing values [8, 13]. Missing values are generally categorized into three types: missing not at random (MNAR), where abundances below the instrument’s detection limit are missed (also referred to as censoring), missing at random (MAR), and missing completely at random (MCAR) [6]. As MAR is generally assumed to be MCAR in proteomics data, the distinction between different missing mechanisms can be achieved by varying proportions of MNAR and MCAR [14–16]. Recently, Li and Smyth proposed the protDP model, which estimates intensity-dependent probabilities of missing values in label-free proteomics through a logit-linear function [17].
Considerable methods have been proposed to address the issue of missing values in MS data. These methods can be classified into two main categories: (i) imputation-based methods, which impute the missing values before conducting statistical tests with complete data, and (ii) imputation-free methods, which use models retaining and accounting for missing values or just eliminate the sample with missing values for test [18]. Imputation methods include left-censored approaches (e.g. minimum imputation) and estimation-based imputation (e.g. bPCA: Bayesian principal component analysis, KNN: k-nearest neighbors) [19, 20]. Imputation-free models consist of the two-part statistical test [21], accelerated failure time (AFT) [22], and semiparametric differential abundance analysis (SDA) [23], among others. In the field of metaproteomics, Plancade et al. proposed a feature selection method that considers both missing and nonmissing data utilizing a similar model as SDA [7].
Extensive research has evaluated the performance of differential analysis strategies across various MS-based data types [15, 18, 24–29]. The recommended methods varied depending on the application scenario and simulation strategy. However, many previous studies did not compare the performance of imputation and imputation-free strategies. Due to variations in data dimension, degrees of missingness, and sample sizes, comparisons of strategies in proteomics and metabolomics may not be directly transferable to metaproteomics. For example, eight proteomic datasets characterized by sample sizes ranging from 9 to 56 were examined in Liu and Dongre’s evaluation, where the number of proteins detected varied from 2000 to 7000, and the missingness rates of the raw intensity matrices ranged from 4% to 32% (for label-free quantification intensity matrices, 15%–47%) [15]. For metabolomics, Taylor et al. investigated three metabolomic datasets comprising sample sizes of 26, 62, and 544. The corresponding missingness rates were 40.6%, 12.7%, and 0.59%, respectively. Only a few hundred metabolites were detected in all three datasets [18]. Both the number of compounds detected and the missingness rate were higher in metaproteomic datasets according to our investigation.
The differences in these characteristics imply that metaproteomic data may differ from other MS data in distribution and missing value composition. The high missingness rate also challenges imputation and statistical tests. Consequently, the performance of different strategies on metaproteomic datasets necessitates further evaluation. Hence, we conducted a thorough comparison of five commonly employed imputation methods and six imputation-free methods using simulated datasets of both DDA and DIA metaproteomics across varying degrees of MNAR. Empirical recommendations were then proposed based on a broad spectrum of sample sizes, missingness ratios, MNAR ratios, and fold changes between control and case samples. We believe that our findings offer practical guidance for the differential abundance analysis of metaproteomics data across diverse scenarios.
Materials and Methods
Metaproteomic datasets
To simulate the metaproteomics datasets that reflect real-world scenarios, we utilized a simulation framework that incorporates the characteristics of real metaproteomic data. We referenced three public datasets, encompassing two DDA and one DIA MS experiments of metaproteomics.
ProteoCardis
The ProteoCardis project reported by Bassignani was an association study between the human intestinal metaproteome and cardiovascular diseases [12]. ProteoCardis includes two classes: patients with acute cardiovascular disease (N = 49) and healthy controls (N = 50). The collected gut microbiota of patients was fractionated into cytosolic and envelope compartments, which were analyzed separately. Details of the MS experiment design can be seen in section 4.1.2 of the thesis [12]. The peptide ions were analyzed with the DDA protocol. ProteoCardis also served as an experiment dataset to develop a feature selection method in metaproteomics by Plancade et al. [7]. We selected the cytosolic subset for analysis. Data are available at https://doi.org/10.15454/ZSREJA.
Ad libitum time-restricted feeding
Palomba et al. aimed to investigate the effects of long-term time-restricted feeding (TR) on gut microbiota protein expression in a rat model with metaproteomics [11]. The researchers collected stool samples from 16 rats, divided into two groups: ad libitum (AL)-fed and TR-fed. Stool samples were collected after 48 weeks of dietary regimen. Peptide mixtures were then analyzed by LC-MS/MS using the DDA mode of the LTQ Orbitrap Velos mass spectrometer. The data are available at the PRIDE database (https://www.ebi.ac.uk/pride/archive/projects/PXD024509).
Data Independent Acquisition-Parallel Accumulation Serial Fragmentation
Gómez-Varela et al. reported the Data Independent Acquisition-Parallel Accumulation Serial Fragmentation (DIA-PASEF) workflow to improve the peptide detection reproducibility and quantification accuracy of metaproteomics [13]. The workflow was applied to a preclinical mouse model of chronic pain. Briefly, they collected fecal samples of age-matched female mice before (Pre) and 14 days (14D) postsurgery. The peptides were analyzed using nanoflow reversed-phase liquid chromatography (Nano-RPLC) coupled with a timsTOF Pro mass spectrometer, employing DIA modes. We take the presurgery samples (N = 12) as the control group and the 14D samples (N = 12) as the case. The dataset is available in the PRoteomics IDEntifications Database (PRIED) (https://www.ebi.ac.uk/pride/archive/projects/PXD040947).
More detailed information on these three datasets is listed in Table 1. Intensity values were total quantity–normalized for each sample to the median total intensity across all samples before subsequent analysis. We excluded features from the three datasets with high missingness rates (>90%) to mitigate their impact on the overall distribution, in alignment with common practices in applications.
Table 1.
Details of the reference metaproteomics dataset.
| Protocol | Dimensiona | Filtered dimensionb | Missingness ratio | Filtered missingness ratiob | |
|---|---|---|---|---|---|
| ProteoCardis | DDA | 120,703 99 99 |
11,433 99 99 |
0.961 | 0.745 |
| ALTR | DDA | 15,691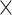 16 16 |
15,482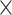 16 16 |
0.377 | 0.332 |
| DIA-PASEF | DIA | 14,507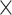 24 24 |
13,486 24 24 |
0.364 | 0.320 |
aFeature size (number of proteins) Sample size.
Sample size.
bFeatures with missingness ratio >90% were filtered out.
Simulation framework
Two-group comparison studies with case–control designs were simulated to evaluate different statistical strategies. Half of the samples were designated as controls. Each dataset was simulated to contain 10 000 proteins (features), of which 50% were differentially abundant. The simulation framework incorporates a nonmissing-value step and a missing-value step to generate data that mimic the distribution of real metaproteomic datasets with specific missingness ratios and compositions (MNAR and MCAR). For clarity, it is assumed that the MNAR ratio + MCAR ratio = 1; the total missingness ratio is independent of the MNAR/MCAR ratio.
In the first step, datasets with no missing values were generated with reference to Ding et al.’s study for phosphoproteomics [29]. We assumed that the intensity of each protein in the case/control group follows a Log-normal distribution
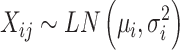 |
(1) |
where  denotes the intensity of protein
denotes the intensity of protein 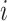 in sample
in sample  . The two parameters of the Log-normal distribution vary for different protein
. The two parameters of the Log-normal distribution vary for different protein 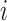 .
. 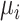 , the log-mean of the protein intensities, was sampled from a normal distribution
, the log-mean of the protein intensities, was sampled from a normal distribution
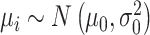 |
(2) |
For the case group of differentially abundant proteins, the  parameters were added with
parameters were added with  . The standard deviation (SD) of the protein intensities on the log scale,
. The standard deviation (SD) of the protein intensities on the log scale, 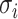 , was sampled from an inverse gamma distribution
, was sampled from an inverse gamma distribution
 |
(3) |
All default simulation parameters (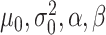 ) in Equations (2) and (3) were calculated from the three reference metaproteomic datasets.
) in Equations (2) and (3) were calculated from the three reference metaproteomic datasets.
Defining the mechanism of missing values is crucial for simulating the metaproteomic datasets. Negative correlations between the intensity of a protein and its missingness ratio were observed (Supplementary Fig. S1A), indicating MNAR in all three reference datasets. In the missing-value step, intensity-related MNARs were generated, and MCARs were then randomly sampled in data matrices. We assigned MNAR ratios across a broad range (0.2, 0.4, 0.6, 0.8) following Lazar et al.’s simulation on proteomics [14]. For MNAR generation, a threshold matrix was initially produced from a normal distribution with 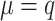 and
and  , where
, where 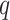 is the
is the  th percentile of the complete intensity distribution generated in the nonmissing-value step (
th percentile of the complete intensity distribution generated in the nonmissing-value step (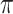 equals to the missingness ratio * 100). Then, from among all the cells in the intensity matrix with values less than the corresponding values in the threshold matrix (occupying approximately
equals to the missingness ratio * 100). Then, from among all the cells in the intensity matrix with values less than the corresponding values in the threshold matrix (occupying approximately 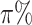 ), a subset (with a number equal to the total number of cells
), a subset (with a number equal to the total number of cells 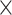 missingness ratio
missingness ratio 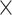 MNAR ratio) was sampled as abundance-dependent missing values. Next, from the remaining non-MNAR cells, cells missing completely at random (MCAR) were randomly selected to achieve a total missingness ratio of
MNAR ratio) was sampled as abundance-dependent missing values. Next, from the remaining non-MNAR cells, cells missing completely at random (MCAR) were randomly selected to achieve a total missingness ratio of  for the dataset. Proteins that consisted entirely of missing values within either the case or control group were subsequently removed.
for the dataset. Proteins that consisted entirely of missing values within either the case or control group were subsequently removed.
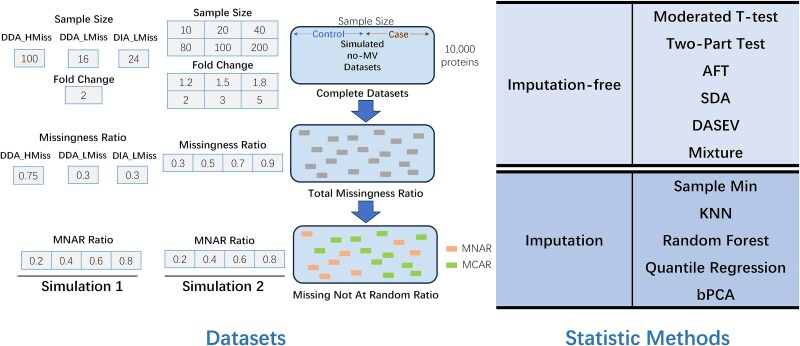
Two simulation studies were conducted sequentially. In Simulation 1, datasets that mirrored the reference ProteoCardis, ALTR, and DIA-PASEF datasets were simulated, with a similar sample size, feature size, total missingness ratio, and distribution of protein intensity means and standard deviations. The ProteoCardis dataset was employed to simulate DDA data with large sample sizes and high rates of missing values, and ALTR represented DDA data with small sample sizes and lower missingness ratios. DIA-PASEF was utilized to simulate emerging DIA metaproteomic experiments with lower levels of data sparsity. The simulated datasets generated based on the characteristics of ProteoCardis, ALTR, and DIA-PASEF were referred to as DDA_HMiss, DDA_LMiss, and DIA_LMiss, respectively, in the following sections. The fold change for differential proteins was set to 2 in simulation 1, and four MNAR ratios were simulated (0.2, 0.4, 0.6, and 0.8). The simulation procedure and the parameters are depicted in Fig. 1. Simulation 2 was applied to evaluate different statistical methods across a broader spectrum of sample sizes, fold changes, and missingness ratios. Given the 96% high missingness rate observed in the whole data matrix of ProteoCardis and previous studies indicating that up to 90% of missingness can still yield unbiased results [30], the upper limit of the missingness ratio in Simulation 2 was set at 90%. Simulation 2 used the distribution of protein intensity means and SDs of ProteoCardis. In Simulation 1, 500 datasets were generated for each parameter combination, totaling 12 combinations. For Simulation 2, each parameter combination was simulated 100 times due to the extensive number of combinations (576 in total) and the substantial computational requirements. The simulation program was executed by R scripts using a single core of the Intel Xeon (R) Scalable Cascade Lake 6248 (2.5GHz) Central Processing Unit (CPU).
Figure 1.
Process for dataset simulation and statistical methods to be assessed. Two simulations (Simulations 1 and 2) were conducted. The parameters used in each simulation (sample size, fold change, missingness ratio, and MNAR ratio) were displayed in the corresponding column. The simulation process encompasses a non-missing value step (to generate complete data) and a missing-value step (to introduce varying ratios of MNAR and MCAR). Six imputation-free methods and five imputation methods were evaluated in the study.
Statistical test methods
Six imputation-free methods were evaluated in this study: moderated t-test (ModT) [31], two-part model (two-part t-test and two-part Wilcoxon test, twoT, and twoWilcox) [32], accelerated failure time (AFT) [22], semiparametric differential abundance analysis (SDA) [23], differential abundance analysis with Bayes shrinkage estimation of variance method (DASEV) [33], and the Mixture model proposed by Taylor et al. [34]. For imputation-free strategies, we also evaluated t-tests and Wilcoxon tests with missing samples eliminated. Five imputation methods were assessed: sample minimum (SMin), KNNs [20], Bayesian principal component analysis (bPCA) [19], random forest (RF) [35], and quantile regression (QR) [36].
Imputed data were tested using both the parametric t-test and the nonparametric Wilcoxon test. For the parametric t-test and the two-part t-test, log2 transformation was applied to the datasets. For the Wilcoxon test and the two-part Wilcoxon test, the datasets remained at the original scale. The P-values derived from statistical tests were adjusted by Benjamini–Hochberg (BH) correction [37]. The proteins with BH-adjusted P-value <0.05 were considered as differentially abundant. The performance of the selected methods was evaluated by standardized partial area under the receiver operating characteristic (pAUROC), area under the precision–recall curve (AUPRC), and false-positive rate (FPR) [38, 39]. Partial AUROC is a more practical metric for evaluation of diagnostic performance, as it focuses solely on ROC regions with high specificity. Detailed information regarding the statistical methods, metrics, and software implementation can be found in Supplementary File S1.
Results
Performance of strategies in simulations of real datasets
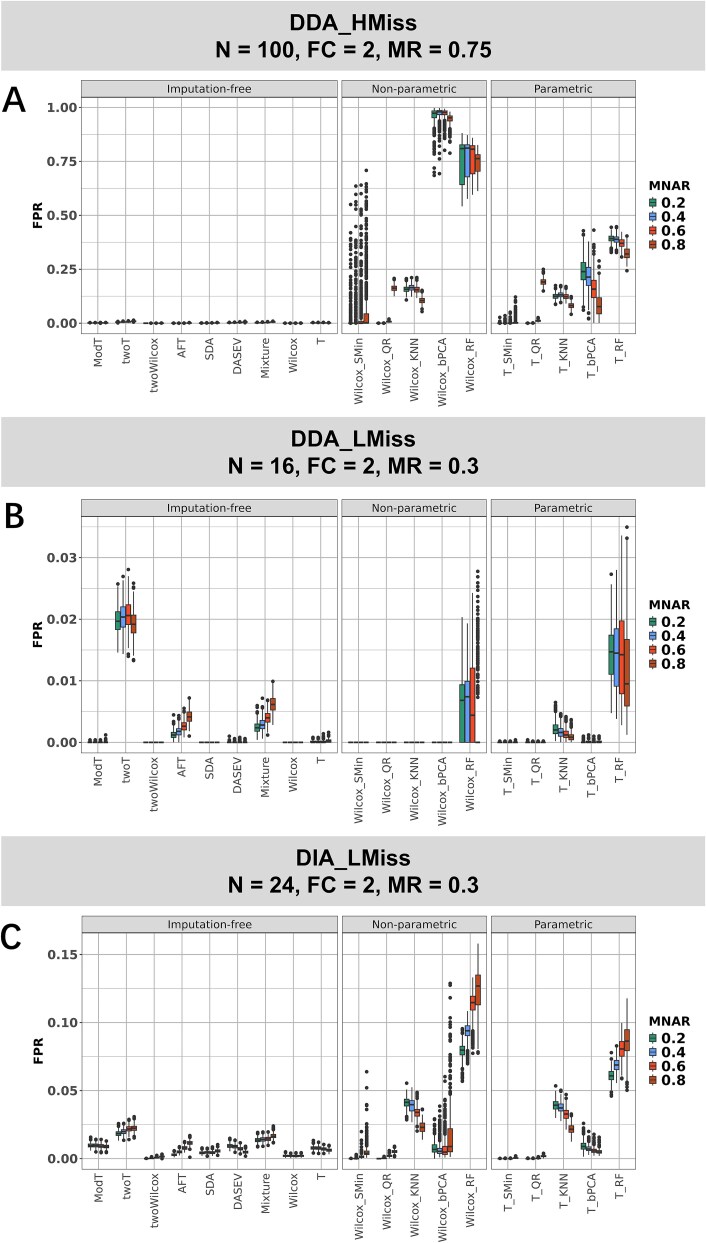
The performance of statistical methods in different MNAR ratios was evaluated in Simulation 1, where the sample size and missingness ratio were consistent with those of three reference metaproteomic datasets. The pAUROC of each method in the three simulated datasets is depicted in Fig. 2. The robustness of methods in different MNAR levels varied. The pAUROC for AFT, SMin imputation, and QR imputation showed substantial increases when MNAR ratios elevated from 0.2 to 0.8, with average improvements of 10.6%, 9.2%, and 18.2% in DDA_HMiss, DDA_LMiss, and DIA_LMiss, respectively. AFT, SMin, and QR are methods designed for left-censored data and hence performed better with high MNAR ratios. Conversely, the pAUROC of three imputation methods (KNN, bPCA, and RF) significantly decreased with increasing MNAR ratios in three simulated datasets, indicating their inapplicability to datasets with a high prevalence of left-censoring missingness. In DDA_HMiss, the most substantial decrease in pAUROC was observed in Wilcox_bPCA (bPCA imputation coupled with Wilcoxon test), with a reduction of ~9.0% from 0.543 (at an MNAR ratio of 0.2) to 0.494 (at an MNAR ratio of 0.8). Wilcox_RF experienced the largest decline in both DDA_HMiss (7.1%, from 0.576 to 0.535) and DIA_LMiss (17.2%, from 0.698 to 0.578).
Figure 2.
PAUROC of statistical tests for imputation and imputation-free methods across different MNAR ratios. (A) pAUROC in the simulation scenario for the DDA_HMiss dataset (sample size = 100, fold change = 2, missingness ratio = 0.75). (B, C) pAUROC for the simulation scenario of DDA_LMiss and DIA_LMiss datasets. Within each panel, boxplots are categorized into three subcolumns based on the types of statistical methods. For imputation methods, “nonparametric” denotes methods coupled with Wilcoxon test, and “parametric” denotes methods coupled with t-test. Wilcoxon test and t-test utilizing data with missing values eliminated were labeled with just Wilcox and T.
Therefore, RF and KNN imputation only exhibited superior performance among imputation methods in low MNAR ratios, but their advantages are not pronounced compared to the remaining imputation-free methods. For example, T_RF and T_KNN both achieved the highest pAUROC of 0.582 among all methods in DDA_LMiss with an MNAR ratio of 0.2 but only 0.004 higher than the T-test with missing values eliminated. However, at an MNAR ratio of 0.8, the median pAUROC of T_KNN (0.568) and T_RF (0.548) was lower than that of the best AFT (0.586) and second-level Wilcox_SMin (0.584). Similarly, in DIA_LMiss, when the MNAR ratio increased to 0.8, Wilcox_SMin (median pAUROC of 0.697) and Wilcox_QR (0.695) outperformed T_KNN (0.690), but they were less effective than ModT (0.711) and twoWilcox (0.705). However, all the imputation methods performed poorly at a high missingness ratio of 0.75 in DDA_HMiss despite the large sample size of 100. Their pAUROCs were much lower than the Wilcoxon and t-test with missing values eliminated. In this case, the maximum median pAUROC across all MNAR ratios of imputation methods was 0.567 for T_RF, compared to 0.6061 for the Wilcoxon test and 0.6058 for the t-test.
Considering all MNAR levels together, ModT exhibited the highest pAUROC in DDA_HMiss and DIA_LMiss, with median pAUROC values of 0.609 and 0.723 across four MNAR ratios, respectively. While at an MNAR ratio of 0.8 in DDA_HMiss, the median pAUROC for Mixture (0.614), DASEV (0.614), and twoWilcox (0.610) is slightly higher than that of ModT (0.604). In DDA_LMiss with a smaller sample size of 16, the Wilcoxon test with missing values eliminated (imputation-free Wilcoxon), imputation-free t-test, and ModT performed similarly and achieved the best median pAUROC of 0.579, 0.578, and 0.576 across four MANR levels.
Imputation resulted in high FPR under a high missingness ratio and a large sample size
The poor performance of RF and KNN imputation at DDA_HMiss attracted our attention, as both methods have been recommended in previous evaluations in proteomics and metabolomics [18, 28]. However, it has also been proposed that imputation may introduce a high proportion of false positives in proteomic analysis [17, 26]. Therefore, we examined the FPR in the test results of the 50% nondifferential proteins. Overall, the imputation methods exhibited a higher FPR compared to the imputation-free methods (Fig. 3). In the scenario of DDA_HMiss with a missingness ratio of 0.75 and a sample size of 100, the median FPR of KNN (0.115 with t-test and 0.146 with Wilcoxon test across four MNAR ratios), bPCA (0.175 and 0.962), and RF (0.368 and 0.757) reached unacceptable levels. In simulations of the DIA_LMiss dataset with a reduced missingness ratio of 0.3 and sample size of 24, KNN (0.034 on average of t-test and Wilcox test across four MNAR ratios) and RF (0.088) imputations also demonstrated higher median FPR compared to imputation-free tests (with a maximum FPR of 0.021 on twoT). The elevated FPR should also be considered when applying imputation to metaproteomic data with a large number of features (for example, >10 000 proteins in our datasets). In DDA_LMiss with a smaller sample size of 16, twoT had the highest median FPR of 0.020 across four MNAR ratios, and T_RF was the second highest (0.014). The other methods all exhibited a median FPR lower than 0.005.
Figure 3.
FPR of statistical tests for imputation and imputation-free methods across different MNAR ratios. (A) FPR in the simulation scenario for the DDA_HMiss dataset (sample size = 100, fold change = 2, missingness ratio = 0.75). (B, C) FPR for the simulation scenario of DDA_LMiss and DIA_LMiss datasets.
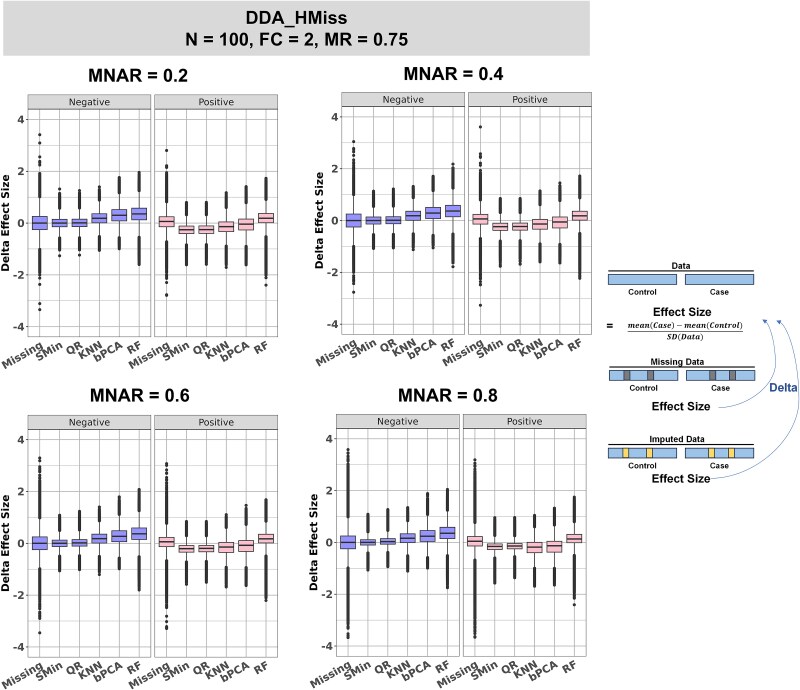
We sought to investigate the effects of imputations to figure out the reason for their poor performance. Effect size was used as the scaled quantitative measure of the difference between the case and control groups. The impact of missing value generation and imputation to effect sizes of each protein in 500 rounds of simulation is depicted in Fig. 4 and Supplementary Fig. S2. In the scenario of DDA_HMiss, for proteins without difference between case and control (negative features), the median bias between missing data and complete data was close to 0, with values of 0.0001 and 0.0006 for MNAR ratios of 0.2 and 0.8. The generation of missing data did not systematically alter the differences between the two groups. Conversely, KNN, bPCA, and RF imputation amplified the difference between case and control for negative features, as their median effect size biases were positive. The maximum bias was observed in RF imputation, which was 0.353 and 0.352 for MNAR ratios of 0.2 and 0.8, respectively. This may account for the high FPR of these three imputations. In the DIA_LMiss scenario with a low missingness ratio and small sample size, KNN, bPCA, and RF imputation also modified the effect size but in a smaller range than in DDA_HMiss (with a maximum bias of 0.117 for bPCA in MNAR ratio of 0.2, Supplementary Fig. S2), corresponding to a lower FPR in Fig. 3C. The effect size bias of DDA_LMiss was similar to that of DIA_LMiss (Supplementary Fig. S2).
Figure 4.
The bias of effect size compared to complete data in each round of simulation in DDA_HMiss. The difference between the effect size of missing data (labeled as “missing” on the x-axis of each panel) or imputed data (labeled with the imputation method names) and the completed data were quantified and visualized. In each panel, scenarios with different MNAR ratios of 0.2, 0.4, 0.6, and 0.8 are displayed. Differentially abundant proteins (labeled as “positive”) and proteins with no difference abundance (labeled as “negative”) were plotted separately.
For proteins differentially abundant between case and control (positive features), SMin and QR imputation also systematically changed the effect size. They reduced the differences for positive features in all three datasets, especially in low MNAR ratios. For example, for an MNAR ratio of 0.2, the median bias was −0.257 and −0.252 for SMin and QR in DDA_HMiss, compared to −0.156 and −0.140 for an MNAR ratio of 0.8 (Fig. 4). This aligns with expectations, as both methods are designed to capture the lower detection limit of the instrument and are more appropriate for censoring mechanisms (high MNAR ratios) [34].
Overall empirical recommendations in broad scenarios
To determine the optimal strategies across various scenarios, 11 statistical methods were assessed in Simulation 2, encompassing a broad spectrum of sample sizes (10–200), fold changes between case and control (1.2–5), and missingness ratios (0.3–0.9). MNAR ratios in Simulation 2 were also set at 0.2, 0.4, 0.6, and 0.8. By manipulating sample sizes and missing value ratios, our findings were further confirmed in scenarios not covered by the reference datasets. After comparing scenarios with small sample sizes of 20 and large sample sizes of 100, as well as missingness ratios from low to high (0.3–0.9), we found that the FPR of the imputation methods indeed increased with sample size and missingness ratio and eventually reached unacceptable levels (Supplementary Fig. S3). Compared to imputation-free methods, imputation only showed nonpronounced advantages in small sample size with low MNAR ratios, consistent with the previous section (Supplementary Fig. S4).
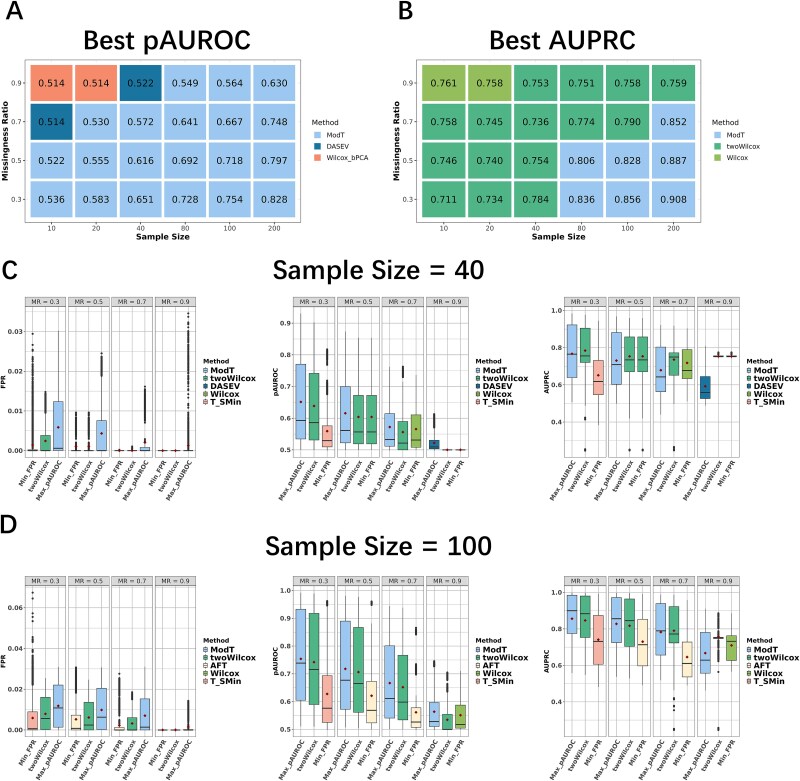
Then, we developed empirical recommendations based on the average pAUROC, AUPRC, and FPR of simulations across four MNAR ratios and six-fold change levels, as the MNAR ratio were difficult to quantify and the dataset is often a mixture of different fold changes in applications. The method with the highest pAUROC in each scenario was presented in Fig. 5A. Wilcox_bPCA and DASEV performed the best in small sample size (≤ 40) with extreme high missingness ratio (≥ 0.7). However, even the optimal pAUROC was very low (equal to about 0.5) in these scenarios, which suggested a significant challenge in metaproteomics analysis with a small sample size and an extremely high missingness ratio. ModT exhibited the highest pAUROC in the remaining scenarios of sample sizes and fold changes. As for FPR, we observed that in some scenarios in Simulation 2, twoWilcox was able to effectively control the FPR while maintaining competitive pAUROC. For example, at sample sizes of 100 (Fig. 5D), the average pAUROC of twoWilcox differed from the top-ranked ModT only by a very low amount (with the maximum difference of 0.029 at a missingness ratio of 0.9). Notably, twoWilcox demonstrated significantly lower FPR compared to ModT, with the maximum reduction of 82.0% observed at missingness ratios of 0.9. Conversely, except for the Wilcoxon test at a missingness ratio of 0.9, the discrepancy in pAUROC between the method exhibiting the lowest FPR and ModT typically exceeded that of twoWilcox (with the minimum difference of 0.097). This conclusion remained consistent across smaller sample sizes (Fig. 5C and Supplementary Fig. S3), where in some scenarios twoWilcoxon itself was the method with the lowest FPR. If considering AUPRC as the metric, twoWilcox showed higher AUPRC compared to ModT except in a large sample size ≥80 with a low missingness ratio ≤0.7 (Fig. 5B).
Figure 5.
Performance of statistical methods in broad scenarios. (A, B) statistical methods with the highest average pAUROC and AUPRC across scenarios with varying sample sizes and missingness ratios. The pAUROC and AUPRC values from 100 rounds of simulations across different MNAR ratios and fold changes were averaged. The color in each grid represents the method with the highest pAUROC and AUPRC in the given scenario, with the corresponding value labeled. (C, D) comparisons of twoWilcox with the methods yielding the highest average pAUROC and AUPRC, and lowest FPR in scenarios with sample sizes of 40 and 100. The boxplots represent the overall distribution of metrics across different MNAR ratios and fold changes, while the average metric was shown as the red diamond mark. Different methods are represented by different colors. See Supplementary Fig. S5 for comparisons of other sample sizes.
In summary, after comprehensive consideration of sensitivity in detection and control of false positives, ModT was recommended for scenarios with large sample sizes (≥80) and low missingness ratios (≤0.7). In contrast, twoWilcox proved more suitable in cases with large sample sizes but higher missingness ratios, or smaller sample sizes with relatively low missingness ratios. However, for the extreme cases in metaproteomic studies involving both small sample sizes and exceptionally high missingness ratios, the differential analysis results warranted a more cautious interpretation, as none of the evaluated methods achieved reliable performance.
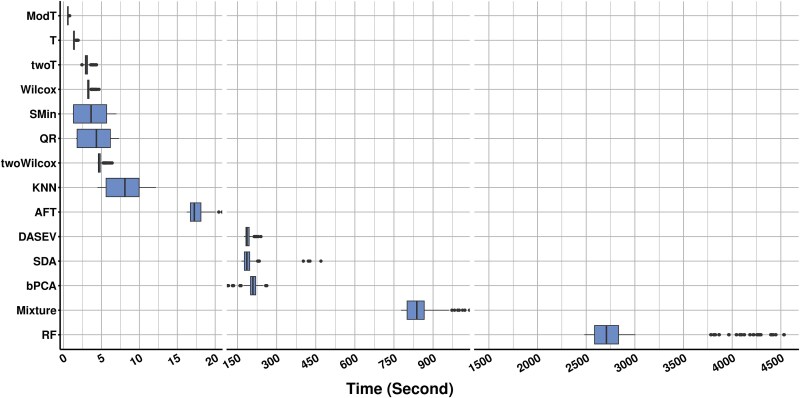
Efficiency was another important factor affecting the choice of strategy. The running time of different statistical methods varied dramatically in the simulation (Fig. 6). For a simulated dataset with 200 samples and 10 000 features, the fastest ModT took only 0.58 s on average to complete a round of tests. TwoWilcox took ~5 s on average. The slowest RF imputation took ~3214 s, making it challenging to be applied in high-dimensional data. DASEV, SDA, and Mixture all require iterative procedures to find maximum likelihood estimates for model parameters, so they are more time-consuming than the other imputation-free methods. The limitation of R scripts to single-thread execution also contributes to the reduced efficiency of certain methods.
Figure 6.
Execution time of statistical methods. The boxplots represent the execution time for each method across 100 simulation rounds with a sample size of 200, a missingness ratio of 0.7, and MNAR ratios of 0.2, 0.4, 0.6, and 0.8.
Discussion
Targeting differential abundance analysis of proteins in metaproteomics, we assessed the performance of five imputation methods and six imputation-free methods in metaproteomic datasets with 588 combinations of simulation parameters. Our results showed data imputation performed poorly in scenarios of high missingness ratio and large sample size, in which KNN, bPCA, and RF imputation showed high FPR in the test results. Overall, based on the balance between pAUROC, AUPRC, FPR, and computational efficiency, we recommend ModT in scenarios of large sample size with low missingness ratio, and twoWilcox in scenarios of small sample size with low missingness ratio or large sample size with high missingness ratio.
Proteomics data are typically close to normally distributed after logarithm transformation and/or normalization [40]. Our simulation datasets were generated with Log-normal distributions, consistent with Ding et al.’s phosphoproteomics simulation framework [29]. No consensus conclusions have been established on the mechanism of missing values in MS data. The recent protDP model for predicting missingness ratio based on protein intensity did not fit well in the ProteoCardis dataset with a high missing value ratio (Supplementary Fig. S1B) [17]. We inferred that it is difficult to fit the intensity and detection probability with a simple logistic regression in metaproteomic datasets such as Proteocardis, as more complex and diverse proteins originating from dynamic microbiomes are detected and more confounding factors could be included. Therefore, we generated missing values with different ratios and different compositions of MNAR and MCAR following Lazar et al. [14].
There has been a huge debate about whether data imputation should be applied to proteomic datasets containing missing values. Some researchers argue that missing value imputation should be applied with caution to MS data. For example, Li and Smyth observed that imputation performed poorly in proteomics data of sample size 12 and missing values generated by protDP, either reducing statistical power or increasing the false discovery rate to unacceptable levels [17]. However, they did not validate it on a larger dataset. Ooijen et al. found that imputation increased sensitivity with the cost of a much higher FDR in peptide-level proteomics [26]. Conversely, other studies have found that imputation methods outperform imputation-free methods. Wang et al. discovered that imputation could enhance the performance of differential analysis when coupled with appropriate statistical methods in proteomics [27]. On isobaric-labeled proteomics datasets, Bramer et al. found that imputation performed better except in small sample sizes and high missingness ratio [28]. But the maximum missingness ratio was 50% in their simulation, which is lower than our metaproteomic data. Taylor et al. reported that RF and KNN imputation yielded the best performance in statistical testing for up to 50% missingness in simulated metabolomics data. None of the imputation-free methods they assessed consistently outperformed the imputation methods [18]. We designed our experiments based on the method selection of Taylor et al. and incorporated ModT and SDA into the imputation-free methods. Our evaluations revealed that at a small sample size and low MNAR ratio, T_KNN achieved a pAUROC higher than that of imputation-free methods, except for ModT in DIA_LMiss. This is partially consistent with the conclusions of Taylor et al. However, imputation methods performed poorly and resulted in high FPR at the high missingness ratio, aligning with the findings of Li and Smyth, and Ooijen et al. We speculated that the discrepancies with Taylor et al.’s conclusions may arise from variations in simulation methods or dataset characteristics. The metabolomics datasets referenced by Taylor et al. have smaller data dimensions and lower missingness ratios compared to our metaproteomic data. Their procedures to generate simulated data involved randomly shuffling samples without missing data to produce non-differentiated data, subsequently introducing data differences and missing values. This process preserved the intrinsic correlation structure among compound intensities, which could be leveraged by certain imputation methods (e.g. kNN, RF, and bPCA) to achieve superior performance [41]. In contrast, our simulated datasets were designed to mirror the scale and missing value patterns observed in real data but were generated under the assumption of independence among proteins.
After evaluation, we found that ModT achieved the highest pAUROC in broad scenarios of metaproteomics. It employs empirical Bayes–moderated statistics, which regularize the variance of the t-test statistic based on Bayesian shrinkage estimation and improve power [31]. Ooijen et al. claimed that ModT with no imputation outperformed halfLocal, random tail, and multiple imputation in peptide-level proteomics [26]. TwoWilcox demonstrated comparable pAUROC, higher AUPRC in a sample size smaller than 80 or a large sample size with a high missingness ratio, and superior control over false positives. The two-part statistical test is proposed for the semicontinuous data. TwoWilcox contains a binomial test for zero parts and a nonparametric Wilcoxon test for nonzero parts and combines the strengths of statistical tests for continuous data and the consideration of zero parts [21, 32]. The two-part models have been evaluated and applied in microbiome analysis of other ‘omics. Wagner et al. demonstrated that the two-part statistic outperforms the t-test and Wilcoxon test in identifying taxa differences between groups in microbial ecology studies due to its ability to handle sequence data with a large proportion of zeros and non-negative skewed counts [42]. In Cho et al.’s evaluation of metatranscriptomic data, the two-part method also exhibited good control of false positives and high sensitivity, especially in large samples and small sample sizes with a missingness ratio < 0.9 [43].
This study is subject to certain limitations. Our simulation was targeted at the currently widely adopted label-free metaproteomics data. However, our simulated dataset did not take into account other metaproteomic experimental platforms and technologies, such as isobaric-labeled metaproteomics and proteomic microarray. The characterization of missing values in such experimental data may be different from that in label-free experiments. This distinction could be considered in further studies.
Key Points
We assessed the performance of five imputation methods and six imputation-free methods in simulated metaproteomic datasets with 588 different scenarios of sample size, fold change between case and control, and missing value ratio at random and nonrandom.
Compared to imputation-free methods, k-nearest neighbors, Bayesian principal component analysis, and random forest imputation performed poorly in datasets with a high missingness ratio and a large sample size and resulted in a high false-positive risk.
Considering the balance of sensitivity in analysis and control of false positives, the moderated t-test is optimal in scenarios of large sample size with a low missingness ratio. The two-part Wilcoxon test is recommended in scenarios of small sample size with a low missingness ratio or large sample size with a high missingness ratio.
Supplementary Material
Acknowledgements
The computations in this paper were run on the Siyuan-1 cluster supported by the Center for High Performance Computing at Shanghai Jiao Tong University.
Contributor Information
Xinyi Mou, Department of Bioinformatics and Biostatistics, School of Life Sciences and Biotechnology, Shanghai Jiao Tong University, 800 Dongchuan Road, Shanghai 200240, China.
Haoyu Du, Department of Bioinformatics and Biostatistics, School of Life Sciences and Biotechnology, Shanghai Jiao Tong University, 800 Dongchuan Road, Shanghai 200240, China.
Guanghua Qiao, Department of Bioinformatics and Biostatistics, School of Life Sciences and Biotechnology, Shanghai Jiao Tong University, 800 Dongchuan Road, Shanghai 200240, China.
Jing Li, Department of Bioinformatics and Biostatistics, School of Life Sciences and Biotechnology, Shanghai Jiao Tong University, 800 Dongchuan Road, Shanghai 200240, China.
Funding
This work was supported by the National Natural Science Foundation of China (32170664, 31871329, and 42327805), the Key Project for Computational Biology of Shanghai (grant no. 23JS1400800), and the Fundamental Research Funds for the Central Universities (YG2023ZD11).
Data availability
The code used for statistical analysis and visualization can be found at GitHub through the following link: https://github.com/Li-Lab-SJTU/metaproteomics_MV_simulation.
References
- 1. Wu E, Xu G, Xie D. et al. Data-independent Acquisition in Metaproteomics. Expert Rev Proteomics 0:1–10. 10.1080/14789450.2024.2394190. [DOI] [PubMed] [Google Scholar]
- 2. Sun Z, Ning Z, Figeys D. The landscape and perspectives of the human gut Metaproteomics. Mol Cell Proteomics 2024;23:100763. 10.1016/j.mcpro.2024.100763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Miller SE, Colman AS, Waldbauer JR. Metaproteomics reveals functional partitioning and vegetational variation among permafrost-affected Arctic soil bacterial communities. mSystems 2023;8:e0123822. 10.1128/msystems.01238-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Quiton-Tapia S, Trueba-Santiso A, Garrido JM. et al. Metalloenzymes play major roles to achieve high-rate nitrogen removal in N-Damo communities: Lessons from Metaproteomics. Bioresour Technol 2023;385:129476. 10.1016/j.biortech.2023.129476. [DOI] [PubMed] [Google Scholar]
- 5. Cohen NR, Krinos AI, Kell RM. et al. Microeukaryote metabolism across the western North Atlantic Ocean revealed through autonomous underwater profiling. Nat Commun 2024;15:7325. 10.1038/s41467-024-51583-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Webb-Robertson B-JM, Wiberg HK, Matzke MM. et al. Review, evaluation, and discussion of the challenges of missing value imputation for mass spectrometry-based label-free global proteomics. J Proteome Res 2015;14:1993–2001. 10.1021/pr501138h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Plancade S, Berland M, Blein-Nicolas M. et al. A combined test for feature selection on sparse Metaproteomics data-an alternative to missing value imputation. PeerJ 2022;10:e13525. 10.7717/peerj.13525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Zhao J, Yang Y, Xu H. et al. Data-independent acquisition boosts quantitative Metaproteomics for deep characterization of gut microbiota. Npj Biofilms Microbiomes 2023;9:1–14. 10.1038/s41522-023-00373-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Jiang X, Zhang Y, Wang H. et al. In-depth metaproteomics analysis of oral microbiome for lung cancer. Res Wash C 2022;2022:9781578. 10.34133/2022/9781578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Abbondio M, Tanca A, De Diego L. et al. Metaproteomic assessment of gut microbial and host functional perturbations in helicobacter pylori-infected patients subjected to an antimicrobial protocol. Gut Microbes 2023;15:2291170. 10.1080/19490976.2023.2291170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Palomba A, Tanca A, Abbondio M. et al. Time-restricted feeding induces lactobacillus- and Akkermansia-specific functional changes in the rat Fecal microbiota. Npj Biofilms Microbiomes 2021;7:1–10. 10.1038/s41522-021-00256-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Bassignani A. Metaproteomics analysis to study functionalities of the gut microbiota in large cohorts. Theses, Sorbonne Université. 2019.
- 13. Gómez-Varela D, Xian F, Grundtner S. et al. Expanding the characterization of microbial ecosystems using DIA-PASEF metaproteomics. bioRxiv 2023;16:2023.03.16.532922. 10.1101/2023.03.16.532922. [DOI] [Google Scholar]
- 14. Lazar C, Gatto L, Ferro M. et al. Accounting for the multiple natures of missing values in label-free quantitative proteomics data sets to compare imputation strategies. J Proteome Res 2016;15:1116–25. 10.1021/acs.jproteome.5b00981. [DOI] [PubMed] [Google Scholar]
- 15. Liu M, Dongre A. Proper imputation of missing values in proteomics datasets for differential expression analysis. Brief Bioinform 2021;22:bbaa112. 10.1093/bib/bbaa112. [DOI] [PubMed] [Google Scholar]
- 16. Karpievitch YV, Dabney AR, Smith RD. Normalization and missing value imputation for label-free LC-MS analysis. BMC Bioinformatics 2012;13:S5. 10.1186/1471-2105-13-S16-S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Li M, Smyth GK. Neither random nor censored: Estimating intensity-dependent probabilities for missing values in label-free proteomics. Bioinforma Oxf Engl 2023;39:btad200. 10.1093/bioinformatics/btad200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Taylor S, Ponzini M, Wilson M. et al. Comparison of imputation and imputation-free methods for statistical analysis of mass spectrometry data with missing data. Brief Bioinform 2022;23:bbab353. 10.1093/bib/bbab353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Oba S, Sato M, Takemasa I. et al. A Bayesian missing value estimation method for gene expression profile data. Bioinforma Oxf Engl 2003;19:2088–96. 10.1093/bioinformatics/btg287. [DOI] [PubMed] [Google Scholar]
- 20. Troyanskaya O, Cantor M, Sherlock G. et al. Missing value estimation methods for DNA microarrays. Bioinforma Oxf Engl 2001;17:520–5. 10.1093/bioinformatics/17.6.520. [DOI] [PubMed] [Google Scholar]
- 21. Taylor S, Pollard K. Hypothesis tests for point-mass mixture data with application to ‘omics data with many zero values. Stat Appl Genet Mol Biol 2009;8:Article 8. 10.2202/1544-6115.1425. [DOI] [PubMed] [Google Scholar]
- 22. Tekwe CD, Carroll RJ, Dabney AR. Application of survival analysis methodology to the quantitative analysis of LC-MS proteomics data. Bioinforma Oxf Engl 2012;28:1998–2003. 10.1093/bioinformatics/bts306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Li Y, Fan TWM, Lane AN. et al. SDA: A semi-parametric differential abundance analysis method for metabolomics and proteomics data. BMC Bioinformatics 2019;20:501. 10.1186/s12859-019-3067-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Wilson MD, Ponzini MD, Taylor SL. et al. Imputation of missing values for multi-biospecimen metabolomics studies: Bias and effects on statistical validity. Meta 2022;12:671. 10.3390/metabo12070671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Jin L, Bi Y, Hu C. et al. A comparative study of evaluating missing value imputation methods in label-free proteomics. Sci Rep 2021;11:1760. 10.1038/s41598-021-81279-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. van Ooijen MP, Jong VL, Eijkemans MJC. et al. Identification of differentially expressed peptides in high-throughput proteomics data. Brief Bioinform 2018;19:971–81. 10.1093/bib/bbx031. [DOI] [PubMed] [Google Scholar]
- 27. Wang J, Li L, Chen T. et al. In-depth method assessments of differentially expressed protein detection for shotgun proteomics data with missing values. Sci Rep 2017;7:3367. 10.1038/s41598-017-03650-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Bramer LM, Irvahn J, Piehowski PD. et al. A review of imputation strategies for isobaric Labeling-based shotgun proteomics. J Proteome Res 2021;20:1–13. 10.1021/acs.jproteome.0c00123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Ding LJ, Schlüter HM, Szucs MJ. et al. Comparison of statistical tests and power analysis for Phosphoproteomics data. J Proteome Res 2020;19:572–82. 10.1021/acs.jproteome.9b00280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Madley-Dowd P, Hughes R, Tilling K. et al. The proportion of missing data should not Be used to guide decisions on multiple imputation. J Clin Epidemiol 2019;110:63–73. 10.1016/j.jclinepi.2019.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Smyth GK. Linear models and empirical bayes methods for assessing differential expression in microarray experiments. Stat Appl Genet Mol Biol 2004;3:1–25. 10.2202/1544-6115.1027. [DOI] [PubMed] [Google Scholar]
- 32. Lachenbruch PA. Comparisons of two-part models with competitors. Stat Med 2001;20:1215–34. 10.1002/sim.790. [DOI] [PubMed] [Google Scholar]
- 33. Huang Z, Lane AN, Fan TW-M. et al. Differential abundance analysis with bayes shrinkage estimation of variance (DASEV) for zero-inflated proteomic and metabolomic data. Sci Rep 2020;10:876. 10.1038/s41598-020-57470-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Taylor SL, Leiserowitz GS, Kim K. Accounting for undetected compounds in statistical analyses of mass spectrometry ‘omic studies. Stat Appl Genet Mol Biol 2013;12:703–22. 10.1515/sagmb-2013-0021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Stekhoven DJ, Bühlmann P. MissForest--non-parametric missing value imputation for mixed-type data. Bioinforma Oxf Engl 2012;28:112–8. 10.1093/bioinformatics/btr597. [DOI] [PubMed] [Google Scholar]
- 36. Lee M, Rahbar MH, Brown M. et al. A multiple imputation method based on weighted quantile regression models for longitudinal censored biomarker data with missing values at early visits. BMC Med Res Methodol 2018;18:8. 10.1186/s12874-017-0463-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Benjamini Y, Hochberg Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J R Stat Soc Ser B Methodol 1995;57:289–300. 10.1111/j.2517-6161.1995.tb02031.x. [DOI] [Google Scholar]
- 38. Ma H, Bandos AI, Rockette HE. et al. On use of partial area under the ROC curve for evaluation of diagnostic performance. Stat Med 2013;32:3449–58. 10.1002/sim.5777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. McClish DK. Analyzing a portion of the ROC curve. Med Decis Making 1989;9:190–5. 10.1177/0272989X8900900307. [DOI] [PubMed] [Google Scholar]
- 40. Välikangas T, Suomi T, Elo LL. A systematic evaluation of normalization methods in quantitative label-free proteomics. Brief Bioinform 2018;19:1–11. 10.1093/bib/bbw095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Frölich N, Klose C, Widén E. et al. Imputation of missing values in lipidomic datasets. Proteomics 2024;24:2300606. 10.1002/pmic.202300606. [DOI] [PubMed] [Google Scholar]
- 42. Wagner BD, Robertson CE, Harris JK. Application of two-part statistics for comparison of sequence variant counts. PLoS One 2011;6:e20296. 10.1371/journal.pone.0020296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Cho H, Qu Y, Liu C. et al. Comprehensive evaluation of methods for differential expression analysis of Metatranscriptomics data. Brief Bioinform 2023;24:bbad279. 10.1093/bib/bbad279. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The code used for statistical analysis and visualization can be found at GitHub through the following link: https://github.com/Li-Lab-SJTU/metaproteomics_MV_simulation.