Explaining basketball game performance with SHAP: insights from Chinese Basketball Association

Abstract

This study explores the Key Performance Indicators (KPIs) influencing the game outcomes of the Chinese Basketball Association (CBA). Utilizing data from 4100 games across 10 CBA seasons (2013–2023), this study constructs CBA game outcome prediction models using seven machine learning algorithms, including XGBoost, LightGBM, Decision Tree, Random Forest, Support Vector Machines, Logistic Regression, and K-Nearest Neighbors. The SHapley Additive exPlanation (SHAP) method is applied to explain the optimal prediction model and analyze the KPIs. The findings are as follows: (1) XGBoost demonstrates excellent performance in predicting CBA game outcomes. (2) eFG%, 3P%, 2P%, ORB%, DRB, and TOV% are key indicators influencing CBA game outcomes. (3) There is a tendency for offensive play over defensive strategies in CBA playoffs. This combined methodology of machine learning and SHAP analysis not only exhibits superior performance but also strong explainability. It effectively reflects the relationship between game outcomes and performance data, providing a scientific basis for enhancing professional basketball performance.

Introduction

Basketball performance analysis is crucial for understanding the factors influencing team success and providing insights for coaching strategies. As basketball continues to evolve tactically and technically, significant performance variations are observed among players from different countries and competitive levels^1–4. Yi Qing’s study using multiple linear regression and quantile regression methods identified two-point shooting percentage, offensive rebounds, assists, and turnovers as key performance indicators (KPIs) affecting the outcomes of WCBA games⁵. Cabarkapa found that shooting percentage and defensive rebounds are critical for determining NBA game outcomes⁶. Further research has shown variations in KPI performance among teams with different win rates and levels⁷, with teams tending towards more conservative tactical choices under higher defensive pressures⁶. Although research on KPIs affecting game outcomes is extensive in top-tier leagues like the NBA and European leagues^8–14, studies focusing on the Chinese Basketball Association (CBA), China’s premier and most influential basketball league, are relatively scarce. This gap underscores the need for in-depth analysis of performance patterns in CBA games.

Retrospective analysis is an imperative method for explaining historical data, offering insights into past performances that guide strategic adjustments in plans. This approach is crucial for CBA as it fills the gap in understanding nuanced aspects of play and decision-making not captured in existing literature. Additionally, existing studies often prioritize model performance over explainability, utilizing complex machine learning models without adequately explaining how specific game data influences outcomes^15–19. This lack of explainability limits the practical application of these models among coaches and athletes, who require actionable insights for decision-making. Explainable machine learning techniques are crucial for bridging the gap between advanced analytics and practical sports applications²⁰. Furthermore, while machine learning models are traditionally leveraged for prospective modeling, their application in retrospective analysis can uncover complex relationships and historical trends that simpler models may not detect. This helps in identifying overlooked performance factors pivotal for retrospective insights.

Considering these factors, this study conducted a retrospective analysis of CBA games from the 2013–2023 seasons, aiming to identify which statistical factors are strongly correlated with outcomes, thereby revealing the intrinsic relationships between game-related statistical data and results. We hypothesized that machine learning algorithms, especially when combined with explainability techniques, can effectively identify and quantify the KPIs influencing CBA game outcomes.

We selected seven mainstream machine learning algorithms for this exploratory analysis: XGBoost, LightGBM, Decision Trees, Random Forests, Support Vector Machines (SVM), Logistic Regression, and K-Nearest Neighbors (KNN). These models were chosen to cover a broad range of modeling approaches, including linear, non-linear, tree-based, and instance-based learning methods. By considering this diverse set of algorithms, we aim to balance explainability and accuracy while capturing the complex non-linear relationships in the data. To enhance the explainability of the best-performing machine learning model, we employed the SHapley Additive exPlanation (SHAP) method²¹. Based on cooperative game theory, SHAP provides consistent and locally accurate feature attributions. Despite the sophisticated nature of SHAP, our methodological framework includes rigorous preprocessing and data validation steps to mitigate potential noise, ensuring clarity and reliability in the insights derived. This careful approach justifies its application in analyzing complex datasets. By applying SHAP, we aim to uncover the intrinsic relationships between game-related statistical data and outcomes, providing valuable insights for coaches and athletes.

Research objectives:

1. To systematically evaluate seven machine learning algorithms in predicting CBA outcomes, identifying context-optimal modeling approaches for basketball analytics.

2. To leverage SHAP explainability frameworks in revealing actionable metric-outcome associations, empirically validating established theories through predictive patterns.

By achieving these objectives, this study bridges the literature gap in explainable machine learning for CBA analytics. The findings offer evidence-backed insights, enabling data-informed coaching strategies grounded in observable performance patterns.

Theory of the selected ML algorithms

XGBoost

Extreme Gradient Boosting (XGBoost) is an ensemble learning algorithm based on gradient boosted decision trees and is notably effective in various fields including sports^22–24. The essence of the XGBoost algorithm lies in its boosting iterative method, which includes an additive model where a strong estimator is formed by linearly adding a series of weak estimators, and a forward stagewise algorithm where each new estimator in the subsequent iteration is trained based on the previous iteration. As an improvement to the GBDT algorithm, XGBoost expands the objective function into a second-order Taylor series, retaining more information about the objective function and incorporating regularization terms to prevent overfitting. The refined objective function is:

1

2

where  represents the discrepancy between the predicted values and the actual values,  is the regularization term of the objective function,  denotes the complexity of each leaf, 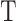 indicates the total number of leaves in the decision tree,  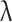is the L2 regularization coefficient, and  represents the L2 regularization score for the j-th leaf. This formulation effectively aids in reducing overfitting while enhancing the robustness and predictive accuracy of the model.

LightGBM

LightGBM (Light Gradient Boosting Machine) is an efficient gradient boosting framework specifically designed to handle large-scale data and high-dimensional scenarios. LightGBM leverages the Histogram algorithm, a depth-limited Leaf-wise approach, and parallel optimization strategies, which offers significant advantages in terms of training speed, memory consumption, and the capacity to manage large-scale distributed data processing²⁵. The objective function of LightGBM, similar to other GBDT models, comprises two parts: a loss function and a regularization term:

3

Here,  represents the loss function for each sample, quantifying the discrepancy between actual values and predictions, while  is the regularization term used to prevent model overfitting. This structure enhances the model’s ability to generalize across complex data sets while maintaining computational efficiency.

Decision tree

The Decision Tree (DT) is a commonly used non-parametric supervised learning algorithm, extensively applied in both classification and regression tasks. Its fundamental principle involves partitioning the dataset recursively into a tree structure, where each division decision is based on maximizing information gain (for classification tasks) or minimizing mean squared error (for regression tasks). This process continues until certain stopping criteria are met, such as the tree reaching a predetermined maximum depth, the number of samples in a node falling below a minimum threshold, or the information gain dropping below a specified value²⁶.

Random forest

The Random Forest (RF) is an ensemble learning algorithm composed of multiple decision trees, capable of handling diverse features while mitigating overfitting²⁷. It randomly selects features from the sample set and constructs multiple decision trees on a randomly generated training set. At each node, a subset of features is randomly chosen for splitting, thereby reducing the model’s variance and the risk of overfitting. The model of Random Forest can be represented as:

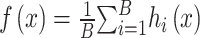4

where is the number of trees in the forest, and denotes the prediction of the -th tree for the sample . This method enhances the robustness of the predictions by averaging the outputs across the ensemble of trees, thus providing a more reliable and generalizable model.

Support vector machine

Support Vector Machine (SVM) is a classification method based on the principle of structural risk minimization. The core idea of SVM is to find an optimal hyperplane that maximizes the margin between different classes, effectively separating the samples of different categories while maximizing the distance from the hyperplane to the nearest data points—known as support vectors²⁸. For datasets that are not linearly separable in the original feature space, SVM introduces kernel functions to map the input data into a higher-dimensional feature space, where a linear separation becomes feasible. The SVM model can be represented as:

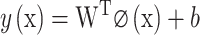5

where 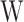is the weight vector, 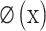is a function that maps the input samples into a higher-dimensional feature space, 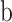is the bias term, and is the predicted value for sample 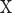. The training of an SVM involves solving the following optimization problem:

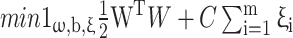6

7

In this formulation, 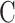is a hyperparameter that controls the trade-off between maximizing the margin and minimizing the classification error, effectively regulating the complexity of the model. The variables are slack variables that allow for misclassification of samples in cases where perfect separation is not possible.

Logistic regression

Logistic Regression is a widely utilized statistical model for binary classification tasks. The core concept of this model involves utilizing the sigmoid function to transform the linear combination of input features into a probability value that ranges between 0 and 1, effectively converting a regression problem into a classification problem²⁹. For a given input feature vector , the model can be expressed as:

8

Here, represents the predicted probability for the input sample , and 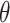denotes the model’s parameter vector, where each parameter corresponds to the weight of an input feature.

K-nearest neighbors

The K-Nearest Neighbors (KNN) algorithm is a non-parametric and intuitive method of supervised learning. It primarily functions by calculating the distance between a query instance and all samples in the training dataset to pinpoint the closest instances³⁰. For classification tasks, predictions for the query instance are determined based on the majority vote of these nearest neighbors’ categories. In the case of regression, the prediction is the average of their values. Commonly used distance metrics include the Euclidean and Manhattan distances, each of which is appropriate for different data distributions.

KNN operates without a formal training phase but requires a computationally intensive prediction stage, particularly in scenarios involving large datasets or high-dimensional spaces. The distance between a test sample and a training sample is computed using the equation:

9

where represents the number of features. After calculating the distances, the 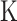samples with the smallest distances are chosen, and their labels or values are utilized to predict the outcome for the test sample. While the simplicity and intuitiveness of KNN are beneficial, its efficiency decreases with the increase in data size or dimensionality. This necessitates a careful selection of the distance metric and the value. For handling high-dimensional data, employing dimensionality reduction techniques or efficient data structures like KD-trees can enhance query performance, making KNN more feasible for large-scale applications.

SHAP

SHAP is a post-hoc explainability framework that quantifies feature contributions to individual predictions, distinct from intrinsic model interpretability methods such as linear regression coefficients^20,21. Post-hoc explainability refers to techniques applied after model training to explain its behavior, whereas intrinsic interpretability arises directly from the model’s structure. This distinction is critical for deriving actionable insights in coaching strategies while preserving model accuracy. Inspired by cooperative game theory, Lundberg and Lee proposed the SHAP framework as a model-agnostic additive feature attribution method based on Shapley values^21,31. Shapley values, rooted in game-theoretic fairness axioms, decompose the contribution of each feature to the model’s prediction and are characterized by uniqueness and theoretical rigor. The SHAP framework is illustrated in Fig. 1.

Fig. 1.

Framework of the SHAP algorithm.

In the SHAP framework, the predictive values (ŷ) of a machine learning model is expressed as:

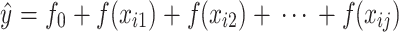10

where f₀ denotes the baseline value, representing the expected model output when no feature information is available (e.g., the mean prediction across the training dataset). SHAP values quantify deviations from this baseline, enabling attribution of feature contributions to individual predictions. f(x_ij) represents the Shapley values of each feature for each sample, reflecting the positive or negative influence of each feature on the model’s prediction outcome.

SHAP was selected for its theoretical consistency (additivity) and ability to handle non-linear interactions inherent in tree-based models like XGBoost²¹. Unlike permutation importance, SHAP provides instance-level explanations aligned with human intuition, making it suitable for coaching applications.

Research methodology

The research flowchart is shown in Fig. 2.

Fig. 2.

CBA game performance analysis flowchart.

Data source and reliability

The dataset analyzed in the study encompasses all game data from the CBA spanning the seasons of 2013–2014 to 2022–2023, sourced from the official website (https://www.cbaleague.com/). Excluding overtime games, preseason games, all-star games, contests not held due to the pandemic, and anomalous games, a total of 4102 valid game records were incorporated. Specific indicators are detailed in Supplementary Table S1, which provides the definition of CBA technical game performance-related variables. Furthermore, this study did not involve human or animal subjects and refrained from including any personal or sensitive information. Consequently, obtaining approval from an Institutional Review Board (IRB) or ethics committee was deemed unnecessary³².

To ascertain the data’s validity, a subset of 50 games, ensuring a minimum of five games per season, was randomly chosen. These games were then reviewed by two seasoned basketball players, both first-class athletes from China, who compared the game footage against the data retrieved from the website. The findings confirmed the data’s high reliability, as evidenced by an intraclass correlation coefficient (ICC) ranging from 0.93 to 0.97.

Modeling the dataset

By employing feature engineering, the problem of predicting game outcomes is transformed into a binary classification problem. The target variable, result, is defined as a binary label indicating the win or loss of the home team, with home team wins and losses assigned values of 1 and 0, respectively. In understanding the specific research on basketball sports and the prediction of game outcomes, combined with the characteristics of the dataset indicators, the final modeling features were obtained by calculating the differences between the values of home and away teams for each technical indicator, such as home_2P% minus away_2P% and home_ORB minus away_ORB. This approach minimizes redundancy from overlapping statistical profiles of home and away teams, like similar 2P% or rebound counts, while maintaining the competitive dynamics essential for accurate outcome prediction.

In regression modeling, multicollinearity refers to the distortion or difficulty in accurately estimating coefficients due to highly correlated explanatory variables. However, in machine learning (e.g., tree-based models like XGBoost), multicollinearity does not inherently degrade predictive accuracy. Instead, it introduces instability in SHAP value attributions, where correlated features compete for credit in explaining predictions³³. To address this, an analysis was conducted by calculating the Pearson coefficient between feature variables and creating a heatmap of correlations. As shown in Fig. 3, there are high correlations between the shooting percentages of 2-point shots, 3-point shots, and free throws with their respective attempts and successful hits. Total rebounds exhibit a strong correlation with both offensive and defensive rebounds (correlation coefficient ≥ 0.7), with highly significant p-values (p < 0.01). Hence, an exploratory analysis was conducted, and related scatter plots were created.

Fig. 3.

Heatmap of technical statistical data in CBA Games. The size of the circle is proportional to the absolute value of the correlation coefficient. Red indicates a positive correlation, blue indicates a negative correlation, and the ‘ × ’ in each box signifies that the Pearson correlation coefficient is not statistically significant (P > 0.01).

Through the analysis of Scatter Fig. 4, it was found that the number of attempts for 2-point shots, 3-point shots, and free throws all have a linear positive correlation with their successful hits, and the shooting percentages increases with the number of successful hits. Additionally, there is a linear positive correlation between defensive rebounds and total rebounds, whereas offensive rebounds decrease as defensive rebounds increase.

Fig. 4.

Exploratory scatter plots of CBA technical statistic relationships.

The shooting percentage, defined as the ratio of successful shots to attempts, accurately reflects the team’s strength and status. To mitigate the instability of SHAP explanations caused by multicollinearity, seven indicators including 2P, 2PA, 3P, 3PA, FT, FTA, and TRB were removed. Given the intricate nature of the dataset, where multiple variables may interact in non-obvious ways and potentially obscure the true influence of each variable on the outcome, there is a substantial risk of compromising the model’s performance and interpretive capacity. To fortify the robustness of the predictive model subsequently developed and to augment the reliability and explanatory power of the research findings, a forward stepwise regression method was employed. This statistical technique incrementally constructs the regression model, initiating with no variables and sequentially incorporating the most statistically significant variables. The process persists until no further variables satisfy the criteria for inclusion. This method proved crucial in mitigating the risks associated with multicollinearity and in enhancing the generalizability of the model. The detailed forward stepwise regression analysis results are presented in Table 1. The following indicators were retained: 2P%, 3P%, FT%, ORB, DRB, AST, TOV, PF. These indicators showed significance in the regression analysis, with all p-values less than 0.05. Although the four-factor indicators are considered to have a significant impact on game outcomes in basketball theory, the information they might provide is already sufficiently represented in the basic data indicators. Therefore, to maintain the model’s simplicity and efficiency, these four-factor indicators were excluded.

Table 1.

Forward stepwise regression analysis results of key performance indicators.

Feature	B	Standard error	Wald	P-value
2P%	37.666479	7.013	28.849	0.000
3P%	33.396	5.285	39.927	0.000
FT%	7.307	2.225	10.781	0.001
ORB	0.391	0.080	24.022	0.000
DRB	0.160	0.075	4.513	0.034
AST	0.122	0.060	4.205	0.040
TOV	− 0.524	0.087	36.181	0.000
PF	− 0.295	0.073	16.520	0.000
const	0.181	0.278	0.424	0.515

Considering the indicator situation and forward stepwise regression results, it was decided to categorize the indicators into three groups: basic indicators, four-factor indicators, and composite indicators (basic data indicators + four-factor indicators). Specific research indicator groupings and descriptive data are detailed in Table 2.

Table 2.

List of feature data for the sample.

Groups	Variables	Mean	std	Min	25%	50%	75%	Max
Basic data indicators	2P%	0.011	0.109	− 0.435	− 0.060	0.011	0.085	0.415
	3P%	0.005	0.134	− 0.563	− 0.087	0.002	0.097	0.478
	FT%	0.005	0.143	− 0.571	− 0.093	0.005	0.102	0.584
	ORB	0.380	5.941	− 22	− 3	0	5	27
	DRB	0.725	7.704	− 24	− 5	1	6	26
	AST	1.500	7.384	− 30	− 3	2	6	30
	PF	− 0.393	5.278	− 22	− 4	0	3	19
	TOV	− 0.711	5.443	− 25	− 4	− 1	3	18
Four factors indicators	eFG%	0.024	1.203	− 21	− 0.058	0.01	0.079	21.7
	TOV%	− 0.029	0.696	− 19.1	− 0.051	− 0.01	0.032	15.2
	ORB%	0.002	1.443	− 30.5	− 0.071	0.014	0.095	34.2
	FTr%	− 0.017	1.278	− 24	− 0.064	0.009	0.086	19.7
Explained variable	Result	0.598	0.490	0	0	1	1	1

The difference in scores between the home and away teams was calculated, with the home team’s values subtracted from those of the away team. Std standard deviation, Min minimum, 25% lower quartile, 50% median, 75% upper quartile, Max maximum.

Model development and explainability

This study collected game data from the CBA spanning the 2013–2014 to 2022–2023 seasons and conducted data preprocessing and feature extraction on the raw data. The dataset was divided into training and test sets in an 80–20% ratio. We constructed seven mainstream machine learning models: XGBoost, LightGBM, Decision Tree, Random Forest, SVM, Logistic Regression, and KNN. Optimal hyperparameters for each model were determined using three hyperparameter optimization methods—the genetic algorithm, Bayesian optimization, and grid search. To ensure the selected models achieved optimal performance, we evaluated the optimal hyperparameters of each algorithm using ten-fold cross-validation. Furthermore, to enhance the reliability and reproducibility of our results, the dataset was partitioned 10 times using distinct random seeds, facilitating the computation of mean values and standard deviations that were ultimately assessed on the test set. These optimized models were then compared against other prevalent predictive models to discern the most efficacious one. Finally, we employed the SHAP method to explain and analyze the predictive results of the top-performing model, aiming to undertake a retrospective analysis of the predictive outcomes.

Evaluation of model performance

In the context of developing machine learning models, it is crucial to rigorously assess model performance to determine both accuracy and efficacy. In this study, the selection of five complementary metrics—AUC, F1 Score, accuracy, precision, and recall—is driven by their distinct roles in addressing multi-dimensional evaluation requirements for basketball game outcome prediction models. Accuracy quantifies the proportion of all correct predictions, reflecting the model’s overall correctness. Precision measures the specificity of positive predictions (i.e., the ratio of true positives to total predicted positives), which is critical for minimizing false-positive errors. Recall evaluates the model’s ability to capture actual positive instances (i.e., the ratio of true positives to all actual positives), ensuring no true home-team victories are overlooked. F1 Score harmonizes precision and recall through their harmonic mean, providing a balanced assessment of model robustness under imbalanced scenarios. AUC (Area Under the ROC Curve) represents the probability that a randomly selected positive instance (e.g., a home team win) is ranked higher than a negative one, offering a threshold-independent evaluation of discriminative power.

These metrics collectively mitigate the limitations of relying on a single measure. For instance, while AUC evaluates performance across all classification thresholds, precision and recall provide actionable insights for specific decision contexts. The confusion matrix (Table 3) systematically categorizes prediction outcomes into True Positives (TP), False Positives (FP), True Negatives (TN), and False Negatives (FN), enabling transparent calculation of accuracy, precision, recall, and F1 Score. This multi-metric framework ensures comprehensive validation of model reliability across both statistical rigor and practical applicability.

Table 3.

Classification results confusion matrix.

Home team win-loss result	Predicted victory	Predicted loss
Actual victory	TP	FN
Actual loss	FP	TN

TP True positives, FP False positives, TN True negatives, FN False negatives.

Based on the confusion matrix, the accuracy, precision, recall, and F1 Score can be calculated as follows.

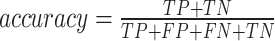11

12

13

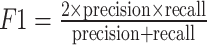14

Results

Evaluation of prediction models for CBA game outcomes

Tables 4, 5 and 6 present the performance evaluation of three sets of indicators (basic data indicators, four-factor indicators, and composite indicators) across seven machine learning algorithms. Figure 5 visualizes the performance evaluation results of the machine learning algorithm models.

Table 4.

Comparative results of CBA game outcome prediction model performance evaluation (basic data indicator model).

Machine learning algorithm	AUC	F1 score	Accuracy	Precision	Recall
XGBoost	0.983 ± 0.002	0.944 ± 0.005	0.932 ± 0.006	0.938 ± 0.005	0.949 ± 0.011
LightGBM	0.982 ± 0.002	0.936 ± 0.007	0.924 ± 0.008	0.934 ± 0.012	0.937 ± 0.009
Decision tree	0.908 ± 0.014	0.877 ± 0.013	0.850 ± 0.014	0.855 ± 0.023	0.901 ± 0.020
Random forest	0.975 ± 0.003	0.927 ± 0.006	0.913 ± 0.006	0.916 ± 0.014	0.939 ± 0.012
SVM	0.957 ± 0.010	0.907 ± 0.009	0.888 ± 0.013	0.896 ± 0.023	0.918 ± 0.007
Logistic regression	0.917 ± 0.014	0.935 ± 0.009	0.922 ± 0.011	0.926 ± 0.018	0.944 ± 0.006
KNN	0.946 ± 0.010	0.894 ± 0.011	0.872 ± 0.014	0.877 ± 0.018	0.912 ± 0.018

Data are presented as “mean ± standard deviation”. SVM Support vector machines, KNN K-Nearest Neighbors.

Table 5.

Comparative results of CBA game outcome prediction model performance evaluation (four-factor indicator model).

Machine learning algorithm	AUC	F1 score	Accuracy	Precision	Recall
XGBoost	0.984 ± 0.001	0.953 ± 0.002	0.944 ± 0.003	0.947 ± 0.005	0.958 ± 0.006
LightGBM	0.985 ± 0.002	0.952 ± 0.003	0.943 ± 0.003	0.949 ± 0.006	0.956 ± 0.006
Decision Tree	0.934 ± 0.011	0.900 ± 0.011	0.880 ± 0.013	0.894 ± 0.022	0.906 ± 0.016
Random Forest	0.983 ± 0.002	0.947 ± 0.001	0.937 ± 0.002	0.943 ± 0.004	0.952 ± 0.002
SVM	0.989 ± 0.002	0.959 ± 0.004	0.951 ± 0.005	0.950 ± 0.008	0.967 ± 0.004
Logistic Regression	0.930 ± 0.013	0.948 ± 0.011	0.937 ± 0.013	0.929 ± 0.013	0.967 ± 0.010
KNN	0.984 ± 0.003	0.947 ± 0.006	0.937 ± 0.006	0.939 ± 0.008	0.956 ± 0.004

Data are presented as “mean ± standard deviation”. SVM Support vector machines, KNN K-nearest neighbors.

Table 6.

Comparative results of CBA game outcome prediction model performance evaluation (composite indicator model).

Machine learning algorithm	AUC	F1 Score	Accuracy	Precision	Recall
XGBoost	0.988 ± 0.002	0.959 ± 0.005	0.951 ± 0.006	0.955 ± 0.003	0.962 ± 0.008
LightGBM	0.988 ± 0.001	0.953 ± 0.005	0.944 ± 0.006	0.946 ± 0.006	0.960 ± 0.005
Decision Tree	0.929 ± 0.008	0.894 ± 0.010	0.875 ± 0.009	0.894 ± 0.011	0.895 ± 0.025
Random Forest	0.982 ± 0.002	0.938 ± 0.006	0.926 ± 0.006	0.932 ± 0.009	0.943 ± 0.011
SVM	0.960 ± 0.009	0.909 ± 0.008	0.891 ± 0.012	0.900 ± 0.022	0.918 ± 0.009
Logistic Regression	0.926 ± 0.011	0.942 ± 0.005	0.930 ± 0.008	0.935 ± 0.015	0.949 ± 0.008
KNN	0.946 ± 0.011	0.894 ± 0.012	0.873 ± 0.015	0.878 ± 0.018	0.911 ± 0.018

Data are presented as “mean ± standard deviation”. SVM Support vector machines, KNN K-nearest neighbors.

Fig. 5.

Comparative chart of performance evaluation metrics for CBA game outcome prediction models. (a) Basic data indicators, (b) four-factor indicators, (c) composite indicators. SVM Support vector machines, KNN K-nearest neighbors.

The comparative experiment based on basic data indicators (Fig. 5a, Table 4) revealed that the XGBoost algorithm demonstrated superior performance across all key metrics, with an AUC of 0.983 ± 0.002, F1 Score of 0.944 ± 0.005, Accuracy of 0.932 ± 0.006, Precision of 0.938 ± 0.005, and Recall of 0.949 ± 0.011.

The comparative experiment using four-factor indicators (Fig. 5b, Table 5) demonstrated that the SVM, XGBoost, and LightGBM algorithms exhibited superior overall performance. Notably, the SVM algorithm ranked highest across five key metrics: AUC, F1 Score, accuracy, precision, and recall.

The comparative experiment based on composite indicators (basic data indicators + four-factor indicators) (Fig. 5c, Table 6) revealed that the XGBoost and LightGBM models delivered robust predictive performance. Notably, the XGBoost algorithm demonstrated the most exceptional performance across all five evaluated dimensions.

In the comparative experiments involving different sets of indicators (basic data indicators, four-factor indicators, and composite indicators), the XGBoost algorithm’s overall performance in predicting CBA game outcomes surpassed that of other mainstream machine learning algorithms. Our experimental results showed that XGBoost not only achieved higher performance across five key metrics—AUC, F1 score, accuracy, precision, and recall—but also maintained lower variability across multiple validations, demonstrating its robustness. This superior performance underscores XGBoost’s capacity to capture the complex nonlinear dynamics between technical indicators and basketball game outcomes.

Alternative algorithms exhibit distinct strengths and limitations that warrant discussion. Decision trees offer human-readable rules with low computational complexity, while logistic regression provides intuitive coefficient interpretations. However, their show limitations in overall performance, as evidenced by their lower AUC values. Machine learning algorithms represented by SVM exhibit higher computational complexity and are sensitive to the choice of kernel functions and parameters. However, they hold advantages in handling small samples, non-linearities, and high-dimensional data recognition challenges. Ensemble learning algorithms, exemplified by XGBoost, despite their higher computational demands, demonstrate exceptional performance in terms of prediction accuracy and robustness when dealing with large-scale datasets, thanks to parallelization and optimization techniques. For instance, XGBoost employs parallel computing and sophisticated algorithmic design to efficiently manage large datasets, thereby excelling in training speed and memory usage. Therefore, the selection of an algorithm should be based on a balance among performance, computational resources, and explainability requirements.

These results justify XGBoost’s selection for subsequent explainability analysis, as detailed in the following sections.

Comparative analysis of explainability

In this section, we conducted a tripartite explainability analysis across 10 CBA seasons (2014–2023) using SHAP values, logistic regression coefficients, and decision tree rules, examining three distinct indicator groups: basic data indicators, four-factor metrics, and composite indicators.

The SHAP feature summary chart allows for an intuitive understanding of the contribution of different features to the outcomes and how variations in feature values influence the final results. Each row represents a feature, with features arranged on the y-axis according to their importance—the higher the placement, the more significant the feature. The x-axis represents the SHAP values, with each data point corresponding to a sample. A shift towards red indicates higher feature values for a sample, while a shift towards blue indicates lower feature values.

Figure 6 displays the SHAP feature summary charts for the basic data indicators, four-factor indicators, and composite indicators for the seasons from 2014 to 2023. In Fig. 6a (basic data indicators), 2P%, 3P%, TOV, and DRB are positioned at the top of the y-axis, indicating they are the top four critical variables affecting CBA game outcomes. Higher values of 2P% and 3P% (represented by red points) correspond to positive SHAP values, suggesting that increased shooting percentages enhance the probability of winning. Conversely, lower 2P% and 3P% values (blue points) are associated with negative SHAP values, indicating a decreased likelihood of victory. Additionally, higher values of TOV are associated with negative SHAP values, indicating that more turnovers reduce the likelihood of victory. DRB shows positive SHAP values with higher feature values, underscoring the importance of securing defensive rebounds for game success.

Fig. 6.

Summary charts of SHAP feature importance. (a) Basic data indicators, (b) four-factor indicators, (c) composite indicators.

In Fig. 6b (four-factor indicators), the significant variables’ importance for affecting game outcomes is ranked as follows: eFG%, ORB%, TOV%, FTr%. In Fig. 6c (composite indicators), eFG%, ORB%, TOV%, TOV, FTr%, and ORB are identified as the top six significant variables influencing CBA game outcomes. Notably, among all the significant indicators, only TOV, PF, and TOV% exhibit high feature values leading to a negative impact on winning probability, as indicated by their negative SHAP values. This implies that increasing numbers of turnovers and personal fouls diminish the chances of winning. In contrast, higher feature values for other indicators generally contribute positively to the likelihood of victory, emphasizing the importance of excelling in these areas.

Figure 7 displays the logistic regression feature importance summary charts for the basic data indicators, four-factor indicators, and composite indicators for the seasons from 2014 to 2023. For basic indicators (Fig. 7a), logistic regression identified TOV (coefficient = − 0.557, OR = 0.57) as the strongest negative predictor, with each unit increase reducing win probability by 42.7%. However, its linear framework disproportionately emphasized turnover reduction while underestimating the impact of 2P% (coefficient = 0.325) and 3P% (coefficient = 0.255)—variables SHAP analysis revealed as top contributors to victory (SHAP = 2.126 and 2.084 respectively). This discrepancy contradicts established basketball analytics principles, where shooting efficiency typically dominates tactical priorities. In four-factor indicators, logistic regression prioritized eFG% (coefficient = 0.498) as the primary positive factor, aligning partially with SHAP rankings. However, it failed to quantify the nonlinear relationship between ORB% and defensive strategies; SHAP values demonstrated ORB%’s context-dependent effects on playoff outcomes, a pattern invisible to linear approximations.

Fig. 7.

Summary charts of logistic regression feature importance. (a) Basic data indicators, (b) four-factor indicators, (c) composite indicators.

Figure 8 displays the decision tree feature importance summary charts for the basic data indicators, four-factor indicators, and composite indicators for the seasons from 2014 to 2023. In composite indicators (Fig. 8c), DTs prioritized eFG% splits (importance = 0.659), generating rules like “eFG% ≤ -0.75 → Loss” that oversimplify multi-feature dynamics (see Supplementary Fig. S1 online). Crucially, DTs ignored FT% (importance = 0) despite SHAP identifying it as moderately influential. For basic indicators (Fig. 8a), DTs hyper-focused on DRB (importance = 0.647) and TOV (importance = 0.243), completely neglecting 2P% (importance = 0 vs. SHAP = 2.126)—a discrepancy stemming from their greedy local optimization.

Fig. 8.

Summary charts of decision tree feature importance. (a) Basic data indicators, (b) four-factor indicators, (c) composite indicators.

Given our research aim to provide decision support for coaches and athletes, utilizing the XGBoost model in conjunction with SHAP analysis is both reasonable and advantageous. This combination not only enhances predictive accuracy but also offers detailed explainability by quantifying each feature’s contribution to the prediction outcomes. Such fine-grained insights are invaluable for strategic decision-making in professional basketball, enabling coaches to optimize tactics based on the quantified impact of specific performance indicators. Therefore, selecting the XGBoost algorithm model for SHAP analysis to explore the KPIs of CBA games is justified and aligns with the objectives of our study.

Annual and stage-specific SHAP analysis for CBA game prediction models

In this study, not only did we construct models for basic data indicators, four-factor indicators, and composite indicators for the seasons from 2014 to 2023 using the XGBoost algorithm, but we also conducted explainability analyses using SHAP. Furthermore, data from ten seasons were grouped by season into ten sets. To ensure the validity of the study results, the XGBoost algorithm was employed to model each dataset under consistent conditions, followed by explainability analysis using SHAP. Finally, the SHAP values of each indicator for every season were converted into percentages to facilitate a more intuitive comparison of their impacts. Considering the issue of multicollinearity among composite indicators, to avoid variable redundancy and explanatory bias in model analysis, we opted to conduct further in-depth exploratory analysis on only the basic and four-factor indicators.

Figure 9 illustrates the changing trends in the importance of basic data indicators (left side) and four-factor indicators (right side) from the 2014 to 2023 seasons. As shown in Fig. 9a, 2P% and 3P% maintained high importance throughout the 2014 to 2023 seasons, while the overall importance of PF was lower. AST, TOV, and DRB experienced some fluctuations over these seasons but remained highly important across all seasons. Figure 9b reveals that eFG% held an absolute advantage over the other three indicators, followed by ORB% or TOV%, with neither having an absolute edge, and FTr% having the lowest SHAP value weight. Overall, eFG% showed an upward trend from the 2014 to 2023 seasons, while TOV% exhibited a general downward trend.

Fig. 9.

Stacked bar chart of SHAP values for performance indicators over ten seasons in the CBA (2014–2023). (a) Basic data indicators, (b) four-factor indicators.

The importance of basic data indicators (left side) and four-factor indicators (right side) varied during different stages of the games. From Fig. 10, it can be observed that the SHAP value weights of 2P%, 3P%, PF, TOV, and ORB were higher in the playoffs compared to the regular season, while FT%, DRB, and AST had lower SHAP value weights in the playoffs. The SHAP value weights of eFG% and ORB% in the playoffs were higher than those in the regular season, whereas TOV% and FTr% experienced varying degrees of reduction in the playoffs compared to the regular season.

Fig. 10.

Stacked Bar Chart of SHAP values for performance indicators in regular season and playoffs in the CBA (2014–2023). (a) Basic data indicators, (b) four-factor indicators.

Discussion

This study pioneers the integration of the ensemble learning algorithm XGBoost with SHAP, applied to the CBA league to quantify the dynamic impacts of technical indicators across ten CBA seasons (2014–2023). Our multi-model framework identifies four-factor metrics—particularly eFG%, TOV%, and ORB%—as superior predictors of game outcomes compared to basic statistics. The analytical supremacy of composite metrics stems from their mathematical integration of fundamental indicators; eFG%, for instance, synthesizes 2P% and 3P% through weighted spatial efficiency, providing a comprehensive and effective evaluation of accuracy. Crucially, we observed an offensive-over-defensive strategy phenomenon in CBA playoffs, which contrasts fundamentally with NBA postseason patterns. These findings establish a data-driven paradigm for optimizing CBA tactical frameworks.

Comparative analysis of the three indicator groups reveals key algorithm performance patterns across different feature dimensions (Fig. 5). Ensemble learning algorithms, such as XGBoost and LightGBM, demonstrate the strongest robustness in composite models, with metrics like AUC and accuracy showing varying degrees of improvement as feature complexity increases. This superiority stems from their ability to integrate diverse weak learners through parallelized gradient boosting, while regularizing the objective function to alleviate overfitting^34,35. Conversely, machine learning algorithms represented by SVM and logistic regression exhibit poorer performance in models using composite indicators (basic data indicators + four-factor indicators) compared to models using only four-factor indicators. This decline in performance (SVM’s AUC value is 0.960 compared to 0.989 for the four-factor model; logistic regression’s AUC value is 0.926 compared to 0.930 for the four-factor model) may be attributed to these algorithms’ sensitivity to multicollinearity among independent variables, confirming the inherent limitations of linear models in handling high-dimensional interactive features³⁶. Therefore, the performance of machine learning predictive models does not simply improve with the increase in feature dimensions; consideration must also be given to variable characteristics, computational resources, and the algorithmic framework, necessitating the selection of appropriate analysis indicators within limited computational resources.

The results of this study indicate that models utilizing four-factor indicators exhibit superior predictive performance compared to those using only basic data indicators (Fig. 5). This advantage arises from their mathematical integration and tactical explainability: for example, eFG% incorporates shooting distribution information through weighted spatial efficiency (2P% × 1 + 3P% × 1.5), overcoming the traditional shooting percentage’s underestimation of three-point strategies³⁷. Consistent with Wang and Fan’s conclusions on the NBA, this study demonstrates the significant advantages of high-level indicators, such as the four-factor indicators, in machine learning models³⁸. High-level indicators integrate information from lower-level metrics, providing richer and more interpretable data features^37,39. Specifically, the four-factor indicators comprehensively cover statistical information for each possession outcome, enabling a thorough understanding of team performance across various dimensions⁴⁰. This comprehensive analysis is supported by recent studies, which emphasize the predictive power and explainability of aggregated metrics in sports analytics^11,41. Therefore, it is recommended that coaches prioritize the use of advanced data indicators, such as the four-factor indicators, for dynamic team assessments and opponent analyses during training and competitions. By leveraging these insights, coaches can develop more targeted and effective tactical strategies, enhancing overall team performance. This approach not only aids in identifying strengths and weaknesses but also facilitates the adaptation of strategies to exploit opponents’ vulnerabilities.

Our machine learning analysis provides strong empirical validation for the central role of eFG% in determining CBA game outcomes. As a composite metric encapsulating spatial scoring efficiency, eFG% consistently achieves SHAP importance scores that significantly surpass those of other indicators across different seasonal contexts. This finding aligns with Oliver’s "Four Factors Theory," which identifies shooting efficiency as a primary determinant of basketball success³⁷. Despite the CBA league’s tactical evolution towards perimeter-oriented offenses, reflected in the increase of three-point attempt rates from 32.3% in 2014 to 38.8% in 2023, eFG%'s predictive advantage remains robust. This metric’s resilience is due to its ability to harmonize competing strategic priorities—while 3P% and 2P% maintain independent significance in basic models (SHAP values of 2.08 and 2.13, respectively), their collective explanatory power is integrated within eFG%'s comprehensive framework. Notably, championship teams consistently achieve eFG% values at least 2.1 percentage points above the league average (2022–2023: 51.4% vs. 49.3%), establishing this metric as a critical benchmark for roster construction and in-game adjustments. This trend is consistent with the findings of Li et al. (2019), who noted that despite the increase in three-point attempt rates, the importance of shooting efficiency metrics remains significant. Through an analysis of team performance across multiple seasons, Li et al. found that eFG% consistently serves as a core element in determining game outcomes⁴².

During the playoffs, the importance of 2P% significantly increases, as evidenced by a 70.9% rise in SHAP weight (from 0.103 in the regular season to 0.176 in the playoffs). This phenomenon highlights a strategic paradox: despite the league-wide increase in three-point attempt rate (3PAr) from 32.3% in 2014 to 38.8% in 2023, playoff success is increasingly reliant on two-point efficiency. This contrasts sharply with NBA playoff patterns, where the importance of 3P% remains stable^43,44, indicating that the CBA is developing along a unique evolutionary trajectory shaped by tactical adjustments. Empirical data suggests that the 4–10 foot zone is a critical scoring area, with playoff FG% differentials significantly surpassing regular season performance, as reflected in a 5.4 percentage point increase in SHAP weight. The studies by Mikołajec and García emphasize the importance of spatial efficiency and shot selection in optimizing team performance, further reinforcing the need for a nuanced understanding of scoring zones^44,45. Player evaluation systems should prioritize athletes who demonstrate sustained efficiency in these key areas. As exemplified by championship teams consistently achieving restricted area FG% values 2.1 percentage points above league averages (51.4% vs. 49.3%), the significance of spatial efficiency is further underscored. These findings advocate for a shift from fixed shot quota systems to dynamic spatial optimization strategies, particularly during critical playoff moments. This transition is not only a response to data but also a profound insight into the unique tactical evolution of the CBA.

The evolving role of DRB is reflected through distinct temporal patterns, with SHAP weight transitioning from sustained stability (2016–2018: 0.170 ± 0.021) to a gradual decline, decreasing by 14.7% between 2019 and 2021, before reaching historical minima in the 2022–2023 seasons (0.119–0.153). This trend inversely correlates with the league’s strategic focus on transition offense, as evidenced by the decline in DRB’s playoff predictive weight (14.7% vs. regular season 24.1%) and contrasting NBA postseason trends⁶. This shift reflects a broader tactical evolution, where teams prioritize transition speed and ball control efficiency over traditional rebounding metrics, as emphasized by studies analyzing game-winning strategies⁶. Moreover, adapting to hybrid defensive schemes that balance rebounding discipline and transition adaptability is crucial, aligning with research findings that underscore the importance of flexible tactical responses in high-stakes games⁴⁵. Strategic implications advocate for preseason prioritization of box-out fundamentals against teams with strong offensive rebounding, while promoting hybrid defensive schemes during playoff contention that balance rebounding discipline and transition adaptability. These findings necessitate context-driven recalibration of traditional rebounding paradigms within CBA coaching frameworks.

Turnover metrics exhibit significant yet differentiated predictive value, depending on the analytical framework employed. In basic indicator models, total TOV emerge as the third most influential feature (SHAP value of 1.835), following 2P% and 3P%. Conversely, in four-factor analyses, TOV% ranks third (SHAP value of 0.901), indicating its ongoing relevance in possession-adjusted evaluations. This dual importance highlights turnovers’ critical role in determining game outcomes, though their operational definitions require distinct strategic interpretations^46,47. The composite model further reinforces TOV%'s analytical robustness, maintaining moderate predictive power (SHAP value of 0.675), while the influence of TOV significantly declines (SHAP value of 0.389). This difference suggests that standardized turnover metrics better capture team-specific efficiency patterns across varying game contexts³⁷. Recent studies emphasize the importance of turnover management as a key determinant of team success, highlighting its impact on maintaining offensive fluidity and defensive stability^48,49. Notably, TOV% exhibits heightened sensitivity during playoffs, with SHAP weight increasing from 14.7% in the regular season to 17.8% in the postseason (a 21.1% increase), contrasting with TOV’s phase-stable profile. This aligns with findings that emphasize ball security in high-pressure environments⁵⁰. Strategic adaptations should focus on possession security during critical game phases, particularly against opponents prone to chronic turnover issues. Coaching protocols should be differentiated based on competitive tiers—teams struggling with ball retention require fundamental error reduction training, while elite teams should optimize risk-calibrated playmaking. These insights advocate for roster compositions that balance creative ball-handlers with low-error specialists during high-stakes rotations.

It is noteworthy that in CBA playoffs, offensive variables (such as 2P%, 3P%, and eFG%) tend to show an increasing trend in importance, indicating that offense has a greater impact on winning during the playoff stage than defense. This stands in stark contrast to the NBA’s philosophy that "defense wins championships"⁵¹. The prevalence of offense over defense in the CBA is closely linked to coaching philosophies and the imbalance in player strengths. In terms of team-building philosophy, Wang’s study indicates that CBA teams are more inclined to prioritize players with strong offensive capabilities over those with balanced defensive skills⁵². This selection strategy might lead to impressive offensive performance but also noticeable defensive shortcomings. Compared to strong international teams, the Chinese men’s basketball team lacks defensive capabilities, making it easier for opponents to penetrate their defense. As the CBA is a cradle for nurturing national team players, future team-building efforts should focus more on achieving a balance between offense and defense to enhance overall competitiveness. The stable performance of foreign players on the offensive end plays a decisive role in determining game outcomes; thus, offensive capabilities can dictate the results of CBA playoff games. However, improving defensive skills is equally crucial to ensure the team remains competitive on both ends of the court.

Limitations of the study and recommendation for future research

Despite the valuable insights provided by this study, several limitations should be acknowledged that point towards avenues for future research. Firstly, our analysis focused primarily on cumulative game data and did not incorporate temporal dynamics during the game. This limits the understanding of in-game decision-making processes. Future studies should consider integrating time-series data to better capture the dynamic changes in KPIs throughout the game, thereby enriching the context of decision-making. Secondly, situational factors such as player injuries, team formations, and overall team strength were not included in our models. The exclusion of these variables might affect the robustness of the model by overlooking critical influences on game dynamics. Additionally, while we conducted a comprehensive analysis of key performance indicators in CBA matches, we did not delve deep into team strength differences and player position variations. Future research that addresses these context variables, possibly through data augmentation or simulation methods, and further investigates these factors, could enhance the precision and robustness of the findings. Lastly, we acknowledge that SHAP can only explain the degree of correlation between each feature and the model’s predictions but cannot be used for causal inference, i.e., identifying the true causes of specific events. Future studies should use causal inference methods to validate these findings. Therefore, it is recommended that future studies further explore these aspects, potentially leading to more nuanced and actionable insights.

Conclusions

This paper applies machine learning algorithms to the prediction of CBA game outcomes and the analysis of key performance indicators, thereby enriching the perspectives and methods for analyzing these crucial performance indicators in the CBA. This approach enhancnes explainability associated with traditional machine learning methods in this research field, providing a scientific basis for coaches’ in-game decisions and daily training. Firstly, a comparative experiment based on seven machine learning algorithms found that the XGBoost algorithm performed best in predicting CBA game outcomes. Secondly, SHAP analysis of the prediction model revealed that eFG%, 3P%, 2P%, ORB%, DRB, and TOV% are KPIs affecting CBA game outcomes. Due to their accuracy and comprehensiveness, high-level data indicators can better reflect a team’s strength and condition. Moreover, an observed trend in the CBA playoffs indicates a preference for offensive gameplay over defensive strategies, with the importance of offensive metrics such as 2P%, 3P%, and eFG% increasing. This method provides a new perspective and approach for the analysis of performance in basketball games. Utilizing this method, factors influencing outcomes in various competitive sports can be explored, building a comprehensive and scientific model for sports performance analysis.

Practical application

This study is the first to apply the SHAP method to predict the outcomes of CBA games, providing a comprehensive and explainable analytical framework. This not only expands the methodological approach to basketball game analysis theoretically but also offers a scientific basis for coaching decisions and team training in practice. The study proposes three main practical applications. Firstly, by identifying key performance indicators, team coaches can develop more targeted tactics and select players who excel in crucial technical indicators, thereby enhancing the overall strength of CBA teams. Secondly, given their accuracy and comprehensiveness, high-level data indicators, compared to lower-level indicators, can more accurately reflect a team’s strength and condition. Hence, coaches should prioritize the use of advanced data indicators for post-game summaries and opponent evaluations. Lastly, considering the observed trend of prioritizing offense over defense in CBA playoffs, teams can strengthen their offensive strategies during the playoff phase while still maintaining solid defense.

Ethics declarations

The study does not involve human or animal subjects and does not include any personal or sensitive information. Therefore, approval from an Institutional Review Board (IRB) or ethics committee was not required.

Author contributions

Conceptualisation: YOY, WH and LMP; methodology: YOY, WH, LMP and XWL; software: YOY and WH; validation: YOY, CXM, WJZ, QW, FQ, SHC, CX and YFW; formal analysis: YOY, WH and LMP; investigation: YOY, CXM, WJZ, QW, FQ, SHC, CX and YFW; resources: LMP and XWL; data curation: YOY, WH and CXM; writing—original draft preparation: YOY; writing—review and editing: YOY, WH, LMP and XWL; visualization: YOY and WJZ; supervision: LMP, WTZ and XWL; project administration: XWL; funding acquisition: XWL and LMP. These authors contributed equally and should be considered co-first authors: YOY, WH and LMP. All authors reviewed the manuscript.

Funding

This research was funded by the 14th Five-Year-Plan Advantageous and Characteristic Disciplines (Groups) of Colleges and Universities in Hubei Province (Grant Number: E Jiao Yan No. [2021] 5), Wuhan Sports University Youth Scientific Research Fund Project "Research on Personalized Learning Path Generation Model for Sports Education Data Resources Based on Association Rule Mining" (Grant Number: 2022S15), Hubei Provincial Social Science Fund General Project “Research on Personalized Recommendation of Online Sports Education Resources Based on Knowledge Graph” (Grant Number: 2021330), and the Scientific and Technological Research Project of Hubei Provincial Education Department (Grant Number: B2021189).

Data availability

Data are available in a public, open access repository and can be freely downloaded from China Basketball Association (https://www.cbaleague.com/). Additionally, the datasets generated during the current study are available from the corresponding author upon reasonable request.

Competing interests

The authors declare no competing interests.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-025-97817-3.