Mining genetic epidemiology data with Bayesian networks I: Bayesian networks and example application (plasma apoE levels)

Abstract

Motivation

The wealth of single nucleotide polymorphism (SNP) data within candidate genes and anticipated across the genome poses enormous analytical problems for studies of genotype-to-phenotype relationships, and modern data mining methods may be particularly well suited to meet the swelling challenges. In this paper, we introduce the method of Belief (Bayesian) networks to the domain of genotype-to-phenotype analyses and provide an example application.

Results

A Belief network is a graphical model of a probabilistic nature that represents a joint multivariate probability distribution and reflects conditional independences between variables. Given the data, optimal network topology can be estimated with the assistance of heuristic search algorithms and scoring criteria. Statistical significance of edge strengths can be evaluated using Bayesian methods and bootstrapping. As an example application, the method of Belief networks was applied to 20 SNPs in the apolipoprotein (apo) E gene and plasma apoE levels in a sample of 702 individuals from Jackson, MS. Plasma apoE level was the primary target variable. These analyses indicate that the edge between SNP 4075, coding for the well-known ɛ2 allele, and plasma apoE level was strong. Belief networks can effectively describe complex uncertain processes and can both learn from data and incorporate prior knowledge.

INTRODUCTION

A fundamental problem in contemporary human genetics is that of ‘imperfect’ genotype-to-phenotype relationship. Owing to recent progress in identification and mapping of transcribed genes, as well as genome-wide mapping for multifactorial traits, a bewildering variety of potential predictive factors can be amassed for any phenotype of interest. As the number of discovered genes contributing to a phenotype and the amount and resolution of sequence variation in those genes increases (Nickerson et al., 2000), so does the complexity and dimensionality of models describing genotype-to-phenotype relationships.

Such a model can be represented visually as a graph consisting of nodes (genes, mutations, haplotypes, environmental factors, metabolite concentration, phenotypes, etc.) and directed edges (or arrows) that link mutually dependent nodes. Dependent nodes are designated as ‘parents’ and ‘children’, often somewhat arbitrarily. Absence of an edge between two nodes indicates their conditional independence. The nodes correspond to random variables such as certain polymorphisms being in one or the other genotype state (or a certain gene being in one or the other allelic state) or the level of a quantitative risk factor. Each edge is accompanied by a Conditional Probability Function or a Conditional Probability Table (CPT, for discrete variables) that defines a conditional distribution for the dependent variable given its parents.

One type of model describing the relationship among nodes is a Bayesian or Belief network (Pearl, 1988). To be more formal, a Belief network (BN) for a set of random variables X = {X₁, . . . , X_n} consists of its structure, or topology T that describes conditional independence assertions about the variables in X and a second component, Θ, describing local probability distributions for each variable (conditional distributions given the variable’s respective parents in T ). The topology is a directed acyclic graph (DAG), and together these two components define a joint probability distribution for X. A detailed treatment of BNs can be found in the overview by Heckerman (1995), but some of the more important technical aspects will be briefly discussed below.

BNs have a number of advantages over alternative representations and data analysis techniques. First, by their very nature BNs allow one to model and study dependencies and, potentially, causal relationships, which is crucial if one is interested in gaining an understanding of underlying mechanisms. Second, the structure of the BN can be easily understood, interpreted and improved upon by human experts. Third, as the result of the second, BNs together with Bayesian statistical analysis techniques can be used to integrate expert knowledge and data. Fourth, strategies for unknown factor (i.e. hidden node) searches are being developed. Fifth, BNs suffer to a much lesser extent from the ubiquitous problem of ‘overfitting’ when proper model scoring criteria are employed. Bayesian methods involved in BN learning generally do not require a separate testing dataset—all available data can be used for training (learning). Finally, BNs can be augmented by traditional statistical validation methods such as cross-validation (CV) or bootstrapping.

Genotype-to-phenotype modeling for complex metabolic and physiological traits is particularly suitable for BN treatment. Edges in the BN models correspond to biological processes and interactions that are readily interpreted and whose relative strengths can be estimated. The variable-to-observation ratio is relatively low, which makes the physiological and genetic networks much easier to model than, for example, gene expression networks (Friedman et al., 2000; Hartemink et al., 2001; Ong et al., 2002). Finally, physiological and genetic networks are, in general, locally structured (or sparse) systems. This means that each node typically interacts directly with only a limited number of other nodes. Structure sparseness bodes well for linear rather than exponential growth in complexity during model selection. Consider a network without the local structure (all nodes are connected) of N discrete variables, S states each. The amount of information required to completely specify all CPTs in such a network is S^N numbers. If, for example, S = 3 and N = 20 (not unreasonable for a small biological network, such as the one detailed later) we would require 3 486 784 401 numbers to specify the CPTs for a network. However, if we assume a local structure (i.e. each node is directly influenced by not more than K other nodes), we would need (at most) S^K numbers for each node and not more than NS^K numbers for the whole network (e.g. only 4860 numbers for K = 5). Also, the local structure allows us to split the complete network into subnetworks of interest, such as subnetworks containing a certain gene or phenotype.

The purpose of this communication is to introduce the BN methodology in the context of phenotype–genotype association studies, specifically apolipoprotein E (apoE), and to show its effectiveness, as a component of general data mining/ knowledge discovery approach in the genetic epidemiology research.

MATERIALS AND METHODS

Belief networks

To the best of our knowledge, this study is the first attempt to use BNs in the context of modeling complex genotype-to-phenotype relationships and, therefore, brief introduction is in order. A detailed treatment can be found in a previous study (Heckerman, 1995).

Learning a BN from data implies learning both its structure, or topology (formally known as an equivalence class), and the conditional probability distributions. (Please see Supplementary Material for the more detailed treatment of BN learning issues, including conditional independence and Markov blankets, equivalence classes, dependency versus causation, structure priors and heuristic search.) For a fixed topology, learning the conditional probability distributions is straightforward (Heckerman, 1995 and references therein). For example, we can treat each node as a discrete variable and learn a multinomial distribution that defines the probabilities of a child’s states given its parents’ states. The obvious disadvantage is that discretization means information loss. However, considering the kinds of variables most likely to be encountered in our problem domain, discretization and the multinomial model might be a better fit than, for example, a linear Gaussian model. In fact, the multinomial model can capture non-linear relationships and is robust to most distributional assumptions.

When learning the network topology, we aim to find a BN that best fits the training set D = {X¹, . . . , X^m} of independent instances of X. An effective approach to learning the network structure would be to apply some objective scoring criterion to various equivalence classes with respect to their fit to the training data and pick the optimal equivalence class. One such criterion, Bayesian in nature, is the posterior probability of an equivalence class given the data (logarithms are used here for computational convenience),

$$\text{log\hspace{0.28em}}P(T|D)=\text{log\hspace{0.28em}}P(D|T)+\text{log\hspace{0.28em}}P(T)+\text{Const}.$$

$$\text{log\hspace{0.28em}}P(D|T)=\int P(D|T,\mathrm{\Theta })P(\mathrm{\Theta }|T)\mathrm{\hspace{0.17em} }\text{d}\mathrm{\Theta }.$$

The first component, log P (D|T ), is also known as the log marginal likelihood. LogP (T ) is a network structure (topology) prior. Under a number of reasonable assumptions both the components can be computed efficiently. For example, in the case of multinomial distributions, parameter independence and fully observable data, parameter priors P (Θ|T ) are Dirichlet-distributed (Geiger and Heckerman, 1994) and the marginal likelihood is easily decomposed into a product of gamma distributions (Cooper and Herskovits, 1992). An important advantage of the posterior probability criterion is that it avoids overfitting implicitly (owing to the ‘smoothing’ by the parameter prior).

Once the BN is studied, the next fundamental question is to how much trust can be put in it or its subnetworks. Unfortunately, this essentially statistical problem has received limited treatment in the field of BN research. One way to test the quality of a particular network is to compute its posterior probability (Heckerman, 1995). We can compute posterior probability for two structures that differ only in absence or presence of one edge, and thus estimate the relative support for this edge. A second way to statistically evaluate BNs is bootstrapping (Efron and Tibshirani, 1993). Bootstrapping is a popular way of estimating statistical significance of edges in other graphical modeling domains (Zharkikh and Li, 1995). In non-parametric bootstrapping, the ‘re-shuffled’ dataset is generated from the original dataset (re-sampling with replacement), the graph is built from this re-shuffled set and then the procedure is repeated a sufficient number of times (usually several hundreds or thousands). Confidence in a particular edge (or feature in general) is measured as a percentage of the number of times when that edge (feature) actually appears in the set of reconstructed graphs.

It is important to emphasize that BNs are primarily an exploratory tool. The goal of BNs is not to prove the correlation between two variables but rather to single out the variables (out of great many) that are likely to be correlated (or causally linked) given the data. In the biological context, BNs should be used to understand the network of dependencies among the factors (variables) involved, to pinpoint the strongest dependencies and clear independencies and to isolate Markov neighborhoods around the variables of interest. Thus, BNs effectively perform the feature selection for the subsequent analysis. Once the feature set is cleared of irrelevant variables and the most interesting dependencies are ascertained, traditional statistical methods (e.g. linear or logistic regression, etc.) can be used to rigorously scrutinize the resulting smaller subnetworks.

Example application (plasma apoE levels)

APOE has become a de facto paradigm for SNP analysis (Martin et al., 2000) and is, therefore, well-suited for an example application of BN modeling in human genetics. In the application presented here, we relate a high density of SNPs in APOE with plasma apoE levels. In general, any kind of polymorphism can be used as a random variable (node) in BN modeling, as BN representation does not ‘discriminate’ between target and predictor variables and the variables belonging to the different generalization levels (e.g. SNPs within a gene, haplotypes, genes, protein products, etc.). However, in this study we were primarily interested in the Markov neighborhood, or ‘blanket’, of the apoE node. The data were first described by Nickerson et al. (2000). Plasma levels of apoE, apoA, apoB, Triglycerides, Cholesterol and HDL were ascertained, as well as gender, age, weight and height. For SNP discovery, the APOE gene was resequenced in a core sample including 24 individuals from Jackson, MS. Twenty variable sites were then typed in a larger sample of 702 individuals from the same population. Four of the twenty sites are located in the coding region of the gene, and two of them (positions 3937 and 4075) are responsible for the well-known E2, E3 and E4 protein isoforms.

Continuous variables (including plasma levels) were discretized into deciles (or fewer categories), and a multinomial model was assumed. Discretizing a variable (node) into fewer categories leads to more dependencies (edges) being reconstructed in its neighborhood, thus counterbalancing the potential loss of information and sensitivity owing to discretization. We are presently implementing a hybrid model, (in which ‘offsprings’ of the multinomial nodes can be linear Gaussian. In our preliminary experiments, ‘hybrid’ BNs did not show any major differences with the purely multinomial BNs in the Markov blankets of the primary nodes of interest (apoE levels), suggesting that the multinomial model with ‘rough’ discretization fits the genetic epidemiology domain well. Searching through the model space was carried out using hill-climbing with random restarts, until the network topology appeared to be stabilized. On an average, ~20 million network topologies were evaluated in each experiment (up to two billion structures in some experiments, to prove convergence). Other search methods, such as simulated annealing and beam search, were tried as well, with similar results. Hill-climbing with random restarts, however, proved to be the fastest to converge. In any case, the Markov blanket of the primary node of interest (apoE level) proved to be robust with respect to the search strategy. To evaluate the network quality, 500-fold bootstrapping was used. Although there is no absolute criterion, in our experience, bootstrap values >92% can be rigorously supported, and values between 75 and 92% are suggestive. All BNs studied were generated from the data only, with no prior/expert biological knowledge of any kind. We considered plasma apoE level as the primary target variable and, therefore, we were especially interested in its Markov blanket. The BNs were constructed, analyzed and visualized using freely available open-source libraries [Intel Research Open-Source Probabilistic Networks Library (PNL), http://www.intel.com/research/mrl/pnl/ and University of Helsinki B-course, http://b-course.cs.helsinki.fi] with various source code modifications related to the model selection and heuristic search algorithms, and bootstrap and simulations framework implementations.

Simulation experiments

Although both bootstrap and posterior probability estimates give a good idea of the validity of the resulting network, we have performed a series of simple simulation experiments to see how well the BN reconstruction algorithm performs on the artificial datasets generated from the known (pre-defined) BNs (in fact, some of the choices we made with respect to fine-tuning the algorithm parameters, such as search strategy and discretization, were based on the results of these simulation experiments). We have followed the simulation schemes described by Sprites and Meek (1995) and Myllymaki et al. (2002), except that our model networks were closer to the actual (APOE) data-sets analyzed in this study. All variables were discrete and only a multinomial model was assumed, for simplicity. The model networks consisted of 25 and 50 nodes and reflected different amount of ‘sparseness’ (average number of edges connected to a node being set at 1, 3 and 5). From the model topologies, 500 and 1000 strong datasets were generated and BN reconstruction algorithm was applied to the datasets. We were interested in reconstructing the correct network topology, not estimating the parameters (CPTs) correctly. Specifically, we were interested in how many dependencies present in the model network were not recovered by the BN reconstruction algorithm. With 25 nodes, both 500 and 1000 datasets were sufficient to recover most of the dependencies (from 76 to 100%, depending on the sparseness factor). With 50 nodes, this figure varied from 47 to 92%. We are presently conducting a series of rigorous simulation experiments aimed at ascertaining the performance of the BN reconstruction algorithms within the genetic epidemiology domain. As an aside note, this type of a simulation experiment (comparing network topologies and computing topological differences) is very similar, conceptually, to a typical simulation study in phylogenetic analysis (see Piontkivska, 2004 and references therein), and we believe that much of the enormous experience accumulated within the latter domain can be profitably applied to design and carry out BN efficiency simulations. We have also carried out a series of simulation experiments aimed at ascertaining how well different model scoring criteria address the overfitting issue (see the Supplementary Material). The Bayesian (marginal-likelihood-based) criteria appear to be the most effective one.

RESULTS

The BN studied from the dataset is shown in Figure 1. The relative strengths of the edges of the network are shown in Table 1. Table 2 contains the bootstrap values for the apoE Markov blanket. Edges between SNPs can be interpreted as frequency dependencies (i.e. linkage disequilibrium). Only SNPs 4036 and 4075 belong to the apoE level node’s Markov blanket. (Note: in this paper BN node labels appear in boldface for clarity.) Boerwinkle and Utermann (1988) first described the effect of the ɛ2 allele (coded for by SNP 4075) on plasma apoE levels. The BN analysis also showed a relationship between plasma apoE level and Triglycerides. The mechanism of this association can either be at the level of the structure and metabolism of the lipoprotein particles themselves (Dergunov and Rosseneu, 1994), or at the level of post-prandial triglyceride metabolism, which is known to be influenced by APOE genetic variation (Boerwinkle et al., 1994).

Fig. 1.

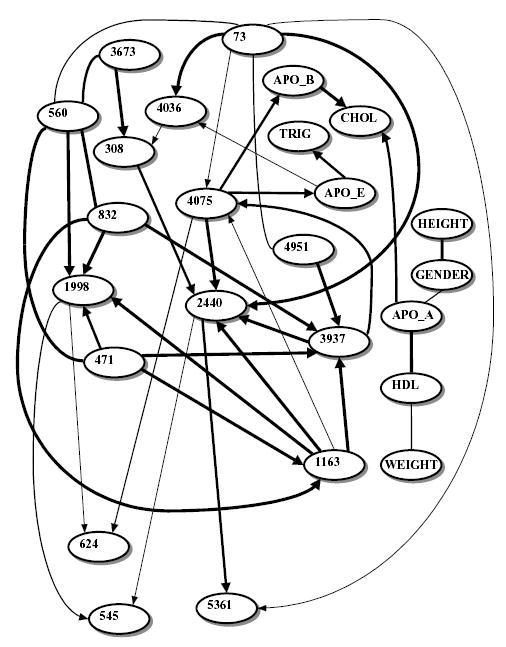
Learned BN relating apolipoprotein E gene SNPs to plasma apoE levels in Jackson, MS. Node legends: numbers refer to corresponding SNPs (see Figure 1 in Nickerson et al. (2000) for an SNP map.) APO_E, APO_A, APO_B, TRIG, CHOL and HDL stand for levels of apolipoproteins E, AI and B, triglycerides, cholesterol and HDL cholesterol, respectively. WEIGHT, GENDER, AGE and HEIGHT labels are self-explanatory. Undirected edges indicate dependencies, directed edges indicate possible causations. Line thickness corresponds to the relative edge strength (Table 1).

Table 1.

Relative edge strengths among plasma apoE levels, APOE gene SNPs and other potential predictive variables

Node 1	Node 2	Edge strength
APO_E	TRIG	970 916
SNP 3937	SNP 4075	190 785
SNP 4075	APO_B	105 196
SNP 471	SNP 1998	73 280
APO_A	CHOL	51 954
SNP 560	SNP 3673	13 854
SNP 2440	SNP 5361	9439
SNP 308	SNP 2440	2505
SNP 4075	APO_E	2221
SNP 4075	SNP 624	880
SNP 73	SNP 560	374
HDL	WEIGHT	261
SNP 1998	SNP 545	50
SNP 73	SNP 4951	45
GENDER	APO_A	18
SNP 1163	SNP 4075	5.95
APO_E	SNP 4036	4.68
SNP 73	SNP 4075	4.04
SNP 1998	SNP 624	3.44
SNP 2440	SNP 545	2.99
SNP 73	SNP 5361	2.81
SNP 4036	SNP 308	1.17

For each edge, its strength is the ratio of the posterior probability of the model containing the edge to the posterior probability of the identical model with the edge removed. Edges with strength >10⁶ are considered highly significant and are not shown here (owing to the limited software resolution there is no significant difference between the values above 1 000 000). However, 20 edges with such values are, drawn in Figure 1.

Table 2.

Bootstrap values for the edges belonging to the Markov blanket of the apoE node (edge strength is also shown for each edge)

Node 1	Node 2	Bootstrap value (%)	Edge strength
SNP 4036	APO_E	76	4.68
SNP 4075	APO_E	85	2221
TRIG	APO_E	98	970 916

The edge between SNP 4036 and apoE level is only moderate in strength. Rall et al. (1989) reported that SNP 4036 was associated with type III hyperlipoproteinemia in a single family. An edge between SNP 3937, the other non-synonymous substitution in the apolipoprotein E gene (Boerwinkle and Utermann, 1988) and the apoE level was not supported for this population. However, this edge was supported (very weakly) in the BN constructed using the ‘hybrid’ (multinomial/linear Gaussian) model (data not shown), and also in the BN constructed using a different scoring criterion (see below). Another interesting result is the strong edge between SNP 4075 and apoB level node. It has been reported previously that APOE gene variation influences plasma apoE and apoB levels.

To summarize, it is gratifying that an unsupervised BN analysis uncovered known relationships (1) between three known APOE coding mutations and apoE/apoB levels, and (2) between apoE and Triglyceride levels.

To further investigate the robustness of BN reconstruction (in addition to bootstrapping and simulation experiments) and the distribution of the BN/edge scores, we have also built a series of networks using a different model scoring criterion—Akaike Information Criterion (AIC) (Akaike, 1973). AIC tends to cause overfitting (please see Supplementary Material for the comparison of model scoring criteria). The extent of overfitting (from slight to severe) can be controlled during the model search stage. Table 3 summarizes the apoE level Markov blankets for the AIC BNs. These results, together with the high bootstrap values and the simulation experiments, suggest that the reconstructed BNs are very robust indeed. By artificially increasing the overfitting, we gain higher sensitivity. Interestingly, the SNP 3937–apoE level edge is present in the most sensitive network. Also, Cholesterol and HDL levels start appearing in the apoE level blanket in more sensitive networks. The underlying biological mechanism for these observed relationships is at least partially attributable to the differential binding affinity of the APOE isoforms to lipoprotein receptors in the liver and elsewhere (Weisgraber et al., 1982).

Table 3.

Relative edge strengths^a for the edges belonging to the Markov blanket of the apoE node in the AIC networks

Overfitting	Node 1	Node 2	Edge strength
Slight	SNP 4075	APO_E	46.55
	TRIG	APO_E	48.89
	CHOL	APO_E	33.06
High	SNP 4075	APO_E	42.28
	TRIG	APO_E	50.51
	CHOL	APO_E	13.14
	HEIGHT	APO_E	18.88
	APOB	APO_E	20.41
	HDL	APO_E	22.12
Severe	SNP 4075	APO_E	46.68
	TRIG	APO_E	56.87
	WEIGHT	APO_E	28.17
	HEIGHT	APO_E	19.40
	APOB	APO_E	14.09
	HDL	APO_E	8.82
	SNP 3937	APO_E	14.66
	SNP 4036	APO_E	7.76

^aNote that AIC edge strength values should not be directly compared with the Bayesian edge strength values (shown in Tables 1 and 2), and only very roughly among ‘slight’, ‘high’ and ‘severe’ AIC BNs.

It should be noted that directed edges in Figure 1 do not unequivocally imply causations. Rather, they mean that the network topology with a directed edge scored higher, in terms of its posterior probability, than the same network but with the edge reversed. If the difference in scores is not statistically significant, the edge is shown as undirected. For example, a (weak) directed edge from apoE to SNP 4036 does not imply that apoE level causally influences SNP 4036. The purpose of introducing directionality into BN reconstruction is mainly for mathematical convenience.

DISCUSSION AND FUTURE DIRECTIONS

In this paper, we introduce the method of BNs to the domain of genotype-to-phenotype analyses in human genetics and provide an example application. Although our approach did not use any prior information, it was successful in uncovering relevant dependencies. From our experience, it appears that BNs are well-suited for gaining insight into the relationship of SNP variation within a gene (e.g. APOE) to interindividual variation in a phenotype of interest (e.g. plasma apoE levels). The utility of the method for analyses of multiple genes or genome-wide SNP association studies remains to be determined.

It is important to distinguish between fitting a single ‘perfect’ model and extracting pronounced (i.e. reliable) features from data. The former is usually impractical since some relationships may be attributable to chance sampling error, overfitting, etc., and no single model is apt to be applicable to all strata within a sample (i.e. hidden heterogeneity). The latter, however, is readily achievable. The primary goal of application of BNs is to extract robust features within the Markov blanket of a target variable, in this case plasma apoE level (or possibly within the Markov blankets of multiple variables of interest). In addition, the dependence and conditional independence relationships between other variables are being ascertained automatically in the BN modeling, thus presenting an effective mechanism for data-driven knowledge discovery. In the genetic epidemiology context, application of BNs also has utility in limiting the number of potential predictor variables that can be the subject of more detailed statistical analyses using more standard statistical methodology. It is worth pointing out that, in our opinion, BNs are being proposed to complement but not replace other methods of SNP site selection (Hoh and Ott, 2001; Nelson et al., 2001; Xiong et al., 2002). In any real application, it may be worthwhile to apply multiple methods of site selection and compare results for similarities and differences.

A straightforward biological interpretation of the apoE Markov blanket at this point would be that SNPs 4075 and likely 4036 influence apoE levels in the blood. No other SNPs provide evidence for a robust relationship (with a possible exception of SNP 3937 when the linear Gaussian model, or AIC scoring criterion, are used). In addition, strongly supported edges between SNP nodes suggest strong linkage disequilibrium. To summarize, the graphical representation generated by the BN technique automatically suggests a number of dependencies (and conditional independencies) between the variables that can be subsequently interpreted in biological context depending on the variable nature (SNP, gene, haplotype, plasma level, phenotype, etc.)

In conclusion, we propose that BNs are valuable data mining tools for the analysis of genotype-to-phenotype relationships in contemporary human genetics. In addition, as the number of SNPs within genes of interest and across the genome increases and the technology for genotyping SNPs becomes more accessible, the utility of such methods will also increase. The advantage of BN method is not that it will identify the ‘functional mutation’, but rather that it will perform initial data exploration to unearth new knowledge in a semi-automated and rapid fashion. In addition, BNs can explicitly combine both expert knowledge from the domain and information studied from the data. Crucially, BNs are effective at combating overfitting. Good data mining processes combine data-driven tools (inferring data-derived model) user-driven tools (combining expert knowledge and data-derived model), and verification-driven tools (estimating statistical significances of particular dependencies in the model). A need for such multi-step processes (hypothesis generation step followed by a traditional hypothesis testing step) has been recognized for other applications, e.g. genome-wide scan analyses (Province, 2001).

Finally, the logical extension to our existing framework would be to consider Bayesian model averaging as an alternative to a single model selection (Hoeting et al., 1999). This extension is currently underway.