Nonlinear structured-illumination microscopy: Wide-field fluorescence imaging with theoretically unlimited resolution

Abstract

Contrary to the well known diffraction limit, the fluorescence microscope is in principle capable of unlimited resolution. The necessary elements are spatially structured illumination light and a nonlinear dependence of the fluorescence emission rate on the illumination intensity. As an example of this concept, this article experimentally demonstrates saturated structured-illumination microscopy, a recently proposed method in which the nonlinearity arises from saturation of the excited state. This method can be used in a simple, wide-field (nonscanning) microscope, uses only a single, inexpensive laser, and requires no unusual photophysical properties of the fluorophore. The practical resolving power is determined by the signal-to-noise ratio, which in turn is limited by photobleaching. Experimental results show that a 2D point resolution of <50 nm is possible on sufficiently bright and photostable samples.

The fluorescence microscope has become a ubiquitous imaging tool in cell biology through its unique ability to image the 3D interior of a living specimen with multicolor molecular labels of extreme specificity, a combination of strengths not shared by higher-resolution techniques such as electron microscopy and scanned-probe methods. It is therefore unfortunate that its spatial resolution is subject to a hard limit caused by diffraction.

Recently, ways have been found to bypass the diffraction limit. 2D resolution in the 30-nm range has been realized by using stimulated emission depletion (STED) (1). STED is based on saturated stimulated emission using two synchronized ultrafast laser sources (2, 3); the underlying concept has been generalized to encompass a class of reversible saturable phenomena (4). STED and other proposed methods (5–7) were conceived in the context of laser-scanning microscopy and are designed to directly minimize the size of a scanned focal point. This article demonstrates an alternative approach that brings theoretically unlimited resolution to a wide-field (nonscanning) microscope by using a nonlinear fluorescence response together with a periodic illumination pattern that fills the field of view.

Both structured illumination light and optical nonlinearity, of course, are established ideas. Patterned light, for example, has been used for measuring surface shapes (8) and deformations (9) and for enhancing the sensitivity of fluorescence-recovery-after-photobleaching experiments (10). Axially structured light has been used to enhance axial resolution in standing-wave fluorescence microscopy (11), 4Pi microscopy (12), and I⁵M (13). Lukosz and Marchand (14) suggested in 1963 that lateral light patterns could be used to enhance resolution, and such patterns have been used for both axial (15) and lateral (16–19) resolution enhancement. They can be more effective than point scanning at retrieving high-resolution information (17, 19). Nonlinear fluorescence is the basis for multiphoton fluorescence microscopy (20), and several other classical optical nonlinearities (21) have also found use in both far-field (22, 23) and near-field (24) microscopy.

The reason that structured illumination can provide resolution extension is that it can render otherwise unresolvable high-resolution information visible in the form of low-resolution moiré fringes (Fig. 1). The strength of this effect is proportional to the spatial frequency of the pattern; the role of nonlinearity is to introduce high-frequency harmonics into the effective pattern and thereby increase its resolution-enhancement power.

Fig. 1.

Resolution extension through the moiré effect. If an unknown sample structure (a) is multiplied by a known regular illumination pattern (b), a beat pattern (moiré fringes) will appear (c). The moiré fringes occur at the spatial difference frequencies between the pattern frequency and each spatial frequency component of the sample structure and can be coarse enough to observe through the microscope even if the original unknown pattern is unresolvable. Otherwise-unobservable sample information can be deduced from the fringes and computationally restored.

Because the nonlinearity does not have to sharpen a focal spot, a larger class of physical phenomena can be exploited. In fact, it was pointed out recently (25) that the method can even use simple saturation of the excited state itself. This well known effect (the fact that once the illumination is intense enough to raise most fluorophore molecules to the excited state, additional intensity increases will not yield proportionate increases in the emission rate) occurs in all fluorophores and can be induced with a single, inexpensive light source. It is ill-suited for point scanning because it would broaden, not sharpen, the focal spot, but that is not a problem in the extended-pattern approach.

The following sections experimentally demonstrate saturated structured-illumination microscopy (SSIM), as an example of the more general concept of nonlinear structured-illumination microscopy, and show that it can achieve 2D resolution of <50 nm.

Principle

The classical resolution limit specifies a maximum spatial frequency k₀ that can be observed through the microscope. For a light microscope, k₀ = 2NA/λ_em, where λ_em is the observation wavelength and NA is the numerical aperture of the objective lens (26). If the frequency content of the sample is described in a 2D frequency space, then this limit defines an “observable region” (a circle with radius k₀ around the origin). Information outside of this region is fundamentally unobservable in the conventional microscope. The goal of resolution extension is to render some of that information observable, that is, to enlarge the observable region.

Structured-illumination microscopy extends resolution beyond the cutoff by moving information into the observable region, from elsewhere in frequency space, in the form of moiré fringes. Moiré fringes are produced by frequency mixing whenever two signals are multiplied. In this case, the multiplication is the one inherent in fluorescence: the observed emission intensity is the product of the local density of fluorescent dye (i.e., the sample) and the local intensity of excitation light.

If the illumination contains a spatial frequency k₁, then each sample frequency k gives rise to moiré fringes at the difference frequency k – k₁. Those fringes will be observable in the microscope if |k – k₁| < k₀, that is, if k lies within a circle of radius k₀ around k₁ (Fig. 2). Thus, the information within that circle has been made indirectly observable; it can be extracted by using a phase-shift method (17). The new information increases the highest observable spatial frequency (the resolution) from k₀ to k₀+ k₁. Thus, to maximize the resolution, it is desirable for the illumination to contain as high spatial frequencies k₁ as possible. Unfortunately, the set of spatial frequencies that can be generated in a light field is limited by diffraction in the same way as the set of frequencies that can be observed. Thus, k₁ cannot be made larger than 2NA/λ_exc ≈ k₀, so the new resolution limit k₀ + k₁ can be at most ≈2k₀. Hence, normal, linear, structured-illumination microscopy (and confocal microscopy, which is a particular case of structured illumination) can extend resolution only by a factor of ≈2.

Fig. 2.

Structured-illumination concept. (a) The set of sample spatial frequencies that can be observed by the conventional microscope defines a circular observable region of radius k₀ in frequency space. (b) If the excitation light contains a spatial frequency k₁, a new set of information becomes visible in the form of moiré fringes (hatched circle). This region has the same shape as the normal observable region but is centered at k₁. The maximum spatial frequency that can be detected (in this direction) is k₀ + k₁.

Even this new limit can be exceeded, however, if the emission rate can be made to depend nonlinearly on the illumination intensity. Such a nonlinearity would cause the effective illumination pattern to contain harmonics with spatial frequencies that are multiples of k₁. A component with frequency 2k₁ would extend resolution by twice as much as the linear method, a 3k₁ component by three times as much, etc. If the nonlinearity can be described by a polynomial of order s, it will give rise to s–1 new harmonics. A nonlinearity that is nonpolynomial (i.e., has an infinite Taylor series) thus produces an infinite number of harmonics, corresponding to theoretically infinite resolution. The resolution in practice will be finite, of course, but bounded only by “soft” matters of signal-to-noise ratio and photostability, not by any hard limit.

The particular nonlinear phenomenon discussed in this article is saturation of the excited state S₁, as suggested in ref. 25. In the normal fluorescence process, a fluorophore molecule in its electronic ground state S₀ is excited to the first excited state S₁ by absorbing a photon at λ_exc and decays back to S₀ after an average time τ (the fluorescence lifetime) as it emits a photon at λ_em. Clearly, on average each molecule can emit at most one photon per lifetime τ. Thus, it cannot respond linearly to illumination intensities above one photon per absorption cross section per lifetime (Fig. 3a). If the sample is illuminated by a sinusoidal light pattern with a peak intensity that is near or above this threshold, then the pattern of emission rate per fluorophore takes on a nonsinusoidal shape (Fig. 3b), which contains the desired series of harmonics with higher spatial frequency than the illumination pattern itself (Fig. 3c).

Fig. 3.

Generation of harmonics by nonlinear fluorescence. (a) The nonlinear dependence of the fluorescent emission rate on the illumination intensity in the saturation regime. (b) The emission pattern resulting from sinusoidally patterned illumination with peak pulse energy densities of (from the bottom to top curve) 0.25, 1, 4, 16, and 64 times the saturation threshold. (c) Amplitude of each Fourier component of such emission patterns as a function of the illumination pulse energy (log scale). Equivalently, the curves indicate the fraction of the image signal that stems from each harmonic of the illumination pattern. As the illumination energy increases, more and more harmonics come into play (lower curves). The calculations used the scalar model of light and were for steady-state illumination (a) and for the pulse length of 0.64 ns used in the experiments and a realistic fluorescent lifetime of 3.5 ns (b and c).

If a sample is illuminated with such a distorted pattern, the observed image will be a superposition of several information components, each displaced in frequency space by an amount corresponding to the spatial frequency of each Fourier component of the pattern (Fig. 4d). The number of pattern harmonics, and thus the number of contributing information components, is infinite, in principle. In practice, however, only a finite number m of information components are strong enough to rise above the noise level.

Fig. 4.

Resolution extension by nonlinear structured illumination. (a) The region of frequency space that is observable by conventional microscopy (compare with Fig. 2a). (b) An example of a sinusoidal illumination pattern. (c) That illumination pattern has three frequency components: one at the origin (black), representing the average intensity, and two at ±k₁, representing the modulation (dark gray). These are also the frequency components of the effective excitation under linear (i.e., nonsaturating) structured illumination. Under conditions of saturation, or other nonlinear effects, a theoretically infinite number of additional components appear in the effective excitation; the three lowest harmonics are shown here (light gray). (d) Observable regions for conventional microscopy (black), linear structured illumination (dark gray), and nonlinear structured-illumination microscopy (light gray) based on those three lowest harmonics. (e) Corresponding observable regions if the procedure is repeated with other pattern orientations. The much larger region of observable spatial frequencies (e) compared with that shown in a makes it possible to reconstruct the sample with correspondingly increased spatial resolution.

The observed image is the sum of these m displaced information components. To move the components back to their true positions in frequency space, they must first be separated, which cannot be done based on a single image. If, however, the pattern is shifted (i.e., its phase is changed by some angle ϕ) and a second image is acquired, then that image is a sum of the same components multiplied by varying powers of e^iϕ. The second image represents an independent linear combination of the m components. If m or more images are acquired at different phase shifts, there are as many equations (images) as there are unknowns (information components); thus, the components can be separated by inverting an m × m matrix and applying the inverse pixelwise to the stack of m images. With the natural choice of m phases equally spaced from 0 to 2π, the separation matrix becomes equivalent to a discrete Fourier transform with respect to the phase-shift variable ϕ.

If an illumination photon flux I is applied to a fluorophore with absorption cross section σ, the emission rate E will increase exponentially with time t toward an equilibrium: E ∝ [Iσ/(Iσ + k_f)]{1 – exp[–(Iσ + k_f)t]}, where k_f = 1/τ is the fluorescent decay rate. Thus, for steady illumination or long pulses (pulse length t_p >> τ), the intensity dependence of E is the rational function [Iσ/(Iσ + k_f)], whereas short pulses (t_p << τ) produce an exponential dependence E ∝ {1 – exp[–(Iσ + k_f) t_p]}, which is somewhat more effective at generating harmonics. For this work, a pulse length of 0.64 ns was chosen, which is shorter than typical lifetimes of 2–4 ns but is not so short as to involve extreme field strengths that could increase the risk of nonlinear damage processes.

Measurements

The light source was a frequency-doubled passively Q-switched diode-pumped solid-state laser (Northrop Grumman PolyScientific, Charlotte, NC), a microchip device that is only 22 mm long. The laser produced 3.6-μJ pulses with 640-ps duration at a wavelength of 532 nm and a repetition rate of 6 kHz. The pulse energy reaching the sample was regulated by a polarization-based variable beam splitter.

In all experiments the illumination pattern was projected onto the sample by an ×100/1.4-numerical aperture planapochromatic oil-immersion objective, which was also used to image the sample onto a cooled charge-coupled device camera through a dichroic mirror and a 580- to 630-nm band-pass filter.

Demonstration of Saturation. An initial experiment was conducted to demonstrate that saturation can generate harmonics. A pattern of parallel lines was produced by passing the laser light through a transmission phase grating and projecting a demagnified image of the grating onto the sample. The pattern period (2.5 μm) was chosen to be much coarser than the resolution limit (0.19 μm), to make it possible to observe the pattern and several of its harmonics directly. The line pattern was made purely sinusoidal (apart from the overall Gaussian profile of the laser beam) by allowing only diffraction orders +1 and –1 from the grating to reach the sample. These two beams intersected at an angle in the sample to produce a sinusoidal interference pattern (which is equivalent to the demagnified grating image).

An effectively uniform thin-layer sample was prepared by diluting a suspension of 120-nm-diameter microspheres (Molecular Probes) in water and allowing a drop of suspension to air-dry on a cover glass. The concentration and volume of the drop were adjusted such that areas of close-packed monolayer formed in the drying step. Such a monolayer appears featureless in the conventional microscope, because its periodicity of 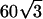nm is unresolvable. Once dry, the sample was mounted in a glycerol-based medium.

The fluorescent layer sample was illuminated by the line-pattern-modulated Gaussian beam described above. Images were exposed for 0.1 s, corresponding to ≈600 excitation pulses. At a relatively low peak energy density per pulse of 0.58 mJ/cm², the observed pattern of emission was approximately sinusoidal (Fig. 5a, bottom trace), not deviating far from the illumination intensity pattern. At a higher peak energy density of 37 mJ/cm², however, the emission pattern changed drastically, taking on broad, flat peaks and sharp, narrow valleys (Fig. 5a, top trace) as fluorescence saturated in the high-intensity regions. This behavior is in good qualitative agreement with expectations (Fig. 3b). Fourier analysis of this pattern revealed five detectable harmonics at higher spatial frequencies than that of the illumination (Fig. 5b, top trace). The lowest harmonic is seen also at the lower pulse energy (Fig. 5b, bottom trace), indicating that the fluorescent response is noticeably nonlinear because of saturation effects already at that energy density.

Fig. 5.

Verification of harmonic production through saturation. (a) Profiles through images of a thin fluorescent layer illuminated by a Gaussian laser beam modulated by sinusoidal stripes with a period of 2.5 μm, with a peak energy density per pulse of 0.58 mJ/cm² (bottom curve) and 37 mJ/cm² (top curve). The bottom curve approximately follows the sinusoidal illumination pattern, because the peak energy density is below the saturation regime. In the top curve, the higher pulse energy causes fluorescence to saturate near the peaks of the pattern, leading to an asymmetric curve form with broad peaks and sharp valleys. (That the observed valleys do not reach zero is expected because of blurring by the observation optics and does not necessarily imply that the actual intensity minima are nonzero.) (b) Fourier transforms corresponding to the profiles shown in a showing five detectable harmonics in the high-energy pattern (arrows). Only the lowest harmonic is detectable in the low-energy pattern (arrowhead). The vertical axis is logarithmic (base 10); the curves in b have been separated vertically for clarity.

SSIM Resolution Test. The hardware used for testing actual SSIM microscopy was similar to the one described above except that the period of the line pattern was decreased by increasing the demagnification from the grating to the sample. Apart from the pulsed light source, the apparatus was similar also to that used earlier for linear structured illumination (17, 18). The two beams corresponding to the +1 and –1 diffraction orders were refocused near opposite edges of the back focal-plane aperture of the objective lens and thus crossed each other in the sample at a maximal angle, generating an interference pattern of maximal spatial frequency. The period of the resulting illumination pattern was 0.20 μm, close to the theoretical limit of 0.19 μm at this wavelength. The orientation and phase of this pattern were controlled by rotating and laterally translating the grating. Capacitive sensing of the grating position, referred to a fixed cylindrical counterelectrode surrounding the piezoelectrically movable grating holder, allowed the pattern phase to be controlled with subnanometer reproducibility at any pattern orientation. To maximize the pattern contrast, the interfering beams were s-polarized by using a corotating linear polarizer on the rotation stage; the incoming beam was polarized circularly so that rotation of the stage would not affect the pulse energy.

A resolution test sample was prepared by depositing 50-nm-diameter fluorescent polystyrene microspheres on a cover glass and covering with a glycerol-based mounting medium. This sample was illuminated by the line pattern at a pulse energy density of 5.3 mJ/cm² and an exposure time of 0.15 s (900 pulses). At these parameters, only the first three harmonics of the pattern were expected to be nonnegligible, corresponding to a total of nine superposed information components (Fig. 4 c and d). Therefore, a sequence of nine images was acquired, with the pattern phase advanced by 2π/9 radians between images. Applying the separation matrix to these nine phase images produced nine separated information components originating from nine regions of frequency space, as indicated in Fig. 4d. This procedure was repeated for 12 different pattern orientations separated by π/12 radians to retrieve complete information from a nearly circular region of frequency space (Fig. 4e).

The precise orientation, line spacing, and starting phase of the pattern were determined from the data by comparing the different information components where they overlapped. The modulation depth of the pattern and each harmonic (or, equivalently, the relative scaling factors between the various information components) could also be determined this way, as has been done in linear structured-illumination microscopy (17, 18). In practice, it was found preferable to enter the modulation depth values manually on an empirical basis, because the signal-to-noise level in the highest information components was insufficient for reliable automatic determination of modulation depths. With a well characterized microscope, it may be possible to treat all these parameters as known system constants.

Processing was also similar to that described in ref. 17 except for the increased numbers of phase images, information components, and pattern orientations. The separated information components were computationally moved to their true position in frequency space. This translation by a vector k₁ in reciprocal space was implemented as a multiplication with the corresponding complex wave e^ik₁^·x in real space so as not to constrain the values of k₁ to integer numbers of pixels of the Fourier transformed data. The components were compensated for the known optical transfer function of the microscope and combined by a weighted average (with weights inversely proportional to the local noise variance) where they overlapped. An additive constant was introduced into the denominator of the average (17, 18) to suppress low signal-to-noise regions as in a Wiener filter (26). When all components had been reassembled into a single data set in this way, a triangular apodization function was imposed to minimize the ringing that would otherwise result from the hard edge of the enlarged observable region. The final reconstruction was produced by retransforming the apodized data set to real space. The pixel size was decreased during processing, from 90 nm in the raw data images to 9 nm in the reconstructions, to accommodate the increased resolution. Comparison reconstructions were also calculated by using fewer orders of information components, with the apodization window resized accordingly.

A subset of the resulting reconstruction is shown in Fig. 6d, which demonstrates the dramatic resolution increase compared with conventional microscopy (Fig. 6a). For additional comparison, Fig. 6c shows a reconstruction from the same data but includes only the center- and first-order information components; thus, the result represents the resolving power of linear structured-illumination microscopy without the saturation effects. Fig. 6b similarly shows a reconstruction in which only the central information component was used, representing conventional microscopy followed by a linear filter that makes the result directly comparable with the processed data.

Fig. 6.

A field of 50-nm fluorescent beads, imaged by conventional microscopy (a), conventional microscopy plus filtering (b), linear structured illumination (c), and saturated structured illumination using illumination pulses with 5.3 mJ/cm² energy density, taking into account three harmonic orders in the processing (d). Because no scanning is necessary, a wide field can be imaged simultaneously.

The successive resolution enhancement is immediately apparent in Fig. 6. The small cluster in the center of the field, for example, appears nearly shapeless in the conventional image, but is seen as a distinct branched rod shape with the help of linear structured-illumination microscopy, and is resolved into its 19 individual beads when the nonlinear saturation effect is used.

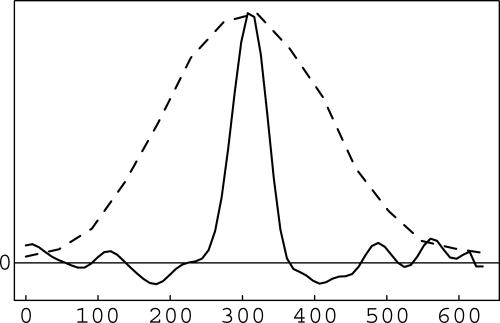
To quantify the resolution of the method, intensity profiles were measured across isolated 50-nm beads (Fig. 7), and their full width at half maximum (FWHM) was determined. The average FWHM of 100 such profiles was 58.6 ± 0.5 nm, an improvement by a factor of 5.5 over the 265-nm lateral FWHM of unfiltered conventional microscopy (Fig. 7, dashed trace). The FWHM value underestimates the resolving power, however, because the object is not a point source but rather a bead of finite diameter (specified by the manufacturer as 51 nm). To allow the true point resolution to be estimated, the known bead shape was removed from the reconstruction by linear deconvolution (i.e., the Fourier transform of the reconstruction was divided by the Fourier transform of a 51-nm sphere and retransformed), and 100 bead profiles were measured as described above. The average FWHM in this corrected data set (i.e., the estimated point resolution) was 48.8 ± 0.5 nm.

Fig. 7.

Lateral profiles through images of an isolated 50-nm red fluorescent bead, acquired by SSIM (solid trace) and conventional microscopy (dashed trace). (The structure along the baseline in the SSIM profile is caused by noise.) The average FWHM of 100 such SSIM profiles through different beads was 59 nm, a dramatic reduction compared with the 265-nm width for unprocessed conventional microscopy.

Discussion

Applicability. Can resolution at the level seen in Figs. 6 and 7 be achieved in cells? In the case of SSIM, the major obstacle is that the photobleaching rate of at least some fluorophores seems to accelerate (in other words, the number of photons that each molecule can emit before being destroyed seems to be smaller) under saturating conditions compared with normal illumination intensities. At the same time, the number of detected photons required for a given signal-to-noise-ratio is greatly increased compared with a single conventional image [by the number of pattern orientations times the squared inverse of the Fourier coefficient (as plotted in Fig. 3c) of the highest harmonic used]. Photostabilities seen in preliminary measurements [for example, ≈50,000 emitted photons per molecule of the DNA stain Po-Pro-3 (Molecular Probes), mounted in an oxygen-depleted medium and exposed to a light pattern with peak pulse energy nine times its estimated saturation threshold] would theoretically support a two-point resolution of 50 nm in 2D with a signal-to-noise ratio above unity even if each point consisted of only a single molecule. In practice, however, SSIM will probably require samples to be brightly labeled as well as photostable. Highly photostable fluorescent labels do exist, including several types of nanoparticles (27–29). Diamond nanocrystals containing nitrogen-vacancy color centers, for example, are known to fluoresce under continuous saturation conditions for hours without bleaching (28).

We have discussed 2D imaging, but the concept of SSIM, and nonlinear structured-illumination microscopy in general, is easily generalized to 3D in the same manner as in the linear case (17, 18) and, in principle, can improve resolution in all three directions. The requirement for photostability of the fluorophore, of course, increases further in proportion to the number of sections. Because the method relies on clean intensity zeros, it will also be more sensitive than conventional microscopy to sample-induced aberrations.

An important question is to what extent the method can be applied to live samples. Apart from photobleaching, the main concern is sample motion: the simple data processing described here assumes that the sample structure is stationary, within a tolerance given by the improved resolution, during acquisition. For a data set as shown in Fig. 6, this would mean <50 nm of motion over many seconds. Many intracellular processes involve much higher speeds. Thus, live imaging will most likely be restricted to slow-moving structures.

Photodamage is always a concern for live specimens. The light intensities used here are lower by >3 orders of magnitude than those commonly used for two-photon microcopy of living specimens, but the saturation conditions may increase phototoxicity.

Alternative Nonlinear Phenomena. It should be stressed that the nonlinearity used here, saturation of the first excited state S₁, is only one example of the general concept of a nonlinear dependence of emission rate on illumination intensity. The same processing and acquisition scheme as described above could be applied equally well to other nonlinear effects, the only requirement being that to provide high resolution the nonlinearity must be nonpolynomial or of high order.

Most classical nonlinear-optics phenomena (21) such as harmonic generation are coherent in the sense that light waves produced at different points of the sample have a fixed relative phase and therefore interfere with each other. This coherence leads to a less direct relationship of the observed image to the sample structure than for fluorescence, where light waves emitted from different sample points are mutually incoherent, so that their intensities simply add. This article covers only the fluorescence case.

Multiphoton absorption fluorescence (20) is one classical nonlinear phenomenon that does produce incoherent emission light and thus fits into the framework described in this article. Two-photon fluorescence has a quadratic nonlinearity and therefore could extend resolution by twice as much as linear structured illumination of the same wavelength. That factor is misleading, however, because it refers to a comparison at constant illumination wavelength. In practice, two-photon microscopy uses nearly twice the illumination wavelength that would be used for linear excitation of the same fluorophore, and that factor of two cancels the resolution doubling from the nonlinearity. Thus, two-photon fluorescence produces no significant resolution improvement, and the same argument applies to higher orders of multiphoton absorption.

One proposed microscopy method called “ground-state depletion” is related to the present one but saturates the triplet state instead of the singlet excited state (5). Because the triplet state is associated with photobleaching (30), it is unattractive to purposely accumulate molecules in this state. In the present method, on the other hand, accumulation into the triplet state can be largely avoided by operating at a pulse-repetition rate that is slow compared to the triplet-state lifetime.

Several nonlinear effects exist, however, that do hold promise for very high resolution, including stimulated emission depletion (1–3), energy transfer in specially designed fluorophores (6), and reversible photoactivation of molecules (4, 31–35). The last category is particularly intriguing in that some promising molecules are proteins of the GFP family (32–35), suggesting the exciting possibility that the extreme resolution of nonlinear structured-illumination microscopy could be combined with the in vivo labeling power of GFP-like genetically encoded protein tags.

Conclusions

SSIM provides fluorescence imaging with in principle unlimited resolution using a single, inexpensive laser. Its ultimate resolution in practice is determined by the measurement signal-to-noise ratio, which in turn is limited by photobleaching. A 2D point resolution of <50 nm was achieved on a bead sample. The method is an example of a general concept of nonlinear structured-illumination microscopy, which has the potential to open a new, nanoscale-sized domain to investigation by wide-field light microscopy.