Structure of stochastic dynamics near fixed points

Abstract

We analyze the structure of stochastic dynamics near either a stable or unstable fixed point, where the force can be approximated by linearization. We find that a cost function that determines a Boltzmann-like stationary distribution can always be defined near it. Such a stationary distribution does not need to satisfy the usual detailed balance condition but might have instead a divergence-free probability current. In the linear case, the force can be split into two parts, one of which gives detailed balance with the diffusive motion, whereas the other induces cyclic motion on surfaces of constant cost function. By using the Jordan transformation for the force matrix, we find an explicit construction of the cost function. We discuss singularities of the transformation and their consequences for the stationary distribution. This Boltzmann-like distribution may be not unique, and nonlinear effects and boundary conditions may change the distribution and induce additional currents even in the neighborhood of a fixed point.

In equilibrium statistical mechanics, the principle of detailed balance and the related fluctuation–dissipation theorem play important roles. Einstein used the principle that the excess energy that is put into each mode of an equilibrium system in the course of thermal fluctuations is also removed from the same mode by dissipative forces. This principle is implicit in his work on Brownian movement (1), and explicit in later works on the photoelectric effect (2), and on the relation between spontaneous and induced emission of electromagnetic radiation (3). It was formulated as the principle of detailed balance by Bridgman (4) and used to explain Johnson noise in electrical circuits by Nyquist (5). It is related to the fact that the same processes that drive fluctuations in the neighborhood of a typical equilibrium configuration also drive the configuration back towards a typical equilibrium or steady-state configuration when it is displaced from equilibrium by an amount that is small, but large compared with the fluctuations in thermal equilibrium. In this situation, the equilibrium distribution in phase space is just the Boltzmann distribution, proportional to e^–βE, where β is inversely proportional to temperature, and E is the energy of the point in phase space. Configurations that differ significantly from those that contribute to the minimum of the free energy are driven back to the neighborhood of this minimum by dissipative effects such as thermal or electrical conduction or viscosity, and the magnitude of these effects is related to the equilibrium fluctuations of related variables.

In many situations, there is no thermodynamic equilibrium, but external steady and fluctuating forces drive the system into a steady or very slowly varying state for which the principle of detailed balance does not hold. A light bulb powered by an external battery or a chemical reaction in which the reactants are introduced at a steady rate and the products of the reaction are removed at a steady rate would both be examples of such a situation. Even in a situation that is almost in equilibrium, such as a system that is started in equilibrium at a local minimum of the free energy but that can go over a saddle point to a deeper minimum, the behavior near the saddle point does not satisfy the principle of detailed balance, because there is a current over the saddle point.

For such systems without detailed balance there is no general method of obtaining the equilibrium distribution from a knowledge of the steady and stochastic forces, such as the Boltzmann distribution provides for a system with detailed balance. In recent work, one of us (6) has developed a method valid near a stable fixed point, which, even when detailed balance does not hold, obtains a cost function analogous to the energy for the Boltzmann distribution. If this method can be extended away from the linear region in the neighborhood of a fixed point, it may provide a new method for dealing with problems of this sort (7, 8).

Great efforts have been spent on finding such a cost function ever since the work of Onsager (9). Results up to 1990 have been summarized, for example, by van Kampen (10). In general, such efforts have been regarded as not very successful (11).

In spite of the difficulty, there have been continuous efforts on the construction of cost function and related topics. Elegant results have been obtained in several directions. Tanase-Nicola and Kurchan (12) have considered explicitly the saddle points of gradient systems. They started from the existence of potential or cost function to avoid the most difficult problem of the irreversibility. The gain is that they can now obtain a powerful computational method to count the saddle points and to compute the escape rate. They also provide an extensive list of related literature.

The study on the mismatch of the fixed points of the drift force and the extremals of the steady-state distribution has been reviewed by Lindner et al. (13). Rich phenomena have been observed, but the mismatch has been treated as “experimental” result. There is no mathematical/theoretical explanation on why it should happen.

In another survey, the useful and constructive role played by the noise has been demonstrated by examples (14). It is argued that the noise is essential to establish the functions of dynamical systems. Again, the mismatch problem is encountered, and the constructed potential function is often regarded as approximation.

From a different perspective, there has been an effort to provide a solid foundation for nonequilibrium processes based on the chaotic hypothesis (15). The chaotic hypothesis presumes that the system is sufficiently chaotic that variation of parameters of the system leads to a unique parameter-dependent steady state, even though the change in Gibbs entropy is not path independent (16). Under this hypothesis an interesting and important fluctuation theorem has been obtained, which further suggests the existence of the Boltzmann-like steady-state distribution function. Hence, a cost function very likely exists under this situation. A difficulty with this approach is that extremely few practical physical systems have been shown to satisfy the chaotic hypothesis.

Because the metastability is such an important phenomenon and because of the difficulty encountered in the construction of cost function, efforts have been made to go around the cost function problem when computing the lifetime of a metastable state. The effort results in the Machlup–Onsager functional method, summarized by Freidlin and Wentzell (17). This approach has been actively pursued recently (18, 19).

In this work, we give a careful discussion of the basis of our method of constructing a cost function in the linear region close to any fixed point, whether stable or unstable. We show that this approach gives an unambiguous prescription under wide conditions. The only case we have found that does not give an unambiguous expression for the cost function has a subspace within which the noise does not act and out of which the force does not carry the state.

In Stating the Problem, we give a general discussion of a linear system with noise. In Decomposition of the Force we show how a cost function can be constructed by a decomposition of the force matrix into two factors, one of which is a symmetric cost function matrix, and that this gives a probability density of exponential form, with the exponent proportional to the cost function. The general proof of this result is obtained in the Appendix, where we exploit the Jordan transformation for matrices with an incomplete set of eigenvectors. In Singularities we discuss the singularities of the transformation and identify two types of singularities, one of which corresponds to a flat subspace of the cost function, whereas the other corresponds to the possibility that the dynamics separates the system into two or more disjoint subspaces. In Other Stationary Solutions we discuss solutions other than the Boltzmann-like solution of the equation for a stationary distribution and argue that such solutions may be significant in any attempt to extend this solution to the nonlinear regime. In Discussion we discuss the significance of this decomposition of the force matrix and its relation to the principle of detailed balance.

Stating the Problem

Many processes in natural sciences can be modeled quantitatively. One particularly important class of such modeling is that described by first-order differential equations (20), supplemented by stochastic terms (10). We start with the nonlinear dynamic equation

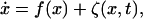[1]

which gives the stochastic evolution of the state represented by the real d-dimensional vector, x^τ = (x₁,..., x_d). Here the superscript τ denotes the transposed vector. The force vector is the d-component f(x), which gives the deterministic time evolution of the system. For simplicity we take the noise term ξ(x, t) to be Gaussian white noise, with zero mean, 〈ζ(t)〉 = 0, and variance 〈ζ(x, t)ζ^τ(x, t′)〉 = 2D(x)δ(t – t′). The angle brackets denote the average over noise distribution, and δ(t) is the Dirac delta function. In this work we assume D(x) to be independent of x. The probability distribution function ρ(x, t) then satisfies the Fokker–Planck equation

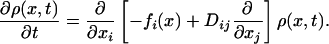[2]

In the neighborhood of a fixed point, which we take to be at the origin, the force can be replaced by its linear approximation

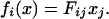[3]

It was noticed by Ao (6) that, in the linear region near a stable fixed point, Eqs. 1 and 3 can be decomposed in the form

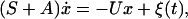[4]

where the symmetric matrix S is semipositive definite and the matrix A is antisymmetric. The noise function ξ has variance given by 〈ξ(x, t)ξ^τ(x, t′)〉 = 2Sδ(t – t′). In this work we adopt an equivalent, but simpler, approach of factorizing the force matrix as

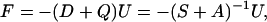[5]

where D is the symmetric diffusion matrix, Q is an antisymmetric matrix that can be determined, and U is the symmetric cost function matrix, which was called a potential matrix in ref. 6. This equation breaks the force Fx into two components, F^(d)x = –DUx, which generates a motion towards the origin if U is positive definite, and F^(c)x =–QUx, which gives a motion on the manifold of constant 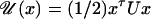. The quadratic form 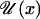is the cost function.

It is immediately obvious that if the vector f is replaced by F^(d)x =–DUx in Eq. 2, a Boltzmann-like stationary distribution of the form

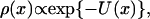[6]

satisfies the equation, since the current density

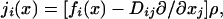[7]

vanishes. Since F^(c)x generates a current density

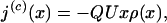[8]

which is divergence free, and conserves 𝒰 and ρ, the combination f(x) = [F^(d) + F^(c)] x also conserves the distribution given by Eq. 6, so that this is a stationary solution of Eq. 2.

This decomposition of the force matrix allows an explicit time-independent solution of the Fokker–Planck equation to be written down. In ref. 6 the solution of the equation for Q was obtained by a power series expansion, without any discussion of the convergence of this series. In the next section, we show that there is a unique solution for the equation for Q under rather wide conditions. It is not even required that the fixed point of F be stable, although if it is not the stationary solution given by Eq. 6 is unbounded and could only, at best, give a useful solution in a neighborhood of the fixed points with boundary conditions that do not perturb this solution too strongly.

It is worth noting that, under the coordinate transformation x → y = M^–1x, the mapping F that relates ẋ to x transforms as

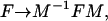[9]

while the symmetric matrices U and D, which represent quadratic forms, transform as

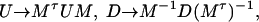[10]

and Q transforms in the same way as D. These transformations preserve the separation of D + Q into symmetric and antisymmetric parts.

Starting from the work of Onsager (9), there has been extensive literature on dynamical behavior near a stable fixed point (21–23). The new construction clearly works for this important situation and has indeed offered a new angle. However, it is not sufficient to generalize the decomposition of the force in Eq. 5 to the nonlinear regime by an equation of the form f = –(D + Q)grad 𝒰, since the Boltzmann form, Eq. 6 may not satisfy the Fokker–Planck Eq. 2 if the antisymmetric matrix Q is space dependent. The generalization to nonlinear systems needs further study. In the next three sections, we establish the decomposition firmly in the linear regime and investigate its limitations and implications.

Decomposition of the Force

In this section, we develop a general method for making the decomposition of the force matrix given in Eq. 5. Since this equation, together with the symmetry of U, D, and antisymmetry of Q, leads to

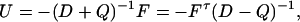[11]

the equation to determine Q is

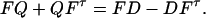[12]

This is a system of d(d – 1)/2 linear equations to determine the same number of independent components of Q, so it has a unique solution unless the set of equations is singular. Inversion of the matrix D + Q then gives the matrix S + A of Eq. 4.

Our method of solution is best illustrated by considering the case that F is real symmetric or has distinct eigenvalues, so that it can be diagonalized in terms of its left and right eigenvectors. Eq. 12 then takes the form

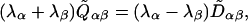[13]

where the λ_α are the eigenvalues of F, and the tilde denotes this representation in terms of eigenvectors. This equation gives an immediate solution for Q provided that no pair of the eigenvalues of F adds up to zero. The eigenvalues can only add to zero when the fixed point is unstable, which is discussed in Singularities.

For completeness, we must consider the general case with degenerate eigenvalues for asymmetric F, in which case there may not be a complete set of eigenvectors. This case is dealt with in Appendix, using the Jordan representation of a nonsymmetric matrix.

Singularities

There are two places in our argument where the transformation from the force matrix F to the symmetric cost function matrix U might be singular. Eq. 12 for the antisymmetric matrix Q can be solved, and we have an explicit solution in Decomposition of the Force unless the determinant of the coefficients in d(d – 1)/2 inhomogeneous equations is zero. The second possibility is that the matrix D + Q whose inverse appears in Eq. 11 might have zero determinant.

In Decomposition of the Force we showed that the conditions for the equation for Q to be singular are that two of the eigenvalues of F sum to zero, or, as can be seen from Eq. 33 in Appendix, when the null space of F² has two or more dimensions. Neither of these cases arise for a stable fixed point. There are two distinct cases of λ_α + λ_β = 0, according to whether the two eigenvalues are real eigenvalues of opposite sign or whether they form a complex conjugate pair. We study the behavior of the eigenvalues and eigenvectors of U in these two cases, assuming that the two eigenvalues of F are nondegenerate and that F has no zero eigenvalue.

Instead of studying the eigenvectors of U directly, we study the eigenvalues and eigenvectors of

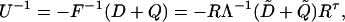[14]

which has the same eigenvectors but reciprocal eigenvalues. Here R is the matrix whose columns are the right eigenvectors of F, and Λ is the diagonal matrix with the eigenvalues of F as its diagonal elements. The generalization of these definitions of R and Λ to the case where the eigenvalues of F are not complete is given in Appendix in Eqs. 28, 30, and 35. For a pair of eigenvalues with λ_α + λ_β ≈ 0, with no other sums of two eigenvalues small and no other small individual eigenvalues, the only large terms in the matrix Ũ^–1 = –Λ^–1(D̃ + Q̃) are, according to Eq. 13,

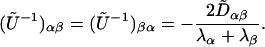[15]

When all other matrix elements are neglected, this approximation, combined with Eq. 14, gives

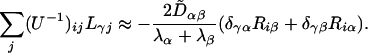[16]

This equation, combined with the relation RL = I, shows that the approximate eigenvector corresponding to a large eigenvalue w^–1 can be written as

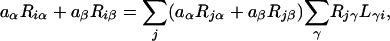[17]

provided the amplitudes and eigenvalues satisfy the equation

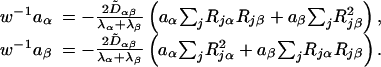[18]

This equation gives the two small real eigenvalues of U as

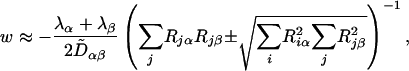[19]

and the corresponding eigenvectors as

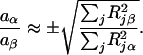[20]

For the case of a pair of real eigenvalues of opposite signs, we can see that, as the sign of λ_α + λ_β is changed by a change in the parameters of F, D, the stable and unstable manifolds of U change places with one another. The stable and unstable manifolds of U bisect the stable and unstable manifolds of F in the original representation, as is obvious if one normalizes the real eigenvectors of Ũ by 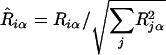and R̂ _iβ similarly, giving eigenvectors R̂_iα ± R̂_iβ. In the limit λ_α = λ_β, U is flat in this two-dimensional subspace.

For a complex conjugate pair of eigenvalues with 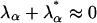the behavior is a little different. Using the property 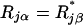, we find the term inside the bracket in Eq. 19 is always positive. The two eigenvalues of U then have the same sign, so U is either stable or unstable, depending on the sign of λ_α + λ_β, in this two-dimensional subspace. As the real part of λ_α changes sign, a two-dimensional stable manifold becomes unstable, or vice versa.

It can be seen from Eq. 32 in Appendix that where one of the eigenvalues satisfying λ_α + λ_β = 0 corresponds to a higher-dimensional subspace, there may be higher-order zeros of the eigenvalues of U.

If the matrix D is positive definite, there is no possibility that D + Q could be singular. If u is a vector in the null space of D + Q, we have

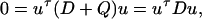[21]

since the antisymmetry of Q makes its expectation value vanish. Therefore, D ± Q cannot be singular when D is positive definite.

However, we do not usually want to specify that the noise acts on all coordinates. Typically, when two of the coordinates are the position and momentum of a particle, people will take the noise to change the momentum but not the position of the particle. However, Eq. 21 shows that for non-negative definite D, vectors in the null space of D + Q are in the intersection of the null spaces of D and Q. Eq. 12 then shows that, for such a vector u in the null space of D and Q,

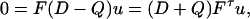[22]

and so u is only in this null space if F^τu, or any power of F^τ acting on u, is still in the null space.

This condition is in agreement with what one should expect. The noise does not have to act directly on all coordinates, but, if there is a subspace in which there is no noise and that is left invariant by the motion, there can be no equilibration within that subspace except collapse towards a stable fixed point.

Other Stationary Solutions

Although the Boltzmann-like form given in Eq. 6 gives a stationary solution of the Fokker–Planck equation, it is only the unique solution under certain rather restrictive boundary conditions. One can see clearly why this might be an issue by considering the one-dimensional form of the equation near a stable fixed point, which can be written as

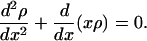[23]

In addition to the Boltzmann-like solution ρ⁽⁰⁾ proportional to exp(–x²/2), this equation has a current-carrying solution of the form

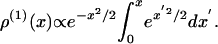[24]

This expression is proportional to 1/x for large values of x, so, if the linear approximation to the equation is valid up to fairly large values of x, the coefficient of such a term must be exponentially small to prevent the probability density given by ρ⁽⁰⁾ + ρ⁽¹⁾ from being negative.

In d-dimensional systems there are similar solutions falling off like 1/|x|^d for large |x|. For such solutions of Eq. 2 the current at large distances from the origin is primarily driven by the linear force Fx, and the diffusive motion is a small correction, so, while the density falls off like |x|^–d, the conserved current falls off like |x|^–d+1. Again, current conservation shows that this contribution to the density must be positive and negative in different parts of space, so that its coefficient at the origin must be exponentially small, with an exponent that depends on the size of the region in which the linear approximation is valid.

Near a maximum, ρ⁽⁰⁾ ∝ exp(x²/2), of the cost function, the one-dimensional current-carrying solution has the form

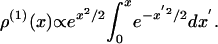[25]

This solution grows at large distances in the same way as ρ⁽⁰⁾, with a change of sign at the origin. In d dimensions a saddle point can sustain a relatively large current across it, because there are current-carrying states for which ρ is of the same order of magnitude as ρ⁽⁰⁾.

To get such a current across a stationary point in a linear system, it is necessary to impose some external current sources and sinks. However, if we want to describe a nonlinear force field in terms of its approximately linear behavior in the neighborhood of its fixed points, adjacent neighborhoods can generate external current sources and sinks for one another, so we should not be surprised to find such currents if we linearize in a local region. These “external” currents will not only produce flows at the boundaries but will shift the flow lines away from the surfaces of constant cost function U shown in Eq. 8.

In the neighborhood of the minimum of the cost function, current-carrying solutions resembling the one-dimensional Eq. 24 shift the maximum of the density away from fixed point, since the gradient of ρ⁽¹⁾ is nonzero. Because, as we remarked in connection with this equation, the amplitude of such a term must fall off exponentially with the size of the region of linearization, to prevent negative densities, it should not be possible to obtain such a term by a conventional perturbation theory in the neighborhood of the stable fixed point. Our numerical exploration of nonlinear systems of this sort suggests that these current-carrying solutions are significant, because the maximum of the density is displaced from the zero of the force. One possibility is to introduce such current-carrying states, in addition to a ρ⁽⁰⁾ determined by the cost function, to make this method applicable to nonlinear systems.

Discussion

The main result of this work is to show that, for a system with a deterministic motion controlled by a linear force and a diffusive motion driven by constant white noise, the force matrix F can be decomposed into two parts, –DU and –QU. Provided the fixed point of F is stable, the first of these components leads to a steady-state distribution of the Boltzmann form, exp(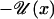), with no probability current, the usual form of an equilibrium distribution when detailed balance holds. The second part gives a flow on the surface of constant 𝒰.

The cost function matrix U can be diagonalized by an orthogonal transformation, and, if it is positive definite, it can be transformed to the identity matrix by choosing a new scale for the variables. In this representation the dissipative part of the force matrix is F^(d) = –D, which is suggestive of Einstein's relation between diffusion and dissipation (1) or of the fluctuation–dissipation theorem (24, 25).

When the cyclic motion induced by F^(c) is included the relation between the eigenvalues of F and D becomes more complicated. If the motion in a two-dimensional subspace is dominated by a fast cyclic motion within the subspace, there will be a complex conjugate pair of eigenvalues of F, so that they have a common relaxation rate given by the real part of the eigenvalues. These possibilities require much more detailed work than we have yet given them.

This situation is actually not so different from the situation usually encountered in statistical mechanics, at least if a classical, rather than a quantum, description is used. For a damped harmonic oscillator, there is a cyclic motion in phase space, as well as the thermal noise and viscous damping acting on the momentum coordinate, whereas for black-body radiation in a cavity there is cyclic motion between electric and magnetic fields, in addition to the resistive damping and noise from the walls of the cavity.

What is remarkable is not that the steady-state density can be written as the exponential of a cost function, because if there is a steady state we could always define the cost function as minus the logarithm of the steady-state density. We find it remarkable that for a linear stochastic system of this sort, it is generally true that the force can be decomposed into two parts, one of which gives detailed balance in its strictest sense, whereas the other gives a cyclic motion on the surfaces of constant cost function.

The question of whether this technique can be extended to nonlinear systems is an important one but requires careful investigation. We have done preliminary work based on perturbative inclusion of nonlinear terms and made comparison with numerical calculations. It is clear that Eqs. 4 and 5 need some modification for nonlinear effects and also that if we try to solve the problem by matching limited regions in which linearity holds approximately, the matching may introduce solutions of the linearized Fokker–Planck equation other than the Boltzmann-like ρ⁽⁰⁾. Different regions will have to serve as sources and sinks for their adjacent regions.

Appendix

For cases in which the force matrix F has degenerate eigenvalues and is not symmetric, so that it may not have a complete set of eigenvectors, we use the Jordan transformation (26) of a general real matrix. The Jordan transformation uses a complete set of independent column vectors v^α with the property

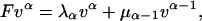[26]

where μ_α is zero if λ_α ≠ λ_α+1 and is either unity or zero for λ_α = λ_α+1. The set of row vectors u^α with the orthonormality property u^αv^β = δ_αβ then satisfies the equation

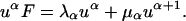[27]

Let us define matrices R and L as 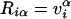and 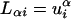. Since the vectors u^α are orthonormal to the set v ^α, we have LR = I, so that these matrices are inverse to one another. R_iα, L_αi are real for real λ_α. For complex λ_α, its complex conjugate is also an eigenvalue, 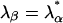, since F is a real matrix. In this case, 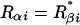, 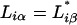. The Jordan transformation is then given by

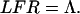[28]

The matrix Λ is now block diagonal, where each nonzero block has identical diagonal elements, which are degenerate eigenvalues, and unity in each place immediately above the diagonal.

With this result, Eq. 12 can be rewritten as

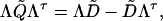[29]

where

[30]

The matrix Q̃ remains antisymmetric and D̃ remains symmetric. In this representation Eq. 29 takes on the form

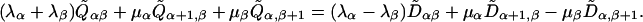[31]

It has the solution, for α < β,

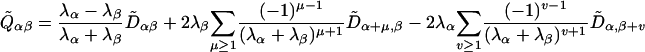[32]

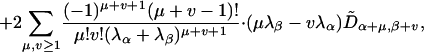where the sums go over all values of μ, ν for which the indices lie within the same block of the block-diagonal matrix Λ. For the case λ_α = λ_β this reduces to

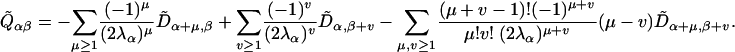[33]

For the case in which all the μ_α are zero, Eq. 32 is equivalent to Eq. 13.

In this Jordan representation of force matrix F, the state variable is transformed by

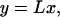[34]

and the corresponding transformation of U is given by

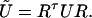[35]

Eq. 11 then becomes

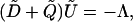[36]

which is form-invariant with Eq. 11 under the Jordan transformation.