Abstract
This study focuses on epilepsy detection using hybrid CNN-SVM and DNN-SVM models, combined with feature dimensionality reduction through PCA. The goal is to evaluate the effectiveness and performance of these models in accurately identifying epileptic patterns. The models were evaluated on two benchmark EEG databases: Epileptic Seizure Recognition and BONN, to ensure robustness and generalization. The integration of Convolutional Neural Networks (CNN) and Deep Neural Networks (DNN) with Support Vector Machines (SVM) is explored, with a particular emphasis on the role of Principal Component Analysis (PCA) in simplifying feature dimensions. In terms of accuracy, for the Epileptic Seizure Recognition dataset, the CNN model achieved a rate of 99.04%, while the DNN model obtained 96.91%. For the BONN dataset, the CNN model achieved an accuracy of 99.78%, and the DNN model reached 96.97%. The introduction of PCA and SVM improved the accuracy of the CNN-SVM-PCA model to 99.42% for the Epileptic Seizure Recognition dataset and 99.96% for the BONN dataset. However, the integration of PCA into the DNN-SVM model led to a significant improvement in accuracy, with a gain of 0.36% for the Epileptic Seizure Recognition dataset and 3.07% for the BONN dataset.
Keywords: Epilepsy detection, Electroencephalogram (EEG), Convolutional Neural Networks (CNN), Deep Neural Networks (DNN), Support Vector Machines (SVM), Principal Component Analysis (PCA)
Subject terms: Learning algorithms, Network models, Electroencephalography - EEG, Pathology, Epilepsy, Epilepsy, Biomedical engineering, Epidemiology, Predictive markers, Computer science, Scientific data
Introduction
Epilepsy is a neurological disorder characterized by recurrent, random seizures caused by abnormal and excessive electrical activity in the brain. Patients must take anti-epileptic medication daily to manage the condition. Epilepsy can affect individuals of any age but is most common in young children and people over the age of 651. There are several types of epileptic seizures depending on the part of the brain affected. The two main types are partial seizures (triggered in a specific part of the brain) and generalized seizures (affecting the entire brain).
Motivation and contributions
To monitor the patient’s condition and define the type of epilepsy, an automatic diagnosis is necessary to determine the appropriate treatment for each patient. The aim of this work is to develop an automatic system capable of detecting epileptic seizures and alerting clinicians to any brain abnormalities without human intervention. Among the most common diagnostic methods today are deep learning methods, which involve extracting features from patient electronic data and categorizing them. Deep learning is commonly used for early diagnosis and providing an accurate examination of a patient’s health status. Machine learning models can detect both epileptic and non-epileptic seizures and alert clinicians to any abnormalities.
This study tests two deep learning models CNN-SVM and DNN-SVM, with two datasets Epileptic Seizure Recognition and BONN, to determine which has the best accuracy in detecting EEG signals. Principal Component Analysis (PCA) is used in the preprocessing phase of the database to simplify and reduce the dimensionality of the data while preserving as much of its variability as possible. The major contributions of this work include the development and evaluation of two EEG signal classification systems based on deep learning models (CNN-SVM and DNN-SVM), the use of PCA to enhance data quality and reduce dimensionality, the presentation of a detailed comparison of the performance of the two systems, highlighting the advantages and limitations of each approach, and the proposal of recommendations for the future improvement of epileptic seizure detection systems based on the obtained results. The implementation section describes the database and the various libraries used in processing, including PCA preprocessing. Finally, two systems, CNN-SVM and DNN-SVM, are presented, discussing the advantages and limitations of each system based on the results obtained by the models used.
Literature survey
There are several prior works in this context that have explored different approaches. For example, Sharmila and Geethanjali2 introduced a DWT model with Naïve Bayes and k-NN classifiers. They utilized an EEG dataset containing 5 sets and 500 unique channels sampled at 173.6 Hz for 23.6 s, collected at the University of Bonn, Germany. Extracting features using DWT, they achieved a precision of 96.47% with 9 data set combinations for classifying both types of epileptic seizures (normal and active).
Ren et al.3 used AR, DWT, WPT, and SampEn for feature extraction, and mRMR, Fisher Score for feature selection to obtain 99.24% Hybrid approach with PCA, 98.95% for Hybrid approach with mRMR and an accuracy ranging from 88.78% to 94.60% for AR, DWT, and WPT. Authors et al.4 used Discrete Wavelet Transform (DWT) for feature extraction, followed by PCA, ICA, and LDA for dimensionality reduction, and classified the fused features using Naive Bayes (NB), Support Vector Machine (SVM), and K-Nearest Neighbor (KNN) to obtain 98.17% for LDA and SVM, 85.58% for PCA and SVM and 90.42% for ICA and SVM. Wang et al.5 employed a dataset of EEG signals from 10 patients at a sampling rate of 200 Hz to build a Directed Transformation Function (DTF) machine learning model. With a fivefold cross-validation, their SVM classifier achieved an accuracy of 98.4% in detecting epileptic seizures.
Wei et al.6 introduced a 3D CNN model for identifying epileptic seizures, achieving a precision of 92.3%. They utilized data from the neurology department of the first hospital affiliated with Xinjiang Medical University, including EEG signals sampled at a frequency of 500 Hz for 13 patients, demonstrating the effectiveness of 3D kernels in classifying epileptic and non-epileptic seizures.
Wang et al.7 proposed an RF model combined with the GSO model for detecting epileptic seizures. They used Fourier transform, multi-paper spectral analysis, partial autocorrelation function (PACF), and short-term Fourier transform (STFT) as feature extractors on a dataset from 25 patients, achieving an accuracy of 96.7%.
Peachap et al.8 introduced an approach based on Laguerre Polynomial Wavelets for decomposing EEG signals in the time and frequency domains, and artificial neural networks (ANN) and support vector machines (SVM) for classification. They utilized a dataset comprising 500 single-channel EEG signals of 5 classes, each lasting 23.6 s, achieving an accuracy rate of 99%.
Matin et al.9 proposed a hybrid model based on PCA, ICA, and SVM to predict epileptic seizures using EEG signals from 5 subsets, each with 100 unique channels sampled at 173.6 Hz for 23.6 s. The accuracy of the proposed model is 99%, which outperforms other models.
Authors10 propose a hybrid method combining PCA, FICA, and KICA for dimensionality reduction, statistical feature extraction, and SVM classification to classify epileptic seizure patterns from EEG signals, achieving an accuracy of 99.60%.
Authors11 combined the Discrete Wavelet Transform (DWT) with dimensionality reduction techniques, including PCA, LDA, and ICA, for feature extraction, followed by SVM for EEG signal classification. The results showed that the LDA + SVM combination achieved the highest accuracy at 96.2%, followed by PCA + SVM with 87.4%, and ICA + SVM with 84.3%. Dhanka S and Maini12 proposed the Random Forest (RF) algorithm to predict heart diseases (HD) based on general physiological parameters. The RF algorithm achieved an accuracy of 90.16%.
Alalayah et al.13 propose the use of discrete wavelet transform (DWT) for feature extraction, as well as dimensionality reduction techniques such as PCA and t-SNE. Five classification algorithms are evaluated: XGBoost, K-nearest neighbors (KNN), decision tree (DT), random forest (RF), and multilayer perceptron (MLP). The results show that the random forest classifier with DWT + PCA achieved an accuracy of 97.96%, while with DWT + t-SNE, the accuracy reached 98.09%. The MLP classifier with PCA + K-means achieved an accuracy of 98.98%.
Dhanka and Maini14 implemented the Min-Max normalization technique for data preprocessing and machine learning models, namely Logistic Regression, Support Vector Classifier, Naïve Bayes, and Random Forest for classification, with the highest accuracy being that of the RF model at 95.93%.
Abhinav et al.15 applies a standard techniques such as handling missing values, formatting, balancing, and directory analysis, as well as Pearson correlation for feature selection to preprocess the UCIML repository database before applying several algorithms such as Random Forest classifier, Linear Discriminant Analysis, Support Vector Machine, Extreme Gradient Boosting, Gaussian Naive Bayes, and Logistic Regression. The proposed optimized RF model achieved impressive performance metrics, including an accuracy of 95.24%, a precision of 100%, a sensitivity of 89.47%, and a specificity of 100%.
Authors16 employed deep learning (BiLSTM) and machine learning models (XGBoost, Random Forest, and SVM) for epileptic seizure classification. The results showed that BiLSTM achieved the highest accuracy of 96.85%, followed by XGBoost and Random Forest with 95.74%, while SVM obtained 94.23%.
Authors17 used Conv1D + LSTM, PCA for feature reduction, and dropout layers, comparing models such as LSTM, CNN, BiLSTM, and GRU for epileptic seizure recognition from EEG recordings. The results showed that LSTM achieved an accuracy of 96,7% before PCA and 97% after PCA with 50% feature retention. CNN models ranged from 79% to 84,9%before PCA and from 79,6% to 82,7% after PCA. BiLSTM achieved 97,1% before PCA and 97,7% after PCA, while GRU reached 97% before PCA and 97,4% after PCA.
In Table 1 below, the characteristics of each method are presented:
Table 1.
Recapitulative main recent research works for EEG analysis.
| Article | Year | Method | Caracteristics | Accuracy |
|---|---|---|---|---|
| 2 | 2016 | DWT model with Naïve Bayes and k-NN classifiers to predict the epileptic seizures | The authors employed both Naïve Bayes and K-NN classifiers for the classification of statistical features derived from DWT | 96.47% |
| 3 | 2016 | Extracting and selecting features from raw EEG signals using techniques such as AR, DWT, WPT, and SampEn for feature extraction, and mRMR, Fisher Score for feature selection and transformation | The authors employed AR, DWT, WPT, and SampEn for feature extraction, and mRMR, Fisher Score for feature selection | Hybrid approach with PCA : 99.24% |
| Hybrid approach with mRMR : 98.95% | ||||
| AR, DWT, and WPT :Accuracy ranging from 88.78% to 94.60% | ||||
| 4 | 2017 | DWT-based feature extraction with dimensionality reduction and Bayesian classification | The authors used Discrete Wavelet Transform (DWT) for feature extraction, followed by PCA, ICA, and LDA for dimensionality reduction, and classified the fused features using Naive Bayes (NB), Support Vector Machine (SVM), and K-Nearest Neighbor (KNN) | LDA and Support Vector Machine (SVM): 89.17% |
| PCA and Support Vector Machine (SVM): 85.58% | ||||
| ICA and Support Vector Machine (SVM): 90.42% | ||||
| 5 | 2018 | Directed transform function (DTF) machine learning model to predict the epileptic seizures |
EEG signal segmentation using a sliding window approach Total brain connectivity classification using SVM |
98.4% |
| 6 | 2018 | 3D CNN model to detect the epileptic seizures |
The initial attempt to utilize a CNN3D model Full utilization of signal information This model outperforms the CNN2D model |
92.3% |
| 7 | 2019 | RF model combined with the GSO model for detecting epileptic seizures |
Visualization of features using Fourier Transform after normalization Dimensionality reduction of features through PCA Involvement of a novel Random Forest algorithm combined with grid search optimization |
96.7% |
| 8 | 2019 | A Laguerre polynomial wavelets, ANN, and SVM models to detect the epileptic seizures | The authors employed EEG signal decomposition using Laguerre Polynomial Wavelets, and either ANN or SVM for classification | 99% |
| 9 | 2019 | Machine learning hybrid model namely PCA, ICA and SVM to predict the epileptic seizures | The authors used SVM for classifying the different components obtained from both PCA and ICA techniques | 99% |
| 10 | 2019 | A hybrid scheme using PCA and ICA based statistical feature for epileptic seizure recognition | The authors propose a hybrid method combining PCA, FICA, KICA for dimensionality reduction, statistical feature extraction, and SVM classification to classify epileptic seizure patterns from EEG signals | 99.60% |
| 11 | 2020 | the DWT-based EEG classification with dimensionality reduction and SVM method | The authors combined the Discrete Wavelet Transform (DWT) with dimensionality reduction techniques (PCA, LDA, ICA) for features extraction and using SVM for EEG signal classification | LDA + SVM: 96.2% |
| ICA + SVM: 84.3% | ||||
| PCA SVM: 87.4% | ||||
| 12 | 2021 | Random Forest (RF) for heart disease detection | Random Forest (RF) with cross validation | 90.16% |
| 13 | 2023 | Classification algorithms based on t-distributed stochastic neighbor embedding and K-means | Multiple Machine Learning Approaches with discrete wavelet transform (DWT) and Principal Component Analysis (PCA) | 98.98% |
| 14 | 2023 | Multiple machine learning intelligent approaches for the heart disease diagnosis | Multiple machine learning approaches with min-max normalization technique | 95.93% |
| 15 | 2024 | Standard preprocessing techniques with Pearson correlation for feature selection, followed by ML algorithms | The authors employed Random Forest, Linear Discriminant Analysis, Support Vector Machine, Extreme Gradient Boosting, Gaussian Naive Bayes, and Logistic Regression classifiers for arrhythmia detection | 95.24 |
| 16 | 2024 | combination of deep learning (BiLSTM) and machine learning (XGBoost, RF, SVM) | The authors employed deep learning (BiLSTM) and machine learning (XGBoost, RF, SVM) | BiLSTM: 96.85% |
| XGBoost: 95.74% | ||||
| Random Forest (RF): 95.74% | ||||
| Support Vector Machine (SVM): 94.23% | ||||
| 17 | 2024 | Conv1D + LSTM with PCA and dropout optimization for epileptic seizure recognition | The authors use Conv1D + LSTM, PCA for feature reduction, dropout layers, and compare models like LSTM, CNN, BiLSTM, and GRU for epileptic seizure recognition from EEG recordings | LSTM: 0.967 (before PCA), 0.970 (after PCA with 50% features). |
| CNN: 0.79 to 0.849 (before PCA), 0.796 to 0.827 (after PCA). | ||||
| BiLSTM: 0.971 (before PCA), 0.977 (after PCA) | ||||
| GRU: 0.970 (before PCA), 0.974 (after PCA) |
However, all these models achieve satisfactory performance, but it is important to note that each method has its own advantages and limitations. For example, in the first method2, the authors found that three statistical features derived from EEG signals are important for better seizure detection, and that the K-NN classifier outperforms Naive Bayes. However, they noted that there is another, more effective method based on decomposing EEG signals into multiple sub-signals and using ANN classification to achieve an accuracy rate of 98.27%.
In the method3, the authors presents a feature extraction method for EEG signals using a combination of techniques like AR, DWT, WPT, and SampEn. After information fusion, feature selection is performed using methods like PCA and mRMR, which enhance the classification performance. The results show that the hybrid approach with PCA achieves an accuracy of 99.24% on test data, while the approach with mRMR achieves 98.95%, outperforming other methods like AR, DWT, and WPT, with performances ranging from 88.78% to 94.60%. The advantages include better exploitation of EEG data through the fusion of different techniques, optimizing classification results. However, this approach can be complex and computationally expensive, which may limit its application on large datasets. The method proposed in4 detects epileptic seizures by decomposing EEG signals using Discrete Wavelet Transform (DWT), followed by dimensionality reduction with PCA, ICA, and LDA. Extracted features are fused and classified using SVM, Naive Bayes (NB), and K-Nearest Neighbor (KNN). The best performance was achieved with LDA and NB, reaching 100% accuracy on the Bonn dataset, followed by 89.17% for LDA+SVM, 80.42% for LDA+KNN, 89.92% for PCA+NB, 85.58% for PCA+SVM, 80.42% for PCA+KNN, 82.33% for ICA+NB, 90.42% for ICA+SVM, and 90% for ICA+KNN. However, its generalization to larger datasets remains uncertain, requiring validation on diverse datasets like CHB-MIT.
As for method5, connectivity derived from DTF can characterize causal and dynamic interaction patterns between brain areas, but its only limitation is its dependence on multi-channel signals and the requirement for a large number of subjects for validation.
Method6 represents a first attempt to use 3D CNN models, allowing for complete exploitation of multi-channel signal information without prior engineering. However, it can serve as a reference for further research facilitating epileptic seizure detection through deep learning.
Moving on to method7, where the authors employed a novel random forest algorithm combined with grid search optimization. However, detection may be affected in case of high noise, so they intend to optimize the model and make it more robust to the high noise present in EEG signals.
In method8, researchers proposed an approach allowing EEG signal decomposition by Laguerre Polynomial Wavelets and ANN model for classification, but they found that a classic case of overfitting occurs when using their model with a quadratic kernel regardless of the wavelet used.
In the method9, the authors found that using PCA with SVM only achieves 70% accuracy, and it is preferable to combine ICA with PCA for better performance.
For the method10, the researchers proposes a hybrid method for classifying epileptic seizure patterns from EEG signals by combining several dimensionality reduction techniques, such as PCA, FICA, and KICA, followed by statistical feature extraction. The significant components from PCA and ICA are used to extract features, and an SVM classifier is applied for seizure classification. The approach achieves an accuracy of 99.60%, and its advantage lies in its ability to extract efficient and robust features through the combination of these dimensionality reduction techniques. However, it may suffer from increased complexity due to the integration of multiple processing steps and the potential impact of hyperparameters on overall performance. The paper11 proposes a method for classifying EEG signals using Discrete Wavelet Transform (DWT) combined with dimensionality reduction techniques such as PCA, LDA, and ICA, followed by classification with an SVM. The EEG signals are first decomposed into frequency sub-bands using DWT, followed by the extraction of statistical features. These reduced features are then used to train an SVM model. The results show that the LDA+SVM combination provides the best performance with a classification rate of 96.2%, followed by ICA+SVM (84.3%) and PCA+SVM (87.4%). This approach is particularly useful for non-stationary biomedical signals and could be applied to the diagnosis of Alzheimer’s disease. However, challenges remain, such as managing generalization error and the diversity of class distributions in EEG signals.
The authors12 demonstrate that this method requires less computational time for prediction without mentioning other limitations.
In the method13, the researchers note that the complexity of the algorithms may require significant computational resources. The results can vary depending on the quality and diversity of the training data. Generalizing the results to other types of data or populations may be limited without additional validation.
In the method14, From this study, the authors concluded that the overall performance of the RF model is the best among all the models used in their work, due to advanced decision rules and better training. The authors mention that with the diversity of large datasets, there is tremendous potential for machine learning models to improve the accuracy of heart disease prediction and to make better-informed decisions.
For the method15, the authors noted that their study requires further exploration of RF hyperparameter optimization using other advanced methods. Additionally, integrating their model with other models or preprocessing techniques could lead to more accurate detection. In the paper16, the authors proposes an epilepsy seizure detection method by combining deep learning and machine learning models to enhance diagnostic accuracy from EEG signals. The approach integrates BiLSTM (96.85%), XGBoost (95.74%), Random Forest (95.74%), and SVM (94.23%), selected after comparison with CNN and MLP. Two aggregation strategies were tested: simple fusion of predictions and performance-based weighting, where BiLSTM, achieving the highest accuracy, received the most weight. The ensemble model reached 98.52% accuracy and a 96.32% F1 score, demonstrating its effectiveness. However, limitations remain, including BiLSTM’s computational cost, XGBoost’s sensitivity to hyperparameters, and SVM’s risk of overfitting. Additionally, the segmentation into 1-s windows may restrict the capture of complex temporal dynamics, requiring further exploration with more diverse datasets and advanced temporal modeling techniques.
Finally, in tis paper17 the researchers proposes an approach to optimize epileptic seizure recognition using deep learning models applied to EEG recordings. Initially, the Conv1D + LSTM architecture achieved 0.975 accuracy. After applying PCA with varying feature reduction percentages, accuracy improved to 0.981 with 80% of features retained, and adding dropout layers maintained 0.981 for Conv1D + LSTM with 50% features. LSTM alone showed 0.967 before PCA, reaching 0.970 with 50% features after PCA. CNN models performed lower, with accuracy ranging from 0.79 to 0.849 before PCA and 0.796 to 0.827 after. BiLSTM and GRU models achieved 0.971 and 0.970 before PCA, improving to 0.977 and 0.974 after. These findings highlight the positive impact of dimensionality reduction on model accuracy for seizure detection. However, challenges such as dataset size, class imbalance, and the lack of real-time evaluation remain, necessitating improvements with larger, more diverse datasets.
Although the methods mentioned above have made significant contributions in the field, they also present limitations that require further research and improvements. These challenges include issues such as signal decomposition, sensitivity to noise, and overfitting, which can hinder the accuracy and reliability of seizure detection systems. In this context, this study aims to address these limitations by evaluating the performance of two deep learning models, CNN-SVM and DNN-SVM, while employing techniques to prevent overfitting and using Principal Component Analysis (PCA) to indirectly mitigate the effects of noise by reducing the dimensionality of the data while preserving the most significant features. This approach aims to enhance the detection of epileptic seizures with greater accuracy and robustness, contributing to the development of more effective and efficient diagnostic systems for clinical use.
Methods
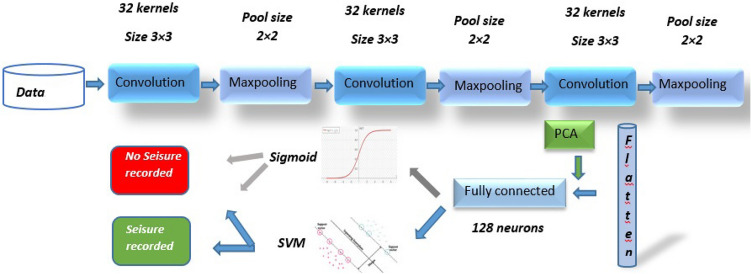
In this study, an implementation of a classification pipeline is proposed using a CNN (Convolutional Neural Network) model to extract features from the data, then applying PCA (Principal Component Analysis) to reduce the dimensionality of these features before training an SVM (Support Vector Machine) model for classification (Fig. 1).
Fig. 1.
The automatic system for epileptic seizure detection.
This comprehensive approach enables gaining insights into the impact of PCA on feature representation, the effectiveness of DNN and CNN models in feature extraction, and the performance of SVM in classification.
Dataset description
Epileptic seizure recognition data set
In this study, the database used is a preprocessed and remodeled version of the popular Epileptic Seizure Recognition Database, consisting of five different sections18. Each section contains 100 recordings of 23.6 s, with a sampling frequency of 173.6 Hz, from 100 patients. In total, the database contains 11,500 instances (rows), where each row represents a vector of 178 dimensions (sensors or columns) and a response variable y with five classes. More precisely, y is included in 1, 2, 3, 4, 5. Class 1 corresponds to the recording of epileptic activity, class 2 to the recording in the epileptic area, class 3 to the recording in a healthy area distant from the epileptic area, class 4 to the recording of the EEG signal with eyes closed, and class 5 to the recording of the EEG signal with eyes open.
The Classes 2, 3, 4, and 5 are assigned a value of 0, indicating that no seizure is recorded, while class 1 is assigned a value of 1, indicating that a seizure is recorded.
BONN dataset
To test the robustness of the models, a dataset used in this research comes from EEG segments obtained from the University of Bonn, Germany19. These signals were recorded from a 128-channel acquisition system in a non-invasive manner using a 12-bit analog-to-digital converter. Each set contains a total of 100 single-channel EEG signals (text files) with 4097 sample points per channel. Each signal has a duration of 23.6 s and a sampling frequency of 173.61 Hz. Five sets of EEG from patients were extracted from multi-channel EEG recordings and are named A, B, C, D, and E. Sets A and B correspond to surface EEGs recorded during eye closure and eye opening in healthy patients, respectively. Sets C and D are intracranial EEGs recorded during seizure-free periods, from seizure-generating zones and regions outside these zones in epileptic patients. Set E is an intracranial EEG of an epileptic patient during a seizure.
Data preprocessing
Epileptic seizure recognition data set
As mentioned earlier, this dataset has already been preprocessed, and the five classes were initially balanced, with each class containing 2300 samples. However, for binary classification, after binarization, classes 0 and 1 became imbalanced. To address this imbalance, the SMOTE (Synthetic Minority Oversampling Technique) method was applied to generate new synthetic instances for the minority class, thus reducing the gap between the classes(Table 2).
Table 2.
Data partition before and after SMOTE with the number of instances for the Epileptic Seizure Recognition Data Set.
| Partition | Before SMOTE sampling | After SMOTE sampling | ||
|---|---|---|---|---|
| Training | Test | Training | Test | |
| 10:90 |
Class 0: 8280 Class 1: 2070 Total: 10350 |
Class 0: 920 Class 1: 230 Total: 1150 |
Class 0: 10350 Class 1: 10350 Total: 20700 |
Class 0: 8280 Class 1: 2070 Total: 10350 |
| 20:80 |
Class 0: 7360 Class 1: 1840 Total: 9200 |
Class 0: 1840 Class 1: 460 Total: 2300 |
Class 0: 9200 Class 1: 9200 Total: 18400 |
Class 0: 1840 Class 1: 460 Total: 2300 |
| 30:70 |
Class 0: 6440 Class 1: 1610 Total: 8050 |
Class 0: 2760 Class 1: 690 Total: 3450 |
Class 0: 8050 Class 1: 8050 Total: 16100 |
Class 0: 2700 Class 1: 690 Total: 3450 |
BONN data set
A band-pass filter with cutoff frequencies of 0.53 Hz and 40 Hz was applied to the data to retain the frequencies of interest while eliminating undesirable frequencies. Additionally, to address the class imbalance, the SMOTE (Synthetic Minority Oversampling Technique) method was used to generate new synthetic instances for the minority class (Table 3).
Table 3.
Data partition before and after SMOTE with the number of instances for the BONN Data Set.
| Partition | Before SMOTE sampling | After SMOTE sampling | ||
|---|---|---|---|---|
| Training | Test | Training | Test | |
| 10:90 |
Class 0: 14751 Class 1: 3685 Total: 18436 |
Class 0: 1637 Class 1: 412 Total: 2049 |
Class 0: 18436 Class 1: 18436 Total: 36872 |
Class 0: 1637 Class 1: 412 Total: 2049 |
| 20:80 |
Class 0: 13096 Class 1: 3292 Total: 16388 |
Class 0: 3292 Class 1: 805 Total: 4097 |
Class 0: 13096 Class 1: 13096 Total: 26192 |
Class 0: 3292 Class 1: 805 Total: 4097 |
| 30:70 |
Class 0: 11446 Class 1: 2893 Total: 14339 |
Class 0: 4942 Class 1: 1204 Total: 6146 |
Class 0: 14339 Class 1: 14339 Total: 28678 |
Class 0: 4942 Class 1: 1204 Total: 6146 |
In Tables 2 and 3 , only the training dataset is subjected to the SMOTE technique to address class imbalance. This approach ensures that the test set remains representative of real, unmodified data, thereby providing an accurate evaluation of the model’s ability to generalize to unseen and naturally distributed data.
The train-test ratio used in this study is 20:80 due to its optimal balance between training and evaluation, ensuring a robust assessment of the model’s performance on a sufficient amount of data while having a large enough test set to evaluate its generalization capability.
As mentioned previously, the Epileptic Recognition dataset used in this study is already pre-processed; however, it is essential to further prepare the data to ensure compatibility with the proposed model. First, the data was normalized to float32 to ensure the consistency of the data type before the model was trained. Next, this data was reshaped while adding an extra dimension 1 at the end of the data shape to represent the channels used.
Once the data was prepared, the model treated it as a one-dimensional time series. In particular, each neuron in the first layer is connected to a window or patch of size 178, which means that each neuron must sequentially process 178 sensor readings (value by value) and consider each value as a separate channel while maintaining the spatial and temporal relationship between them to ensure good feature extraction.
For the BONN dataset, the CNN model processes the input data in a similar manner to the first dataset. By reshaping the data to have a shape of (100, 1), each neuron in the first layer of the CNN model is connected to a window or patch of size 100. This means that each neuron sequentially processes 100 sensor readings (value by value) and considers each value as a separate channel. This approach maintains the spatial and temporal relationship between the values to ensure good feature extraction.
In this step, two deep learning models, CNN and DNN, were tested to determine which one of them is the optimal feature extractor.
Feature extraction
After data collection and preprocessing, two neural network architectures, DNN and CNN, will be evaluated to determine the optimal feature extractor. Additionally, a custom PCA layer will be integrated between the layers of each model to reduce the dimensionality of the extracted features.
-
The Convolutional Neural Network (CNN):
A convolutional neural network architecture with three convolutional layers and three max-pooling layers has been developed for extracting features from EEG data stored in a CSV file.-
The convolutional neural network (CNN):A convolutional neural network architecture with three convolutional layers and three max-pooling layers has been developed for extracting the features of EEG data stored in a CSV file.

- Convolution: The convolution operation for an input
 and a filter
and a filter  is given by:
is given by:
where
1 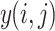 is the output of the convolution at position
is the output of the convolution at position  ,
,  and
and 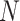 are the dimensions of the filter, and
are the dimensions of the filter, and  and
and  are indices iterating over the filter dimensions.
are indices iterating over the filter dimensions. 
- Pooling: The pooling operation (e.g., max-pooling) for an input
 is given by:
is given by:
where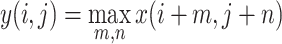
2 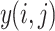 is the output of the pooling operation at position
is the output of the pooling operation at position  , and
, and  and
and  iterate over the pooling window.
iterate over the pooling window. 
- Activation function: The most commonly used activation function in CNNs is the Rectified Linear Unit (ReLU), defined by:
This function retains positive values and eliminates negative values, introducing non-linearity into the model.
3
The input data was introduced as univariate time sequences at the input layer, which consists of 178 neurons. Each neuron corresponds to a sensor reading in the sequence. Then, at the output of this layer, 32 feature maps are generated through the convolutional filter (eq.1). Subsequently, following this Maxpooling operation20, the length of the features is reduced to 89 while maintaining 32 feature maps (eq.2). A dense layer21 with 128 units using the RELU activation function is added (eq.3). Before adding a dense output layer with a sigmoid activation function suitable for binary classification, PCA was incorporated to reduce the dimensions of the features extracted by the CNN model layers.
-
-
The Deep neural network DNN :

- Forward propagation: The output of a neuron
 in layer
in layer  is given by:
is given by:
where:
4 
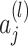 is the activation of neuron
is the activation of neuron  in layer.
in layer.
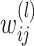 is the weight between neuron
is the weight between neuron 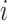 in layer
in layer 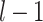 and neuron
and neuron 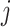 in layer
in layer  .
.
 is the activation of neuron
is the activation of neuron  in layer
in layer  .
.
 is the bias of neuron
is the bias of neuron  in layer
in layer  .
.
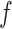 is the activation function applied to the weighted sum of inputs.
is the activation function applied to the weighted sum of inputs.
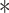
- Backpropagation: The update of weights
 and biases
and biases 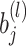 during training is given by:
during training is given by:
and:
5
where: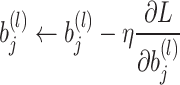
6 
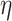 is the learning rate.
is the learning rate.
 is the loss function.
is the loss function.
 is the gradient of the loss with respect to the weight
is the gradient of the loss with respect to the weight  .
.
 is the gradient of the loss with respect to the bias
is the gradient of the loss with respect to the bias  .
.
A simple DNN model with three dense layers was also used for the extraction of features from the EEG data, as shown in (Fig. 3).
The model starts with three dense layers containing respectively 128, 64, and 32 neurons, each using a ReLU activation function. Finally, the output layer utilizes a sigmoid activation function to obtain class probabilities in a binary classification problem. Unlike CNN models, PCA was used at the beginning of the DNN model process to reduce feature dimensionality because DNN models are highly sensitive to overfitting. Therefore, right from the start, the amount of redundant or non-significant data that could be introduced into the later layers of the DNN model was limited.
Fig. 2.
The architecture of the CNN.
Fig. 3.
The architecture of the DNN.
However, the focus is on feature extraction, and the classification part will involve integrating another algorithm, such as a classifier.
Dimensionality reduction of features using PCA
In this work, the PCA principal component analysis is used during feature extraction to reduce the dimensionality of features while retaining their important information for classification and minimizing execution time22.
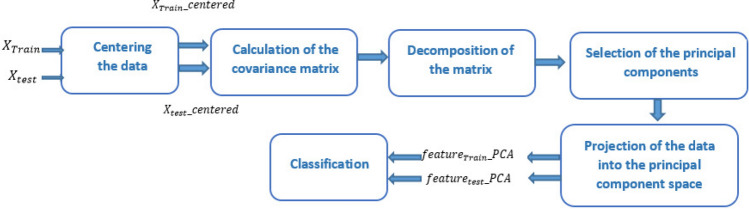
Here are the key steps in Principal Component Analysis (PCA) (Fig. 4):
Centering the data: To calculate the covariance matrix, it is necessary to center the data by subtracting the mean of each variable (column) from each observation (row) in the dataset. In this case, the data matrix is the set of training data. To center this data, the average of each column is subtracted from each sensor reading associated with that column, and the same calculation is performed for the test data.
- Calculating the covariance matrix: After centering the data, the covariance matrix is calculated using the following formula:
where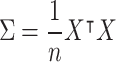
7  is the matrix of the centered data (each column represents a variable, each row represents an observation), and
is the matrix of the centered data (each column represents a variable, each row represents an observation), and  is the number of observations23.
is the number of observations23. - Decomposition of the covariance matrix: In this step, the covariance matrix
 is decomposed into its eigenvectors and associated eigenvalues. This is expressed by the following formula:
is decomposed into its eigenvectors and associated eigenvalues. This is expressed by the following formula:
where
8  is the matrix whose columns are the eigenvectors of
is the matrix whose columns are the eigenvectors of  , and
, and  is the diagonal matrix containing the eigenvalues.
is the diagonal matrix containing the eigenvalues. Selection of principal components: In this step, the eigenvalues
 and the resulting eigenvectors
and the resulting eigenvectors 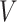 are ranked in descending order. The first
are ranked in descending order. The first  eigenvectors corresponding to the highest
eigenvectors corresponding to the highest  eigenvalues are the selected principal components, where
eigenvalues are the selected principal components, where  is the fixed number of principal components to be retained after dimensionality reduction.
is the fixed number of principal components to be retained after dimensionality reduction.- Data projection: Assuming that
 is the centered data matrix, the projection is done by multiplying
is the centered data matrix, the projection is done by multiplying  by the first
by the first  eigenvectors:
eigenvectors:
where
9  is the projected data matrix,
is the projected data matrix,  is the centered data matrix, and
is the centered data matrix, and 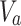 is the matrix containing the first
is the matrix containing the first  eigenvectors. After projecting the training data into the principal component space, the new transformed features are stored in feature_PCA_Train. Similarly, for the entire test set, the new transformed features are stored in feature_PCA_Test to be classified by the classifier.
eigenvectors. After projecting the training data into the principal component space, the new transformed features are stored in feature_PCA_Train. Similarly, for the entire test set, the new transformed features are stored in feature_PCA_Test to be classified by the classifier.
Fig. 4.
The dimensionality reduction of features using PCA.
Feature classification using SVM
In the classification phase, the SVM classifier’s performance in assigning the PCA-reduced features to specific classes will be assessed, and its potential as an alternative to the sigmoid activation function in neural networks will be explored. The Support Vector Machine (SVM) is a machine learning algorithm used for classification and regression. It can be used for the classification of linear models, but it can also be used for nonlinear data using the functions of its kernels RBF, linear, sigmoid, and poly24. This algorithm seeks to find an optimal separation hyperplane in feature space that maximizes the margin between the two classes. This equation (4) represents the decision boundary that the SVM algorithm uses to classify data points into two classes.
 |
10 |
where: f(x) is the decision function that determines the class of the sample x.
w is the weight vector.
x is the feature vector of the sample.
b is the bias term.
The sign function, which returns +1 if the expression is positive, indicating that  belongs to the positive class, and -1 if the expression is negative, indicating that
belongs to the positive class, and -1 if the expression is negative, indicating that  belongs to the negative class.
belongs to the negative class.
Results and discussion
Performance comparison of different methods
After 50 epochs, the results from different machine learning models (CNN, DNN) with different configurations (with or without SVM, PCA) were achieved, showing several performance metrics, including accuracy, error, execution time, CPU usage, and memory usage:
The models was also evaluated using different partition ratios, including 70:30, 80:20, and 90:10, to compare performance in the Table 4.
Table 4.
Performance comparison of CNN-PCA-SVM and DNN-PCA-SVM on Epileptic Seizure Recognition Database and BONN datasets.
| Dataset | Partitions | CNN-PCA-SVM | DNN-PCA-SVM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Acc | Loss | Spe | Sens | F1-score | Acc | Loss | Spe | Sens | F1-score | ||
| ESR | 10:90 | 99.13 | 0.0087 | 98.23 | 97.36 | 97.8 | 97.47 | 0.0252 | 19.82 | 100 | 33.07 |
| 20:80 | 99.34 | 0.0065 | 98.67 | 96.95 | 97.8 | 97.26 | 0.0274 | 95.21 | 90.86 | 93 | |
| 30:70 | 98.81 | 0.0118 | 97.26 | 96.84 | 97.06 | 97.30 | 0.0269 | 97.007 | 92.75 | 93 | |
| BONN | 10:90 | 99.90 | 0.00098 | 99.51 | 100 | 99.94 | 99.85 | 0.0014 | 99.27 | 100 | 99.91 |
| 20:80 | 99.96 | 0.00036 | 99.25 | 99.37 | 99.84 | 99.95 | 0.00048 | 99.75 | 100 | 99.87 | |
| 30:70 | 99.95 | 0.00049 | 99.83 | 99.75 | 99.97 | 99.93 | 0.00066 | 99.75 | 99.91 | 99.96 | |
The results show that the model maintains remarkable and reliable performance across these different partitions, confirming the robustness of the approach. The train-test ratio used in this study is 20:80, providing an optimal balance between training and evaluation. This ensures a thorough assessment of the model’s performance on a sufficient amount of data while maintaining a large enough test set to evaluate its generalization capability.
For Epileptic Seizure Recognition Database:
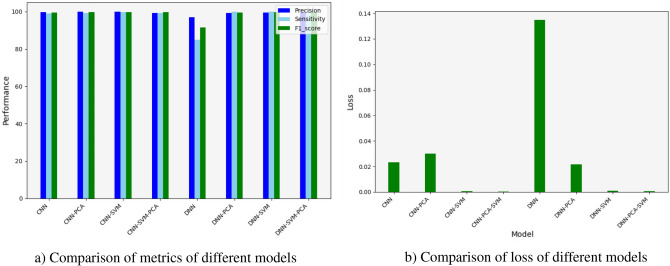
The results presented in Figs. 5 and 6 show that the CNN model outperforms the DNN model in terms of feature extraction, although it requires significant execution time. This result was expected due to the use of a complex architecture with many parameters, demanding substantial CPU resources and large memory capacity to achieve an accuracy of 99,04% and an error rate of 0.0359. In comparison, the DNN model only achieves an accuracy of 96,91% and an error rate of 0.1119 (Fig. 5a and b) due to the simplicity of its architecture. The time complexity of these models is directly influenced by the feature extraction, dimensionality reduction, and classification stages. The CNN models, particularly without dimensionality reduction, account for about 35% of the total cumulative execution time of the various models due to the intensive convolution operations across multiple layers (Fig. 6a and b). Adding PCA reduces this execution time by approximately 35%, demonstrating the efficiency of dimensionality reduction in alleviating computational costs.
Fig. 5.
(a) Comparison of metrics of different models. (b) Comparison of loss of different models.
Fig. 6.
(a) Execution time for each model. (b) CPU usage and memory usage for each model.
In contrast, models combining CNN and SVM, such as CNN-SVM and CNN-SVM-PCA, show increased execution times, representing about 36% and 25% of the total, respectively, as SVM training, especially with complex kernels, requires substantial resources to optimize the decision boundaries. On the other hand, DNN-based models exhibit significantly lower execution times, contributing to only about 5% of the overall time due to the simplicity of the architecture, making them a more computationally efficient alternative.
According to graph 6.b, it is observed that the CNN and CNN-PCA models have the highest CPU consumption, reaching around 55%, while their memory usage remains low. In contrast, the DNN models and their variants (with PCA and SVM) consume significantly fewer CPU resources, with a notable reduction when dimension reduction (PCA) is applied. Models incorporating SVM, such as CNN-SVM and DNN-SVM, exhibit slightly higher memory usage compared to the other models. These results suggest that integrating PCA helps reduce the overall computational cost, particularly for DNN models.
The Table 5 highlights the differences in execution time, CPU usage, and memory usage across various models for the ESR dataset. The CNN-PCA model shows substantial time consumption for classification (218.33 s) and high memory usage (305.34 MB). The CNN-SVM model, while having a long training time (516.59 s), is efficient in terms of feature extraction (6.92 s) and classification (2.11 s). The CNN-PCA-SVM model balances time and resource usage effectively, with a total of 13.57 s for feature extraction, PCA, and classification. The DNN-PCA model is quick in PCA reduction (0.10 s) but has minimal CPU usage during feature extraction.
Table 5.
Summary of model results for the ESR dataset.
| Model | Time (s) | CPU usage (%) | Memory usage (MB) |
|---|---|---|---|
| CNN-PCA | |||
| Feature extraction | 7.39 | 1.60 | 52.61 |
| PCA analysis | 5.67 | 99.40 | 27.49 |
| CNN-SVM | |||
| Feature extraction | 6.92 | – | – |
| SVM classification | 2.11 | − 0.20 | 0.0 |
| CNN-PCA-SVM | |||
| CNN feature extraction | 7.62 | 1.30 | 0.40 |
| PCA reduction | 0.16 | 93.80 | − 0.20 |
| SVM classification | 5.79 | 98.10 | 0.10 |
| DNN-PCA | |||
| DNN training | 5.76 | 0.40 | − 0.20 |
| PCA reduction | 0.10 | 100.00 | 0.00 |
| DNN-SVM | |||
| Feature extraction | 4.52 | – | – |
| SVM classification | 0.74 | 0.90 | 0.80 |
| DNN-PCA-SVM | |||
| DNN feature extraction | 7.80 | 0.70 | − 0.03 |
| PCA reduction | 0.39 | 98.50 | 0.01 |
| SVM classification | 60.26 | 96.90 | − 0.04 |
| CNN | |||
| Execution time | 321.012 | 54.10 | 0.5 |
| DNN | |||
| Execution time | 38.174 | 35.80 | 0.40 |
The DNN-SVM model demonstrates efficient classification (0.74 seconds), with low CPU (0.90%) and memory usage (0.80 MB). Lastly, the DNN-PCA-SVM model has higher computational costs, especially in SVM classification (60.26 s), which results in significant CPU usage (96.90%) but relatively low memory use (− 0.04 MB).
For BONN Database:
The results presented in Figs. 7 and 8 show that the CNN model outperforms the DNN model in terms of feature extraction, although it requires significant execution time. This result was expected due to the use of a complex architecture with many parameters, demanding substantial CPU resources and large memory capacity to achieve an accuracy of 99.78% and an error rate of 0.02320. In comparison, the DNN model only achieves an accuracy of 96,97% and an error rate of 0.1349 (Fig. 7a and b) due to the simplicity of its architecture.
Fig. 7.
(a) Comparison of metrics of different models. (b) Comparison of loss of different models.
Fig. 8.
(a) Execution time for each model. (b) CPU usage and memory usage for each model.
According to the graph (8.a), the time complexity of these models is directly influenced by the feature extraction, dimensionality reduction, and classification stages. The CNN models, without dimensionality reduction, account for a significant portion of the total cumulative execution time, with CNN taking about 32% of the total time due to the costly convolution operations across multiple layers. Adding PCA reduces this time by approximately 28%, as it helps compress the feature dimensions, speeding up the process. On the other hand, combined models such as CNN-SVM and CNN-SVM-PCA increase the total execution time, reaching 35% and 38% respectively, as training the SVM requires substantial computational resources to find the optimal separating hyperplane, especially with nonlinear kernels.
In contrast, DNN-based models are much faster, contributing to only about 5% of the total execution time, as they do not involve the complex convolutional layers present in CNNs. Although adding PCA or SVM to DNN models increases their execution time slightly, they still remain faster than their CNN counterparts. For instance, DNN-PCA reduces the classification time while preserving essential discriminative features. These findings highlight the role of PCA in reducing execution time while maintaining system performance, thus achieving a balance between time constraints and accuracy requirements. However, the integration of an SVM into DNN models, similar to CNNs, improves accuracy but comes at the cost of increased computational resources and processing time.In terms of CPU and memory usage, as shown in graph 8.b, each model exhibits distinct behavior over 50 epochs. CNN-based models, such as ’CNN’ and ’CNN-PCA’, show low CPU and memory usage, with minimal variations throughout the epochs. Models combining SVM or PCA with CNN or DNN, like ’CNN-SVM’ and ’DNN-SVM-PCA’, display moderate costs, with a slight increase in both CPU and memory usage as the epochs progress. DNN-based models, such as ’DNN’ and ’DNN-PCA’, show higher CPU consumption, reaching up to 28.3% in the early epochs, but remain relatively efficient in terms of memory. The ’DNN-SVM’ model is also more CPU-intensive but has lower memory usage in comparison. Overall, adding PCA or SVM seems to improve memory efficiency without significantly affecting CPU usage.
The Table 6 summarizes the performance of various models in terms of execution time, CPU usage, and memory usage. The CNN-PCA model has high time consumption for classification (428.54 s) and significant memory usage (150.16 MB). The CNN-SVM model requires long training time (240.86 s), but has efficient feature extraction (11.91 s) and classification (2.39 s). The CNN-PCA-SVM model balances time and resources, with 10.13 s total for feature extraction, 0.47 s for PCA, and 40.55 s for classification. The DNN-PCA model shows fast PCA reduction (7.70 s) with minimal CPU usage, while the DNN-SVM model is efficient in classification (2.43 s) with low CPU (98.80%) and memory usage (-0.30 MB). Finally, the DNN-PCA-SVM model shows significant CPU usage during classification (2.08 s) but has relatively low memory usage (0.00 MB).
Table 6.
Interpretation of Model Results for the dataset BONN.
| Model | Time (s) | CPU usage (%) | Memory usage (MB) |
|---|---|---|---|
| CNN-PCA | |||
| Feature extraction | 11.48 | 1.20 | 285.23 MB |
| PCA analysis | 1.70 | −0.90 | 21.39 MB |
| CNN-SVM | |||
| Feature extraction | 11.91 | – | – |
| SVM classification | 2.39 | − 1.50 | 0.0 |
| CNN-PCA-SVM | |||
| CNN feature extraction | 10.13 | 0.60 | 0.60 |
| PCA reduction | 0.47 | 0.00 | 0.00 |
| SVM classification | 40.55 | 97.90 | 0.60 |
| DNN-PCA | |||
| DNN training | 7.70 | 2.50 | 0.30 |
| PCA reduction | 0.20 | − 3.70 | 0.00 |
| DNN-SVM | |||
| Feature extraction | 10.72 | 1.80 | 0.50 |
| SVM classification | 2.43 | 98.80 | −0.30 |
| DNN-PCA-SVM | |||
| DNN feature extraction | 10.20 | 1.70 | − 1.90 |
| PCA reduction | 0.33 | 0.00 | 0.10 |
| SVM classification | 2.08 | 96.60 | 0.00 |
In summary, the results show that CNN models generally have better accuracy and lower error rates compared to DNN models. While integrating SVM may improve accuracy, it leads to a significant increase in execution time, CPU usage, and memory requirements. However, the use of PCA provides a significant advantage, and the speed gains achieved during training can offset other additional costs.
In general, the choice of model will ultimately depend on the specific priorities of the context, including desired accuracy, time constraints, and resource availability. Therefore, both performance and real-time system requirements must be considered.
Stability study
In this section, the performance and characteristics of the proposed models are presented, comparing them with other well-established techniques in the scientific literature and existing alternatives.
Study of stability between the feature extractors CNN and DNN
To study the stability of each model over the 50 epochs and test which model is robust to data variations, their behaviors over time before and after the addition of PCA were visualized in the following graphs (Figs. 9 and 10):
Fig. 9.
(a) Training accuracy comparison. (b) Training loss comparison.
Fig. 10.
(a) Training accuracy comparison. (b) Training loss comparison.
For Epileptic Seizure Recognition Database:
The two graphs illustrate the performance of the CNN, DNN, CNN-PCA, and DNN-PCA models in terms of accuracy and loss over 50 training epochs. The first graph (9.a) shows that all models achieve high accuracy, exceeding 95% within the initial epochs and gradually converging towards nearly 100%, with slight variations among the models. The CNN model appears to exhibit better overall stability in terms of accuracy. The second graph (9.b) indicates that the loss decreases rapidly during the initial epochs for all models, suggesting a strong initial learning phase. However, the loss fluctuations in the later epochs are more pronounced for the PCA-based models, which could indicate a higher sensitivity to data variations. Overall, all models demonstrate good performance, with minimal differences in accuracy and convergence.
For BONN Database:
According to the two previous graphs (Fig. 10a and b), For BONN dataset the CNN models exhibit notably high performance compared to other models during the initial epochs. This can be attributed to the convolutional layers’ ability to extract local patterns in the data, facilitating efficient initial feature recognition. Additionally, the incorporation of Maxpooling layers serves to reduce data dimensions, leading to better data generalization and less variability in the training process. Furthermore, DNN models are observed to be less stable than CNN models and exhibit more fluctuations due to their sensitivity to training data and their more intricate optimization process.
It is important that the CNN model is better than the CNN-PCA model during the initial epochs. This explains that the addition of PCA can potentially lead to a loss of important information for classification at the beginning of learning when features are still being learned. But subsequently, PCA begins to extract more discriminative features, reduce over-fitting, and achieve better overall performance (Fig. 11).
Fig. 11.
(a) Impact of the number of PCA components on model performance for ESR database. (b) Impact of the number of PCA components on model performance for BONN database.
Based on the Fig. 11a, the results show that the CNN-PCA-SVM model achieves the highest and most stable performance, with accuracies ranging from [99.08%, 99.42%] across all values of N. The DNN-PCA-SVM model follows with lower but consistent performance, within the range [97.50%, 97.77%]. In contrast, CNN-PCA exhibits slight fluctuations in performance, ranging from [98.52%, 99.13%], while DNN-PCA shows a declining trend, with accuracies dropping to 95.65% at ( N = 128) within the range [95.65%, 97.22%]. The inclusion of SVM improves model stability, highlighting the importance of selecting the appropriate number of PCA components for DNN models.
According to the Fig. (11b), the results indicate that the CNN-PCA-SVM model is the most performant and stable, with accuracies ranging from [99.92%, 99.96%] across all values of N. The DNN-PCA-SVM model closely follows, showing slight variability within the range [99.87%, 99.95%]. In contrast, **CNN-PCA** improves as N increases, achieving accuracies between [95.53%, 99.87%], while DNN-PCA exhibits instability, dropping to 91.01% at (N = 100) within the range [91.01%, 99.85%]. Similarly to the ESR dataset, the addition of SVM enhances robustness, and selecting the optimal number of PCA components remains crucial for DNN architectures in the BONN dataset.
The Table 7 below compares the performance of our approach with that of the methods presented in the state of the art, using different numbers of principal components on the ESR and BONN datasets.
Table 7.
Results of models on ESR and BONN datasets with different PCA reductions.
| Model | Dataset | PCA 50 | PCA 60 | PCA 80 | PCA 90 |
|---|---|---|---|---|---|
| Conv1D_LSTM17 | ESR | 0.981 | 0.976 | 0.979 | 0.972 |
| DNN17 | ESR | 0.826 | 0.819 | 0.812 | 0.81 |
| BiLSTM17 | ESR | 0.977 | 0.977 | 0.973 | 0.971 |
| GRU17 | ESR | 0.974 | 0.961 | 0.963 | 0.97 |
| CNN-PCA-SVM | ESR | 0.9830 | 0.9804 | 0.9835 | 0.9809 |
| BONN | 0.9985 | 0.9983 | 0.9954 | 0.9988 | |
| DNN-PCA-SVM | ESR | 0.9743 | 0.9696 | 0.9687 | 0.9648 |
| BONN | 0.9993 | 0.9990 | 0.9988 | 0.9978 |
In summary, CNN-PCA-SVM stands out as the most performant model on the ESR and BONN datasets, with high accuracies and narrow confidence intervals. For ESR, its accuracies range from 0.9830 to 0.9809, with confidence intervals from [0.9812, 0.9848] to [0.9791, 0.9827]. On BONN, its accuracies range from 0.9985 to 0.9988, with confidence intervals from [0.9967, 0.9993] to [0.9970, 0.9996]. DNN-PCA-SVM follows closely, with accuracies from 0.9743 to 0.9648 for ESR, and confidence intervals from [0.9725, 0.9761] to [0.9630, 0.9666]. On BONN, its accuracies range from 0.9993 to 0.9978, with confidence intervals from [0.9975, 0.9997] to [0.9960, 0.9990].
Other models17, such as Conv1D_LSTM , BiLSTM, and GRU, show less consistent results, with wider confidence intervals indicating greater variability in performance. For example, Conv1D_LSTM on ESR achieves accuracies from 0.981 to 0.972, with confidence intervals from [0.9792, 0.9828] to [0.9702, 0.9738]. BiLSTM yields similar results, ranging from 0.977 to 0.971, with confidence intervals from [0.9742, 0.9798] to [0.9694, 0.9726]. Finally, GRU achieves accuracies from 0.974 to 0.961 on ESR, with confidence intervals from [0.9713, 0.9767] to [0.9575, 0.9645].
The DNN17 model demonstrates the lowest performance across all, with accuracies on ESR ranging from 0.826 to 0.81, and wider confidence intervals, indicating lower stability.
Nevertheless, all these models achieve satisfactory final performances. It is worth noting that incorporating PCA between the layers of the CNN model proves beneficial, enhancing accuracy and minimizing execution time, thus making it an effective feature extractor.
Study of stability between the two classifiers sigmoid and SVM
The CNN and DNN models were tested before and after incorporating SVM to monitor their performance over epochs and analyze their behavior throughout the learning process (Figs. 12 and 13):
Fig. 12.
(a) Training accuracy comparison. (b) Training loss comparison.
Fig. 13.
(a) Training accuracy comparison. (b) Training loss comparison.
For Epileptic Seizure Recognition Database:
An analysis of the two graphs (Fig. 12a and b) indicates that the CNN-PCA-SVM and CNN-PCA models demonstrate better convergence and outperform the DNN-PCA and DNN-PCA-SVM models. This can be attributed to the use of convolutional layers, which extract local patterns in the data, as well as the utilization of Maxpooling layers, which reduce the dimensionality of the data for improved generalization.
Furthermore, it appears that the CNN-PCA-SVM model tends to have slightly better performance than the CNN-PCA model, although the differences are not significant over the epochs. Additionally, integrating SVM as a classifier in the DNN architecture can lead to remarkable improvements in results over the epochs. This can be attributed to the fact that CNNs can generate high-dimensional feature representations compared to DNNs due to their ability to extract local spatial information. Sometimes, this can make classification more challenging for the SVM when applied directly to features extracted by the CNN, whereas the lower-dimensional features produced by the DNN may be easier to separate.
For BONN Database:
Figure 13 illustrates the behavior of each model in terms of accuracy and loss during the training process. The left graph (13.a) shows that the CNN-PCA-SVM model quickly achieves an accuracy close to 100%, outperforming the other models in terms of convergence speed. The DNN-PCA-SVM model exhibits a slower convergence with steady progress, while CNN-PCA reaches high performance faster than DNN-PCA. The right graph (13.b) indicates that the losses of the CNN-PCA and DNN-PCA-SVM models decrease rapidly and stabilize at very low values, suggesting good convergence. In contrast, the CNN-PCA-SVM model shows a faster loss reduction, whereas the DNN-PCA model exhibits significant fluctuations, indicating potential instability due to its sensitivity to hyperparameters such as learning rate, batch size, and weight initialization, which can lead to variations in convergence. Overall, the results suggest that models incorporating SVM enhance performance and convergence, but the stability of the DNN-PCA-SVM model requires special attention.
In conclusion, incorporating the SVM classifier into the classification process can have a positive impact on performance. SVM helps delineate decision boundaries between different classes, leading to better generalization and improved performance.
To study the impact of kernel choice in the classification process, various kernels for the SVM classifier (RBF, Sigmoid, Linear, Polynomial with several polynomial degree values 1, 2, 3, 4) were tested. This empirical study enabled the assessment of how different kernel functions affect the classification accuracy and overall performance of the SVM classifier in the classification process (Fig. 14).
Fig. 14.
(a) The impact of kernel choice for ESR dataset. (b) The impact of kernel choice for BONN dataset.
According to graph (14.a) The CNN-SVM model achieves its best performance with the rbf kernel (99.21% [98.95%, 99.47%]), while the linear, poly, and sigmoid kernels show slightly lower performances (98.434%, 98.869%, and 96.347%, respectively). The DNN-SVM model exhibits lower performance, achieving 97.08% with rbf, but experiencing a significant drop to 83.826% with sigmoid. The CNN-PCA-SVM model outperforms all others with 99.42% for rbf [99.25%, 99.59%], confirming its superiority in accuracy and stability. In contrast, the DNN-PCA-SVM model shows lower performance, ranging from 97.26% for rbf to 96.043% for sigmoid. Overall, CNN-PCA-SVM provides the best performance and the highest stability, as confirmed by the confidence intervals. This may explain why RBF kernels are effective for CNN models due to their ability to capture nonlinear relationships between extracted features. Conversely, linear kernels are effective for DNN models in cases where the data is linearly separable in the feature space.
As shown in the graph (14.b), the CNN-SVM model achieves its best performance with the rbf kernel (99.95% [99.70%, 100.00%]) and shows a slight decrease with sigmoid (98.68% [98.30%, 99.06%]). The DNN-SVM model, while effective with rbf (99.90% [99.60%, 100.00%]) and linear (99.92% [99.62%, 100.00%]), experiences a significant drop with poly (88.79% [87.90%, 89.68%]) and sigmoid (87.80% [86.89%, 88.71%]). The CNN-PCA-SVM model achieves the best overall results, with 99.96% [99.71%, 100.00%] for rbf, while the sigmoid kernel leads to lower performance (90.45% [89.50%, 91.40%]). Finally, the DNN-PCA-SVM model offers high and stable performance, with scores ranging from 99.90% [99.60%, 100.00%] to 99.95% [99.70%, 100.00%] across all kernels except poly (99.19% [98.80%, 99.58%]). These results highlight the superiority of the rbf and linear kernels, while poly and sigmoid exhibit greater variability depending on the model.
For Epileptic Seizure Recognition Database:
According to the Table 8, The results show that the CNN-PCA-SVM model achieves an average accuracy of 99.342% with an average loss of 0.00658, indicating high and stable performance across the different folds. In comparison, the DNN-PCA-SVM model achieves an average accuracy of 97.768% with an average loss of 0.02232, which is lower than that of the CNN model, but still demonstrates good stability in the results. The integration of PCA improves both models by reducing the loss while maintaining high accuracy levels.
Table 8.
Performance of CNN-PCA-SVM and DNN-PCA-SVM models across different folds.
| Folds | CNN-PCA-SVM accuracy | CNN-PCA-SVM loss | DNN-PCA-SVM accuracy | DNN-PCA-SVM loss |
|---|---|---|---|---|
Fold  1 1 |
98.840 | 0.0116 | 96.763 | 0.03237 |
Fold  2 2 |
99.275 | 0.00725 | 97.632 | 0.02368 |
Fold  3 3 |
99.130 | 0.0087 | 97.198 | 0.02802 |
Fold  4 4 |
99.903 | 0.00097 | 98.599 | 0.01401 |
Fold  5 5 |
99.565 | 0.00435 | 98.647 | 0.01353 |
| Average | 99.342 | 0.00658 | 97.768 | 0.02232 |
For BONN Dataset:
Based on the Table 9, the CNN-PCA-SVM and DNN-PCA-SVM models show excellent performance, with high accuracy and low error rates across all folds. The CNN-PCA-SVM model achieves an average accuracy of 99.963% and an error rate of 0.0372%, while the DNN-PCA-SVM model achieves an average accuracy of 99.975% and a slightly lower error rate of 0.0248%. The differences in performance are minimal, suggesting both models are highly effective, with the DNN-based model having a marginally lower error rate.
Table 9.
Performance and error rates for CNN-PCA-SVM and DNN-PCA-SVM models across different folds.
| Folds | CNN-PCA-SVM accuracy | CNN-PCA-SVM loss | DNN-PCA-SVM accuracy | DNN-PCA-SVM loss |
|---|---|---|---|---|
Fold  1 1 |
99.969 | 0.031 | 99.969 | 0.00031 |
Fold  2 2 |
99.969 | 0.031 | 100 | 0.00000 |
Fold  3 3 |
99.938 | 0.062 | 99.938 | 0.00062 |
Fold  4 4 |
99.938 | 0.062 | 100 | 0.00000 |
Fold  5 5 |
100 | 0.000 | 99.969 | 0.00031 |
| Average | 99.963 | 0.0372 | 99.975 | 0.000448 |
However, it is important to note that the effectiveness of adding SVM may depend on the specific nature of the problem and the data. Therefore, a thorough evaluation of results is necessary to ascertain the benefits of incorporating SVM into the classification process of epileptic seizures.
Comparison of the proposed scheme with other state of the art methods
In this section, the performance of the proposed models, CNN-PCA-SVM and DNN-PCA-SVM, is compared with other methods from the literature, as shown in Fig. 15:
Fig. 15.

Comparison of performance of different models.
According to the graph 15, the DNN-SVM-PCA (BONN) model achieves the highest accuracy (99.97%), closely followed by CNN-SVM-PCA (BONN) (99.96%) and CNN-SVM-PCA (ESR)(99.34%), demonstrating their strong performance. The CWT-PCA-ANN and (PCA+ICA)-SVM models also perform well at 99%. The Hybrid approach + mRMR (98.95%) and BiLSTM+XGBoost (95.74%) show competitive results, while DWT+LDA+SVM (89.17%) and DWT+ICA+SVM (90.42%) achieve the lowest accuracies among the compared models.
In the Table 10, the results indeed include the calculation of the confidence intervals (CIs) for the accuracy of each model. These intervals were computed assuming  , based on a fivefold cross-validation.
, based on a fivefold cross-validation.
Table 10.
Model accuracy with 95% confidence intervals.
| Model | Accuracy (%) | 95% confidence interval (%) |
|---|---|---|
| DWT+LDA+SVM4 | 89.17 | [61.93, 116.41] |
| BiLSTM+XGBoost16 | 95.74 | [78.04, 113.44] |
| DWT+ICA+SVM4 | 90.42 | [64.62, 116.22] |
| Hybrid Approach + mRMR3 | 98.95 | [90.02, 107.88] |
| 3DCNN6 | 92.30 | [68.93, 115.67] |
| BiLSTM+Random Forest16 | 94.23 | [73.79, 114.67] |
| CWT+PCA+ANN8 | 99.00 | [90.28, 107.72] |
| (PCA+ICA)+SVM9 | 99.00 | [90.28, 107.72] |
| CNN+SVM+PCA (ESR) | 99.34 | [92.24, 106.44] |
| DNN+SVM+PCA (ESR) | 97.76 | [84.79, 110.73] |
| CNN+SVM+PCA (BONN) | 99.96 | [98.21, 101.71] |
| DNN+SVM+PCA (BONN) | 99.97 | [98.45, 101.49] |
The results indicate that the CNN-SVM-PCA and DNN-SVM-PCA models applied to the BONN dataset achieve the highest accuracies, 99.96% [98.21%, 101.71%] and 99.97% [98.45%, 101.49%] respectively, with very narrow confidence intervals, indicating high reliability and stability. The CNN-SVM-PCA model on the ESR dataset also shows a high accuracy of 99.34% [92.24%, 106.44%], while the DNN-SVM-PCA on ESR achieves an accuracy of 97.76% [84.79%, 110.73%], with a wider confidence interval, suggesting greater variability in performance. In comparison, traditional models like DWT+LDA+SVM4 (89.17% [61.93, 116.41]) and 3DCNN6 (92.30% [68.93%, 115.67%]) show relatively lower accuracies and wider confidence intervals, reflecting greater uncertainty. These results highlight the effectiveness of combining PCA and SVM to enhance accuracy and reduce prediction uncertainty across both datasets.
It can be inferred that adding PCA to machine learning algorithms yields better results, without the need to combine PCA with other techniques. Additionally, it is observed that SVM can be considered as an alternative solution to the sigmoid function of neural networks, provided that a secondary feature extractor is added after the neural network to extract features from its intermediate layers.
Conclusion
In summary, the application of deep learning in epilepsy detection offers significant benefits in terms of early diagnosis, personalized treatment, reduced healthcare costs, and improved quality of life for patients. The results highlight the trade-offs between different model types. CNN models generally provide better accuracy and reduced errors but require more computation time, CPU power, and memory compared to DNN models. Integrating SVM can enhance system performance but at the cost of a significant increase in execution time. However, this constraint can be alleviated by adding PCA, which reduces the dimensionality of the data while preserving essential information, potentially speeding up SVM model training. By combining SVM and PCA in the classification pipeline, it is possible to leverage the increased accuracy of SVM while reducing the overall execution time of the model.
Future research should focus on optimizing hybrid architectures (CNN, DNN, SVM), particularly by exploiting the advantages of deep models such as ResNet or Transformer for EEG data. Computational efficiency can be improved by using low-cost neural networks (MobileNets, EfficientNet) or quantization techniques, while utilizing hardware accelerators. Other dimensionality reduction methods, such as LDA, ICA, or autoencoders, could also be explored. Robustness to EEG artifacts should be enhanced with models capable of detecting and eliminating them. Finally, the practical applicability of these models in real-world clinical settings requires overcoming challenges such as computational cost, artifact removal, and integration into hospital systems. By addressing these issues, these models could support clinicians in real-time monitoring, leading to better patient outcomes, particularly in epilepsy care.
Abbreviations
- ML
Machine learning
- DL
Deep learning
- EEG
Electroencephalogram
- ESR
Epileptic Seizure Recognition Database
- CNN
Convolutional Neural Network
- ReLU
Rectified Linear Unit
- DNN
Deep Neural Network
- PCA
Principal Component Analysis
- SVM
Support Vector Machine
- DWT
Discrete Wavelet Transform
- RBF
Radial basis function
- CPU
Central processing unit
- SMOTE
Synthetic Minority Oversampling Technique
Author contributions
Yousra BERRICH wrote the main manuscript text and prepared all the figures. All authors contributed to the review and analysis of the manuscript.
Data availability
Two datasets were utilized during the current study: the first being ESR, available at https://www.kaggle.com/datasets/harunshimanto/epileptic-seizure-recognition, and the second being BONN, available at https://www.ukbonn.de/epileptologie/arbeitsgruppen/ag-lehnertz-neurophysik/downloads/.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.https://www.epilepsy.org.au/about-epilepsy/facts-and-statistics.
- 2.Sharmila, A. et al. DWT based detection of epileptic seizure from EEG signals using naive Bayes and k-NN classifiers. IEEE Access4, 7716–7727 (2016). [Google Scholar]
- 3.Ren, W. et al. Efficient feature extraction framework for EEG signals classification. In 7th International Conference on Intelligent Control and Information Processing. December 1-4, 2016; Siem Reap, Cambodia (2016).
- 4.Guharoy, R. et al. Novel epileptic seizure detection techniques and their empirical analysis. IEEE Access. 2017. (2017).
- 5.Wang, G. et al. EEG-based detection of epileptic seizures through the use of a directed transfer function method. IEEE Access6, 47189–47198 (2018). [Google Scholar]
- 6.Wei, X. et al. Automatic seizure detection using three-dimensional CNN based on multi-channel EEG. BMC Med. Inform. Decis. Mak.18(5), 71–80 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wang, X. et al. Detection analysis of epileptic EEG using a novel random forest model combined with grid search optimization. Front. Hum. Neurosci.13, 52 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Peachap, A. B. et al. Epileptic seizures detection based on some new Laguerre polynomial wavelets, artificial neural networks and support vector machines. Inform. Med. Unlocked16, 100209 (2019). [Google Scholar]
- 9.Matin, A. et al. A hybrid scheme using PCA and ICA-based statistical features for epileptic seizure recognition from EEG signal. In In 2019 Joint 8th International Conference on Informatics, Electronics Vision (ICIEV) and 2019 3rd International Conference on Imaging, Vision Pattern Recognition (icIVPR) 301–306 (IEEE, 2019).
- 10.Matin, A. et al. Hybrid scheme using PCA and ICA based statistical feature for epileptic seizure recognition from EEG signal. In 8th International Conference on Informatics, Electronics Vision (ICIEV) 3rd International Conference on Imaging, Vision Pattern Recognition (IVPR) (2019).
- 11.Sharmila, A. & Shiny Angel, T. Performance analysis of dimensionality reduction techniques in EEG signal classification. Int. J. Adv. Res. Eng. Technol.11(10), (2020).
- 12.Dhanka, S. & Maini, S. Random forest for heart disease detection: a classification approach. In In 2021 IEEE 2nd International Conference On Electrical Power and Energy Systems (ICEPES), 1–3. (IEEE, 2021).
- 13.Alalayah, K. M. et al. Effective early detection of epileptic seizures through EEG signals using classification algorithms based on t-distributed stochastic neighbor embedding and K-means. Artif. Intell. Neuroimaging Diagn. (2023). [DOI] [PMC free article] [PubMed]
- 14.Dhanka, S. & Maini, S. Multiple machine learning intelligent approaches for the heart disease diagnosis. In In IEEE EUROCON 2023-20th International Conference on Smart Technologies, 147–152. (IEEE, 2023).
- 15.Sharma, A. et al. A comparative study of heterogeneous machine learning algorithms for arrhythmia classification using feature selection technique and multi-dimensional datasets. Eng. Res. Express6(3), 035209 (2024). [Google Scholar]
- 16.Hosseinzadeh, M. et al. A model for epileptic seizure diagnosis using the combination of ensemble learning and deep learning. IEEE Access.2024, 3457018 (2024). [Google Scholar]
- 17.Omar, A. & El-Hafeez, T. Optimizing epileptic seizure recognition performance with feature scaling and dropout layers. Neural Comput. Appl.36, 2835–2852 (2024). [Google Scholar]
- 18.Qiuyi, W. & Fokoue, E. Epileptic Seizure Recognition Data Set. (2017).
- 19.Andrzejak, R. G. et al. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: dependence on recording region and brain state. Phys. Rev. E64, 061907 (2001). [DOI] [PubMed] [Google Scholar]
- 20.Gardy, N. Détection automatique multi-échelle et de grande envergure d’oscillations intracérébrales pathologiques dans l’épilepsie par réseaux de neurones artificiels. In: theses.hal.science (2021).
- 21.Valenchon, N. Développement D’Un Système de Stimulation en Temps Réel de L’Activité Cérébrale. In: search.proquest.com (2021).
- 22.Erkki, O. A Simplifed Neuron Model as a Principal Component Analyser. Vol. 15 (Springer, 1982).
- 23.Subasi, A. & Gursoy, M. I. EEG signal classification using PCA, ICA, LDA and support vector machines. Expert Syst. Appl.2010, 5. 10.1016/j.eswa.2010.06.065 (2010). [Google Scholar]
- 24.Wang, C. J. & Huang, C. L. A GA-based feature selection and parameters optimization for support vector machines. Expert Syst. Appl.31, 231–240 (2006). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Two datasets were utilized during the current study: the first being ESR, available at https://www.kaggle.com/datasets/harunshimanto/epileptic-seizure-recognition, and the second being BONN, available at https://www.ukbonn.de/epileptologie/arbeitsgruppen/ag-lehnertz-neurophysik/downloads/.