Experimental study on the bending performance of a precast, pretensioned high-strength concrete I-girder with pretensioned double broken strands

Abstract

Precast, pretensioned concrete girders are extensively used in bridge engineering to prevent damage to concrete girders, such as the loss of prestress and the corrosion of strands. Existing studies of the mechanical performance and failure characteristics of bridge girders had shortcomings, resulting in potential safety hazards. This study conducted a full-scale model experiment and theoretical analysis of the bending performance of a 35-m long precast, pretensioned concrete I-girder with pretensioned double broken strands. The cracks and bending damage were investigated. The results showed that the maximum vertical displacement of the composite girder was much lower than the required standard value, with a crack factor and bearing capacity factor of 1.31 and 1.54, respectively. The bending stiffness of the composite girder decreased by 70%. Many cracks occurred in the concrete, resulting in excess stress of the steel bars and prestressed strands. The crack width during loading was much smaller than the theoretical one in the Specifications for Highway Reinforced Concrete Prestressed Concrete Bridge Culverts (JTG 3362–2018). Therefore, the girder exhibited optimum bending stiffness, sufficient crack resistance, acceptable ultimate bending capacity, and ductile failure performance. The mechanical behavior and failure mechanism during loading were investigated. This study provides recommendations for the design, maintenance, and damage assessment of this bridge type to improve the service lives of bridges.

Introduction

Pretensioned, prestressed concrete composite girders are widely used in bridge construction in China and internationally to prevent damage and improve safety. However, the mechanical characteristics and failure modes of these girders have not been sufficiently investigated, resulting in safety risks. Therefore, it is critical to research the potential failure of pretensioned, prestressed concrete girders.

Han et al.¹ proposed a modified thick‐walled cylinder model to estimate the elongation of precast, pretensioned concrete members in 2016, which is lack of a simplified approach for its practical application. In the same year, Mantawy et al.² performed a field test and found that precast, pretensioned concrete columns had good seismic performance, but the reduction in damage also prevented visual inspection of the reinforcement. Salazar et al.³ investigated precast, pretensioned girders with 18 mm diameter strands, reducing the material use by 35% in 2017. And Guo et al.⁴ proposed the Paris model for analyzing the expansion rate of fatigue cracks in a concrete beam reinforced with prestressed carbon fiber plates at the same time, while Naji et al.⁵ analyzed four types of failures in pretensioned concrete girders and examined 15 characteristics. In 2018, Wang et al.⁶ proposed a model for estimating the elongation length, expansion stress, and bond stress of corroded strands in pretensioned, prestressed concrete beams. And Dang et al.⁷ developed a simple and reliable technique to quantify the elongation length based on the slip theory. They used the free-end slip (FES) as an indicator of the elongation length. Naji et al.⁸ conducted experiments and established a model to analyze the shear capacity of precast, pretensioned girders in the same year. The measured capacity was greater than the theoretical one based on the AASHTO LRFD Bridge Design Specifications 2017. Jayaseelan et al.⁹ observed that using fully tensioned top strands and mild reinforcing steel in the precompression zones of prestressed concrete bridge girders reduced the camber by 72% in 2019. Williams et al.¹⁰ found that the AASHTO LRFD 2017 and the ACI 318–14 provided conservative estimates for the shear strengths of precast, pretensioned concrete girders, and additional testing should be conducted for more splice regions featuring a wide range of details. Yan et al.¹¹ revealed that the number of strands and the corrosion length were critical indicators of the degradation of the bending capacity of precast, pretensioned girders in the same year, but bond failure and shear failure were not considered in this study. Alirezaei et al.¹² investigated three end-region reinforcement methods to reduce the crack width and stress in steel girders. Then, Honarvar et al.¹³ used a probabilistic method for the stress analyses of concrete beams and stated that thermal effects should be considered in 2020. The stress exceeded the limit according to AASHTO. Lee et al.¹⁴ established a model to estimate the prestress loss in steel strands in 2022. The thermal effect caused a prestress loss of 5.2%-5.5% after releasing the strands. Al-Omaishi¹⁵ found that the time-dependent losses in the AASHTO LRFD specifications did not reflect the effect of beam configuration on the creep and shrinkage multipliers in the same year. And Babarinde¹⁶ observed that using ultra-high performance concrete (UHPC) improved the crack resistance and suggested the prestress of the strands should not exceed 139.7 MPa to limit the crack width, thus anchors should be carefully selected to minimize the anchor set losses and leverage recovery stress. Alateeq¹⁷ observed that adequate details in the bridge deck decreased the torsion deflection of precast, pretensioned multi-girders, but the live load was not applied as a patch area. Xiong et al.¹⁸ also found that precast, pretensioned, prestressed UHPC beam-column interior joints provided the same seismic performance as the ones using reinforced concrete in the same year.

In summary, previous studies have focused on the mechanical behavior of precast, pretensioned concrete simply supported girders and investigated the bonding performance between the steel strands and the concrete under normal operating conditions. However, few studies analyzed the bearing capacity of these girders and the evolution and mechanism of cracking failure. A full-size model experiment was conducted using a 35-m long precast, pretensioned I-girder concrete bridge. The deformation evolution of the composite girder is assessed to determine the force in the steel bars and strands, analyze cracks due to bending deformation and failure, and evaluate the girder’s mechanical performance. The research results enable the optimization of the design, construction, and maintenance of precast, prestressed concrete bridges and the evaluation of carrying capacity and failure patterns to improve the safety and service lives of bridges.

Bending capacity and stiffness of beam with cracks

An analysis model is established to obtain the bending capacity in precast-pretensioned composite girder with double-broken pretensioning strands in Fig. 1, according to the "Code for the Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts" (JTG 3362–2018)¹⁹, as shown in Eq. (1) and (2).

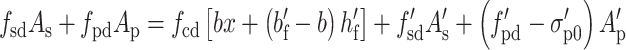1

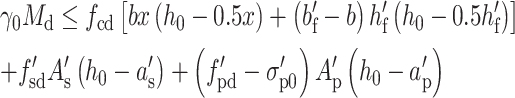2

where γ₀ is the significant factor of structure, M_d is the design bending moment, f_cd is the ultimate compressive strength of concrete, f_sd and f’_sd are the yield strength of steel bar, f_pd and f’_pd are the ultimate tensile strength of steel strand, A_s and A’_s are the rea of steel bars, A_p and A’_p are the area of steel strand, b is the width of web, h₀ is the effective height in cross section, a and a’ are the distance between the joint force points of steel bars and prestressed strands and their edges in the tension area respectively, a’_s and a’_p are the distance between the joint force points of steel bars and prestressed strands and their edges in the compression area respectively, σ’_p0 is the position of the resultant force of the prestressed strands without the compression stress in concrete.

Fig. 1.

Analysis mode of bending capacity in precast-pretensioned composite girder with double-broken pretensioning strands.

The test beam under a symmetric load is shown in Fig. 2a. A_s the load increases, the cracks at the bottom of the beam cause significant decreases in the bending stiffness and bearing capacity. The bending stiffness of the cracked section is reduced by γ_sEI (γ_s is the degradation coefficient of the bending stiffness), whereas the bending stiffness in the uncracked sections does not change under a load, as shown in Fig. 2(b)²⁰.

Fig. 2.

Simply supported beam under a bending load.

The relationship between the bending moment and the deflection of the beam is described by Eq. (3):

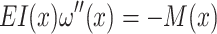3

where E is the material’s elastic modulus, I is the moment of inertia of the cross-section, M(x) is the bending moment in the cross-section.

The equivalent bending stiffness is calculated from the midspan deflection as follows:

4

where P is the single-point load (Fig. 2), a is the distance between the load point and the support, L is the span, and f_L/2 is vertical deflection in the midspan of the beam. After cracks appear in the test beam, the measured vertical deflection in the midspan, the load, the crack position, and the bending stiffness degradation coefficient γ_s derived from a model describing the two-point symmetric loading of a variable stiffness beam are shown in Eq. (5).

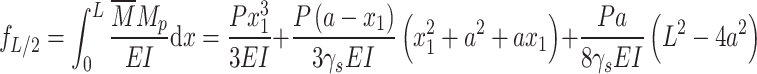5

where 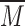is the influence of the bending moment, M_p is the bending moment caused by an external load, x₁ is the distance between the edge crack and the support, γ_s is the degradation coefficient of the bending stiffness of the cross-section, which is defined in Eq. (6).

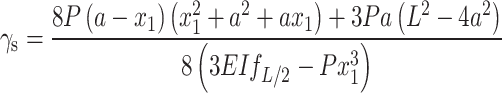6

The maximum crack width is obtained using Eq. (7) according to the Code for the Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts (JTG 3362-2018)¹⁹:

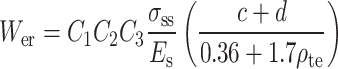7

where σ_ss is the stress of the steel bars, E_s is the elastic modulus of steel, and ρ_te is the effective reinforcement ratio of the longitudinal tensile steel bars.

Field test procedures

A field test was conducted on a 35-m long precast, pretensioned composite I-girder with pretensioned double broken strands. The bending moment, bending deformation, strain of the concrete, steel bars, and steel strands, and the cracks in the concrete were analyzed.

Precast, pretensioned composite girder

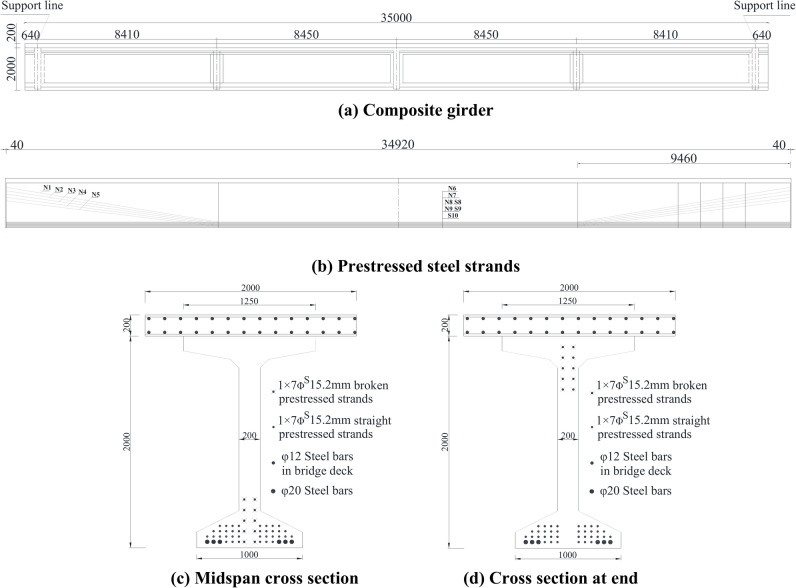
A plenty of express highway bridges are built in a 71.345 km long express highway in Guangdong province. And most of these bridges are built using 35 m long precast, pretensioned composite I-girder with pretensioned double broken strands, as well as the substructure with double-columns piers, central single column with double large cantilever and portal frame piers, as shown in Fig. 3.

Fig. 3.

Express highway bridge.

The top and bottom widths of the girder were 1.25 m and 1 m, respectively, and the thickness of the web was 20 cm. Three 20-cm thick transverse partitions were located in the middle, and two 30-cm thick transverse partitions were located at the end of the girder. The cast-in-situ concrete deck was 20 cm thick, and nine groups of prestressed strands were used; five groups of strands had bends, as shown in Fig. 4.

Fig. 4.

Precast, pretensioned concrete I-girder with pretensioned double broken strands (mm).

The 1 × 7Φ^S15.2mm prestressed strands has the tensile strength of 1860 MPa, maximum tensile force of 260 kN, yield force of 229 kN, elongation of 3.5% and relaxation ratio of 2.5%. The concrete contains slag powder and flyash with highly active mineral material, optimum water reducer, medium-coarse sand and crushed stone with diameter of 5 to 20 mm. Thus, this type of concrete has slump of 250 mm and expansion degree of 600 mm, with 6 to 8 h and 10 to 12 h for pre-hardening and permanent set respectively, as shown in Table 1. Therefore, the collocation strength of C70 concrete is f_cu,0 ≥ 1.15f_cu,k = 1.15 × 70 MPa = 80.5 MPa, where f_cu,0 and f_cu,k are the collocation and specification compressive strength of C70 concrete²¹.

Table 1.

Mix proportion for C70 concrete.

NO	Mix proportion (kg/m3)								Water-binder ratio
	Cement	Flyash	Mineral	Sand	Megalith	Pebble	Water	Admixture
1	470	40	60	653	778	333	126	8.55	0.22
2	470	40	70	652	776	333	126	8.595	0.22

C70 and C50 concrete were used for the girder and cast-in-situ concrete deck, respectively. The material properties, determined through preliminary tests, are listed in Table 2. The effective prestress of the steel strands was reduced due to the friction of the bending device, the elastic compression of the girder, and the shrinkage and creep of the concrete during prefabrication and tensioning (Table 3).

Table 2.

Material properties.

Number	Items	Value (MPa)
1	Ultimate compressive strength of C70 concrete	80.5
2	Ultimate tensile strength of C70 concrete	3.0
3	28-day elastic modulus of C70 concrete	44,000
4	Ultimate compressive strength of C50 concrete	32.4
5	Ultimate tensile strength of C50 concrete	2.65
6	28-day elastic modulus of C50 concrete	41,650
7	Ultimate tensile strength of steel strand	1950
8	Elastic modulus of steel strand	194,000
9	Yield strength of φ12 steel bar	450
10	Yield strength of φ20 steel bar	465
11	Elastic modulus of steel bar	200,000

Table 3.

Effective prestresses of the strands.

Number	Steel strand number	Bending Angle (Degree)	Effective prestress (MPa)
1	N1	9.26	1288
2	N2	8.67	1295
3	N3	8.08	1301
4	N4	7.49	1308
5	N5	6.89	1314
6	N6-N9	0	1390

Crack failure test

Loading test device

A field crack failure test was conducted on a 35-m long precast, pretension composite girder (Fig. 5). The load was increased from 0 kN until the girder cracked and failed. The vertical deflection, strain of the concrete and steel bars, tensile stress of the prestressed strands, and cracking of the concrete were analyzed (Fig. 6).

Fig. 5.

Bending experiment of precast, pretensioned concrete I-girder with pretensioned double broken strands.

Fig. 6.

Bending failure test.

Loading test procedure

The limit design loads were 5595 kN·m and 13083kN·m under normal conditions and at the ultimate bearing capacity, respectively, as well as the theoretical bending moment was 16986kN·m, obtained by Eq. (1) and (2). The single-point crack load was 530 kN, corresponding to a cracking moment of 7346 kN·m. The single-point failure load was 1890 kN, corresponding to a bending moment of 26195kN·m. The loading procedure is shown in Fig. 7, and the data is collected in each loading steps, as the load suspension.

Fig. 7.

Loading procedure during the bending experiment.

Experimental methods

The deflection, concrete strain, strains in the steel bars, and tension in the prestressed strands of the girder were assessed.

Vertical deflection

Seven test sections were used in the longitudinal direction of the girder to assess vertical deflection. Two dial gauges were placed in each test section to monitor the vertical displacement. Their positions are shown in Fig. 8.

Fig. 8.

Measurement points for vertical displacement (mm).

Concrete strain

Three test cross-sections (B-B, C-C, and D-D) were used near the middle span of the girder to measure the concrete strain (Fig. 9). Resistance strain gauges were used in the test sections to measure the strain during loading and bending failure. The locations of the gauges are shown in Fig. 10a, and the measuring points in the B-B section are shown in Fig. 10b. The locations were the same for the C-C and D-D sections.

Fig. 9.

Measurement points for concrete strain in the cross-section (mm).

Fig. 10.

Measurement points for concrete strain (mm).

Strain in steel bars

Three sections were used to measure the strain of the steel bars with resistance strain gauge near the middle of the girder (F-F, G-G, and H-H) (Fig. 11). The locations of the measuring points are shown in Fig. 12.

Fig. 11.

Measurement points for the strain of the steel bars in the cross-section (mm).

Fig. 12.

Measurement points for strain (mm).

Tension of steel strands

Three sections were used to measure the tensile forces of the prestressed strands near the middle of the girder (I-I, II-II, and III-III) (Fig. 13). Embedded magnetic flux sensors were used. The prestressed strands N1-1, N1-2, N5-1, N5-2, S9-3, and S9-4 were selected for testing. Three longitudinal sections were used for the bent strands N1-1, N1-2, N5-1, and N5-2, and one longitudinal section in the midspan was used for the straight strands S9-3 and S9-4. The locations of the measuring points are shown in Fig. 14a, and the numbers of the sensors for the steel bars are shown in Fig. 14b.

Fig. 13.

Measurement points for tensile forces in the strands (mm).

Fig. 14.

Measurement points for tensile forces.

Experimental results of bending and cracking test

Deformation

The deformation curve of the composite girder under a single-point load of 0 kN-530 kN is symmetrical around the midspan during bending and cracking. The maximum deflection is 25.5 mm in the midspan, amplified by the long-term load to 31.5 mm, significantly lower than the allowable vertical displacement of 55.7 mm under normal conditions, as outlined in the Code for the Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culvert (JTG 3362–2018)¹⁹ (Fig. 15a). The deflection increases linearly with the load, indicating that the composite girder has sufficient stiffness and remains in the elastic state as cracks are formed (Fig. 15b).

Fig. 15.

Deflection of composite girder.

Concrete strain

The concrete strain of the composite girder under a load is shown in Fig. 15. The strain in the tension/compression zone of the B-B section increases linearly with the load. The strain distribution is consistent with the plane section assumption, indicating that the concrete is in the linear elastic state (Fig. 16a). The tensile strain (CDi-5 and DDi-2) at the bottom of the C–C and D-D sections increases rapidly when the load exceeds 430 kN. The strain starts changing nonlinearly when the strain reaches about 200 με, as shown in Fig. 16c. The strain range at the upper and lower edges of the test sections is listed in Table 4. The maximum strain reaches 467 με at the lower edge of the D-D cross-section, suggesting that cracks have formed (Fig. 17). As the load increasing to 450kN, the crack moment, regarding the dead load, in the midspan is 7346 kN·m (it is 5595kN·m under normal conditions), and the crack safety factor is 1.31. The bending moment increases as cracks are formed, and the bending stiffness decreases slightly due to vertical displacement after unloading.

Fig. 16.

Relationship between load and concrete strain.

Table 4.

Concrete strain in the crack stage.

Section	Test location	Strain value range (με)
B-B	Lower edge	257 ~ 290
	Upper edge	− 185 ~ − 170
C–C	Lower edge	231 ~ 414
	Upper edge	− 232 ~ − 251
D-D	Lower edge	274 ~ 467
	Upper edge	− 248 ~ − 221

Fig. 17.

First crack in the D-D section.

Strain of the steel bars

The relationship between the load and the strain of the steel bars on the top/bottom plate in the crack stage is shown in Fig. 18. The concrete cracks when the load reaches 530 kN, and the strain has a linear relationship with the load. The strain values are similar to that of the concrete at the same section height, indicating that the steel bars and concrete are well bonded; thus, the steel bars remain in the elastic stage. The strain of the steel bars in the G-G and H–H sections is slightly higher than that in the F-F section under the same load due to cracks in the concrete.

Fig. 18.

Relationship between the load and the strain of the steel bars.

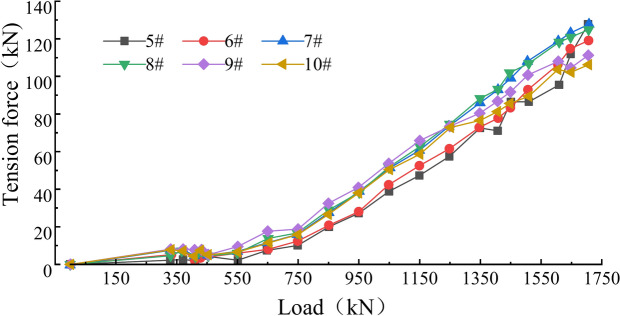
Tensile force of prestressed strands

Since cracks occurred only in the midspan test section, we analyze the tensile forces of the prestressed strands. The tension in the midspan strands increases linearly. It fluctuates significantly at measuring point 9 of strand N9 because there are cracks in the midspan. However, the relationship is predominantly linear, as shown in Fig. 19. The increase in the tensile force of the strands in the midspan is consistent with the plane section assumption, and the growth rate is the same for the lower strands. The maximum increment of the tensile force is 11.7 kN for strand N9 near the central axis at the bottom of the girder. The minimum increment is 6.1 kN for strand N1 (Table 5).

Fig. 19.

Relationship between the load and the tensile force of the strands.

Table 5.

Tension increment of strands.

Strands	Sensor number	Tension in strands (kN)
N1	5	6.1
N1	6	8.3
N9	7	11.7
N9	8	8.3
N9	9	10.0
N9	10	9.3

Experimental results of bending failure

Deformation

The deformation curve of the girder under different loads is symmetrical around the midspan in the bending failure process, as shown in Fig. 20a. Under a single-point load of 0 kN-750 kN, the maximum deflection of the midspan and the L/4 section are 4.0 cm and 2.5 cm, respectively. As the load increases from 750 to 1350 kN, cracks occur, resulting in a decrease in the bending stiffness and increases in the deflection of the midspan and L/4 section of 10.9 cm and 18.5 cm, respectively. The deflection of the composite girder increases nonlinearly when the load exceeds 1350 kN, and the girder is destroyed when the midspan deflection reaches 60 cm. Therefore, the ductility coefficient of the composite girder is 15.0, indicating ductile failure (Fig. 20b).

Fig. 20.

Deflection of composite girder.

Concrete strain

The strain-load curves for the B-B, C-C, and D-D sections are shown in Fig. 21. The number, width, and length of cracks at the bottom of the composite girder increase significantly with the load. Under a single-point load of 0 kN-750 kN, the strain in the three sections increases linearly with the load. When the load exceeds 750 kN, cracks result in a decrease in the bending stiffness of the composite girder and an increase in the growth rate of the strain. These effects are the most pronounced in the C-C section in the middle span. When the load reaches 1250 kN, the damage in the C-C section causes a further decrease in the bending stiffness, resulting in a nonlinear change in the strain in the B-B and D-D sections. The strain increases linearly when the load reaches 1450 kN, significantly increasing the damage level. The maximum strain is -1287 με, and the bending moment at the ultimate bearing capacity in the midspan is 26,195 kN·m. The coefficient of the bending bearing capacity is 1.54 at the ultimate bearing capacity. Thus, this specimen meets the requirements of 16,986 kN·m in the Code for the Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts (JTG 3362-2018). The composite girder bend and failed at a load of 1890 kN, indicating ductile failure.

Fig. 21.

Relationship between the load and the concrete strain.

The maximum principal tensile stress in the A-A and E-E sections exhibits a linear-nonlinear relationship with the load. At loads ranging from 0 to 1150 kN, the tensile strain increases linearly in the A-A and E-E sections. The reduction in the bending stiffness caused by the midspan cracks had a negligible effect on the stress at the supports. As the load increases to 1250 kN, the bending stiffness decreases substantially due to the failure in the midspan section, increasing the growth rate of the tensile strains. The maximum principal tensile strain increases nonlinearly to 133 με as the load increases to 1450 kN, and no shear cracks appear near the web of the two test sections, as shown in Fig. 22.

Fig. 22.

Relationship between load and maximum concrete principal tensile strains.

Strains of the steel bars

The strain-load relationship of the steel bars during the bending failure process is shown in Fig. 23. The strain of the upper steel bars increases linearly as the load increases from 0 to 750 kN. After the girder cracks, the concrete at the bottom does not provide sufficient support, and only the tensile steel bars bear the load. The tensile strain of the steel bars at the bottom increases linearly as the load increases to 534 με. When the load reaches about 750 kN, the bending stiffness of the composite girder is lower due to numerous cracks at the bottom. An inflection point occurs in the strain curve at this location. Subsequently, the strain increases rapidly, and the steel bars fail. The maximum strain is 3286 με at the bottom and -389 με on the top plate, and no yielding occurs.

Fig. 23.

Relationship between the load and the strain of the steel bars.

Tensile force of prestressed strands

The tensile force of the prestressed strands does not increase substantially as the load increases to 550kN. The rate of increase of the tensile force rises significantly after the load exceeds 750 kN. Few cracks are formed as the load increases to 550 kN due to the combined bearing capacity of the steel strands and the concrete. Once the load reaches 750 kN, the strain increases rapidly due to a decrease in the bending stiffness of the composite girder because of increases in the number, width, and depth of cracks. A significant increase in the tensile strain occurs in the range of 104.9 kN to 130.3 kN due to the separation between the concrete and the strands, as shown in Fig. 24.

Fig. 24.

Relationship between the load and the tensile force of the strands.

Degradation in bending stiffness and failure types

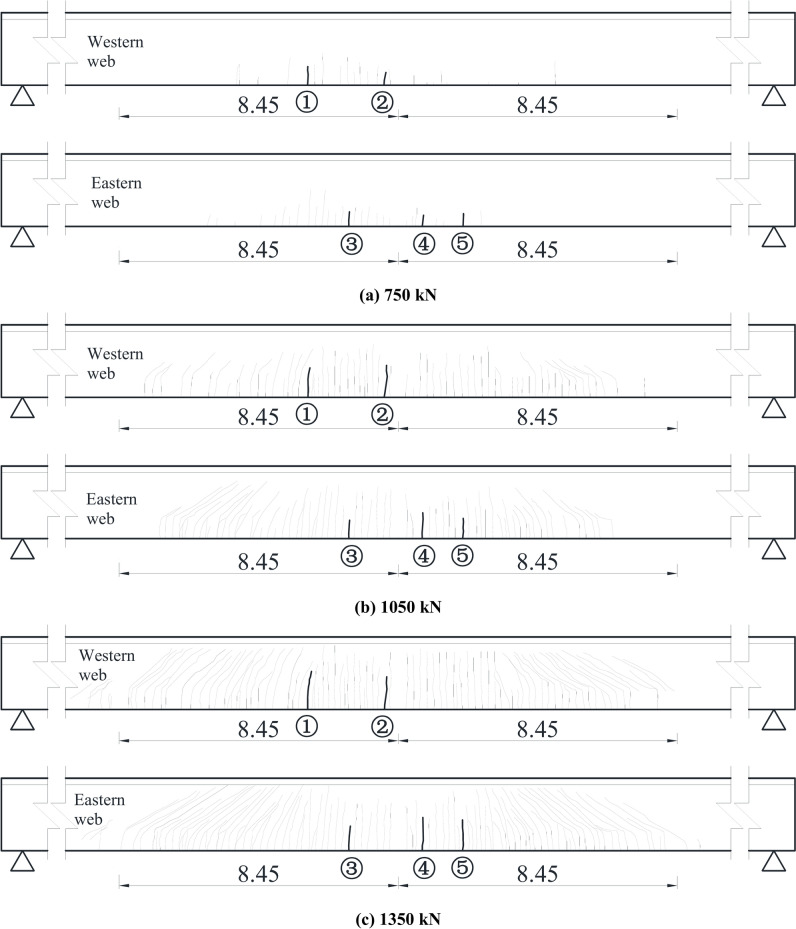
The number, width, and depth of cracks increase when the load exceeds 750 kN, resulting in a significant degradation in the bending stiffness, an increase in damage, and the failure of the girder. The width and length of 5 typical cracks are listed in Table 6.

Table 6.

Width and length of typical cracks (mm).

Load	Crack No.1		Crack No.2		Crack No.3		Crack No.4		Crack No.5		Calculated Maximum width
	Width	Length	Width	Length	Width	Length	Width	Length	Width	Length
750 kN	0.10	46	0.06	27	0.08	37	0.05	27	0.08	31	0.10
850 kN	0.15	58	0.10	69	0.12	50	0.15	66	0.15	45	0.16
950 kN	0.18	78	0.14	75	0.14	49	0.20	75	0.18	58	0.21
1050 kN	0.20	80	0.16	85	0.18	57	0.22	81	0.20	63	0.27
1150 kN	0.24	92	0.20	104	0.19	62	0.23	88	0.20	82	0.31
1250 kN	0.28	112	0.18	110	0.20	65	0.24	104	0.22	87	0.38
1350 kN	0.38	123	0.22	115	0.22	78	0.25	106	0.28	99	0.43

Vertical and horizontal cracks occur in the web as the load increases. The bottom edge of the girder cracks laterally at the southern loading point as the load increases to 450 kN. The crack length and width are 5 cm and 0.02 mm, respectively. The cracks close after unloading. When the load exceeds 450 kN, new cracks appear, extending from the span to the supports, and their width increases. The cracks are vertical in the midspan, and the angle is about 45° in the bent area. As the load increases to 950 kN, the maximum width of the crack is 0.2 mm. Crack No. 1 is 0.38 mm wide and 123 mm long. It is formed as the load increases to 1350 kN, as shown in Fig. 25. The measured widths of the 5 typical cracks are lower than the calculated maximum crack width derived from Eq. (7), indicating that the girder exhibits good performance with minor cracks, which is caused by the much less prestress loss in precast pretensioned concrete girders than those post-pretensioned ones.

Fig. 25.

Cracks in the girder (unit: m).

As the load increases from 750 to 1350 kN, the bending stiffness of the girder decreases significantly with the crack region (x₁) expanding in the composite girder, which also affects the vertical displacement in the girder (f_L/2). The degradation coefficient of the bending stiffness γ_s is shown in Table 7. The cracks occur at a distance of 7.28 m to 11.09 m from the fulcrum, and the midspan deflection increases sharply from 28.27 mm to 153.83 mm as the load increases. The degradation coefficient γ_s rapidly decreases from 0.70 to 0.39 and from 0.39 to 0.30 as the load increases from 750 to 1050 kN and from 1050 to 1350 kN, respectively.

Table 7.

Degradation Coefficient of the Bending Stiffness.

P (kN)	x1 (m)	EI (N·m2)	fL/2 (mm)	a (m)	L (m)	γs
750	11.09	3.44 × 1010	38.27	13.86	33.72	0.70
850	11.08		42.76			0.54
950	10.23		59.75			0.48
1050	9.43		76.73			0.39
1150	8.85		105.09			0.36
1250	7.80		126.62			0.33
1350	7.28		153.83			0.30

The bridge deck failed with a loud noise at a load of 1890 kN. Subsequently, the composite girder broke due to damage to the reinforcement. The prestressed steel strands and concrete did not fail during the test, but local sag occurred at the end of the girder, indicating a slip between the prestressed steel strands and the concrete. The collapsed concrete bridge deck due to the buckling of the longitudinal steel bars and the exposure of the stirrup and steel bars is shown in Fig. 26a. The bending stiffness decreased rapidly after the bridge deck was crushed. The redistribution of the stress in the failed section caused damage to the web. The steel bars yield, as the load increasing to 750 kN, resulting in the length of cracks and tensile forces in prestressed strands rising significantly, which leads the bending stiffness decreasing dramatically in the following load procedure. Then, as the compressive part, the bridge concrete deck provides significant ductile deformation in this composite girder, caused by a plenty of steel bars in bridge deck. The web damage and the exposed longitudinal steel bars and stirrups in the web are shown in Fig. 26b. The ductile failure of the composite girder included the collapse of the C50 concrete deck and the yielding of the steel bars; thus, the C70 concrete did not fail immediately.

Fig. 26.

Damage patterns.

Service in real-world conditions

To assess the mechanical performance of these girders, a long-term monitoring is conducted for a simply supported bridge with 8 I-girders, as shown in Fig. 27. The results show that the load is identically divided for each girder, with the identical vertical displacement (6.8 mm) for each girder in the middle span, as shown in Figs. 28 and 29a. Besides, there are not large differences in strains between each girder, without larger than the limit of tensile and compression of C70 concrete (Fig. 29b). Therefore, the 35-m long precast, pretensioned concrete I-girder with pretensioned double broken strands provides good mechanical performance in real-world conditions.

Fig. 27.

Monitoring for bridge.

Fig. 28.

Load proportion.

Fig. 29.

Deflections of girders under loads.

The temperature gradient is large in cross sections of the girder, especially in the top plate. And the large tensile stresses would occur in the bottom of top plate, which would lead cracks in girder. Besides, the height of girder also triggers large temperature stress.

The humidity affects the deformation of the concrete girder by influencing the concrete creep, and the low humidity leads the fast water loss in concrete with the large creep deformation. The upward vertical deflections are greatly different in the 35-m long precast, pretensioned concrete I-girder with pretensioned double broken strands in the environments with humidity of 55%, 80% and 95% respectively. The upward vertical displacement is 46.8 mm in middle span in the environments with humidity of 55%, much larger than the ones in the environments with humidity of 80% and 95%, as shown in Fig. 30.

Fig. 30.

Upward vertical deflections in middle span.

Conclusion

A full-scale model test was used to investigate the mechanical performance of a 35-m long precast, pretensioned high-strength composite I-girder with pretensioned double broken strands. The deformation of the composite girder, the strain of the concrete and steel bars, the tensile force of the prestressed strands, and the concrete cracks were examined. The equivalent bending stiffness in different sections was derived, and the mechanical behavior of the girder during bending, cracking, and failure was evaluated. The main conclusions are as follows.

1. The maximum vertical deflection in the midspan during bending and cracking was significantly lower than the allowable value according to the Code for the Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts (JTG 3362-2018). The deflection of the composite girder increased nonlinearly after the load exceeded 1350 kN and was 60 cm at failure. The ductility coefficient was 15.0, indicating satisfactory performance and ductile failure.

2. The crack resistance coefficient was 1.31. As the load increased to 1450 kN, numerous cracks caused significant damage to the composite girder. The maximum strain of the bridge deck was -1287 με, and the composite girder failed at a load of 1890 kN. The C50 concrete on the bridge deck significantly improved the girder’s bending ductility. The coefficient of the bending bearing capacity was 1.54, indicating that this girder had good bending and cracking resistance and an appropriate ultimate bearing capacity.

3. After the load exceeded 750 kN, the bending stiffness of the composite girder decreased due to numerous cracks in the concrete. The strain of the steel bars on the bottom increased rapidly until fracture occurred, and the maximum strain was3286 με. Separation between the steel strands and the concrete resulted in a significant increase in the tensile strain in the load range of 104.9 kN-130.3 kN. This result indicated that the steel bars and steel strands improved the bending ductility and significantly delayed the failure of the composite girder during bending.

4. As the load increased from 750 to 1350 kN, the maximum crack width rose from 0.10 mm to 0.38 mm, which is lower than the maximum allowable crack width according to the Code for the Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts (JTG 3362-2018). Therefore, this structure exhibited good crack resistance, although the degradation coefficient of the bending stiffness γ_s decreased from 0.70 to 0.30. The composite girder exhibited ductile failure at a load of 1890 kN. The bridge deck collapsed, and the steel bars yielded, demonstrating ductile failure during bending.

5. Load is identically divided for each girder, and there are not large differences in strains between each girder, indicating that the 35-m long precast, pretensioned concrete I-girder with pretensioned double broken strands provides good mechanical performance in real-world conditions. Besides, the low humidity leads the fast water loss in concrete with the large creep deformation, thus leading larger upward vertical displacement in the environments with low humidity.

Author contributions

T. L. and X.Z. contributed to the conception of the study; T. L. and J.C. performed the experiment; T. L. and X.Z. contributed significantly to analysis and manuscript preparation; Y.Y. performed the data analyses and wrote the manuscript; Y.L. provided guidance throughout the process and made revisions to the language of the paper; X.Z. helped perform the analysis with constructive discussions.

Funding

This article was funded by Key Research and Development Program of Shaanxi (No. 2024SF-YBXM-616), Innovation Capability Support Programme of Shaanxi (No. 2023-CX-TD-38), Natural Science Basic Research Program of Shaanxi (No. 2022JC-23 & 2024JC-YBMS-321), and Shaanxi Teacher Development Research Project (No. SJS2022ZQ019).

Data availability

The datasets used in this study were obtained from field tests. All data generated or analyzed during this study are included in this published article.

Declarations

Competing interests

The authors declare no competing interests.