Finite element analysis of mandibular fracture fixation authenticated by 3D printed mandible mechanical testing

Abstract

Finite element analysis (FEA) for mandibular fracture fixation in craniomaxillofacial surgery remains promising but has been restricted due to the absence of an authenticated FEA model. This study aims to create an authenticated FEA model. This model was verified through a series of 3D printed mandible mechanical testing (3D-MMT) in a universal tensile machine using an indistinguishable set-up. Non-comminuted mandibular symphysis, parasymphysis, and angle fracture fixation stability were evaluated using a 2.0 mm 4-hole miniplate in three different plate configurations. Both FEA and 3D-MMT outcomes were reproducible and in agreement with the present understanding of stable mandibular fracture treatment. The results show favourable fracture stability with the dual plating, followed by the superior border, with the least stability observed in the inferior border plating. Furthermore, the FEA and the 3D-MMT outcomes were consistently similar, with a systematic 0.56 ± 0.12 mm total displacement difference (standard deviation). An excellent interclass relation coefficient (0.93, 95% confidence interval: 0.80–0.96) was found between the FEA model and the 3D-MMT mechanical test, indicating that both results were consistent with each other. The authenticated FEA can accurately study the recognised biomechanical behaviour of non-comminuted mandibular fractures and shows a potential application for complex fracture fixation analysis.

Introduction

The application of three-dimensional (3D) modelling and finite element analysis (FEA) in craniomaxillofacial surgery (CMF) has been promising, particularly for mandibular fracture fixation^1–13. FEA is a powerful non-invasive tool known for its high precision, which can effectively replace the time-consuming and costly in vivo studies, such as mechanical testing of polymeric or cadaveric mandibles^14–18. As a flexible in silico instrument, FEA can enhance the understanding of fracture treatment by: (1) evaluating the distribution of stress, strain, displacement, or forces; and (2) providing a direct visual overview of what is happening to the fracture stability in terms of reduction and fixation^{1–3,9–14,19,20}. Especially, in case of complex fractures (e.g., severely atrophic or comminuted), FEA can enhance the optimal fracture treatment (e.g., visualisation and localisation of the forces, stress, or displacement), and lead to improvement of the existing osteosynthesis or development of new implants (e.g., patient-tailored 3D printed implant)^1,2,21–23. However, FEA applicability for mandibular fracture treatment has been limited due to the lack of an available authenticated model that could be routinely utilised in the clinical setting^1,2,14,21,24.

In our previous studies, we systematically took the steps towards developing an FEA model authenticated by a series of polymeric mandible mechanical tests^1,2. We observed that the developed FEA model was a proper tool to evaluate non-comminuted mandibular fracture fixation stability; however, optimised adjustments were necessary in both the FEA model and the authentication process to achieve an excellent agreement between the FEA and the mechanical test setup (e.g., mandibular material properties, fracture reduction, and mechanical test configuration).

The aim of this study is to develop an authenticated in silico FEA model principle for mandibular fracture fixation. This will be investigated by evaluating common mandibular fracture treatment using a precisely fine-tuned FEA model, authenticated through a series of 3D printed mandible mechanical testing (3D-MMT). First, we hypothesise that our FEA principle is a valid tool for evaluating mandibular fracture fixations (e.g., in case of complex fractures), and can assist in optimal selection or development of osteosynthesis materials. This may reduce the future need for the use of costly and time-consuming model experiments and in vivo physical tests. Second, we hypothesise that the current FEA model is significantly improved compared to our previous model by substantially reducing the displacement difference between the FEA and 3D-MMT outcomes.

Material and methods

Study outline

The FEA principle was applied to evaluate the fixation of the mandibular symphysis, parasymphysis, and angle fracture using different miniplate configurations. For the fracture fixation, the study used a 2.0 mm 4-hole 1.0 mm thick titanium miniplate (reference nr. 25-551-04-09) and the maxDrive 2.0 × 6 mm screws (reference nr. 25-872-05-09) (KLS-Martin, Gebrüder Martin GmbH & Co., Tuttlingen, Germany). Three different miniplate configurations were tested, namely: superior border (in accordance with the ideal line of osteosynthesis), inferior border (the lower mandibular border), and dual plating (using two miniplates at the mandibular superior and inferior border). Solidworks software (version SP5.0, 2021, Waltham, Massachusetts, USA) was used for the in silico numerical simulations. FEA authentication was attained by conducting the 3D mandible mechanical testing (3D-MMT), which used 3D printed polymeric mandibles placed in a universal tensile machine using a custom-made fixture device. Both FEA and 3D-MMT were conducted under identical conditions, specifically identically matched: fracture type, fracture reduction, miniplate configuration, miniplate location, applied load, mandibular condylar fixture region, connections, and constraints.

Creating 3D model

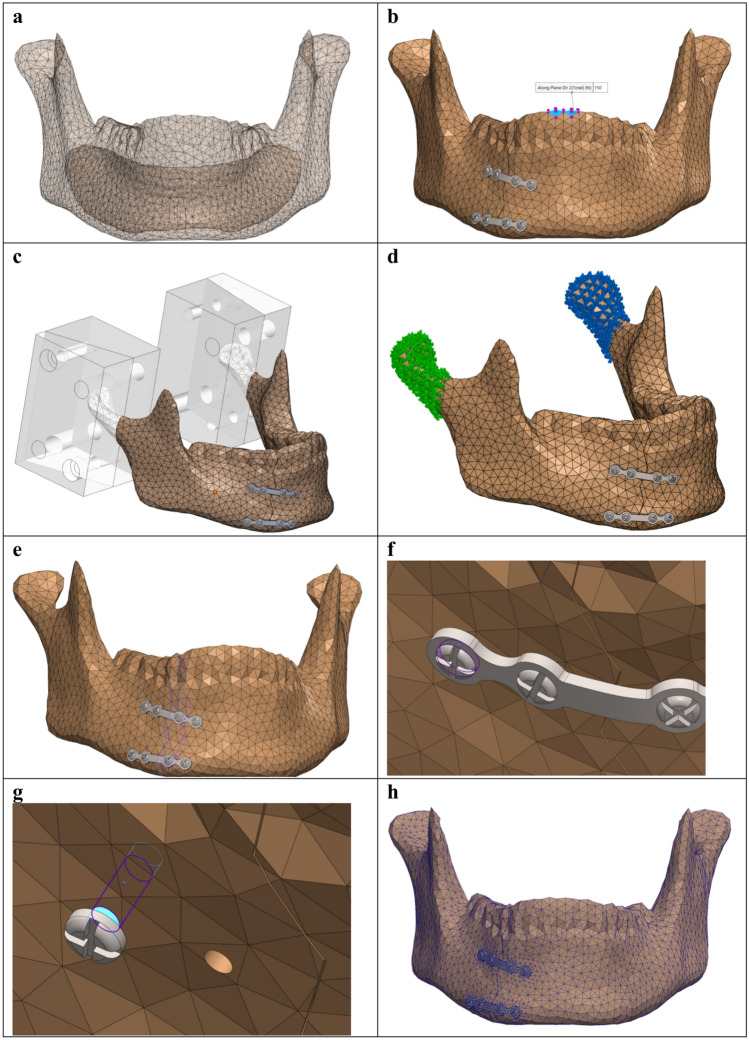
The study contains the same geometrically shaped mandible model as used in our previous study¹. The 3D mandible model was obtained by a cone beam computed tomography (CBCT) scan (Planmeca Promax dental imaging device, 3D-Max ProFace, Helsinki, Finland) of a polymeric mandible (bone setting, 120 kVp tube potential, 2.5 mAs tube current, and 400 µm voxel size). Mimics software (version 20.0, Materialise, Leuven, Belgium) enabled cortical and trabecular mandibular bone segmentation using different Hounsfield units (HU) thresholds. Further, 3-Matic software (version 15, Materialise, Leuven, Belgium) was used to smooth and wrap the 3D model. Afterwards, Geomagic (Solidworks 2021 add-in, 3D systems, Rock Hill, South Carolina, USA) was used to create a single mandible assembly file by adding the cortical and trabecular bone segments. This way the segmentation geometrical mesh errors were resolved, and an organic functional file was made to import to Solidworks in a stereolithography (STL) file format (Fig. 1a). The rest of the analysis was conducted in Solidworks.

Fig. 1.

3D model assembly and FEA set up in Solidworks. (a) Mandible 3D model with the segmented cortical bone and trabecular cavity. (b) Bite load of 150 N applied downward on the two frontal incisor teeth of the mandible, identical to the 3D-MMT load application. (c–d) Mandibular fixtures at the condylar region using fixed geometry, identical to the mandible holder’s fixation used in the 3D-MMT: (c) defining the regions where fixtures are applied, and (d) the applied fixtures on the right and left condylar regions. (e) Fracture surfaces constraints using contact sets with no penetration and a fracture distance of 0.1 mm. (f) Contact connection interaction between the screw and the miniplate. (g) Bounded connection constraints between the screw and the mandible. (h) Illustrating the applied converged mesh.

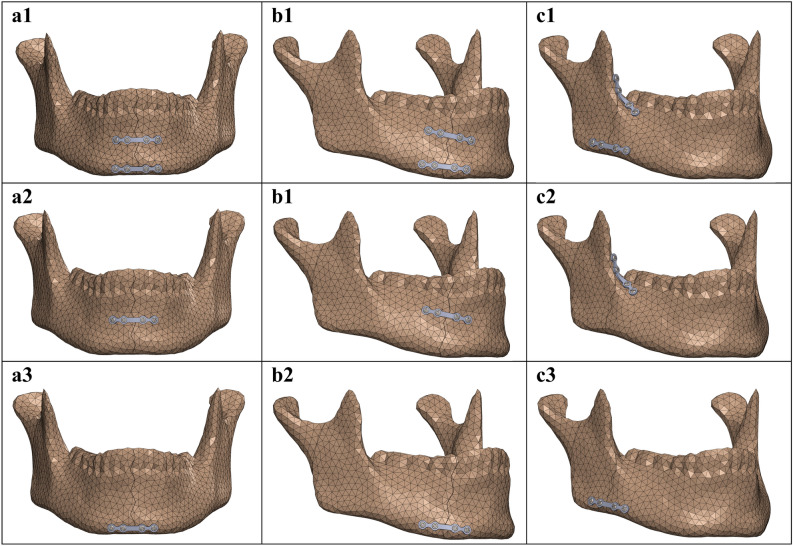
In the study, three clinically realistic non-comminuted jagged line fractures were created in the mandibular symphysis, parasymphysis, and angle regions (Fig. 2). The fracture surface distance was set at 0.1 mm, identical to the fracture surface distance measured from the fixated 3D printed mandibles used in the 3D-MMT. For the fracture fixation, a precise model of a 2.0 mm 4-hole titanium miniplate (1 mm thickness, 26 mm length, and 4.3 mm width) and 6 mm titanium screw (6 mm length and 2 mm diameters) was created in Solidworks. These were applied for the in silico fracture fixation in three different configurations (Fig. 2).

Fig. 2.

In silico mandibular fracture fixation in the region of (a) symphysis, (b) parasymphysis, and (c) angle using the following miniplate configurations: (1) dual plating configuration, (2) superior border plating, and (3) inferior border plating.

Finite element analysis (FEA)

Creating assembly

The 2.0 mm miniplate was positioned at the fracture site in three different plating configurations (Fig. 2). The miniplate was held against the mandibular surface using the maxDrive screws tightened in the mandibular screw holes, in accordance with the non-locking compression plating system. The assembling setup in the in silico study was identical to the 3D-MMT study, ensuring matched fracture configurations and fixation setups in both studies (Fig. 2).

Load and fixture

The applied load and fixtures were matched to the setup used in the 3D-MMT. A load of 150 N was inserted on the two mandibular frontal incisor teeth, corresponding to the identical position of the applied load in the 3D-MMT (Fig. 1b). The 150 N load was selected for two reasons, namely: first, it is the average postoperative incisal maximum bite force according to the literature for a non-comminuted mandibular fracture treated with miniplate osteosynthesis^25,26; and second, at this load, the FEA results can be best compared to the 3D-MMT outcomes.

The fixtures were precisely matched to the custom-made mandible holder clamp system used in the 3D-MMT (Fig. 3). This was done by first positioning the 3D modelled mandible clamp system on the 3D mandible model at an exact location as applied in the 3D-MMT (Fig. 1c). Next, the fixture nodes were selected according to the reference lines from the mandible holders (Fig. 1d). Finally, the fixed geometry option in Solidworks was used for defining the fixtures at the selected regions (Fig. 1d).

Fig. 3.

3D printed mandible mechanical testing (3D-MMT). (a) Total overview of test setup used in the 3D-MMT. (b) Overview of the custom-made device including the mandible holders for positioning the mandible onto the mechanical test bench. (c) The 3D printed mandible inserts used for positioning the mandible inside the aluminium mandible holder frames. (d) Overview of how mandible inserts are positioned inside the mandible holder aluminium frames. (e) The back view of the custom-made device front plate, showing four M6 bolts used for tightening the mandible holder aluminium frames to the frontal plate of custom-made device. (f) Applied load through a custom 3D printed adaptor attached to the load cell of the universal tensile machine.

Material properties

The material model used is linear elastic isotropic. The mechanical material properties of the material, used for 3D printing the mandible replicas, was provided by the manufacturer’s datasheet^27,28. The material properties of the cortical bone segment were set at an elastic modulus of 1700 megapascal [MPa], mass density of 0.93 g/cm³, and Poisson’s ratio of 0.34^27,28. Though not used in the model but relevant in the interpretation of the results, we mention that the yield strength is 40 MPa. The trabecular bone segment was set as a cavity, identical to the 3D printed mandibles used in the 3D-MMT. Therefore, there was no need to define the material properties of the trabecular bone.

The titanium osteosynthesis (miniplate and screws) mechanical properties were defined with an elastic modulus of 104,800 MPa, yield strength of 827.40 MPa (not used in the model), mass density of 4.43 g/cm³, and Poisson’s ratio of 0.31²⁹.

Connections and constraints

The constraints between the mandible and osteosynthesis were defined by using the local interactions property manager in Solidworks. This was achieved based on the present knowledge of mandibular fracture fixation in accordance with non-locking compression osteosynthesis plating^1,30–33, identical to the setup used in the 3D-MMT. The constraints between most of the assembly parts were set as contact, namely the connection between the fracture surfaces (Fig. 1e), the miniplate and the mandible, and the miniplate and the screws (Fig. 1f). Contact was defined without friction, whereupon a load application, only normal forces would be exchanged between the surfaces of the components. Further, the fracture surfaces were set at a fixed distance of 0.1 mm, illustrating optimal reduction and in line with the measured fracture surfaces in the 3D-MMT after placing the mandible onto the universal tensile machine. Finally, the interactions between the screws and the mandible screw holes were set as bonded (Fig. 1g). This means that the screw is tight inside the mandible screw hole, holding the miniplate fixed against the mandibular surface.

FEA mesh convergence

Sensitivity analyses were conducted to determine the proper mesh size for the FEA. Convergence of the solution was attained by progressively reducing the mesh size until the peak Von-Mises stress [MPa] became independent of the mesh size (Supplementary Fig. S1: mesh convergence plot). This advanced to a controlled mesh which was used in the FEA simulations. The applied mesh was set at a 0.15 mm minimum and 5 mm maximum element size (Fig. 1h). The applied mesh had an average computation time of 45 min per simulation run, on a 12th Gen Intel Core i9-12950HX CPU 2.30 GHz processor with 32 GB RAM memory.

3D printed mandible mechanical testing (3D-MMT)

Solidworks mandibular 3D models with three different fractures were used for 3D printing the polymeric mandible replicas (Fig. 1a, Supplementary Fig. S2). The study used 3D printed mandibles made from a substance with known mechanical material properties. The fractured mandible replicas were 3D printed based on selective laser sintering (SLS) method in an EOS-P-369 printer (Electro Optical System, model P 369, EOS GmbH, Munich, Germany) using polyamide 12 (PA12) (EOS fine polymer powder, trade name: PA 2200 Performance, PA12 medical grade) material. The 3D printer could only print the cortical section of the mandible due to the limitations of the available 3D printer. The trabecular section was left empty as a cavity inside the cortical bone segment (Fig. 1). Hence, this was also applied in the FEA mandibular 3D model. Afterwards, assemblies of the fractured mandibles with the miniplates were created with the assistance of an experienced OMF surgeon; however, only one person did the assembling process (e.g., miniplate bending, drilling screw holes, and screwing) to eliminate any interindividual variations. The assembling process was done by using the manufacturer’s original tools (Supplementary Fig. S2).

For the mechanical testing, a calibrated Instron 3400 universal tensile machine (Instron, 3400 series, dual column table 34TM-5 model, Norwood, USA) was used. A computerised test protocol was meticulously predefined using Instron’s mechanical test bench software (version 4.34, BlueHill Universal, Illinois Tool Working Inc.) to establish an identical testing condition for all the mechanical experiments.

The study used a custom-made device for positioning the mandible onto the universal tensile machine, similar to the device used in Daqiq et al.¹; however, the mandible holders were significantly improved (Fig. 3a–d). The redesigned mandible holders were constructed of outer frame blocks made of A6061 aluminium alloy with 3D printed inner inserts from nylon (polyamide type 6, PA6) (Fig. 3c–d). This design allowed the holders to function as a clamp system, securely holding the mandible at the mandibular condylar region (Fig. 3c–d). Each mandible holder frame consisted of two individual blocks connected by four M6 stainless-steel bolts, ensuring a fixed tight clamp system that facilitated easy placement and removal of the mandible onto the device (Fig. 3d). The outer frame of the mandible holders was securely fixed tight to the front plate of the custom-made device using M6 bolts, effectively eliminating any movement, translation, or rotation of the mandible (Fig. 3e). The nylon inner inserts (Fig. 3c) were replaced after every nine tests due to the potential of deformation from repeated use, with a total of four pairs of inserts used for each side.

To apply load on the mandible, a custom 3D printed adaptor was mounted on the load cell of the universal tensile machine (Fig. 3f). This adaptor, made of nylon (PA6), was further strengthened by an AISI 316 stainless-steel flat ring inserted into the centre hole where it was connected to the load cell of the tensile machine. The load cell was capable of 5 kilonewtons [kN] maximum load. The mechanical load was applied on the two mandibular frontal incisors via the 3D printed adaptor (Fig. 3f).

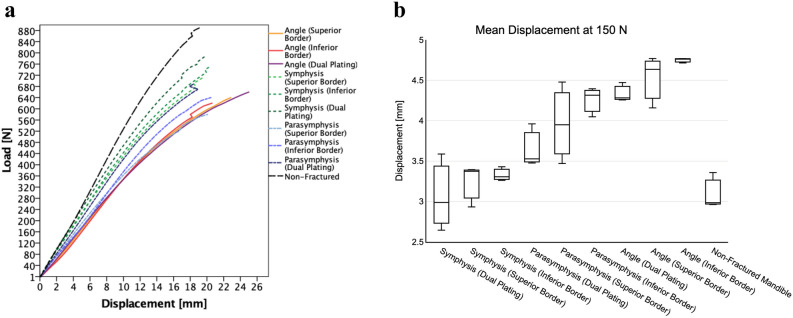
Prior to the start of each test, the mandibles were positioned onto the universal tensile machine at an identical location using the custom-made device with mandible holders (Fig. 3). Before starting with the experiments, the load cell was calibrated to a predefined zero position. The testing started by running the pre-programmed test protocol in the universal tensile machine software. A preload of 5 Newton [N] was applied, after which the load increased continuously at the rate of 1 Newton per second [N/s]. Each test was automatically terminated upon reaching the failure point (e.g., mandible breaks, or the fixation fails), defined at a load drop threshold of 40%. In the study, only the compressive displacement in relation to the applied load could be measured by the tensile machine. The compressive displacement in the downward direction was registered based on the movement of the load cell from the initial zero position up to the failure point (Appendix: 3D-MMT results at the failure load). All the test data were logged in the tensile machine software and were exported for further analysis.

Finally, the mechanical testing was performed three times for each of the fractures and each of the plate configurations with a total of twenty-seven tests (e.g., angle fracture with dual plating was tested three times). Furthermore, an additional three tests were conducted for non-fractured mandible replicas for the comparison.

Data analysis

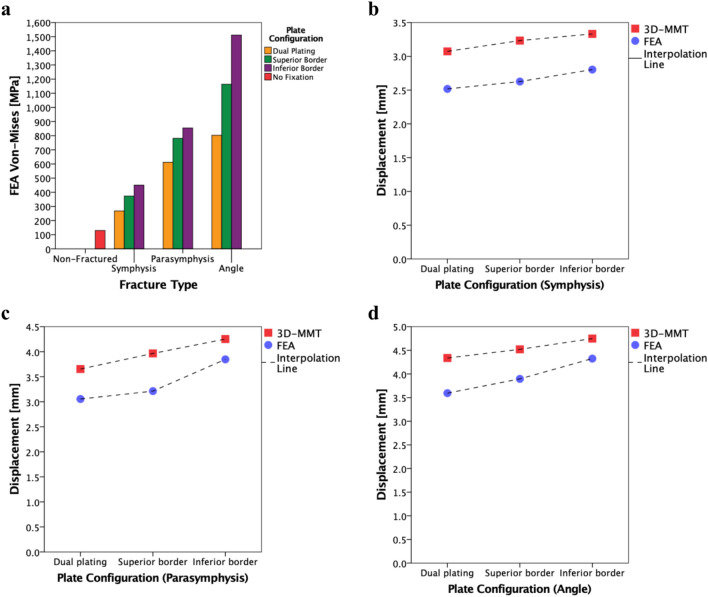
Firstly, in the FEA simulations: the Von-Mises stress distribution and the maximum Von-Mises stress in megapascal [MPa] (Table 1, Figs. 4, 5 and 6) as well as the displacement in millimetre [mm] were assessed (Table 2, Fig. 7). The presence of small amount of stress at the fixture regions was visualised by applying iso clipping property manager option (set at 4 or 40 MPa), which is the smallest stress value that could be chosen to properly show the stress around the fixture sites in the figures (Supplementary Figs. S3b-c and S4). Secondly, the 3D-MMT displacement [mm] outcomes were evaluated (Table 2). Lastly, the displacement results of the FEA were compared to the outcomes from the 3D-MMT. This was achieved by comparing the displacement pattern for the different fracture types and miniplate configurations at 150 N load (Table 2, Fig. 8). For displacement comparison, the FEA displacement in the Z-axis was used, as this corresponds to the direction of applied load in the 3D-MMT.

Table 1.

FEA maximum Von-Mises stress [MPa] outcomes.

Mandibular fracture	Miniplate configuration	Von-Mises stress (MPa)
Symphysis	Dual plating	267.70
	Superior border	373.43
	Inferior border	450.51
Parasymphysis	Dual plating	612.38
	Superior	781.84
	Inferior	854.16
Angle	Dual plating	802.90
	Superior	1163.67
	Inferior	1511.57
Non-Fractured mandible*	Not applicable	129.98

*Non-Fractured mandible: as a baseline for comparison.

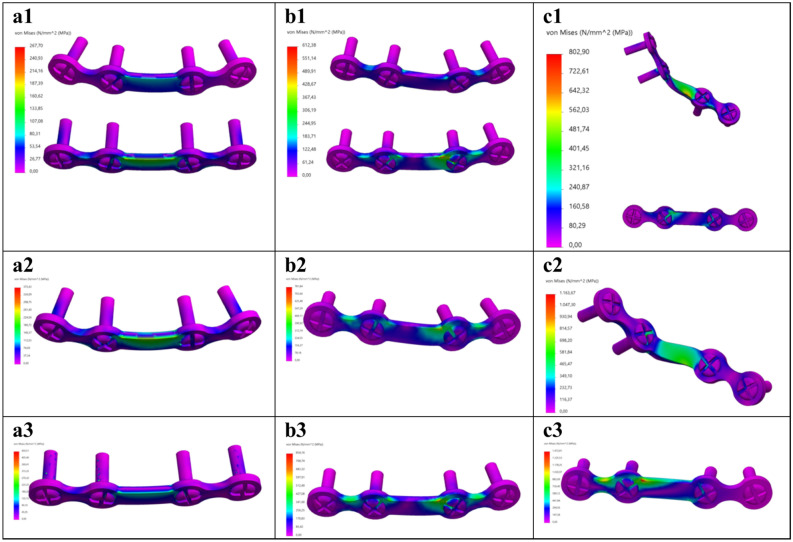
Fig. 4.

FEA Von-Mises stress distribution at 150 N load for the mandibular (a) symphysis, (b) parasymphysis, and (c) angle fracture fixated using the following miniplate configurations: (1) dual plating, (2) superior border plating, and (3) inferior border plating. Colour coding: the minimum stress is indicated by bright pink colour; and the maximum, as indicated in Table 1, by red colour.

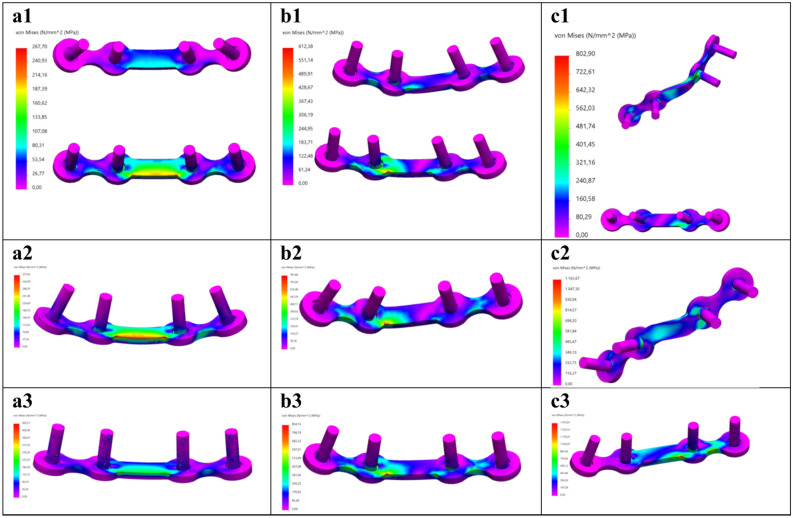
Fig. 5.

Anterior overview of the osteosynthesis (miniplate and screws) FEA Von-Mises stress distribution at 150 N load for the mandibular (a) symphysis, (b) parasymphysis, and (c) angle fracture using the following fixation configurations: (1) dual plating, (2) superior border plating, and (3) inferior border plating. Colour coding: the minimum stress is indicated by bright pink colour; and the maximum, as indicated in Table 1, by red colour.

Fig. 6.

Posterior overview of the osteosynthesis (miniplate and screws) FEA Von-Mises stress distribution at 150 N load for the mandibular (a) symphysis, (b) parasymphysis, and (c) angle fracture using the following fixation configurations: (1) dual plating, (2) superior border plating, and (3) inferior border plating. Colour coding: the minimum stress is indicated by bright pink colour; and the maximum, as indicated in Table 1, by red colour.

Table 2.

The 3D-MMT displacement compared to the FEA displacement in mm at 150 N load.

Mandibular fracture	Miniplate configuration	Test number 3D-MMT*	Displacement (mm) at 150 N		Displacement difference***
			3D-MMT*	FEA**
Symphysis	Dual plating	1	2.65
		2	2.99
		3	3.59
		Mean ± SD	3.07 ± 0.39	2.52	0.55
	Superior border	1	3.37
		2	3.39
		3	2.93
		Mean ± SD	3.23 ± 0.21	2.63	0.60
	Inferior border	1	3.26
		2	3.43
		3	3.31
		Mean ± SD	3.33 ± 0.07	2.80	0.53
Parasymphysis	Dual plating	1	3.96
		2	3.48
		3	3.53
		Mean ± SD	3.65 ± 0.22	3.05	0.60
	Superior border	1	3.95
		2	3.47
		3	4.48
		Mean ± SD	3.97 ± 0.41	3.21	0.76
	Inferior border	1	4.05
		2	4.39
		3	4.31
		Mean ± SD	4.25 ± 0.15	3.85	0.40
Angle	Dual plating	1	4.26
		2	4.47
		3	4.28
		Mean ± SD	4.34 ± 0.10	3.59	0.75
	Superior border	1	4.77
		2	4.16
		3	4.63
		Mean ± SD	4.52 ± 0.26	3.90	0.62
	Inferior border	1	4.76
		2	4.71
		3	4.77
		Mean ± SD	4.75 ± 0.02	4.33	0.42
Non-Fractured		1	2.96
		2	3.36
		3	2.99
		Mean ± SD	3.10 ± 0.18	2.41	0.69

*3D-MMT (3D printed mandible mechanical testing) displacement: each scenario (fracture mandible with three different miniplate configurations and non-fractured mandible) was repeated three times under identical conditions (Test number 1–3). Italic: mean and standard deviation (SD) of the three repeated tests.

**FEA displacement represents the exact values from the numerical simulations at 150 N load.

***Displacement differences between the FEA versus the 3D-MMT at 150 N load.

Fig. 7.

FEA displacement distribution in the Z-axis (same direction as the applied force) at 150 N load for the mandibular (a) symphysis, (b) parasymphysis, and (c) angle fracture with the following miniplate configurations: (1) dual plating, (2) superior border plating, and (3) inferior border plating. Colour coding: on the left side showing the displacement pattern (with the red colour representing the maximum displacement), and the coordinate axis.

Fig. 8.

(a) FEA simulation maximum Von-Mises stress outcomes [MPa] at 150 N load. (b–d) Displacement [mm] pattern of 3D-MMT (red) versus FEA (blue) of each fracture fixated with three different miniplate configurations at 150 N load; respectively: (b) symphysis, (c) parasymphysis, and (d) angle fracture.

The outcomes of the FEA and the 3D-MMT were evaluated using IBM SPSS (version 28, IBM Corporation, Chicago, IL, USA) and R (version 4.1.1, r-project.org) with NLME package (version 3.1.166, Mixed Effects Models package). Firstly, descriptive statistics were used to determine the mean displacement and standard deviation (SD) of the three repeated 3D-MMT tests. Secondly, the FEA versus the 3D-MMT displacement differences were calculated for each fracture type and miniplate configuration as well as determining the total mean displacement difference. Finally, the interclass correlation coefficient (ICC) was calculated by estimating variance components in a mixed effect model, allowing for different variances for the experiment (σ²_e) and the simulation (σ²_s), as well as a fixed (systematic) difference between these modes; the ICC was then calculated as the correlation between simulation and experimental measurements, σ²_t/√(σ²_t + σ²_s) (σ²_t + σ²_e), where σ²_t is the estimated true variance of the displacement, and confidence intervals were estimated from the variance–covariance matrix of the variance estimates. ICC values were interpreted as follows: 0.00–0.20 is poor, 0.20–0.40 is fair, 0.40–0.60 is moderate, 0.60–0.80 is good, and 0.80–1.00 is excellent agreement³⁴.

Results

Finite element analysis (FEA)

The Von-Mises stress outcomes [MPa] are presented in Table 1. Different fracture types and miniplate configurations led to the variation in the Von-Mises stress distributions and the maximum Von-Mises stress location (Figs. 4, 5, 6 and 8a). In all the FEA models, the maximum stress (267.70–1511.57 MPa) remains on the miniplate which is responsible for holding the fracture segments into a fixed stable position (Figs. 4, 5 and 6). In terms of miniplate configurations, the dual plating method exhibited the lowest Von-Mises stress (267.70–802.90 MPa) (Fig. 4a1–c1), followed by superior border plating (373.43–1163.67 MPa) (Fig. 4a2–c2), and the highest stress was observed in the inferior border plate positioning (450.51–1511.57 MPa) (Fig. 4a3–c3). Regarding the fracture type, the angle fracture produced the highest stress (802.90–1511.57 MPa), followed by the parasymphysis fracture (512.38–854.16 MPa), with the lowest stress observed in the symphysis fracture (267.70–450.51 MPa). Further, a non-fractured mandible illustrates much lower stress (129.98 MPa) compared to a fractured mandible (Table 1, Supplementary Fig. S3). Furthermore, a small stress distribution was observed along the condylar fixture region where the mandible is held tight using the mandible holders (Supplementary Fig. S4). However, the stress is much lower at this condylar fixture region compared to the stress located on the miniplate.

Table 2 and Fig. 7 present the FEA displacement results [mm]. The displacement varied for different fracture types and miniplate configurations, revealing a similar pattern compared to the Von-Mises stress results (Table 1, Fig. 8). In all the fractures, the dual plating method demonstrated smaller displacements compared to a single plating (Table 2, Fig. 8b–d). Additionally, the displacement is greater in the inferior border compared to the superior border plating in all the fracture types, with displacement differences of 0.17, 0.64, and 0.43 mm (respectively for the symphysis, parasymphysis, and angle fracture) (Fig. 8b–d). Furthermore, displacement observed in a non-fractured mandible remains lower compared to the fractured mandibles (Table 2, Supplementary Fig. S3).

Third, the fracture stability using different miniplate configurations is illustrated (Figs. 5 and 7). Placement of the miniplate at the lower border results in the least stability, as the fracture faces tend to open, leading to reduced fixation stability. This effect is more visible in the angle fracture compared to the parasymphysis and the symphysis fractures. In contrast, dual plating demonstrates the most optimal fracture stability, maintaining intact and stable fracture surfaces.

Three-dimensional mandible mechanical testing (3D-MMT)

The 3D-MMT compressive displacement [mm] outcomes at a 150 N load are presented in Table 2 which is compared to the FEA displacement. In the mechanical tests, the load was gradually increased until reaching the failure point, which resulted in either the mandible breaking or the fixation failure (Fig. 9, Appendix: 3D-MMT outcomes at the failure load). Hence, at this failure point, all the mandible assemblies broke at the condylar fixture region (Appendix: Fig. A1–A4). The lowest displacement is found in the dual plate combination for all the fractures compared to the single plating (Table 2, Fig. 8b–d). In the single plate positioning, the displacement in the superior border plating was lower compared to the inferior border plating with the displacement difference of 0.10, 0.28, and 0.23 mm (respectively for the symphysis, parasymphysis, and angle fracture).

Fig. 9.

(a) Load (Y-coordinate) and displacement (X-coordinate) curve of the 3D-MMT mechanical tests from the start to the breakage load; and (b) displacement boxplot at 150 N load. The plots are based on the mean displacement of the three repeated tests conducted under identical conditions.

FEA versus 3D-MMT

Table 2 illustrates the displacement variations between the 3D-MMT and the FEA. The 3D-MMT demonstrates slightly higher displacement compared to the FEA, with a mean total displacement difference and SD of 0.59 ± 0.12 mm. Furthermore, the displacement patterns for different miniplate configurations across the various fracture types remain comparable and similar in both studies (Fig. 8b–d). Finally, the displacement ICC between the 3D-MMT and the FEA was 0.93 (95% CI 0.80–0.96) indicating excellent correlation between the two analyses. Note that ICC is based on covariances; thus, subtracting the displacement difference 0.59 mm or any other number will give the same result.

Discussion

The purpose of this study was to develop an authenticated 3D FEA model principle for the simulation of mandibular fracture treatment. This was achieved through a systematic approach to enhance our previous attempt to develop such a model by improving both the FEA methodology and the mechanical testing authentication process¹.

Three major outcomes were observed. Firstly, the results of mandibular FEA were similar to the present interpretations of mandibular fracture treatment. As the literature demonstrates, superior border plating results in eliminating the tensile forces on the mandible^35–38, while inferior border plating is necessary during functional load movements to stabilise the fracture against the torsional and bending forces^{31–33,39–43}. This study confirms these effects, showing that dual plating provides the most optimal fracture stability, followed by superior border plating, and the least stability was observed in inferior border plating (Fig. 8). In a dual plating method (Fig. 8, Fig. 4a1–a3), tensile forces are neutralised by the superior border miniplate, while the inferior border miniplate counterbalances compression forces during the application of a load. Furthermore, applying a single miniplate at the inferior border results in the least fracture stability (Fig. 4a3–c3). A similar effect was observed in our previous study, only with less correlation between the FEA and the 3D-MMT outcomes¹.

A key point to discuss is that the stress results show that the stress distribution on the fractured mandibles is almost constant, with most deformations occurring at the miniplate region. Using the Solidworks iso clipping property manager set at 40 MPa reveals a small amount of stress around the mandibular condylar fixture site (replicating the mandible holders used in the 3D-MMT) (Supplementary Fig. S4). This effect is more visible when examining a non-fractured mandible (Supplementary Fig. S3). The maximum stress observed in the non-fractured mandible is 129.98 MPa, located at the condylar fixture site (Supplementary Fig. S3a–c). However, this peak stress occurs in the outer mandibular bone surface region, while the stress in the rest of the mandible remains below 4 MPa (Supplementary Fig. S3c). When observing the colour bar stress pattern between the fractured and non-fractured mandibles (Fig. 4, Supplementary Figs. S3c and S4), it is evident that the stress in the remainder of the mandible (except the condylar fixture region and the osteosynthesis fixation site) is less than 4 MPa, illustrating that the mandible possibly can be considered as a rigid body^44–49. Currently, a single simulation run takes approximately 45 min using the converged mesh, with multiple runs often required to achieve accurate outcomes for clinical practice. This extended duration can lead to a lengthy decision-making process. To speed up the performance, one possibility is to model certain parts of the mandible as a rigid body, thereby reducing the degrees of freedom and, consequently, the computation time.

Secondly, the 3D-MMT results were consistently in line with the FEA outcomes and comparable (Fig. 8c–d). Both had an identical setup, each containing the same fracture type, fracture reduction, miniplate configuration, miniplate positioning, load application on the mandible, condylar fixture, and connections or interactions between the components. The universal tensile machine used in the 3D-MMT could only generate load–displacement relationships as output. This means that in the mechanical tests, the load was applied downward in the gravitational direction on the mandibular frontal incisors (Fig. 3f), with displacement changes measured in the same direction (Figs. 3 and 9a). For this reason, the FEA displacement in the Z-axis (same direction as mechanical tests) was used for comparison with the 3D-MMT displacement. The displacement patterns in both studies were consistently similar (Table 2, Fig. 8): the dual plating system resulted in a lower displacement compared to single plating, followed by superior border plating, and most displacement was observed in the inferior border plating. This agreement resulted in an excellent interclass correlation (ICC between the FEA and the 3D-MMT displacement, 0.93; 95% CI 0.80–0.96), where the ICC is based on covariances and will not change by a systematic error. The absolute displacement difference between the FEA and the 3D-MMT was consistently low, with a mean difference and SD of 0.59 ± 0.12 mm. This systematic error is substantially lower compared to our previous study¹ (1.13 mm).

Several biomechanical factors likely contribute to the remaining small but consistent displacement difference between the FEA and the 3D-MMT. First, in this study, Solidworks software was used to best compare the outcomes with our previous publication¹, which used the same software. In the follow-up studies, we will consider using software programs that may be more suitable for complex FEA models and could filter out small mismatches (e.g., Abaqus, Ansys, or Comsol). Second, we used bonded condition between the screws and the mandible screw hole connection (Fig. 1g), while a friction condition might be more correct. However, in a clinical setting, it is impossible to measure this; therefore, the assumption of bondedness is reasonable. Third, a substantial fraction of the systematic error is likely due to the mandible holders (Figs. 1c and 3). We modelled rigid mandible holders with zero displacement at the interface with the mandible. Both are approximations of reality since the holder will deform too, and the holder-mandible interface is a friction boundary (see Appendix 2). So due to the force acting at the incisal teeth region (Figs. 2b and 3f), the moment at the mandible holder is at its maximum and a non-negligible strain may occur there. The largest differences occur when the peak stress is about the yield stress or higher. Hence, plasticity is expected to play a role in the measurements too, whereas this was not taken into account in the FEA model. Recall that we set the mandibular material model as linear elastic isotropic, which neglects the nonlinear effect of large deformations. It is only valid as long as the stresses remain below the yield stress. This is a limitation of the present model which is to be relaxed in a next model. Furthermore, in future studies, we recommend using stress–strain sensor gauges during mechanical testing (e.g., at the peak strain zone predicted in the FEA) to quantify the stress or strain on the miniplate and the fixtures. Further, if possible, more studies should be conducted to measure friction and define its effect on the fixation and fixture regions as well as between the fracture fragments. Because of the numerous potential causes of the systematic error, it will likely be difficult to fully account for this systematic error. However, for clinical practice a small systematic error is not truly relevant. The computational model clearly shows which fixation configuration is most favourable for each fracture. A practical solution is to subtract 0.59 from all predicted “displacement difference” values in Table 2, making the new difference always less than 5% of the computed value.

Thirdly, using 3D printed mandibles made from materials with known mechanical properties appears to be the best replacement of the commercially available mandible replicas (e.g., Synbone, Sawbone). This enables a more accurate and precise comparison between the FEA and the 3D-MMT. The primary challenge of 3D printing lies in replicating the mandibular trabecular region. In our study, it was only possible to print the mandibular cortical segment with the trabecular segment being an empty cavity. However, the influence of trabecular bone on fracture stability is very limited; therefore, it is doubtful whether a precise simulation of the trabecular part contributes to an even more reliable FEA model. Additionally, it remains crucial that the mechanical testing process aligns precisely with the FEA setup for effective validation; therefore, the mandibles in the FEA and the 3D-MMT studies were identical. Furthermore, in future studies, it would be valuable to explore 3D printable materials with mechanical material properties identical to those of human mandibular bone. Finally, both in silico and experimental analyses were conducted using a polymeric material, which is inherently isotropic. However, cortical bone exhibits highly anisotropic behaviour, and when combined with the influence of the trabecular structures, differing mechanical responses from the miniplates are to be expected in clinical settings.

The strength of this study is the improvements over our previous study¹ and the inclusion of new scientific findings. Compared to the earlier model¹, this study includes five significant adjustments: 1) Synbone mandible replicas were used in our previous study¹. We tried to determine the Synbone mandibular cortical and trabecular mechanical properties by mechanical experiments using Synbone specimens, as these properties were not provided by the manufacturer. The found material properties (e.g., elastic modulus) were in line with earlier studies^50–52, with a slight variation observed in the composition of the Synbone trabecular and cortical segments at the end of the experiments, probably caused by the moulding process. Such variations could lead to differences in the biomechanical behaviour of the mandible replica. In contrast, the current study used 3D printed mandible replicas made from PA12, a material with exactly known mechanical properties. This approach ensured that the geometrical shape, composition, and mechanical material properties of the mandible were identical in both FEA and 3D-MMT. 2) In our earlier study, we could not say for sure whether the fracture reduction in both the FEA and the 3D-MMT were identical¹. Therefore, in the current study, the fracture surface distance in the 3D-MMT was measured, and a similar reduction was created in the FEA (Figs. 1e and 2). (3) The previous study contained mandibles with a non-comminuted straight-line fracture, resembling a saw cut rather than a realistic fracture¹; therefore, this study used true jagged-line fractures, which more accurately resemble the non-comminuted clinical fractures (Fig. 2). (4) The mandibular clamp system used in the earlier study was entirely made of nylon (PA6) and it was secured in the custom-made device using two stainless-steel rod bars¹. This setup might have led to non-observable mandibular movements at the fixture regions during the application of load, slight alterations in the positioning of the new mandible replica due to the sliding mechanism, and in a too rigid fixture since the mandible was fixed from the condyle to the mid-ramus region. In response, the current study redesigned and significantly optimised the mandible holders. This was achieved by creating aluminium frame blocks with nylon inserts, with the outer frame blocks fixed tight to the front plate of the custom-made device (Fig. 3). This design effectively eliminated any mandibular movement, translation, or rotation at the fixture region. Further, it ensured the precise placement of each mandible replica onto the mechanical test bench without any variations. Furthermore, this setup is considerably more realistic, as it holds the mandible only in the condylar region (Fig. 3c–d). (5) The previous study used a 200 N load in the FEA simulations and displacement comparisons¹. In contrast, this study applied a more realistic load of 150 N (Fig. 1b), based on literature reporting the maximum incisal bite force following surgery for a non-comminuted mandibular fracture fixated with miniplate osteosynthesis^25,26.

In conclusion, this study presents our authenticated and accurate FEA model for the assessment of mandibular fracture fixation. The in silico FEA outcomes of the non-comminuted fractures are in line with the present understanding of the mandibular fracture treatment and authenticated with the in vivo mechanical experiments. This means that the in silico FEA model can be used to analyse complex fractures (e.g., comminuted, or atrophic), compare or improve the current osteosynthesis (e.g., titanium versus biodegradable miniplates), and develop new implants (e.g., 3D printed patient specific implants), without the need for costly or time-consuming models and in vivo experiments. Therefore, the next step would be to use this model to study complex mandibular fracture fixations and compare the simulation results with the clinical outcomes. Perhaps, ultimately it can be routinely used as a tool in the clinical setting for enhancing the treatment approach of complex mandibular fractures.

Author contributions

O.D. conducted the study design, 3D modelling, FEA computer studies, 3D printed mandible mechanical testing (3D-MMT), and wrote the manuscript. F.W.W., C.C.R, F.K.L.S and B.v.M. were responsible for supervision, helping with data analysis, and providing guidance. G.L. assisted with the interclass correlation coefficient statistical analysis. The authors approve the manuscript.

Funding

The materials used for the three-dimensional mandible mechanical testing (3D-MMT) were funded by the Maxim Champy research grant awarded by S.O.R.G. (Strasburg Osteosynthesis Research Group). The funding organisation had no influence on the study design, conducting the study (including collection, management, evaluation, and interpretation of the data), and the writing of the manuscript.

Data availability

All data are available from corresponding author upon reasonable request.

Declarations

Competing interests

The authors declare no competing interests.

Ethical approval

Not applicable. This study does not contain any procedure with human participants or animals performed by any of the authors. All applicable international, national, and/or institutional guidelines were followed.

Informed consent

Not applicable. For this type of study, formal consent is not required.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-025-98732-3.