Machine learning-based prediction of heating values in municipal solid waste

Abstract

In this research, our objective was to utilize different machine learning techniques, such as XGBoost, Extra Trees, CatBoost, and Multiple Linear Regression (MLR), to model the heating values of municipal solid waste. The input parameters considered for the constructed models included the weight of the dry sample (kg) and the content of carbon (C), hydrogen (H), oxygen (O), nitrogen (N), sulfur (S), and ash in kg. The Extra Trees model, fine-tuned for hyperparameters, demonstrated outstanding performance, achieving R² values of 0.999 in the training set and 0.979 in the testing set. Notably, the model has shown robust accuracy, as evidenced by a low Mean Squared Error (MSE) of 77,455.92 on the testing dataset. Furthermore, the Mean Absolute Error (MAE) and Mean Absolute Percentage Error (MAPE) were 245.886 and 16.22%, respectively, further proving the model’s substantial predictive accuracy and reliability. Although XGBoost and CatBoost demonstrated strong predictive capabilities with high R² values, Extra Trees outperformed them by achieving significantly lower error metrics. On the contrary, MLR, utilized as a conventional technique, demonstrated moderate performance, suggesting a distinct trade-off between explanatory power and predictive accuracy. In the feature importance examination of the optimal model, Extra Trees, nitrogen content emerged as the most impactful factor, succeeded by sulfur content, ash content, and dry sample weight in a descending hierarchy of significance.

Introduction

The substantial increase in global waste production has raised alarming concerns regarding its environmental consequences, emphasizing the urgency for efficient waste management approaches^1,2. Inadequate management of waste introduces risks to ecosystems, public health, and natural resources. Urgent attention is required to tackle this issue and implement sustainable solutions to alleviate the negative impacts of waste^3,4. Effective waste management is crucial in reducing the environmental impact of human activities. By adopting effective waste management approaches, we can decrease the volume of waste directed to landfills and encourage the recuperation of resources through recycling and waste-to-energy methods⁵. Prudent waste management not only safeguards natural resources but also diminishes emissions of greenhouse gases, contributing to the promotion of a circular economy⁶.

An alternative for MSW involves harnessing energy through diverse thermal techniques like combustion, pyrolysis, and gasification⁷. Waste harbors energy that can be captured and transformed into electrical power or heat using advanced technologies⁸. Harnessing the thermal potential of waste allows us to diminish dependence on fossil fuels, contributing to the advancement of a more sustainable energy system⁹.

Heating values (HVs) are illustrated to significantly impact the planning and functioning of thermal disposal systems for MSW¹⁰. Estimating the heating value (HV) of MSW is essential for optimizing the design and functioning of technologies based on waste-to-energy conversion¹¹. The heating value of waste is significantly influenced by its physical parameters¹². The computation of the overall heat content of waste is affected by various crucial factors, encompassing waste composition, moisture content, density, ash content, and the greater heating value (HHV) of individual waste components^13,14. The analysis of waste composition offers valuable information about the variety and proportions of materials present, facilitating a more precise evaluation of their thermal value¹⁵. By taking into account these physical parameters, a holistic comprehension of waste and its energy potential can be established, enhancing the efficiency of waste-to-energy conversion processes¹⁶.

The heating value is experimentally measured utilizing a bomb calorimeter with excess oxygen. Nonetheless, determining heating values experimentally with a bomb calorimeter is associated with certain constraints. Representing MSW’s substantial volume and heterogeneity with a small sample mass of just 1 g poses significant challenges. Moreover, numerous waste-to-energy facilities lack the necessary experimental infrastructure for bomb calorimeter measurements¹⁷. Additionally, the results may be susceptible to various experimental errors. Furthermore, the experimental procedures are both time-intensive and costly. Various empirical correlations have been developed to overcome these challenges to estimate the HHV of different biomass materials, utilizing either proximate or ultimate analysis¹⁸. While empirical models based on ultimate analysis show significant potential, many exhibit inconsistencies when compared to experimental results. Consequently, modeling approaches are often regarded as valuable tools for predicting the heating value of MSW¹⁸.

Machine learning methodologies have become potent instruments in the implementation of waste management strategies^19,20. These methodologies empower us to scrutinize extensive datasets and derive significant patterns and associations^20,21. Within the realm of predicting waste thermal value, machine learning models provide a data-centric approach for precise heat content forecasts¹⁸. Through training on historical data encompassing waste composition and pertinent physical parameters, these models can acquire intricate relationships and produce dependable predictions²². Artificial intelligence models like neural networks have exhibited outstanding performance in this domain, surpassing conventional regression methods²³. Utilizing these machine learning models has the potential to transform waste management, improve decision-making, optimize resource allocation, and maximize the utilization of the thermal value of waste²⁴.

Among machine learning approaches, regression analysis is widely employed in constructing predictive models for estimating the heating value of MSW. However, it has certain limitations in predicting dependent variables (such as LHV) when the resolution of independent variables (e.g., waste composition) is low. Additionally, regression models are highly sensitive to the accuracy of the input data²⁵. Numerous inquaries have explored the use of alternative machine learning methods for predicting HHV. For instance, Xing et al.²⁶ applied three distinct ML algorithms of Artificial Neural Network (ANN), Support Vector Machine (SVM), and Random Forest (RF), to estimate the HHV of biomass based on proximate and ultimate analyses. Among these, the RF algorithm demonstrated the highest performance, achieving an R² value greater than 0.94. In a comparable study, Taki et al.²⁷ employed four machine learning methods of Radial Basis Function Artificial Neural Network (RBF-ANN), Multilayer Perceptron Artificial Neural Network (MLP-ANN), Support Vector Machine (SVM), and Adaptive Neuro-Fuzzy Inference System (ANFIS) to model the HHV using six different inputs: carbon, water, hydrogen, oxygen, nitrogen, sulfur, and ash. The results indicated that the RBF-ANN model outperforms the other models in predicting the HHV of MSW with greater accuracy. A study by Wang et al.²⁵ employed multiple linear regression and artificial neural network (ANN) techniques to estimate the LHV. The results demonstrate that models developed using both methods displayed comparable and satisfactory performance levels in predicting the LHV, as indicated by various statistical measures. In a study conducted by Kumar et al.¹⁷, both linear and non-linear methods were employed to develop prediction models for the LHV, utilizing the physical composition, proximate analysis, and ultimate analysis of mixed MSW as well as combustible components individually. In total, six models based on multiple linear regression (MLR) and six models using artificial neural networks (ANN) were created. The models developed utilizing combustible components demonstrated marginally slightly superior predictive performance compared to those based on mixed MSW. Afolabi et al.¹⁸ investigated the prediction of the HHV for various biomass classes utilizing three machine learning models: artificial neural network (ANN), decision tree (DT), and random forest (RF). The RF model was recognized to be most dependable, as it exhibited the lowest mean absolute error (MAE) of 1.01 and mean squared error (MSE) of 1.87. The literature review clearly indicates that specific ML models, including CatBoost, Extra Trees (ET), and XGBoost, have not been evaluated for predicting MSW heating values.

Therefore, In this research, our aim is to create a sophisticated data-driven framework for predicting the thermal value of waste. Through the utilization of waste’s physical composition, ultimate analysis, and employing machine learning models including MLR, CatBoost, Extra Trees (ET) and XGBoost CatBoost. Our objective is to achieve accurate predictions of heat content. The proposed framework will entail gathering extensive data on waste composition. Through meticulous training and validation of the models, we will evaluate their performance using relevant metrics. This thorough methodology will offer waste management professionals valuable insights into the thermal value of waste, facilitating more informed decision-making and resource optimization. In the end, this framework will play a role in fostering sustainable waste management practices and supporting the transition to a circular economy.

Materials and methods

Data sources

This inquiry centers on gathering and examining data from 24 counties within the Khorasan Razavi Province, Iran. Khorasan Razavi Province, covering a total area of 118,851 km², had a population exceeding 6 million according to the 2016 census. The province’s annual generation of MSW amounts to 1.2 million tons. The data utilized in this study were sourced from the solid waste management organization of Mashhad municipality. The typical categorization of reported MSW compositions encompasses various components comprising food waste, bone, bread, paper and cardboard, wood and cellulosic materials, plastics, glass, metals, rubber, hazardous waste, textiles, electronic components, and debris. Nevertheless, certain types of waste can be further subdivided. For instance, plastic waste encompasses soft plastics, hard plastics, polystyrene, PET, and similar categories. Data on the physical composition were documented for both spring and summer seasons. The final dataset for each parameter in the respective counties was derived from the average composition obtained during spring and summer. Table 1. illustrates the seasonal average of the physical composition of 24 cities in the study area. To ascertain the thermal content of solid waste, the calculation involved considering waste components such as food waste, paper and cardboard, wood and cellulosic materials, textiles, plastics, glass, and rubber. The adjusted Dulong formula was utilized to compute the heating value, incorporating ultimate analysis (determination of carbon, hydrogen, oxygen, nitrogen, and sulfur percentages by weight). This dataset offers significant insights into the heat content of diverse waste materials across the 24 counties within Khorasan Razavi Province.

Table 1.

Physical components of wastes produced in study area (%).

City name	Physical composition of the wastes used to calculate heating values
	Food waste	Paper and cardboard	Wood and cellulosic materials	Fabrics and textiles	Plastic	Glass	Rubber
Torbat Heydarieh	55.355	5.2	5.285	2.25	13.275	1	0
Jangal	41.050	9	0.6	8.65	25.25	3.25	5.1
Roshtkhar	16.5	6.25	8.75	9	7.5	7.5	7.5
Bayg	37.6	3	7.85	5.25	6	5.1	1.5
Dolatabad	41.45	6.35	2.75	4.3	6.75	2	1.9
Kadkan	56.4	6.15	0.95	4.45	5.9	4.25	1.1
Robatsang	67.59	3.925	1.415	3.555	6.955	2.925	0.69
Sarakhs	27.86	7.46	6.72	4.82	13.72	1.2	0.71
Mazdavand	55.15	3.6	4.31	9.21	12.98	5.5	1.23
Quchan	68.7	3.4	4.4	3.3	13.25	4.6	0.505
Bajgiran	53.650	10.105	1.1	2.38	8.5	3.55	1.6
Chekneh	46.66	3.89	1.430	4.46	10.43	2.085	1.11
Kalat	19.215	14.31	4.39	3.55	12.245	10.420	2.365
Zavin	9.04	4.95	2.1	13.75	13.11	2.6	1.25
Dargaz	53.8	6.2	5.5	2.9	13.85	1.65	0.1
Chapeshlu	53.65	2.45	2.6	3.55	7.45	0.65	0
Lotfabad	39.75	14.15	5.65	2.4	15.45	1.85	1
Nokhandan	60.35	2.2	2	13.95	5.1	1.8	0.4
Neyshabur	61.05	10.685	0.69	2.735	4.245	1.745	0.77
Darud	21.16	0.955	0.97	1.665	4.06	0.415	0.055
Kharv	35.64	4.285	0.54	1.84	9.235	1.34	0.55
Taybad	68.8	7	5.05	2.4	16.3	1.2	1.4
Kariz	5.05	6.3	1.45	2.6	11.6	1.45	1
Mashhad Rizeh	35.55	1.993	4.74	1.495	3.115	1.085	1.04
Mean	42.96	5.99	3.39	4.77	10.25	2.88	1.37
Std	18.79	3.55	2.44	3.55	5.04	2.38	1.67

According to the physical composition of MSW and ultimate analysis, the heating value can be computed as follows using the modified Dulong formula²⁸:

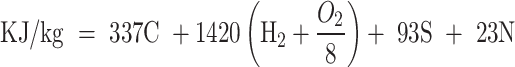1

Data description

Processing of data

Before developing machine learning models, the dataset gathered from 24 cities was randomly divided into two subsets for training and testing, with proportions of 80% and 20%, respectively.

ML techniques

This study involved developing and evaluating four different models: CatBoost, Extra Trees (ET), XGBoost, and Multiple Linear Regression (MLR). Concise descriptions of these models are presented below.

CatBoost

CatBoost is an advanced machine learning algorithm tailored to manage categorical features within tabular datasets. Distinguished by its innate capability to handle categorical variables with minimal preprocessing, CatBoost extends the principles of gradient boosting. The algorithm sequentially builds an ensemble of decision trees, showcasing notable proficiency in both classification and regression tasks. CatBoost is characterized by its automatic management of categorical variables and its robustness against overfitting. This algorithm proves especially beneficial in situations where tabular datasets encompass diverse feature types, showcasing its efficiency in handling large datasets during training^29,30.

Extra trees (ET)

Extra Trees, also known as Extremely Randomized Trees, RF by introducing further randomization in the decision tree construction. This involves selecting random thresholds for feature splits, enhancing the overall randomness in the process. Extra Trees proves advantageous in high-dimensional data scenarios, specifically focusing on mitigating overfitting^31–33.

XGBoost

XGBoost, short for eXtreme Gradient Boosting, is a highly efficient machine learning algorithm renowned for its exceptional accuracy and speed. Functioning within the gradient boosting framework, XGBoost builds an ensemble of weak learners, commonly decision trees, in an iterative manner to progressively rectify errors made by preceding models. Employing a gradient descent optimization approach, XGBoost employs strategies to minimize residual errors, thereby improving predictive accuracy. Distinguishing features include the incorporation of regularization techniques, effective management of missing values, and the implementation of parallel processing for expedited computations. Renowned for its adaptability, XGBoost is widely applicable in tasks involving classification, regression, and ranking, gaining popularity in both competitive settings and practical scenarios due to its consistent and robust performance across varied datasets^34–36.

MLR

MLR, the forecasted values of the dependent variable are determined by a linear combination of various independent variables, each with an assigned regression coefficient. The MLR model posits a broad linear connection between the dependent and independent variables. For instance, when predicting Heating values with factors such as Dry Sample Weight, carbon (C), hydrogen (H), oxygen (O), nitrogen (N), sulfur (S), and ash, the MLR equation is designed to encapsulate the combined impact of these variables on the resultant outcome. The coefficients in the equation signify the degree of influence exerted by each independent variable on the dependent variable, offering insights into the interconnections within the dataset. Python is widely employed in the creation of machine learning (ML) models, establishing itself as the predominant programming language within the field. The widespread use of Python in ML is attributed to its extensive array of ML libraries and frameworks, including scikit-learn, TensorFlow, and PyTorch, offering a resilient environment for constructing, training, and deploying ML models. In this research, Python, coupled with scikit-learn, was employed for the development of machine learning models.

Comparison between MLR and other machine learning (ML) models

This study centered on forecasting Heating values and assessing the model’s effectiveness using critical metrics, such as R-squared (R²)³⁷, Mean Squared Error (MSE)³⁸, Mean Absolute Percentage Error (MAPE), and Mean Absolute Error (MAE). These comprehensive metrics provide a nuanced comprehension of the models, covering accuracy and error analysis aspects by thoroughly examining these metrics against the actual values. The research aimed to evaluate both the model’s fitting capability and the accuracy of predictions. An ideal model is typically distinguished by attaining minimal error values (MSE, MAE, MAPE) and highest correlation coefficients (R²). For additional elucidation, the pertinent formulas for computing these statistical indices can be referenced in Table 2, as outlined by Hosseinzadeh et al. in 2020³⁹.

Table 2.

Formulas for the performance metrics applied in this study.

Index	Equation
Mean absolute error
Mean square error
R-squared
Mean absolute percentage error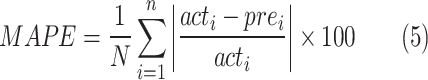

where N indicates the number of observations; 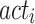and Illustrate the observed and predicted heating values, respectively; Show the average of predicted heating values; Indicates the mean of the observed heating values.

Feature importance analysis

The assessment of feature importance in a model’s output entails examining the effect of individual input features on the model’s overall predictive effectiveness. It furnishes a quantitative gauge of the significance of individual features in impacting the output or predictions of the model. This analysis assists in pinpointing the most impactful features, enabling researchers to prioritize and concentrate on those that substantially contribute to the model’s accuracy⁴⁰. Comprehending feature importance provides insights into the inherent relationships within the data, potentially revealing crucial variables influencing the model’s decision-making process. The analysis of feature importance is essential for interpreting the model, directing the selection of features, and enhancing the model to enhance its ability to generalize and capture fundamental patterns within the dataset more effectively. In this research, tree-based feature importance analysis was utilized using Python’s scikit-learn library to identify the most influential features in the best-performing model. The methodology employed in this study is comprehensively depicted in Fig. 1, offering a detailed visual representation of the overall process.

Fig. 1.

Overview of the Methodology Employed in the Study.

Results and discussion

Descriptive statistics for dry sample weight, elemental composition, and heating value

Table 3 presents the descriptive statistics for the dry sample weight (DSW), elemental composition (including carbon, hydrogen, oxygen, nitrogen, sulfur, and ash), as well as the heating value (HV). The dataset comprises 24 samples, with DSW values varying between 13.96 kg and 62.01 kg and an average of 40.33 kg. Among the elemental constituents, carbon (C) exhibits the highest average concentration at 19.30 kg, whereas sulfur (S) has the lowest mean contribution, measuring 0.10 kg. The heating value, a critical factor for energy applications, has an average of 11,582.18 kJ/kg with a standard deviation of 2,667.86 kJ/kg, reflecting significant variability across the samples. The median values for most variables are closely aligned with their respective means, indicating relatively symmetrical distributions. Nevertheless, the highest recorded ash content (13.02 kg) and maximum heating value (18,134.61 kJ/kg) highlight the presence of upper extremes in the dataset.

Table 3.

Descriptive statistics for dry sample weight, elemental composition, and heating value.

Statistic	DSW (Kg)	C (kg)	H (kg)	O (kg)	N (kg)	S (kg)	Ash (kg)	HV (kJ/kg)
Count	24	24	24	24	24	24	24	24
Mean	40.33	19.30	2.47	12.74	0.47	0.10	5.26	11,582.18
Standard deviation	10.16	5.01	0.63	2.91	0.13	0.03	2.67	2667.86
Min	13.96	6.97	0.89	4.63	0.20	0.03	1.24	8749.74
25%	37.15	17.09	2.22	11.41	0.36	0.08	3.76	9853.36
50% (Median)	39.56	19.22	2.47	12.98	0.48	0.10	4.46	10,942.34
75%	48.08	21.88	2.78	14.61	0.55	0.11	6.39	11,779.39
Max	62.01	31.92	4.03	17.37	0.76	0.17	13.02	18,134.61

DSW dry sample weight.

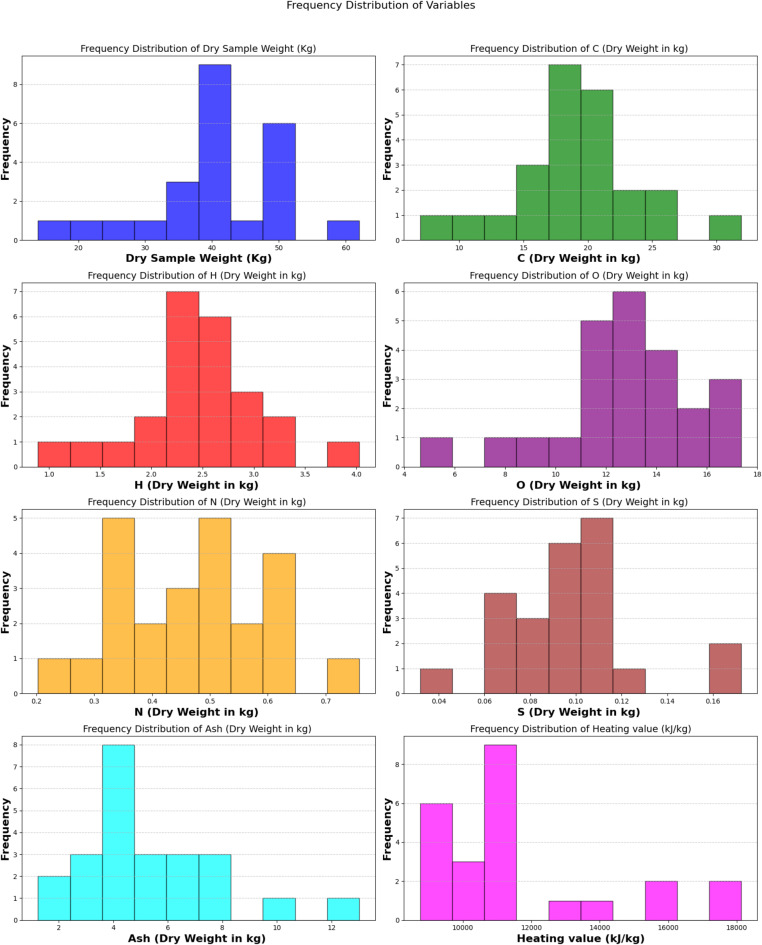
Figures 2 and 3 illustrate the frequency distribution of the parameters presented in Table 3, along with the correlation matrix depicting their interrelationships. The frequency distribution provides a visual representation of the variability in every parameter, while the correlation matrix reveals the relationships between variables, offering a deeper understandings of the dataset^40,41. These statistics and visual representations offer thorough insights into the physical and chemical properties of municipal solid waste from Khorasan Razavi Province. As illustrated in Fig. 3, the heating value demonstrates a moderate positive correlation with dry sample weight (0.45), carbon content (0.43), and hydrogen content (0.41), indicating their substantial influence on energy production, with carbon being the most significant contributor. Additionally, weak positive correlations are found with oxygen content (0.23) and sulfur content (0.30), suggesting they have a limited but noticeable influence on heating value. On the other hand, nitrogen content shows a moderate negative correlation (-0.43), indicating that it may lower the overall energy potential.

Fig. 2.

Frequency distribution of key variables in the dataset.

Fig. 3.

Relationship analysis of key variables in the dataset.

Heating value modeling by XGBoost

Multiple models were generated to construct a reliable model for predicting heating values using XGBoost, and hyperparameter optimization was conducted through an iterative trial-and-error process to construct a reliable model for predicting heating values. The optimal hyperparameters for the XGBoost model, including a learning rate of 0.1(range 0.01–0.3), a maximum depth of 3 (range 2–8), a minimum child weight of 1(range 1–5), a gamma value of 0.001 (range 0.001 –0.5), and a column subsample rate of 0.6 (range 0.4–0.8), were determined for enhanced performance. Utilizing these hyperparameters in conjunction with input variables, including Dry Sample Weight (kg), carbon (C) content (kg), hydrogen (H) content (kg), oxygen (O) content (kg), nitrogen (N) content (kg), sulfur (S) content (kg), and ash content (kg), yielded optimal model performance. Figure 4a–b present scatter plots depicting the predicted Heating values (XGBoost output) compared to the actual values within the training and testing datasets.

Fig. 4.

Heating value prediction: XGBoost model performance for training (19 cities) and testing data (5 cities).

The R² values for the training and testing datasets in the XGBoost models developed for Heating values were found to be 0.999 and 0.975, respectively. Moreover, Fig. 4c–d incorporate the forecasted Heating value corresponding to each data point, offering an understanding of the model’s effectiveness across diverse city points in comparison to their actual values in the train and test datasets. The obtained R² values of 0.999 for the training set and 0.975 for the testing set validate that the XGBoost model, constructed with a learning rate of 0.1, a max depth of 3, a min child weight of 1, a gamma value of 0.001, and a column subsample rate of 0.6, accounts for 99.9% and 97.5% of the variability between the actual and predicted heating values, respectively. Moreover, the model’s effectiveness is assessed through the Mean Squared Error (MSE), a metric quantifying the average squared disparity between predicted and actual values. In this instance, the testing dataset exhibits an MSE of 148,696.869, while the training dataset demonstrates a notably lower value of 0.007. A reduced MSE signifies superior model accuracy, underscoring the XGBoost model’s proficiency in minimizing prediction errors on the training data.

Heating value modeling by extra trees

We utilized a comparable iterative and trial-and-error methodology in developing Extra Trees, much like we did with XGBoost. Several models were generated, and hyperparameter optimization was carried out to improve the performance of the Extra Trees model. Through an exhaustive optimization process, we identified the optimal hyperparameters for the Extra Trees model, which included n_estimators = 300 (range 100–300), max_features = 3 (range 3–7), and max_depth = 10 (range 5–10). Figure 5a–b visually demonstrate the efficacy of the Extra Trees model, presenting scatter plots that juxtapose predicted Heating values (output from Extra Trees) with the actual values in both the training and testing datasets. The R² values, representing the coefficient of determination, were calculated for both the training and testing datasets. In the training set, the R² value stood at an exceptional 0.999, indicating an extraordinarily high level of variability accounted for by the model. This suggests that the Extra Trees model explains 99.9% of the variance in the Heating values within the training dataset. In the testing dataset, the R² value remained remarkably high at 0.979, demonstrating the model’s robust ability to generalize well to new and unseen data. This indicates that the Extra Trees model accounts for 97.9% of the variability in the Heating values within the testing data. These elevated R² values emphasize the strong explanatory capacity and predictive precision of the constructed Extra Trees model for Heating values.

Fig. 5.

Heating value prediction: Extra Trees model performance for training (19 cities) and testing data (5 cities).

Furthermore, the illustration comprehensively explains the model’s predictions by incorporating a forecasted Heating value for each data point (Fig. 5c–d). It appears that both the XGBoost and Extra Trees models exhibit outstanding performance in forecasting heating values for both the training and testing datasets. Nevertheless, upon a more detailed analysis of Figs. 4 and 5, it becomes apparent that the Extra Trees model surpasses XGBoost in forecasting the heating value for the city of Mazdavand (point 5 in the test data) with a value of 1137.39. The forecasted value from the Extra Trees model closely corresponds to the observed value, demonstrating a more precise prediction compared to the noticeable disparity observed in the XGBoost model. This implies that, particularly for the city of Mazdavand, the Extra Trees model offers a superior and more accurate estimation of heating values. Furthermore, the model’s effectiveness was evaluated through the MSE. The MSE for the testing dataset was 77,455.91, suggesting precise predictions on unfamiliar data. In contrast, the MSE for the training dataset was 1.12, demonstrating successful model training with minimal error on the provided data. This highlights the model’s resilience in providing accurate predictions while maintaining the ability to generalize to new observations.

Heating value modeling by CatBoost

The CatBoost model exhibited outstanding predictive performance for heating values, attaining an R² value of 0.999 in the training dataset and 0.951 in the testing dataset. This indicates a significant level of explained variability in both the training and testing datasets. The model’s accuracy is further supported by the MSE, which is 713.59 for the training dataset and 547,119.35 for the testing dataset. These MSE values suggest minimal errors in predictions on the training data and a successful generalization to new, unseen data. The model underwent fine-tuning with the following hyperparameters: learning_rate = 0.1 (range 0.05–0.3), max_depth = 5 (range 3–10), iterations = 150, random_seed = 5, logging_level = Silent, and loss_function = MAE. This setup embodies the ideal combination that resulted in the remarkable performance metrics observed in both training and testing situations. Figure 6a–d illustrate the predictive powers of the CatBoost model in estimating heating values, showcasing the closeness between predicted and actual values.

Fig. 6.

Heating value prediction: CatBoost model performance for training (19 cities) and testing data (5 cities).

Heating value modeling by MLR

Utilizing the Multiple Linear Regression (MLR) model as a conventional method, we observed a moderate performance in forecasting heating values. The R² values were calculated as 0.748 for the training dataset and 0.709 for the testing dataset, indicating a reasonable level of explained variability in both sets. Evaluation of the model’s accuracy through MSE values indicated 1,910,554.9 for the training dataset and 941,272.5 for the testing dataset.

While MLR continues to be a conventional and widely-applied technique, the observed MSE values suggest potential challenges in minimizing prediction errors, particularly on the testing data. Exploring alternative algorithms or refining the model further may be considered to improve predictive accuracy. Figure 7a–d provide a visual representation of the model’s predictive performance, illustrating the relationship between the predicted and actual heating values. Equation 6, derived from the MLR modeling of the heating value using the software, yielded a P-value of 0.0044, signifying the statistical significance of the developed models since the value is below the standard threshold of 0.05. Importantly, both the dependent variable (heating value) and the independent variables are maintained in their original scales.

6

Fig. 7.

Heating value prediction: MLR model performance for training (19 cities) and testing data (5 cities).

Evaluating the developed models for predicting heating values

Here is an evaluation of the constructed models for forecasting heating values, employing metrics like Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), Mean Squared Error (MSE), and R² for both the training and testing datasets (Table 4). The evaluation underscores notable variations in performance metrics among different models. XGBoost and Extra Trees exhibit outstanding accuracy, characterized by low MSE and MAE, high R² values, and relatively modest MAPE percentages. In contrast, the Multiple Linear Regression model demonstrates elevated MSE and MAE and lower R² values, suggesting relatively diminished predictive accuracy. This thorough assessment emphasizes the efficacy of ensemble methods, specifically XGBoost and Extra Trees, in contrast to conventional linear regression models, for the prediction of heating values. In the assessment of the test data, both XGBoost and Extra Trees demonstrate robust predictive capabilities. While XGBoost exhibits a slightly higher MSE of 148,696.9 compared to Extra Trees’ 77,455.92, indicating that Extra Trees achieves slightly better precision. Extra Trees excels in terms of MAE, achieving 245.886 compared to XGBoost’s 279.439. Additionally, Extra Trees exhibits a lower MAPE at 16.22%, surpassing XGBoost’s 17.181%. Both models attain high R² values of 0.975 and 0.979 for XGBoost and Extra Trees, respectively, indicating strong explanatory power. In summary, the analysis of the constructed models for forecasting heating values indicates that Extra Trees surpasses other models, showcasing higher accuracy and precision in both the training and test datasets. In Fig. 8, the forecasted outcomes for four cities in Mashhad County are presented using the Extra Trees model in the testing dataset. The visual depiction suggests a remarkably strong correlation between the actual and predicted data.

Table 4.

Performance comparison of the developed techniques for testing and training dataset^43–45.

Model	Train data				Test data
	MSE	MAE	MAPE (%)	R2	MSE	MAE	MAPE (%)	R2
XGBoost	0.007	0.065	23.884	0.999	148,696.9	279.439	17.181	0.975
Extra Trees	1.127	0.626	23.88	0.999	77,455.92	245.886	16.22	0.979
CatBoost	713.59	9.035	23.816	0.999	547,119.4	636.869	14.573	0.951
MLR	1,910,554.9	902.5	6.98	0.748	941,272.5	843.09	7.7	0.709

Fig. 8.

Prediction results for 4 cities in Mashhad County using Extra Trees model in Testing Dataset.

The Taylor diagram serves as a valuable tool for assessing the performance of models and simulations in comparison to actual data. In the particular illustration shown in Fig. 9, key metrics such as the correlation coefficient (r), standard deviation (SD), and centered root mean square difference (CRMSD) are succinctly included. This visual representation enables a comprehensive evaluation of the model’s ability to accurately capture essential data points, offering immediate insights into its accuracy. The Taylor diagrams effectively highlight crucial performance aspects of the model, employing CRMSD to gauge the distance from the observed data point. A closer alignment with the data point suggests improved agreement with the model. The angle formed between the reference point and model points quantifies the correlation coefficient, where smaller angles indicate a higher correlation in model performance. The horizontal distance from the observed data signifies SD, and models closer to the reference point demonstrate comparable variability to the observed data⁴². This visualization simplifies the model evaluation process, assisting in the selection and improvement of models. Based on the figure, it can be inferred that Extra Trees, boasting an R-value surpassing 0.99, a CRMSD of 544.67, and an SD of 1617.62, stands out as the top-performing model.

Fig. 9.

Performance assessment of XGBoost, Extra Trees, CatBoost and MLR on test data and their comparison with observed data using Taylor diagram.

In 2016, Akkaya employed three ANFIS-based models to estimate the heating value of biomass, using fixed carbon, ash, and volatile matter as primary input parameters. The results highlight the enhanced accuracy of the sub-clustering-based ANFIS model, which achieved an R² value of 0.8836 during the testing phase⁴⁶. In a separate study, Kumar and Samadder (2023) constructed both MLR and ANN models to predict the lower heating value of municipal solid waste. They developed six MLR models and six ANN models, each utilizing a variety of input parameters. The MLR models demonstrated slightly superior predictive accuracy, with R² values ranging between 0.834 and 0.912, compared to the ANN models, which achieved R² values within the range of 0.734–0.91417¹⁷. The models developed in this study exhibited enhanced performance relative to previous research findings.

Feature importance analysis for extra trees (best model)

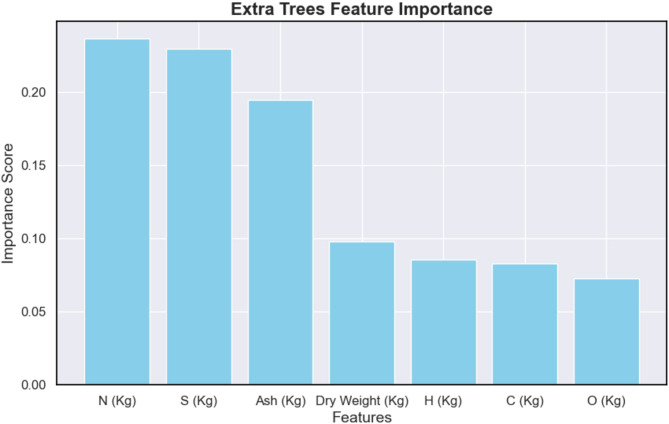
In the evaluation of feature importance in the best-performing model, Extra Trees, four crucial parameters were identified: nitrogen (N) content (kg), sulfur (S) content (kg), ash content (kg), and Dry Sample Weight (kg). In Extra Trees, the hierarchy of importance is as follows: nitrogen (N) content (kg) > sulfur (S) content (kg) > ash content (kg) > Dry Sample Weight (kg). The significance of these features is visually represented in Fig. 10 using a bar chart, where nitrogen (N) content (kg) and sulfur (S) content (kg) exhibit the tallest bars, underscoring their considerable influence on the model’s predictive accuracy. Nitrogen content ranked highest, accounting for 27.5%, followed by sulfur content at 26%. In comparison, the combined contribution of ash, dry weight, H, C and O amounted to 51.9%. This visual representation underscores the importance of nitrogen (N) content and sulfur (S) content in shaping the predictive outcomes of the Extra Trees model.

Fig. 10.

Feature importance analysis for Extra Trees developed model.

To gain a deeper understanding of the relationships, we employed Partial Dependence Plots (PDPs) to explore how these features impact the predicted heating value (HV), highlighting both linear and non-linear dependencies between the variables. The Partial Dependence Plots shown in Fig. 11 illustrate the relationships between different features in the data, providing a comprehensive view of how variations in one feature affect the predicted outcome while holding other features constant. These plots demonstrate both linear and non-linear relationships, as well as potential interactions between feature pairs. The analysis indicates that the heating value of municipal solid waste is strongly affected by the weights of carbon, hydrogen, oxygen, dry sample weight, ash, and sulfur, all show a positive correlation with the heating value. In a study conducted by Afolabi et al., the findings revealed that the most significant input features contributing to HHV predictions are ash content, C, VM, N contents, and biomass classes. Ash content was identified as the most influential factor, contributing 15.6%, followed by C content, which ranked second with a contribution of 12.9%¹⁸. Alternatively, Abdollahi et al. employed multiple linear regression and Pearson’s correlation coefficients, demonstrating that volatile matter, N, and O content have minimal impact on HHV, suggesting that these factors can be excluded from HHV modeling⁴⁷. In two studies by Nieto et al. different variables were found to have varying levels of significance for HHV prediction in different models. In the SVM–SA model, the most crucial factor was Fixed C, followed by the Atomic O/C ratio, Reaction temperature, Atomic H/C ratio, Residence time, and Volatile matter⁴⁸. In the PSO–SVM model, however, Volatile matter emerged as the most influential variable for HHV prediction, with Fixed C, Atomic O/C ratio, Reaction temperature, Atomic H/C ratio, and Residence time following in order of importance⁴⁹. Carbon and hydrogen are key contributors to heating value, as they are rich in energy and generate significant heat when combusted, while oxygen improves combustion efficiency by promoting more complete burning. According to the Dulong formula, carbon content is a dominant factor in the typical analysis of HHV for conventional fuels⁴⁹. The discrepancies between the results of the current research and those reported by others can be attributed to differences in the physical composition of the waste materials. Dry sample weight represents the overall mass of combustible material, where heavier samples tend to contain greater amounts of energy-rich substances such as plastics, paper, and organic matter (like food waste or biomass), thereby enhancing energy production. In contrast, non-combustible components like metals, glass, and partially combusted residues primarily contribute to ash production. Although sulfur is not a major source of energy, it can indirectly affect combustion processes or serve as a marker for the presence of other energy-dense components. Conversely, nitrogen demonstrates a negative association with heating value, as its non-combustible nature reduces the overall energy potential by decreasing the concentration of energy-rich components. This in-depth study underscores the intricate relationships among various features and their differing influences on heating value, offering a valuable understanding of the key factors shaping the model’s predictions.

Fig. 11.

Interaction effects of input parameters on HV using two-way partial dependence plots (best model).

Conclusion

In summary, the study sought to develop models for predicting the heating values of municipal solid waste, employing various machine learning techniques, with a specific emphasis on XGBoost, Extra Trees, CatBoost, and MLR. The Extra Trees model, constructed using optimal hyperparameters, demonstrated exceptional performance, achieving R² values of 0.999 for the training set and 0.979 for the testing set. This model displayed strong explanatory capability and accuracy, as reflected in its minimal Mean Squared Error (MSE) of 77,455.92 on the testing dataset. Examining the predictive efficacy of alternative models, XGBoost and CatBoost also exhibited notable proficiency in projecting heating values. These models demonstrated elevated R² values, signifying a significant explanatory correlation between predicted and actual values. While Extra Trees distinguished itself with remarkably low error metrics, XGBoost and CatBoost exhibited competitive performance, presenting valuable alternatives in predicting heating values. Conversely, the MLR model, utilized as a conventional approach, exhibited moderate performance with relatively lower R² values and higher error metrics. This research presented an innovative approach to waste management and energy recovery, contributing to policy development and advancing sustainability initiatives. Nevertheless, the limited dataset may restrict the model’s generalizability and statistical robustness. To enhance predictive accuracy and broader applicability, future research should focus on expanding the dataset by incorporating data from additional cities and a more diverse range of waste characteristics.

Abbreviations

MLR

Multiple linear regression

MSE

Mean squared error

MAPE

Mean absolute percentage error

MSW

Municipal solid waste

HV

Heating values

ANN

Artificial neural network

SVM

Support vector machine

RF

Random fores

RBF-ANN

Radial bias function artificial neural network

MLP-ANN

Multilayer perceptron artificial neural network

ANFIS

Adaptive nero-fuzzy inference system

LHV

Lower heating value

MAE

Mean absolute error

ET

Extra trees

DSW

Dry sample weight

C

Carbon

H

Hydrogen

O

Oxygen

N

Nitrogen

S

Sulfur

ML

Machine learning

R²

Determination coefficients

SD

Standard deviation

CRMSD

Centered root mean square difference

SVM–SA

Support vector machine–simulated annealing

PSO–SVM

Particle swarm optimization–support vector machin

Author contributions

Mansour Baziar: Conceptualization, Methodology, Investigation, Formal analysis, Writing–original draft. Mahmood Yousefi, Vahide Oskoei, Ahmad Makhdoomi, Reza Abdollahzadeh: Methodology, Writing–review & editing. Aliakbar Dehghan: Methodology, Writing–review & editing, Supervision. All authors reviewed the manuscript.

Data availability

The datasets used during the current study available from the corresponding author on reasonable request.

Declarations

Competing interests

The authors declare no competing interests.