Abstract
Rocks in deep geological settings are subjected to elevated in-situ stresses, and blasting excavation often induces significant damage to the surrounding rock mass, thereby complicating its stability assessment and support design. This damage may undermine the stability assessment and support design of tunnels. Therefore, it is crucial to characterize the nature of blasting-induced damage in tunnel surrounding rocks under high in-situ stress conditions. In light of this, this study employs the LS-DYNA software coupled with a fluid–structure interaction algorithm to simulate full-face smooth blasting excavation in tunnels, accounting for scenarios both with and without in-situ stress. This study examines the excavation-induced destruction in the three-dimensional profile of tunnels and investigates the influence of in-situ stress on rock damage zoning, aiming to reveal the failure patterns of the surrounding rock in deeply buried tunnels. Furthermore, the Basic Quality Index (BQ) of the rock mass is used as a classification criterion to evaluate the impact of blasting-induced damage on the surrounding rock of the tunnel, and the influence of such damage on rock mass classification is discussed. The results indicate that ground stress substantially limits the depth of blasting-induced damage in the surrounding rock. Additionally, the study classifies the intact surrounding rock into five categories based on the severity of blasting damage, with ground stress playing a pivotal role in the evolution of each class of surrounding rock areas. The findings of this study offer theoretical underpinnings for assessing the safety and stability of deep tunnel surrounding rocks and for developing disaster prevention strategies.
Keywords: Full-face blasting, In-situ stress, Damage characteristics, Rock mass classification
Subject terms: Engineering, Civil engineering, Mechanical engineering
Introduction
Modern projects, including mining1, transportation2, and hydropower projects3, are increasingly advancing into deeper operational depths, where they are subjected to high in-situ stress conditions characterized by hydrostatic pressure. Among the various excavation methods in underground engineering, drilling and blasting are frequently employed, yet they can readily cause damage to surrounding rocks, thereby reducing their stability4. Therefore, in the stability assessment and safety protection of tunnel blasting in the deep and high in-situ stress environment, it is crucial to fully understand how blasting operations influence the cumulative evolution of damage in the surrounding rock under varying ground stress conditions. Studies on blasting-induced damage in surrounding rock can primarily be divided into single-hole and multi-hole blasting studies blasting investigations. Numerous studies have concentrated on characterizing the damage resulting from single-hole blasting5. For instance, He6 demonstrated through numerical simulations that the degree and severity of damage to the surrounding rock are roughly 50% greater with cyclic blasting than with single blasting. Yue et al.⁷ found that the damaged rock area in the cross-section is approximately 35 times larger than the blast hole area, while it is approximately 8 times larger in the longitudinal section. While studies on single-hole blasting have provided valuable insights into rock damage mechanisms, their practical limitations in engineering have prompted a shift in research focus toward multi-hole blasting technologies. Multi-hole blasting mainly comprises two types: zoned blasting and full-face blasting. In terms of zoned blasting, Yao et al.8 employed comprehensive in-situ monitoring methods to demonstrate that although zoned blasting can mitigate local vibration effects, significant particle velocity and tensile stress still exist at critical locations, including the arch top and arch foot. Chen et al.9 further indicated that the damage range induced by a single vertical blast hole diminishes with increasing depth. Despite these advantages, the uneven damage control limits the application of zoned blasting in complex engineering environments. In contrast, Ji et al.10 have focused their research on full-face blasting, analyzing the damage depth at different positions through numerical simulations under various full-face blasting sequences. The findings indicate that the minimum damage depth typically occurs at the arch foot, while the maximum damage depth is observed at the midpoint of the inverted arch. Ling et al.11 also identified distinct phases in the evolution of rock damage through numerical simulations, demonstrating that the rate of damage accumulation varies significantly with depth. Combining field tests with numerical simulations, Lyu et al.12 analyzed that the damage depth on the tunnel cross-section is deepest at the arch soffit of each step and shallowest at the arch foot. The above studies mainly investigate the evolution law of surrounding rock damage under blasting loads, focusing on the cumulative damage depth, range, and other characteristics of the surrounding rock.
The aforementioned studies primarily explore the evolution laws of surrounding rock damage under blasting loads, focusing on the cumulative damage depth, range, and other characteristics of the surrounding rock. However, with engineering projects delving deeper, research on blasting damage should increasingly focus on high in-situ stress environments. Numerous studies have demonstrated that high in-situ stress significantly inhibits rock damage13–15. Models testing, field monitoring, and numerical simulations are commonly employed to predict blasting-induced rock damage in such conditions. Model testing, for instance, has been used by Sun et al.16 to investigate the stress redistribution patterns and failure processes of soft rock under different loading conditions. Meanwhile, Huang et al.17 demonstrated that rock damage evolution under multiple blasting disturbances in high in-situ stress conditions exhibits nonlinear cumulative characteristics, albeit at considerable cost and time expense with a limited site similarity. In terms of field monitoring, the single-hole ultrasonic test method is predominantly employed to evaluate the extent and range of surrounding rock damage. Chen et al.18 highlighted the directional influence of ground stress on the excavation damage zone during high-stress blasting. Cui et al.19 identified periodic damage characteristics in the retained rock mass during tunnel excavation utilizing cyclical blasting. Meanwhile, Yan et al.20, Yang et al.21, and Fan et al.22 employed the single-hole longitudinal wave velocity method to delineate the excavation damage zone in projects such as the Jinping II Water Diversion Tunnel. However, given the complex mechanical properties of rock masses in practical engineering applications and the poor experimental repeatability in blasting, numerical simulations have become a pivotal research avenue for studying the evolution of rock damage. In terms of numerical simulations, the majority of studies employ the equivalent blasting load method. For instance, Xie et al.23 examined the effects of in-situ stress on the damage zone under single blasting loads, while Li et al.24 showed that in-situ stress suppresses damage area expansion. Luo et al.25 analyzed the impact of ground stress on excavation blasting damage in deep-buried tunnels, revealing a trend where damage depth and area initially decrease before increasing, with a critical threshold of 12.5 MPa. Some studies employ fluid–solid coupling algorithms; for example, Wang et al.26 investigated the impacts of in-situ stress on different damage zones under single blast actions, while while Liu et al.27 demonstrated that in-situ stress significantly reduces the extent of damage in rock from single-hole blasting.
Collectively, these studies have significantly enhanced our understanding of deep tunnels. Regrettably, the above studies primarily focus on the mechanical responses at the small-specimen scale and the damage characteristics in two-dimensional sections. However, they fail to elucidate the impact of blasting disturbances on the damage characteristics and classification of deep tunnels at the engineering scale, particularly the damage characteristics in the three-dimensional excavation direction. This research gap poses significant risks to the stability evaluation and reinforcement strategies for the surrounding rock. Blasting damage is a complex, multifactorial phenomenon, with overbreak being a particularly critical issue28. Relevant studies have shown through statistical analysis that geological mechanical properties and in-situ stress conditions significantly influence the extent of overbreak29. Additionally, research based on rock mechanics parameters has proposed models for predicting the depth of the excavation damage zone (EDZ). Studies combining rock strength factors with numerical simulations have successfully predicted overbreak depths in tunnels30. Furthermore, optimization of blasting parameters through experiments and numerical simulations has significantly reduced overbreak in underground excavations31. Systematic analyses of the cumulative damage effects of multiple full-face blasting in large cross-section tunnels have also been conducted, with corresponding safety criteria proposed32.
Consequently, leveraging indoor static tests to ascertain model parameters, this study employs the LS-DYNA finite element software in conjunction with a fluid–solid coupling algorithm to investigate the damage effects on deep tunnel surrounding rock and examines how blasting-induced damage impacts the classification of the surrounding rock.
Mechanical parameter determination of surrounding rocks
Static tensile mechanical properties of surrounding rocks
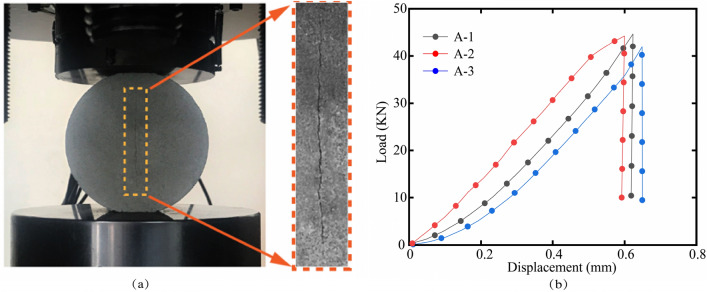
The rock samples were extracted from intact blocks of the tunnel surrounding rock and were prepared into Flat Brazilian Discs specimens in accordance with the International Society for Rock Mechanics (ISRM) suggestions, with a diameter of 87 mm and thickness of 43.5 mm. The specimens were subjected to loading at an angle of 25° using an MTS815 rock mechanics testing machine at a loading rate of 0.2 mm/min. The relationship between tensile strength and the applied peak load was established based on the methodology reported Liu et al.33, as illustrated in Eqs. (1). Figure 1 illustrates the stress–strain curves from the static uniaxial compression of the rock, with the test results summarized in Table 1 indicating an average static tensile strength of the specimens at 6.68 MPa.
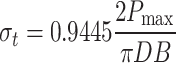 |
1 |
where  represents the load at which the platform disc fails;
represents the load at which the platform disc fails;  is the diameter of the specimen;
is the diameter of the specimen; 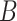 is the thickness measured at the center of the specimen.
is the thickness measured at the center of the specimen.
Fig. 1.
(a) Crack Initiation at the Center of the Specimen, and (b) load–displacement curve.
Table 1.
Results of the FBD Test.
| No. | Peak load (KN) | Tensile strength (MPa) |
|---|---|---|
| A-1 | 43.41 | 6.90 |
| A-2 | 42.33 | 6.73 |
| A-3 | 40.32 | 6.41 |
| Average | 42.02 | 6.68 |
Static compressive mechanical properties of surrounding rocks
To obtain parameters such as the static compressive strength (fc), elastic modulus (E), and Poisson’s ratio ( ) of the rock, static uniaxial compression tests were conducted using an MTS815 rock mechanics testing machine. The loading rate was fixed at 0.3 mm/min. The stress–strain curves from the static uniaxial compression of the rock are depicted in Fig. 2. The test results, as presented in Table 2, indicate that the average values for the uniaxial compressive strength, elastic modulus, and Poisson’s ratio of the tunnel surrounding rock are 70 MPa, 8 GPa, and 0.22, respectively.
) of the rock, static uniaxial compression tests were conducted using an MTS815 rock mechanics testing machine. The loading rate was fixed at 0.3 mm/min. The stress–strain curves from the static uniaxial compression of the rock are depicted in Fig. 2. The test results, as presented in Table 2, indicate that the average values for the uniaxial compressive strength, elastic modulus, and Poisson’s ratio of the tunnel surrounding rock are 70 MPa, 8 GPa, and 0.22, respectively.
Fig. 2.
(a) Static compression test, (b) Stress–strain curve.
Table 2.
Uniaxial compression test results.
| No. | Peak load (KN) | Compressive strength (MPa) | Secant elastic modulus (GPa) | Poisson’s ratio |
|---|---|---|---|---|
| C-1 | 78.7 | 69.4 | 8.2 | 0.22 |
| C-2 | 80.9 | 71.3 | 7.8 | 0.24 |
| C-3 | 79.2 | 69.8 | 8.0 | 0.21 |
| Average | 79.7 | 70.0 | 8.0 | 0.22 |
Dynamic compressive mechanical properties of surrounding rocks
To accurately calibrate the parameters of the constitutive model for rock materials, dynamic compression tests were conducted using the Split Hopkinson Pressure Bar (SHPB) apparatus in this study., obtaining the dynamic stress–strain curves of the rock material, as shown in Fig. 3. These curves reflect the mechanical behavior of rock under high-strain-rate conditions, providing essential data for determining the parameters of the RHT constitutive model. The dynamic compressive strength parameters of the sandstone specimens are summarized in Table 3.
Fig. 3.
(a) Dynamic compressive test, (b) Dynamic stress–strain curve.
Table 3.
Dynamic compression test results.
| No. | Strain rate (s−1) | Cross-sectional area (mm2) | Dynamic compressive strength (MPa) |
|---|---|---|---|
| C-1 | 46.7 | 1962.7 | 109.1 |
| C-2 | 45.4 | 1962.3 | 112.4 |
| C-3 | 46.2 | 1962.2 | 116.5 |
Numerical model setup
Materials parameters determination
Parameters determination of surrounding rock material
In the realm of rock blasting damage simulation, the triad of dominant damage ontology models includes the Holmquist–Johnson–Cook (HJC) model34, the JH series model35, and the Riedel–Hiermaier–Thoma (RHT) model36. The RHT model, an extension of the HJC model, encompasses a total of 34 parameters as detailed in Table 4 and serves as a plastic damage constitutive model that integrates an equation of state with a strength model to characterize the dynamic response of brittle materials like rock and concrete when subjected to high strain rates and significant deformations. Following the calibration based on the results of the basic physical tests described in the previous chapters, parameters such as fc, E, G, and ν have been determined. Other model parameters are determined as follows.
Table 4.
Parameters for RHT model for rock.
| Variable | Description | Variable | Description |
|---|---|---|---|

|
Mass density | N P | Porosity exponent |

|
Initial porosity |
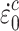 , ,  , ,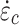 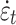
|
Reference compressive |

|
Crush pressure |
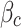
|
Compressive strain rate |

|
Compaction pressure |
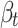
|
Tensile strain rate |
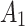 , , 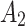 , ,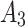
|
Hugoniot polynomial coefficient |
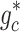
|
Compressive yield surface parameter |
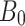 , ,  , , 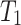 , , 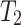
|
Parameter for polynomial EOS |
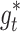
|
Tensile yield surface parameter |

|
Elastic shear modulus |
|
Shear modulus reduction factor |
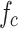
|
Compressive strength | D1, D2 | Damage parameter |
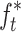
|
Relative tensile strength |

|
Minimum damaged residual strain |

|
Relative shear strength |
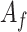 , , 
|
Residual surface parameter |
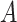 , N , N
|
Failure surface parameter |
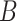 , , 
|
Lode angle dependence factor |
Strain rate parameters
The influence of strain rate on rock strength was captured by Eq. (1), which defines the relationship between strength and strain rate under both compression and tension32.
 |
2 |
where 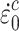 is the reference strain rate under compression,
is the reference strain rate under compression,  s−1;
s−1; 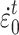 is the reference strain rate under tension,
is the reference strain rate under tension,  s−1; P is the compressive stress;
s−1; P is the compressive stress; 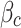 and
and  are the compression and tension strain rate index respectively,
are the compression and tension strain rate index respectively,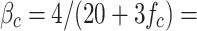 0.017,
0.017, 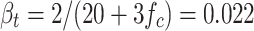 .
.
-
(b)
Determination of parameters in the p-α equation of state
In the RHT model, the p-α equation of state is expressed as:
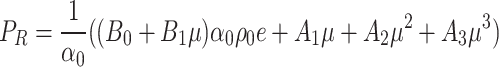 |
3 |
where  is the pressure of the equation of state;
is the pressure of the equation of state; 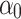 is the initial porosity;
is the initial porosity; 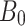 and
and 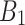 are the parameters of the equation of state of material,
are the parameters of the equation of state of material, 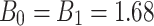 ; e is the internal energy per unit mass;
; e is the internal energy per unit mass; 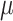 is the volumetric strain;
is the volumetric strain; 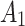 ,
, 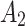 , and
, and 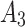 are coefficients of the Hugoniot polynomial determined by the following formulae:
are coefficients of the Hugoniot polynomial determined by the following formulae:
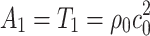 |
4 |
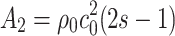 |
5 |
 |
6 |
where 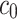 is the wave velocity of material when the pressure is zero;
is the wave velocity of material when the pressure is zero; 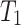 is the material constant; s is an empirical constant, taken as 1.34. Equations (4)–(6) give
is the material constant; s is an empirical constant, taken as 1.34. Equations (4)–(6) give 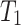 ,
, 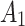 ,
,  , and
, and 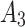 as 28.4 GPa,28.4 GPa, 47.7 GPa and 91.9 GPa, respectively.
as 28.4 GPa,28.4 GPa, 47.7 GPa and 91.9 GPa, respectively.
-
(c)
Determination of damage parameters
The damage variable  is defined as the accumulation of plastic strain
is defined as the accumulation of plastic strain 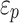 :
:
 |
7 |
where  is the failure strain.
is the failure strain.
When a stress state reaches the ultimate strength of the material on failure surface, damage is accumulated during further inelastic deformation or plastic strain. The failure strain is
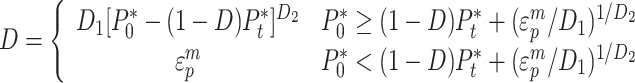 |
8 |
where 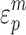 is the minimum damage residual strain;
is the minimum damage residual strain; 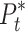 is the failure pressure; D is the damage variable of the RHT model, and D1 = 0.04 and D2 = 1.0 are damage constants.
is the failure pressure; D is the damage variable of the RHT model, and D1 = 0.04 and D2 = 1.0 are damage constants.
-
(d)
Determination of failure surface parameters
Next, the parameters A and N will be further calibrated. Under quasi-static loading conditions, Fr is set to 1, and the failure surface expression of the model is as follows:
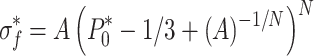 |
9 |
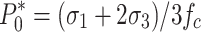 |
10 |
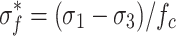 |
11 |
In the absence of empirical data, according to the literature23, it is known that:
 |
12 |
where 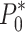 is the normalized compressive strength parameter,
is the normalized compressive strength parameter, 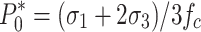 ;
; 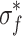 represents the normalized strength relative to compression,
represents the normalized strength relative to compression, 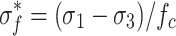 ;
; 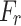 is the dynamic strain rate increase factor, under quasi-static loading conditions, Fr is set to 1; A and N are parameters of the failure surface;
is the dynamic strain rate increase factor, under quasi-static loading conditions, Fr is set to 1; A and N are parameters of the failure surface; 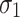 and
and  are the maximum and minimum effective stresses of failure, respectively. The fitting results are shown in Fig. 4, with the ultimate determined values of A and N being 2.54 and 0.71, respectively.
are the maximum and minimum effective stresses of failure, respectively. The fitting results are shown in Fig. 4, with the ultimate determined values of A and N being 2.54 and 0.71, respectively.
Fig. 4.

Fitting of failure surface parameters.
-
(e)
Parameter adjustment and optimization
The remaining parameters, initially sourced from the literature37, due to the complexity of their acquisition, serve as starting values for optimization. Accordingly, an enhanced Split Hopkinson Pressure Bar (SHPB) setup was utilized to perform dynamic compression tests on sandstone specimens, as depicted in Fig. 5a. The experimental configuration included an incident bar and a transmitted bar with lengths of 300 cm and 200 cm, respectively, which were designed to accommodate a sandstone specimen measuring 50 mm in diameter and 50 mm in height. The numerical model, shown in Fig. 5b, was meticulously crafted to mirror the physical dimensions and conditions of the experimental setup, ensuring that the model dimensions were an exact replica of those used in the lab tests. The numerical simulations were instrumental in determining the remaining parameters that were not directly measurable through experimentation. Figure 5c presents a comparison between the experimentally obtained stress–strain curves and those predicted by the numerical model. The close alignment between the test results and numerical results, as evidenced by the overlapping curves, serves as a validation of the numerical model’s accuracy in capturing the dynamic response of the sandstone under high strain rates. The final set of constitutive parameters, as determined, are presented in Table 5.
Fig. 5.
Comparison of Experimental and Simulated SHPB Results. (a) Test sample, (b) Numerical model, and (c) Validation of the Stress–strain Response.
Table 5.
RHT constitutive model parameter calibration results.
| Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|---|---|
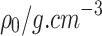
|
2.32 | B | 0.05 | fc/MPa | 70 |
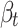
|
0.022 |

|
23.33 | B 0 | 1.68 | f t * | 0.1 |

|
3  10–5 10–5
|

|
6 | B 1 | 1.68 | f s * | 0.45 |

|
3 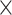 10–6 10–6
|
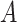
|
2.54 | T1/GPa | 0.227 |
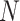
|
0.71 |

|
3  1025 1025
|
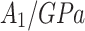
|
28.4 | T2/MPa | 0 |

|
3.25 |

|
3 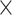 1025 1025
|

|
47.7 | n | 3 |
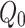
|
0.68 |
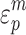
|
0.01 |

|
91.9 |

|
1.09 |
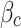
|
0.017 |
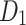
|
0.04 |

|
0.3 | A f | 1.63 |
|
0.3 |

|
1.0 |
|
0.7 | n f | 0.59 |
-
(2)
Parameters determination of explosive material
The utilized explosive is the Type 2 rock-emulsified explosive employing *MAT_HIGH_EXPLOSIVE_BURN (material type 8) as the material model. The Jones-Wilkins-Lee (JWL) equation of state is utilized to describe the functional relationship between pressure, volume, and energy of the detonation products during the explosion. The expression is defined as:
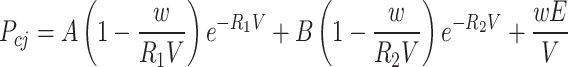 |
13 |
where E represents the specific internal energy per unit volume; V is the relative volume; e denotes the specific internal energy of the detonation products; A, B, R1, R2, and w are constants. The material equation describing the explosive is presented in Table 6.
Table 6.
Explosive equation of state parameters.

|
A/(GPa) | B/(MPa) | R 1 | R 2 | W | E/(GJ.m−3) | Pcj/(MPa) |
|---|---|---|---|---|---|---|---|
| 1.00 | 214.4 | 232 | 0.9 | 0.15 | 0.15 | 4.0 | 9530 |
-
(3)
Parameters determination of Air material
The air material is modeled using the *MAT_NULL material model. The linear polynomial equation of state describing the state of air under high pressure is expressed as follows:
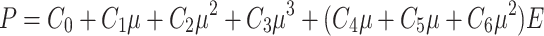 |
14 |
where  to
to  are the polynomial equation parameters;
are the polynomial equation parameters; 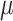 is the bulk modulus parameter. The specific parameters defining the air material equation are listed in Table 7.
is the bulk modulus parameter. The specific parameters defining the air material equation are listed in Table 7.
Table 7.
Air material equation parameters.
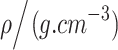
|
C 0 | C 1 | C 2 | C 3 | C 4 | C 5 | C 6 | E (MPa) | V 0 |
|---|---|---|---|---|---|---|---|---|---|
| 0.0013 | − 0.1 | 0 | 0 | 0 | 0.4 | 0.4 | 0 | 0.25 | 1 |
-
(4)
Parameters determination of plug material
The muck-filling section of the borehole is modeled using a soil material, with material parameters defined using the LS-DYNA keyword *MAT_SOIL_AND_FOAM. The relevant parameters for the muck-filling material are presented in Table 8.
Table 8.
Plug material parameters.
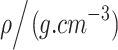
|
G(MPa) | u | a 0 | a 1 | a 2 | P c |
|---|---|---|---|---|---|---|
| 1.8 | 64 | 0.3 | 3.4 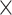 10–13 10–13
|
7.0  10–7 10–7
|
0.3 | − 6.9 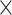 10–8 10–8
|
Finite element model of tunnel excavation using full-face smooth blasting
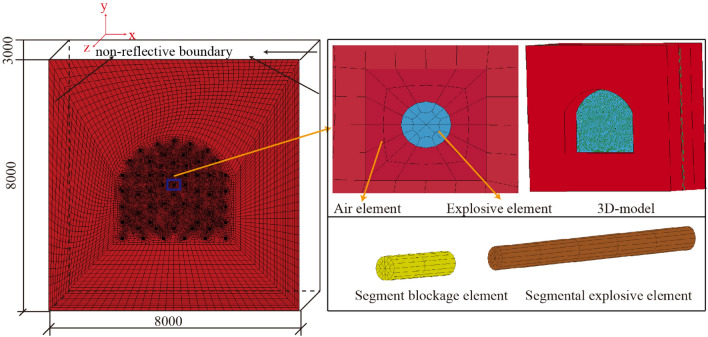
The mining tunnel project extends to a total length of 2016 meters38, featuring a face layout that encompasses pilot holes, auxiliary holes, peripheral holes, and bottom plate holes as depicted in Fig. 6. The tunnel is characterized by a burial depth ranging from 40 to 1800 m and traverses highly weathered sandstone, faulted zones, and water-bearing fracture zones. These geological complexities, combined with an in-situ stress range of 1.05–48.5 MPa, pose significant challenges for design and construction. This study leverages a blasting strategy utilizing seven segments of millisecond delay detonators for tunnel excavation. The smooth blasting layer thickness is set at 0.5 m, with each full-face smooth blasting cycle progressing by 2.0 m and borehole plug lengths at 0.2 m. A comprehensive model for full-face smooth blasting tunnel excavation is constructed using LS-DYNA software, as illustrated in Fig. 7. This model employs a unit system of g-cm-μs with a solution time of 2000 μs. he model dimensions are 8 × 8 × 3 m and consists of 561,000 SOLID elements. The Arbitrary Lagrangian–Eulerian (ALE) method is applied for computations, with the Lagrange algorithm designated for the surrounding rock, while the ALE algorithm is designated for explosives, plug sections, and air. Non-reflective boundaries are implemented at the model boundaries, and the initiation method involves segmented millisecond delay blasting.
Fig. 6.
Drill hole distribution and structural diagram. (a) Blast-hole arrangement for construction, (b) Top view of excavation, and (c) Blast-hole structure diagram.
Fig. 7.
Numerical calculation model of the tunnel. The 3D images were generated using ANSYS 19.0 (ANSYS, Inc., www.ansys.com, version 19.0).
Rock damage zone classification criteria
Commonly used damage variables for the surrounding rock are defined as follows39:
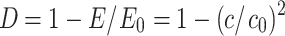 |
15 |
where D represents the damage to the surrounding rock; E0 and E denote the elastic moduli of the rock mass before and after blasting, respectively; and c0 and c are the velocities of the P-waves (primary or compressional waves) in the rock mass before and after blasting, respectively.
Material failure primarily occurs due to plastic deformation. In the RHT (Hoek–Brown failure criterion) constitutive model, the relationship between the plastic strain of the rock and the critical damage parameter can be described by:
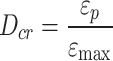 |
16 |
In this model, the damage parameter is defined by:
 |
17 |
 |
18 |
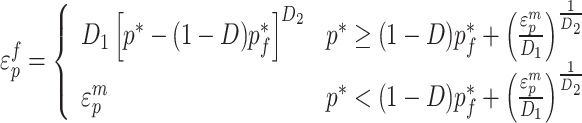 |
19 |
The stress states marking the onset of rock crushing and complete compaction serve as critical thresholds for measuring the rock damage zone and the rock crushing zone. The plastic strain and the ultimate strain are calculated via Eqs. (20)–(23).
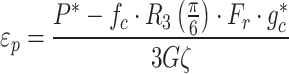 |
20 |
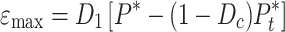 |
21 |
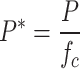 |
22 |
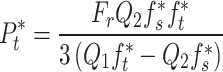 |
23 |
where 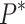 represents the normalized pressure of the compressive strength parameter;
represents the normalized pressure of the compressive strength parameter; 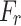 is the dynamic increase factor; and
is the dynamic increase factor; and  denotes the stress at failure cutoff. The meanings of the other parameters are detailed in Table 4. Based on the RHT constitutive model parameters and Eqs. (16)–(23), the critical damage threshold Dcr and the critical fracture threshold Dcf for the rock sample are calculated to be 0.2 and 0.73, respectively. The criteria for determining the blasting damage in terms of the RHT constitutive mode are shown in Table 9.
denotes the stress at failure cutoff. The meanings of the other parameters are detailed in Table 4. Based on the RHT constitutive model parameters and Eqs. (16)–(23), the critical damage threshold Dcr and the critical fracture threshold Dcf for the rock sample are calculated to be 0.2 and 0.73, respectively. The criteria for determining the blasting damage in terms of the RHT constitutive mode are shown in Table 9.
Table 9.
Rock damage zone classification criteria.
| Damage zones | D values |
|---|---|
| Crushing zone | 0.73<D≤1 |
| Crack damage zone | 0.2<D≤0.73 |
| Elastic vibration zone | D≤0.2 |
Numerical model verification
A comprehensive dual-hole ultrasonic survey was conducted using the RSM-SY6 ultrasonic detection instrument to assess the damage to the tunnel surrounding rock under blasting loads, as depicted in Fig. 8. The testing procedure began with strategically drilling two parallel test holes, each 1 m deep at the tunnel’s arch waist, inclined at a 3° angle to the horizontal, and spaced 50 cm apart. Ultrasonic transducers were installed within each test hole, ensuring intimate contact with the hole walls to facilitate effective ultrasonic wave transmission. Initial measurements of ultrasonic wave velocities were recorded prior to excavation to establish a baseline. Subsequently, following each blasting event, ultrasonic wave velocity measurements were repeated to monitor the dynamic response of the surrounding rock. Over the course of 21 experimental sets, the ultrasonic probe was progressively repositioned outward by 5 cm after each test to capture changes in the longitudinal wave velocity both before and after excavation. The velocities recorded were denoted as 1# for Test Hole 1, 2# for Test Hole 2, and 1–2# for the velocity between the two holes. By comparing these datasets, the integrity and degree of damage to the surrounding rock were evaluated. All tests were conducted under stringent quality control to ensure the precision and reliability of the data obtained. This comprehensive field testing procedure provided a scientific basis for assessing the impact of blasting on the tunnel’s surrounding rock.
Fig. 8.
Schematic of acoustic wave test. The 3D visualization was created using Blender 3.3 (Blender Foundation, www.blender.org, version 3.3).
Figure 9 compares the results of damage verification. The experimental testing indicated a damage value of 0.1 and a depth of 21.2 cm. In parallel, the simulation results indicated a damage of 0.13, demonstrating a significant alignment with the experimental data.
Fig. 9.

Comparison of field test and numerical simulation results.
Characteristics of damage evolution in tunnel surrounding rock by full-face smooth blasting
Characteristics of accumulated damage in tunnel surrounding rock under various explosive sections
The evolution of damage in the tunnel surrounding rock under different explosive segments is illustrated in Fig. 10. In Fig. 10a, the pilot hole explosive segment MS1 initiates the blasting. At 300 μs, circular damage begins around the borehole, intensifying near the source. By 360 μs, stress wave convergence induces radial damage. By 420 μs, damage near the pilot hole evolves into a strip-like pattern and starts to penetrate and connect in the tunnel face section. Figure 10b shows the progression from the MS3 explosive segment to the completion of the MS11 bottom plate hole explosive blasting. Both the degree and distribution range of damage in the surrounding rock increase significantly. After MS9 blasting, substantial damage appears in the outer contour area. Following MS11 blasting, the damage to the tunnel surrounding rock stabilizes.
Fig. 10.
Cumulative damage evolution process of rock mass in tunnel. (a) Initiation of cutting holes (MS1) and (b) Initiation of critical holes (MS3), Initiation of peripheral holes (MS9), and Initiation of bottom holes (MS11).
Figure 11 provides a statistical analysis of the tunnel surrounding rock’s damage evolution under different explosive segments, highlighting a positive correlation between the extent of damage and the number of blasts. The most significant increase in the damaged area occurred after the MS5 blast, reaching 3.8 m2, and then stabilized at 15.33 m2 following the MS11 blast. The damaged depth peaked at 4.42 m after MS11, with an initial notable rise of 1.9 m after MS1. It was only after the blasting at the MS8 segment that a significant increase in both damaged area and depth began to appear, with increases of 1.22 m2 and 0.11 m, respectively. The most substantial increase in damaged depth outside the contour occurred after the MS9 segment, reaching 0.38 m; after the MS11 blasting, the maximum damaged depth reached 0.68 m. When the cyclic blasting load exceeds the yield strength of the surrounding rock, the damaged area exhibits a nonlinear trend of change.
Fig. 11.
Damage curves of tunnel surrounding rock in full section and contour area. (a) Damaged depth and (b) Damaged area.
Damage evolution characteristics of tunnel surrounding rock at different locations
An analysis of damage evolution at the tunnel’s arch crown, shoulders, and foot was conducted, with monitoring unit distribution shown in Fig. 12 and damage evolution in the surrounding rock for various explosive segments is illustrated in Fig. 13. Taking the arch crown as an example, damage initiated at Point A1 after the MS8 blast during the rock’s elastic vibration phase. The MS9 blast significantly increased the damage value by approximately 250%, entering the crack damage phase, while the MS11 blast caused the damage to peak at 0.63. Damage diminished with increasing depth, remaining within the elastic vibration zone beyond a vertical depth of 20 cm from the crown. The crown experienced the highest damage, followed by the foot and shoulders. Notably, the final damage values of all monitoring units did not exceed the threshold Dcf (the crushed zone), indicating an absence of crushed zones in the external surrounding rock. This suggests that the tunnel blasting excavation parameters were well-designed.
Fig. 12.

Layout of measuring points. The 3D visualization was created using Blender 3.3 (Blender Foundation, www.blender.org, version 3.3).
Fig. 13.
Damage evolution of the tunnel at different locations. (a)Vault, (b) Spandrel, and (c) Arch foot.
Characteristics of damage evolution in deep tunnels with full-face smooth blasting
Damage evolution process in different tunnel cross-sections
Deep rock formations are situated within high in-situ stress environments. Consequently, three scenarios of mining under hydrostatic stress conditions at burial depths of 500, 1000, and 1500 m are selected for analysis, as outlined in Table 10 detailing various stress distributions in deep tunnels. Understanding the progression of damage under elevated in-situ stress is crucial for the design and implementation of drilling and blasting operations in deep rock. Simulations, by sectioning along the x–y plane of the tunnel’s surrounding rock mass, expose the evolving distribution of final damage clouds under varying in-situ stress conditions, illustrated in Fig. 14. In the absence of in-situ stress, the damage intensity at the tunnel face is the highest, affecting a larger area of crushed rock near the blasting holes due to the stress waves generated by the explosion. The extent of damage to the surrounding rock at the tunnel face is inversely proportional to the magnitude of in-situ stress. Higher in-situ stress, suppresses the impact of blasting on the surrounding rock, resulting in less effective excavation damage. In the unexcavated regions of the tunnel, an increase in in-situ stress correlates with a decrease in both the extent and severity of damage at multiple locations within the tunnel.
Table 10.
In-situ stress distribution scenarios for different deep tunnels.
| Stress field | Scheme | Depth H (m) |
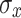 (MPa) (MPa) |
 (MPa) (MPa) |
|---|---|---|---|---|
| Zero initial stress condition | 1 | 0 | 0 | 0 |
| Hydrostatic stress field | 2 | 500 | 13.5 | 13.5 |
| 3 | 1000 | 27 | 27 | |
| 4 | 1500 | 40.5 | 40.5 |
Fig. 14.
Damage nephogram of full-face blasting under in-situ stresses. (a) 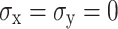 (MPa), (b)
(MPa), (b) 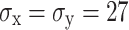 (MPa), and (c)
(MPa), and (c) 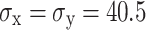 (MPa).
(MPa).
This study analyzes the characteristics of damage evolution of tunnel surrounding rock under varying in-situ stress conditions in three-dimensional space, focusing on the damage depth z in the direction of blasting excavation. The analysis involves sectioning the x–z cross-section of the tunnel’s surrounding rock at the arch foot and shoulder, and plotting the final distribution of blasting damage evolution cloud maps under hydrostatic pressure stress conditions, as shown in Fig. 15. At the arch shoulder section, with 0 MPa in-situ stress, the excavation damage depth, horizontal damage depth, and overall area are maximized, nearly encompassing the entire excavation process. As in-situ stress increases, both the excavation damage depth and the damaged area exhibit a decreasing trend. At 40.5 MPa in-situ stress, the reduction rates of damage depth along the z and x directions are only 18.5% and 8.8%, respectively. Regarding the arch foot section, damage at 0 MPa in-situ stress appears in a strip-like pattern. As the in-situ stress increases from 0 to 40.5 MPa, the excavation damage depth decreases from 182 to 101 cm, and the horizontal damage depth also decreases from 471 to 297 cm. Increased in-situ stress diminishes the excavation effect of blasting, with greater suppression on the horizontal damage depth compared to the excavation depth.
Fig. 15.
Damage nephogram of spandrel and arch soffit under in-situ stresses. (a) 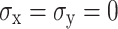 (MPa), (b)
(MPa), (b) 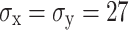 (MPa), and (c)
(MPa), and (c) 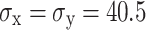 (MPa).
(MPa).
To delve deeper into evolutionary patterns of tunnel surrounding rock blasting under blast-induced loads at varying in-situ stress conditions, this study mapped out the damage area index and the damage area curves, as illustrated in Fig. 16. It is apparent that damage at the arch shoulders originates from the MS1 explosive segment across all levels of in-situ stress. Conversely, at the arch foot, damage emerges only from the subsequent MS8 explosive segment when the in-situ stress is elevated to 27 MPa, which is not observed at 0 MPa. Across all explosive segments, in-situ stress mitigates the blasting-induced damage area of the full-face surrounding rock in the x–y plane. This inhibitory effect diminishes as the in-situ stress value escalates. Notably, damage only appears at the external contour of the surrounding rock starting from the MS8 segment. Under a 0 MPa condition, the damage area peaks following the MS8 explosive blast, then gradually diminishes with increasing in-situ stress.
Fig. 16.
Damage area curves of the tunnel under different sections. (a) Vault, (b) Full section, (c) Contour area, and (d) Arch soffit.
Damage evolution process and zoning in tunnel surrounding rock at different locations
Figure 17 displays the damage cloud maps for the tunnel contour cross-section under diverse in-situ stress scenarios, indicating that the regions at the arch crown and shoulders sustain the most significant damage. The shoulders of the arch show the most pronounced damage depth, which initially drops from 0.41 m at 0 MPa to 0.33 m at 40.5 MPa, then marginally ascends to 0.35 m. At 27 MPa in-situ stress, damage progression at the arch shoulders is notably suppressed, and at 40.5 MPa, it experiences a slight upsurge. Conversely, the damage depth at the arch crown consistently decreases from 0.31 to 0.02 m, with in-situ stress consistently suppressing the evolution of the damage depth.
Fig.17.
Damage nephogram of contour area under in-situ stresses. (a) 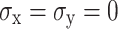 (MPa), (b)
(MPa), (b) 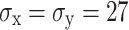 (MPa), and (c)
(MPa), and (c) 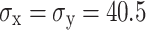 (MPa).
(MPa).
This study delves into the damage evolution patterns at the arch crown and shoulders of tunnel surrounding rock under fluctuating in-situ stress conditions, as depicted in Fig. 18. The arch crown exhibits higher damage values than the shoulders, with all measurements situated within the crack damage zone across the spectrum of in-situ stress levels. Increasing in-situ stress suppresses the damage values of the monitoring units to varying extents. For example, monitoring unit A1 demonstrates damage post-blast in segments MS8, MS9, and MS11 under in-situ stresses of 0 MPa, 27 MPa, and 40.5 MPa, respectively. Once the damage depth surpasses 20 cm, the surrounding rock enters the elastic vibration zone under diverse in-situ stress scenarios. In-situ stress exerts a more pronounced impact on reducing damage at the arch crown compared to the shoulders. Consequently, reinforced bolting and support measures are crucial for the arch shoulder region during deep rock tunneling and progression.
Fig. 18.
Damage evolution of the tunnel at typical locations under different in-situ stresses.
Huang et al.40 proposed a computational method for rock damage zoning based on the rock damage criterion and RHT constitutive equation, but it lacks considerations of the impact of in-situ stress on rock damage zoning. Therefore, this study illustrates the distribution of blasting damage zoning in the surrounding rock of tunnels under hydrostatic pressure, adhering to the principles of rock damage zoning. Figure 18 provides cloud maps that visualize the extent of damage at the arch shoulders under two distinct in-situ stress scenarios: 0 MPa and 27 MPa. In Fig. 19a, under 0 MPa, indicates that the tunnel face’s surrounding rock is almost entirely crushed. In contrast, under 27 MPa, certain sections remain intact, as they have not exceeded the damage threshold for crushing, highlighting the stress’s inhibitory effect on blasting damage. Comparing the two stress conditions in Fig. 19b, it is evident that the central region of the tunnel face under 27 MPa exhibits less damage compared to the 0 MPa scenario, where the rock is uniformly crushed. This transformation arises because the in-situ stress partially converts the crushed rock into cracked damaged rock, demonstrating its mitigating influence. Furthermore, Fig. 19c underscores the distinct impact of elevated in-situ stress on the elastic vibration zone at the base of the tunnel arch. Simulations indicate that in-situ stress exerts a varying degree of inhibition on the horizontal extent and depth of damage in the excavation direction, across all damage zones: crushed, cracked, and elastic vibration.
Fig. 19.
Different damage zones under in-situ stress of 0 MPa and 27 MPa. (a) Crushing zone, (b) Crack damage zone, and (c) Elastic vibration zone.
Impact of blasting-induced damage on classification of tunnel surrounding rock
The Basic Quality Index (BQ) value can reflect the degree of blasting impact on basic quality indicators of the rock mass: the higher the BQ value shows, the greater stability the surrounding rock has41. Using BQ as an analytical indicator for assessing the effects of blasting damage on the classification of surrounding rock, the calculation formula is defined as follows:
 |
24 |
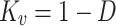 |
25 |
where 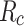 represents the uniaxial compressive strength (assumed as 70 MPa);
represents the uniaxial compressive strength (assumed as 70 MPa); 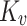 is the integrity coefficient of the surrounding rock; D denotes damage. When
is the integrity coefficient of the surrounding rock; D denotes damage. When 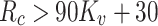 , the equation should be substituted with
, the equation should be substituted with 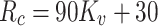 and
and  . The relationship between BQ values and D for different grades of surrounding rock is represented in Fig. 20.
. The relationship between BQ values and D for different grades of surrounding rock is represented in Fig. 20.
Fig. 20.

Curves of BQ and damage under different levels of surrounding rock grades.
Continuing with the evaluation of the surrounding rock classification for the arch crown and shoulders, the evolution of the surrounding rock damage in the contour areas of the arch crown and shoulders is recorded relative to distance, as depicted in Fig. 21. As the cyclic blasting of explosive segments persists, the BQ values of the surrounding rock progressively decrease. The blasting-induced damage reclassifies the arch crown and shoulder contour areas from Class I to Class III. Meanwhile, the presence of in-situ stress substantially mitigates the reduction in BQ values, facilitating the transition of the arch crown and shoulder regions into Class II surrounding rock.
Fig. 21.
BQ curves under different in-situ stress conditions.
According to the grade-based classification of surrounding rock areas depicted in Fig. 22, it is apparent that in-situ stress impedes the progression of Class II, III, and V rock zones, while facilitating the evolution of Class I and IV areas. Notably, in-situ stress exerts the greatest impact on Class I rock areas and the least on Class III. As in-situ stress escalates from 0 to 40.5 MPa, the evolution of Class I rock areas rises from 75 to 80%, while that of Class III rock areas diminishes from 1.53 to 1.34%.
Fig. 22.

Distribution of surrounding rock areas under different in-situ stress conditions.
Conclusion
This study examines the patterns governing damage progression in deep tunnel surrounding rock through full-face smooth blasting. It delves into the cyclic blasting damage progression under various in-situ stress conditions and evaluates its impact on the classification of the deep tunnel surrounding rock. The principal findings are summarized as follows:
The analysis of damage progression in deep tunnels utilizing full-face smooth blasting techniques discloses that he damaged area and depth of the surrounding rock increase with the number of blasts during the cyclic blasting process of different explosive segments. Concurrently, damage severity decreases farther away from the blasting source. Notably, the measured damage depths at the crown, springline, and base of the unexcavated contour regions are recorded at 44.2 cm, 63.5 cm, and 45.4 cm, respectively.
This study delineates the damage patterns of surrounding rocks in the deep underground tunnel subjected to full-face smooth blasting, underscoring the pivotal role of in-situ stress in attenuating blast-induced damage. It examines the three-dimensional excavation profile’s damage, assessing the impact of in-situ stress on rock damage zoning. Results indicate that increasing in-situ stress from 0 to 40.5 MPa significantly reduces excavation and horizontal damage depths at the arch foot by 81 cm and 174 cm, respectively. Furthermore, comparing damage areas at 0 MPa and 27 MPa in-situ stress shows that the influence of in-situ stress effectively suppresses the expansion of the crushed, crack, and elastic vibration zones, particularly in horizontal and excavation damage depths.
Using the Basic Quality Index (BQ) of the rock mass for the classification assessment of tunnel surrounding rock, the study shows that blasting damage can categorize intact surrounding rock into five classes. It further establishes that in-situ stress significantly suppresses the evolution of the areas of Classes V, III, and II, while promoting the evolution of the areas of Classes I and IV.
Employing the Basic Quality Index (BQ) to appraise the classification of tunnel surrounding rock, this study elucidates that blasting-induced damage delineates the rock into five distinct classes. Additionally, it ascertains that in-situ stress markedly inhibits the progression of Classes V, III, and II, concurrently fostering the advancement of Classes I and IV.
Acknowledgements
This work was supported by the Natural Science Foundation of China (52209121), the Natural Science Foundation of Chongqing (cstc2021jcyj-msxmX0952), the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJZD-K202300703).
Author contributions
H.D.: Conceptualization, Investigation, Methodology, Formal analysis, Writing original draft, Funding acquisition; W.L.: Supervision, Methodology, Writing review & editing; X.H. & H.W.: Formal analysis, Methodology, Investigation, Validation; Y.W. & S.H.: Investigation, Validation.
Data availability
Data and material used in preparation of this manuscript are available from the corresponding authors upon reasonable request if not already in the public domain.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Chen, M., Lu, W. & Yi, C. Blasting vibration criterion for a rock-anchored beam in an underground powerhouse. Tunn. Undergr. Space Technol.22(1), 69–79 (2007). [Google Scholar]
- 2.Lu, S., Zhou, C., Jiang, N. & Xu, X. Effect of excavation blasting in an under-cross tunnel on airport runway. Geotech. Geol. Eng.33, 973–981 (2015). [Google Scholar]
- 3.Chen, Y. et al. Shaping characteristics of excavation contours in sequential controlled fracture blasting of rock-anchored beams in Shuangjiangkou underground powerhouse. Sci. Rep.13(1), 15645 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Verma, H. K., Samadhiya, N. K., Singh, M., Goel, R. K. & Singh, P. K. Blast induced rock mass damage around tunnels. Tunn. Undergr. Space Technol.71, 149–158 (2018). [Google Scholar]
- 5.Shadabfar, M., Gokdemir, C., Zhou, M., Kordestani, H. & Muho, E. V. Estimation of damage induced by single-hole rock blasting: A review on analytical, numerical, and experimental solutions. Energies14(1), 29 (2020). [Google Scholar]
- 6.He, R. Research on cumulative damage induced by cyclic blasting of tuff. J. Phys. Conf. Ser.2694, 012057 (2024). [Google Scholar]
- 7.Yue, H. Z. et al. The effect of blast-hole arrangement, delay time, and decoupling charge on rock damage and vibration attenuation in multihole blasting. Shock Vib.2022(1), 2110160 (2022). [Google Scholar]
- 8.Yao, Q., Yang, X. G., Chen, X. Z. & Li, H. T. Numerical simulation of vibration dynamic response during excavation blasting of large underground powerhouses. J. Vib. Shock.33(6), 66–70 (2014). [Google Scholar]
- 9.Chen, J. H., Zhang, J. S. & Li, X. P. Study on the damage influence range and evaluation of excavation blasting in large underground power stations. J. Vib. Shock.34(23), 54–61 (2015). [Google Scholar]
- 10.Ji, L., Zhou, C., Lu, S., Jiang, N. & Li, H. Modeling study of cumulative damage effects and safety criterion of surrounding rock under multiple full-face blasting of a large cross-section tunnel. Int. J. Rock Mech. Min.147, 104882 (2021). [Google Scholar]
- 11.Ling, T., Li, S., Liu, D. & Liang, S. Blasting damage of tunnel rock mass based on cumulative effect. Rock Mech. Rock. Eng.56(3), 1679–1695 (2023). [Google Scholar]
- 12.Lyu, G., Zhou, C. & Jiang, N. Experimental and numerical study on tunnel blasting induced damage characteristics of grouted surrounding rock in fault zones. Rock Mech. Rock Eng.56(1), 603–617 (2023). [Google Scholar]
- 13.Yang, J. H., Jiang, Q. H., Zhang, Q. B. & Zhao, J. Dynamic stress adjustment and rock damage during blasting excavation in a deep-buried circular tunnel. Tunn. Undergr. Space Technol.71, 591–604 (2018). [Google Scholar]
- 14.Yang, J. H., Yao, C., Jiang, Q. H., Lu, W. B. & Jiang, S. H. 2D numerical analysis of rock damage induced by dynamic in-situ stress redistribution and blast loading in underground blasting excavation. Tunn. Undergr. Space Technol.70, 221–232 (2017). [Google Scholar]
- 15.Lu, A. et al. Crack propagation mechanism of smooth blasting holes for tunnel excavation under high in-situ stress. Eng. Fract. Mech.304, 110144 (2024). [Google Scholar]
- 16.Sun, F., Sun, Z., Zhang, D. & Li, M. Large-scale model test and numerical analysis of load-bearing arch characteristics of large cross-section tunnel under high geostress. Eng. Fail Anal.163, 108600 (2024). [Google Scholar]
- 17.Huang, J., Chen, S. H., Liu, M. L. & Li, K. P. Physical model test and numerical simulation study of cumulative damage to deep tunnel surrounding rock under cyclic blasting load. Int. J. Damag. Mech.32(2), 161–184 (2023). [Google Scholar]
- 18.Chen, M., Lu, W. B., Yan, P. & Hu, Y. G. Blasting excavation induced damage of surrounding rock masses in deep-buried tunnels. Ksce J. Civ. Eng.20, 933–942 (2016). [Google Scholar]
- 19.Cui, Y., Wu, B., Meng, G. & Xu, S. Research on blasting cumulative dynamic damage of surrounding rock in step construction tunnel. Sci. Rep.13(1), 1974 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yan, P. et al. Contributions of in-situ stress transient redistribution to blasting excavation damage zone of deep tunnels. Rock Mech. Rock Eng.48, 715–726 (2015). [Google Scholar]
- 21.Yang, J. et al. Comparative study of the excavation damage and rockburst of the deeply buried Jinping II diversion tunnels using a TBM and the drilling-blasting method. Adv. Civ. Eng.2020(1), 8876214 (2020). [Google Scholar]
- 22.Fan, Y. et al. Damage zones induced by in situ stress unloading during excavation of diversion tunnels for the Jinping II hydropower project. B Eng. Geol. Environ.80, 4689–4715 (2021). [Google Scholar]
- 23.Xie, L. X. et al. Damage evolution mechanisms of rock in deep tunnels induced by cut blasting. Tunn. Undergr. Space Technol.58, 257–270 (2016). [Google Scholar]
- 24.Li, Z. et al. Study on cyclic blasting failure characteristics and cumulative damage evolution law of tunnel rock mass under initial in-situ stress. Eng Fail Anal.150, 107310 (2023). [Google Scholar]
- 25.Luo, S. et al. Effects of in-situ stress on blasting damage during deep tunnel excavation. Arab. J. Sci. Eng.46(11), 11447–11458 (2021). [Google Scholar]
- 26.Wang, H. L., Gao, S. & Zhang, H. Y. Study on the evolution of damage in high geostress rock by dual-hole blasting. Eng. Blast.28(2), 1–6 (2022). [Google Scholar]
- 27.Liu, S., Wang, W. H., Zhang, H. G. & Zhang, L. W. Three-dimensional numerical simulation study of single hole blasting damage in rock mass. Eng. Blast.29(1), 10–18 (2023). [Google Scholar]
- 28.Mandal, S. K., Singh, M. M., Bhagat, N. K. & Dasgupta, S. Evaluating extent and causes of overbreak in tunnels. Tunn. Undergr. Space Technol.24, 22–36 (2009). [Google Scholar]
- 29.Perras, M. A. & Diederichs, M. S. Predicting excavation damage zone depths in brittle rocks. J. Rock Mech. Geotech. Eng.8, 60–74 (2016). [Google Scholar]
- 30.Daraei, A. & Zare, S. Prediction of overbreak depth in Ghalaje road tunnel using strength factor. Int. J. Min. Sci. Technol.28, 679–684 (2018). [Google Scholar]
- 31.Elshorbagy, A. M. et al. Experimental and numerical investigation of the effects of blasting parameters on overbreak in underground excavations. Tunn. Undergr. Space Technol.45, 1–10 (2015). [Google Scholar]
- 32.Li, G., Zhou, C., Lu, S., Jiang, N. & Li, H. Modeling study of cumulative damage effects and safety criterion of surrounding rock under multiple full-face blasting of a large cross-section tunnel. Int. J. Rock Mech. Min. Sci.147, 104882 (2021). [Google Scholar]
- 33.Liu, Y., Dai, F., Xu, N., & Zhao, T. Cyclic flattened Brazilian disc tests for measuring the tensile fatigue properties of brittle rocks. Rev. Sci. Instrum. 88(8), 083902 (2017). [DOI] [PubMed]
- 34.Liu, K. et al. A modified HJC model for improved dynamic response of brittle materials under blasting loads. Comput. Geotech.123, 103584 (2020). [Google Scholar]
- 35.Baranowski, P., Kucewicz, M. & Janiszewski, J. JH-2 constitutive model of sandstone for dynamic problems. Sci. Rep.14(1), 3339 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Xie, L. X. et al. Analysis of damage mechanisms and optimization of cut blasting design under high in-situ stresses. Tunn. Undergr. Space Technol.66, 19–33 (2017). [Google Scholar]
- 37.Li, H., Chen, Y., Liu, D., Huang, D. & Zhao, L. Sensitivity and determination method of main parameters of rock RHT model. J. Beijing Inst. Technol.38(8), 779–785 (2018). [Google Scholar]
- 38.Zhou, H. et al. Study on smooth blasting technology of short pilot tunnel in small cross-section and steep slope long tunnel. Modern Tunn. Technol.58(2), 228–237 (2021). [Google Scholar]
- 39.Zhao, M. J. & Xu, R. Ultrasonic velocity study on rock damage characteristics and strength. Chin. J. Geotech. Eng.2, 720–722 (2000). [Google Scholar]
- 40.Huang, Y. et al. Optimization and verification of blasting fragmentation judgment method for RHT constitutive model of rock. Trans. Beijing Inst. Technol.43(6), 565–574 (2023). [Google Scholar]
- 41.Cui, Z., Sheng, Q., Zhang, G. M. & Liu, H. A modified rock mass classification considering seismic effects in the basic quality (BQ) system. B Eng. Geol. Environ.80, 2249–2260 (2021). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data and material used in preparation of this manuscript are available from the corresponding authors upon reasonable request if not already in the public domain.