Analysis of rare events in healthcare intervention using department of defense data: intravenous immune globulin therapy for bullous pemphigoid

Abstract

Introduction

Rare events data have proven difficult to explain and predict. Standard statistical procedures can sharply underestimate the probability of rare events, such as intravenous immune globulin therapy (IVIg) for bullous pemphigoid.

Methods

This retrospective cross-sectional study used Department of Defense TRICARE data to determine factors associated with IVIg therapy among bullous pemphigoid patients. We used prior and weighted correction methods for logit regression to solve rare event bias.

Results

We identified 2,720 individuals diagnosed with bullous pemphigoid from 2019 to 2022, of which 14 were treated with IVIg. Patients who received IVIg therapy were younger (65.07 vs. 75.85, P =.0016) and more likely to be female (13 vs. 1, P =.0036). The underestimation with the standard regression model for event probabilities ranged from 11% to 102% using the prior correction method and from 15% to 107% using the weighted correction method.

Conclusion

Rare events are low-frequency, high-severity problems that can have significant consequences. Rare diseases and rare therapies are individually unique but collectively contribute to substantial health and social needs. Therefore, correct estimation of the events is the first step toward assessing the burden of rare diseases and the pricing of their therapies.

Background

In outcomes research data, we deal with rare cases frequently. Currently, about 7,000 rare diseases have been identified, with an estimated 300 million people affected globally [1]. Rare diseases, although individually unique, collectively represent substantial unmet health and social care needs and a significant public health challenge to society as a whole [1]. Definitions of rare diseases vary: [1] under the U.S. Orphan Drug Act, a rare disease is defined as a disease or condition affecting fewer than 200,000 individuals [2], whereas it is defined as a condition that affects fewer than 5 people per 10,000 population in Europe [1].

It is estimated that 95% of rare diseases have no approved treatment [1, 3, 4]. The treatments for the remaining 5% are frequently expensive and relatively unknown. In addition to the high research and development costs associated with largely limited treatment options, the rather small market for rare diseases is conducive to prohibitive pricing. Rare diseases present a challenge for clinicians in reaching a conclusive diagnosis and determining an appropriate course of treatment due to their low prevalence, heterogenicity, and complexity [1, 5, 6]. Thus, it can be challenging to predict and estimate rare-disease outcomes in a real-world setting.

A rare event is defined as a binary dependent variable characterized by dozens to thousands of times fewer 1’s (i.e., rare diseases, treatments, newly approved medications) than 0’s (“nonevents”) [7]. There are two main reasons for the difficulty in estimating rare events.

First, standard logistic regression can sharply underestimate the probability of events. Therefore, the estimates would be biased. One real-life example is working with data on a rare disease such as bullous pemphigoid (BP), a rare skin condition. It is estimated that BP affects fewer than 50,000 people in the U.S., primarily older people [8]. The most common treatment is prednisone, but long-term use increases the risk of weak bones, diabetes, high blood pressure, high cholesterol, and infection. As an alternative, intravenous immunoglobulin (IVIg) is effective, although optimal use of IVIg is yet to be determined. Most adverse effects of IVIg infusions are transient, infusion-related symptoms that do not have long-term sequelae, although serious adverse events such as thrombosis, renal dysfunction, and acute renal failure have been noted [9]. Additional concerns about IVIg treatment include its potential toxicity and cost. While a single infusion starts at $5,000 to $10,000, treatment usually requires repeated cycles for which insurance coverage is not always covered. Therefore, it is essential to know the probability of using IVIg treatment for a rare disease.

To study the usage pattern of IVIg therapy in BP, we can formulate the model as follows: Let the outcome variable (e.g., whether the patient had IVIg therapy) be and follow a Bernoulli probability function that takes on the value 1 with probability . Let be the vector of explanatory variables such as age, comorbid conditions, gender, or insurance type. Then it can be shown that the variance matrix takes the following form:

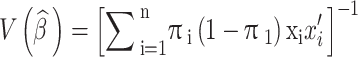Rare events have small estimates for observations. Standard logit models that use approximation rather than actual values will usually have larger values for . Thus, will be larger for 1’s than 0’s, stating that 1’s are more informative than 0’s in rare events. Since rare events have small sample sizes (usually < 200 observations), the logit models will yield a suboptimal result [7]. Therefore, logit models need to be adjusted to control this effect.

The second problem is related to how the data are collected. There is a fear among analysts that collecting data sets with no events (and thus with no variation on outcome measures) has led researchers to choose very large data sets with few, and often poorly measured, explanatory variables. For example, to avoid rare events, a researcher could include a broader sample by including a wide variety of International Classification of Disease (ICD) codes, a Healthcare Common Procedure Coding System (HCPCS) Level II alphanumeric code issued by the Center for Medicare and Medicaid Services (J-Codes), or Current Procedural Terminology (CPT) codes rather than specific codes. This technique will cloud the estimates, making it challenging to see the true effect of treatment on an actual targeted sample.

The twofold problem outlined above arises when predicting health outcomes of rare diseases, rare treatments, or small numbers of recently approved medications. The objective of this study is to apply correction methods used in other rare event studies such as major stock market crashes to solve the aforementioned issues in performing research on rare diseases.

Methods

For this retrospective cross-sectional study, we extracted de-identified patient data for fiscal years (FYs) 2019 to 2022 from the Department of Defense TRICARE data. Each FY (October 1–September 30) is based on the U.S. federal budget calendar. The data from Military Health Services (MHS) has been recognized as a model of equitable healthcare access across socioeconomic and racial groups. The U.S. MHS is a global healthcare network with a diverse population that is more representative of the U.S. population than other data sets, with fewer disparities in healthcare services. The system serves 9.6 million beneficiaries, including active-duty service members, retirees, and family members, on an annual budget of $53 billion. The MHS delivers care through a direct-care/health maintenance organization system for Department of Defense military treatment facilities and a purchased-care/preferred provider organization system for civilian facilities. In addition, the MHS provides universal coverage for its beneficiaries under its TRICARE program. The data do not capture healthcare delivery in combat zones or care received in the Veterans Administrative system. All individuals were in the TRICARE Prime^® managed care option.

Patients with BP were identified using the International Classification of Diseases, Tenth Revision, Clinical Modification (ICD-10-CM) diagnosis codes (L12.0). Our outcome variable was the use of IVIg therapy and identified by J codes (J1459, J1554, J1556, J1557, J1561, J1566, J1568, J1569, J1572, J1599). The inclusion criteria used were adults (≥ 18 years), diagnosed with BP and treated with or without IVIg. IVIg date was the index date; the index date for the non-event cohort was randomly assigned between the earliest IVIg date and latest IVIg date.

Patient age, gender, and comorbidities were available in the data sets. We identified the top 10 comorbidities associated with BP. Hypertension emerged as one of the most prevalent comorbidities in patients with BP, with studies reporting its occurrence in up to 76% of cases [10]. The association between hypertension and BP is hypothesized to stem from shared inflammatory pathways or medication effects. Esophageal involvement is another frequent complication in BP cases, potentially manifesting as reflux symptoms or, in some instances, esophagitis dissecans superficialis [11]. Dermatological comorbidities are also common in patients with BP. Research has demonstrated an increased risk of BP in patients with pre-existing dermatitis, and BP may initially present with eczematous or urticarial lesions before the characteristic blistering occurs [12]. Rash, a primary symptom of BP itself, often manifests as urticarial plaques preceding blister formation [13]. Urinary tract involvement is another significant comorbidity in patients with BP. One study reported characteristic lower urinary tract lesions in 93% of BP cases [14]. The increased prevalence of urinary tract infections in patients with BP is attributed to advanced age and the use of immunosuppressive treatments [14]. Neurological comorbidities are frequently observed in patients with BP, often manifesting as limb pain. Multiple sclerosis (MS) has been found to have a significant association with BP, with one study reporting an odds ratio of 5.36 for neurological diseases, including MS, in patients with BP [15]. Cardiovascular comorbidities are also prevalent in patients with BP, with dyspnea being a common related symptom [16]. Additionally, several studies have reported an increased risk of squamous cell carcinoma in patients with BP [17]. A flag was created for patients who had at least three of the following comorbidities: hypertension, hyperlipidemia, esophagitis reflux, dermatitis, urinary tract infection, limp pain, rash, skin cancer, dyspnea, and MS prior to treatment to proxy for severity.

For descriptive analysis, we compared the patients with and without IVIg therapy. Numbers and percentages were provided for dichotomous and polychotomous variables. Means and standard deviations were provided for continuous variables. For dichotomous and polychotomous variables, P values were calculated according to the chi-square test, and for continuous variables, t-tests were used to calculate P values. Nonparametric tests (e.g., the Mann-Whitney U test, log-rank test, or McNemar test) were applied if there was a deviation from asymptotical assumptions.

Since it is well documented that logit coefficients are biased in small samples, we proposed a correction method to solve the possible “rare event” bias in log estimation. Consider a logit model for outcome variable y and set of k explanatory variables x:

where G is the logistic function:

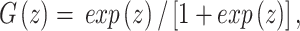which is between 0 and 1 for all real numbers z.

To apply the first correction method, we obtained information about the fraction of 1’s in the population and then the observed fraction of ones in the sample 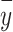. Then the adjusted coefficient in the logit model is

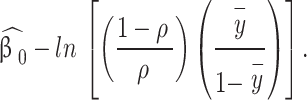Note that prior correction affects only constant terms (therefore, not the odds ratio), but since most of the time interest lies in estimated probabilities:

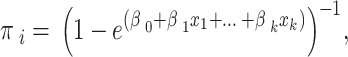it is necessary to estimate a rare-event bias-adjusted constant term, with the first correction technique, called prior correction.

For the second correction technique, we used weights determined by the proportion of 1’s and 0’s in the sample to equal the true proportion in the population, letting and be the dependent variable and weighting independent variables by if and if Then, we ran a standard logistic regression of weighted dependent and independent variables. In other words, the second correction technique aims to address the issue of imbalanced data in logistic regression by applying weights to both the dependent and independent variables. The rationale for this technique is to adjust the influence of each observation in the model to reflect the true events (1’s) and nonevents (0’s) in the population. By doing so, it attempts to correct for the bias introduced by imbalanced samples, where one class may be overrepresented or underrepresented compared with the true population. For example, if age=75 and w=1, the age variable would remain 75, but the observation would be a given weight of 1.5 in the model fitting process. This means that this observation would have 1.5 times the influence on the model parameters compared with an observation with a weight of 1. To solve commonly used data collection biases under rare-event data, King and Zeng have proposed collecting all (or all available) 1’s and a small random sample of 0’s to avoid losing consistency or even much efficiency relative to the full sample [7]. Wang et al. have also proposed an adjusted logistic propensity weighting method, a more advanced version of this approach [18]. Both methods were validated under different scenarios (e.g., varying sample sizes, different event rates) using Monte Carlo simulation techniques, as described in previous research [7].

For the second part of the analysis, we tested differences in predicted probabilities. We proposed nonparametric tests since these tests are most appropriate when the sample sizes are small. The Mann-Whitney U test and the Kolmogorov-Smirnov two-sample test were used on predicted probabilities of logit regressions to see whether differences exist. To assess the independence of our predictor variables in the regression model, we employed two established methods: variance inflation factor analysis and examination of pairwise correlations.

The analysis used SAS version 9.4 (SAS Institute Inc.) and STATA 17 (STATA Corp., LLC).

Results

We identified 2,720 unique individuals diagnosed with BP in FY 2019–2022. Among these patients diagnosed with BP, 14 were treated with IVIg. The remaining sample was a non-event cohort (n = 2,706). Overall, 54.19% of individuals were women, and 85% of our sample was 65 years or older (mean, 78 years). We identified the most frequent 10 comorbidities from our sample. According to Table 1, the most frequent comorbidity prior to treatment with IVIg was hypertension (61.32%), followed by hyperlipidemia (37.20%), pemphigoid (34.70%), pain limp (24.15%), dyspnea (23.82%), dermatitis (23.49%), skin cancer (22.31%), urinary tract infection (20.25%), esophageal reflux (19.44%), and rash (16.43%). Within this sample, 54.08% of patients had more than three comorbidities within one year prior to treatment.

Table 1.

Demographic characteristics of BP patients with and without IVIg therapies

	Total	With IVIg therapy	Without IVIg therapy	P value
Sample size (n)	2,720	14	2,706
Age, mean (SD)	75.79 (12.72)	65.07 (17.54)	75.85 (12.67)	.0016
Age, median (IQR)	78 (70–85)	72 (54–76)	78 (70–85)
Female, n (%)	1,474 (54.19)	13 (92.85)	14 (53.99)	0.0036
Diseases
Hypertension	1,668 (61.32)	11 (78.57)	1,657 (61.23)	.1841
Hyperlipidemia	1,012 (37.20)	8 (57.14)	1,004 (37.10)	.1219
Pemphigoid	944 (34.70)	8 (57.14)	936 (35.58)	.0771
Esophagitis reflux	529 (19.44)	6 (42.85)	523 (19.32)	.0265
Dermatitis	639 (23.49)	8 (57.14)	631 (23.31)	.0029
Urinary tract infection	551 (20.25)	7 (50.00)	544 (20.10)	.0055
Pain limp	657 (24.15)	5 (35.71)	652 (24.09)	.3112
Rash	447 (16.43)	6 (42.85)	441 (16.29)	.0075
Skin cancer	607 (22.31)	5 (35.71)	602 (22.24)	.2275
Dyspnea	648 (23.82)	5 (35.71)	643 (23.76)	.2952
≥3 comorbidities	1,471 (54.08)	11 (78.57)	1,460 (53.95)	.0653

Abbreviations: IQR, interquartile range; IVIg, intravenous immune globulin; SD, standard deviation

Patients with BP receiving IVIg therapy were younger (65.07 vs. 75.85, P =.0016) and more likely to be female (13 vs. 1, P =.0036). Overall, patients with IVIg treatment had significantly more comorbidities than patients without IVIg therapy. (78.57% vs. 53.95%, P =.0653). Patients receiving IVIg therapy also had a significantly higher likelihood of esophageal reflux (42.85% vs. 19.44%, P =.0265), dermatitis (57.14% vs. 23.49%, P =.0029), urinary tract infection (50.00% vs. 20.25%), P =.0055), and rash (42.85% vs., 16.43%, P =.0075).

Table 2 shows the coefficients from standard logistic regression, prior correction regression, weighting regression, and reduced non-event sample regression.

Table 2.

Coefficient estimates from logistic, rare-event corrected logistic, and reduced non-event sample regressions

	Coefficient	Standard error	P Value	Lower CI	Upper CI
Standard logistic regression
Age ≥65 years	-1.517	0.557	.007	-2.602	-0.424
Male	-2.213	1.044	.034	-4.260	-0.167
≥3 comorbidities	1.428	0.665	.032	0.124	2.731
Constant	-4.619	0.624	.624	-5.841	-3.396
Prior correction logistic regression
Age ≥65 years	-1.534	0.567	.007	-2.645	-0.421
Male	-1.757	1.078	.103	-3.870	0.357
≥3 comorbidities	1.307	0.651	.045	0.032	2.582
Constant	-4.360	0.608	.60834	-5.552	-3.168
Weighting logistic regression
Age ≥65 years	-1.533	0.567	.007	-2.645	-0.421
Male	-1.757	1.078	.103	-3.870	0.357
≥3 comorbidities	1.307	0.651	.045	0.032	2.582
Constant	-4.360	0.608		-5.552	-3.168
Reduced sample size
Age ≥65 years	-1.145	0.630	.069	-2.380	0.090
Male	-1.863	1.076	.083	-3.972	0.246
≥3 comorbidities	1.235	0.706	.080	-0.148	2.619
Constant	-1.945	0.666	.004	-3.250	-0.639

The correction rate for the prior correction technique assumes that the IVIg rate for BP is 0.00538918 (. This rate is obtained from an open-claims database that covers 330 million patients in the United States. When comparing unadjusted rates for IVIg treatment, our rates were lower (0.00515). There was agreement on the sign of the coefficients across regressions. Older age, male self-identification, and fewer comorbidities decreased the likelihood of BP being treated with IVIg. Coefficients from weighting and prior correction logistic regression were statistically similar, but both were statistically different from and standard logistic regression (P =.0001). The coefficients from the regression that used the reduced random sample of non-events were also different from standard logistic regression (P =.004) (Table 2).

We randomly selected 140 patients from 2,706 non-event patients, so the total regression sample was 154, with 10% of the sample in the IVIg cohort (i.e., the rare-event proportion increased from 0.5% to 10%). The reduced random sample increased the event proportion in the regression sample. We calculated event probabilities for each group of patients with respect to age, gender, and comorbidities (Table 3). As expected, standard logistic regression significantly underestimated the event probabilities. The underestimation ranged from 11% to 102% using the prior correction method and from 15% to 107% using the weighting correction method. For example, standard logistic regression predicted that male patients 18 to 64 years old with few comorbidities have a 0.1% probability of receiving IVIg treatment; however, the actual probability was double according to prior correction and weighting correction. Random selection of non-event samples significantly biased the results and found probabilities 10 times larger than corrected probabilities and 20 times larger than probabilities calculated by standard logistic regression.

Table 3.

Standard and corrected predicted probabilities for different sets of groups

Age (years)	Gender	Comorbidities	Actual probabilities	Standard logistic regression	Prior correction method		Weighting method		Random reduction of non-event sample
					Point estimate	Underestimation of probabilities	Point estimate	Underestimation of Probabilities	Point estimate	Deviation of probabilities
18–64	Male	High	0.00798	0.0044769	0.00831	-85.62%	0.0085	-89.86%	0.0755036	108.82%
≥65	Male	High	0.00163	0.0009856	0.00171	-73.50%	0.0017	-72.48%	0.0156083	102.12%
18–64	Female	High	0.04253	0.0395085	0.04662	-18.00%	0.04552	-15.22%	0.4761266	364.52%
≥65	Female	High	0.01125	0.0089435	0.00997	-11.48%	0.01031	-15.28%	0.1499854	230.68%
18–64	Male	Low	0.00222	0.0010776	0.00218	-102.30%	0.00223	-106.94%	0.0230371	102.25%
≥65	Male	Low	0.00039	0.0002366	0.00047	-98.65%	0.00048	-102.87%	0.0045571	100.46%
18–64	Female	Low	0.01128	0.0097704	0.01253	-28.24%	0.01216	-24.46%	0.2078657	173.60%
≥65	Female	Low	0.00299	0.00216	0.00275	-27.31%	0.0027	-25.00%	0.0484764	100.79%

Rare-event correction affected the constant term the most. Table 3 shows the constant term for each model with its lower and upper confidence intervals.

Discussion

The development of rare-event sampling techniques can be traced back to the early 1950s, primarily motivated by the need to solve complex problems in nuclear physics, particularly the neuron shielding problem that was crucial for designing nuclear facilities [19]. Later, researchers addressed the challenge of extremely rare events using Monte Carlo random sampling [20]. The importance of sampling methods, another key technique in rare-event simulation, also emerged during this period, setting the stage for the evolution of rare-event sampling techniques that continue to be refined and applied in various fields today [21]. For example, in physics, the search for dark matter involves detecting extremely rare particle interaction [22]. In earth sciences, methods were developed to analyze extremely rare natural disasters with occurrence rates of 1% or less [23]. In the telecommunication sector, researchers have focused on detecting and analyzing rare network anomalies [24]. In political science, case study approaches are used to analyze rare events like successful coups or the peaceful dissolution of countries [7, 25]. In economics, agent-based modeling used to simulate complex financial systems and identify conditions that may lead to rare market crashes [26]. In health care, researchers are used genomic sequencing techniques to identify genetic markers associated with rare disorders or Bayesian hierarchal models applied to analyze small sample sizes typical in rare diseases [27, 28]. Here, we applied a logistic regression technique for rare event rates among large sample sizes.

Due to the structured data entry system used by TRICARE, the data set used in this study had minimal missing data. Across all variables included in the analysis, less than 1% of data points were missing. This extremely low rate of missingness did not warrant the use of advanced imputation techniques or separate complete case analyses. The completeness of the TRICARE data contributes to the robustness of the findings and minimizes potential bias from missing information.

While the traditional rule of thumb for logistic regression suggests 10 to 20 events per variable are necessary, recent research has shown that this guideline can be relaxed under certain circumstances [29]. When dealing with rare events, total sample size becomes more critical than the number of events alone. The large sample size of 2,720 provides substantial information even with only 14 events. The empirical example provided here illustrates why specialized techniques for rare events logistic regression were developed. Several correction techniques were applied to a rare treatment for BP using a military health data set. As expected, the results yielded that standard logistic regression significantly underestimated the event probabilities. The underestimation in this study ranged from 11% to 102% using the prior correction method and from 15% to 106% using the weighting correction method. For example, in this study, standard logistics regression predicted that male patients 18 to 64 years old, with fewer comorbidities, have a 0.1% probability of receiving IVIg treatment; however, the actual probability was more than double according to prior correction and weighting correction. This discrepancy could give rise to a large margin of error and, ultimately, cost-ineffective decisions.

Furthermore, this study showed that the random selection of non-event samples significantly biased the results. The probabilities were found to be 10 times larger than the corrected probabilities and 20 times larger than the probabilities calculated by standard logistic regression. These results support King and Zeng’s findings, which indicated that a second, more important common problem in analyzing rare events lies in how data are collected [7]. The reduced sample size in this study demonstrated the most bias, supporting the idea that data collection can greatly influence results.

Other techniques such as meta-analysis have been suggested for rare event bias correction. However, meta-analyses of binary data can be problematic when the proportion of events is low [30, 31]. Meta-analyses of binary data are frequently performed using the standard inverse-variance fixed-effects model, based on large-sample normal approximation, or fixed-effects methods, based on exact distributional theory such as the Mantel–Haenszel (MH) or Peto model, or the standard random-effects DerSimonian-Laird (DL) model [31]. These methods, based mostly on large-sample normal approximation (particularly inverse-variance) [31–33], lack power to investigate the incidence of rare events. Therefore, their statistical properties for estimating treatment effects are often judged as suboptimal either through biased results, inappropriately wide confidence intervals, or insignificant statistical power to detect true differences.

The Cochrane guidelines (version 6.1, 2020) recommend the use of methods mostly accessible in Review Manager (RevMan), a free-access software developed by the Nordic Cochrane Centre [31, 33]. Its guideline suggests that, at event rates less than 1%, the Peto odds ratio should be utilized [31]. In circumstances where event rates are above 1% and meta-analyses involves many studies with imbalanced treatment groups, the MH odds ratio should be used [31, 34]. However, some of these methods, notably, the MH without continuity correction, logistic regression, and exact methods, are not available in RevMan. Second, meta-analysts must often revert from inverse-variance weighting to a random-effects DL model to reduce bias in estimation when heterogeneity is present.

Most recently, new methods, including maximum likelihood, profile likelihood, and restricted maximum likelihood or the nonparametric “permutations” methods, have been proposed for improved estimation of variance (τ) [31, 35, 36]. The nonparametric bootstrap of the DL estimator was shown to be a better performer in small meta-analyses that were falsely assumed to be homogenous under the standard DL model [31]. Although this nonparametric bootstrap of the DL model has now been extended for both the MH and Peto models, little is known about the performances of these methods in meta-analyses involving rare events when heterogeneity is an issue.

Limitations

This study utilizes data from the Department of Defense TRICARE system, which primarily serves military personnel, veterans, and their families. We acknowledge that this population may have unique characteristics that could affect the generalizability of the findings to the broader U.S. population [37]. TRICARE beneficiaries may have different healthcare access patterns, comorbidity profiles, and treatment preferences compared to civilians [38]. For instance, active-duty personnel might have better overall health due to physical fitness requirements, while veterans may have higher rates of certain conditions related to military service [39]. Additionally, TRICARE’s structured healthcare system and coverage policies may influence treatment choices and outcomes in ways that differ from other insurance plans [39].

This study also has several limitations related to the use of administrative data sets and retrospective analysis. Although retrospective studies are an important tool to study rare diseases, manifestations, and outcomes, their design is subject to limitations [40]. Since the analysis was done on the review of claims data that were not originally designed for research, some information is bound to be missing. Selection, recall, and loss of follow-up biases may affect how representative the data is for the rare event of interest.

Using an administrative database has many strengths as it includes a large population/base sample size, which provides an established denominator [41]. The data include patient demographics, clinical characteristics, detailed healthcare use, and cost information allowing for identification and comparison of treatments and outcomes across populations included in the data [41]. However, some limitations warrant mentioning. First, as with most claims-based data sources, there is a time lag between an individual’s receipt of services and when the files become available for research (average, 2–3 years) [41]. Thus, the data may not be generalizable to the entire population, as some information may be missed in processing or reimbursement. Also, not all health data are captured in the claims. Although diagnoses are included, information such as health-related behaviors, anthropomorphic data, and nonprescription medication use that may be found in medical records are not captured in the claims. Further, claims for which services were recommended but not yet received would not be captured in the data set. Additionally, administrative claims data lack information about the decision-making process (e.g., who made the decisions, how or why the decisions were made, the correlation between planned and received treatment, why treatment was altered or discontinued) and other patient-reported outcomes [41].

We recognize the potential for overfitting in our model given the limited number of rare-event cases (14 IVIg patients). To address this concern, we have included confidence around regression (see Table 2). Additionally, we acknowledge that the small sample size may limit the generalizability of our results. In future analyses, one can plan to explore regularization techniques such as ridge or LASSO regression to mitigate overfitting and improve model performance. These methods can help reduce model complexity and potentially enhance the robustness of our predictions, especially when dealing with high-dimensional data or limited sample sizes.

Conclusion

Rare events are low-frequency, high-severity problems that can have significant consequences including major stock market crashes, pandemics, wars, rare diseases, and small counts of recently approved medications. While rare diseases are individually unique, they collectively contribute to substantial health and social care needs. Additionally, rare diseases present a challenge for clinicians in reaching a conclusive diagnosis and determining an appropriate course of treatment due to their low prevalence, heterogenicity, and complexity [1, 5, 6]. Predicting and estimating rare-disease outcomes in a real-world setting can be challenging to researchers and can have significant public health implications. While caution is warranted when analyzing rare events, dismissing the potential for meaningful results based solely on the event counts overlooks the complexities of rare event analysis and the compensating factor of large sample size.

Therefore, improving statistical techniques to understand rare events is a tremendous analytical challenge that can have major impacts on health care. In technical terms, the maximum likelihood-based logit model can generate heavily biased parameter estimates and is prone to overfitting rare-event data even in low-dimensional models. Such issues have forced scientists to get creative and explore unconventional analytic methods. We have proposed the application of several correction techniques used in public economics to outcomes research studies dealing with rare-event estimation bias from standard logistic regression or inefficient data collection techniques.

Author contributions

O.B. provided the supervision, conceptualization, methodology, validation, and visualization of the research and participation in the writing process from the original draft preparation to the reviewing and editing of the manuscript. H.Y. participated in the supervision and participated in the writing process from the original draft to the reviewing and editing of the manuscript. G.S. participated in the project management, supervision, and investigation of the literature review and in the writing process from the original draft preparation to the reviewing and editing of the manuscript.

Funding

This research received no external funding.

Data availability

No datasets were generated or analysed during the current study.

Declarations

Ethics approval and consent to participate

Informed consent was not required as the data were from an anonymous, de-identified database.

Consent for publication

All authors have approved the manuscript and agree to its submission for publication.

Competing interests

The authors declare no competing interests.