Abstract
Accelerated degradation test is an effective way for the rapid reliability assessment of mechanical systems. Most of the existing optimization methods for accelerated degradation tests aim to optimize objective functions with a single objective, which leads to inappropriate optimization results. To solve the problem, a multi-objective optimization design method is presented for accelerated degradation tests based on game theory in this work. First, the multi-objective optimization model is established to optimize the prediction precision of lifetime distribution, the estimation precision of model parameters, and the robustness of model parameter deviation under the constraint that the total experimental cost does not exceed the predetermined budget. Based on game theory, the multi-objective optimization model is transformed into a cooperative game problem. The fuzzy clustering method is applied to calculate the strategy space owned by each player. Each player considers the benefits of other players in the construction of its benefit function to form a collusive cooperation model. Under the condition of maximizing the collective interest, the multi-objective optimization model is solved to obtain a compromised optimal test plan which balances the multiple optimization objectives. Finally, the necessity and effectiveness of the proposed method have illustrated a group of examples of motorized spindles.
Keywords: Accelerated degradation test, Fuzzy clustering, Game theory, Multi-objective optimization, Reliability
Subject terms: Mechanical engineering, Scientific data
Introduction
Reliability is an important attribute of the product1–4. For a product with high reliability and long life, only a few or even no failures occur during the traditional life test, it is difficult to evaluate its lifetime accurately within the allowable engineering time5,6,7. The researchers have discussed that some performance indicators of a product gradually degrade over time, and the increase in performance degradation gradually leads to operational degradation and eventually failure8–10. Under these circumstances, the accelerated degradation test (ADT) can be utilized in the rapid reliability assessment. In the ADT, the products are subjected to stress levels that are higher than the normal working stress levels to improve their degradation rates11. Based on the statistical analysis of degradation test data, an accelerated degradation model can be established to describe the degradation process and calculate the lifetime distribution under normal working stress levels12.
For implementing ADT, an effective test plan not only saves the test resources and consumption time but also obtains sufficient degradation information. This information lays the foundation of statistical analysis for obtaining correct lifetime distribution13. However, due to increasingly complex engineering test requirements, a single optimization objective no longer meets the actual requirements, and the optimization results of ADT under different optimization objectives are often different or even contradictory14. For instance, to maintain the best consistency of the degradation mechanism, the fitting accuracy and prediction accuracy must be reduced to a certain extent. Nevertheless, fitting accuracy and prediction accuracy are often contradictory15. In addition, due to the long computation time and high cost of ADT for highly reliable and long-lifetime products, it is urgent to obtain the optimal test plan that balances multiple optimization objectives under limited test time and cost. It is noteworthy that as compared to single-objective optimization, each optimization objective in the multi-objective optimization problem restricts or even conflicts with other objectives. Consequently, the optimal solution of a multi-objective optimization problem is usually not the global optimal solution. Instead, it is a compromised optimal solution that balances all optimization objectives16.
The traditional methods for solving multi-objective optimization problems transform multi-objective problems into single-objective problems. This is accomplished by weighing or ranking the objectives based on their importance17–19. However, please note that each objective represents different performance functions in the engineering paradigm. Consequently, it is difficult to determine a reasonable weight indicator or perform an accurate importance ranking leading to inaccurate optimization results. In addition, with the development of intelligent optimization algorithms, genetic algorithms20–23, particle swarm optimization algorithm24–27, and quantum-inspired evolutionary algorithm28–30, etc. have also been used to solve multi-objective optimization problems. Nevertheless, intelligent optimization algorithms are prone to local minima and it is difficult to get the global optimal solution. Moreover, in numerical optimization methods, several independent operations are usually required, and some heuristic information cannot be used effectively, which results in a large computation time and low optimization efficiency.
To address the aforementioned problems, this work proposes a multi-objective optimization design method for ADT based on game theory. The multi-objective optimization model is established for ADT in order to improve the prediction accuracy of the time to failure (TTF), the estimation precision of model parameters, and the robustness of model parameter deviation. Based on game theory, the multi-objective optimization model is transformed into a cooperative game problem. The strategy space of each player is obtained by using the fuzzy clustering method and the benefit function of the players is constructed based on the collusion cooperation model. By solving the multi-objective optimization model, the compromised optimal ADT plan that balances the multiple optimization objectives is obtained. Finally, the necessity and effectiveness of the proposed method are illustrated by a group of examples of motorized spindles.
The main contributions of this article are shown as follows.
(1) The multi-objective optimization model of ADT is established so that a compromised test plan can be obtained to balance the multiple optimization objectives, including improving the prediction precision of lifetime distribution, the estimation precision of model parameter, and the robustness of model parameter deviation under the constraint that the total experimental cost does not exceed the predetermined budget. Compared with the single-objective optimization model of ADT, the obtained optimum test plan is more in line with the actual engineering requirements.
(2) To solve the multi-objective optimization model, the multi-objective optimization model is transformed into a cooperative game problem. The fuzzy clustering method is applied to calculate the strategy space owned by each player. Each player considers the benefits of other players in the construction of its benefit function to form a collusive cooperation model. Through this transformation, the difficulty of solving the multi-objective optimization model is greatly reduced. Besides that, the collusion cooperation model is adopted to establish the benefit functions of game players, in which each game player should consider the benefits of other game players to form the collusion mechanism. Each player adopts a balance between cooperation and competition and introduces a weight coefficient to combine its absolute and relative benefits. By this method, the searching efficiency is significantly improved and meanwhile the globally optimal solution can be obtained.
This paper is organized as follows. Section "Related works" provides a literature review on existing research. Section "Assumption of accelerated degradation model" describes the basic assumptions of the accelerated degradation model. The multi-objective optimization model is established in Section "Multi-objective optimization model of ADT", including the multi-objective optimization function, decision variables, and test constraints. Section "Multi-objective optimization method based on game theory" introduces the multi-objective optimization method based on game theory. Section "Numerical example" demonstrates the feasibility and effectiveness of the proposed method by using a group of numerical examples. Finally, Section "Conclusions" concludes this work.
Related works
In the existing literature, optimization objectives adopted in optimization models of ADT are mainly divided into three categories. Designers choose the most necessary optimization objective based on actual needs.
The first category is for improving the estimation precision of the degradation model parameters, i.e. improving the fitting degree between the ADT data and the accelerated degradation model. Generally, the asymptotic variance–covariance matrix of the maximum likelihood estimator of model parameters, which is the inverse of the Fisher information matrix, is utilized as the optimality criterion. Based on this, the A-optimality criterion is established by minimizing the trace of the inverse of the variance–covariance matrix, and the D-optimality criterion is established by maximizing the determinant of the Fisher information matrix of the estimated model parameters. Duan et al.31 addressed the optimization problems in the constant-stress accelerated degradation test (CSADT) under the A-optimality criterion and proved that the optimal CSADT plans with multiple stress levels degenerate to two-stress-level test plans by only using the minimum and maximum stress levels. Zhao et al.32 proposed an optimization design method for step-stress accelerated degradation test (SSADT) based on the Bayesian method and optimized stress levels, and the allocation of inspections under the A-optimality criterion, as well as the D-optimality criterion. Based on the D-optimality criterion, Ge et al.33 proposed an optimization design method for SSADT. Based on this method, the number of test units, total test time, stress levels, and test time under each stress level are obtained as the optimal test plan. Si et al.34 adopted the D-optimality criterion for SSADT with the expenditure function and decision variable function as constraint conditions and obtained the optimal sample size and the optimal test time under each stress level. Fang et al.35 adopted two common planning criteria (D-optimality criterion and C-optimality criterion) to find the optimal set of test conditions and allocation of test units for a single-variable case, and then the initial solution was transformed into the test plan for the case of two stress variables.
The second category is for improving the prediction accuracy of the lifetime indicators, such as the mean time to failure and the p-th percentile of the lifetime distribution at normal working conditions. Tang et al.36 presented an SSADT to minimize the asymptotic variance of mean life at the use stress level. Park et al.37 developed the optimal accelerated degradation test plans in such a way that the asymptotic variance of the maximum likelihood estimator of the mean lifetime at the use condition is minimized. Lim et al.38 optimized the test stress levels and the proportion of sample size allocated to each stress level in CSADT to minimize the asymptotic variance of the maximum-likelihood estimator of the q-th quantile of the lifetime distribution. Li et al.39 proposed an optimization design method for SSADT based on the competing failure rule, minimized the asymptotic variance of the estimated hundred percentile of the competing reliability model with limited budgets, and presented the optimal sample size and inspection times at each stress level. Ye et al.40 considered the ADT planning for the inverse Gaussian (IG) process, and the objective of the planning is to minimize this variance by properly choosing the testing stresses and the number of samples allocated to each stress level. In the optimal design of hybrid ADT, Ma et al.41 were concerned with the estimation precision of the p-quantile of the product’s failure time under the normal using condition.
The third category is for keeping the consistency between the acceleration factors in ADT maintained to ensure that the failure mechanism of the products under accelerated stress levels is consistent with that under normal working conditions. Teng et al.42 derived the exact expression of the acceleration factor based on the Wiener degradation model. The authors adopted the asymptotic variance of the acceleration factor as the objective function. Wang et al.43 proposed the M-optimality criterion for CSADT based on the IG process model with covariates and random effects, and determined the combination of stress levels, the sample size allocated to each stress level, test time, and the stress region.
In addition, few other works have established other optimization criteria for ADT based on Bayesian theory. Zhang, Liu, Nasir et al. established optimization criteria based on the Kullback–Leibler divergence and Hellinger distance to solve the problem of inaccurate optimization results in case of a small number of samples44–46.
However, due to increasingly complex engineering test requirements, a single optimization objective no longer meets the actual requirements, and the optimization results of ADT under different optimization objectives are often different or even contradictory.
Assumption of accelerated degradation model
Nonlinear degradation process
The Wiener process is one of the most widely used stochastic processes for degradation models and has been widely studied, covering various areas such as confidence intervals and parameter estimation, Bayesian analysis, and residual life prediction. The Wiener process can have a better description of the dynamic characteristics of the system47. Assuming that the degradation process of the product performance {X(t), t ≥ 0} is a nonlinear degradation process based on the Wiener process model, it can be mathematically expressed as:
 |
1 |
where X(t) is the degraded performance of the product at time t, X(0) is the initial degraded performance, μ is the drift parameter describing the rate of performance degradation, Λ(t) represents a monotone time function with Λ(0) = 0, σ is the diffusion parameter describing the fluctuations in the degradation process over time, and B(t) ~ N(0, t) is the standard Brownian motion process.
The failure threshold ω of the product is described based on the product’s functional characteristics, working condition requirements, and the engineering experience of the testers. When the degraded performance of a product reaches the failure threshold ω for the first time, the product is considered to have a failure. Therefore, based on the continuity of the degradation process, the lifetime T of the product is defined as:
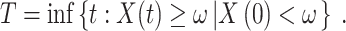 |
2 |
The probability density function (PDF) of T is expressed as follows:
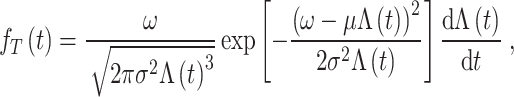 |
3 |
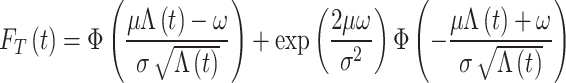 |
4 |
where Φ(∙) represents the standard normal distribution function.
Accelerated degradation model
When SSADT is performed, the performance degradation of a product is affected by H kinds of stresses. Each of these stresses comprises K stress levels. Let Shk denote the value of the K-th stress level of stress H, where h = 1, 2, …, H and k = 1, 2, …, K. In SSADT, all test samples experience the same stress loading process. The test profile is shown in Fig. 1, where tk denotes the time to complete the acceleration stress at step k and t0 = 0.
Fig. 1.

The SSADT profile with H acceleration stresses and K stress levels.
The first step is to conduct the test on the product till t1 under the combination of the stress levels S11, S21, …, SH1, and then conduct the test till t2 under the combination of increased stress levels S12, S22, …, SH2, and so on. When the stresses are increased to the combination of the stress levels S1K, S2K, …, SHK, the test is completed at tK. The combination of stress levels throughout the test is expressed as follows:
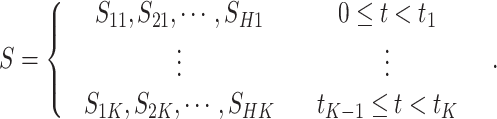 |
5 |
In order to facilitate the statistical analysis of the accelerated degradation model, the stress Shk is normalized to shk by using the following expression:
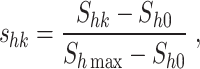 |
6 |
where Sh0 denotes the stress level of stress Sh in normal working conditions, and Shmax denotes the maximum stress level of stress Sh based on the consistency of the failure mechanism.
Let Mk denote the number of measurements under the stress level combination S1k, S2k, …, SHk. The total number of measurements during the whole test is  . Let Xi,j,k be the j-th measurement of the i-th test unit under S1k, S2k, …, SHk, where i = 1, 2, …, N, j = 1, 2, …, Mk, then:
. Let Xi,j,k be the j-th measurement of the i-th test unit under S1k, S2k, …, SHk, where i = 1, 2, …, N, j = 1, 2, …, Mk, then:
 |
7 |
In the accelerated degradation model, the drift parameter μ in the Wiener process characterizes the degradation rate, which is a function of stresses. Assuming that there is no interaction between H stresses, and sk = (s1k, s2k, …, sHk) represents the combination of acceleration stress levels at the k-th stage in SSADT, the acceleration model is expressed as follows:
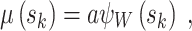 |
8 |
where 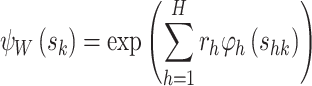 , a and rh are the parameters to be estimated, φh is the known function of acceleration stress shk. The exponential relationship is a commonly used and well-studied model. Along with its simplicity, the exponential link represents several life–stress relationships built from physical principles such as Arrhenius, inverse power law, Eyring, temperature-humidity, and temperature-non-thermal48.
, a and rh are the parameters to be estimated, φh is the known function of acceleration stress shk. The exponential relationship is a commonly used and well-studied model. Along with its simplicity, the exponential link represents several life–stress relationships built from physical principles such as Arrhenius, inverse power law, Eyring, temperature-humidity, and temperature-non-thermal48.
The PDF of an increase in degradation is expressed as follows:
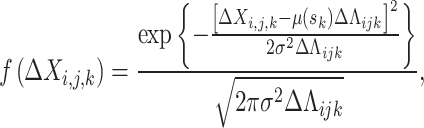 |
9 |
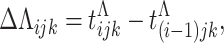 |
10 |
where Λ is the parameter to be estimated.
So, the function of SSADT data is expressed by the following mathematical expression:
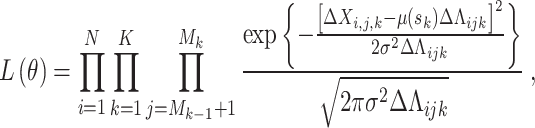 |
11 |
where θ = (a, r1, r2, …, rH, σ, Λ) is the parameter vector to be estimated in the accelerated degradation model.
Multi-objective optimization model of ADT
Optimization objectives
The selection of optimization criteria is crucial for the multi-objective optimization design of ADT. Firstly, the degradation data collected from ADT will be used to predict the lifetime of the same type of products. For example, some samples are selected randomly to carry out ADT, so as to evaluate the reliability level of the newly manufactured products from the same batch. So the prediction accuracy of the reliability indexes of products should be considered as one of the optimization objectives of ADT. Secondly, in the engineering paradigm, the researchers need to extrapolate the reliability of a system or a whole machine based on the reliability model of some key functional components or allocate the reliability based on the reliability model of each key functional component. For example, the established degradation model of the motorized spindle will be used to model the degradation path and formulate the reliability level of the CNC machine tool. So the estimation precision of the parameters of the accelerated degradation model for reducing the cumulative error in the subsequent models. In addition, ADT optimization design is the reverse process of the test data evaluation. When designing the test plan, it is necessary to refer to the product design information, and a small amount of pre-test and engineering experience. Thus there will be some deviations between these estimated values and the real values, and the inaccuracy of the estimated values of model parameters will inevitably affect the accuracy of the optimal design of the test. Therefore, in the fluctuation range of model parameters, reducing the deviation of test evaluation accuracy can fully improve the robustness of optimization results.
The three aforementioned aspects are considered the optimization objectives of ADT and a multi-objective optimization model of ADT is established.
(a) Objective I: minimize the asymptotic variance of the estimated mean time to failure (MTTF) under the normal working condition.
The asymptotic variance reflects the degree of deviation in the estimated TTF under normal conditions. The purpose of objective I is to improve the accuracy of lifetime precision under normal working conditions, i.e.,
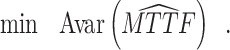 |
12 |
(b) Objective II: maximize the determinant of the Fisher information matrix of the estimated parameters.
The estimated model parameters are closely related to the determinant of Fisher information matrix. The confidence interval width of the estimated parameters is inversely proportional to the square root of the determinant of Fisher information matrix. The purpose of objective II is to improve the estimation precision of the accelerated degradation model parameters, i.e.,
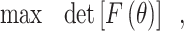 |
13 |
where F(θ) is the Fisher information matrix of the model parameter θ.
(c) Objective III: minimize the relative ratio of the asymptotic variances between, before, and after changing the parameters.
In order to study the sensitivity of the ADT plan toward the change in estimated parameters, the asymptotic variance of the estimated MTTF is calculated based on the prior parameters. Then, after slightly adjusting the prior parameters, the asymptotic variance of the estimated MTTF is calculated based on the adjusted parameters. The objective III ensures the sensitivity of the ADT plan towards the change in the model parameters, i.e.,
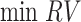 |
14 |
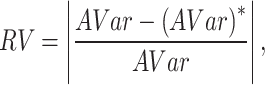 |
15 |
where AVar is the asymptotic variance of the estimated MTTF based on the prior parameters and (AVar)* is the asymptotic variance of the estimated MTTF based on the adjusted parameters.
Design variables
The sample size N, the number of stress types H, the number of stress levels K, the stress level Sk = (S1k, S2k, …, SHk), the measurement interval Δtk under each stress level, and the measurement times Mk allocated to each stress level, etc. are regarded as the design variables. Thus the design variables of ADT are {N, H, K, Sk, Δtk, Mk…}. In practical applications, the design variables are simplified to reduce the search dimension of optimization as well as the quantity of computations.
Constraints
The total experimental cost of ADT can be divided into four categories, namely the sample unit cost, the degradation measurement cost, the consumption cost, and the operation cost. Let Cit, Co, and CM denote the unit cost of a sample, the cost of human and public resources per unit of time under various stress levels, and the unit cost of measurement, respectively. Then, the total experimental cost is mathematically expressed as:
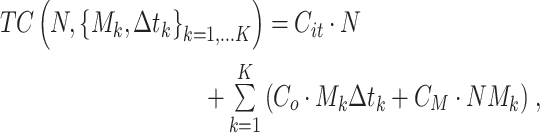 |
16 |
The constraint of ADT is expressed as follows:
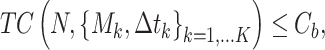 |
17 |
where Cb denotes the experimental budget.
At the same time, in order to ensure sufficient degradation data, the sample size of ADT should not be less than 5, and the measurement times allocated to each stress level should not be less than 2.
Optimization model
The multi-objective optimization model is expressed in (18). It is noted that the optimization result is not related to the sequence of these three objectives.
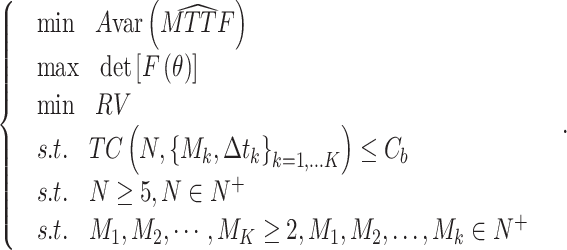 |
18 |
Multi-objective optimization method based on game theory
Game theory
Game theory is an alternative method for studying the behavioural interaction and mutual balance among multiple decision-making subjects for maximizing the utilities of players. The game theory has been widely applied in many fields, such as politics, military, diplomacy, public choice, criminology, and so on49.
The basic elements of the game theory include players, actions, information, strategies, and payoffs. The players tend to maximize their benefits by choosing the most appropriate actions or strategies. Action denotes the decision-making variable of the game subject. Information refers to players’ knowledge in the game process, such as other players’ characteristics and action knowledge. Strategy is the action rule under the given information. Payoff represents the utility level obtained by the game players based on performed actions. The game players tend to maximize the expected utility value by choosing their strategy.
Multi-objective optimization method based on game theory
The mathematical model of the multi-objective optimization design is expressed as follows.
Solve the design variable 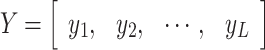 ,
,
so that the objective function  ,
,
s.t.  , l = 1, 2, …, L,
, l = 1, 2, …, L,
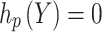 , p = 1, 2, …, P,
, p = 1, 2, …, P,
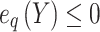 , q = 1, 2, …, Q,
, q = 1, 2, …, Q,
where m is the number of optimization objectives, al and bl are the upper and lower limits of design variable yl, respectively, L is the number of design variables, P is the number of equality constraints, and Q is the number of inequality constraints. If it is to maximize the objective function, zi (Y) (i = 1, 2, …, m) should be converted to
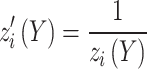 |
19 |
where 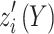 participates in the multi-objective optimization process as a new optimization objective.
participates in the multi-objective optimization process as a new optimization objective.
According to game theory, m optimization objectives are regarded as m game players. The set of design variables 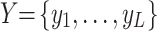 is decomposed into the strategy space D1, D2, …, Dm owned by each player, where
is decomposed into the strategy space D1, D2, …, Dm owned by each player, where 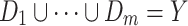 ,
, 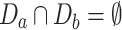 , (a, b = 1, 2, …, m, a ≠ b), and the constraints in the multi-objective optimization problem are regarded as the constraints on the optional strategies in the game. The solution of the multi-objective optimization problem is finally transformed into the solution of the game problem
, (a, b = 1, 2, …, m, a ≠ b), and the constraints in the multi-objective optimization problem are regarded as the constraints on the optional strategies in the game. The solution of the multi-objective optimization problem is finally transformed into the solution of the game problem 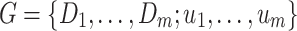 , where um denotes the benefits of the i-th player.
, where um denotes the benefits of the i-th player.
The Nash equilibrium50 is defined as a strategy combination 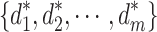 comprising a strategy of each player, if the strategy
comprising a strategy of each player, if the strategy  of any player i is the best strategy for the strategic combination
of any player i is the best strategy for the strategic combination 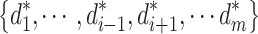 of the other game parties, i.e.,
of the other game parties, i.e.,
 |
20 |
where 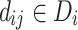 denotes the j-th strategy of the i-th player. If it is true for any
denotes the j-th strategy of the i-th player. If it is true for any 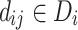 ,
, 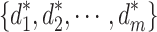 is called a Nash equilibrium of the game.
is called a Nash equilibrium of the game.
Strategy spaces of game players
The key technology for transforming a multi-objective optimization problem into a game problem is to reasonably decompose the design variables Y into the strategy space D1, D2, …, Dm owned by each game player. The decomposition of the strategy set requires the construction of an impact factor set to form the classification samples. Compared with the traditional cluster analysis method that classifies objects based on certain characteristic indicators, the fuzzy clustering method fully considers the multi-attribute intermediate state of each sample and the uncertainty of each category, which is more suitable for the clustering of design variables in this paper. Therefore, the fuzzy clustering method51 is used to classify the samples for obtaining the strategy set of each game player. The specific steps of decomposition are as follows:
Step 1: Calculate a single objective optimal solution for each objective among m objectives  , where
, where 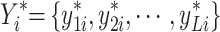 ;
;
Step 2: Define the impact factor of the l-th design variable yl on the i-th game player as
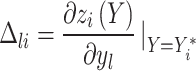 |
21 |
If the impact factor cannot be obtained directly by calculating the partial derivative of the objective function, the numerical calculation is applied.
Step 3: Construct the fuzzy similarity matrix. Let  represent the set of impact factors of l-th design variable for all m optimization objectives, and
represent the set of impact factors of l-th design variable for all m optimization objectives, and 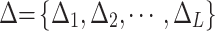 represent the set of impact factors of the design variable Y on all optimization objectives. Before fuzzy clustering, it is necessary to establish the fuzzy similarity relationship of the impact factor set Δ, i.e., the fuzzy similarity matrix
represent the set of impact factors of the design variable Y on all optimization objectives. Before fuzzy clustering, it is necessary to establish the fuzzy similarity relationship of the impact factor set Δ, i.e., the fuzzy similarity matrix 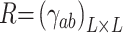 , where γab is the similarity between Δa and Δb (a, b = 1, 2, …, L),
, where γab is the similarity between Δa and Δb (a, b = 1, 2, …, L), 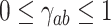 , the mathematical expression of γab is
, the mathematical expression of γab is
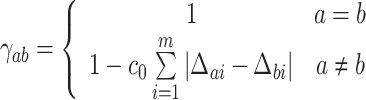 |
22 |
where c0 is a constant, which is properly selected to make 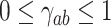 .
.
Step 4: Construct the fuzzy equivalence matrix 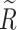 . Please note that the fuzzy similarity matrix does not satisfy transitivity, so it cannot be clustered directly. As a result, a square method is applied to construct the fuzzy equivalent matrix of R. Calculate
. Please note that the fuzzy similarity matrix does not satisfy transitivity, so it cannot be clustered directly. As a result, a square method is applied to construct the fuzzy equivalent matrix of R. Calculate  successively until
successively until 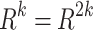 appears for the first time, where k = 1, 2, …, then
appears for the first time, where k = 1, 2, …, then  is obtained.
is obtained.
Step 5: Perform fuzzy cluster analysis. Let ξ denote the confidence level and  , and select an appropriate value of ξ and intercept according to the following rules. In the optimization process, ξ needs to be constantly adjusted to make the clustering results meet the number of optimization objectives. In matrix
, and select an appropriate value of ξ and intercept according to the following rules. In the optimization process, ξ needs to be constantly adjusted to make the clustering results meet the number of optimization objectives. In matrix 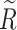 , the element greater than or equal to ξ becomes 1, and the element less than ξ becomes 0. As a result,
, the element greater than or equal to ξ becomes 1, and the element less than ξ becomes 0. As a result, 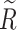 only consists of 0 and 1. Then observe the elements of each row in the matrix, put the rows with equal elements into the same category, and then get the classification results of the impact factor set Δ, i.e., the classification result of the design variable set Y.
only consists of 0 and 1. Then observe the elements of each row in the matrix, put the rows with equal elements into the same category, and then get the classification results of the impact factor set Δ, i.e., the classification result of the design variable set Y.
The clustering results show that Y is decomposed into m strategy sets, i.e., the strategy space D1, D2, …, Dm. The sum of the impact factors of the design variables contained in Di on all the optimization objectives is calculated. Based on the sum of impact factors, Di is allocated to the corresponding game player.
Establishment of benefit functions of game players
In a cooperative game, each player pursues the maximization of collective interests. The final optimization result is not necessarily the optimal result for each player, but it is a relatively better result under the condition of ensuring the maximization of collective interests. The collusion cooperation model is adopted to establish the benefit functions of game players. This model advocates that each game player should consider the benefits of other game players to form the collusion mechanism. Each player adopts a balance between cooperation and competition and introduces a weight coefficient to combine its absolute and relative benefits. The benefit function ui of game player i is expressed as follows:
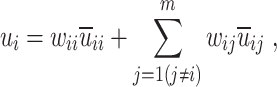 |
23 |
where 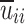 denotes the absolute utility of the i-th game player to itself when taking a certain action. Please note that it is a dimensionless value after the normalization of the objective function zi.
denotes the absolute utility of the i-th game player to itself when taking a certain action. Please note that it is a dimensionless value after the normalization of the objective function zi. 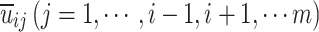 denotes the utilities of other game players when game player i takes a certain action. It is a dimensionless value after the normalization of the objective function zj. wij denotes the weight coefficient, whose value reflects the direct cooperation and competition degree of each game player. The larger value of wij represents low cooperation and high competition. When wij = 1, only competition exists, and the cooperative game model degenerates to the non-cooperative game model, where
denotes the utilities of other game players when game player i takes a certain action. It is a dimensionless value after the normalization of the objective function zj. wij denotes the weight coefficient, whose value reflects the direct cooperation and competition degree of each game player. The larger value of wij represents low cooperation and high competition. When wij = 1, only competition exists, and the cooperative game model degenerates to the non-cooperative game model, where 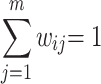 and
and 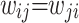 .
.
Solving algorithm of multi-objective optimization model based on game theory
The major steps of the multi-objective optimization model of ADT based on game theory are as follows:
Step 1: Calculate the impact factors of all design variables on the utilities of game players and the strategy space D1, D2, …, Dm owned by each game player through fuzzy clustering.
Algorithm 1.

Algorithm Step 1.
Step 2: Randomly generate the initial feasible strategies in the strategy space of each game player to form the strategy combination 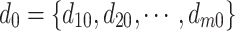 .
.
Algorithm 2.

Algorithm step 2.
Step 3: Let  be the corresponding complement of
be the corresponding complement of 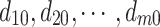 in the strategy combination d0. For the i-th game player, its utility ui is considered as the optimization objective,
in the strategy combination d0. For the i-th game player, its utility ui is considered as the optimization objective,  is fixed, and the corresponding single-objective optimization design is carried out in the strategy space Di owned by the game player. Then, search for the optimal strategy
is fixed, and the corresponding single-objective optimization design is carried out in the strategy space Di owned by the game player. Then, search for the optimal strategy  that implements
that implements
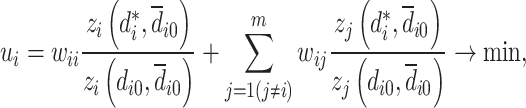 |
24 |
under the following constraints:
 |
25 |
Algorithm 3.

Algorithm step 3.
Step 4: Let the strategy combination 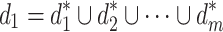 , and test the feasibility of d1. If the constraints are not satisfied, go to Step 2. If the constraints are satisfied, analyse whether the distance between the two strategies satisfies the convergence criterion, i.e.,
, and test the feasibility of d1. If the constraints are not satisfied, go to Step 2. If the constraints are satisfied, analyse whether the distance between the two strategies satisfies the convergence criterion, i.e., 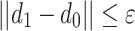 . If the criterion is satisfied, the game is ended, otherwise, replace d0 with d1 and go to Step 3 to continue the cyclic operation.
. If the criterion is satisfied, the game is ended, otherwise, replace d0 with d1 and go to Step 3 to continue the cyclic operation.
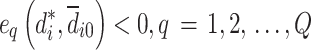 |
26 |
Algorithm 4.

Algorithm step 4.
Numerical example
To verify the feasibility and effectiveness of multi-objective optimization method for ADT based on game theory proposed in this work. This section presents a specific example to optimize the SSADT plan of a motorized spindle by using the proposed method. The rotating speed and the cutting force of the spindle are regarded as the acceleration stresses.
Let 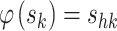 , the acceleration model is mathematically expressed as:
, the acceleration model is mathematically expressed as:
 |
27 |
Based on the stress levels presented in Table 1, the multi-objective optimization model of accelerated degradation test is established, and the multi-objective optimization design for SSADT is performed based on game theory.
Table 1.
Stress levels of SSADT for the motorized spindle.
| Number of stress levels | Stress levels | |
|---|---|---|
| Rotating speed (rpm) | Radial cutting force (N) | |
| 3 | (4000, 6311, 10,000) | (40, 152, 580) |
| 4 | (4000, 5431, 7405, 10,000) | (40, 98, 238, 580) |
| 5 | (4000, 5014, 6310, 7942, 10,000) | (40, 78, 152, 297, 580) |
In order to explore the degradation failure mechanism of the motorized spindle and the maximum accelerated stress level to keep the degradation failure mechanism unchanged, the baseline test of the motorized spindle has been carried out in the early stage. Based on the statistical analysis of the preliminary baseline test data, the values of prior parameters of the accelerated degradation model are obtained, which are presented in Table 2.
Table 2.
Value of prior parameters.
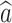 |
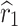 |
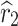 |
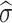 |
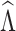 |
|---|---|---|---|---|
| 0.0083 | 1.5322 | 2.3997 | 0.0687 | 0.732 |
Mathematical optimization model
Objective functions
Based on the property of the Wiener process, the PDF of the T0 is obtained by substituting the prior parameters 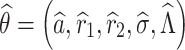 into (3), i.e.,
into (3), i.e.,
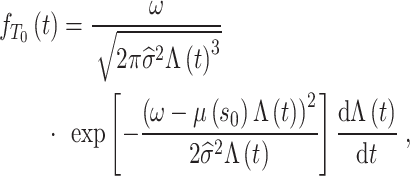 |
28 |
where 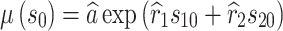 is the acceleration model under normal working conditions.
is the acceleration model under normal working conditions.
The MTTF of test sample under normal working stresses is given as:
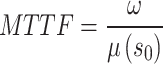 |
29 |
and the asymptotic variance of the MTTF is expressed as follows:
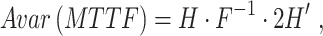 |
30 |
where 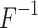 is the inverse of the Fisher information matrix F, which is expressed in the Appendix, H′ is the transpose of H, and is expressed as:
is the inverse of the Fisher information matrix F, which is expressed in the Appendix, H′ is the transpose of H, and is expressed as:
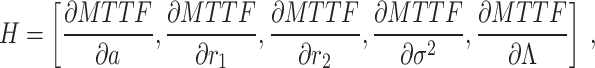 |
31 |
where 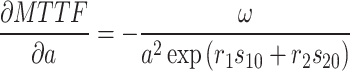 ,
, 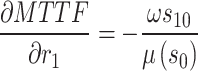 ,
, 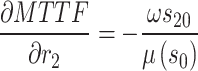 ,
, 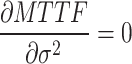 ,
, 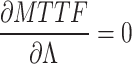 .
.
The function of objective I is expressed as:
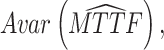 |
32 |
And the function of objective II is expressed as:
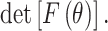 |
33 |
The prior parameter estimates are 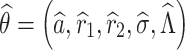 , and the corresponding deviations in the prior estimates are ε1, ε2, ε3, ε4, and ε5, respectively. As a result, the model parameters after fluctuation are
, and the corresponding deviations in the prior estimates are ε1, ε2, ε3, ε4, and ε5, respectively. As a result, the model parameters after fluctuation are 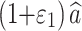 ,
, 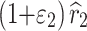 ,
, 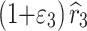 ,
,  and
and 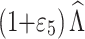 . When the deviations ε1, ε2, ε3, ε4, and ε5 are too large, it will lead to an inappreciable result that is not the optimum plan of ADT. In this paper, the optimization process is carried out under the assumption that the deviations in the prior estimates of parameters do not exceed 10%. Therefore, let ε1 = ε2 = ε3 = ε4 = ε5 = 10%, then, the function of objective III is expressed as (15).
. When the deviations ε1, ε2, ε3, ε4, and ε5 are too large, it will lead to an inappreciable result that is not the optimum plan of ADT. In this paper, the optimization process is carried out under the assumption that the deviations in the prior estimates of parameters do not exceed 10%. Therefore, let ε1 = ε2 = ε3 = ε4 = ε5 = 10%, then, the function of objective III is expressed as (15).
Design variables
Considering the engineering applications, the design variables include the test sample N, the measurement interval Δtk under each stress level, and the number of measurements Mk for each stress level, i.e., {N, Δtk, Mk}.
Constrains
The detailed cost of the motorized spindle for SSADT includes the unit cost of sample Cit = 25(thousand yuan), the cost of human and public resources per unit of time Co = 0.03 (thousand yuan), and the unit cost of measurement is CM = 0.2 (thousand yuan).
Optimization results
Based on the fuzzy clustering method proposed in Strategy spaces of game players, the strategy spaces of the game players for ADT with three stress levels are determined as D1 = {N, M1, M2, M3}, D2 = {Δt1, Δt3}, and D3 = {Δt2}, the strategy spaces for ADT with four stress levels are determined as D1 = {N, M1, M2, M3, M4}, D2 = {Δt1, Δt3}, and D3 = {Δt2, Δt4}, and the strategy spaces for ADT with five stress levels are determined as D1 = {N, M1, M2, M3, M4}, D2 = {Δt1, Δt3, Δt5, M5}, and D3 = {Δt2, Δt4}. Considering the equal degree of competition and cooperation among the three optimization objectives, the weight coefficients are determined as w11 = w22 = w33 = 0.5, w12 = w21 = w13 = w31 = w23 = w32 = 0.25. Finally, the optimal SSADT plans under three different test budgets are obtained.
When Cb = 200, the game process of solving the multi-objective optimization model with 3, 4 and 5 stress levels are shown in Fig. 2, and the optimization process has gone through 12, 18, and 18 rounds of games, respectively. The optimal test plan under the constraint Cb = 200 is shown in Table 3. When Cb = 250, the game process of solving the multi-objective optimization model is shown in Fig. 3, and the optimization process has gone through 11, 17, and 17 rounds of games, respectively. The optimal test plan under the constraint Cb = 250 is shown in Table 4. When Cb = 300, the game process of solving the multi-objective optimization model is shown in Fig. 4, and the optimization process has gone through 8, 17, and 20 rounds of games, respectively. The optimal test plan under the constraint Cb = 300 is shown in Table 5.
Fig. 2.
Game process of multi-objective optimization (Cb = 200).
Table 3.
Optimal SSADT test plans of the motorized spindle (Cb = 200).
| Number of stress levels | N | Δt1, Δt2, …, ΔtK | M1, M2, …, MK |  |
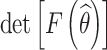 |
RV | CT |
|---|---|---|---|---|---|---|---|
| 3 | 5 | (22, 21, 17) | (23, 22, 19) | 1.89 × 1015 | 5.85 × 108 | 0.17 | 192.8 |
| 4 | 5 | (20, 17, 11, 9) | (21, 19, 19, 10) | 2.41 × 1015 | 1.96 × 108 | 0.19 | 197.1 |
| 5 | 5 | (19, 18, 12, 11, 9) | (17, 13, 12, 7, 7) | 2.18 × 1016 | 2.04 × 107 | 0.20 | 183.5 |
Fig. 3.
Game process of multi-objective optimization (Cb = 250).
Table 4.
Optimal SSADT test plans of the motorized spindle (Cb = 250).
| Number of stress levels | N | Δt1, Δt2, …, ΔtK | M1, M2, …, MK | 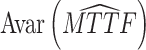 |
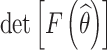 |
RV | CT |
|---|---|---|---|---|---|---|---|
| 3 | 6 | (14, 12, 10) | (14, 13, 9) | 2.20 × 1015 | 7.75 × 108 | 0.17 | 226.7 |
| 4 | 7 | (17, 15, 12, 11) | (15, 13, 10, 10) | 7.00 × 1015 | 3.64 × 108 | 0.21 | 244.2 |
| 5 | 6 | (17, 15, 14, 10, 7) | (16, 15, 12, 9, 7) | 1.17 × 1016 | 1.38 × 108 | 0.25 | 223.2 |
Fig. 4.
Game process of multi-objective optimization (Cb = 300).
Table 5.
Optimal SSADT test plans of the motorized spindle (Cb = 300).
| Number of stress levels | N | Δt1, Δt2, …, ΔtK | M1, M2, …, MK | 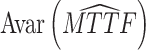 |
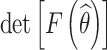 |
RV | CT |
|---|---|---|---|---|---|---|---|
| 3 | 7 | (27, 23, 19) | (29, 23, 17) | 1.98 × 1014 | 3.39 × 109 | 0.18 | 276.5 |
| 4 | 7 | (22, 19, 17, 14) | (22, 20, 15, 10) | 3.26 × 1014 | 7.36 × 108 | 0.24 | 272.6 |
| 5 | 6 | (20, 18, 17, 13, 12) | (21, 20, 18, 17, 11) | 1.17 × 1016 | 1.51 × 108 | 0.29 | 258.7 |
Comparing the optimization results in Tables 3, 4, 5 it can be seen that the measurement interval under the high stress level is smaller than that under the low stress level, and the number of measurements is also less. It is due to the fact that the high stress level increases the degradation rate, and in order to ensure the accuracy of the test results, it is necessary to increase the sampling frequency.
From the results of the optimal plans under different stress levels with the same test budget constraint, it can be seen that with the increase of the number of stress levels, there is no significant change in the sample size, and the number of measurements under the low stress level is significantly higher than that under the high stress level, indicating that the test resources are more allocated to low stress levels. This is due to the fact that the cost of test samples is much higher than the cost of test measurements, and the sample size does not have the ability to be increased with a certain test budget, then by increasing the number of measurements under the low stress level and reducing the measurement interval under the high stress level, it is possible to improve the testing efficiency and guarantee the accuracy of the evaluation results. In addition, under the same test budget constraint, the test plan with fewer number of stress levels has better evaluation results. Whereas increasing the number of stress levels leads to an increase in the asymptotic variance of estimated MTTF, a decrease in the determinant of the Fisher information matrix of unknown parameters, and an increase in the relative ratio of the asymptotic variances before and after the parameter fluctuation, which indicates that the prediction accuracy of the test results, the estimation accuracy of the model parameters and the stability of the test results have decreased.
From the results of the optimal plan under the same stress level with different test budget constraints, it can be seen that the allowable sample size of the test increases as the test budget increases, resulting in a significant improvement in the accuracy of the evaluation results of the optimized plan. Furthermore, with an increase in the test budget, the test resources become more abundant, thus significantly increasing the sample size and the measurement times. This consequently decreases the asymptotic variance of estimated MTTF, increases the determinant of the Fisher information matrix of unknown parameters, and decreases the relative ratio of the asymptotic variances before and after the parameter fluctuation. It indicates that the prediction accuracy of the lifetime distribution, the estimation precision of the model parameters, and the stability of the optimization results are improved significantly.
Test simulation and robustness analysis
In order to investigate which design variable has the greater influence on the optimization results, the Monte Carlo simulation method is applied to study the robustness of the optimal plans.
To ensure the estimation accuracy of the objective function, the sampling number should be large enough. Let NMC = 1000. The specific method for simulation and evaluation of the test plan is as follows:
Step 1: The parameters of the accelerated degradation model are set in Table 2.
Step 2: According to the optimization plan to be simulated, based on the property that the degradation increment satisfies ΔXi, j, k ~ N(μ(sk)Δtj, σ2Δtj), random numbers that satisfy one of the candidate models mentioned above are generated to obtain a set of simulated experimental data for accelerating degradation trajectory. The maximum likelihood estimation theory is used to statistically analyze the simulated degradation data of this set, and the maximum likelihood estimation values of the degradation model parameters are obtained.
Step 3: Using the maximum likelihood estimation values of the degradation model parameters obtained in Step 2, the asymptotic variance of the estimated MTTF under normal working stress, the determinant of the Fisher information matrix of the model parameters, and the relative ratio of the asymptotic variances before and after the parameter fluctuation are obtained.
Step 4: By repeating Steps 2–3 NMC times, the asymptotic variance of the estimated MTTF under normal working stress, the determinant of the Fisher information matrix of the model parameters, and the relative ratio of the asymptotic variances before and after the parameter fluctuation for NMC motorized spindles are obtained separately.
Step 5: By repeating Steps 1–5, the mean values of the evaluation indicators under each optimization plan are calculated and the sensitivity of the experimental plan is evaluated.
For example, under the constraint that Cb = 300, the degradation data are simulated for different test plans and the three objective function values are calculated, which are shown in Table 6. Comparing with these altered test plans, the influence of design variables on different optimization objectives is shown in Fig. 5. It can be seen that the increase of the sample size will significantly improve the determinant of Fisher information matrix of the estimated parameters, that is, increase the test sample size in ADT helps to improve the estimation precision of the model parameters. The measurement times and the measurement interval significantly influence the asymptotic variance of the estimated product’s MTTF. The increase of the measurement times under lower stress levels (M1 < M2 < … < MK), or the increase of the measurement interval under lower stress levels (Δt1 > Δt2 > … > ΔtK), helps improve the prediction accuracy of lifetime. Besides that, more stress levels lead to a higher relative rate of the asymptotic variances before and after the parameter fluctuation, which is caused by an increase in the number of model parameters.
Table 6.
Robustness analysis results.
| N | Δt1, Δt2, …, ΔtK | M1, M2, …, MK | 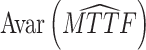 |
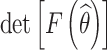 |
RV | |
|---|---|---|---|---|---|---|
| Optimum plan | 7 | (27, 23, 19) | (29, 23, 17) | 1.98 × 1014 | 3.39 × 109 | 0.18 |
| Simulation plan | 6 | (27, 23, 19) | (29, 23, 17) | 2.01 × 1014 | 2.83 × 109 | 0.18 |
| 8 | (27, 23, 19) | (29, 23, 17) | 2.37 × 1014 | 5.76 × 109 | 0.18 | |
| 7 | (27, 23, 19) | (23, 23, 23) | 2.28 × 1014 | 3.58 × 109 | 0.18 | |
| 7 | (27, 23, 19) | (17, 23, 29) | 1.15 × 1014 | 2.97 × 109 | 0.19 | |
| 7 | (27, 23, 19) | (35, 23, 11) | 4.14 × 1014 | 6.01 × 109 | 0.18 | |
| 7 | (23, 23, 23) | (29, 23, 17) | 2.51 × 1014 | 3.87 × 109 | 0.18 | |
| 7 | (19, 23, 27) | (29, 23, 17) | 4.83 × 1014 | 3.23 × 109 | 0.19 | |
| 7 | (31, 23, 14) | (29, 23, 17) | 1.58 × 1014 | 3.57 × 109 | 0.18 | |
| Optimum plan | 7 | (22, 19, 17, 14) | (22, 20, 15, 10) | 3.26 × 1014 | 7.36 × 108 | 0.24 |
| Simulation plan | 6 | (22, 19, 17, 14) | (22, 20, 15, 10) | 3.06 × 1014 | 5.25 × 108 | 0.24 |
| 8 | (22, 19, 17, 14) | (22, 20, 15, 10) | 1.83 × 1014 | 1.73 × 109 | 0.23 | |
| 7 | (22, 19, 17, 14) | (17, 17, 17, 17) | 4.36 × 1014 | 8.01 × 108 | 0.24 | |
| 7 | (22, 19, 17, 14) | (10, 15, 20, 22) | 2.87 × 1014 | 5.12 × 108 | 0.24 | |
| 7 | (22, 19, 17, 14) | (27, 25, 10, 5) | 4.01 × 1014 | 8.77 × 108 | 0.25 | |
| 7 | (18, 18, 18, 18) | (22, 20, 15, 10) | 3.02 × 1014 | 5.52 × 108 | 0.24 | |
| 7 | (14, 17, 19, 22) | (22, 20, 15, 10) | 3.87 × 1014 | 6.07 × 108 | 0.24 | |
| 7 | (26, 23, 13, 10) | (22, 20, 15, 10) | 2.05 × 1014 | 6.98 × 108 | 0.24 | |
| Optimum plan | 6 | (20, 18, 17, 13, 12) | (21, 20, 18, 17, 11) | 1.17 × 1016 | 1.51 × 108 | 0.29 |
| Simulation plan | 5 | (20, 18, 17, 13, 12) | (21, 20, 18, 17, 11) | 9.88 × 1015 | 5.53 × 108 | 0.28 |
| 7 | (20, 18, 17, 13, 12) | (21, 20, 18, 17, 11) | 3.12 × 1016 | 5.74 × 108 | 0.29 | |
| 6 | (20, 18, 17, 13, 12) | (18, 18, 18, 18, 18) | 2.72 × 1016 | 2.50 × 108 | 0.29 | |
| 6 | (20, 18, 17, 13, 12) | (11, 17, 18, 20, 21) | 6.85 × 1015 | 1.14 × 108 | 0.29 | |
| 6 | (20, 18, 17, 13, 12) | (24, 23, 18, 14, 7) | 2.83 × 1016 | 3.29 × 108 | 0.29 | |
| 6 | (17, 17, 17, 17, 17) | (21, 20, 18, 17, 11) | 2.77 × 1016 | 2.02 × 108 | 0.27 | |
| 6 | (12, 13, 17, 18, 20) | (21, 20, 18, 17, 11) | 1.73 × 1016 | 3.75 × 108 | 0.29 | |
| 6 | (25, 23, 17, 13, 7) | (21, 20, 18, 17, 11) | 1.10 × 1016 | 2.65 × 108 | 0.29 |
Fig. 5.
Influence of design variables on optimization objectives.
Comparison analysis of single optimization objective
In order to verify the necessity and effectiveness of the proposed multi-objective optimization method and test the accuracy of the above multi-objective optimization results, this section presents the single-objective optimization of SSADT. The optimization objective is to minimize the asymptotic variance of estimated MTTF, maximize the determinant of the Fisher information matrix of the model parameters, and minimize the relative ratio of the asymptotic variances before and after parameter fluctuation respectively. The optimization results are shown in Tables 7, 8 and 9.
Table 7.
Optimal SSADT test plans with single optimization objective (Cb = 200).
| Number of stress levels | N | Δt1, Δt2, …, ΔtK | M1, M2, …, MK | Objective function | Function value | CT |
|---|---|---|---|---|---|---|
| 3 | 5 | (15, 13, 10) | (21, 17, 16) |  |
1.02 × 1015 | 199.9 |
| 6 | (15, 11, 10) | (12, 10, 10) |  |
1.22 × 109 | 198.6 | |
| 5 | (14, 13, 9) | (18, 18, 16) | RV | 0.16 | 195.9 | |
| 4 | 5 | (15, 12, 9, 9) | (17, 16, 11, 10) | 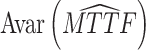 |
1.34 × 1015 | 198.1 |
| 6 | (10, 9, 9, 7) | (10, 10, 7, 7) | 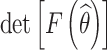 |
3.23 × 109 | 199.9 | |
| 5 | (17, 16, 10, 10) | (12, 12, 11, 10) | RV | 0.20 | 188.2 | |
| 5 | 5 | (7, 7, 6, 5, 5) | (16, 13, 13, 11, 10) |  |
1.18 × 1016 | 199.6 |
| 6 | (10, 8, 7, 6, 6) | (8, 7, 8, 6, 6) | 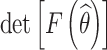 |
5.17 × 108 | 199.9 | |
| 5 | (18, 17, 10, 6, 5) | (13, 10, 11, 9, 8) | RV | 0.23 | 194.2 |
Table 8.
Optimal SSADT test plans with single optimization objective (Cb = 250).
| Number of stress levels | N | Δt1, Δt2, …, ΔtK | M1, M2, …, MK | Objective function | Function value | CT |
|---|---|---|---|---|---|---|
| 3 | 7 | (12, 9, 9) | (16, 14, 10) | 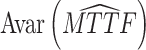 |
7.35 × 1014 | 243.2 |
| 8 | (10, 9, 7) | (10, 8, 8) |  |
1.08 × 1010 | 248.4 | |
| 7 | (16, 10, 6) | (15, 10, 9) | RV | 0.15 | 234.4 | |
| 4 | 6 | (15, 13, 10, 10) | (18, 18, 14, 12) | 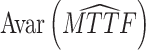 |
9.44 × 1014 | 247.3 |
| 7 | (13, 12, 12, 11) | (13, 13, 9, 7) | 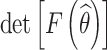 |
2.91 × 1010 | 249.1 | |
| 7 | (15, 13, 8, 8) | (12, 11, 9, 10) | RV | 0.20 | 248.1 | |
| 5 | 6 | (10, 9, 10, 8, 7) | (18, 14, 14, 12, 10) | 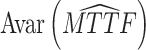 |
8.63 × 1015 | 250.0 |
| 7 | (11, 12, 10, 10, 9) | (10, 11, 9, 7, 6) | 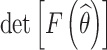 |
5.66 × 109 | 248.9 | |
| 7 | (10, 12, 9, 9, 7) | (10, 10, 9, 7, 7) | RV | 0.21 | 247.6 |
Table 9.
Optimal SSADT test plans with single optimization objective (Cb = 300).
| Number of stress levels | N | Δt1, Δt2, …, ΔtK | M1, M2, …, MK | Objective function | Function value | CT |
|---|---|---|---|---|---|---|
| 3 | 7 | (18, 17, 11) | (20, 18, 15) | 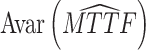 |
1.05 × 1014 | 274.1 |
| 8 | (22, 22, 17) | (18, 13, 10) | 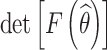 |
3.51 × 1010 | 291.2 | |
| 7 | (22, 15, 11) | (20, 17, 15) | RV | 0.15 | 273.6 | |
| 4 | 7 | (16, 13, 11, 10) | (22, 20, 15, 12) | 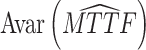 |
2.83 × 1014 | 298.5 |
| 7 | (22, 19, 16, 14) | (20, 18, 14, 10) | 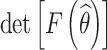 |
2.92 × 1010 | 296.2 | |
| 7 | (21, 20, 18, 11) | (19, 18, 16, 11) | RV | 0.18 | 299.6 | |
| 5 | 6 | (15, 16, 14, 10, 7) | (25, 22, 18, 16, 14) | 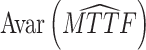 |
6.78 × 1015 | 299.5 |
| 7 | (22, 18, 17, 15, 12) | (14, 15, 10, 11, 9) |  |
1.09 × 1010 | 288.2 | |
| 6 | (20, 20, 15, 11, 11) | (19, 17, 18, 17, 12) | RV | 0.10 | 288.9 |
The aforementioned analysis shows that under the same test budget, the optimal test plans under different optimization objectives are significantly different. When the optimization objective is to minimize the asymptotic variance of the estimated product’s MTTF, the measurement interval under each stress level decreases, the measurement times increase significantly, and more test resources are added to the measurement cost. Hence, increasing the measurement times for the product’s degradation performance in ADT helps to improve the prediction accuracy of lifetime. When the optimization objective is to maximize the determinant of Fisher information matrix of the estimated parameters, the test sample size increases, and more test resources are added to the cost of test samples. Hence, increasing the test sample size in ADT helps to improve the estimation precision of the model parameters. When the optimization objective is to minimize the relative ratio of the asymptotic variances before and after the parameter fluctuation, more stress levels lead to a higher relative change rate. This is caused by an increase in the number of model parameters. Hence, reducing the number of stress levels in ADT helps to improve the stability of parameter fluctuation in the degradation model.
In short, the optimal test plans under different optimization objectives are considerably different. The optimal solution for the multi-objective optimization problem of ADT is not a globally optimal solution under a single objective optimization condition, instead, the optimal test plan is to balance all the optimization objectives. Therefore, to save test resources and make full use of the ADT, it is necessary and effective to propose a multi-objective optimization method for ADT based on game theory.
Comparison with other multi-objective optimization algorithms
To verify the efficiency of the proposed method based on game theory, the multi-objective particle swarm optimization (MOPSO) method, nondominated sorting genetic algorithm II (NSGA II), multi-strategy differential evolution (MSDE) algorithm52 and fast one-to-many multicriteria shortest path search (MSOS) method53 are applied to solve the established multi-objective optimization model. The comparative analysis of the optimization results is shown in Tables 10, 11 and 12.
Table 10.
Optimal SSADT test plans with different multi-objective optimization algorithms (Cb = 200).
| Optimization algorithm | Number of stress levels | N | Δt1, Δt2, …, ΔtK | M1, M2, …, MK | 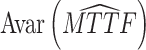 |
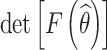 |
RV | CT |
|---|---|---|---|---|---|---|---|---|
| Game theory | 3 | 5 | (22, 21, 17) | (23, 22, 19) | 1.89 × 1015 | 5.85 × 108 | 0.17 | 192.8 |
| 4 | 5 | (20, 17, 11, 9) | (21, 19, 19, 10) | 2.41 × 1015 | 1.96 × 108 | 0.19 | 197.1 | |
| 5 | 5 | (19, 18, 12, 11, 9) | (17, 13, 12, 7, 7) | 2.18 × 1016 | 2.04 × 107 | 0.20 | 183.5 | |
| MOPSO | 3 | 5 | (19, 15, 11) | (18, 16, 13) | 3.78 × 1015 | 1.37 × 108 | 0.19 | 193.8 |
| 4 | 5 | (16, 14, 12, 10) | (16, 12, 10, 9) | 5.26 × 1015 | 7.11 × 107 | 0.22 | 191.0 | |
| 5 | 5 | (18, 16, 11, 6, 5) | (12, 10, 9, 9, 7) | 3.41 × 1016 | 9.56 × 106 | 0.27 | 188.9 | |
| NSGA II | 3 | 5 | (15, 12, 8) | (21, 19, 15) | 6.52 × 1015 | 3.37 × 108 | 0.20 | 199.9 |
| 4 | 5 | (16, 14, 10, 9) | (18, 14, 12, 10) | 1.04 × 1016 | 3.22 × 107 | 0.22 | 199.8 | |
| 5 | 5 | (16, 15, 11, 10, 9) | (15, 12, 10, 9, 8) | 8.88 × 1016 | 3.48 × 106 | 0.28 | 199.8 | |
| MSDE | 3 | 5 | (19, 16, 10) | (19, 13, 13) | 3.16 × 1015 | 8.89 × 107 | 0.21 | 194.3 |
| 4 | 5 | (17, 15, 11, 11) | (14, 13, 9, 9) | 4.29 × 1015 | 5.76 × 107 | 0.23 | 195.6 | |
| 5 | 5 | (17, 16, 11, 5, 5) | (13, 12, 10, 9, 7) | 3.09 × 1016 | 7.31 × 106 | 0.29 | 195.3 | |
| MSOS | 3 | 5 | (21, 21, 16) | (20, 21, 19) | 2.05 × 1015 | 4.68 × 108 | 0.20 | 192.9 |
| 4 | 5 | (19, 17, 11, 9) | (21, 18, 19, 9) | 3.33 × 1015 | 8.76 × 107 | 0.21 | 192.0 | |
| 5 | 5 | (20, 18, 13, 12, 9) | (19, 11, 11, 7, 6) | 2.67 × 1016 | 1.63 × 107 | 0.21 | 196.2 |
Table 11.
Optimal SSADT test plans with different multi-objective optimization algorithms (Cb = 250).
| Optimization algorithm | Number of stress levels | N | Δt1, Δt2, …, ΔtK | M1, M2, …, MK |  |
 |
RV | CT |
|---|---|---|---|---|---|---|---|---|
| Game theory | 3 | 6 | (14, 12, 10) | (14, 13, 9) | 2.20 × 1015 | 7.75 × 108 | 0.17 | 226.7 |
| 4 | 7 | (17, 15, 12, 11) | (15, 13, 10, 10) | 7.00 × 1015 | 3.64 × 108 | 0.21 | 244.2 | |
| 5 | 6 | (17, 15, 14, 10, 7) | (16, 15, 12, 9, 7) | 1.17 × 1016 | 1.38 × 108 | 0.25 | 223.2 | |
| MOPSO | 3 | 7 | (16, 10, 9) | (13, 11, 7) | 3.29 × 1015 | 4.93 × 108 | 0.18 | 229.8 |
| 4 | 7 | (15, 10, 9, 9) | (14, 10, 9, 9) | 9.64 × 1015 | 1.02 × 108 | 0.23 | 248.0 | |
| 5 | 6 | (13, 10, 9, 8, 7) | (17, 16, 15, 9, 9) | 3.20 × 1016 | 8.94 × 107 | 0.27 | 248.7 | |
| NSGA II | 3 | 6 | (22, 15, 11) | (24, 20, 13) | 5.74 × 1015 | 6.31 × 108 | 0.19 | 247.5 |
| 4 | 6 | (21, 19, 16, 15) | (19, 15, 13, 10) | 1.01 × 1016 | 2.99 × 107 | 0.23 | 249.7 | |
| 5 | 6 | (15, 11, 11, 9, 8) | (14, 13, 12, 7, 9) | 7.21 × 1016 | 9.35 × 106 | 0.27 | 234.6 | |
| MSDE | 3 | 7 | (17, 11, 9) | (15, 10, 6) | 3.77 × 1015 | 1.20 × 108 | 0.10 | 231.9 |
| 4 | 7 | (17, 13, 9, 6) | (13, 11, 10, 9) | 9.89 × 1015 | 8.97 × 107 | 0.23 | 240.7 | |
| 5 | 6 | (14, 11, 10, 8, 7) | (18, 15, 15, 8, 9) | 5.21 × 1016 | 6.11 × 107 | 0.29 | 233.8 | |
| MSOS | 3 | 6 | (15, 11, 10) | (15, 13, 10) | 4.31 × 1015 | 5.23 × 108 | 0.21 | 241.5 |
| 4 | 7 | (15, 15, 12, 10) | (17, 12, 11, 10) | 8.57 × 1015 | 2.18 × 108 | 0.23 | 232.2 | |
| 5 | 6 | (18, 15, 13, 9, 7) | (18, 14, 12, 8, 8) | 3.33 × 1016 | 8.75 × 107 | 0.28 | 246.5 |
Table 12.
Optimal SSADT test plans with different multi-objective optimization algorithms (Cb = 300).
| Optimization algorithm | Number of stress levels | N | Δt1, Δt2, …, ΔtK | M1, M2, …, MK | 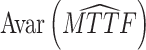 |
 |
RV | CT |
|---|---|---|---|---|---|---|---|---|
| Game theory | 3 | 7 | (27, 23, 19) | (29, 23, 17) | 1.98 × 1014 | 3.39 × 109 | 0.18 | 276.5 |
| 4 | 7 | (22, 19, 17, 14) | (22, 20, 15, 10) | 3.26 × 1014 | 7.36 × 108 | 0.24 | 272.6 | |
| 5 | 6 | (20, 18, 17, 13, 12) | (21, 20, 18, 17, 11) | 1.17 × 1016 | 1.51 × 108 | 0.29 | 258.7 | |
| MOPSO | 3 | 7 | (22, 18, 11) | (24, 20, 8) | 3.40 × 1014 | 8.23 × 108 | 0.20 | 273.0 |
| 4 | 6 | (20, 16, 12, 9) | (22, 19, 17, 12) | 1.08 × 1015 | 4.77 × 108 | 0.25 | 265.7 | |
| 5 | 6 | (17, 14, 12, 10, 9) | (22, 20, 17, 15, 10) | 5.37 × 1016 | 9.82 × 107 | 0.33 | 283.7 | |
| NSGA II | 3 | 7 | (23, 20, 16) | (27, 20, 15) | 8.20 × 1014 | 8.11 × 108 | 0.20 | 299.6 |
| 4 | 6 | (22, 21, 18, 13) | (25, 21, 19, 14) | 8.01 × 1015 | 6.58 × 107 | 0.23 | 290.3 | |
| 5 | 7 | (17, 12, 10, 7, 6) | (16, 13, 24, 10, 6) | 5.75 × 1016 | 5.29 × 107 | 0.30 | 277.8 | |
| MSDE | 3 | 7 | (20, 19, 12) | (22, 21, 10) | 5.34 × 1014 | 6.11 × 108 | 0.21 | 291.1 |
| 4 | 6 | (21, 17, 10, 9) | (21, 20, 16, 13) | 3.21 × 1015 | 3.27 × 108 | 0.26 | 270.7 | |
| 5 | 6 | (19, 13, 12, 11, 9) | (20, 18, 17, 15, 13) | 6.78 × 1016 | 7.33 × 107 | 0.33 | 274.0 | |
| MSOS | 3 | 7 | (24, 22, 20) | (29, 25, 15) | 2.08 × 1014 | 2.51 × 109 | 0.21 | 273.1 |
| 4 | 7 | (23, 20, 16, 12) | (23, 21, 13, 9) | 3.97 × 1014 | 5.29 × 108 | 0.24 | 282.6 | |
| 5 | 6 | (20, 17, 17, 12, 12) | (22, 21, 17, 17, 10) | 5.26 × 1016 | 8.99 × 107 | 0.30 | 297.3 |
The comparison of the results obtained using the three algorithms shows that the performance of the proposed method is better than other methods. For instance, the optimal test plans with three stress levels, when Cb = 200, there are 6.52 × 1015 > 3.78 × 1015 > 3.16 × 1015 > 2.05 × 1015 > 1.89 × 1015, 8.89 × 107 < 1.37 × 108 < 3.37 × 108 < 4.68 × 108 < 5.85 × 108, 0.21 > 0.20 > 0.19 > 0.17. This shows that the multi-objective optimization design method based on game theory for ADT has a better optimization result.
In addition, to compare the computational complexity of two optimization algorithms, the average operation times of different optimization algorithms and the execution time of the optimization process under the same hardware environment are shown in Tables 13, 14.
Table 13.
Comparison of average operation times of different multi-objective optimization algorithms.
| Optimization algorithm | Number of stress levels | Average operation times | ||
|---|---|---|---|---|
| Cb = 200 | Cb = 250 | Cb = 300 | ||
| Game theory | 3 | 1584 | 1440 | 1440 |
| 4 | 800 | 900 | 950 | |
| 5 | 2436 | 2436 | 2784 | |
| MOPSO | 3 | 6419 | 15,043 | 67,433 |
| 4 | 14,217 | 47,865 | 107,623 | |
| 5 | 51,372 | 69,511 | 235,334 | |
| NSGA II | 3 | 36,557 | 63,655 | 425,125 |
| 4 | 67,346 | 251,324 | 435,526 | |
| 5 | 200,789 | 377,068 | 756,174 | |
| MSDE | 3 | 650 | 1614 | 2861 |
| 4 | 11,961 | 23,955 | 36,876 | |
| 5 | 59,411 | 84,030 | 114,602 | |
| MSOS | 3 | 1436 | 2325 | 4793 |
| 4 | 6714 | 14,498 | 17,730 | |
| 5 | 41,845 | 59,418 | 64,307 | |
Table 14.
Running time of different multi-objective optimization algorithms.
| Optimization algorithm | Number of stress levels | Elapsed time (s) | ||
|---|---|---|---|---|
| Cb = 200 | Cb = 250 | Cb = 300 | ||
| Game theory | 3 | 93.22 | 96.78 | 98.41 |
| 4 | 123.45 | 136.96 | 152.18 | |
| 5 | 123.80 | 137.80 | 170.33 | |
| MOPSO | 3 | 213.66 | 238.92 | 249.87 |
| 4 | 502.98 | 521.32 | 547.63 | |
| 5 | 1147.21 | 1233.02 | 1350.28 | |
| NSGA II | 3 | 1273.21 | 1874.63 | 1031.76 |
| 4 | 3093.27 | 1834.27 | 3098.25 | |
| 5 | 6012.56 | 6305.93 | 8782.36 | |
| MSDE | 3 | 198.38 | 199.15 | 190.14 |
| 4 | 487.21 | 479.18 | 481.16 | |
| 5 | 950.60 | 922.38 | 962.43 | |
| MSOS | 3 | 150.04 | 159.21 | 152.06 |
| 4 | 204.92 | 206.83 | 205.75 | |
| 5 | 280.34 | 284.61 | 285.14 | |
It is evident from Tables 13, 14 that the complexity of the proposed method based on game theory decreased significantly. Besides that, the optimization speed of the proposed method is significantly higher as compared to the speed of other methods. Especially, when the number of stress levels increases, the execution time of other methods increases sharply, but the execution time of the method based on game theory does not increase significantly.
In short, the proposed multi-objective optimization method for ADT based on game theory significantly improves the optimization result and solution efficiency of ADT.
Conclusions
In this work, we propose a multi-objective optimization design method for ADT based on game theory. The multiple optimization objectives improve the precision accuracy of the lifetime distribution by minimizing the asymptotic variance of the estimated product’s MTTF under normal working conditions. In addition, it improves the estimation precision of the model parameters by maximizing the determinant of the Fisher information matrix of model parameters and improves the robustness of model parameter deviation by minimizing the relative ratio of the asymptotic variances before and after the fluctuation in model parameters. Based on game theory, the multi-objective optimization model is transformed into a cooperative game problem. The fuzzy clustering method is used to calculate the strategy space of each player, and the utility function of the game is constructed based on the collusion cooperation model. Finally, a compromised optimal test plan to balance multiple optimization objectives can be obtained.
To verify the feasibility and effectiveness of the proposed method, a motorized spindle is considered as the research object for obtaining the optimal SSADT plan with 3, 4, and 5 stress levels under different test budgets. As compared with the single objective optimization results, it is proved that the optimal test plans with multiple optimization objectives reduce the sample size, shorten the test cycle, and reduce the test cost, while ensuring the accuracy of optimization results. In addition, as compared with the optimization results obtained by using the MOPSO algorithm, the proposed multi-objective optimization design method for ADT not only obtains better optimization results, but also greatly improves the optimization efficiency. The proposed multi-objective optimization design method of ADT has high engineering application value.
Acknowledgements
This work was supported by National Natural Science Foundation of China (Grant No. 52305537 and U22B2087), Key Scientific and Technological Research Project of Jilin Province (Grant No. 20230201104GX), Natural Science Foundation of Chongqing Municipality (Grant No. CSTB2022NSCQ-MSX0902 and cstc2021jcyj-msxmX0935).
Appendix
 |
34 |
where 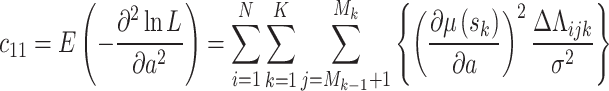 ,
,
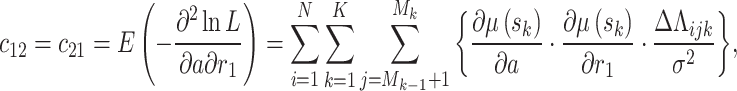 |
 |
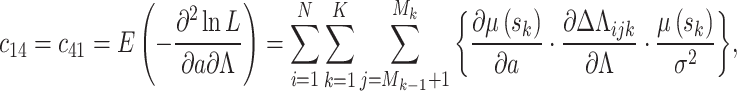 |
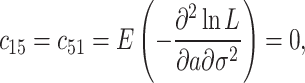 |
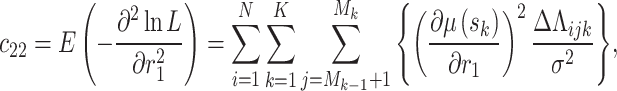 |
 |
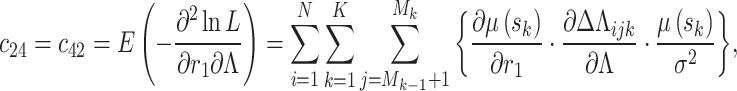 |
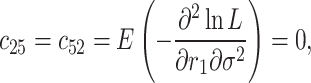 |
 |
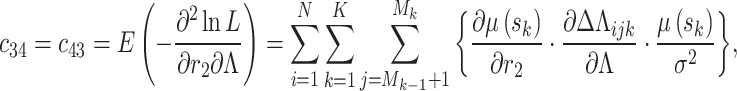 |
 |
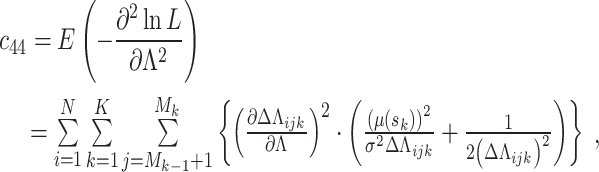 |
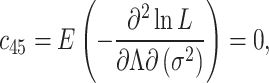 |
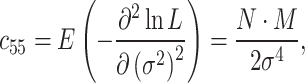 |
where 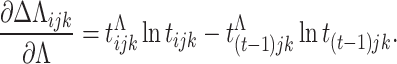
Author contributions
J. Y. G. proposed the conceptualization and conducted the writing- reviewing; Z. W. H. conducted the visualization and data curation; S. F. W. conducted the Investigation and data curation; J. Q. L. proposed the methodology and conducted the validation, writing- original draft preparation; C. H. C. conducted the conceptualization, data curation and supervision; Z. F. L. conducted the investigation and supervision.
Data availability
The data that support the findings of this study are available from the corresponding author, [J. Long and C. Chen], upon reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Junqi Long, Email: longjq_jlu@163.com.
Chuanhai Chen, Email: cchchina@foxmail.com.
References
- 1.Li, G. F., Zhong, Y., Chen, C. H., Jin, T. T. & Liu, Y. Reliability allocation method based on linguistic neutrosophic numbers weight Muirhead mean operator. Expert Syst. Appl.193, 116504 (2022). [Google Scholar]
- 2.Meng, D. B. et al. Kriging-assisted hybrid reliability design and optimization of offshore wind turbine support structure based on a portfolio allocation strategy. Ocean Eng.295, 116842 (2024). [Google Scholar]
- 3.Guo, Y., Meng, D., Pan, L., Zhang, J. & Yang, S. Reliability evaluation of precision hot extrusion production line based on fuzzy analysis. Structures64, 106553 (2024). [Google Scholar]
- 4.Yang, S., Meng, D., Wang, H. Y. & Yang, C. A novel learning function for adaptive surrogate-model-based reliability evaluation. Philos. Trans. R. Soc. A382, 20220395 (2024). [DOI] [PubMed] [Google Scholar]
- 5.Kang, M. et al. Lifetime estimation for optocouplers using accelerated degradation test. Qual. Reliab. Eng. Int.38, 560–573 (2021). [Google Scholar]
- 6.Zhao, X. J., Chen, P., Gaudoin, O. & Doyen, L. Accelerated degradation tests with inspection effects. Eur. J. Oper. Res.292, 1099–1114 (2021). [Google Scholar]
- 7.Chen, W. Z., Yang, Z. J. & Ding, Z. A. Identifying and evaluating spindle tool-tip dynamic response under different workloads. Mech. Syst. Signal Pr.185, 109728 (2023). [Google Scholar]
- 8.Draudviliene, L. & Meskuotiene, A. The methodology for the reliability evaluation of the signal processing methods used for the dispersion estimation of lamb waves. IEEE Trans. Instrum. Meas.71, 1001607 (2022). [Google Scholar]
- 9.Sheng, Z. D., Hu, Q. P., Liu, J. & Yu, D. Residual life prediction for complex systems with multi- phase degradation by ARMA-filtered hidden Markov model. Qual. Technol. Quant. Manag.16, 19–35 (2019). [Google Scholar]
- 10.Chen, C. H., Long, J. Q., Chen, W. Z., Liu, Z. F. & Guo, J. Y. Modeling and prediction of spindle dynamic precision using the Kriging-based response surface method with a novel sampling strategy. Nonlinear Dynam.111, 559–579 (2022). [Google Scholar]
- 11.Guo, J. Y., Yang, Z. J., Chen, C. H., Luo, W. & Hu, W. Real-Time prediction of remaining useful life and preventive maintenance strategy based on digital twin. J. Comput. Inf. Sci. Eng.21, 031003 (2021). [Google Scholar]
- 12.Wang, H., Liao, H. T. & Ma, X. B. Stochastic multi-phase modeling and health assessment for systems based on degradation branching processes. Reliab. Eng. Syst. Saf.222, 108412 (2022). [Google Scholar]
- 13.Tseng, S. T., Yao, Y. C. & Wong, D. S. H. The effects of model misspecification on shelf-life prediction of nano-sols under pH acceleration. Qual. Technol. Quant. M.17, 383–398 (2019). [Google Scholar]
- 14.Hu, C. H., Lee, M. Y. & Tang, J. Optimum step-stress accelerated degradation test for Wiener degradation process under constraints. Eur. J. Oper. Res.241, 412–421 (2015). [Google Scholar]
- 15.Liu, X. P., Guo, B., Xia, L. J., Tian, X. & Zhang, L. J. Multi-objective optimization design of accelerated degradation test based on Wiener process. Commu. Stat.-Theor. M.51, 1–18 (2022). [Google Scholar]
- 16.Garg, H., Rani, M., Sharma, S. P. & Vishwakarma, Y. Intuitionistic fuzzy optimization technique for solving multi-objective reliability optimization problems in interval environment. Expert Syst. Appl.41, 3157–3167 (2014). [Google Scholar]
- 17.Kogiso, N., Kodama, R. & Toyoda, M. Reliability-based multi-objective optimization using the satisficing trade-off method. Mech. Eng. J.1, 1–12 (2014). [Google Scholar]
- 18.Ma, X. L. et al. A multi-objective evolutionary algorithm based on decision variable analyses for multi-objective optimization problems with large-scale variables. IEEE Trans. Evolut. Comput.20, 275–298 (2016). [Google Scholar]
- 19.Zhang, X. Y., Tian, Y., Cheng, R. & Jin, Y. C. A decision variable clustering-based evolutionary algorithm for large-scale many-objective optimization. IEEE Trans. Evolut. Comput.22, 97–112 (2018). [Google Scholar]
- 20.Shafaie, V. & Rad, M. M. Multi-objective genetic algorithm calibration of colored self-compacting concrete using DEM: An integrated parallel approach. Sci. Rep.14, 4126 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hu, Y. S., Ding, Y. & Zeng, Z. G. Redundancy optimization for multi-state series-parallel systems using ordinal optimization-based-genetic algorithm. P. I. Mech. Eng. O-J. Ris.236, 66–78 (2022). [Google Scholar]
- 22.Chi, F. A. & Xu, Y. Building performance optimization for university dormitory through integration of digital gene map into multi-objective genetic algorithm. Appl. Energ.307, 118211 (2022). [Google Scholar]
- 23.Yokoyama, A. M., Ferro, M. & Schulze, B. Multi-objective hyperparameter optimization approach with genetic algorithms towards efficient and environmentally friendly machine learning. AI Commun.37, 429–442 (2024). [Google Scholar]
- 24.Wu, Z. Y., Liu, X. P., Guo, B., Cui, D. J. & Zhang, L. J. Multi-objective optimization design of constant stress accelerated degradation test using inverse Gaussian process. IEEE Access7, 28757–28768 (2019). [Google Scholar]
- 25.Ye, Q. L. et al. A clustering-based competitive particle swarm optimization with grid ranking for multi-objective optimization problems. Sci. Rep.13, 11754 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wang, F., Zhang, H. & Zhou, A. M. A particle swarm optimization algorithm for mixed-variable optimization problems. Swarm Evol. Comput.60, 100808 (2021). [Google Scholar]
- 27.Li, B. & Guo, Q. Particle swarm optimization-based multi-objective planning model for marketing strategy decision. J. Circuit. Syst. Comp.33, 2450279 (2024). [Google Scholar]
- 28.Fan, W., Liu, Q. & Wang, M. Y. Bi-level multi-objective optimization scheduling for regional integrated energy systems based on quantum evolutionary algorithm. Energies14, 4740 (2021). [Google Scholar]
- 29.Wang, Y., Li, Y. Y. & Jiao, L. C. Quantum-inspired multi-objective optimization evolutionary algorithm based on decomposition. Soft Comput.20, 3257–3272 (2016). [Google Scholar]
- 30.Antonio, L. M. & Coello, C. A. C. Use of cooperative coevolution for solving large scale multi-objective optimization problems. In Proc. IEEE CEC, 2758–2765 (2013).
- 31.Duan, F. J. & Wang, G. J. Optimal design for constant-stress accelerated degradation test based on gamma process. Commu. Stat.-Theor. M.48, 2229–2253 (2019). [Google Scholar]
- 32.Zhao, X. J., Pan, R. & Xie, M. Bayesian planning of step-stress accelerated degradation tests under various optimality criteria. Appl. Stoch. Model. Bus.35, 537–553 (2019). [Google Scholar]
- 33.Ge, Z. Z., Li, X. Y., Jiang, T. M. & Huang, T. T. Optimal design for step-stress accelerated degradation testing based on D-optimality. In Proc. Annual RAMS (2011).
- 34.Si, S., Zhai, G. F., Zheng, B. K., Ye, X. R. & Wang, S. J. Optimal design for step-stress accelerated degradation testing based on D-optimality. In Proc. QR2MSE, 967–972 (2019).
- 35.Fang, G. Q., Pan, R. & Stufken, J. Optimal setting of test conditions and allocation of test units for accelerated degradation tests with two stress variables. IEEE Trans. Reliab.70, 1096–1111 (2021). [Google Scholar]
- 36.Tang, L. C., Yang, G. & Xie, M. Planning of step-stress accelerated degradation test. In Proc. RAMS, 287–292 (2004).
- 37.Park, J. I. & Yum, B. J. Optimal design of accelerated degradation tests for estimating mean lifetime at the use condition. Eng. Optimiz.28, 199–230 (1997). [Google Scholar]
- 38.Lim, H. & Yum, B. J. Optimal design of accelerated degradation tests for estimating mean lifetime at the use condition. J. Appl. Stat.38, 309–325 (2011). [Google Scholar]
- 39.Li, X. Y. & Jiang, T. M. Optimal design for step-stress accelerated degradation with competing failure modes. In Proc. RAMS, 64–68 (Fort Worth, 2009).
- 40.Ye, Z. S., Chen, L. P., Tang, L. C. & Xie, M. Optimal design of accelerated degradation tests for estimating mean lifetime at the use condition. IEEE Trans. Reliab.63, 750–763 (2014). [Google Scholar]
- 41.Ma, Z. H. et al. Optimal design of hybrid accelerated test based on the inverse Gaussian process model. Reliab. Eng. Syst. Saf.210, 107509 (2021). [Google Scholar]
- 42.Teng, F., Wang, H. W. & Zhou, Y. Design of an optimal plan of accelerated degradation test via acceleration factor constant principle. Int. J. Reliab. Qual. Saf. Eng.25, 1850021 (2018). [Google Scholar]
- 43.Wang, H., Zhao, Y., Ma, X. B. & Wang, H. Y. Optimal design of constant-stress accelerated degradation tests using the M-optimality criterion. Reliab. Eng. Syst. Saf.164, 45–54 (2017). [Google Scholar]
- 44.Zhang, Y. & Meeker, W. Q. Bayesian methods for planning accelerated life tests. Technometrics48, 49–60 (2006). [Google Scholar]
- 45.Liu, X. & Tang, L. C. A Bayesian optimal design for accelerated degradation tests. Qual. Reliab. Eng. Int.26, 863–875 (2010). [Google Scholar]
- 46.Nasir, E. A. & Pan, R. Simulation-based Bayesian optimal ALT designs for model discrimination. Reliab. Eng. Syst. Saf.134, 1–9 (2015). [Google Scholar]
- 47.Hou, Y. D., Du, Y. H., Peng, Y. & Liu, D. T. An improved random effects Wiener process accelerated degradation test model for lithium-ion battery. IEEE Trans. Instrum. Meas.70, 3520611 (2021). [Google Scholar]
- 48.Han, D. Time and cost constrained optimal designs of constant-stress and step-stress accelerated life tests. Reliab. Eng. Syst. Saf.140, 1–14 (2015). [Google Scholar]
- 49.Xiao, M., Shao, X. Y., Gao, L. & Luo, Z. A new methodology for multi-objective multidisciplinary design optimization problems based on game theory. Expert Syst. Appl.42, 1602–1612 (2015). [Google Scholar]
- 50.Nash, J., Kuhn, H. W. & Nasar, S. Equilibrium points in n-person games. In The Essential John Nash (eds Nash, J. & Nasar, S.) 49–50 (Princeton University Press, 2016). [Google Scholar]
- 51.Isaza, C. V., Sarmiento, H. O., Kempowsky-Hamon, T. & LeLann, M. V. Situation prediction based on fuzzy clustering for industrial complex processes. Inf. Sci.279, 785–804 (2014). [Google Scholar]
- 52.Zhang, L. M. & Wen, Y. A. A multi-strategy differential evolution algorithm with adaptive similarity selection rule. Symmetry-Basel15, 697 (2023). [Google Scholar]
- 53.Kucukkoc, I., Karaoglan, A. D. & Yaman, R. Fast one-to-many multicriteria shortest path search. IEEE Trans. Intell. Transp.24, 10410–10419 (2023). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, [J. Long and C. Chen], upon reasonable request.






