基于自动轮廓勾画求取体模空间分辨率的方法

Abstract

本研究提出了一种自动轮廓勾画测量自制自动管电流调制（ATCM）体模空间分辨率的方法，通过勾画体模图像的边缘轮廓，选取感兴趣区域（ROI），测算电子计算机断层扫描（CT）体模图像的空间分辨率特征。具体而言，该方法通过自动化快速区域卷积神经网络（AFRCNN）模型勾画出的体模图像轮廓，得到二值化图像；并测量不同管电流和层厚的CT体模图像的边缘扩散函数（ESF），对ESF进行微分以获得线扩展函数（LSF）。最后，通过傅里叶变换，对经过零点处的值进行归一化，以获得自动测量调制传递函数（MTF）的CT空间分辨率指数（RI）。本文将此算法与使用聚甲基丙烯酸甲酯（PMMA）测算体模边缘MTF的算法对比，以验证此方法的可行性。结果显示，AFRCNN 模型不仅提高了体模轮廓勾画的效率与准确性，还能够通过自动化分割得到更为精准的空间分辨率值。综上所述，本文提出算法的体模图像空间分辨率测算结果精确，而且在真实临床CT图像中也有广泛应用潜力。

0. 引言

电子计算机断层扫描（computer tomography，CT）的图像质量是由一系列关键参数共同决定的，包括高对比度分辨率、低对比度分辨率、噪声和信噪比等^[1-2]。图像质量中的空间分辨率通常通过使用体模进行测量来评估。体模，通常是指用来模拟人体组织特性的物理模型，可用于评估和测量CT设备的空间分辨率。即，通过将体模放置在CT扫描仪中进行扫描，并分析得到的图像，可以评估CT设备在成像时区分物体最小细节的能力。将体模用于空间分辨率的测量，不仅可用于验证CT设备的性能，而且对于确保诊断的准确性和有效性也极为重要。

CT体模图像受到点扩散函数（point spread function，PSF）的影响^[3]，而PSF受到X射线源的有限尺寸、图像重建算法的限制滤波反投影（filtered back projection，FBP）方法或迭代重建（iterative reconstruction，IR）方法^[4]的影响，均会影响到空间分辨率的测算。空间分辨率可以通过观察 CT 影像中体模图像的线对数来主观评价，也可以使用计算调制传递函数（modulation transfer function，MTF）的方法进行客观评价^[5]。MTF测量方法通常基于PSF^[6]、线扩展函数（line spread function， LSF）或者使用线对法（back projection，BP）^[7]进行评估。MTF的计算可以使用边缘扩散函数（edge spread function，ESF）、PSF或LSF进行分析^[8-11]，即通过微分将ESF转换为LSF^[8]，或者通过平均处理将PSF转换为LSF^[9]，然后对LSF进行傅里叶变换后求取。MTF也可以通过使用LSF曲线或ESF曲线的拟合方法进行计算^[12]，或者直接根据体模条形图来计算。但，使用上述方法计算MTF，不仅耗时且高度依赖相关医务人员的专业知识，尚需进一步优化改良。通常基于PSF、LSF、ESF或BP的MTF计算需要特定的体模，而常见的体模包括：美国医学物理学家协会（American association of physicists in medicine，AAPM）CT性能体模（CT performance phantom，Catphan）、美国放射学委员会（American college of radiology，ACR）CT认证体模^[13]或专门设计的边缘体模。本文采用了复旦大学放射医学研究所自制的自动管电流调制（automatic tube current modulation，ATCM）体模来测试体模图像的空间分辨率。

综上，为提高体模空间分辨率，本文提出了一种从自制体模图像中测量CT空间分辨率指数的算法。该算法包括三个主要步骤：① 使用自动化快速区域卷积神经网络（automated fast region convolutional neural network，AFRCNN）模型从体模图像中自动分割出边缘轮廓；② 生成二值化图像；③ 测量自制体模图像边缘的ESF，并根据ESF测量计算空间分辨率。在不同管电压和层间距参数的情况下，本文研究通过考察CT体模图像空间分辨率的变化，并将本文算法和体模边缘自动测量MTF算法对比，以期AFRCNN模型可以自动并精确勾画轮廓求取体模的空间分辨率。

1. 方法

1.1. ATCM体模

本文实验采用一种自制模拟人体胸部的ATCM体模^[14]，该体模由聚甲基丙烯酸甲酯（polymethyl methacrylate，PMMA）制成。PMMA性能几乎与组织等效，且易于制造。体模实物图如图1所示，长度为20 cm。

图 1.

Photo of the phantom

体模实物图

1.2. 数据预处理

1.2.1. 数据采集

本文自制体模图像采集于CT扫描设备United Imaging UIHuCT960+（联影医疗科技股份有限公司，中国）。将自制体模图像根据不同管电流和层间距分为50张，其层厚都为5.0 mm，管电压为120 kV。用图像标注软件Labelme 4.5.6（Massachusetts Institute of Technology，美国）对体模图像进行分割，筛选出10张大小为512×512矩阵的图像（编号为：B10f、B20f、B30f、B40f、B50f、B60f、B70f、B80f、D10f、D20f）作为结果呈现，CT体模数据均以医学数字成像和通信标准（digital imaging and communications in medicine，Dicom）格式储存，具体扫描参数如表1所示。

表 1. Phantom scanning parameters.

体模扫描参数

扫描参数	默认值
管电压/kV	120
旋转时间/s	0.5
准直宽度/mm	40
调制水平	L15
螺距/mm	1.0
重建核	B
重建层厚/mm	5

1.2.2. AFRCNN自动分割网络设计

本文使用图像标注软件Labelme 4.5.6对体模边界以点的形式进行标注，原始图像经过标注后结果如图2所示。在标注完成后，会得到包含体模边界的位置信息，并通过解析库得到边界位置信息的数据结构。遍历数据结构，提取图像信息和体模边界标注信息，并将其转换为数据集格式用来训练模型。

图 2.

CT phantom images before and after software annotation

软件标注前后的CT体模图像

将前文所述图像数据放入AFRCNN模型中处理，而AFRCNN模型结构基于快速卷积神经网络，旨在提高目标检测和分割的自动化水平。AFRCNN模型包括数据增强模块、定位模块和分割模块^[15-18]。首先，普通样本通过数据增强模块输入生成网络，训练后获得增强后的数据集。然后，定位模块用于预测目标位置，结合水平集方法进行目标区域的精准分割，构建出一种精准分割模型。将普通样本和增强样本一同输入特征提取网络，使用101层深度残差网络（residual network 101，ResNet101）进行抽象特征提取，生成包含样本抽象特征的特征图，进而输入到区域提议网络（region proposal network，RPN），在其中生成一系列锚框^[19]，锚框会被判断在图像中是属于前景还是后景，即判断锚框在图像中是否具有语义。然后，RPN 网络会计算能够完整包裹这些锚框的目标框的回归偏移量。最后，通过结合特征图和感兴趣区域（region of interest，ROI）进行池化，筛选出候选区域，并得到待检目标的边界框和分类信息，输出网络对目标位置的预测。本研究需将RPN 网络的损失函数进行优化，RPN 网络损失L({p_i}, {t_i})的计算如式(1)所示：

1

其中，i代表错框在该批次锚框集合的索引，p_i代表锚框被预测为是待检目标还是背景的概率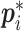，则代表真值的标签。当其为待检目标时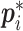，为 1，否则为0。t_i为代表预测包围框的坐标向量，代表锚框真值对应的真实标注框的坐标值，N_cls代表参与计算的候选框的数量，N_reg代表回归候选框的数量，L_cls为二分类交叉熵损失，以评估模型的分割效果。

对于定位模块，本研究采用平均精确率均值（mean average precision，mAP）作为模型的评价指标，计算公式如式(2)所示：

2

其中，ΣAP为平均精确率（average precision，AP）求和，N(Classes)为总的类别数。

最后，分割模块对该区域进行分割，输出分割结果。对于分割模块的评价指标，选取了戴斯（Dice）系数来评估分割出的边界曲线和真实边界曲线之间的相似性。整个流程旨在通过引入生成对抗网络和优化分割模块，提高自动化分割网络的性能，计算公式如式(3)所示：

3

其中，m代表经专家手动分割的物体真实边界曲线，p代表本文模型所得出的分割结果。

本研究对训练集与验证集进行了规划，将1.2.1小节采集的50张自制CT体模图像分为训练集和验证集，以评估模型的泛化能力。具体而言，本文采用80%和20%的比例分配，即40张图像作为训练集，用于模型的训练；剩余的10张图像作为验证集，用于评估模型在未见数据上的性能。本文初始学习率为0.005，训练2 000次之后为0.003，训练5 000次之后为0.001；反向传播算法为随机最速下降法，动量为0.8，权重衰减为0.000 5，轮次为10 000次，超参数为2.5^[20]。

提取CT体模图像中包含体模边界的图像序列，然后将其输入上述如图3所示AFRCNN 自动化分割网络模型中，对边界进行分割，由分割结果对图像进行二值化，然后对 CT 体模图像进行二值化^[21]。对于体模轮廓线内部区域，将其像素赋值为 1，而轮廓线外部区域则赋值为0，如图4所示。因为选取整个轮廓范围数据量庞大，所呈现的结果图有一定波动，所以选择左下角（x < 130，y > 340）这一特定区域。

图 3.

AFRCNN automated segmentation network architecture

AFRCNN自动化分割网络结构

图 4.

Binary image of CT phantom

CT体模图像二值化

1.3. 求取ESF

由于均匀体模的两侧，一侧是空气，另一侧为用等效组织材料替代的人体器官，因此在CT体模图像当中，沿体模轮廓的外侧面至内侧面的CT值将出现由低至高的变化。通过这个区域的CT值的变化，使用微元法来模拟CT体模图像的ESF。为了保证统一，对上图经二值化后的CT体模图像中的体模边界构建多个微元，根据每个微元的长度来确定法向量，通过法向量将圆心坐标和边缘轮廓点连线来得到ESF，同时以圆心坐标来保证ESF对同一中心的径向依赖，如图5所示，黄线为法向量，红线为微元的ESF。

图 5.

ESF of the phantom

体模ESF

在求取ESF前，首先要寻找刃边点并对图像相邻各点灰度值进行差值分析，差值较大的点为刃边点，即ESF曲线中的关键点。为了减少噪声及其他因素对刃边点的影响，采用最小二乘法对刃边点进行直线拟合，以获得更精确的刃边直线。同时，由于曲线上点数量较多，每条 ESF 曲线均通过三次样条插值处理，使曲线更光滑、采样区间更均匀，从而提高 MTF计算的精度。对于生成的ESF曲线，使用Sanders等^[22] 提出的一种称为尾部置换的特殊程序，将左尾翼旋转了180°来替换右尾翼。

在求取ESF时，运用带有高斯权重的四阶移动多项式拟合对ESF阵列数组进行平滑处理，如图6所示。局部平滑的使用，不限于将ESF约束为特定的数学形式，而是通过拟合ESF数组元素的多项式函数来实现，将预测值替换原始值，并对中心点附近赋予高权重，权重函数呈高斯分布，如式(4)所示^[23]：

图 6.

The result of the ESF

ESF结果图

4

其中，w是窗宽，i是以［−(w − 1)/(2), (w − 1)/(2)］定义的局部变量。

1.4. LSF生成MTF曲线

LSF表示系统对线源的响应，可用于估计MTF的轮廓，如图7所示。其中，在PSF(x, y)和MTF(x, y)中，x和y表示二维空间坐标，u表示空间频率。在ESF_x(x)和LSF_x(x)中，x表示单方向上的空间坐标。一般而言，如使用狭缝法需要非常精确的对齐，这给实际应用带来了限制。本文采用刀锋法，从图像中检测并提取刃边直线，用标准的中心差分算法对阵列进行数值微分得到LSF^[23]，如式(5)所示：

图 7.

Transformation image for MTF calculation

MTF求取转换图

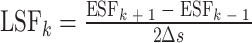5

其中，LSF_k表示在k点位置计算得到的LSF值，ESF _{k + 1}和ESF _{k − 1}表示k点前后两个位置的ESF数值，Δs表示空间采样步长。再对LSF做傅里叶变换，得到图像的频率域表示，如式(6)所示：

6

其中，x_i表示采样点i的空间位置，x_i+1表示相邻点的空间位置，y_i表示采样点i的信号值，y_i+1表示相邻点的信号值，f是估计MTF的空间频率的幅度，W是窗口函数，且常数C使MTF（0）=1。然后，选用汉宁（Hanning，Hann）窗，如式(7)所示：

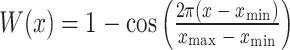7

其中，x_min和x_max是数据间隔的极限^[24]。此时，图像中不同的空间频率对应于频率域中不同的位置，并通过零点处的值进行归一化，取幅值频谱，假定 0 频率的传输函数为 1，即可得到MTF，结果如图8所示。

图 8.

MTF generation

MTF生成

1.5. 边缘自动测量MTF算法

CT体模图像的轮廓是自动勾画的^[25]，并且使用质心方程确定图像的中心。即，从体模中心至图像顶部边缘绘制一条贯穿顶部边界的线，体模上边缘的中点是ROI中心，坐标为（x_c，y_c）。创建ROI，x从（x_c − 20）像素到（x_c + 20）像素，y从（y_c − 20）像素至（y_c + 20）像素。ROI中x值的平均值用于给出ESF，质心方程如式（8）所示：

8

其中，x_j表示每个像素向上的位置，y_j为像素值。由于像素之间的距离相对较大^[26]，该ESF曲线对数据采样不足，需通过样条插值增加像素间的数据点，以确保所得MTF具有更高的空间分辨率，如图9所示。

图 9.

Algorithm for automatic edge measurement of MTF

边缘自动测量MTF算法

2. 结果和讨论

2.1. 结果

分别使用亚历克斯卷积神经网络(Alex convolutional neural network，AlexNet)、视觉几何组16（visual geometry group 16，VGG 16）模型、ResNet101进行特征提取，并对这三种不同的特征提取网络的分割结果进行对比，其分割结果评价指标对比如表2所示。

表 2. Comparative evaluation metrics of segmentation results using different feature extraction networks.

不同特征提取网络分割结果评价指标对比

特征提取网络	mAP	Dice系数
AlexNet	78.38%	83.33%
VGG16	85.63%	87.26%
ResNet101	91.35%	90.93%

由表2结果可知，当使用 ResNet101作为特征提取网络时，其定位框恰好能包裹住目标区域，mAP为91.35%，比AlexNet和VGG16都略有增加。同时，其对目标区域的定位精度最高，分割最为精准。分割结果的Dice系数为90.93%，大于使用AlexNet和VGG16作为特征提取网络最后所取得的Dice系数。这表明在AFRCNN模型中，ResNet101能够更有效地拟合目标函数，其学习特征的能力也优于AlexNet和VGG16。这一优势源于ResNet101采用残差块扩展了模型深度，有效防止了梯度消失问题。

2.2. 讨论

管电流、层间距对AFRCNN模型自动轮廓勾画测量空间分辨率的影响，如图10所示，先以点的形式个性化分割得到体模轮廓，其次使用AFRCNN模型提取特征，自动选取轮廓。过程中需要先将格式为Dicom的CT体模图像二值化，再通过微元法求取法向量，接着通过刃边法得到平均ESF，再求导得到LSF，进一步通过傅里叶变化和归一化处理得到MTF曲线，最后用非线性最小二乘法将函数进行拟合得到空间分辨率具体数值。

图 10.

Steps in the algorithm for automatic contour delineation and measurement of MTF

自动勾画轮廓测量MTF算法步骤

实际测量的MTF曲线可能受到噪声和测量误差等因素影响，这些因素会使MTF曲线出现波动或不规则性，故直接从图像中读取MTF调制度50%（MTF 50%，MTF50）时的空间频率的值可能会降低准确度。为此，文献[27]中，以非线性最小二乘法基于解析模型从CT胸腔图像中提取过采样ESF，并用多个单独函数的总和进行拟合，通过最小化残差均方根值优化ESF模型参数，从而提高拟合效果并提升评估精度。本文实验选取了10张不同管电流和层间距的体模图（编号为：B10f、B20f、B30f、B40f、B50f、B60f、B70f、B80f、D10f、D20f）进行差异分析，如图11所示。

图 11.

Differential map of MTF results obtained from automatic contour delineation

自动勾画轮廓求取MTF结果差异图

因为体模图像的管电流和层间距不同，结果也存在一定差异，如表3所示。根据表3数据结果显示，随着管电流的增加，MTF50的值逐渐增长；而随着层间距的增加，MTF50的值逐渐减小。

表 3. Comparative analysis of different tube currents and interlayer spacing.

不同管电流和层间距的比较分析

序号	管电流/mA	层间距/mm	层厚/mm	管电压/kV	边缘自动MTF50/（lp·cm−1）	AFRCNN勾画MTF50/（lp·cm−1 ）
B10f	529	1 360.3	5	120	8.101	7.806
B20f	552	1 330.3	5	120	7.106	7.522
B30f	559	1 335.3	5	120	7.649	7.765
B40f	525	1 320.3	5	120	8.810	8.381
B50f	547	1 350.3	5	120	8.198	7.154
B60f	546	1 355.3	5	120	8.554	8.507
B70f	544	1 345.3	5	120	5.504	5.558
B80f	549	1 340.3	5	120	8.072	8.295
D10f	537	1 325.3	5	120	7.699	7.796
D20f	461	1 300.3	5	120	8.250	8.697

综上所述，一定条件下管电流增加，空间分辨率有一定提高，这主要是管电流增加了光子数，提高了信噪比，但管电流增加到一定程度，高对比度分辨率变化不明显。此外，对于图像的层间距，层间距越大，空间分辨率降低；因为层间距的增加代表成像系统对细节的捕捉能力下降，影响了图像的整体清晰度。

本文所提出的自动勾画轮廓来求取空间分辨率方法可以用于测算体模的MTF50数值，并且总结出不同管电流、层间距的体模图像的空间分辨率变化。此算法通过AFRCNN模型自动勾画体模轮廓，选取的范围更广。此方法可以应用于CT真实人体图像上，图像质量一定程度地反映了实际临床图像的属性；并且可以通过像素平均的方式得到三维化模型的空间分辨率MTF50的值，比测算二维化图像的MTF50的值更具直观性。

3. 结论

本文提出了一种个性化分割模型用于对CT体模图像自动勾画轮廓来求取空间分辨率，其中AFRCNN模型的主要结构为数据增强模块、定位模块和分割模块，其作用分别是提高数据集影像质量、回归预测目标的位置、根据坐标信息实现目标分割。通过本文模型可实现对CT体模影像数据的自动化分割，解决了传统建模法中专业医生勾画轮廓工作量大、耗时久的问题。本文采用自制的 ATCM体模来测算体模图像空间分辨率，利用所提出的自动分割模型对体模图像进行自动化分割，并通过对二维CT体模图像求取ESF，得到特定区域的空间分辨率数值，验证了其与不同管电流以及层距之间的关系。总之，本文算法不仅提高了分割边界的准确性，还减少了人工干预，提升了操作的效率。

重要声明

利益冲突声明：本文全体作者均声明不存在利益冲突。

作者贡献声明：刘颖负责实验设计、理论指导；孙明浩负责实验与数据分析、论文写作；章浩伟负责方案与方法设计；刘海宽负责实验分析。

Funding Statement

国家自然科学基金（12075064）；上海介入医疗器械工程技术研究中心（18DZ2250900）