Variotherm assisted precision injection molding of plastic optical lenses based on improved cooling stage control model

Yuwang Hu; Changxi Xue

doi:10.1038/s41598-025-96659-3

. 2025 May 2;15:15451. doi: 10.1038/s41598-025-96659-3

Variotherm assisted precision injection molding of plastic optical lenses based on improved cooling stage control model

Yuwang Hu ¹, Changxi Xue ^1,^✉

PMCID: PMC12048522 PMID: 40316621

Abstract

Precision injection-molded plastic optical lenses are extensively utilized in imaging optical systems. The residual stress and surface deformation produced during the injection molding of plastic optical lenses will immediately result in impairments in imaging quality. Conventional injection molding enhances molding quality by the optimization of process parameters, necessitating increased raw materials and multiple procedures, but it still fails to produce satisfactory results. This study proposed a variotherm assisted precision injection molding method based on an improved cooling control model. The cooling phase of variotherm assisted injection molding is controlled by determining the cooling time according to the thickness distribution derived from the surface equation of the plastic optical lens, achieving optimisation of residual stress and deformation. The residual stress and deformation of a precision injection molded aspherical plastic optical lens for imaging optical systems were studied through simulation and experimentation under different maximum and minimum temperature and cooling time conditions. The results indicate that the simulation outcomes for residual stress and deformation align with the experimental data trends, suggesting that the proposed method can further minimize the residual stress and deformation inherent in traditional variotherm assisted forming techniques.

Subject terms: Mechanical engineering, Optoelectronic devices and components

Introduction

Precision Injection Molding (PIM) is a primary technique for the mass production of plastic optical lenses, including products with diverse optical surfaces, including free-form surfaces¹, diffractive surfaces², and array surfaces³. The residual stress and surface quality of plastic optical lenses post-injection molding will directly influence the imaging quality of these lenses⁴. Conventional precision injection molding techniques, including Artificial Neural Network⁵, single and multi-objective optimization^6–8, Particle Swarm Optimisation⁹, Nonlinear constrained optimisation¹⁰, Genetic Algorithm¹¹, Nondominated Sorting Genetic Algorithm(NSGA-ll)¹², Firefly algorithm¹³,grey correlation¹⁴, response surface methodology¹⁵, injection compression molding¹⁶, are frequently employed to reduce residual stress and deformation. However, since the mentioned method is optimized only within the mold temperature range below the glass transition temperature, it fails to alter the distribution of the solidification layer during the injection and pressure holding processes, as well as the arrangement of molecular chains during the cooling process. Consequently, it cannot effectively reduce residual stress and deformation. Therefore, there is an urgent need for a method to optimize the molding of plastic optical lenses.

Variotherm assisted injection molding, commonly referred to as rapid thermal cycling molding (RHCM)¹⁷, is an innovative auxiliary injection molding technique that has been developed and implemented in the industry^18,19. In the variotherm assisted injection molding process, the mold temperature during the filling and holding stages is higher than the glass transition temperature of the material to reduce the viscosity and flow resistance of the material, thereby improving the cavity filling behavior of the melt. Through this process, the frozen layer formed during the filling process is reduced or eliminated, achieving a reduction in residual stress and deformation. During the cooling phase, the mold temperature drops to the material deformation temperature until the material strength is sufficient to eject^20,21. Chen et al.²² found that when the mold temperature approaches above the glass transition temperature of the material, birefringence weakens. When the mold temperature reaches 180 ℃, birefringence completely disappears. Yao et al.²³ used high proximity heating to assist in filling PC rectangular parts with a thickness of 0.5 mm. As the mold temperature nears 265 ℃, the mold achieves total filling, resulting in a substantial reduction of molecular orientation and residual stress induced by flow. Park et al.²⁴ studied the effect of rapid heating of molds on birefringence distribution. Through experiments, it was found that the increase in mold temperature reduced the maximum birefringence and average birefringence, reaching up to 50%. Hong et al.²⁵ studied the effects of steam dynamic temperature control system assisted injection molding on the replication and birefringence of microstructured optical elements. The experimental results showed that the optical elements formed by temperature controlled assisted molding had high thickness uniformity and low birefringence index of. However, traditional variotherm assisted injection molding technology uses rapid heating and rapid cooling temperature curve control to control the production of plastic optical components, which only considers the highest temperature during the injection stage and ignores the influence of the cooling stage on residual stress and deformation. Therefore, it is necessary to add optimization to the cooling stage on the basis of traditional variotherm assisted molding. Table 1 illustrates the primary approaches employed and their respective limitations.

Table 1.

Optimization methods and limitations in constant temperature injection molding and variotherm injection molding.

Molding condition	Optimisation approach	Limitation	References
Constant temperature injection molding	Artificial Neural Network	The model training process is time-consuming; The state of the solidified layer cannot be changed	⁵
	Single and multi-objective optimization	Must depend on pre-established measurement outcomes or CAE simulation analysis results; The state of the solidified layer cannot be changed	^6–8
	Genetic Algorithm/Nondominated Sorting Genetic Algorithm (NSGA-ll)	The initial analysis data set needs to be obtained through simulation or data collection.; The state of the solidified layer cannot be changed	^11,12
	Firefly algorithm	Before starting optimization, initial analysis data needs to be obtained through simulation or experimentation; The state of the solidified layer cannot be changed	¹³
	Grey correlation	Single objective optimization can only be carried out after obtaining simulation or experimental data; The state of the solidified layer cannot be changed	¹⁴
	Response surface methodology	The initial analysis data set needs to be obtained through simulation or data collection. The state of the solidified layer cannot be changed	¹⁵
	Injection compression molding	The mold necessitates a compressible mechanical structure or an injection molding machine equipped with an injection compression capability; The state of the solidified layer cannot be changed	¹⁶
Conventional variotherm assisted injection molding	The mold temperature during the injection and holding stages is higher than the glass transition temperature	Only focussing on controlling temperatures during the injection and pressure holding phases, while neglecting the influence of the cooling phase	^22–25

Open in a new tab

At present, the main research is focused on the calculation of cooling time. Tayalati et al.²⁶ explored five algorithms for predicting cooling time parameters, including random forest, decision tree, KNN (k-nearest neighbor), XGBoost, and multiple regression, and compared their performance. Research has shown that machine learning can still effectively capture and predict cooling time parameters. Park et al.²⁷ calculated the cooling time of a plate based on the cooling time calculation method proposed by Ballman and verified its accuracy through experiments. Carlos et al.²⁸ analyzed and calculated the cooling time of a rectangular flat plate using the cooling time calculation method proposed by Liang, and verified the accuracy of their model through experiments. However, the current cooling time control methods for the cooling stage only consider the time required for the melt to reach the mold temperature, ignoring the contribution of molecular chain relaxation behavior during the cooling process. In addition, the traditional way to characterize the variotherm assisted forming process is through computational fluid dynamics simulation²⁹, which involves a large amount of grid partitioning and time step analysis, requiring a significant amount of computing power and time. Compared with traditional simulation methods, the multi physics field approximation method can simplify the calculation during the injection molding process of plastic optical lenses of any shape³⁰. The solidification layer theory establishes the relationship between residual stress and deformation and temperature and pressure history, providing a way to analyze products of any shape³¹. At present, research on temperature dependent assisted molding is mainly focused on the manufacturing of microstructured optical, such as microarrays³²and microstructures³³, rather than imaging optical lenses with complex curved surfaces with large to medium thickness ratios. The comprehensive modeling of deformation analysis after precision injection molding of plastic optical lenses with complex surfaces and large central edge thickness ratios has been lacking.

Therefore, we propose a variotherm assisted precision injection molding model for plastic optical lenses based on an improved cooling stage control model. The improved cooling time analysis model is used to establish the relationship between the surface equation of the plastic optical lens and the cooling time. The purpose is to analyze the residual stress and deformation of plastic optical lenses with complex surfaces and large centre edge thickness ratios after temperature assisted molding. Detailed analysis and discussion were conducted on the residual stress and deformation of plastic optical lenses after variotherm assisted injection molding under the main process parameters. Finally, the proposed model was validated through temperature assisted precision injection molding experiments to manufacture aspherical optical plastic lenses.

Solidification layer model

Due to the close relationship between stress formation, solidification process, and temperature history, without considering convection and dissipation effects, assuming constant thermal performance and uniform initial temperature, the dimensionless energy equation for the cooling process of a static slab can be expressed as³⁴:

in the formula, T_i is the initial temperature, T_w is the mold cavity wall temperature, x is the thickness coordinate, D is half the thickness, t is time, and a is the thermal diffusion coefficient of the polymer plate. According to the length of time, there are two solutions:

Equation (2) is applicable to situations with shorter time, while Eq. (3) is applicable to situations with longer time. The position of the thickness layer of the solidification isotherm is denoted as D_s, and from Eqs. (2) and (3), we can obtain³⁰:

the subscripts a and b respectively represent the short-term solution (according to Eq. (2)) and the long-term solution (according to Eq. (3)), and T_s represents the solidification temperature. The short-term solution will be used for the injection phase, while the long-term solution will be used for the pressure holding and cooling phase. According to the characteristics of optical components, the residual stress model can be expressed as³⁵:

The lens deformation after precision injection molding mainly includes warpage behavior and shrinkage behavior. According to the warpage equilibrium after demolding³⁶ and the shrinkage behavior of the relative melt layer³⁷, there are:

Improved cooling stage control model

Under the temperature control system of variotherm assisted injection molding, the mold temperature is raised to or above the glass transition temperature of the material to reduce material viscosity and flow resistance to facilitate surface replication. During the cooling phase, the mold temperature is lowered to below the deformation temperature of the material in order to safely eject the parts³⁸, as shown in Fig. 1.

Fig. 1 — Temperature curves of variotherm assisted and conventional mold temperature control method.

During the pressure holding cooling stage, the molecular chain activity exhibits temperature dependence and tends to stabilize over time. When the temperature is high, molecular chains that are flexible move in an active Brownian motion and can stretch back and reorient themselves. This makes the conformational entropy go up until it reaches a new equilibrium. During the cooling process, the temperature decreases, the thermal motion of the molecular chains weakens, and the oriented molecular chains are difficult to dissociate. After cooling, they are “frozen”. Consequently, a reduced holding pressure cooling duration and an accelerated cooling rate will result in heightened residual stress within the product’s internal flow, thereby increasing deformation post-molding³⁹.

While conventional variotherm assisted injection molding can achieve mold temperatures exceeding the glass transition temperature during the injection and holding phases, the cooling duration is often minimised to enhance cycle efficiency. To optimise the cooling stage, we offer a cooling time design model grounded in the molecular chain relaxation model. Calculating the relaxation time at the local thickness and incorporating it into the total cooling calculation facilitates adequate relaxing of the molecular chains throughout the cooling phase, hence preventing orientation freezing due to an excessively rapid cooling rate. In comparison to conventional variotherm injection molding, it can optimise the cooling phase duration and diminish residual stress and deformation post-molding.

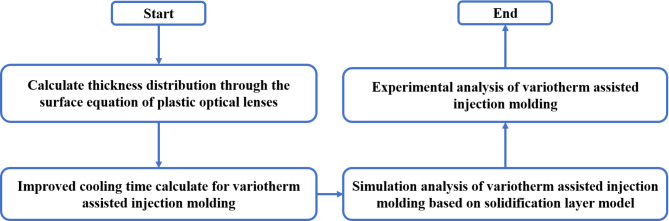
As shown in Fig. 2, initially, compute the thickness distribution of the fabricated plastic optical lens. Subsequently, the cooling time is computed based on the thickness distribution and material, and then rounded for ease of input into the mould temperature control apparatus. Upon finalising the design of the primary process parameters, a simulation analysis will be performed utilising the theoretical model of the solidification layer. Experimental procedures will ultimately validate the simulation results.

According to our previous work³⁵, the thickness D of the plastic optical lens can be written as the sum of the surface sag of Z₁(X), Z₂(X), and the central thickness Z₃(X), X represents the coordinate value along the diameter axis:

Assuming that the shear stress of the melt during injection is proportional to the compression factor, and the relationship between processing parameters and orientation, i.e. the flow induced stress distribution is related to the injection rate, product thickness, and solidification layer thickness, internal expression⁴⁰:

µ_∞ is the power law viscosity, ν is the power law viscosity coefficient, α is the thermal conductivity coefficient, v_max is the maximum injection velocity, D is the half thickness, Ds is the thickness of the solidification layer, and x is the depth of the solidification layer. After the flow stops, the stress in the hot core partially relaxes. The variation of relaxation time with temperature can be expressed as:

τ_Ro and a_T respectively represent the relaxation time constant and temperature displacement factor at the initial melt temperature (Ti). T represents the relaxation time variable (also known as shortening time), calculated at Tin. This is a direct measurement of the amount of relaxation. If t = 0, no relaxation occurs, but as t increases, relaxation monotonically increases. By simplifying the power law function, we can obtain:

in the formula, q is the cooling rate, and β is the Boltzmann calculation coefficient. As shown in the above formula, the relaxation time of the molecular chain exhibits a negative correlation with the cooling rate. In order to provide more opportunities for molecular chain groups to relax during the cooling stage, an additional time factor is added to the cooling time to achieve longer cooling time for plastic melts at the same thickness, while reducing the cooling time rate:

In the formula, D is the thickness, α is the coefficient of thermal expansion, w_p is the weight, and N_cav is the number of cavities inside the mold.

As shown in Fig. 3, the improved temperature curve exhibits a characteristic of rapid heating and gradual decrease. The cooling time is partially prolonged throughout the cooling phase, allowing molecular chains additional time to further relax into a low orientation state, hence reducing stress and deformation.

Simulation analysis

To further validate the proposed method, based on the characteristics of plastic materials and the geometric conditions of the lens, the model proposed in the previous section was used to simulate the stress and deformation of an aspherical plastic optical lens after injection molding.

As shown in Fig. 4, an imaging aspherical plastic lens has an effective light passing diameter of 38 mm, flange edge width of 0.5 mm, center thickness of 11 mm, edge thickness of 2 mm, and a center edge thickness ratio of 6:1. Z₁ is aspherical, Z₂ is spherical, and their coefficients are shown in Table 2. For the convenience of future discussions, five locations (A, B, C) were selected as discussion points along the direction of the melt advance. These points include the sprue, half diameter distance (located at the center of the lens), and the end of the lens. The position under discussion falls within the effective light transmission area, and the calculation does not include the outer flange edge.

Table 2.

Coefficients of the aspheric and spheric surface.

Coefficients	R	K	A2	A4	A6	A8
Aspheric	− 30	− 0.1	0	− 2.339E−006	3.8457E−007	2.5501E−008
Spheric	70	–	0	–	–	–

Open in a new tab

in the formula, c is the aspherical curvature, c = 1/R, k₁ and k₂ are quadratic factors, and A_i is the aspherical coefficient.

The optical plastic used is ACRERT VH001 polymethyl methacrylate produced by Mitsubishi (Nantong) Co., Ltd. Table 3^41–43 shows the main features.

Table 3.

Physical and thermal properties of the PMMA.

Material properties	ACREPT VH001
Young’s modulus E (E_∞) (MPa)	3.29 × 10² (3.3 × 10²)
Poisson’s ratio v	0.32
Brewster’s constant	4.6
Coefficient of thermal expansion α (1/℃)	7.07*E−5
Compressibility β (cm²/kg)	3.56
Solid-state densities ρ₀ (g/cm³)	1.178421
Melt density densities ρ₁ (g/cm³)	1.04
Transition temperature T_g (℃)	105

Open in a new tab

From Eq. (26), it can be observed that the deformation of plastic optical lenses after injection molding is mainly determined by the material properties of the plastic material, the thickness distribution of the injected parts, and the main process parameters. The process parameters that have an impact include mold temperature, melt temperature, holding pressure, and holding time of⁴⁴. In our previous work¹⁵, we established benchmark process parameters for constant temperature forming. These parameters include injection speed of 10 mm/s, mold temperature of 90 ℃, melt temperature of 245 ℃, packaging pressure of 120 Mpa, and holding time of 20 s. In order to verify the effect of variotherm assisted injection molding, the high and low temperature settings and cooling time were discussed separately, and the experimental parameters are shown in Table 4.

Table 4.

Experiment parameters.

Experiment no.	High temperature (℃)	Low temperature (℃)	Cooling time (s)
1	135	80	120
2	130	80	120
3	125	80	120
4	130	90	120
5	130	80	120
6	130	70	120
7	130	80	150
8	130	80	120
9	130	80	100

Open in a new tab

Import the geometric model data of the mold and plastic lens into Matlab and conduct simulation analysis. The result is shown in Fig. 5.

The high mold temperature is the maximum temperature supplied by the mold temperature control mechanism in injection molding, which directly influences the flow characteristics of the melt upon entering the mold cavity. The experimental parameters for mold temperature are presented in trials 1–3 in Table 4. Figure 5a–c, illustrate the expected results of residual stress under different maximum mold temperature conditions. The residual stress has a pattern of greater magnitudes at the edges and lesser magnitudes at the centers. The proximity to the center correlates with a reduction in residual stress values, with the center exhibiting the minimal residual stress. This phenomenon occurs because the mold temperature exceeds that of the polymer, resulting in the molecular chains remaining in a fluid condition. The thickness of the solidified layer diminishes during the cooling phase, and the maximum residual stress is reduced. An increase in the maximum mold temperature results in a peak phenomena, characterized by a rise in residual stress from the edge to the center. As the temperature rises, the free quenching stress correspondingly increases, exhibiting greater intensity near the thinner edge and progressively diminishing towards the center. The minimum mold temperature will determine the cooling phase of the molten plastic and influence the development of the solidification layer. The experimental parameters are presented in Table 4, specifically for experiments 4–6. As illustrated in Fig. 4d–f, with a certain cooling duration, an increase in the minimum temperature corresponds to a reduction in residual stress. This effect occurs because, for the same cooling duration, a lower temperature correlates with a higher cooling rate, leading to an increase in orientation residual stress. The simulation findings indicate that an increase in maximum temperature correlates with a reduction in residual stress. In practical manufacturing, mold temperature cannot rise indefinitely; extremely high temperatures necessitate the selection of appropriate injection molding machines and mold temperature control systems during processing. Figure 5g–i illustrates the impact of cooling duration on residual stress. As the cooling duration extends, the cooling rate diminishes, resulting in a downward trend in overall stress, including residual stress in the peripheries.

Figure 6 illustrates the anticipated deformation outcomes under various experimental conditions, as seen in Fig. 6a–c. Figure 6a illustrates that when the maximum temperature increases, the extent of warpage during deformation diminishes. This represents a favorable numerical aspect; nonetheless, the behavior of shrinking increases, which constitutes the complex numerical aspect. This is attributable to the rise in maximum temperature, necessitating an extended duration for plastic to transition from molten to solid state, while the cooling time remains constant. Figure 6b illustrates that maintaining a constant cooling duration while reducing the minimum temperature accelerates the cooling process. This aligns the molecular chains more effectively during cooling, resulting in distortion and warpage post-demolding. The relatively high and low temperatures exacerbate the shrinking characteristic. Figure 6c illustrates that increased chilling duration results in less overall shrinkage and warpage when examining the extreme temperature variations. Nonetheless, temperature variations dictate the ultimate values of both. Extending the chilling duration mitigates warpage or shrinkage tendencies.

Experiment

The experiment used FANUC α 150iA precision injection molding machine and an improved TOPSTAR TTW1210 mold temperature control machine, as shown in Fig. 7a. The aspherical mold insert is located on the front mold, while the spherical mold insert is located on the rear mold, as shown in Fig. 7c, d. The deformation measurement is carried out using TAYLORHOBSON PGI1240, as shown in Fig. 7b. The measurement results are shown in Fig. 8.

Fig. 7 — Experimental equipment: (a) Injection molding machine with opened mold, (b) Mold temperature control machine, (c) Ejector side mold plat, (d) Nozzle side mold plate.

Fig. 8 — (a) Molded plastic lenses; (b) Consistent temperature conditions; (c) Variotherm conditions; (d) Improving Variotherm conditions.

Measure the residual stress of the injected lens using a WYL-3 stress gauge. The device used birefringence method to measure residual stress in the product. The different stress conditions inside the injection molded lens cause interference when polarized light passes through, resulting in different levels of fringes and representing the birefringence optical path difference caused by stress. According to the law of stress optics, there are⁴⁵:

Δl is the optical path difference, n₁ and n₂ are the optical refractive indices parallel to the principal stresses σ₁ and σ₂, respectively. C is the material’s photoelastic coefficient, also known as the Brewster coefficient. N is the contour level of the isochromatic lines, d is the lens thickness at the measurement point, and λ is the wavelength of the light. The WYL-3 stress meter can be used to measure the optical path difference Δl. According to the relationship Eq. (17) between residual stress and optical path difference, the residual stress Δσ of the lens after injection molding can be calculated.

d is the lens thickness and C is the Brewster constant of the material.

The plastic lens after injection molding is shown in Fig. 8a. Select A, B, and C at the same position as the simulation to measure and analyze the stress on the surface of the formed lens. Use a WYL-3 stress field meter to measure and calculate the residual stress of the injection molded lens, as shown in Fig. 8a–c. The experimental results, as shown in Fig. 8b, c, showed a significant improvement in residual stress after variotherm assisted injection molding. And the lens after improved variotherm assisted molding exhibited lower stress levels, as shown in Fig. 8d.

Figure 9 illustrates that the comparative analysis of residual stress in injection molded plastic lenses indicates a consistent trend between simulation results and experimental findings across various conditions. Figure 9a–c illustrates that an increase in the highest mold temperature corresponds to a gradual decrease in residual stress. At elevated temperatures, the molten plastic retains its liquid state following heat exchange with the cavity wall, resulting in a slower molecular orientation. The residual stress in the injection molded lens is diminished. When the lowest temperature increases, the central melt layer experiences extended relaxation time, resulting in a reduction of overall residual stress. With an increase in cooling time, the residual stress continues to decrease, demonstrating a low residual stress condition; however, some residual stress remains at the gate, as illustrated in Fig. 8d. The strong shear behavior occurring as the melt traverses the gate results in significant molecular chain orientation, which is challenging to mitigate through cooling time.

Fig. 9 — Measure stress values and simulate stress values.

Analyze the deformation simulation outcomes of the aspherical lens post-injection in relation to the experimental data presented in Figs. 6 and 10. The simulation results align with the experimental findings across various process parameter settings. Figure 10a illustrates that warpage behavior diminishes as the highest mold increases post-demolding, while shrinkage behavior concurrently escalates. The molecular chains at the edges can relax, whereas the cooling time at the center is prolonged, despite the cooling time remaining constant. Figure 10b illustrates that elevating the minimum mold temperature facilitates heat transfer from the core, thereby enhancing the continuous flow of the melt. This process further relaxes the peripheral molecular chains and mitigates warpage, while concurrently exacerbating the shrinkage in the thicker central region. Figure 10c indicates that an increase in cooling time results in a reduction of both warpage and shrinkage behavior; however, the extent of these changes remains dependent on the maximum and minimum temperatures. This phenomenon can be ascribed to the decrease in the solidified layer during the molding process and the relaxation of molecular chains in the molten layer over an extended duration.

Conclusion

This study proposes a variotherm assisted precision injection molding method with improved cooling stage control model through theoretical analysis and experimental verification, and discusses the influence of process parameters on residual stress and deformation. The results indicate that compared with traditional temperature assisted methods, the improved temperature assisted method can improve the residual stress and deformation of plastic lenses with aspherical surfaces after injection molding. This model has the potential to predict residual stress and deformation after injection molding of plastic lenses with free-form or complex optical surfaces. In summary, the conclusion can be succinctly expressed as:

An analytical model was established for variotherm assisted precision injection molding of aspherical optical plastic lenses. This model is based on the solidification layer theory in injection molding, and calculates the effect of cooling rate on residual stress during the cooling stage.
An improved variotherm assisted precision injection molding method was proposed, and the effects of different maximum and minimum mold temperatures, as well as cooling times, on the variotherm assisted injection of aspherical plastic lenses were simulated and discussed through the established model.
Verify the proposed model through injection molding experiments, and measure residual stress and deformation using stress gauges and profilometers. The simulation results of residual stress and deformation are consistent with the experimental data trend, proving that the model can analyze the residual stress and deformation of plastic optical lenses after temperature assisted injection molding.

Acknowledgements

Authors thanks for Prof. Xue for his academic guidance.

Author contributions

Yuwang Hu proposed the model construction and simulated the model.Yuwang Hu conceived the experiments, Yuwang Hu and Changxi Xue conducted the experiments, Yuwang Hu and Changxi Xue analysed the results. Yuwang Hu wrote the main manuscript text and prepared figures. All authors reviewed the manuscript.

Funding

Natural Science Foundation of Jilin Province [China] (No. 20220101124JC).

Data availability

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request. For data from this study, please contact Prof.Xue (xcx272479@sina.com).

Declarations

Competing interests

The authors declare no competing interests.

Footnotes

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

References

1.Xia, R. et al. Surface astigmatism correction using segmented freeform surfaces for a progressive addition lens. Opt. Express. 30, 43384–43397. 10.1364/OE.476678 (2022). [DOI] [PubMed] [Google Scholar]
2.Dong, B. et al. Design of adjustable multifocal diffractive optical elements with an improved smooth phase profile by continuous variable curve with multi-subperiods method. Opt. Express. 31, 28338–28354. 10.1364/OE.497346 (2023). [DOI] [PubMed] [Google Scholar]
3.Chakrabarti, M., Dam-Hansen, C., Stubager, J., Pedersen, T. F. & Pedersen, H. C. Replication of optical microlens array using photoresist coated molds. Opt. Express. 24, 9528–9540. 10.1364/OE.24.009528 (2016). [DOI] [PubMed] [Google Scholar]
4.Liu, J. & Chen, X. Study on the relationship between surface error and optical performance for polymer optical lenses. Optik194, 163119. 10.1016/j.ijleo.2019.163119 (2019). [Google Scholar]
5.Feng, Q., Liu, L. & Zhou, X. Automated multi-objective optimization for thin-walled plastic products using Taguchi, ANOVA, and hybrid ANN-MOGA. Int. J. Adv. Manuf. Technol.106, 559–575. 10.1007/s00170-019-04488-2 (2020). [Google Scholar]
6.Kariminejad, M., Tormey, D., Hara, C. O. & McAfee, M. In 9th International Conference on Control, Decision and Information Technologies (CoDIT) 309–314. (2023).
7.Moayyedian, M., Qazani, M. R. C., Amirkhizi, P. J., Asadi, H. & Hedayati-Dezfooli, M. Multiple objectives optimization of injection-moulding process for dashboard using soft computing and particle swarm optimization. Sci. Rep.14, 23767. 10.1038/s41598-024-62618-7 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Kariminejad, M. et al. Single and multi-objective real-time optimisation of an industrial injection moulding process via a bayesian adaptive design of experiment approach. Sci. Rep.14, 29799. 10.1038/s41598-024-80405-2 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Nguyen, H. T., Nguyen, M. Q., Manh, N. Q. & Vu, N. C. In Proceedings of the International Conference on Advanced Mechanical Engineering, Automation, and Sustainable Development 2021 (AMAS2021) (eds Long, B. T. et al.) 199–205 (Springer International Publishing).
10.Mukras, S. M. S. Experimental-based optimization of injection molding process parameters for short product cycle time. Adv. Polym. Technol. 2020, 1309209. 10.1155/2020/1309209 (2020).
11.Mukras, S. M. S., Omar, H. M. & al-Mufadi, F. A. Experimental-based multi-objective optimization of injection molding process parameters. Arab. J. Sci. Eng.44, 7653–7665. 10.1007/s13369-019-03855-1 (2019). [Google Scholar]
12.Fang, M., Zhu, Z. & Zhang, Z. Numerical simulation of closed plastic impeller molding process and its parameter optimization. Sci. Rep.12, 17335. 10.1038/s41598-022-22260-7 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Sudsawat, S. & Sriseubsai, W. Warpage reduction through optimized process parameters and annealed process of injection-molded plastic parts. J. Mech. Sci. Technol.32, 4787–4799. 10.1007/s12206-018-0926-x (2018). [Google Scholar]
14.Li, J. et al. Optimization of injection molding process parameters for the lining of IV hydrogen storage cylinder. Sci. Rep.13, 665. 10.1038/s41598-023-27848-1 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Lan, X., Li, C., Yang, C. & Xue, C. Optimization of injection molding process parameters and axial surface compensation for producing an aspheric plastic lens with large diameter and center thickness. Appl. Opt.58, 927–934. 10.1364/AO.58.000927 (2019). [DOI] [PubMed] [Google Scholar]
16.Lin, C. M. & Lin, Y. Q. Injection-compression molding process on optical quality optimization of plastic lens array. Polym. Adv. Technol.34, 3569–3585. 10.1002/pat.6166 (2023). [Google Scholar]
17.Yao, D., Chen, S. C. & Kim, B. H. Rapid thermal cycling of injection molds: An overview on technical approaches and applications. Adv. Polym. Technol.27, 233–255. 10.1002/adv.20136 (2008). [Google Scholar]
18.Fang, F., Zhang, N. & Zhang, X. Precision injection molding of freeform optics. Adv. Opt. Technol.5, 303–324. 10.1515/aot-2016-0033 (2016). [Google Scholar]
19.Peixoto, C. et al. Injection molding of high-precision optical lenses: A review. Precis Eng.76, 29–51. 10.1016/j.precisioneng.2022.02.002 (2022). [Google Scholar]
20.Kitayama, S. Process parameters optimization in plastic injection molding using metamodel-based optimization: A comprehensive review. Int. J. Adv. Manuf. Technol.121, 7117–7145. 10.1007/s00170-022-09858-x (2022). [Google Scholar]
21.Kitayama, S., Ishizuki, R., Takano, M., Kubo, Y. & Aiba, S. Optimization of mold temperature profile and process parameters for weld line reduction and short cycle time in rapid heat cycle molding. Int. J. Adv. Manuf. Technol.103, 1735–1744. 10.1007/s00170-019-03685-3 (2019). [Google Scholar]
22.Chen, M., Yao, D. & Kim, B. Eliminating flow induced birefringence and minimizing thermally induced residual stresses in injection molded parts. Polym. -Plast Technol. Eng.40, 491–503. 10.1081/PPT-100002072 (2001). [Google Scholar]
23.Yao, D., Kimerling, T. E. & Kim, B. High-frequency proximity heating for injection molding applications. Polym. Eng. Sci.46, 938–945. 10.1002/pen.20548 (2006). [Google Scholar]
24.Park, K., Kim, B. & Yao, D. Numerical simulation for injection molding with a rapidly heated mold, part II: Birefringence prediction. Polym. Plast. Technol. Eng.45, 903–909. 10.1080/03602550600718167 (2006). [Google Scholar]
25.Hong, S., Min, I., Yoon, K. & Kang, J. Effects of adding injection–compression to rapid heat cycle molding on the structure of a light guide plate. J. Micromech Microeng. 24, 015009. 10.1088/0960-1317/24/1/015009 (2014). [Google Scholar]
26.Tayalati, F., Azmani, A. & Azmani, M. Application of supervised machine learning methods in injection molding process for initial parameters setting: Prediction of the cooling time parameter. Prog. Artif. Intell.10.1007/s13748-024-00318-z (2024). [Google Scholar]
27.Ballman, R. & Shusman, T. Easy way to calculate injection molding set-up time. Mod. Plast.194, 130–131 (1959). [Google Scholar]
28.Liang, J. Z. & Ness, J. N. The calculation of cooling time in injection moulding. J. Mater. Process. Technol.57, 62–64. 10.1016/0924-0136(95)02044-6 (1996). [Google Scholar]
29.Wang, L., Hu, Y. & Xue, C. Stress analysis of a large diameter aspheric plastic lens in the variable temperature assisted injection molding process. Appl. Opt.63, 1320–1329. 10.1364/AO.511657 (2024). [DOI] [PubMed] [Google Scholar]
30.Jansen, K. M. B. Calculation and control of heat transfer in injection moulding (1993).
31.Jansen, K. M. B. In AIP Conference Proceedings (AIP Publishing).
32.Zhang, N., Zhang, H., Zhang, H., Fang, F. & Gilchrist, M. Geometric replication integrity of micro features fabricated using variotherm assisted micro injection moulding. Procedia CIRP. 71, 390–395. 10.1016/j.procir.2018.05.049 (2018). [Google Scholar]
33.Michaeli, W., Klaiber, F. & Scholz, S. Investigations in variothermal injection moulding of microstructures and microstructured surfaces. Multi-Material Micro Manuf. (2008).
34.Carslow, H. S., Jaeger, J. C. & Morral, J. E. Conduction of heat in solids, second edition. J. Eng. Mater. Technol.108, 378–378 (1986). [Google Scholar]
35.Hu, Y., Wang, L. & Xue, C. Prediction of residual stress in precision injection molding of plastic optical lenses based on an improved solidification layer model. Opt. Express. 32, 37716–37731. 10.1364/OE.537891 (2024). [DOI] [PubMed] [Google Scholar]
36.Landau, L. & Lifshitz, E. Theory of Elasticity, Vol. 7 (1986).
37.Jansen, K. M. B. & Titomanlio, G. Effect of pressure history on shrinkage and residual stresses—Injection molding with constrained shrinkage. Polym. Eng. Sci.36, 2029–2040. 10.1002/pen.10598 (1996). [Google Scholar]
38.Su, Q., Zhang, N. & Gilchrist, M. D. The use of variotherm systems for microinjection molding. J. Appl. Polym. Sci.133. 10.1002/app.42962 (2016).
39.Adam, G. & Gibbs, J. H. On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J. Chem. Phys.43, 139–146. 10.1063/1.1696442 (1965). [Google Scholar]
40.Janeschitz-Kriegl, H. Injection moulding of plastics: Some ideas about the relationship between mould filling and birefringence. Rheol Acta. 16, 327–339. 10.1007/BF01534086 (1977). [Google Scholar]
41.Deng, Z., Cheng, D., Hu, Y., Huang, Y. & Wang, Y. Design and Fabrication of concave-convex lens for Head Mounted Virtual Reality 3D Glasses, Vol. 9618 (OIT (SPIE, 2015).
42.Koji, M. Optical plastics. In Handbook of Plastic Optics, 123–160 (2010).
43.Shtarkman, B. P., Monich, I. M., Arzhakov, S. A. & Averbakh, N. Y. The isothermal compressibility of polymethylmethacrylate in various physical States. Polym. Sci. U S S R. 18, 1203–1209. 10.1016/0032-3950(76)90521-9 (1976). [Google Scholar]
44.Otieno, S. O. et al. A predictive modelling strategy for warpage and shrinkage defects in plastic injection molding using fuzzy logic and pattern search optimization. J. Intell. Manuf.10.1007/s10845-024-02331-4 (2024). [Google Scholar]
45.Rastogi, P. K. & Hack, E. Optical Methods for Solid Mechanics: A Full-field Approach (Wiley, 2013).

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

[CR1] 1.Xia, R. et al. Surface astigmatism correction using segmented freeform surfaces for a progressive addition lens. Opt. Express. 30, 43384–43397. 10.1364/OE.476678 (2022). [DOI] [PubMed] [Google Scholar]

[CR2] 2.Dong, B. et al. Design of adjustable multifocal diffractive optical elements with an improved smooth phase profile by continuous variable curve with multi-subperiods method. Opt. Express. 31, 28338–28354. 10.1364/OE.497346 (2023). [DOI] [PubMed] [Google Scholar]

[CR3] 3.Chakrabarti, M., Dam-Hansen, C., Stubager, J., Pedersen, T. F. & Pedersen, H. C. Replication of optical microlens array using photoresist coated molds. Opt. Express. 24, 9528–9540. 10.1364/OE.24.009528 (2016). [DOI] [PubMed] [Google Scholar]

[CR4] 4.Liu, J. & Chen, X. Study on the relationship between surface error and optical performance for polymer optical lenses. Optik194, 163119. 10.1016/j.ijleo.2019.163119 (2019). [Google Scholar]

[CR5] 5.Feng, Q., Liu, L. & Zhou, X. Automated multi-objective optimization for thin-walled plastic products using Taguchi, ANOVA, and hybrid ANN-MOGA. Int. J. Adv. Manuf. Technol.106, 559–575. 10.1007/s00170-019-04488-2 (2020). [Google Scholar]

[CR6] 6.Kariminejad, M., Tormey, D., Hara, C. O. & McAfee, M. In 9th International Conference on Control, Decision and Information Technologies (CoDIT) 309–314. (2023).

[CR7] 7.Moayyedian, M., Qazani, M. R. C., Amirkhizi, P. J., Asadi, H. & Hedayati-Dezfooli, M. Multiple objectives optimization of injection-moulding process for dashboard using soft computing and particle swarm optimization. Sci. Rep.14, 23767. 10.1038/s41598-024-62618-7 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR8] 8.Kariminejad, M. et al. Single and multi-objective real-time optimisation of an industrial injection moulding process via a bayesian adaptive design of experiment approach. Sci. Rep.14, 29799. 10.1038/s41598-024-80405-2 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR9] 9.Nguyen, H. T., Nguyen, M. Q., Manh, N. Q. & Vu, N. C. In Proceedings of the International Conference on Advanced Mechanical Engineering, Automation, and Sustainable Development 2021 (AMAS2021) (eds Long, B. T. et al.) 199–205 (Springer International Publishing).

[CR10] 10.Mukras, S. M. S. Experimental-based optimization of injection molding process parameters for short product cycle time. Adv. Polym. Technol. 2020, 1309209. 10.1155/2020/1309209 (2020).

[CR11] 11.Mukras, S. M. S., Omar, H. M. & al-Mufadi, F. A. Experimental-based multi-objective optimization of injection molding process parameters. Arab. J. Sci. Eng.44, 7653–7665. 10.1007/s13369-019-03855-1 (2019). [Google Scholar]

[CR12] 12.Fang, M., Zhu, Z. & Zhang, Z. Numerical simulation of closed plastic impeller molding process and its parameter optimization. Sci. Rep.12, 17335. 10.1038/s41598-022-22260-7 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR13] 13.Sudsawat, S. & Sriseubsai, W. Warpage reduction through optimized process parameters and annealed process of injection-molded plastic parts. J. Mech. Sci. Technol.32, 4787–4799. 10.1007/s12206-018-0926-x (2018). [Google Scholar]

[CR14] 14.Li, J. et al. Optimization of injection molding process parameters for the lining of IV hydrogen storage cylinder. Sci. Rep.13, 665. 10.1038/s41598-023-27848-1 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR15] 15.Lan, X., Li, C., Yang, C. & Xue, C. Optimization of injection molding process parameters and axial surface compensation for producing an aspheric plastic lens with large diameter and center thickness. Appl. Opt.58, 927–934. 10.1364/AO.58.000927 (2019). [DOI] [PubMed] [Google Scholar]

[CR16] 16.Lin, C. M. & Lin, Y. Q. Injection-compression molding process on optical quality optimization of plastic lens array. Polym. Adv. Technol.34, 3569–3585. 10.1002/pat.6166 (2023). [Google Scholar]

[CR17] 17.Yao, D., Chen, S. C. & Kim, B. H. Rapid thermal cycling of injection molds: An overview on technical approaches and applications. Adv. Polym. Technol.27, 233–255. 10.1002/adv.20136 (2008). [Google Scholar]

[CR18] 18.Fang, F., Zhang, N. & Zhang, X. Precision injection molding of freeform optics. Adv. Opt. Technol.5, 303–324. 10.1515/aot-2016-0033 (2016). [Google Scholar]

[CR19] 19.Peixoto, C. et al. Injection molding of high-precision optical lenses: A review. Precis Eng.76, 29–51. 10.1016/j.precisioneng.2022.02.002 (2022). [Google Scholar]

[CR20] 20.Kitayama, S. Process parameters optimization in plastic injection molding using metamodel-based optimization: A comprehensive review. Int. J. Adv. Manuf. Technol.121, 7117–7145. 10.1007/s00170-022-09858-x (2022). [Google Scholar]

[CR21] 21.Kitayama, S., Ishizuki, R., Takano, M., Kubo, Y. & Aiba, S. Optimization of mold temperature profile and process parameters for weld line reduction and short cycle time in rapid heat cycle molding. Int. J. Adv. Manuf. Technol.103, 1735–1744. 10.1007/s00170-019-03685-3 (2019). [Google Scholar]

[CR22] 22.Chen, M., Yao, D. & Kim, B. Eliminating flow induced birefringence and minimizing thermally induced residual stresses in injection molded parts. Polym. -Plast Technol. Eng.40, 491–503. 10.1081/PPT-100002072 (2001). [Google Scholar]

[CR23] 23.Yao, D., Kimerling, T. E. & Kim, B. High-frequency proximity heating for injection molding applications. Polym. Eng. Sci.46, 938–945. 10.1002/pen.20548 (2006). [Google Scholar]

[CR24] 24.Park, K., Kim, B. & Yao, D. Numerical simulation for injection molding with a rapidly heated mold, part II: Birefringence prediction. Polym. Plast. Technol. Eng.45, 903–909. 10.1080/03602550600718167 (2006). [Google Scholar]

[CR25] 25.Hong, S., Min, I., Yoon, K. & Kang, J. Effects of adding injection–compression to rapid heat cycle molding on the structure of a light guide plate. J. Micromech Microeng. 24, 015009. 10.1088/0960-1317/24/1/015009 (2014). [Google Scholar]

[CR26] 26.Tayalati, F., Azmani, A. & Azmani, M. Application of supervised machine learning methods in injection molding process for initial parameters setting: Prediction of the cooling time parameter. Prog. Artif. Intell.10.1007/s13748-024-00318-z (2024). [Google Scholar]

[CR27] 27.Ballman, R. & Shusman, T. Easy way to calculate injection molding set-up time. Mod. Plast.194, 130–131 (1959). [Google Scholar]

[CR28] 28.Liang, J. Z. & Ness, J. N. The calculation of cooling time in injection moulding. J. Mater. Process. Technol.57, 62–64. 10.1016/0924-0136(95)02044-6 (1996). [Google Scholar]

[CR29] 29.Wang, L., Hu, Y. & Xue, C. Stress analysis of a large diameter aspheric plastic lens in the variable temperature assisted injection molding process. Appl. Opt.63, 1320–1329. 10.1364/AO.511657 (2024). [DOI] [PubMed] [Google Scholar]

[CR30] 30.Jansen, K. M. B. Calculation and control of heat transfer in injection moulding (1993).

[CR31] 31.Jansen, K. M. B. In AIP Conference Proceedings (AIP Publishing).

[CR32] 32.Zhang, N., Zhang, H., Zhang, H., Fang, F. & Gilchrist, M. Geometric replication integrity of micro features fabricated using variotherm assisted micro injection moulding. Procedia CIRP. 71, 390–395. 10.1016/j.procir.2018.05.049 (2018). [Google Scholar]

[CR33] 33.Michaeli, W., Klaiber, F. & Scholz, S. Investigations in variothermal injection moulding of microstructures and microstructured surfaces. Multi-Material Micro Manuf. (2008).

[CR34] 34.Carslow, H. S., Jaeger, J. C. & Morral, J. E. Conduction of heat in solids, second edition. J. Eng. Mater. Technol.108, 378–378 (1986). [Google Scholar]

[CR35] 35.Hu, Y., Wang, L. & Xue, C. Prediction of residual stress in precision injection molding of plastic optical lenses based on an improved solidification layer model. Opt. Express. 32, 37716–37731. 10.1364/OE.537891 (2024). [DOI] [PubMed] [Google Scholar]

[CR36] 36.Landau, L. & Lifshitz, E. Theory of Elasticity, Vol. 7 (1986).

[CR37] 37.Jansen, K. M. B. & Titomanlio, G. Effect of pressure history on shrinkage and residual stresses—Injection molding with constrained shrinkage. Polym. Eng. Sci.36, 2029–2040. 10.1002/pen.10598 (1996). [Google Scholar]

[CR38] 38.Su, Q., Zhang, N. & Gilchrist, M. D. The use of variotherm systems for microinjection molding. J. Appl. Polym. Sci.133. 10.1002/app.42962 (2016).

[CR39] 39.Adam, G. & Gibbs, J. H. On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J. Chem. Phys.43, 139–146. 10.1063/1.1696442 (1965). [Google Scholar]

[CR40] 40.Janeschitz-Kriegl, H. Injection moulding of plastics: Some ideas about the relationship between mould filling and birefringence. Rheol Acta. 16, 327–339. 10.1007/BF01534086 (1977). [Google Scholar]

[CR41] 41.Deng, Z., Cheng, D., Hu, Y., Huang, Y. & Wang, Y. Design and Fabrication of concave-convex lens for Head Mounted Virtual Reality 3D Glasses, Vol. 9618 (OIT (SPIE, 2015).

[CR42] 42.Koji, M. Optical plastics. In Handbook of Plastic Optics, 123–160 (2010).

[CR43] 43.Shtarkman, B. P., Monich, I. M., Arzhakov, S. A. & Averbakh, N. Y. The isothermal compressibility of polymethylmethacrylate in various physical States. Polym. Sci. U S S R. 18, 1203–1209. 10.1016/0032-3950(76)90521-9 (1976). [Google Scholar]

[CR44] 44.Otieno, S. O. et al. A predictive modelling strategy for warpage and shrinkage defects in plastic injection molding using fuzzy logic and pattern search optimization. J. Intell. Manuf.10.1007/s10845-024-02331-4 (2024). [Google Scholar]

[CR45] 45.Rastogi, P. K. & Hack, E. Optical Methods for Solid Mechanics: A Full-field Approach (Wiley, 2013).

PERMALINK

Variotherm assisted precision injection molding of plastic optical lenses based on improved cooling stage control model

Yuwang Hu

Changxi Xue

Abstract