Experimental determination of TNT equivalence values for binary energetic materials

Abstract

TNT equivalency quantifies the impact of energetic materials relative to TNT, aiding in safety guidelines and performance evaluations. Despite widespread use in industry, military, and research, many binary energetics lack published TNT equivalence values. This study experimentally determines TNT equivalency values for Helix, Texpak, Rimfire, Tannerite, and Kinepak using three tests: (1) plate dent, (2) reaction velocity and (3) air blast. Each test evaluates distinct aspects of energetic performance, addressing both close-in destructive power and downstream effects. Helix produced TNT equivalence values from 0.64 to 1.10, comparable to TNT, while Kinepak had lower values (0.18 to 0.58) indicating limited brisance, but higher air-blast impulse. Tannerite and Rimfire did not produce dent values due to low brisance; with reaction velocity and air blast TNT equivalence values ranging from 0.18 to 0.71. Commercial AN-based energetics consistently produced low TNT equivalence values, while commercial liquid energetics show values closer to TNT. Synthetic AN-based energetics lack the brisance found in other energetics but effectively produced gas and overpressure. These findings emphasize the importance of considering the characteristics of energetic materials and test type when determining TNT equivalence. Plate dent and reaction velocity tests are suggested for assessing close-in destructive power, while air-blast tests are suitable for evaluating downstream effects.

Introduction

The field of energetics relies on physical measurements such as quantifying the impact of energetic materials on the environment to ensure safety, establish minimum safe distances, and assess storage requirements. Central to these considerations is the concept of TNT equivalence, a benchmark used to relate the effects of various energetic materials to the well-understood characteristics of Trinitrotoluene (TNT)¹. TNT equivalence not only aids in estimating potential blast damage and risks for individuals, but also supports the determination of safety factors for energetic material storage and handling. However, the definition of TNT equivalence is complex, and there are many experimental bases for the comparison of energetics, including the sand crush test^1–3, ballistic mortar test^1–3, plate dent test^1–3, air blast^1,4–6, and reaction velocity^2,3,5,6. Comparing the reaction energy for an energetic to that of TNT allows estimation of the TNT equivalence with respect to peak pressure, while comparison of the heat of combustion allows estimation of TNT equivalence with respect to quasi-static pressure⁴. Calculating TNT equivalence lacks a universally accepted method due to diverse test parameters, resulting in published measurements varying by as much as 50%^7,8. Theoretical predictions often overlook factors like aluminum content or additional gas production, while experimental approaches tend to focus on one aspect of detonation such as shock, brisance, or overpressure^1,7. Despite this apparent methodological disparity and the resultant diverse outcomes, TNT equivalence remains a quick and reasonably accurate means to acquire data, contingent upon the selection of an appropriate test.

The TNT equivalence values for energetic materials are used to compare the effects of the output of a given energetic to that of TNT, which has a TNT equivalence of 1.00 and serves as the baseline against which other energetics are compared. The TNT equivalence of Composition B (Comp B) typically falls within a range of values due to the range of tests possible. A range of 1.10 to 1.36 can be found with the most commonly cited value being 1.32^1,2,5. It’s important to note that the data available for comparing different energetics often lack consistency and comprehensiveness, making it essential to define the context in which a TNT equivalence value is stated. Notably, the TNT equivalence of C4 at a consistent density is 1.16 based on the sand crush test, 1.30 based on the ballistic mortar test, 1.15 based on the plate dent test, and 1.47 based on the heat of explosion^4,5. Alternative values for TNT equivalence can be calculated according to which property is being compared and when in the reaction or downstream processes the values are measured^6,9. These known values have been widely accepted and utilized in safety assessments, blast modeling, and regulatory guidelines^10–12. This measure helps researchers and practitioners gauge the relative destructive power of different energetics and assess their potential impact on structures, environments, and human lives^1,10,11. Not knowing the TNT equivalence of an energetic can have implications on research, usage, and safety^4,6,9.

While some energetics have well-documented TNT equivalence values, numerous binary energetic materials lack such published data. Binary energetics, which are composed of two separate components that only become energetic when mixed, are increasingly used in industry due to their safety in handling and storage¹³. This research aims to determine TNT equivalence values for such materials, including Tannerite, Rimfire, Texpak, Helix, and Kinepak. As of the current literature, no published TNT equivalence values have been found for these materials^1,2. This research seeks to address this gap by employing a comprehensive testing approach to derive TNT equivalence values experimentally for these commonly used energetic materials. A series of tests were conducted, focusing on three distinct parameters: (1) dent depth measured through the plate dent tests, (2) reaction velocity, using a two-channel time of arrival system, and (3) air blast time-pressure waveforms to measure air overpressure and calculate impulse.

Methods

Three different tests (plate dent, reaction velocity, and air blast) were used to determine the TNT equivalence of different energetic charges. TNT was used as the baseline charge for comparison, and then six different energetics, shown in Table 1, were evaluated based on their various energetic properties. All charges had a net energetic weight near 100 g (g), and consistent densities between the repeats as shown by the low error in each average. The charges were placed inside 2.54 cm diameter PMMA casing for consistency between tests. This charge size was chosen as it is similar to the casing diameter of commercial off the shelf binary products. A charge mass of 100 g was chosen based on the ability to press TNT charges to a maximum 2.54 cm (1 inch) diameter to a density around 90% of the theoretical maximum density (TMD). This resulted in a charge length to diameter ratio of 5, which is in the range of acceptable use for the plate dent test²³. Three repeats were conducted for each energetic type, with an additional repeat for Kinepak due to not initially capturing the reaction velocity measurement. One of the energetics in the study, Tannerite, has a critical diameter of 2 inches and manufacturer recommendation to not use less than 230 g of Tannerite²⁴. To compare Tannerite to the rest of the charges, Rimfire (another Tannerite product with a smaller critical diameter) was evaluated at both charge sizes. The larger charges with a 5.08 cm diameter and mass of 250 g are designated as Rimfire (L) and Tannerite (L). Table 1 includes data for the energetic materials, as tested.

Table 1.

Diameter, density, mass, and height for each energetic charge.

Energetic	Diameter (cm)	Density (g/cc)	Mass (g)	Height (cm)
TNT	2.54	1.54 ± 0.00	98.7 ± 0.20	12.90 ± 0.03
Helix	2.54	1.13 ± 0.05	98.7 ± 4.56	17.30 ± 0.00
Texpak	2.54	1.13 ± 0.00	100.4 ± 0.54	17.45 ± 0.09
Kinepak	2.54	1.20 ± 0.06	100.0 ± 5.83	16.46 ± 0.04
Rimfire	2.54	1.31 ± 0.01	90.8 ± 2.14	13.67 ± 0.32
Rimfire (L)	5.08	1.36 ± 0.13	250.0 ± 0.00	9.03 ± 0.84
Tannerite (L)	5.08	0.77 ± 0.01	251.9 ± 5.12	16.19 ± 0.32

Table 2 shows the formulations of the binary energetics used in the study. Some energetics have weight percentages included in safety data sheets provided by manufacturers while others are proprietary mixes. These materials can be categorized into three groups based on their composition. Commercial AN-based energetics: Kinepak, commercial liquid-based energetics: Texpak and Helix, and synthetic AN-based energetics: Rimfire and Tannerite.

Table 2.

Components of binary explosives.

Energetic	Component 1	Component 2
Kinepak14,15	Nitromethane	Ammonium nitrate (90–95%) and glass oxide (5–10%) powder
Texpak16,17	Nitromethane	Diethylenetriamine
Helix18,19	Nitromethane	Coated aluminum powder
Tannerite20,21	Powder of 90% ammonium nitrate and 10% ammonium perchlorate	Catalyst blend of 90% aluminum powder, 5% titanium powder and 5% zirconium
Rimfire22	Prills of ammonium nitrate and potassium perchlorate	Aluminum powder

Plate dent test

The plate dent test is a standard method of estimating the Chapman-Jouguet (CJ) pressure of an energetic using a linear correlation with the depth of a dent formed in a metal witness plate^25–28. The traditional plate dent test uses steel plates under the energetic charge as a measure of brisance^25–28. However, since the binary energetic materials examined in this study were low brisance materials and would not produce a measurable dent in steel plates, a more malleable material, aluminum, was used. Charges were situated on a 7.62 × 7.62 × 5.08 cm plate for the smaller charges and 15.24 × 15.24 × 5.08 cm plates for the larger charges. A thin layer of petroleum jelly was applied between the charge surface and the plate surface to eliminate air gaps. The charge was initiated with a 10 g cast pentolite booster, and an electric detonator^29,30. Figure 1 shows the setup for the 2.54 cm Kinepak charge and 5.08 cm Tannerite (L) charge with booster and detonator centered on top of the charge.

Fig. 1.

Charge set up for (A) Kinepak 2.54 cm charge and (B) Tannerite (L) 5.08 cm charge.

The resultant dents were scanned using a portable laser scanner, the Ametek HANDYSCAN 3D, which provided 3D images of each dent to an accuracy of 0.1 microns³¹. Due to extra noise resulting from the laser interaction with the aluminim plates, the dents were smoothed over every three points measured using a linear approximation. Each dent’s 3D scan was used to generate a cross-sectional view, highlighting differences across various materials. These cross-sectional views were generated by analyzing multiple sub-sections extracted from each dent. A total of 180 sub-sections were generated along a single, straight line traversing the center of the dent. These crosscuts through the center of the dent were overlayed and averaged to produce a single representative crosscut of the full dent.

The TNT equivalence was calculated from these tests as a ratio of the reaction pressures. Since the dent depth produced by each energetic is known to be linearly correlated to the CJ pressure, a ratio of energetic dent depth to TNT dent depth is equivalent to a ratio of the energetic material CJ pressure and TNT CJ pressure.

Reaction velocity test

Piezoelectric time of arrival pins³² were used to determine the reaction velocity of each energetic. For each charge, the pins were placed in holes at 2 cm and 8 cm from the bottom of the PMMA. This created a 6 cm separation between pins to achieve uniform wave propagation. The distances between the holes were measured using digital calipers to ensure precise reaction velocity calculations. Each time of arrival pin was connected to a separate channel on a PicoScope to record the voltage and corresponding time of arrival of the wave at 250 MegaSamples per second. The PicoScope was connected to a laptop and the PicoScope 7 T8M program was used to collect the time–voltage waveforms. The waveforms were subsequently analyzed to extract the time interval between the top and bottom pins, which were then divided by the distance between the pins. The reaction velocity for each material was recorded and averaged before being compared to the reaction velocity of TNT to calculate the TNT equivalence.

Air blast test

Air blast was measured with two sets of three PCB Piezotronics ICP blast pressure pencil probes (model 137B23B)³³. The six pencil probes were connected to a Synergy Hi-Techniques data acquisition system sampling at two million hertz (MHz)³⁴. Pencil probes were placed in both the near (1.25 m and 1.65 m) and far field (3.73 m and 5 m) at distances designed to achieve comparable pressures for both the 100 g and 250 g charges. Pencil probe sensors were mounted on tripod stands and angled towards the center of the charge. In consultation with the sensor manufacturer, the sensor distances were designed to be located outside the fireball to not affect the pressure reading. The distinction between near and far fields was determined based on the pressure profile of the shockwave as well as examining figures in previous research^35,36, with near field regions typically experiencing minimal attenuation and faster pressure rise, while far field measurements showed greater attenuation and slower pressure changes. For 2.54 cm diameter charges, the near field sensors were positioned at 1.25 m, and the far field sensors at 3.73 m, implementing three sensors in each field to calculate an average pressure and remove outliers. Similarly, for 5.08 cm diameter charges, the near field sensors were placed at 1.65 m, and the far field sensors at 5 m, ensuring that the near field (1.25 m and 1.65 m) and far field (3.73 m and 5 m) distances would yield similar pressure readings for both charge sizes. In the far field, blast effects are predominantly characterized by the propagation of shock waves and air overpressure, which diminish with distance from the explosion point. In contrast, the near field experiences high-intensity shock waves, intense pressures, and fragmentation, resulting in more immediate and concentrated damage^35,37–40. To prevent the disturbance of the sensors due to shockwaves, the sensors were mounted on tripods anchored by sandbags.

TNT equivalence for each energetic material was determined by computing an average peak pressure derived from the three pressure-versus-time waveforms recorded in both the near and far fields. Impulse, also considered in evaluating the performance and characteristics of energetic materials, comprehensively accounts for the full waveform. It represents the change in momentum imparted to the surrounding air or other media due to the reaction of an energetic substance, reflecting the cumulative effect of pressure over time. The impulse for each waveform was calculated by estimating the area under the pressure–time curve at each discrete interval. This provides a more accurate representation of the total impulse by considering the average pressure within each time step. Subsequently, the TNT equivalence was determined by averaging the impulse in both the near and far fields before comparing it to that of TNT.

Results and analysis

Three test series were conducted to establish TNT equivalence values for Helix, Texpak, Kinepak, Rimfire, and Tannerite: (1) plate dent test, (2) reaction velocity, and (3) air blast. Each will be discussed individually, followed by a comparative analysis.

Plate dent test

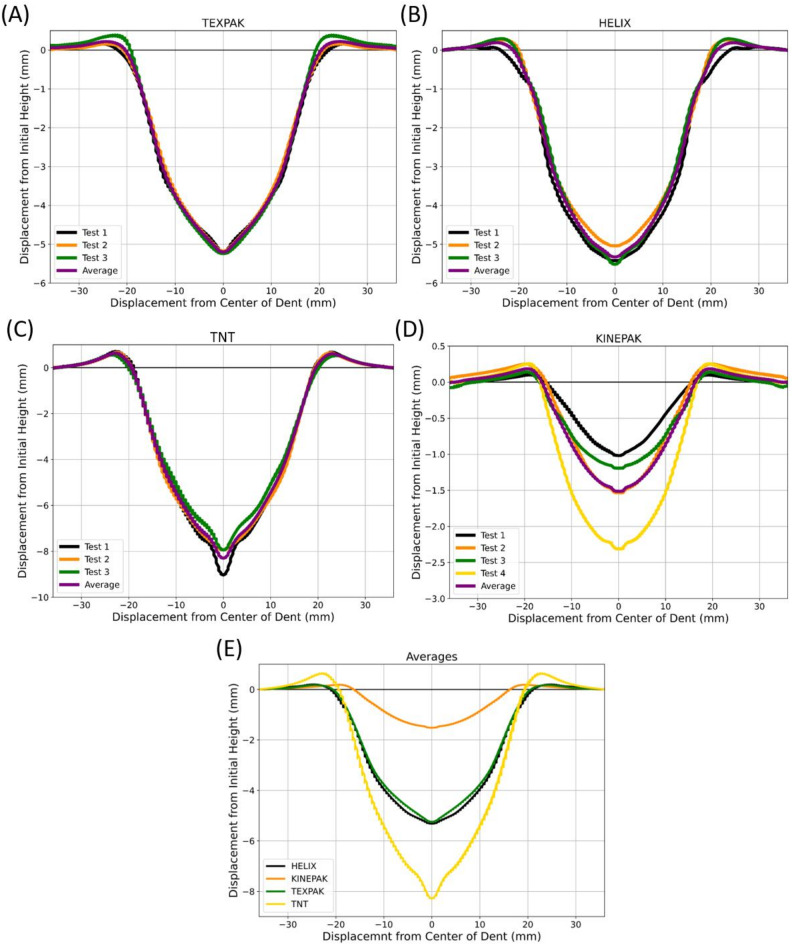
The plate dent tests were conducted to compare the dent depths of lesser studied materials to that of TNT. It’s important to note that some plates showed no visible dents, resulting in no calculated TNT equivalence values for Tannerite or Rimfire. Outputs from this analysis were compared across three repeated tests.

The energetic material dents were captured in aluminum witness plates and are compared in Fig. 2. TNT, in Fig. 2C, showed great consistency between repeats up to about 7 mm from the center of the dent. The two commercial liquid energetics, Texpak in Fig. 2A and Helix in Fig. 2B, had great consistency between repeats. There is some variability in the width of the two liquid dents which is a result of the direct contact between the energetic and the plate. No sealing material or glue could be used around the edge of the casing as it would have affected the dent. As a result, some of the energetic leaked between the casing and the plate.

Fig. 2.

Plate dents: (A) Texpak, (B) Helix, (C) TNT, (D) Kinepak, and (E) average comparison.

Kinepak, in Fig. 2D, showed the most variability between repeated tests. This material needed to be packed into the casing material by hand. This created less control than with the TNT charges, which were pressed at the same mass, to the same pressure, for the same amount of time using a hydraulic press. Given how shallow the dents produced by Kinepak are compared to the other materials, the variability observed in Fig. 2D is negligible. It should also be pointed out, that while the depth of the repeats in Fig. 2C and B are different, the width remains constant and the overall shape of the dents are similar between repeats.

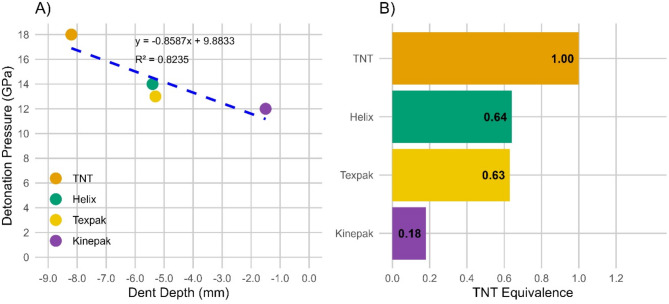
All dent depths were graphed against their respective detonation pressures in Fig. 3. The detonation pressure for TNT have been studied extensively^41–47, providing well-established reference values. The pressures for Helix, Kinepak, and Texpak were broad estimations given by their manufacturers and assumed to be precise for this study^17,18,48. The linear fit line connecting the points showed good alignment with a R² value of 0.82.

Fig. 3.

(A) Plate dent depth versus detonation pressure and (B) TNT equivalence.

The TNT equivalence of each energetic was calculated as a ratio of its average dent depth to the average dent depth of TNT in Fig. 3B. The dent depth has been quantified, so it can be compared to the values found by the remaining methods in this study. From the plate dent test, it is found that the commercial AN energetics have a lower TNT equivalence than the commercial liquid energetics.

Reaction velocity test

The reaction velocity tests measured the velocity upon initiation for each energetic material and then compared the velocities to the baseline energetic, TNT. Utilizing known measurements of the inter-hole distances on the casing of each material, reaction velocity was determined using the time difference between the two time of arrival pin measurements. Additionally, the three repeats of each energetic material were averaged to calculate TNT equivalence. However, due to unattainable data for two Kinepak tests, its reaction velocity calculation is based on two repeat tests. Similarly, some Tannerite L and Rimfire data was insufficient to calculate reaction velocity, thus two data points were used for analysis. Presented in Table 3 are the average reaction velocities and the TNT equivalence values for the energetics. The TNT equivalence was calculated using the ratio between the reaction velocity of the energetic of interest and that of TNT. The included coefficient of variation, expressed as a percentage, is defined as the ratio of the standard deviation to the mean, providing a measure of relative dispersion in the data.

Table 3.

The reaction velocity for each energetics TNT equivalence.

Energetic	Average reaction velocity (m/s)	TNT equivalence	Coefficient of variation (%)
TNT	6603	1.00	27.07
Helix	5727	0.87	130.2
Texpak	6033	0.91	55.85
Kinepak	2528	0.38	6435
Rimfire	1370	0.21	156.6
Rimfire (L)	1511	0.21	1.597
Tannerite (L)	1346	0.18	27.43

Table 3 shows a significant difference in velocity for Kinepak highlighting the influence of density variations on the behavior of commercial AN energetics. Despite maintaining constant length and diameter during testing, the inability to consistently control the compaction of the commercial AN material results in differing densities across tests. This variability in density directly impacts the reaction characteristics of the energetic material, leading to fluctuations in velocities ultimately affecting blast performance. The inconsistency in density across tests poses significant challenges in determining an accurate TNT equivalence that can reliably represent the performance of commercial AN energetics.

Air blast test

The air blast tests aimed to determine the TNT equivalence values by recording time-pressure waveforms in air. Both pressures in the far field and near field were measured using three sensors each and then averaged to calculate the TNT equivalence. TNT equivalence values, average pressure values and the coefficient of variation are shown in Table 4. The results revealed a distinction in TNT equivalence values between near and far field among the tested materials. Energetic materials lacking published TNT equivalence values displayed unexpectedly higher TNT equivalence when compared to the plate dent test results. These variations highlight the importance of using multiple testing methods to assess TNT equivalency, as different tests may yield divergent results due to unique material characteristics.

Table 4.

Pressure in near and far field TNT equivalence.

Energetic	Near field			Far field
	Average pressure (kPa)	Coefficient of variation (%)	TNT Equivalence	Average pressure (kPa)	Coefficient of variation (%)	TNT equivalence
TNT	196.8	2.89	1.00	21.81	10.5	1.00
Helix	188.8	6.83	0.96	23.42	4.06	1.07
Texpak	150.2	9.72	0.76	19.49	9.18	0.89
Kinepak	69.85	1.80	0.35	12.75	4.00	0.58
Rimfire	79.73	5.00	0.41	14.33	3.49	0.66
Rimfire (L)	76.52	6.56	0.41	14.32	10.3	0.66
Tannerite (L)	75.44	3.02	0.40	12.58	9.46	0.57

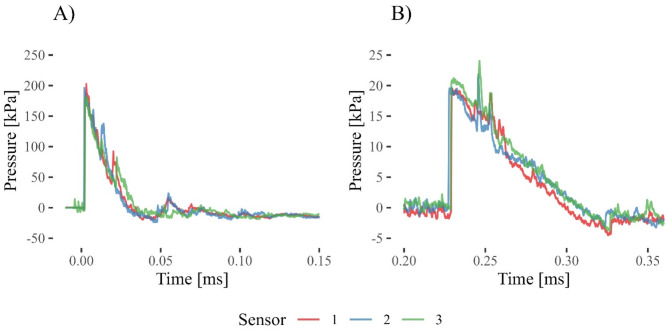
As seen in Table 4, the near field pressure resulted in TNT equivalence values that are lower than the far field pressure TNT equivalence values. Interestingly, the average coefficient of variance is greater in the far field compared to the near field. This contrasts with predictions suggesting that variance would be greater in the near field due to the challenges associated with measurement. Given the fast rise time and rapid decay characteristic of near-field measurements, pinpointing the exact sensor location and angle directed towards the charge becomes more crucial. Figure 4 shows the time-pressure waveforms for TNT in the near and far fields. There is good agreement between the three measurements and a faster decay rate in the near field is clear. A higher coefficient of variance in the far field in this instance is due to the lower pressure overall, accentuating the effect of any small change in the waveforms. Further analysis reveals intriguing nuances in the performance of different energetics within the near and far fields. For instance, Kinepak exhibits lower TNT equivalence values compared to Tannerite, but Kinepak produces dents while Tannerite does not, highlighting variations in their shockwave propagation characteristics. This discrepancy underscores the importance of understanding the specific dynamics of energetic materials in different scenarios.

Fig. 4.

TNT Pressure versus Time waveforms with same time scale starting at 0 in the near field and arriving at the far field sensor 0.23 ms later for (A) near field and (B) far field.

Comparing the near and far field pressure TNT equivalence values across various types of energetics offers insights into the distinct compositions and reaction characteristics inherent to each. This comparison sheds light on how differences in formulation and behavior contribute to varying peak pressures and duration. In the pressure measurements, commercial AN based energetics like Kinepak, exhibit lower TNT equivalence values. This could be attributed to the tendency of commercial AN-based energetics to hold together rather than rapidly disperse after reaction. Commercial liquid-based energetics such as Helix and Texpak show slightly higher TNT equivalence values, likely due to their more homogeneous nature, allowing for more efficient energy release. Synthetic AN-based energetics like Rimfire and Tannerite demonstrate moderate TNT equivalence values, because of the efficient conversion of AN into gas during reaction. Pressed energetics like TNT have denser and more compact compositions, leading to greater propagations of energetic force over longer distances.

While pressure measures the force exerted by an explosion at a specific point in time, impulse accounts for the cumulative effect of that force over a duration. This distinction is crucial as it provides a more comprehensive understanding of how energetics interact with their surroundings. Hence, exploring impulse alongside pressure offers a more detailed perspective on the behavior and impact of the different energetic materials. TNT equivalence values, average impulse values, and the coefficient of variance are shown in Table 5.

Table 5.

Impulse in near and far field TNT equivalence.

Energetic	Near			Far
	Average impulse (kPa ms)	Coefficient of variation (%)	TNT equivalence	Average impulse (kPa ms)	Coefficient of variation (%)	TNT equivalence
TNT	57.00	1.85	1.00	18.85	11.8	1.00
Helix	62.83	2.26	1.10	19.95	1.63	1.06
Texpak	51.48	3.58	0.90	16.50	1.83	0.88
Kinepak	29.42	2.05	0.52	9.469	0.85	0.50
Rimfire	38.53	11.7	0.68	13.38	2.73	0.71
Rimfire (L)	38.01	0.55	0.68	12.87	1.35	0.71
Tannerite (L)	32.06	1.87	0.56	10.48	1.97	0.56

Table 5 demonstrates a closer relation between TNT equivalence values calculated for the near and far field impulse compared to the air overpressure near and far field values. The coefficient of variation for impulse values are below 3.6% for all other than Rimfire in the near field and TNT in the far field. While the highest coefficient of variation being TNT in the far field seems concerning as the reference material, the fact that both the near and far field TNT equivalence values are in such close agreement for all energetics reduces this concern, since the TNT coefficient of variation in the near field is low at 1.85%. Impulse, being a measure of the total momentum imparted to the surrounding medium, is less susceptible to the localized effects that contribute to air overpressure variability. The reliability of impulse as a parameter can be attributed to its integration over time, capturing the cumulative effect of the energetic event. This provides a more stable and consistent metric that reflects the overall impact of the reaction.

Comparing the impulse values with those of pressure across both near and far fields reveals notable differences and similarities among the energetics tested. In the near field, while the order of energetics by impulse generally follows a similar trend to that of pressure, there are some variations. Kinepak, despite its lower pressure values, shows higher impulse values in both near and far fields. This discrepancy implies that Kinepak might sustain its energetic force for a longer duration despite generating lower pressure, potentially due to its unique composition and reaction characteristics. Similarly, in the far field, the order of energetics by impulse generally corresponds with their pressure based rankings, with a few exceptions. Notably, Rimfire exhibits higher impulse values relative to its pressure based TNT equivalence, indicating a longer duration of energetic force release. This divergence suggests that while Rimfire may not generate the highest pressure, it might sustain its energetic force for a longer period, leading to greater impulse values. This finding highlights the multifaceted nature of energetic behavior and emphasizes the need for comprehensive testing to capture various aspects of their performance accurately.

Comparative analysis

All TNT equivalence values obtained from the plate dent tests, air blast tests, and reaction velocity tests are compiled into Table 6. This consolidation allows for a comprehensive analysis of all calculated values across the different tests, providing a holistic understanding of the relative performance of various energetic materials.

Table 6.

TNT equivalence values from each experimental test method.

TNT equivalence
Energetic	Plate dent	Near field pressure	Far field pressure	Near field impulse	Far field impulse	Reaction velocity
TNT	1.00	1.00	1.00	1.00	1.00	1.00
Helix	0.64	0.96	1.07	1.10	1.06	0.87
Texpak	0.63	0.76	0.89	0.90	0.88	0.91
Kinepak	0.18	0.35	0.58	0.52	0.50	0.38
Rimfire	-	0.41	0.66	0.68	0.71	0.21
Rimfire (L)	-	0.41	0.66	0.68	0.71	0.21
Tannerite (L)	-	0.40	0.57	0.56	0.56	0.18

Comparing the results obtained from the plate dent test, air blast test, and reaction velocity test in Table 6 revealed variations in TNT equivalence values for the commercial AN, commercial liquid, and synthetic AN-based energetic materials. These tests revealed several findings including possible dependency on brisance, packing method, grain size, and material hardness. The commercial AN energetics exhibit a noticeable variation in TNT equivalence order when compared to synthetic AN-based energetics for both the reaction velocity and air blast test results. An explanation for this might be based on the purpose of the energetic materials produced as well as the type. Commercial AN-based energetics such as Kinepak are manufactured with agricultural blasting and demolition in mind, while Tannerite and Rimfire are synthetic AN-based energetics manufactured for target practice. As a result, the synthetic AN-based energetics exhibit more consistent performance in the air blast test. The differences in design and optimization of these energetics for their respective applications contribute to the observed variations in their TNT equivalence for each different test. The unique composition and packing method of these energetics renders them more responsive to certain experimental conditions, leading to their distinct performance in each test. Such disparities underscore the intricate interplay at hand when determining the TNT equivalence.

When evaluating the energetic material reaction characteristics, destructive power is evident in metrics such as plate dent and reaction velocity. Close alignment in destructive power, as indicated by plate dent tests, suggests comparable effectiveness in causing physical damage to targets. Similarly, reaction velocity values offer insights into the speed at which the energy propagates, influencing its ability to cause destructive effects. However, if downstream air blast effects are of interest, metrics like air blast pressure and impulse become essential. These measures capture the force exerted by the explosion on surrounding structures over time, providing information for assessing the potential impact on the environment and infrastructure downstream from the explosion. Therefore, the choice of metric depends on the specific application and the desired focus for safety, whether it be immediate destructive effects or the broader downstream consequences of the explosion.

Conclusion

This research used three experimental tests to determine TNT equivalence for materials not found in literature but commonly used in the military, in research, and by law enforcement. Test methods included, (1) plate dent test, (2) reaction velocity, and (3) air blast. Materials tested were Tannerite, Rimfire, Texpak, Helix, Kinepak, and TNT.

Consistent with the same tests performed in literature, each test produced a different TNT equivalence value, as each evaluates a different effect of the energetic power. Analyzing the correlation between the TNT equivalence values obtained provides valuable insights into the behavior and performance of a range of energetic materials, including commercial AN, commercial liquids, and synthetic AN-based energetics. Across multiple tests, the commercial AN-based energetic, Kinepak, consistently exhibits lower TNT equivalence values compared to other materials. Kinepak TNT equivalence values produced for near and far field impulse are 0.52, 0.50, and 0.58, 0.58, while the values from the plate dent test are 0.18 and 0.11, respectively. This suggests that while commercial AN-based materials may have sufficient impulse for downstream air blasts, their effectiveness in generating destructive power is relatively limited. Commercial liquids, represented by Helix and Texpak, demonstrate TNT equivalence values close to those of TNT in most tests, indicating their comparable performance in terms of energetic power. Helix produced TNT equivalence values ranging from 0.64 to 1.10 and Texpak produced values ranging from 0.63 to 0.91 across all three tests. These findings suggest that commercial liquid energetics are effective for applications requiring rapid energy release and are capable of propagating energy downstream as pressure. Synthetic AN-based energetics, including Rimfire and Tannerite, exhibit moderate TNT equivalence values across the air blast tests relative to others in this study, while being unable to produce a dent. Rimfire and Tannerite’s TNT equivalence values for the air blast test ranged from 0.41 to 0.71 and 0.40 to 0.57, while reaction velocity values were 0.21 and 0.18, respectively. This reflects their efficiency in converting AN into gas during reaction while being unable to produce dents showing their limitations in destructive power.

The consistent trends observed among the various types of energetic materials highlight the importance of considering their specific characteristics and behaviors when assessing their TNT equivalency. Commercial AN-based energetics, while effective in certain applications, may not exhibit the same level of performance as commercial liquids or pressed energetics. Similarly, synthetic AN-based energetics demonstrate moderate TNT equivalence values for air blast, reflecting their unique composition and reaction characteristics, but lack the energetic power demonstrated in the other energetics. Overall, TNT equivalency values will vary under different experimental conditions including diameter and confinement. Values found through this work should be used with caution, ensuring that appropriate safety factors are applied if test parameters are changed. Selection should be based on the most suitable value for the specific application at hand. Values from the plate dent test or reaction velocity test are suggested if close in destructive power is of interest, or impulse if downstream air blast effects are being calculated.

Author contributions

G.M.J, R.L.B, E.M.J. and C.E.J. all performed formal analysis, investigation, methodology design, and writing of the original draft and review and editing. C.E.J additionally provided supervision, resources, project administration, and funding.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Declarations

Competing interests

The authors declare no competing interests.