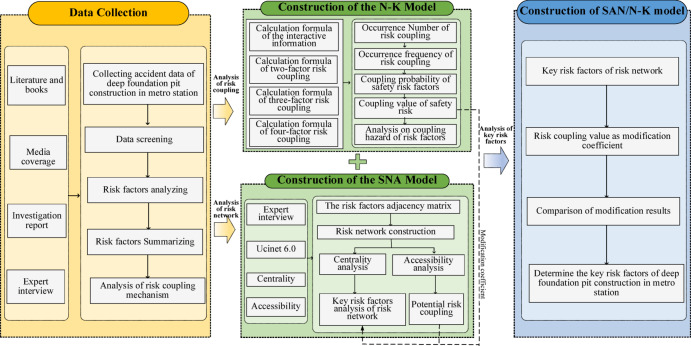
Abstract
From a systematic perspective, the triggering mechanism of safety risks in deep foundation pit construction at metro stations results from the coupling among multiple risk factors. To scientifically explore the mechanisms of risk factors in deep foundation pit construction at metro stations and prevent safety accidents, the N-K model and SNA model are introduced to explore the interaction and coupling of safety risks. According to the collected data of 197 metro station foundation pit accidents over the past 30 years, a risk factor system comprising five primary risk factors and 36 secondary risk factors is established. Subsequently, based on the analysis of coupling mechanisms and risk network characteristics, key risk factors are determined by combining the coupling effect evaluation from the N-K model with the centrality and accessibility analyses from the SNA model. The results indicate that multi-risk coupling should be avoided during the construction stage of deep foundation pits at metro stations. Considering the coupling effect, the risk factors such as poor awareness of personnel security, insufficient professional skills, and insufficient safety investment are the key risk factors that require attention. These research results can serve as a theoretical reference for enhancing safety management and control for deep foundation pits at metro stations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-025-00526-0.
Keywords: Deep foundation pit of metro station, Construction safety, Risk factor coupling, N-K model, Social network analysis (SNA)
Subject terms: Risk factors, Engineering, Mathematics and computing
Introduction
Amid the global urban modernization drive, the metro systems have rapidly developed, effectively alleviating the congestion issues plaguing urban ground transportation, and have gradually become the dominant choice for urban rail transit, particularly in developing countries like China. According to the data of Statistics and Analysis Report of Urban Rail Transit 2022 issued by China Urban Rail Transit Association, 6,350.55 km of rail lines were under construction, with 3,860 stations being built and an additional 3,284 stations planned in China by the end of 2022. The station is a critical component of metro construction, and the excavation work, as a key aspect of station construction, often encounters various challenges, including complex and varied construction environments, large excavation depth, diverse cross-working procedures, extensive machinery and equipment use, and complex construction management, all of which heighten the risk of safety incidents. For instance, the collapse at Xianghu Station of Hangzhou Metro on November 15, 2008, led to 21 fatalities and 49.61 million yuan in direct economic losses. Similarly, the collapse of Baimang Station of Shenzhen Metro Line 13 on August 22, 2022, resulted in one fatality and direct economic losses of one million yuan, highlighting the persistent severity of safety concerns in recent years. Safety accidents during metro station excavation often result in serious casualties and property losses, requiring urgent attention. Therefore, it is crucial to effectively control and manage risks in deep foundation pit construction of metro stations to mitigate safety accidents.
The construction of deep foundation pits for metro stations is a complex systems engineering project. The impact of any single factor on safety accidents is limited. Safety accidents are often influenced by multiple risk factors which interact within or between risk subsystems to breed risks. Although risk coupling has garnered attention in various safety research fields as an interdisciplinary topic, the interaction and coupling of risks are seldom addressed in studies on the safety of deep foundation pit construction in subway stations. Therefore, a comprehensive study on scientific methods for risk coupling analysis is essential. This will enable a deeper understanding of the interrelationships among risk factors in accidents during deep foundation pit construction at metro stations, thereby revealing the underlying cause mechanism of safety accidents and enabling the formulation of effective risk control strategies.
Based on the preceding research background, the second section reviews the relevant literature on construction safety of deep foundation pit in metro station, and puts forward the research ideas. The third section analyzes the risk coupling mechanism based on risk factor identification, and introduces the application framework, along with the integration of the N-K and SNA models. The fourth section delves into the application results of N-K and SNA model in the safety risk analysis. Finally, the fifth section draws conclusions and summarizes the article.
Literature review
The excavation depth of metro station foundation pits is increasing, exhibiting characteristics such as greater depth, larger scale, closer proximity to surrounding structures, and more compressed construction schedules1. The construction safety of these projects is a primary focus for scholars and engineers. Research on safety in deep foundation pit construction at metro stations has primarily focused on risk analysis methods and management strategies. Chen et al. proposed an integrated framework for risk identification in deep foundation pit construction by leveraging knowledge management and BIM2. Sharafat et al. proposed an information modeling framework for underground engineering projects utilizing BIM technology, with the aim of enhancing project data management and risk assessment3. Zhou et al. employed a Bayesian network to establish a risk analysis model focusing on diaphragm wall deflection using the data of subway construction site4. Sharafat et al. applied the Bow-Tie Risk Analysis method to conduct a systematic risk analysis of geological factors, construction management factors and design factors in tunneling projects under complex geological conditions5. Similarly, Sharafat et al. utilized a risk assessment methodology utilizing Event Tree Analysis in an additional study6. Zhou et al. combined complex network and Association Rule Miming as a new risk analysis method to uncover associations between security risk monitoring types and risk coupling, thereby enhancing the identification of risks from abnormal monitoring combinations7. Lin et al. improved the accuracy of risk assessment grades of foundation pit excavation through machine learning by using 3 S technology and massive amounts of data collected by sensors8. Based on fuzzy evidential reasoning-based approach, Wei et al. proposed a comprehensive risk assessment method for deep excavation construction projects9. Considering the characteristics of fuzziness, randomness and uncertainty present in metro deep foundation pit construction risks, Zhang et al. presented an enhanced fuzzy comprehensive evaluation method that combines the triangular intuitionistic fuzzy cloud model with probability density function10. Wu et al. proposed a Multi-Source Intelligent Fusion Assessment Method taking the monitoring data as the analysis sample11. Some studies have pointed out that there remains a degree of one-sidedness in risk studies related to metro deep foundation pits. Specifically, the mutual coupling effects between risk factors are largely neglected in risk factor analysis, leading to an insufficient exploration of their impact on construction safety12,13.
In recent years, an increasing number of scholars have focused on the understanding that the triggering mechanism of risk arises from the interaction and coupling of multiple factors. Fang et al. employed the four-module analysis approach to identify the key causes of metro collapse accidents and their coupling risk effect, and analyzed the evolution process of the accidents14. Qiao contended that the coupling effect among various risks was the significant cause of coal mine accidents, and conducted measurements to evaluate this risk coupling effect15. Some academics have begun to focus on investigating the risk coupling mechanisms and mathematical models of multiple factors. Currently, their research primarily targets the fields of transportation16, fire17,18, coal mine19, and especially, they have made rich research achievements in the study of the risk coupling mechanisms in construction projects. Xiang et al. explored the risk coupling mechanisms of cross-regional mega projects using system dynamics method and proposed the decoupling control method20. Zhang et al. utilized the N-K and system dynamics methods to assess coupling modes of tunnel construction risks from four dimensions: personnel, equipment, environment, and management, and established the conduction path of risk factors21. To quantitatively analyze the coupling degree of risk factors in shield tunnel construction, Pan et al. utilized the improved coupling model for quantitative calculations and applied it to actual cases to evaluate the risk coupling levels22. The mainstream models for studying coupling mechanisms in existing research systems include the N-K model, the SD model, and the coupling model. Comparatively, the N-K model proposed by Kauffman23 is an important tool for researching risk coupling in complex systems. By utilizing objective data from past accidents, risk coupling utility can be assessed using the N-K model, which can reduce subjectivity and is widely applied in the coupling risk analyses in transportation24,25, aviation safety26, fire27, and project construction28,29. In the safety management of metro construction, Fang et al. quantified the risk coupling effects of personal, mechanical, material, management and environmental factors during subway tunnel construction through the application of the N-K model30. Guo et al. utilized the N-K model to compute the risk coupling values of complex geological and construction factors in tunnel construction, and their findings proved that the coupling risk of these components exceeded their individual effects31. The aforementioned research demonstrates the feasibility and applicability of the N-K model in risk analysis and security state evaluation. Nevertheless, due to data constraints, the N-K model focuses on analyzing primary risk indicators and assesses the likelihood of accidents resulting from the coupling of different risk factors, it cannot provide more targeted information on sub-risk factors.
Risk factors are interconnected and influence one another, presenting a complex network relationship. The research by Pryke and Chinowsky pioneered the application of SNA in the engineering field32,33, and it is currently utilized by numerous scholars to analyze how risk factors relate to one another in the field of engineering construction. Ding et al. integrated the complex network theory with the risk analysis method of association rule mining, proposing the association law of monitoring types of engineering construction safety risks and risk coupling34. Chen et al. established the risk factor network for underground engineering from the dimensions of management, environment, technology, and personnel elements, and important risk factors were then identified through SNA analysis of each risk component’s position and degree of interaction35. Qin et al. employed the SNA model to identify critical risk factors of green buildings36. Yuan et al. applied social networks to explore the life cycle risks in prefabricated building projects, evaluating key risks and their interactions while formulating corresponding strategies37. The aforementioned research indicates that the perspective of social network analysis emphasizes the interaction between risk factors and focuses on the analysis of the relationships among causal factor nodes. However, it lacks an examination of the differences in risk nodes concerning the accident’s hazardousness.
Given that most existing literature on the safety management of deep foundation pits in metro stations does not address the mechanism linking risk coupling values to sub-risk factors, the complementary use of the N-K model and SNA model can yield more reliable conclusions. The risk coupling value obtained by N-K model is utilized for evaluating the coupling hazard, while SNA model is employed to identify the factor relationship and evaluate key risks within the network. By optimizing the network key risks using risk coupling values and further quantifying the risk factors and their internal relations, the key risk factors are identified. This will enhance understanding of the interrelationships among risk factors in accidents during deep foundation pit construction at metro stations, hereby revealing the underlying causes behind safety accidents and providing a valuable reference for the scientific prevention of safety risks.
Materials and methods
Analysis on risk factors
Identification of risk factors
To quantitatively analyze the coupling effect of safety risks in deep foundation pit construction of metro stations, relevant construction safety accidents are collected and compiled to form a case database. The following steps are undertaken to identify and analyze the risk factors.
Data collection: Collecting data on safety accidents in deep foundation pit construction of metro stations by searching for research literature published on academic websites, books, news media reports, accident investigation reports and conducting expert interviews.
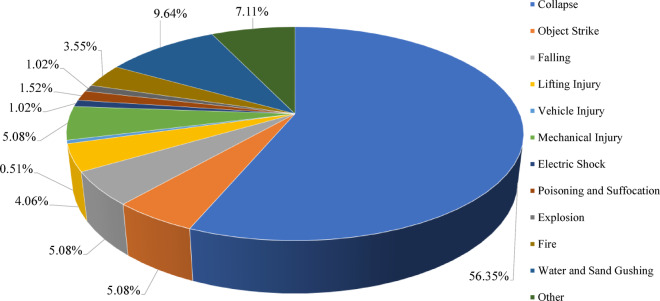
Data screening: An analysis framework was utilized, encompassing the basic information of deep foundation pit projects, including time, place, accident type, accident process, accident consequence, accident cause and treatment measures of the safety accident in the construction process of deep excavation of metro stations. Cases where the reasons could not be identified or the data were unreliable were excluded to ensure data quality. Ultimately, a total of 197 safety accident cases related to deep foundation pit construction for metro stations were collected from 1991 to 2023. These cases include various incidents such as collapses, falls, mechanical injuries, and other types of accidents. The distribution of various types of safety accidents in metro stations during deep foundation pit construction is shown in Fig. 1.
Fig. 1.
Type and proportion of safety accidents in deep foundation pit construction of metro station.
-
(3)
Risk factors analysis: On the basis of the collected accident process and causes, a further analysis is conducted on the risk factors influencing the construction safety of deep foundation pit construction of metro stations. This analysis is supplemented by a review of relevant literature and draws upon established causation analysis patterns from existing safety incidents and systematic thinking. The “4M1E” system safety theory and Wuli-Shili-Renli (WSR) system approach38 are used to construct a risk factor framework based on the safety system, primary risk factors, and secondary risk factors. This framework encompasses five dimensions, leading to the further categorization and compilation of 36 secondary risk factors, as detailed in Table 1. The “p”, “w”, “m”, “e” and “t” represent “Personnel”, “Material”, “Management”, “Environmental” and, “Technical” risk factors respectively in the following discussion.
Personnel risk factors refer to risks associated with all individuals present at the construction site.
-
2)
Material risk factors include hazardous elements associated with machinery, equipment and materials.
-
3)
Management risk factors are primarily concerned with safety rules and regulations, organization scheme management, hidden danger investigation management and safety investment.
-
4)
Environmental risk factors refer to hazards and harmful factors arising from the construction environment.
-
5)
Technical risk factors consider the complexity of construction methods and techniques involved in deep foundation pit construction, including inaccurate survey data and conclusions, design risks, and irregular construction practices.
Table 1.
Safety risk factors of deep foundation pit construction in metro station.
| Primary risk factor | Secondary risk factor | Typical accident cases |
|---|---|---|
|
Personnel risk factors (p) |
Poor awareness of personnel security11,40 (p1) | Falling accident at Memorial Hall Station of Guangzhou Metro |
| Insufficient professional skills10,13,41 (p2) | Collapse accident at Chongwen Men Station of Beijing Metro | |
| Poor safety emergency response ability13 (p3) | Collapse accident at Daxin Station of Shenzhen Metro | |
| Inadequate personnel protection30 (p4) | Falling accident at Songjiazhuang Station on Beijing Metro | |
| Poor physical or mental health30 (p5) | The other accident at Xiaomeisha Station of Shenzhen Metro | |
| Violation of operating regulations13,40 (p6) | Object strike accident at Jixiang’an Station of Nanjing Metro | |
|
Material risk factors (w) |
Inadequate equipment maintenance30 (w1) | Mechanical injury accident at Yan’an 3rd Rd Station of Qingdao Metro |
| Equipment failure13,41 (w2) | Lifting injury accident at Fuzimiao Station of Nanjing Metro | |
| Unreasonable equipment selection13 (w3) | Lifting injury accident at Bid 3 of Guangzhou Metro | |
| Unreasonable arrangement of mechanical work13 (w4) | Lifting injury accident at Fuzimiao Station of Nanjing Metro | |
| Improper construction material storage30 (w5) | Collapse accident of Heyu Road on Hangzhou Metro | |
| Defective retaining structure10,40,41 (w6) | Collapse accident at Zhejiang Chinese Medical University Station of Hangzhou Metro | |
| Insufficient strength and stability of internal support10,39,41 (w7) | Collapse accident of the Nicoll Highway in Singapore metro | |
| Substandard strength of anchor rod and pull rod13,39 (w8) | Collapse accident at Bayi memorial Station of Nanchang Metro | |
| Unqualified construction materials30,41 (w9) | Collapse accident at Shengli Bridge Station of Qingdao Metro | |
|
Management risk factors (m) |
Inadequate safety education and training30,41 (m1) | Collapse accident at Zhenxing Road Station of Hefei Metro |
| Incomplete rules and regulations10,30 (m2) | Collapse accident at Dujiaping Station of Changsha Metro | |
| Insufficient safety investment (m3) | Collapse accident at Jinshanqiao Sub-center Station of Xuzhou Metro | |
| Inadequate safety supervision and hidden danger inspection1,30,40 (m4) | Object strike Accident at Lingling Road Station of Shanghai Metro | |
| Inadequate security disclosure (m5) | Collapse accident at Baimang Station of Shenzhen Metro | |
| Illegal subcontracting (m6) | Collapse accident at Xianghu Station of Hangzhou Metro | |
| Unreasonable safety construction organization design13,30 (m7) | Collapse accident at Shuijing Station of Shenzhen Metro | |
|
Environmental risk factors (e) |
Poor engineering geological and hydrological conditions5,10,40 (e1) | Collapse accident at Dashi Station of Guangzhou Metro |
| Harsh weather or natural disasters40,41 (e2) | Collapse accident at Zhejiang Chinese Medical University Station of Hangzhou Metro | |
| Complicated underground pipeline laying39,40 (e3) | Collapse accident at Shiliuzhuang Station of Beijing Metro | |
| Closing to large high-rise buildings10,39 (e4) | Collapse accident at Harbin East Railway Station of Harbin Metro | |
| Complicated peripheral traffic39 (e5) | Collapse accident at Haidian Huangzhuang Station of Beijing Metro | |
| Harsh operating environment41 (e6) | Electric shock accident in phase II Project of Wuhan Metro | |
|
Technical risk factors (t) |
Unspecified or deviation of geological and hydrological survey1,10,39 (t1) | Collapse accident at Chengzhan Station of Hangzhou Metro |
| Improper design scheme5,10 (t2) | Collapse accident of the Nicoll Highway in Singapore metro | |
| Not prepared special construction scheme10 (t3) | Collapse accident at Xidan Station of Beijing Metro | |
| Over-excavation40,41 (t4) | Collapse accident at Middle Yanji Road of Shanghai Metro | |
| Improper construction method of retaining structure13 (t5) | Collapse accident at Dujiaping Station of Changsha Metro | |
| Error in setting and demolishing supports13,40 (t6) | Collapse accident at Daxin Station of Shenzhen Metro | |
| Insufficient monitoring of foundation pit1,10,39 (t7) | Collapse accident at Jiangxi Road Station of Qingdao Metro | |
| Untimely dewatering and drainage39,41 (t8) | Collapse accident at Luban Road of Shanghai Metro |
For instance, the collapse of the North 2 foundation pit at Xiang hu Station in Hangzhou on November 15, 2008, occurred in a soft foundation area, characterized by significant soil layers, including high-water-content silt and silty soil. The groundwater level was shallow, with no confined water. The excavation base primarily rested on silty clay, which exhibited poor engineering properties and was prone to quicksand phenomena. The foundation pit measures 107.8 m in length, 21.05 m in width, and has a depth of 15.7 to 16.3 m. The excavation utilized a “diaphragm wall with four levels of steel pipe internal supports” for shoring. The incident resulted in 21 fatalities and direct economic losses amounting to 49.61 million yuan. Analyzing the cause of the accident, the direct reason was over-excavation, with weaknesses in the supporting system and delayed installation of the steel pipe supports. Additionally, the monitoring system was ineffective. Indirect causes included illegal subcontracting and inadequate safety education and training. Following the five-dimensional risk factor system, the risk factors can be categorized as technical risk factors (t4, t6, t7), and management risk factors (m1, m6).
Coupling mechanism of safety risk
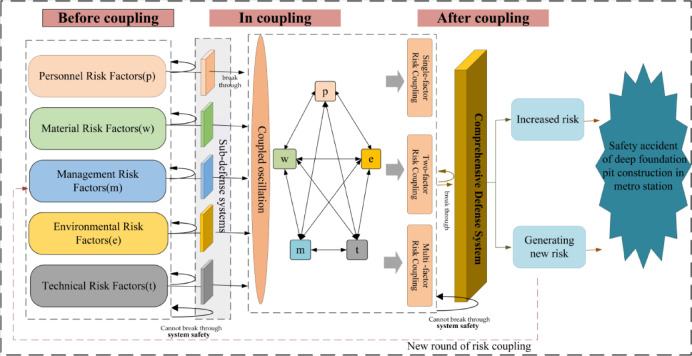
Risk coupling refers to the phenomenon in which risk factors within a system interact and reinforce one another, resulting in changes in the system’s stability and risk levels. The risk system in deep foundation pit construction for metro stations is a complex dynamic system comprised of numerous subsystems, including construction personnel, machinery and materials, project management, construction environment, and technical methods. Within this system, risk factors are intricately intertwined, influencing and interacting with each other, thus leading to the occurrence of risk coupling. The combined effects of multiple risk factors during the construction process reduce the system stability, thereby increasing the likelihood of safety accidents. Figure 2 qualitatively analyzes the coupling mechanism of the risk system in deep foundation pit construction for metro stations.
Fig. 2.
Analysis of risk coupling mechanism.
During the construction process of deep foundation pits for metro stations, the risk control system can achieve proactive risk management through self-recovery and adaptive adjustment mechanisms when risks emerge. The system remains secure as long as risk factors are effectively contained and isolated by five independent sub-defense systems operating. However, when escalating risks break through these subsystem defenses while active control measures of the safety system fail, the risk factors begin to manifest multiple coupling effects. The system maintains operational safety provided that the magnitude and impact of this coupling remain constrained within the tolerance threshold of the comprehensive defense system. A critical transition occurs when the interaction intensity of risk factors after coupling increases through oscillation coupling, leading to a sharp rise in risk, or the emergence of new risk factors. Under these conditions, coupled risks that surpass the capacity of the comprehensive defense system result in complete safety system failure and subsequent accidents. Unaddressed risks will lead to a new cycle of risk coupling, further exacerbating systemic vulnerabilities.
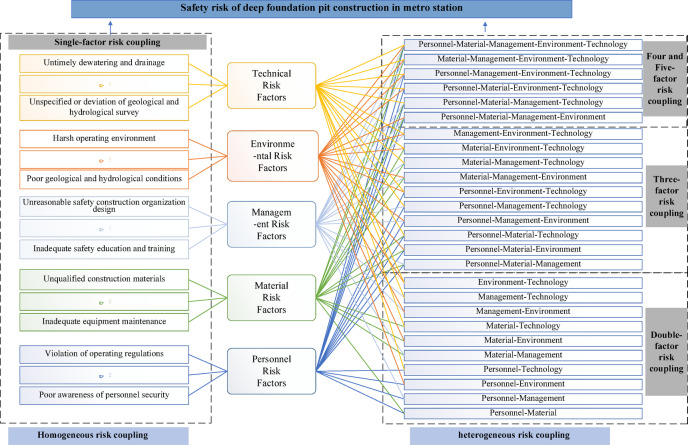
Risk coupling in deep foundation pit construction at metro stations can be categorized into three types based on the number of factors involved: single-factor risk coupling, double-factor risk coupling and multi-factor risk coupling which include three, four or five factors. More specifically, single-factor risk coupling is deemed homogeneous, whereas the others are considered to be heterogeneous (Fig. 3). In terms of factor composition, single-factor risk coupling refers to the internal influence of a single type among the five types of risk factors, for example, inadequate equipment maintenance can affect equipment failure which will cause accidents. Double-factor risk coupling pertains to the interaction between two distinct categories of risk factors, for example, personnel physiological and psychological state or professional and technical level will affect the maintenance of equipment. Multi-factor risk coupling is a relationship in which three or more types of risk factors interact and influence each other, for example, harsh environment will adversely affect safety behavior and the condition of equipment.
Fig. 3.
Sketch of coupling types of risk factors.
Establishment of the N-K/SNA model
Construction of the N-K model
The N-K model serves as a widely used tool for investigating complex system issues, and its applicability in construction engineering has been validated through various studies, allowing for the examination of interactions among different risks within the safety system of deep foundation pit construction at metro stations. The N-K model consists of two key parameters: N represents the number of elements in the system, which corresponds to the number of risk factors. If the system consists of N elements and each element has n states, then there are nN possible states within the system. K denotes the number of dependencies between elements, indicating the number of coupled risk elements, with K ranging from [0, N-1]. In the context of deep excavation construction systems at metro stations, N refers to the number of categories of risk factors (five in this case), with each category having two states: occurrence and non-occurrence. K represents the number of interactions among these risk factors which lead to coupling. The fundamental principle of using the N-K model to analyze coupling risks during deep excavation construction at metro stations is the calculation of the interaction information value (T) among various factors, including personnel, material, management, environment, and technology. A higher value of T indicates an increased likelihood of safety risks occurring.
In the study of safety risk coupling in deep foundation pit construction at metro stations, interactive information 
that considers the coupling of five distinct categories of risk factors is shown in the Calculation Formula (1):
 |
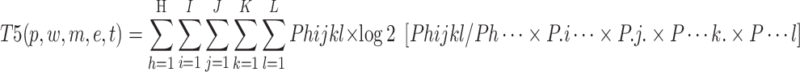1 |
where, 
denotes the probability of coupling between the condition of personnel risk factors in state h, the condition of material risk factors in state i, the condition of management risk factors in state j, the condition of environmental risk factors in state k and the condition of technical risk factors in state l;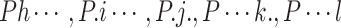 
respectively represent the probability of the condition of personnel risk factors being in state h, the condition of material risk factors being in state i, the condition of management risk factors being in state j, the condition of environmental risk factors being in state k and the condition of technical risk factors being in state l; The “.” signifies that the condition of the corresponding risk factor is unknown.
Partial coupling exists in the interaction among risk factors, which includes homogenous single-factor coupling, heterogenous double-factor coupling, heterogenous three-factor coupling and heterogenous four-factor coupling. Homogeneous single-factor coupling reflects the internal factors of each risk subsystem, making the previous formula inapplicable. In heterogeneous two-factor coupling, there are ten risk combinations: “Personnel-Material”, “Personnel-Management”, “Personnel-Environmental”, “Personnel-Technical”, “Material-Management”, “Material-Environmental”, “Material-Technical”, “Management-Environmental”, “Management-Technical”, and “Environmental-Technical”, whose coupling values are respectively labeled as 
, 
, 
, 
, 
,
, 
, 
,
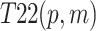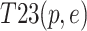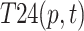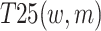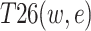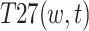and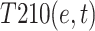 
. The total risk coupling value for heterogeneous two-factor coupling is denoted as T2 in Calculation Formula (2):
 |
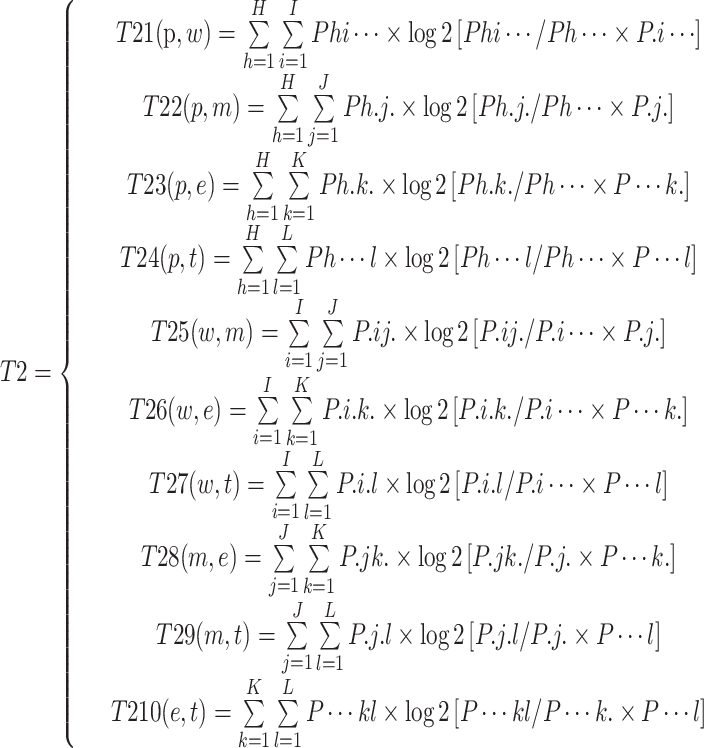2 |
In heterogeneous three-factor coupling, there are ten risk combinations, whose coupling values are respectively labeled as 
, 
, 
, 
, 
, 
, 
,
, 
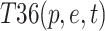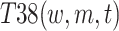and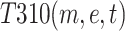 
. The total risk coupling value for heterogeneous three-factor coupling is denoted as T3 in Calculation Formula (3):
 |
3 |
In heterogeneous four-factor coupling, there are five risk combinations,, whose risk coupling value are respectively labeled as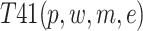 
, 
, 
, 
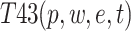and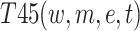 
. The total risk coupling value for heterogeneous four-factor coupling is denoted as T4 in Calculation Formula (4):
 |
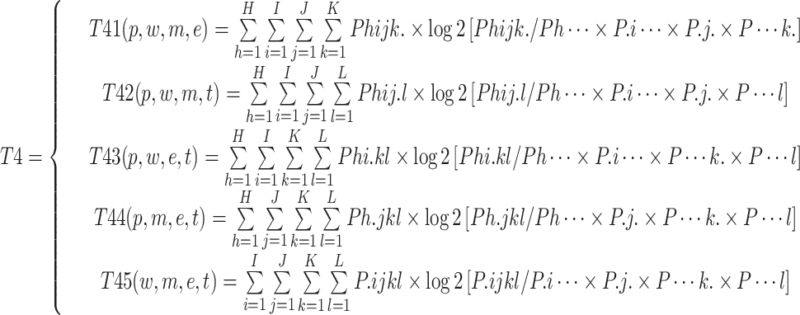4 |
Construction of the SNA model
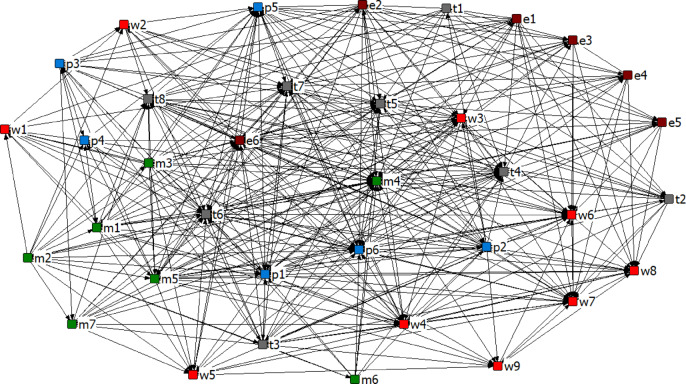
Social Network Analysis (SNA) was initially developed by experts and scholars in the social sciences. It integrates graph theory and mathematical models to construct the complex network structures of relevant entities within a specific system, enabling quantitative analysis of interactions between nodes and node sets in the network. In risk research, this method transcends the limitations of assuming risk independence, facilitating a more comprehensive understanding of the intrinsic relationships and interactions among different risks. SNA is employed to analyze the risk network relationships in deep foundation pit construction at metro stations. Key risk factors of network are derived from analyzing the influence degree among risk factors. The risk impact adjacency matrix was established based on expert interviews, and a visual network model was constructed (Fig. 4). In the network, risk factors are represented as nodes and the interactions between factors are represented as edges. The edges in the risk network are directed because there is an induced relationship between risk factors.
Fig. 4.
Risk network model of deep foundation pit construction in metro station.
The safety risk network of deep foundation pit construction at metro stations forms a directed complex social network. In our analysis, we select two indicators—closeness centrality (CC) and betweenness centrality (CB)—to ascertain the extent to which risk factors influence system risk. Specifically, CC reflects the connection relationships between risk factors and the risk network. In directed networks, CC is determined by the joint contributions of out-degree closeness centrality (CCO) and in-degree closeness centrality (CCI). The calculation methods for these indicators are presented in Calculation Formulas (5)-(6). The value of CCO indicates the capacity of a risk factor to induce other risks within the security system. Conversely, CCI indicates the extent to which a risk factor is influenced by other factors within the safety system. Additionally, CB reveals the role of risk factors in risk communication and indicates the degree to which they control risk transmission within the network, as shown in Calculation Formula (7).
 |
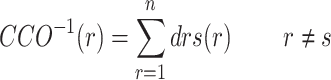5 |
 |
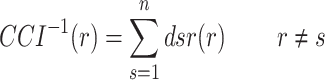6 |
 |
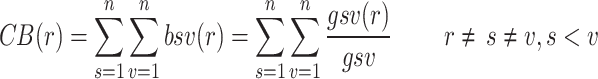7 |
where,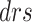 
represents the network distance from risk factor r to risk factor s; 
represents the network distance from risk factor s to risk factor r; 
represents the shortest path probability of risk factor r between risk factor s and risk factor v;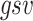 
represents the quantity of shortest paths from risk factor s to risk factor v; 
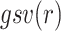represents the quantity of risk factors r, which is on the shortest path from risk factor s to risk factor v.
The analytical framework of N-K/SNA model
This research employs an integrated approach that combines SNA and the N-K model to quantitatively analyze multi-factor risk coupling mechanism and identify key safety risk factors associated with deep foundation pit construction at metro stations, utilizing actual safety accident data and expert knowledge (Fig. 5). Both models are applicable for analyzing complex systems, but they have different focuses. The N-K model emphasizes adaptability and complexity within the system, reflecting the hazard implications of various risk type combinations on the safety system associated with deep foundation pit construction at metro stations. While the N-K model reflects the coupling risk of various risk combinations, it does not facilitate further analysis of secondary risk factors. On the other hand, the SNA model emphasizes network structures and relationships. It can identify important factors and their transmission routes, while also emphasizing factor-to-factor relationships. However, it is more subjective and the coupling effects between factors are overlooked in this approach. The two models can complement each other in the analysis of complex systems. By combining the two models, the limitations of conclusions drawn from a single model can be mitigated.
Fig. 5.
Flow chart of N-K/SNA model.
Initially, we identify and classify the risk factors based on accident data from deep foundation pit construction at metro stations. Furthermore, utilizing the actual occurrence probability of coupling risks in this context, the N-K model is employed to calculate the coupling effects of different risk factors, quantified by the risk coupling value. Subsequently, we employ the SNA model to analyze the network structure among various risk factors, determining the key network factors through network centrality analysis. Additionally, the possible coupling forms of risk factors are identified based on accessibility analysis. Ultimately, the core risk factors of the network obtained by the SNA model are adjusted according to the corresponding risk coupling values obtained from the N-K model to ascertain the final key risk factors.
Results and findings
Analysis of calculation results of the N-K model
Coupled risk statistics of safety accidents
In the safety system of deep foundation pit construction at metro stations, personnel, material, management, environmental and technical risk factors exhibit two states: whether they have breached the defense system or not. During the N-K model calculation, “1” indicates that the defense system has been broken through, meaning the risk factor participates in the coupling effect, while “0” indicates that the defense system has not been broken through, meaning the risk factor does not participate in the coupling effect. For instance, “11100” denotes that the personnel, material and management risk factors have broken through the defense system, while environmental and technical risk factors have not yet occurred. In the metro station foundation pit construction safety system, there are 32 possible types of risk coupling across three categories. Based on the collected risk coupling data of 197 foundation pit construction safety accidents at metro stations from 1991 to 2023, the number and corresponding probabilities of various coupled risk factors are recorded, as shown in Table 2.
Table 2.
Number and corresponding probability of deep foundation pit construction accidents in metro stations from 2000 to 2023.
| Type of coupling | Risk factor | Accident code | Accident count | Accident probability | Type of coupling | Risk factor | Accident code | Accident count | Accident probability |
|---|---|---|---|---|---|---|---|---|---|
| Single-factor coupling | - | P00000 | 0 | 0.0000 | Multi-factor coupling | p-w-m | P11100 | 5 | 0.0254 |
| p | P10000 | 7 | 0.0355 | p-w-e | P11010 | 9 | 0.0457 | ||
| w | P01000 | 4 | 0.0203 | p-w-t | P11001 | 2 | 0.0102 | ||
| m | P00100 | 1 | 0.0051 | p-m-e | P10110 | 15 | 0.0761 | ||
| e | P00010 | 12 | 0.0609 | p-m-t | P10101 | 2 | 0.0102 | ||
| t | P00001 | 3 | 0.0152 | p-e-t | P10011 | 5 | 0.0254 | ||
| Double-factor coupling | p-w | P11000 | 9 | 0.0457 | w-m-e | P01110 | 4 | 0.0203 | |
| p-m | P10100 | 1 | 0.0051 | w-m-t | P01101 | 3 | 0.0152 | ||
| p-e | P10010 | 3 | 0.0152 | w-e-t | P01011 | 2 | 0.0102 | ||
| p-t | P10001 | 8 | 0.0406 | m-e-t | P00111 | 4 | 0.0203 | ||
| w-m | P01100 | 3 | 0.0152 | p-w-m-e | P11110 | 17 | 0.0863 | ||
| w-e | P01010 | 3 | 0.0152 | p-w-m-t | P11101 | 14 | 0.0711 | ||
| w-t | P01001 | 3 | 0.0152 | p-w-e-t | P11011 | 16 | 0.0812 | ||
| m-e | P00110 | 1 | 0.0051 | p-m-e-t | P10111 | 12 | 0.0609 | ||
| m-t | P00101 | 3 | 0.0152 | w-m-e-t | P01111 | 4 | 0.0203 | ||
| e-t | P00011 | 2 | 0.0102 | p-w-m-e-t | P11111 | 20 | 0.1015 |
Calculation and analysis of safety risk coupling
For calculating the safety risk coupling level “T”, the risk coupling probability needs to be determined based on the occurrence probabilities of five types of risk factors, as detailed in Table 3. The probability of single-factor coupling under various situations was calculated using Formula (1). The calculation process for P0\cdots. is exemplified to explain the probability calculation methods for different coupling forms under the condition of single factor determined.
Table 3.
Coupling probability of risk factors in different situations.
| Type of coupling | Coupling probability | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Single-factor coupling | P0…. | 0.2640 | P.0… | 0.4010 | P..0.. | 0.4467 | P…0. | 0.3452 | P….0 | 0.4772 |
| P1…. | 0.7360 | P.1… | 0.5990 | P..1.. | 0.5533 | P…1. | 0.6548 | P….1 | 0.5228 | |
| Double-factor coupling | P00… | 0.1320 | P0.0.. | 0.1472 | P0..0. | 0.1015 | P0…0 | 0.1421 | P.00.. | 0.2030 |
| P01… | 0.1320 | P0.1.. | 0.1168 | P0..1. | 0.1624 | P0…1 | 0.1218 | P.01.. | 0.1980 | |
| P10… | 0.2690 | P1.0.. | 0.2995 | P1..0. | 0.2437 | P1…0 | 0.3350 | P.10.. | 0.2437 | |
| P11… | 0.4670 | P1.1.. | 0.4365 | P1..1. | 0.4924 | P1…1 | 0.4010 | P.11.. | 0.3553 | |
| P.0.0. | 0.1269 | P.0..0 | 0.2030 | P..00. | 0.1827 | P..0.0 | 0.2386 | P…00 | 0.1523 | |
| P.0.1. | 0.2741 | P.0..1 | 0.1980 | P..01. | 0.2640 | P..0.1 | 0.2081 | P…01 | 0.1929 | |
| P.1.0. | 0.2183 | P.1..0 | 0.2741 | P..10. | 0.1624 | P..1.0 | 0.2386 | P…10 | 0.3249 | |
| P.1.1. | 0.3807 | P.1..1 | 0.3249 | P..11. | 0.3909 | P..1.1 | 0.3147 | P…11 | 0.3299 | |
| Multi-factor coupling | P000.. | 0.0863 | P00.0. | 0.0355 | P00..0 | 0.0711 | P0.00. | 0.0508 | P0..00 | 0.0406 |
| P001.. | 0.0457 | P00.1. | 0.0964 | P00..1 | 0.0609 | P0.01. | 0.0964 | P0..01 | 0.0609 | |
| P010.. | 0.0609 | P01.0. | 0.0660 | P01..0 | 0.0711 | P0.10. | 0.0508 | P0..10 | 0.1015 | |
| P100.. | 0.1168 | P10.0. | 0.0914 | P10..0 | 0.1320 | P1.00. | 0.1320 | P1..00 | 0.1117 | |
| P110.. | 0.1827 | P11.0. | 0.1523 | P11..0 | 0.2030 | P1.10. | 0.1117 | P1..10 | 0.2234 | |
| P101.. | 0.1523 | P10.1. | 0.1777 | P10..1 | 0.1371 | P1.01. | 0.1675 | P1..01 | 0.1320 | |
| P011.. | 0.0711 | P01.1. | 0.0660 | P01..1 | 0.0609 | P0.11. | 0.0660 | P0..11 | 0.0609 | |
| P111.. | 0.2843 | P11.1. | 0.3147 | P11..1 | 0.2640 | P1.11. | 0.3249 | P1..11 | 0.2690 | |
| P0.0.0 | 0.0964 | P.000. | 0.0914 | P.00.0 | 0.1117 | P.0.00 | 0.0457 | P..000 | 0.1015 | |
| P0.0.1 | 0.0508 | P.001. | 0.1117 | P.00.1 | 0.0914 | P.0.01 | 0.0812 | P..001 | 0.0812 | |
| P0.1.0 | 0.0457 | P.010. | 0.0355 | P.01.0 | 0.0914 | P.0.10 | 0.1574 | P..010 | 0.1371 | |
| P1.0.0 | 0.1421 | P.100. | 0.0914 | P.10.0 | 0.1269 | P.1.00 | 0.1066 | P..100 | 0.0508 | |
| P1.1.0 | 0.1929 | P.110. | 0.1269 | P.11.0 | 0.1472 | P.1.10 | 0.1675 | P..110 | 0.1878 | |
| P1.0.1 | 0.1574 | P.101. | 0.1523 | P.10.1 | 0.1168 | P.1.01 | 0.1117 | P..101 | 0.1117 | |
| P0.1.1 | 0.0711 | P.011. | 0.1624 | P.01.1 | 0.1066 | P.0.11 | 0.1168 | P..011 | 0.1269 | |
| P1.1.1 | 0.2437 | P.111. | 0.2284 | P.11.1 | 0.2081 | P.1.11 | 0.2132 | P..111 | 0.2030 | |
| P0000. | 0.0152 | P000.0 | 0.0609 | P00.00 | 0.0051 | P0.000 | 0.0203 | P.0000 | 0.0355 | |
| P0001. | 0.0711 | P000.1 | 0.0254 | P00.01 | 0.0305 | P0.001 | 0.0305 | P.0001 | 0.0558 | |
| P0010. | 0.0203 | P001.0 | 0.0102 | P00.10 | 0.0660 | P0.010 | 0.0761 | P.0010 | 0.0761 | |
| P0100. | 0.0355 | P010.0 | 0.0355 | P01.00 | 0.0355 | P0.100 | 0.0203 | P.0100 | 0.0102 | |
| P1000. | 0.0761 | P100.0 | 0.0508 | P10.00 | 0.0406 | P1.000 | 0.0812 | P.1000 | 0.0660 | |
| P0011. | 0.0254 | P001.1 | 0.0355 | P00.11 | 0.0305 | P0.011 | 0.0203 | P.0011 | 0.0355 | |
| P0110. | 0.0305 | P011.0 | 0.0355 | P01.10 | 0.0355 | P0.110 | 0.0254 | P.0110 | 0.0812 | |
| P1100. | 0.0558 | P110.0 | 0.0914 | P11.00 | 0.0711 | P1.100 | 0.0305 | P.1100 | 0.0406 | |
| P0101. | 0.0254 | P010.1 | 0.0254 | P01.01 | 0.0305 | P0.101 | 0.0305 | P.0101 | 0.0254 | |
| P1010. | 0.0152 | P101.0 | 0.0812 | P10.10 | 0.0914 | P1.010 | 0.0609 | P.1010 | 0.0609 | |
| P1001. | 0.0406 | P100.1 | 0.0660 | P10.01 | 0.0508 | P1.001 | 0.0508 | P.1001 | 0.0254 | |
| P1110. | 0.0964 | P111.0 | 0.1117 | P11.10 | 0.1320 | P1.110 | 0.1624 | P.1110 | 0.1066 | |
| P1101. | 0.1269 | P110.1 | 0.0914 | P11.01 | 0.0812 | P1.101 | 0.0812 | P.1101 | 0.0863 | |
| P1011. | 0.1371 | P101.1 | 0.0711 | P10.11 | 0.0863 | P1.011 | 0.1066 | P.1011 | 0.0914 | |
| P0111. | 0.0406 | P011.1 | 0.0355 | P01.11 | 0.0305 | P0.111 | 0.0406 | P.0111 | 0.0812 | |
| P1111. | 0.1878 | P111.1 | 0.1726 | P11.11 | 0.1827 | P1.111 | 0.1624 | P.1111 | 0.1218 | |
| P00000 | 0.0000 | P10010 | 0.0152 | P11100 | 0.0254 | P01011 | 0.0102 | |||
| P10000 | 0.0355 | P10001 | 0.0406 | P11010 | 0.0457 | P00111 | 0.0203 | |||
| P01000 | 0.0203 | P01100 | 0.0152 | P11001 | 0.0102 | P11110 | 0.0863 | |||
| P00100 | 0.0051 | P01010 | 0.0152 | P10110 | 0.0761 | P11101 | 0.0711 | |||
| P00010 | 0.0609 | P01001 | 0.0152 | P10101 | 0.0102 | P11011 | 0.0812 | |||
| P00001 | 0.0152 | P00110 | 0.0051 | P10011 | 0.0254 | P10111 | 0.0609 | |||
| P11000 | 0.0457 | P00101 | 0.0152 | P01110 | 0.0203 | P01111 | 0.0203 | |||
| P10100 | 0.0051 | P00011 | 0.0102 | P01101 | 0.0152 | P11111 | 0.1015 | |||
P0.... =P00000 + P01000 + P00100 +P00010 +P00001 +P01100 +P01010+P01001+P00110+P00101 +P00011 +P01110 +P01101 +P01011 + P00111 + P01111= 0.2640.
The probabilities of double-factor, multiple-factor coupling under different situations were calculated using Formulas (2)-(4).
The coupling values presented in Table 4 are obtained by summarizing the data in Table 3. A higher risk coupling value signifies a greater degree of coupling, which poses a more significant threat to the safety system of deep foundation pits in metro stations and increases the likelihood of safety accidents.
Table 4.
Risk coupling values and ranking.
| Coupling mode | Coupling value | Ranking | Coupling mode | Coupling value | Ranking |
|---|---|---|---|---|---|
| T21(p, w) | 0.010428 | 19 | T34(p, m, e) | 0.035836 | 7 |
| T22(p, m) | 0.012845 | 17 | T35(p, e, t) | 0.014890 | 16 |
| T23(p, e) | 0.001762 | 25 | T36(p, m, t) | 0.030576 | 10 |
| T24(p, t) | 0.003895 | 22 | T37(w, m, e) | 0.033974 | 8 |
| T25(w, m) | 0.006941 | 21 | T38(w, m, t) | 0.015623 | 15 |
| T26(w, e) | 0.001771 | 24 | T39(w, e, t) | 0.015944 | 13 |
| T27(w, t) | 0.001647 | 26 | T310(m, e, t) | 0.028225 | 11 |
| T28(m, e) | 0.010503 | 18 | T41(p, w, m, e) | 0.122861 | 2 |
| T29(m, t) | 0.007576 | 20 | T42(p, w, m, t) | 0.064166 | 5 |
| T210(e, t) | 0.001977 | 23 | T43(p, w, e, t) | 0.053705 | 6 |
| T31(p, w, m) | 0.031384 | 9 | T44(p, m, e, t) | 0.096162 | 3 |
| T32(p, w, e) | 0.023129 | 12 | T45(w, m, e, t) | 0.082290 | 4 |
| T33(p, w, t) | 0.015866 | 14 | T5(p, w, m, e, t) | 0.210310 | 1 |
By comparing and analyzing the risk coupling values, insights can be gained into the following:
Compared with the occurrence probabilities of single factor, two factors, three factors and four factors, the occurrence probability of five factors is low, accounting for only 10.15% of the collected data. However, it has the largest risk coupling value of 0.210310, indicating that five-factor coupling exerts the greatest impact on system security and poses the highest risk. Comparing vertically, the risk coupling values reflect the hierarchical relationship T5>T4>T3>T2. A significant correlation has been observed between the risk coupling value and the number of risk factors. The risk level of the system increases in conjunction with the number of coupled risk factors. Therefore, it is imperative to prevent multi-factor coupling during safety control procedures for deep foundation pit construction at metro stations.
In double-factor risk coupling, the coupled risks associated with “Personnel-Management”, “Management-Environment”, and “Personnel-Material” are relatively high. All three incorporate subjective factors as a common feature, indicating that during the actual excavation construction process at metro stations, system safety is influenced more by the coupling of subjective factors than by that of objective elements. Therefore, coupling of subjective factors should be avoided.
In three-factor risk coupling, the coupled risks resulting from “Personnel-Management-Environment”, “Material-Management-Environment” and “Personnel-Material-Management” are relatively high. A common feature is the presence of management factors in all three couplings, which underscores the impact of the participation of management factors on the coupling effect. This indicates that shortcomings in safety management processes and irregular management actions significantly elevate risks. In the context of safety management for deep foundation pit construction at metro stations, management measures such as refining the management system, reviewing management procedures and troubleshooting potential safety hazards should be taken seriously.
In four-factor risk coupling, the coupled risks arising from “Personnel-Material-Management-Environment”, “Personnel-Management-Environment-Technology”, and “Material-Management-Environmental-Technology” are relatively high, and a common feature is the inclusion of both management and environmental factors. This indicates that management and environmental risk factors tend to couple with other factors, inducing system risks, thus posing a threat to the safety system of deep foundation pit construction at metro stations.
Analysis of calculation results of the SNA model
Analysis of risk factor centrality
UCINET 6.0 software is employed to calculate the closeness centrality (CC) and betweenness centrality (CB) of each risk node within the complex risk network. The safety network for deep foundation pit construction at metro stations is a directed complex social network, wherein CC comprises both out-degree closeness centrality (CCO) and in-degree closeness centrality (CCI). Table 5 displays the results of the calculations.
Table 5.
Normalized centrality of risk factors.
| Risk factor | CC | CB | |
|---|---|---|---|
| CCI | CCO | ||
| Poor awareness of p security (p1) | 59.32203 | 72.91666 | 4.30614 |
| Insufficient professional skills (p2) | 50.72464 | 70.0000 | 4.34672 |
| Poor safety emergency response ability (p3) | 54.68750 | 53.84615 | 2.83973 |
| Inadequate p protection (p4) | 50.00000 | 46.66667 | 0.25287 |
| Poor physical or mental health (p5) | 66.03773 | 61.40351 | 5.79575 |
| Violation of operating regulations (p6) | 79.54546 | 57.37705 | 13.44474 |
| Inadequate equipment maintenance (w1) | 55.55556 | 37.23404 | 0.19858 |
| Equipment failure (w2) | 51.47059 | 50.72464 | 1.52208 |
| Unreasonable equipment selection (w3) | 53.03030 | 54.68750 | 0.40065 |
| Unreasonable arrangement of mechanical work (w4) | 54.68750 | 55.55556 | 0.41481 |
| Improper construction material storage (w5) | 54.68750 | 44.87180 | 0.52188 |
| Defective retaining structure (w6) | 71.42857 | 37.23404 | 0.23399 |
| Insufficient strength and stability of internal support (w7) | 71.42857 | 37.23404 | 0.25920 |
| Substandard strength of anchor rod and pull rod (w8) | 61.40351 | 37.63441 | 0.18777 |
| Unqualified construction materials (w9) | 49.29578 | 46.05263 | 0.22378 |
| Inadequate safety education and training (m1) | 42.16867 | 64.81481 | 1.96594 |
| Incomplete rules and regulations (m2) | 45.45454 | 64.81481 | 6.37966 |
| Insufficient safety investment (m3) | 31.81818 | 67.30769 | 0.09020 |
| Inadequate safety supervision and hidden danger inspection (m4) | 76.08696 | 77.77778 | 24.66474 |
| Inadequate security disclosure (m5) | 46.05263 | 67.30769 | 0.60250 |
| Illegal subcontracting (m6) | 31.81818 | 54.68750 | 0.05415 |
| Unreasonable safety construction organization design (m7) | 37.63441 | 54.68750 | 0.21102 |
| Poor engineering geological and hydrological conditions (e1) | 46.05263 | 61.40351 | 2.32271 |
| Harsh weather or natural disasters (e2) | 50.72464 | 67.30769 | 4.54072 |
| Complicated underground pipeline laying (e3) | 51.47059 | 47.94521 | 0.55122 |
| Closing to large high-rise buildings (e4) | 50.72464 | 54.68750 | 1.77538 |
| Complicated peripheral traffic (e5) | 53.03030 | 53.03030 | 1.62492 |
| Harsh operating environment (e6) | 61.40351 | 66.03773 | 6.87056 |
| Unspecified or deviation of geological and hydrological survey (t1) | 36.08247 | 55.55556 | 0.12545 |
| Improper design scheme (t2) | 39.32584 | 54.68750 | 0.28284 |
| Not prepared special construction scheme (t3) | 47.29730 | 61.40351 | 1.01669 |
| over-excavation (t4) | 68.62745 | 41.66667 | 1.55159 |
| Improper construction method of retaining structure (t5) | 70.00000 | 44.87180 | 2.84119 |
| Error in setting and demolishing supports (t6) | 77.77778 | 37.63441 | 2.53083 |
| Insufficient monitoring of foundation pit (t7) | 74.46809 | 47.94521 | 1.35703 |
| Untimely dewatering and drainage (t8) | 68.62745 | 49.29578 | 0.66679 |
According to the calculation results and the 80/20 Principle, the top seven factors were selected for analysis as important factors.
The calculation results for in-degree closeness centrality indicate that seven risk factors rank higher, including: Violation of operating regulations(p6), Defective retaining structure(w6), Insufficient strength and stability of internal support(w7), Inadequate safety supervision and hidden danger inspection(m4), Improper construction method of retaining structure(t5), Error in setting and demolishing supports(t6), Insufficient monitoring of foundation pit(t7). In safety management practice, unsafe states of materials, unsafe behaviors of construction workers and managers, and improper operation of construction technology can directly lead to risk accidents. Factors with high in-degree closeness centrality are direct causes of safety accidents and contribute significantly to risk aggregation.
The calculation results for out-degree closeness centrality indicate that seven risk factors rank higher, including: Poor awareness of personnel security(p1), Insufficient professional skills(p2), Insufficient safety investment(m3), Inadequate safety supervision and hidden danger inspection(m4), Inadequate security disclosure(m5), Harsh weather or natural disasters(e2), Harsh operating environment(e6). In terms of safety management practice, unfavorable conditions of personnel, management and environmental factors play a significant role in triggering other risk factors and are the fundamental contributors to safety accidents, although their direct impact on such accidents is limited.
The calculation results for betweenness centrality indicate that seven risk factors ranked higher, including: Insufficient professional skills(p2), Poor physical or mental health(p5), Violation of operating regulations(p6), Incomplete rules and regulations(m2), Inadequate safety supervision and hidden danger inspection(m4), Harsh weather or natural disasters(e2), and Harsh operating environment(e6). The results indicate that personnel, management and environmental factors reside within the interactive path of the risk transmission network, playing a significant intermediary role in risk transmission. Effectively controlling the occurrence of these risk factors can disrupt the risk transmission path and help avoid safety accidents.
Analysis of accessibility of risk factors
Accessibility refers to the likelihood that each node in the risk network induces other factors to occur. Potential risk coupling forms that may induce safety accidents can be analyzed through accessibility analysis based on the risk network. For example, the risk factors “Inadequate safety education and training” can readily induce or affect the occurrence of risk factors such as “Unreasonable arrangement of mechanical work”, “Violation of operating regulations”, “Inadequate safety supervision and hidden danger inspection”, “Harsh operating environment”, “Error in setting and demolishing supports”, representing a “Personnel-Material-Management-Environment-Technology” risk coupling. As shown in Fig. 5, the accessibility of 36 secondary risk factors is mapped to five primary risk factors, and Table 6 presents the outcomes of the possible coupling forms. The results of the accessibility analysis indicate that management and environmental factors can mostly cause the coupled risk of “Personnel-Material-Management-Environment-Technology”.
Table 6.
Accessibility analysis of risk factors.
| Secondary risk factor | Personnel factors | Material factors | Management factors | Environmental factors | Technical factors | Potential coupling |
|---|---|---|---|---|---|---|
| p1 | 1 | 1 | 1 | 1 | 1 | p-w-m-e-t |
| p2 | 1 | 1 | 1 | 1 | 1 | p-w-m-e-t |
| p3 | 1 | 0 | 1 | 0 | 1 | p-m-t |
| p4 | 1 | 0 | 1 | 0 | 1 | p-m-t |
| p5 | 1 | 1 | 1 | 0 | 1 | p-w-m-t |
| p6 | 1 | 1 | 1 | 0 | 1 | p-w-m-t |
| w1 | 0 | 1 | 0 | 0 | 1 | w-t |
| w2 | 0 | 1 | 1 | 0 | 1 | w-m-t |
| w3 | 1 | 1 | 1 | 1 | 1 | p-w-m-e-t |
| w4 | 1 | 1 | 1 | 1 | 1 | p-w-m-e-t |
| w5 | 0 | 1 | 0 | 1 | 1 | w-e-t |
| w6 | 1 | 1 | 0 | 0 | 0 | p-w |
| w7 | 1 | 1 | 0 | 0 | 0 | p-w |
| w8 | 1 | 1 | 0 | 0 | 0 | p-w |
| w9 | 0 | 1 | 1 | 0 | 0 | w-m |
| m1 | 1 | 1 | 1 | 1 | 1 | p-w-m-e-t |
| m2 | 1 | 1 | 1 | 0 | 1 | p-w-m-t |
| m3 | 1 | 1 | 1 | 1 | 1 | p-w-m-e-t |
| m4 | 1 | 1 | 1 | 1 | 1 | p-w-m-e-t |
| m5 | 1 | 1 | 1 | 1 | 1 | p-w-m-e-t |
| m6 | 1 | 0 | 1 | 0 | 1 | p-m-t |
| m7 | 1 | 1 | 1 | 1 | 1 | p-w-m-e-t |
| e1 | 1 | 1 | 1 | 1 | 1 | p-w-m-e-t |
| e2 | 1 | 1 | 1 | 1 | 1 | p-w-m-e-t |
| e3 | 1 | 1 | 0 | 1 | 1 | p-w-e-t |
| e4 | 1 | 1 | 1 | 1 | 1 | p-w-m-e-t |
| e5 | 1 | 1 | 1 | 1 | 1 | p-w-m-e-t |
| e6 | 1 | 1 | 1 | 1 | 1 | p-w-m-e-t |
| t1 | 0 | 0 | 1 | 1 | 1 | m-e-t |
| t2 | 1 | 1 | 1 | 0 | 1 | p-w-m-t |
| t3 | 1 | 1 | 1 | 1 | 1 | p-w-m-e-t |
| t4 | 1 | 0 | 0 | 1 | 1 | p-e-t |
| t5 | 0 | 1 | 0 | 1 | 0 | w-e |
| t6 | 0 | 1 | 0 | 1 | 0 | w-e |
| t7 | 1 | 1 | 1 | 0 | 1 | p-w-m-t |
| t8 | 1 | 1 | 1 | 1 | 0 | p-w-m-e |
Identification of core risk factors
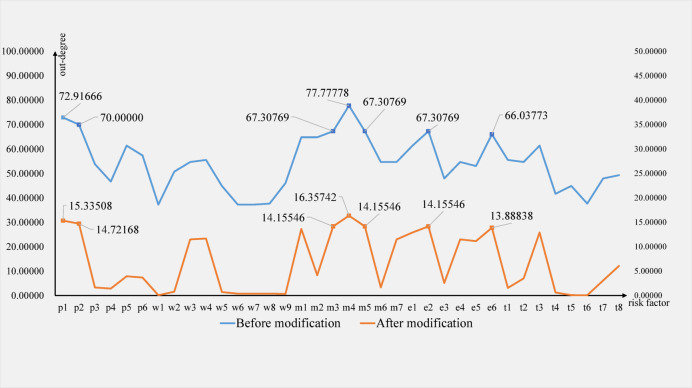
Section 3.2 quantified the influence degree, affected degree and risk transmission function of each risk factor by analyzing the out-degree closeness centrality, in-degree closeness centrality and betweenness centrality in the complex risk network of deep foundation pit construction at metro stations. Specifically, the out-degree closeness centrality reveals the capacity of risk factors to induce system risks, and can be used as a key index to control and prevent safety accidents at their source. However, the data supporting the calculation of out-degree closeness centrality relies on expert knowledge, which is subjective as a key risk identification index, and can be further modified by using objective risk accident data in conjunction with N-K coupling model. According to the accessibility matrix of risk factors from the SNA model, possible coupling forms are analyzed, and the corresponding risk coupling values determined by the N-K model are employed as modification coefficients for the out-degree closeness centrality. Figure 6 illustrates the modified results of the out-degree closeness centrality values.
Fig. 6.
Comparison of out-degree values based on coupling modification.
Based on the modified results, the risk factors such as Poor awareness of p security(p1), Insufficient professional skills(p2), Insufficient safety investment(m3), Inadequate safety supervision and hidden danger inspection(m4), Inadequate security disclosure(m5), Harsh weather or natural disasters(e2), Harsh operating environment(e6) remain highly ranked, which is consistent with the results obtained from the SNA model, indicating that personnel, environmental and management factors tend to induce multi-factor risk coupling and should be controlled emphatically. Through a comparative analysis of the key risk factors identified in this study and actual data from engineering cases, a high frequency of these risk factors was observed in the engineering reports, accompanied by severe outcomes in the corresponding cases. This closely aligns with actual risk scenarios, further validating the effectiveness and practicality of our research methodology.
Conclusion
Based on the analysis of risk identification and coupling mechanism in deep foundation pit construction at metro stations, this research employed a risk factor analysis approach integrating the SNA and N-K model to analyze the risk factors.
The research results from the N-K model indicate a significant impact of multi-factor risk coupling on the safety level of deep foundation pit construction at metro stations. The coupling level of safety risk in deep foundation pit construction at metro stations is increasing with the number of coupled risk factors, underscoring the importance of mitigating such coupling to reduce safety incidents. Furthermore, it is crucial to avoid subjective risk coupling and remain vigilant regarding risk coupling stemming from environmental and managerial factors during the safety management processes of deep foundation pit construction at metro stations.
The analysis conducted with the SNA model demonstrates that risk factors with high in-degree closeness centrality, such as “Violation of operating regulations”, contribute to risk aggregation and are more likely to be influenced by additional risk factors. Risk factors with high out-degree closeness centrality, such as “Poor awareness of personnel security”, are more likely to trigger other risk factors. Risk factors, such as “Insufficient professional skills”, exhibit significant intermediary and transmission functions within the risk network, which makes the subway station deep foundation pit construction system generate more risk propagation paths. Effective management and control of these risk factors can disrupt the transmission paths within the risk network, thereby avoiding further expansion of system risks.
The research utilizing the SNA/N-K model indicates that, when considering the network relationships and coupling effects of risk factors, the key risk factors during the construction phase of deep foundation pits at metro stations include: “Poor awareness of personnel security”, “Insufficient professional skills”, “Insufficient safety investment”, “Inadequate safety supervision and hidden danger inspection”, “Inadequate security disclosure”, “Harsh weather or natural disasters”, and “Harsh operating environment”. Remarkably, these factors exhibit a significant capacity to induce multi-factor risk coupling of “Personnel-Material-Management-Environment-Technology”, necessitating emphasized control measures. The formulation and implementation of corresponding control measures throughout the entire risk coupling process can effectively avoid safety accidents in deep foundation pit construction at metro stations.
In this paper, the SNA/N-K model is employed to thoroughly analyze the key risk factors and multi-factor risk coupling mechanism associated with the construction phase of deep foundation pit at metro stations, providing valuable theoretical support for safety risk management during this critical phase. However, the accident data utilized in this paper is based on incomplete statistics from relevant departments, which may affect the analysis results of the N-K model. Future research should focus on more comprehensive data analysis, which will facilitate more detailed risk factor identification and analysis. Additionally, to align more closely with the realities of construction projects and to quantify the degree of influence of various risk factors, future research will increase the investigation into the hierarchical calculation of these influences and construct a weighted network model to enhance the optimization of the risk network structure.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Author contributions
J.H. was mainly responsible for establishing models and writing the paper. J.F. was responsible for checking the rationality and logical coherence of the paper. P.G. was mainly responsible for organizing data and analyzing the results. J.W. was mainly responsible for data collation and chart production. All authors reviewed the manuscript.
Data availability
The datasets used and analysed during the current study are available from the corresponding author on reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Tian, S. C., Zhang, X. Y., Yang, P. F. & Chen, L. G. Study on the Accident-causing of Foundation Pit Engineering. IOP Conference Series-Earth and Environmental Science. 153(6), 062012 (2018).
- 2.Chen, D. W., Zhou, J. L., Duan, P. S. & Zhang, J. Q. Integrating knowledge management and BIM for safety risk identification of deep foundation pit construction. Eng. Constr. Architectural Manage.30 (8), 3242–3258 (2023). [Google Scholar]
- 3.Sharafat, A., Khan, M. S., Latif, K. & Seo, J. BIM-based tunnel information modeling framework for visualization, management, and simulation of drill-and-blast tunneling projects. J. Comput. Civil Eng.35 (2), 04020068 (2021). [Google Scholar]
- 4.Zhou, Y., Li, C. S., Zhou, C. & Luo, H. B. Using bayesian network for safety risk analysis of diaphragm wall Deflection based on field data. Reliab. Eng. Syst. Saf.180, 152–167 (2018). [Google Scholar]
- 5.Sharafat, A., Latif, K. & Seo, J. Risk analysis of TBM tunneling projects based on generic bow-tie risk analysis approach in difficult ground conditions. Tunneling Undergr. Space Technol.111, 103860 (2021). [Google Scholar]
- 6.Sharafat, A., Latif, K., Park, S. & Seo, J. Risk Assessment of TBM Advanced Rate in the Difficult Ground Using Event Tree Analysis (ETA). In Proceedings of the KSCE. 9, 39–40 (2021).
- 7.Zhou, Y. et al. Combining association rules mining with complex networks to monitor coupled risks. Reliab. Eng. Syst. Saf.186, 194–208 (2019). [Google Scholar]
- 8.Lin, S. S., Shen, S. L., Zhou, A. & Xu, Y. S. Risk assessment and management of excavation system based on fuzzy set theory and machine learning methods. Autom. Constr.122 (4), 103490 (2021). [Google Scholar]
- 9.Wei, D. J., Xu, D. S. & Zhang, Y. A fuzzy evidential reasoning-based approach for risk assessment of deep foundation pit. Tunn. Undergr. Space Technol.97 (3), 1032321–10323216 (2020). [Google Scholar]
- 10.Zhang, W., Huang, Z., Zhang, J. B., Zhang, R. F. & Ma, S. K. Multifactor uncertainty analysis of construction risk for deep foundation pits. Appl. Sci.12 (8122), 8122 (2022). [Google Scholar]
- 11.Wu, B. et al. A Multi-Source intelligent fusion assessment method for dynamic construction risk of subway deep foundation pit: A case study. Sustainability15 (13), 10162 (2023). [Google Scholar]
- 12.Li, X. X., Tan, Z. S., Lei, K. & Ding, Y. Study on construction risk of Multi-factor coupling in urban underground space. Highway66 (12), 217–226 (2021). [Google Scholar]
- 13.Wang, Q. K., Kang, X. W. & Zhu, K. Coupling evaluation method of the construction risk for subway deep foundation pit. J. Northeastern Univ. (Natural Science). 42 (08), 1152–1158 (2021). [Google Scholar]
- 14.Fang, M., Zhang, Y., Zhu, M. J. & Chen, S. P. Cause mechanism of metro collapse accident based on risk coupling. Int. J. Environ. Res. Public Health19(4), 2102 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Qiao, W. G. Analysis and measurement of multifactor risk in underground coal mine accidents based on coupling theory. Reliab. Eng. Syst. Saf.208, 46–48 (2021). [Google Scholar]
- 16.Liu, J. et al. Integrated fuzzy DEMATEL-ISM-NK for metro operation safety risk factor analysis and Multi-Factor risk coupling study. Sustainability15 (5898), 5898 (2023). [Google Scholar]
- 17.Liu, J. et al. Based on ISM-NK tunnel fire Multi-Factor coupling evolution game research. Sustainability14 (12), 7034 (2022). [Google Scholar]
- 18.Lv, Q. Q., Ning, H. M., Chen, K. Z., Ye, J. H. & Research on Fire Risk Coupling of Petrochemical Enterprises Based on Improved N-K Model. 2nd International Conference on Big Data & Artificial Intelligence & Software Engineering (ICBASE). (2021). (2021).
- 19.Li, X. C., Han, J. L. & Qiao, W. G. Study on coupling mechanism of mine accident risk factors. Saf. Coal Mines. 46 (08), 240–242 (2015). [Google Scholar]
- 20.Xiang, P. C. & Liu, Y. L. Research on risk coupling mechanism of Cross-regional Meja construction projects. Constr. Econ.39 (07), 97–101 (2018). [Google Scholar]
- 21.Zhang, M. Y., Yu, D. M., Wang, T. Y. & Xu, C. Coupling analysis of tunnel construction safety risks based on N-K model and SD causality diagram. Buildings13 (1081), 1081 (2023). [Google Scholar]
- 22.Pan, H. Z. et al. Research on Coupling Degree Model of Safety Risk System for Tunnel Construction in Subway Shield Zone. Mathematical Problems in Engineering. 1–20 (2019). (2019)(1).
- 23.Kauffman, S. A. Origins of order in evolution: self-organization and selection. Underst. Origins. 130, 153–181 (1992). [Google Scholar]
- 24.Xu, H., Liao, H. M., Yue, J. C. & Tan, Y. T. Coupling of Operational Risks of Urban Rail Transit Based on N-K Model. Proceedings of the 26th International Symposium on Advancement of Construction Management and Real Estate. (2022).
- 25.Zhang, W. J. Research on coupling mechanism of intelligent ship navigation risk factors based on N-K model. J. Mar. Sci. Technol.28 (1), 195–207 (2023). [Google Scholar]
- 26.Pan, D., Li, Y. Z. & Luo, F. Aircraft operational safety risk coupling based on N-K model. J. Saf. Environ.22 (02), 606–614 (2022). [Google Scholar]
- 27.Huang, W., Shuai, B. & Sun, Y. Study on coupling risk formation mechanism of railway dangerous goods transportation system based on N-K model. J. China Railway Soc.41 (5), 1–9 (2019). [Google Scholar]
- 28.Wu, B. J., Jin, L. H., Zheng, X. Z. & Chen, S. Coupling analysis of crane accident risks based on bayesian network and the N-K model. Sci. Rep.14 (1), 1133 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Shan, Z., Qiu, L. J., Chen, H. H. & Zhou, J. S. Coupled analysis of safety risks in Bridge construction based on N-K model and SNA. Buildings13 (2178), 2178 (2023). [Google Scholar]
- 30.Fang, J., Guo, P. W., Zhu, K. & Chen, Z. F. Coupling evolution analysis of subway tunnel construction safety risk based on N-K model. China Saf. Sci. J.32 (06), 1–9 (2022). [Google Scholar]
- 31.Guo, D. S., Song, Z. P., Xu, T., Zhang, Y. W. & Ding, L. B. Coupling analysis of tunnel construction risk in complex geology and construction factors. J. Constr. Eng. Manage.148 (9), 1–13 (2022). [Google Scholar]
- 32.Pryke, S. D. Analysing construction project coalitions: exploring the application of social network analysis. Constr. Manage. Econ.22 (8), 787–797 (2004). [Google Scholar]
- 33.Chinowsky, P., Diekmann, J. & Galotti, V. Social network model of construction. J. Constr. Eng. Manage.134 (10), 804–812 (2008). [Google Scholar]
- 34.Ding, L. Y. & Zhou, Y. Combining association rule mining with complex networks complex networks to monitor coupled risks. Reliab. Eng. Syst. Saf.186, 194–208 (2019).
- 35.Chen, W. Q., Deng, J. J. & Niu, L. C. Identification of core risk factors and risk diffusion effect of urban underground engineering in China: A social network analysis. Saf. Sci.147, 105591 (2022). [Google Scholar]
- 36.Qin, X., Li, H. Q. & Mo, Y. Y. Research on risk network construction and evaluation of green Building projects based on SNA. J. Civil Eng.50 (02), 119–131 (2017). [Google Scholar]
- 37.Yuan, M. Q., Li, Z. F., Li, X. D. & Luo, X. W. Managing stakeholder-associated risks and their interactions in the life cycle of prefabricated Building projects: A social network analysis approach. J. Clean. Prod.323, 129102 (2021). [Google Scholar]
- 38.Xu, N. J., Wan, A. X., Elahi, E. & Peng, B. H. Evaluating Investment Risks in Overseas Renewable Energy Projects: A WSR and D-AHP Based Approach (ENVIRONMENTAL PROGRESS & SUSTAINABLE ENERGY, 2023).
- 39.Pan, M. Z. & Guo, C. G. Safety evaluation of foundation pit construction based on improved interaction matrix. J. Saf. Sci. Technol.16 (3), 125–130 (2020). [Google Scholar]
- 40.Liu, Y. et al. FDEMATEL-TOPSIS model and its application for safety assessment of deep foundation pit construction of subway. Sci. Technol. Eng.22 (10), 4253–4260 (2022). [Google Scholar]
- 41.Shen, J. H. & Liu, S. P. Application of fuzzy dynamic bayesian network in risk evolution analysis of deep foundation pit construction. J. Saf. Environ.23 (12), 4211–4221 (2023). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets used and analysed during the current study are available from the corresponding author on reasonable request.