Anisotropic DLVO-like interaction for charge patchiness in colloids and proteins

Abstract

The behaviour and stability of soft and biological matter depend significantly on electrostatic interactions, as particles such as proteins and colloids acquire a charge when dispersed in an electrolytic solution. A typical simplification used to understand bulk phenomena involving electrostatic interactions is the isotropy of the charge on the particles. However, whether arising naturally or by synthesis, charge distributions are often inhomogeneous, leading to an intricate particle-particle interaction landscape and complex assembly phenomena. The fundamental complexity of these interactions gives rise to models based on distinct assumptions and varying degrees of simplifications which can blur the line between genuine physical behaviour and artefacts arising from the choice of a particular electrostatic model. Building upon the widely-used linearized Poisson-Boltzmann theory, we propose a theoretical framework that – by bridging different models – provides a robust DLVO-like description of electrostatic interactions between inhomogeneously charged particles. By matching solely the single-particle properties of two different mean-field models, we find a quantitative agreement between the pair interaction energies over a wide range of system parameters. Our work identifies a strategy to merge different models of inhomogeneously charged particles and paves the way to a reliable, accurate, and computationally affordable description of their interactions.

Electrostatic interactions play a key role in the behavior of soft and biological matter, yet their complexity increases when particle charge distributions are inhomogeneous. This work presents a unified theoretical framework that bridges different electrostatic models to accurately and efficiently describe interactions between inhomogeneously charged particles.

Introduction

Electrostatics is omnipresent in soft matter and biology since colloids and proteins dispersed in an electrolytic medium are inevitably charged due to the dissociation of ionizable groups and/or preferential adsorption of ions from the surrounding solvent^1–3. On colloidal surfaces, these processes typically lead to charged particles with charge inhomogeneities that are negligible with respect to particle size (100 nm–1 μm). However, they have been recently exploited to synthesize colloids with charged surface patterns engineered to drive material assembly^4–8. In contrast, proteins are intrinsically charged in a highly uneven fashion as the (de)protonation of their ionizable amino acids leads to charge inhomogeneities comparable in scale to the protein size (~1 nm). The resulting surface charge distribution of a protein is then dictated by the configuration of acidic and basic groups along its backbone³.

Charge inhomogeneity—or patchiness—has a significant impact on the behaviour of charged systems, as it is not only highly directional^9,10 but can induce attraction between neutral and even like-charged objects^11,12. Control over charge patchiness can be achieved both directly via targeted synthesis of colloids or mutagenesis of proteins and indirectly by inducing changes in the solvent pH^3,13. This makes charge patchiness a convenient parameter for tuning the properties of electrostatic interactions. Despite the synthesis of charged patchy colloids with simple surface patterns still being in its infancy, the experiments conducted thus far highlight the fact that the anisotropic nature of interparticle interactions can guide the formation of aggregates with nontrivial, nonclose-packed architectures^14–17. In protein systems, the intrinsic inhomogeneity of surface charge has recently emerged as a powerful feature that influences protein aggregation^18,19 and liquid-liquid phase separation^3,20,21.

When describing electrostatic interactions between inhomogeneously charged particles, the level of detail is usually adjusted to the phenomenon under consideration. Analytical approaches, which typically rely on the linearized Poisson-Boltzmann (PB) approximation, have a long history (see refs. ^22,23 for an overview), with the recent decade bringing notable advances in analytical solutions for the interactions between inhomogeneously charged particles^23–29. These are, however, difficult to efficiently evaluate when particles carry complicated patterns of charge and become prohibitively expensive when applied to large-scale systems. Models of charged patchy particles consequently rely on simplifications to make them computationally feasible^27,28,30,31 and enable large-scale simulations of their assembly in two and three dimensions^32–35. Yet the same simplifications often make it unclear which assembly properties are a true consequence of patchy particle interactions and which properties are an artefact of a given model.

We develop a unifying analytical framework that connects mean-field descriptions of inhomogeneously charged particles at different levels of approximation. Within this framework, we obtain an excellent agreement for pairwise interactions predicted by two distinct electrostatic models^25,27,28 across a wide range of system parameters, which is achieved solely by matching their single-particle properties. This approach allows better control over the approximations used in the models, resulting in a reliable and easy-to-implement description of interactions between inhomogeneously charged particles. As such, it works as an anisotropic generalization of the electrostatic component of the DLVO theory^23,36.

Reconsidering existing models of charged patchy particles

The two models on which we build our theoretical framework describe electrostatic interactions between inhomogeneously charged spherical particles in the linearized Debye-Hückel (DH) regime. To distinguish between the two models, we will term them IC ("internal charge”) and CS ("charged shell”) and use a suffix to describe whether or not the ions from the solvent outside the particles are present also inside them (suffix “i” standing for impermeable and suffix “p” for permeable particles). By rigorously relating these two models to each other, we can develop a unified mean-field description of interactions between charged patchy particles which also allows for a further refinement of the two models.

The IC model was introduced by Bianchi et al.^27,28 to describe interaction patterns of colloids synthesized with differently charged surface regions^4–8. These inhomogeneously charged colloids are typically ion-impenetrable and thus modelled as impermeable dielectric spheres carrying a discrete number of point charges {Z_i} in their interior (ICi; Fig. 1a, left). The number and positions of the point charges are chosen in such a way that they qualitatively reproduce the symmetries of the charge pattern on the particle surface. The effective pair interaction energy in the ICi model is determined by first calculating the electrostatic potential around a single particle and then approximating the pairwise interaction as the energy of a “probe” particle in the electrostatic potential of the “source” particle. In the interior of the probe particle, the original charges must be dressed with an excluded volume factor that takes into account that the {Z_i} are embedded in an impermeable sphere and thus cannot be approached by solution ions (Methods and Fig. 1b, left). In the original model by Bianchi et al.^27,28 the effective charge was approximated using the excluded volume factor of the DLVO theory^23,36, i.e., $Z_i^{*}=\exp \left(\kappa R\right)/\left(1+\kappa R\right)Z_i$ for all charges {Z_i}. We improve on this approximation by determining the effective charges in a general fashion. Specifically, we require that the surface electrostatic potential generated by a permeable particle containing effective point charges matches the one generated by the point charges of its impermeable counterpart. Notably, this is done at the single-particle level by matching the leading terms of the multipole expansion of the electrostatic potentials of the two particles (Methods and Supporting Information (SI)).

Fig. 1. Sketch of the proposed theoretical framework to determine the electrostatic interactions between inhomogeneously charged particles, where red and blue represent opposite charges.

Detailed formulation is given in Methods and SI. a Essential properties of impermeable internal charge (ICi) and permeable charged shell (CSp) models. b Basic steps in the determination of the pair interaction energies within the two models. c Mapping between the two models achieved by redefining the surface charge distribution of the CSp model so that the surface potential of a single CSp particle matches the one of an ICi particle. d Comparison of the resulting electrostatic pair interaction energies of the potential-matched models.

The CS model was introduced by Božič and Podgornik²⁵ with the aim to describe the electrostatic interactions between virus particles, which typically possess icosahedrally symmetrical inhomogeneous charge distributions³⁷. As virus capsids are permeable to solution ions, this model features inhomogeneously charged particles as permeable charged spherical shells with a continuous surface charge distribution σ (CSp; Fig. 1a, right). The CSp model allows for an analytical derivation of the exact pair electrostatic potential of the two-particle system, expressing the free energy of pair interaction as the work associated with moving ions from the bulk of the solution to the particle surfaces (Methods and Fig. 1b, right).

On the one hand, the IC model allows for a fast numerical evaluation of pair energies but involves several simplifications and cannot reproduce any arbitrary surface charge distribution. On the other hand, the ability of the CS model to reproduce a wide array of surface charge distributions comes at the expense of a larger computational demand. Another important difference between the two models lies in the fact that ICi particles are ion-impenetrable while CSp particles are ion-penetrable.

Unifying different electrostatic models by matching single-particle potentials

In order to unify the two electrostatic models into a single framework, we define an analytical procedure that maps discrete charges of the ICi model to a continuous surface charge distribution of the CSp model and bridges the gap between impermeable and permeable particles. The mapping procedure is based on single-particle properties of the two descriptions with the aim to extend this match to their pair interaction energies. This approach is motivated by the recent work of Everts³⁸, who has shown that such a mapping in the other direction—from impermeable bodies with a continuous surface charge density to permeable bodies with point, line, or surface charges—while not unique, can in specific cases guarantee the preservation of the pair interaction energy.

Since particle radius R, dielectric constant of the solvent ε_w, and Debye screening length κ⁻¹ are all shared between the two models by construction, the only particle feature that remains to be defined via this mapping is the particle charge. Note that, for the sake of simplicity, we assume there is no dielectric jump. To obtain the relation between the ensemble of the discrete charges of the ICi model, {Z_i}, and the surface charge distribution of the CSp model, σ, we require that the single-particle electrostatic potential ψ^ICi at the surface of an impermeable particle must be identical to the single-particle electrostatic potential ψ^CSp at the surface of its permeable counterpart (Fig. 1c). This can be synthetically expressed as

$${\left({\psi }^{\mathrm{ICi}}\right.∣}_{r=R}{\left(={\psi }^{\mathrm{CSp}}\right.∣}_{r=R}\Rightarrow \sigma =f\left(\left\{Z_i\right\}\right),$$ 1

where f(…) represents a generic functional form relating the angular dependence of the surface charge distribution and the positions of internal charges. This determines the charge distribution of the CSp model in such a way that it generates a surface potential identical to the one of its ICi counterpart (see SI for detailed derivations). Potential-matching the two models at the level of single particles results in two pair energy landscapes: (i) the interaction energy V^ICi between impermeable spheres with a discrete distribution of point charges in their interior (ICi) and (ii) the interaction energy V^CSp between permeable spheres (CSp) with a continuous surface charge distribution that has been tailored on the basis of the ICi counterpart. The pair interaction energies of the two models can now be compared, V^ICi ↔ V^CSp, to verify whether and to what extent they match (Fig. 1d).

From potential-matching to pair interaction energy: homogeneously charged particles

An instructive example of our framework is the case of homogeneously charged particles. In the ICi model, this corresponds to a single charge Z placed at the centre of the particle; in the CSp model, this corresponds to a uniform surface charge distribution σ(Ω) = σ₀ = Q/4πR² imparting total charge Q to the particle. Our approach to determine the effective charges used in the ICi pair potential in this case yields the DLVO excluded volume factor, as expected^23,36. Matching the surface potentials of individual ICi and CSp particles leads to (see SI)

$$\frac{Q}{Z}=\frac{\kappa R}{1+\kappa R}\frac{e^{\kappa R}}{\sinh \left(\kappa R\right)}.$$ 2

In other words, the total charge of the CSp particle Q has to be modified in a κ-dependent fashion in order for the surface potentials to match. The resulting pair interaction energies then also match exactly, V^IC/V^CS = 1. If one would instead equate the total charge on the ICi and CSp particles, Z = Q, this would lead to a κ-dependent difference in the interaction energies, $V^{\mathrm{IC}}/V^{\mathrm{CS}}={\left[\kappa R/\left(1+\kappa R\right)\right]}^2\left[e^{2\kappa R}/{\sinh }^2\left(\kappa R\right)\right]$.

This procedure can be applied to an arbitrary number and distribution of internal charges in the ICi model and a corresponding inhomogeneous surface charge distribution in the CSp model. While the potential-matching between the two models at the level of single particles is exact, the approximation of the pair energy involves calculation of effective charges $\left\{Z_i^{*}\right\}$ which only corrects for the excluded volume contribution up to a finite number of terms of the multipolar expansion (see SI). Evaluating the effects of this approximation for the effective charges is not straightforward as charge inhomogeneity also leads to intricate interaction landscapes of interparticle orientations that are not trivial to scan and compare.

Orientational interaction landscapes of charged triblock and Janus patchy particles

In colloids and proteins alike, the two types of charge anisotropy with the lowest symmetry – that of a dipolar Janus particle and of a quadrupolar triblock particle – still exhibit a rich and complex array of assembly and aggregation phenomena also seen in particles with more complex charge distributions and as such represent excellent model systems^16,39. Moreover, Janus and triblock charge distributions provide a good first-order approximation for charge distributions of globular proteins^40–42. The pair interaction energy between these particles encapsulates the properties of the interactions in the system needed for both simulations and theoretical evaluations and in general depends on orientations and relative positions of both particles. Even for axisymmetric particles, the configuration space is three-dimensional and thus unfeasible to visualize in its entirety. In order to carry out a comparison between the pair interaction energies of CSp and ICi models, we construct a one-parametric rotational path that includes all highly-symmetric relative orientations of the two particles at a fixed interparticle distance ρ and interpolates them in a continuous fashion. This method is inspired by Brillouin zone paths used to sample electronic band structures in crystal lattices. Figure 2 shows the rotational paths with corresponding sketches at most symmetric orientations, used for triblock particles with quadrupolar symmetry (panel (a)) and for Janus particles with dipolar symmetry (panel (b)). In the Janus case, we trace the path twice, with one of the particles reversed the second time around. Negative energies correspond to attraction in the radial direction and vice-versa, with expected maxima where like charges are in close proximity. The radial dependence of the interaction energy is less relevant because it will generally display an exponential fall-off as the interparticle distance increases. We thus typically study the orientational interaction landscapes when the two particles are in contact, ρ = 2R. We also note that orientational paths such as the ones presented in Fig. 2 can be constructed for any charge distribution by choosing an appropriate set of mutual orientational configurations of particles and the transitions between them. This set does not need to be exhaustive (and in fact cannot be for complicated charge distributions) in order to characterize the orientational pair interaction profiles to a satisfying degree.

Fig. 2. Sketches of one-parametric orientational pathways tracing the interaction energy along the main orientations between two patchy particles at a fixed interparticle distance.

a Patchy particles with the symmetry of a linear quadrupole (Triblock) and b patchy particles with the symmetry of a dipole (Janus, with two symmetric off-centre charges); red and blue represent opposite charges. The main orientations of the two particles relate the relative orientations of their equators (E) and poles (P): EP, EE, PP, tEE (transverse equator-equator), sEE (staggered equator-equator), and sEP (staggered equator-pole). Rotations (r) between configurations along the pathway either rotate one particle around the other (p) or the particle itself (o) along one of the three coordinate axes (x, y, z). In both panels, symbols label selected pair configurations and colors mark rotations between two consecutive ones along the chosen pathway. The empty star in the Janus pathway mark the PP configuration where one of the particles is flipped upside-down compared to the PP configuration marked by the full star; analogously, the empty circle in the Janus pathway marks the EP configuration where one of the particles is flipped left-right compared to the EP configuration marked by the full circle. The interaction energy curves in panels (a) and (b) are sketches that qualitatively summarize the interparticle interactions.

From potential-matching to pair interaction energy: triblock and Janus particles

We start by examining the interaction energies of triblock patchy particles, as their orientational pathway is simpler because of their symmetry (Fig. 2a). To define the size of the charge patches on the particle poles in a consistent fashion, we use the polar angle θ₀ at which the surface potential vanishes (Fig. 3a), which is the same for both models by construction (continuous versus dashed lines in Fig. 3c). The patch size θ₀ in the ICi model is varied by changing the eccentricity $ā=a/R$ of the off-centre charges Z_p (Fig. 3b). The patch size is the largest when the off-centre charges are close to the central one, and decreases in size as they are moved closer to the surface. This, in turn, increases the values of the potential at the poles. Two other important parameters influencing θ₀ are the total charge on the particles, expressed by the dimensionless ratio η = Z_tot/∣Z_p∣ (Fig. 3c) and the screening in the system given by κR (Fig. 3d). Going from zero net charge on the particle to negative or positive net charge acts to either decrease or increase θ₀, respectively (Fig. 3c). As the total charge increases, it is possible to reach a limit beyond which the surface potential does not change sign anymore; in that case we do not consider the particles to have charged patches even if their surface potential is not isotropic. When the net particle charge is fixed, θ₀ decreases upon increasing κR (Fig. 3d), i.e., patches become smaller when the screening in the system is higher.

Fig. 3. Triblock symmetry.

a Sketch of the electrostatic potential around a triblock particle, with patch size θ₀ defined as the angle of vanishing surface potential. b Point charge distribution of a triblock particle in the ICi model, where $ā=a/R$ describes the relative displacement of positive (patch) charges Z_p from the centre, referred to as eccentricity. c Electrostatic potential of a single triblock particle with R = 150 nm after potential-matching as a function of the polar angle, at κR = 3 and $ā=0.5$. The two models are depicted by solid (ICi) and dashed (CSp) lines. The potential is shown for particles with different total charge, given by parameter η = Z_tot/∣Z_p∣, where we used Z_p = 280e. Dotted lines highlight the patch size θ₀ for neutral particles (η = 0). d Patch size θ₀ as a function of the distance between the centre and off-centre charges, $ā$, in the ICi model at different values of κR. e Orientational pair interaction energy pathways for the ICi and CSp models, shown at three different interparticle distances ρ. The particles are overall neutral (η = 0) and the other parameters are fixed ($ā=0.5$, κR = 3).

After mapping the single-particle electrostatic potential at the surfaces of triblock ICi and CSp particles, we observe that the resulting pair interaction energies show striking near-equivalence, as they are almost identical along the entire orientational pathway (Fig. 3e). This is true not only at contact but also at larger interparticle distances. Indeed, for most particle-particle orientations, the interaction energies in the two models are in excellent agreement (Fig. 4) regardless whether we vary the strength of screening κR (panel (a)), the patch size by varying $ā$ (panel (b)), or the total charge on the particles η (panel (c)). Differences between the two models only become apparent when the screening becomes large, in particular at the local extrema of the orientational pathway. We compare the absolute energy values of three extrema – one minimum (EP) and two maxima (PP and sEP) – over a large range of κR at fixed values of $ā$ for neutral particles (panels (d–f) of Fig. 4) and over a range of total charge η at fixed values of $ā$ and κR (panels (g–i)). Differences between ICi and CSp models become visible only when κR ≳ 10 as the effects of local charge patterns become more pronounced. This highlights the importance of higher-order terms in the potential expansion (Fig. S2 in SI) as the determination of effective charges in the ICi model less accurately reproduces the features of the original potential, since only a finite number of expansion terms can be matched. This effect is the most pronounced at large $ā$ where patches are small in size and large in magnitude, especially in the PP orientation of the particles (Fig. 4e).

Fig. 4. Pair interaction energy of triblock particles in the ICi (full lines) and CSp (dashed lines) models.

The particles are in contact, ρ/R = 2, and we vary a screening (κR), b patch size ($ā$), and c net particle charge (η). Parameter values, when not varied, are κR = 3, $ā=0.5$, and η = 0. d–i Comparison of interaction energies in the two models at specific particle orientations between two particles (EP, PP, and sEP; cf. Fig. 2) with (d–f) changing screening and (g–i) changing net particle charge. Dotted vertical lines in panels (d–f) highlight the values of the corresponding parameters in panels (a) and (c).

Next, we consider the case of two Janus particles with off-centre charges in a similar fashion as we did for triblock particles. Due to the additional asymmetry of Janus particles compared to the triblock ones, the orientational pathway is more complicated and splits into two branches upon flipping one of the particles (full and empty symbols in Fig. 2b). Despite this, once the Janus particles are potential-matched between the ICi and CSp models, their interaction energies exhibit the same degree of equivalence as they did in the triblock case (Fig. 5). The discrepancies between the two models again become apparent only when the screening is large (κR ≳ 10), and are most prominent in the interaction peaks and in the PP orientation of the two particles in particular (Fig. 5a). Furthermore, as soon as the particles are not net neutral, the symmetry around zero between the two orientational pathway branches is lost due to the interaction of the additional monopole contribution with the (odd) higher order multipole expansion terms that change sign on particle reversal (Fig. 5b). This effect is most obvious in the PP orientation where both branches show markedly different net charge dependence. In the lowest order, the monopolar contribution cancels out for parallel dipoles (full star, Fig. 5c), while for antiparallel dipoles (empty star, Fig. 5d) it results in additional attraction or repulsion of the dipoles, depending on its sign. For larger net charges, nontrivial higher order effects can be observed.

Fig. 5. Pair interaction energy of Janus particles in the ICi (full lines) and CSp (dashed lines) models.

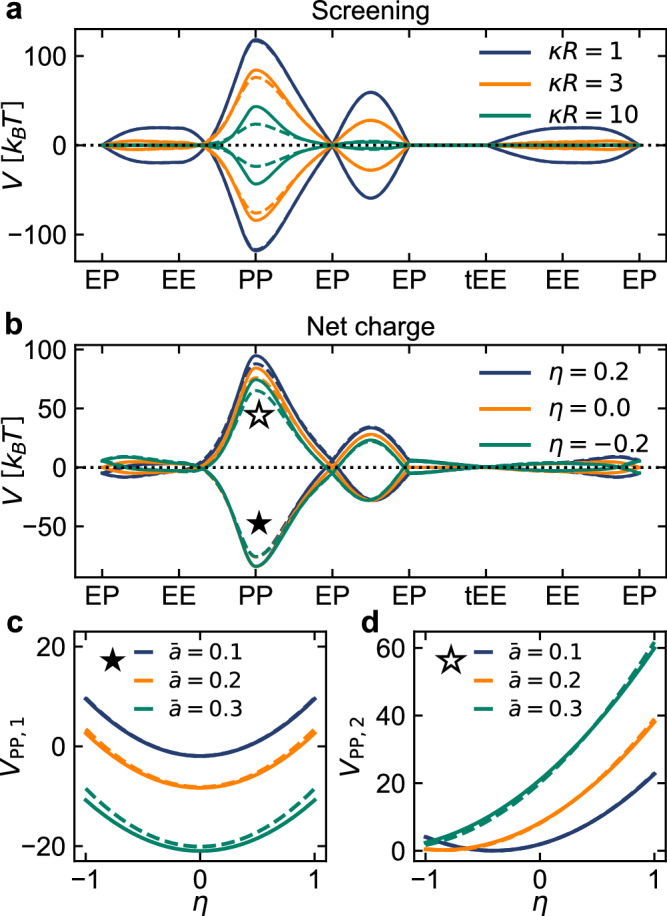
The particles are in contact, ρ/R = 2, and we vary a screening (κR) and b net particle charge (η). Parameter values, when not varied, are κR = 3, $ā=0.5$, and η = 0. Panels c and d show the dependence of PP peak energies on the total charge η for both path branches (full and empty symbols, respectively).

Discussion

Our work demonstrates the connection between different mean-field representations of pairwise electrostatic interactions between charged patchy particles with their correspondence based on matching solely the single-particle surface electrostatic potentials. Using this approach, we are able to match IC and CS models to have the same interparticle interaction up to the accuracy that the two models can provide. The proposed framework serves as a self-consistent tool for designing and refining anisotropic DLVO-like models, suitable for large-scale simulations.

Both IC and CS models resort to similar simplifications. Foremost, they are derived in the linear DH approximation, with all its caveats, and they can be extended to the non-linear (PB) regime using charge renormalization^43,44. In particular, Boon et al.⁴⁵ developed a method that allows for the decoupling of different modes in the multipole expansions of surface charge and electrostatic potential, enabling the extension of charge renormalization to the non-linear regime also in the case of inhomogeneous surface charge distributions. This approach could in principle be applied to our case, provided that the charge renormalization step is correctly incorporated into the larger framework of the mapping between IC and CS models. The two models further assume that the dielectric constant both inside and outside the particles is that of water, which is a simplification as systems of colloids or proteins are typically characterised by a dielectric jump. Our potential-mapping approach can be extended to dielectric particles by resorting to the known single-particle solution for the electrostatic potential of a dielectric CSp model⁴⁶ and using it in the CS pair interaction energy to obtain a first-order approximation for the interaction of impermeable dielectric particles. Both models also assume perfectly spherical particles, which is not the case when modelling biological molecules such as proteins. This could be partially alleviated by using multiple spherical particles as a coarse-grained model of a more complex building block⁴⁷. To describe proteins, the assumption of fixed charge distributions that do not depend on pH should also be revisited. However, the inclusion of charge regulation or changes in particle conformation, both relevant for protein electrostatics^3,48, presents a significant challenge, as it requires dynamic adjustments to the model in response to external stimuli. Nonetheless, once this challenge is addressed by developing a suitable model, our framework provides a method to assess the reliability of the model and test it against explicit electrostatic solutions.

The classic Janus and triblock charge distributions examined in this work can be realized with reasonable accuracy in synthetic charged patchy colloids by using state-of-the-art techniques. More importantly, they represent the leading terms of the multipole expansion that describes charge distributions of many globular proteins^40–42. If more internal charges are needed to model a complex charge pattern, the IC and CS models can still be matched: when the internal charge positions and charges are already given, the corresponding surface charge distribution can be determined to exactly match the surface potential between the two models. More care is required in the calculation of effective charges that compensate for absent screening in the excluded volume within the ICi model. However, if a suitable finite subset of expansion terms can be found that best describe the potential features, the relation connecting the real and effective charges is linear and thus trivial to evaluate (Sec. II of SI). A similar procedure can also be constructed for the inverse connection between the models, i.e., when the charge position can be inferred from the symmetries of the charge pattern, their magnitude could be determined from the CS multipole expansion coefficients.

The general inverse problem of finding an IC model for a known surface potential in a CS model – relevant for modelling complex proteins – is fully non-linear and thus more challenging, because both optimal positions of internal charges, as well as their number have to be determined. This requires an iterative procedure that is not limited to surface charge distributions, but could match volumetric charges without bringing much additional complexity. Obtaining a carefully selected point charge distribution as an approximation to a general charge distribution, permeable or impermeable, can thus be considered as its own step of the procedure; one such approach has been described by Hoppe⁴⁰. Our results demonstrate that the single-particle (IC or CS) model obtained from this generalized problem will result in an accurate pair interaction energy and subsequently a well-behaved model of a large-scale system.

A particularly useful application of our framework is the design of coarse-grained models of proteins, which are typically characterized by intricate charge distributions. The introduced orientational pathway (Fig. 2) provides a reference for coarse-grained models and allows to tune coarse-grained parameters to minimize the differences with respect to more detailed (and computationally expensive) models. Such a procedure would preserve the most important electrostatic features of modelled particles and enable simulation of large multi-particle systems.

Methods

Governing equations of ICi and CSp models

In both ICi and CSp models, the particles are immersed in a dielectric solvent with dielectric constant ε (we use that of water, ε_w = 80) in the presence of a symmetric monovalent salt with bulk concentration c₀. For simplicity, the dielectric constant inside the particle is assumed to be the same as outside and there is therefore no dielectric jump across the particle boundary.

We describe the system in terms of mean-field electrostatics and use linear Debye-Hückel (DH) theory to derive the electrostatic potential ψ(r) of two interacting particles:

$${\nabla }^2\psi ={\kappa }^2\psi ,$$ 3

where, for sake of clarity and generality, we have dropped the dependency of the potential on spatial coordinates r. Here, $\kappa =\sqrt{8\pi l_B{c}_0}$ is the inverse DH screening length which arises due to the screening of monovalent salt ions; l_B = βe²/4πεε₀ is the Bjerrum length, with β = 1/k_BT and e the elementary charge.

The DH equation (3) determines the electrostatic potential outside the two particles ${\psi }_{\mathrm{out}}^{\mathrm{IC}/\mathrm{CS}}$ in both ICi and CSp models. Furthermore, the same equation holds also for the electrostatic potential in the interior of the permeable particles of the CSp model, ${\psi }_{\mathrm{in}}^{\mathrm{CS}}$. On the other hand, the potential inside the impermeable particles of the ICi model must satisfy

$${\nabla }^2{\psi }_{\mathrm{in}}^{\mathrm{ICi}}=-\frac{\rho }{\epsilon {\epsilon }_0},$$ 4

where the charge density inside the particles ρ is given in terms of the positions of the internal (point) charges {Z_i}.

Pair interaction energies

The solutions for the pair interaction energies in both ICi and CSp models are known and have been derived previously^25,27,28; here, we provide a brief summary.

Interaction energy in the ICi model

We approximate the pair interaction energy of two ICi particles, V^ICi, as a symmetrized energy of a probe particle in the field generated by a source particle²⁷. To properly carry out this calculation, the probe particle needs to contain effective charges $\left\{Z_i^{*}\right\}$ that take into account the lack of ions inside it, i.e., the excluded volume around the bare charges {Z_i}. Our derivation of the effective charges, given in the next Section, improves on the existing DLVO correction used previously in this model^27,28.

The probe particle with effective charges is placed in the single-particle external potential of an unmodified ICi particle. Since the pair energy between two particles must be symmetric, we symmetrize the pair interaction energy by including both the energy of the first particle in the field generated by the second particle and vice versa:

$$V^{\mathrm{ICi}}=\frac{1}{2}\left[{\sum }_{i\in 2}{\psi }_1^{\mathrm{ICi}}\left({\mathbf{r}}_i\right)Z_i^{*}+{\sum }_{i\in 1}{\psi }_2^{\mathrm{ICi}}\left({\mathbf{r}}_i\right)Z_i^{*}\right].$$ 5

The form of the effective potential energy in Eq. (5) is of the utmost importance from the viewpoint of simulations, as it can be used, for instance, as an effective Hamiltonian in Monte Carlo simulations.

Interaction energy in the CSp model

To determine the pair energy of two CSp particles, we can derive the electrostatic potential of the system of two particles as a whole, Ψ₁₂²⁵. Due to the linearity of the DH equation, the electrostatic potential of the system is the sum of the individual potentials generated by each particle, namely:

$${\mathrm{\Psi }}_{12}=A_1{\psi }_1^{\mathrm{CSp}}+A_2{\psi }_2^{\mathrm{CSp}},$$ 6

where each single-particle potential ${\psi }_i^{\mathrm{CSp}}$ is written in the coordinate system of its source particle i and A_i are (some) constants. The solution of the governing DH equation that determines the coefficients A_i can be obtained by writing the electrostatic potential in the coordinate system of a single particle while satisfying the boundary conditions on both particles simultaneously. To achieve this, one can resort to addition theorems for the potentials ${\psi }_i^{\mathrm{CSp}}$, resulting in an exact analytical expression for the electrostatic potential of the entire system of two particles in the coordinate system of either the first or the second particle, namely, ${\tilde{\mathrm{\Psi }}}_1$ or ${\tilde{\mathrm{\Psi }}}_2$.

The free energy of this system is obtained via the charging integral over the surface of both charged particles:

$$F^{\mathrm{CSp}}{\left(=\frac{1}{2}{\sum }_{i=1,2}{\oint }_{S_i}{\sigma }_i{\tilde{\mathrm{\Psi }}}_i\right.∣}_{r=R_i}\mathrm{d}{S}_i,$$ 7

where the integral runs over the closed surface of each particle. Finally, the interaction energy between two CSp particles is obtained as the free energy required to bring them from infinite separation to a distance ρ:

$$V^{\mathrm{CSp}}=F^{\mathrm{CSp}}\left(\rho \right)-F^{\mathrm{CSp}}\left(\infty \right).$$ 8

This leads to a free energy of pairwise particle interaction that can be written as a multipole expansion²⁵.

Effective charges of probe particle in the ICi model

We determine the effective charges $Z_i^{*}$ of the probe particle within the IC model by requiring that the single-particle electrostatic potential at the particle surface of an impermeable sphere is equal to the potential of its permeable counterpart, namely

$${\left({\psi }^{\mathrm{ICp}}\right.∣}_{r=R}{\left(={\psi }^{\mathrm{ICi}}\right.∣}_{r=R}\Rightarrow \forall i{Z}_i^{*}=g\left(\left\{Z_i\right\}\right).$$ 9

As both potentials can be expressed through multipole expansions, the aforementioned mapping consists of matching the expansion coefficients. While the equivalence is thus exact for an infinite number of terms, we consider only the leading ones, a choice that depends on the number and distribution of the point charges. Detailed derivations for charge distributions with different symmetries are given in Sec. II of SI.

Author contributions

E.B. and A.B. conceived the idea. A.G., E.L. and S.Č. performed the theoretical calculations. All authors contributed to the development of the theoretical framework, discussed the results, and wrote the manuscript.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.

Data availability

Figure data generated in this study are provided as a Source Data file in the Zenodo database at 10.5281/zenodo.15065195. Other data related to the manuscript can be made available upon request.

Code availability

Data for this study have been produced using the codes made available at ref. ⁴⁹.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-025-58991-0.