Abstract
We investigate the linear absorption spectra of the organic photovoltaic nonfullerene acceptor Y6 in chloroform using perturbative and nonperturbative approaches with atomistic details. Direct nonadiabatic semiclassical mapping dynamics reveal population and coherence evolution during and after ultrafast light pulse, revealing dominant absorption to the S1 state and subsequent oscillatory polarization. The simulated spectra accurately reproduce experimental peak positions and broadening, corresponding to transitions from the ground state to the S1, S2, and S6 excited states. Time-dependent radial distribution functions offer atomistic insights into solvent reorganization in response to charge redistribution. These findings enhance the understanding of nonadiabatic dynamics in Y6 and provide a consistent protocol for simulating electronic spectroscopy in condensed-phase systems.
Electronic spectroscopy is a fundamental tool for characterizing molecular properties pertinent to photochemistry, photosynthesis, and solar energy conversion.1−6 Over the past few years, significant theoretical efforts have been dedicated to computing electronic spectra, aiming to interpret experimental results7−11 and develop novel spectroscopic methods that provide deeper physical insights.12−17 Simulating electronic spectra for disordered condensed matter, such as liquid solutions, presents challenges due to the complexities of light-matter interactions, environmental effects, and nonadiabatic dynamics involved in spectroscopic measurements.18−28 In electronic absorption spectroscopy, incident light induces coherence between the ground state and an electronically excited state, probably involving vibrational excitation and leading to vibronic features in the measured spectra. Accurately capturing chromophore-environment interactions, including solute–solvent rearrangements and complex hydrogen bonding—which can be highly anharmonic and exhibit many-body characteristics—is essential. Therefore, faithful simulation of the spectroscopic process is critical for determining the absorption line shape.
One widely adopted approach for calculating the absorption spectra of chromophores involves optimizing the molecular geometry of the chromophore and employing time-dependent density functional theory (TD-DFT) combined with a polarizable continuum model (PCM) to account for implicit solvent effects.29 This method yields excitation energies corresponding to the peak positions in the spectrum. However, since single-point calculations do not inherently include vibronic effects, the resulting discrete spectral sticks are often broadened using arbitrary parameters. This arbitrary broadening may not accurately capture finite temperature effects or the fine structure arising from vibronic coupling.
Incorporating realistic broadening into absorption spectra calculations can be achieved through ensemble averaging of molecular conformations sampled from the ground-state potential energy surface (PES) with explicit solvent, utilizing methods such as molecular dynamics (MD)12,30 or quantum mechanics/molecular mechanics (QM/MM)31−34 at finite temperatures. This approach addresses inhomogeneous and temperature-dependent thermal broadening by sampling the static nuclear density distribution of molecular structures within their environment;35−37 however, it does not account for dynamical or vibronic effects. Conversely, the Franck–Condon approach38,39 considers the vibronic effects of the chromophore molecule, typically within an implicit solvent framework. This method relies on calculating Franck–Condon overlaps between vibrational states of the ground and electronically excited states, necessitating optimized geometries for both states, corresponding normal modes, and the electronic-vibrational coupling. While this approach effectively captures vibronic structures, it can be computationally intensive for large systems and often omits explicit environmental interactions. Recent advancements have demonstrated that combining nuclear ensemble averaging with the Franck–Condon method yields improved predictions of electronic spectra than the ensemble approach.32
The cumulant method40,41 offers an alternative approach to modeling spectral line shapes by incorporating dynamical effects besides the vibronic and environmental effects that are captured by the above-mentioned static methods. This technique formulates the linear response function in terms of cumulant expansion that is typically truncated after the second-order cumulant. It effectively assumes Gaussian distribution for the energy gap between the ground and excited states, thereby invoking harmonic approximation. In other words, if a system is accurately described by shifted harmonic potentials of identical curvature, then the Gaussian distribution of energy gap and hence the second order cumulant expansion would be exact, but for realistic systems, the second order cumulant method is an approximation. The second-order cumulant can be written as a function of the spectral density, which is the Fourier transform of the time correlation function (TCF) of the energy gap between two electronic states. This energy-gap TCF could be obtained with all-atom MD simulations with explicit solvent, for instance, which encompasses the system-specific dynamical information with solute–solvent interactions. Optionally, the continuous spectral density can be further discretized to parametrize a Brownian oscillator model (BOM),40 which features displaced harmonic oscillators on two states. It should be distinguished between the anharmonic PES effects from sampling and dynamical perspectives. Sampling on anharmonic PES is widely adopted when obtaining energy-gap TCFs,32,42 but it does not fully capture the anharmonic effect in the dynamics of spectroscopic response. It is noted that whether or not to construct BOM explicitly, using spectral density in the second-order cumulant approach invokes the harmonic approximation to the effective PES that will be used subsequently for dynamics, which is known analytically. Despite that the spectral density may be derived from atomistic input, the mapped BOM or equivalently using the spectral density loses the atomistic details when performing the dynamical calculation for spectroscopy. Thus, a main drawback of the second-order cumulant approach is that it cannot describe dynamical effects on anharmonic PES, which may be important for complex condensed phase systems and some nonlinear spectroscopic features that will vanish for purely harmonic systems.
In this work, we present a direct dynamical protocol of simulating the linear electronic spectroscopy of molecules in liquid solution with atomistic details, which has a consistent theoretical treatment for several aspects, including anharmonic PES, environmental effect, vibronic effect, finite temperature effect, as well as nonadiabatic dynamics that could allow population transfer and coherences between multiple electronically excited states,43 plus a realistic simulation of the field-matter interaction in both the perturbative and the nonperturbative approaches.18,19 Additionally, various nonadiabatic semiclassical mapping dynamics are tested in the spectroscopic simulations. In both perturbative and nonperturbative treatments, the required TCFs involving electronic coherences are naturally defined. To ensure consistency in treating these coherences, we include the mean-field Ehrenfest dynamics, while the fewest switches surface hopping is not considered, as defining such coherence-related TCFs within that framework is not straightforward.
Figure 1(a) emphasizes that the current method lies at the intersection of all-atom multistate anharmonic Hamiltonian, nonadiabatic dynamics, and perturbative and nonperturbative spectroscopic observables. In particular, we will investigate the linear spectroscopy of an organic photovoltaic (OPV) nonfullerene acceptor (NFA) Y644−48 dissolved in chloroform (trichloromethane, TCM) solution.49 As a representative novel NFA, Y6 blended with polymer donors such as PM6 exhibits power conversion efficiency as high as 19.3%.50 Additionally, the Y6 molecule has an Acceptor–Donor–Acceptor (A-D-A) complex structure (Figure 1(b)), which may exhibit intramolecular charge transfer (CT) upon photoexcitation in the solution phase (Figure 1(c)), and the most significant excited states including S1, S2, and S6 are shown in Figure 1(d). It would be interesting to see the nonadiabatic dynamics under the direct influence of the explicit external ultrafast light pulse as in the spectroscopic experiment.49
Figure 1.

Methodology features and system of interest: (a) the three aspects in spectroscopic simulation: Hamiltonian, dynamics, and spectroscopic observable; (b) the A-D-A molecular structure of organic photovoltaic nonfullerene acceptor Y6; (c) Y6 dissolved in explicit chloroform solution; (d) the detachment–attachment plot of S1, S2, and S6 excited states of Y6.
We employ both perturbative and nonperturbative approaches for simulating the linear absorption spectra.18,19,40,41,51 We start by expressing the total Hamiltonian as the sum of F-state material Hamiltonian ĤM and the time-dependent light-matter interaction Ĥint(t) as follows
| 1 |
| 2 |
| 3 |
Here, in the material Hamiltonian, M = {mi |i = 1, ···, N}, P̂ = {P̂i |i = 1,..., N} and R̂ = {R̂i |i = 1,..., N} are masses, momenta and positions for N nuclear DOF, correspondingly, Vjj(R̂)≡ Vj(R̂) is the PES of the j-th electronic state, Vjk(R̂) (j≠ k) is the electronic coupling between the j-th and the k-th states. Additionally, in the interaction part, the dipole moment operator
| 4 |
where μeg (e ≠ g) is the transition dipole moment between the e-th excited and the ground (g) states, and E(t) = êE(t) cos(ω t–k·r) is the time-dependent external electric field with the polarization unit vector ê, pulse envelope E(t), leading frequency ω, and wave vector k.
First, the perturbative approach is based on the time-dependent perturbation theory where the light-matter interaction is assumed to be weak, and it formulates the absorption line shape I(ω) in terms of the linear optical response function R(t):40
| 5 |
 |
6 |
Here, θ(t) is the Heaviside function and Tr(·) is the trace over both electronic and nuclear DOF and the TCF of the dipole moment operator along the electric field is given by
 |
7 |
where the equilibrium density matrix is ρ̂eq = ρ̂g |g⟩⟨g| and the ground state nuclear density is ρ̂g = e–βĤg/TrN{e–βĤg}. The second line of eq 7 was obtained by applying rotational average for an isotropic liquid system, and μ̂ = (μ̂x, μ̂y, μ̂z) is the transition dipole of the chromophore in 3-dimensional space and each component μ̂a (a = x, y,z) is an electronic operator. Within the Condon approximation where the transition dipole moment is assumed constant in the molecular frame, one can simplify the TCF J(t) as a linear combination of coherence-to-coherence TCFs:19,40
| 8 |
Here, using the quantum evolution operator 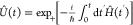 with time-ordered exponential, we express
the TCF of the elementary electronic operators Mjk = |j⟩ ⟨k| and Mmn =
|m⟩⟨n| as
with time-ordered exponential, we express
the TCF of the elementary electronic operators Mjk = |j⟩ ⟨k| and Mmn =
|m⟩⟨n| as
| 9 |
Second, the nonperturbative approach19,51 does not assume weak light-matter interaction and simulates the realistic nonadiabatic process starting from population of the ground state |g⟩⟨g| followed by explicit light-matter interaction Ĥint(t) that induces the electronic coherence between the ground state and the excited states, i.e. |g⟩⟨e| and |e⟩⟨g|. The light pulse of short duration τ creates a nonequilibrium state of the system that will undergo the free-induction decay (FID) back to equilibrium, whose dynamics is governed by the field-free Hamiltonian ĤM. In this case, the absorption spectrum measures the time evolution of the polarization. The polarization at time t after the laser pulse is written as the expectation value of the dipole moment operator projected to the detection polarization direction:
 |
10 |
where the reduced density matrix (RDM) is obtained by performing partial trace for density matrix over the nuclear DOF, namely σ̂(t) = TrN [ρ̂(t)]and the population-to-coherence TCF CMgg Mge (t) and CMgg Meg (t) correspond to starting from a ground-state population and observe a coherence at time t, in contrast to the coherence-to-coherence TCF CMjgMkg (t) as used in the perturbative approach. The line shape function in the nonperturbative approach is given by
| 11 |
where AE = ∫τ0dtE(t) is the total electric field exposure for duration τ.
We consider the most important three excited states of the Y6 molecule, i.e., S1, S2, and S6 (Figure 1(d)), which have large oscillator strengths from the ground state, S0. Among these states, S2 shows the most significant CT character. In the framework of nonadiabatic mapping dynamics that we employ in this study, the Meyer-Miller-Stock-Thoss Hamiltonian52,53 for Y6 dissolved in chloroform with time-dependent light-matter interaction can be represented as below
| 12 |
where the number of electronic states F = 4, the electronic couplings Vjk (j≠ k) are assumed constants under Condon approximation, q = {qi |i = 1, ···, F} and p = {pi |i = 1, ···, F} are the position and momentum mapping variables, respectively, γ is the zero-temperature-energy (ZPE) parameter (default γ = 1/2 if not mentioned otherwise in this work), and the transition dipole moments μjk only exist between the ground state and the excited states. Detailed information on the electronic states of Y6 can be found in Supporting Information.
Once the initial conditions for (R,P, q,p) are known, the nonadiabatic propagation of the mapping Hamiltonian reduces to solving its corresponding Hamilton’s equations.42 In this sense, the equations of motion for the nonadiabatic propagation is the same for the linearized semiclassical (LSC),54−59 symmetrical quasiclassical (SQC),60,61 classical mapping model (CMM),62−64 spin mapping model (SPM),65,66 as well as the mixed quantum-classical mean-field (MF) Ehrenfest dynamics67 (γ = 0). These nonadiabatic mapping dynamical methods differ in the initial sampling of the mapping variables, observable evaluation, and ZPE choice.
In particular, TCF CMjkMmn(t) evaluated in the mapping dynamics is written as
| 13 |
Here, ρN(R0,P0) is the initial nuclear phase space distribution such as the equilibrated ground state, ρe(q0,p0) is the initial distribution of the electronic mapping variables, for example, in LSC methods
| 14 |
and in CMM method, mapping variables are sampled on a hypersphere such that the total electronic population is unity:
| 15 |
For the observable evaluation in eq 13, the time t observable in LSC1 (or Poisson bracket mapping equation)58 and LSC2 (or LSC-initial value representation)56 correspond to
| 16 |
| 17 |
respectively, where γ = 1/2 and  . The time-0 observable in both LSC1 and
LSC2 will be the same as M(2)jk (q0, p0) in eq 17 with G(q0, p0) used for the electronic initial
sampling
. The time-0 observable in both LSC1 and
LSC2 will be the same as M(2)jk (q0, p0) in eq 17 with G(q0, p0) used for the electronic initial
sampling  . The resolution of identity (RI) for the
electronic DOF could improve the estimation of population,54,59 and combining the RI trick with the LSC approaches yields resolution-of-identity
linearized semiclassical 1–3 (RI-LSC1–3) methods (see Supporting Information for details).
. The resolution of identity (RI) for the
electronic DOF could improve the estimation of population,54,59 and combining the RI trick with the LSC approaches yields resolution-of-identity
linearized semiclassical 1–3 (RI-LSC1–3) methods (see Supporting Information for details).
Additionally, in CMM method, the time-0 and time-t observables are given by
| 18 |
| 19 |
respectively, where 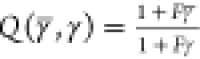 and
and  . The Q, P, and W schemes in the SPM method
correspond to choosing
. The Q, P, and W schemes in the SPM method
correspond to choosing 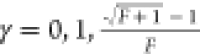 , respectively. It is noted that the uniform
sampling across all electronic states employed in the LSC and CMM
methods makes them suitable for obtaining the multiple coherence-to-coherence
and population-to-coherence TCFs with the same batch of nonadiabatic
dynamical trajectories in the perturbative approach. This is in contrast
with the methods such as Ehrenfest and SQC methods, where the initial
sampling of the electronic mapping variables are focused on a single
state, thus requiring multiple batches of nonadiabatic simulation
as in the perturbative approach. The nonperturbative approach, however,
would only require to start from the equilibrated ground state, so
it could combine with the Ehrenfest and SQC more straightforwardly
than the perturbative approach. If not mentioned otherwise, the time
step in all dynamical calculations is chosen to be δt = 0.1 fs. In the nonperturbative approach, the applied square laser
pulse of strength E = 2.57 × 1010 V/m lasts for 0.1 fs. For more details of other dynamical methods
such as Ehrenfest and SQC methods, refer to ref (43) and the Supporting Information.
, respectively. It is noted that the uniform
sampling across all electronic states employed in the LSC and CMM
methods makes them suitable for obtaining the multiple coherence-to-coherence
and population-to-coherence TCFs with the same batch of nonadiabatic
dynamical trajectories in the perturbative approach. This is in contrast
with the methods such as Ehrenfest and SQC methods, where the initial
sampling of the electronic mapping variables are focused on a single
state, thus requiring multiple batches of nonadiabatic simulation
as in the perturbative approach. The nonperturbative approach, however,
would only require to start from the equilibrated ground state, so
it could combine with the Ehrenfest and SQC more straightforwardly
than the perturbative approach. If not mentioned otherwise, the time
step in all dynamical calculations is chosen to be δt = 0.1 fs. In the nonperturbative approach, the applied square laser
pulse of strength E = 2.57 × 1010 V/m lasts for 0.1 fs. For more details of other dynamical methods
such as Ehrenfest and SQC methods, refer to ref (43) and the Supporting Information.
Figure 2 shows the time-domain response function R(t) as in the perturbative approach and the polarization P(t) as in the nonperturbative approach of the Y6 chloroform solution. With the amplitude of both quantities normalized, the time profiles of both R(t) and P(t) are rather similar, which indicates the validity of the perturbative treatment. Their similarity could be traced back to the fact that the external light pulse used in the direct nonperturbative nonadiabatic simulation is rather narrow (one time step), so the polarization that is the convolution of the response function and the narrow external electric field is close to the material-only response function. The slightly augmented oscillation in polarization than the response function at time t > 40 fs is probably due to the finite width of the pulse as opposed to a true δ-function pulse shape. It is observed that the response functions obtained with different nonadiabatic dynamical methods are similar and so are the polarizations. The Y6 solution at room temperature is probably represented by the BOM that falls in the friendly parameter space where different mixed quantum-classical and semiclassical nonadiabatic dynamics generate agreeing results, which was discussed in a recent benchmark work.68 Even if there were some slight differences in the time-domain results across different dynamical methods, they might be easier to be observed in the frequency domain.
Figure 2.
Time-domain response function of Y6 dissolved in chloroform calculated with the perturbative approach (left panels) via nonadiabatic dynamics including LSC1 and LSC2 (a1), and CMM with ZPE parameters γ = 0.309 (SPM-W) and γ = 0.5 (a2); the time-dependent polarization after the external laser pulse of strength E = 2.57 × 1010 V/m and duration 0.1 fs calculated with the nonperturbative approach (right panels) via nonadiabatic dynamics including LSC1, LSC2, and RI-LSC1–3 (b1) and MF, SQC, and CMM with ZPE parameters γ = 0.309 (SPM-W) and γ = 0.5 (b2). The results are normalized according to their maximal amplitudes.
The main result of the paper is Figure 3, which depicts the frequency-domain linear absorption spectra of the Y6 chloroform solution, as obtained by Fourier transforming the response function and the polarization in the perturbative (eq 5) and nonperturbative approaches (eq 11), respectively. The main spectroscopic features of Y6 solution from the simulation agree well with the experimental measurement49 in terms of peaks at about 1.7, 2.1, and 2.7 eV corresponding to S0 to S1, S2, and S6 absorption, respectively. The main peak at 1.7 eV from the simulation is seen to reproduce the line shape broadening compared with the experiment, except for the shoulder around 1.9 eV. The shoulder might have originated from the Y6 dimer formation, which was not explicitly treated in this work. Also, the experimental peaks at 2.1 and 2.7 eV have a higher baseline than the simulation result. The spectra calculated with the perturbative and nonperturbative approaches are rather similar and the nonadiabatic dynamical methods including LSC1, LSC2, RI-LSC1–3, CMM (γ = 0.309, or SPM-W), CMM (γ = 0.5), and Ehrenfest lead to the same spectra. The only exception is SQC method in the nonperturbative approach, which shows a negative peak at 2.3 eV and the reason is that the underlying binning algorithm leads to an unphysical oscillatory S1 population. Additionally, the nonadiabatic effects can be tested by turning off the electronic coupling between excited states but still having the vibronic coupling between electronic and nuclear DOF. The simulation without nonadiabatic effects yields a lower S2 peak and a higher S6 peak, which is more distinct from the experimental results than the original simulated spectra with nonadiabatic effects. This highlights the importance of the nonadiabatic effects in calculating the absorption spectroscopy.
Figure 3.
Linear absorption spectra of Y6 dissolved in chloroform solution obtained via the perturbative approach (left panels) and nonperturbative approach (right panels) using various nonadiabatic dynamics including LSC1, LSC2, RI-LSC1–3, MF, SQC, and CMM with γ = 0.309 (SPM-W) and CMM with γ = 0.5, in comparison with the experimental spectra (black circles) adapted from ref (49). The spectral line shapes are normalized according to their maximal amplitudes, but the peak positions are not shifted.
We also test the perturbative approach on coumarin 153 (C153)’s benzene solution at 300 K (refer to the Supporting Information for details). The ground S0 state and the first excited S1 state of C153 are considered here. The response function and the linear spectra are shown in Figures S5 and S6 in the Supporting Information. The simulated spectra reproduce the peak position of the experimental result and about 60% peak width for the absorption of S0→S1 transition. Additionally, the simulated spectra of the C153 solution obtained with various semiclassical dynamics methods are very similar, also seen in the Y6 case. Overall, we believe the theoretical spectra capture the main experimental features remarkably, especially considering that the theoretical spectra are obtained directly from the nonadiabatic dynamical simulation without frequency-shifting or artificial broadening.
Besides the spectra, we can also obtain detailed nonadiabatic dynamics from the direct simulation of the nonperturbative approach. For example, the population dynamics during and after the external light pulse are plotted in Figure 4. The system was prepared to be in equilibrium with the ground state, and during the light pulse (see Figure 4(a)), there is a rapid population transfer from the ground state to the three excited states, and the transition to S1 state is the most significant to about 0.55. After the light-matter interaction period, the population transfer dramatically slows down, which relies completely on the electronic couplings that are smaller than the light-matter interaction. In the long time scale, however, the populations of S2 and S6 exhibit complementary oscillatory dynamics until reaching the plateau after 30 fs, as shown in Figure 4(b). The similar population dynamics obtained with other nonadiabatic dynamical methods are shown in Figure S1 in the Supporting Information. Moreover, the charge transfer amount dynamics of Y6 after the photoexcitation as depicted in Figure S2 in the Supporting Information is seen to reflect the population oscillation between S2 and S6 states.
Figure 4.
Population transfer dynamics of Y6 dissolved in chloroform via RI-LSC2 method with time step δ t = 0.02 fs during the light pulse (duration 0.1 fs) (left to the dashed line in (a)) and after the light-matter interaction (right to the dashed line in (a)) in the short time (a) and long time (b) scales simulated in the nonperturbative approach. A total of four electronic states are involved in the nonadiabatic dynamics, including the excited S1, S2, S6 states, and the ground state (GS).
Moreover, we can also obtain the entire RDM dynamics from the direct nonadiabatic dynamical simulations in the nonperturbative approach. Figure 5 shows the RDM dynamics obtained with RI-LSC2, CMM (γ = 0.309), and SQC methods, where the upper and lower triangle panels are the real and imaginary parts of the coherences, respectively. It is seen that the coherence between the ground state and the first excited state, i.e., σ14(t), contributes the most to the polarization in Figure 2(b). This is expected since the S0→S1 transition is the main electronic transition for the absorption spectra, thus a large coherence between the two states. In contrast, the coherences between other excited states (S2 and S6) and the ground state are small in amplitude, which slightly modulates the polarization. Furthermore, the coherences between S1 and S2/S6 show a larger amplitude than the coherence between S2 and S6, which could be attributed to the relatively large population of S1 state about 0.75. We note that the S1 population in Figure 5 about 0.75 is larger than in Figure 4 about 0.55, and the reason is that the time affected by the external laser pulse (i.e., the pulse duration plus one time step) is longer in Figure 5, hence more population transfer to S1 would occur. As shown in Figure 5, RI-LSC2 and CMM (γ = 0.309) produce almost the same RDM dynamics. However, the SQC generates more oscillatory S1 population and weaker coherences than the other methods [see Figure 5 and Figure S1(g)]. It might result from the trajectories that fall out of the population window functions in SQC simulation60 and in turn, give rise to the negative peak in the absorption line shape in Figure 3.
Figure 5.

Reduced density matrix dynamics of Y6 dissolved in chloroform obtained with RI-LSC2, CMM (γ = 0.309, SPM-W), and SQC methods with time step δt = 0.1 fs after the external light pulse (duration 0.1 fs) in the nonperturbative approach. The state labels 1–4 correspond to the excited S1, S2, S6, and the ground states, respectively.
Figure 6 shows atomistic information involved in the nonadiabatic dynamics in the direct nonperturbative approach — the radial distribution function (RDF) change for a specific atom in the solvent with respect to the surface of the donor moiety of Y6 molecule. The first row in Figure 6 is the equilibrated ground state RDF for the hydrogen atom and the chlorine atom with respect to the donor moiety of Y6, i.e., the time-0 structural property. The second to the fourth rows of Figure 6 show the RDF change up to 0.1 and 0.4 ps when simulated with Ehrenfest, LSC, and CMM (γ = 0.309) dynamical methods, respectively. After the explicit light-matter interaction, the hydrogen of chloroform with respect to the donor moiety of Y6 (Figure 6(a)) is seen decreased by 10% at around 0.25 nm, which is driven by the populated excited states with CT character and the donor moiety gets more positively charged, thereby repelling the hydrogen atom in chloroform. The opposite trend is observed in the RDF changes between the chlorine atom in solvent and the donor of Y6 (Figure 6(b)), where the more positively charged donor moiety of Y6 attracts the negatively charged chlorine atom in chloroform from 0.5 nm region to 0.4 nm region. The opposite RDF trend can be observed between the solvent and the acceptor moieties of Y6 as shown in Figures S3 and S4 in the Supporting Information.
Figure 6.
Radial distribution function (RDF) of the hydrogen (left) and chlorine (right) atoms of chloroform with respect to the surface of donor moiety of Y6. The first row (a1,b1) corresponds to the RDF of the equilibrium ground state, the rows 2 to 4 correspond to the RDF changes up to 0.1 ps (blue) and 0.4 ps (orange) after the applied light pulse in nonperturbative approach via MF (a2,b2), LSC (a3,b3), and CMM with γ = 0.309 (SPM-W) (a4,b4).
We have systematically investigated the linear absorption spectra of Y6 in chloroform using perturbative and nonperturbative methodologies, providing a detailed analysis of nonadiabatic population and coherence dynamics. These computational approaches account for the vibronic effect, environmental effect, and anharmonic realistic interactions in a consistent manner within direct nonadiabatic dynamics for liquid solutions and yield an agreement with the experimental spectra. The direct dynamical simulation of the nonperturbative approach enabled us to resolve the transient population transfer under light excitation and subsequent electronic transition dynamics. Our study reveals that the LSC, MF, SPM, and CMM methods yield consistent results, while the SQC method exhibits small discrepancies in absorption features. However, high temperature and small reorganization energy alone are not sufficient to guarantee agreement among various nonadiabatic dynamics methods. A benchmark comparison with exact results using reduced effective models—such as the multistate harmonic (MSH) model42—is ultimately necessary, especially when all-atom quantum dynamics are not feasible. Additionally, solvent structural reorganization following photoexcitation has been demonstrated with time-dependent RDF, reflecting CT-induced solvent redistribution around the donor and acceptor moieties of Y6. These findings contribute to the broader understanding of excitonic and solvent-mediated effects in organic photovoltaic systems and pave the way for refined theoretical approaches in modeling electronic spectroscopy in complex molecular environments using a consistent treatment for atomistic multistate Hamiltonian, nonadiabatic dynamics, and spectroscopic observables.
Simulation Summary. The excitation energies, transition dipoles from the ground state to excited states, diabatic couplings, and atomic charges were calculated with time-dependent density functional theory (TDDFT) on the level of ω*B97X-D/6–31G(d,p) using polarizable continuum model of ε0 = 3.0 and the tuned range separation parameter is ω = 0.11 using Q-Chem 6.0. The excited states (S1, S2, S6) were selected with the minimal oscillator strength threshold of 0.2 and maximum excitation energy threshold of 3.0 eV. The all-atom PESs are based on the generalized Amber force field, where the atomic charges and the excitation energies correspond to the TDDFT calculation for the ground state and the three excited states. The initial nuclear positions and momenta are sampled from equilibrated ground state Y6 with 1632 explicit chloroform solvent molecules in box 60.9 × 60.9 × 60.9 Å3 with periodic boundary conditions at 300 K. The nonadiabatic dynamics simulations of the Y6 molecule dissolved in the explicit solvent environment for the linear absorption spectra are performed using a nuclear time step of 0.1 fs and an electronic time step of 0.005 fs by averaging over 2 × 104 trajectories in the perturbative approach and 105 trajectories in the nonperturbative approach. For more details of the simulation, refer to the Supporting Information.
Acknowledgments
We greatly appreciate Dr. Xing Gao for helpful discussions regarding the spectroscopy simulation and Dr. Yuanping Yi for sharing the Y6 molecular structure. X.S. acknowledges support from the National Natural Science Foundation of China (No. 22273059). Computing resources were provided by NYU Shanghai HPC.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.5c00714.
Details of the nonadiabatic semiclassical mapping dynamics, quantum chemistry calculation of Y6, and all-atom simulations, population dynamics obtained with all nonadiabatic dynamics, charge transfer amount dynamics, and radial distribution function change between solvent and acceptor moieties of Y6, simulation details of quantum chemistry calculation and nonadiabatic dynamics for C153 in benzene solution at 300 K, and the response function and linear absorption spectroscopy (PDF)
Transparent Peer Review report available (PDF)
The authors declare no competing financial interest.
Special Issue
Published as part of The Journal of Physical Chemistry Lettersspecial issue “Wei-Hai Fang Festschrift”.
Supplementary Material
References
- Yoneda Y.; Arsenault E. A.; Yang S.-J.; Orcutt K.; Iwai M.; Fleming G. R. The Initial Charge Separation Step in Oxygenic Photosynthesis. Nat. Commun. 2022, 13, 2275. 10.1038/s41467-022-29983-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz J. D.; Yuly J. L.; Arsenault E. A.; Parker K.; Chowdhury S. N.; Dani R.; Kundu S.; Nuomin H.; Zhang Z.; Valdiviezo J.; et al. Coherence in Chemistry: Foundations and Frontiers. Chem. Rev. 2024, 124, 11641–11766. 10.1021/acs.chemrev.3c00643. [DOI] [PubMed] [Google Scholar]
- Marcolin G.; Tumbarello F.; Fresch E.; Agostini A.; Büchel C.; Carbonera D.; Collini E. Two-Dimensional Electronic Spectroscopy Characterization of Fucoxanthin-Chlorophyll Protein Reveals Excitonic Carotenoid-Chlorophyll Interactions. J. Phys. Chem. Lett. 2024, 15, 2392–2399. 10.1021/acs.jpclett.3c03609. [DOI] [PubMed] [Google Scholar]
- Brey D.; Binder R.; Martinazzo R.; Burghardt I. Signatures of Coherent Vibronic Exciton Dynamics and Conformational Control in the Two-Dimensional Electronic Spectroscopy of Conjugated Polymers. Faraday Discuss. 2022, 237, 148–167. 10.1039/D2FD00014H. [DOI] [PubMed] [Google Scholar]
- Cheng C.; Zhang J.; Zhu B.; Liang G.; Zhang L.; Yu J. Verifying the Charge-Transfer Mechanism in S-Scheme Heterojunctions Using Femtosecond Transient Absorption Spectroscopy. Angew. Chem., Int. Ed. 2023, 62, e202218688. 10.1002/anie.202218688. [DOI] [PubMed] [Google Scholar]
- Song Y.; Schubert A.; Liu X.; Bhandari S.; Forrest S. R.; Dunietz B. D.; Geva E.; Ogilvie J. P. Efficient Charge Generation via Hole Transfer in Dilute Organic Donor-Fullerene Blends. J. Phys. Chem. Lett. 2020, 11, 2203–2210. 10.1021/acs.jpclett.0c00058. [DOI] [PubMed] [Google Scholar]
- Huang C.; Bai S.; Shi Q. Simulation of the Pump-Probe Spectra and Excitation Energy Relaxation of the B850 Band of the LH2 Complex in Purple Bacteria. J. Phys. Chem. B 2024, 128, 7467–7475. 10.1021/acs.jpcb.4c02059. [DOI] [PubMed] [Google Scholar]
- Segatta F.; Russo M.; Nascimento D. R.; Presti D.; Rigodanza F.; Nenov A.; Bonvicini A.; Arcioni A.; Mukamel S.; Maiuri M.; et al. In Silico Ultrafast Nonlinear Spectroscopy Meets Experiments: The Case of Perylene Bisimide Dye. J. Chem. Theory Comput. 2021, 17, 7134–7145. 10.1021/acs.jctc.1c00570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu C.; Lin K.; Hu D.; Gu F. L.; Gelin M. F.; Lan Z. Ultrafast Internal Conversion Dynamics through the on-the-Fly Simulation of Transient Absorption Pump-Probe Spectra with Different Electronic Structure Methods. J. Phys. Chem. Lett. 2022, 13, 661–668. 10.1021/acs.jpclett.1c03373. [DOI] [PubMed] [Google Scholar]
- Zhang J.; Borrelli R.; Tanimura Y. Probing Photoinduced Proton Coupled Electron Transfer Process by Means of Two-Dimensional Resonant Electronic-Vibrational Spectroscopy. J. Chem. Phys. 2021, 154, 144104. 10.1063/5.0046755. [DOI] [PubMed] [Google Scholar]
- Wiethorn Z. R.; Hunter K. E.; Zuehlsdorff T. J.; Montoya-Castillo A. Beyond the Condon Limit: Condensed Phase Optical Spectra from Atomistic Simulations. J. Chem. Phys. 2023, 159, 244114. 10.1063/5.0180405. [DOI] [PubMed] [Google Scholar]
- Soh J. H.; Jansen T. L. C.; Palacino-González E. Controlling the Nonadiabatic Dynamics of the Charge-Transfer Process with Chirped Pulses: Insights from a Double-Pump Time-Resolved Fluorescence Spectroscopy Scheme. J. Chem. Phys. 2024, 160, 024110. 10.1063/5.0177073. [DOI] [PubMed] [Google Scholar]
- Keefer D.; Schnappinger T.; de Vivie-Riedle R.; Mukamel S. Visualizing Conical Intersection Passages via Vibronic Coherence Maps Generated by Stimulated Ultrafast X-Ray Raman Signals. Proc. Natl. Acad. Sci. U.S.A. 2020, 117, 24069–24075. 10.1073/pnas.2015988117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kowalewski M.; Bennett K.; Dorfman K. E.; Mukamel S. Catching Conical Intersections in the Act: Monitoring Transient Electronic Coherences by Attosecond Stimulated X-Ray Raman Signals. Phys. Rev. Lett. 2015, 115, 193003. 10.1103/PhysRevLett.115.193003. [DOI] [PubMed] [Google Scholar]
- Everitt K. F.; Geva E.; Skinner J. L. Determining the Solvation Correlation Function from Three-Pulse Photon Echoes in Liquids. J. Chem. Phys. 2001, 114, 1326–1335. 10.1063/1.1332811. [DOI] [Google Scholar]
- McRobbie P. L.; Geva E. Coherent Control of Population Transfer via Linear Chirp in Liquid Solution: The Role of Motional Narrowing. J. Phys. Chem. A 2016, 120, 3015–3022. 10.1021/acs.jpca.5b09736. [DOI] [PubMed] [Google Scholar]
- Cho M.; Scherer N. F.; Fleming G. R.; Mukamel S. Photon Echoes and Related Four-wave-mixing Spectroscopies Using Phase-locked Pulses. J. Chem. Phys. 1992, 96, 5618–5629. 10.1063/1.462686. [DOI] [Google Scholar]
- Gao X.; Geva E. A Nonperturbative Methodology for Simulating Multidimensional Spectra of Multiexcitonic Molecular Systems via Quasiclassical Mapping Hamiltonian Methods. J. Chem. Theory Comput. 2020, 16, 6491–6502. 10.1021/acs.jctc.0c00843. [DOI] [PubMed] [Google Scholar]
- Gao X.; Lai Y.; Geva E. Simulating Absorption Spectra of Multiexcitonic Systems via Quasiclassical Mapping Hamiltonian Methods.. J. Chem. Theory Comput. 2020, 16, 6465–6480. 10.1021/acs.jctc.0c00709. [DOI] [PubMed] [Google Scholar]
- Ka B. J.; Geva E. A Nonperturbative Calculation of Nonlinear Spectroscopic Signals in Liquid Solution. J. Chem. Phys. 2006, 125, 214501. 10.1063/1.2359440. [DOI] [PubMed] [Google Scholar]
- Polley K.; Loring R. F. One and Two Dimensional Vibronic Spectra for an Exciton Dimer from Classical Trajectories. J. Phys. Chem. B 2020, 124, 9913–9920. 10.1021/acs.jpcb.0c07078. [DOI] [PubMed] [Google Scholar]
- Polley K.; Loring R. F. Two-Dimensional Vibronic Spectroscopy with Semiclassical Thermofield Dynamics. J. Chem. Phys. 2022, 156, 124108. 10.1063/5.0083868. [DOI] [PubMed] [Google Scholar]
- Dunnett A. J.; Gowland D.; Isborn C. M.; Chin A. W.; Zuehlsdorff T. J. Influence of Non-Adiabatic Effects on Linear Absorption Spectra in the Condensed Phase: Methylene Blue. J. Chem. Phys. 2021, 155, 144112. 10.1063/5.0062950. [DOI] [PubMed] [Google Scholar]
- Provazza J.; Segatta F.; Coker D. F. Modeling Nonperturbative Field-Driven Vibronic Dynamics: Selective State Preparation and Nonlinear Spectroscopy. J. Chem. Theory Comput. 2021, 17, 29–39. 10.1021/acs.jctc.0c01035. [DOI] [PubMed] [Google Scholar]
- Kumar M.; Provazza J.; Coker D. F. Influence of Solution Phase Environmental Heterogeneity and Fluctuations on Vibronic Spectra: Perylene Diimide Molecular Chromophore Complexes in Solution. J. Chem. Phys. 2021, 154, 224109. 10.1063/5.0054377. [DOI] [PubMed] [Google Scholar]
- van der Vegte C. P.; Prajapati J. D.; Kleinekathöfer U.; Knoester J.; Jansen T. L. C. Atomistic Modeling of Two-Dimensional Electronic Spectra and Excited-State Dynamics for a Light Harvesting 2 Complex. J. Phys. Chem. B 2015, 119, 1302–1313. 10.1021/jp509247p. [DOI] [PubMed] [Google Scholar]
- Petit A. S.; Subotnik J. E. How to Calculate Linear Absorption Spectra with Lifetime Broadening Using Fewest Switches Surface Hopping Trajectories: A Simple Generalization of Ground-State Kubo Theory. J. Chem. Phys. 2014, 141, 014107. 10.1063/1.4884945. [DOI] [PubMed] [Google Scholar]
- Fujita T.; Hoshi T. Ab Initio Study of Charge Separation Dynamics and Pump-Probe Spectroscopy in the P3HT/PCBM Blend. J. Phys. Chem. B 2023, 127, 7615–7623. 10.1021/acs.jpcb.3c02458. [DOI] [PubMed] [Google Scholar]
- Cammi R.; Corni S.; Mennucci B.; Tomasi J. Electronic Excitation Energies of Molecules in Solution: State Specific and Linear Response Methods for Nonequilibrium Continuum Solvation Models. J. Chem. Phys. 2005, 122, 104513. 10.1063/1.1867373. [DOI] [PubMed] [Google Scholar]
- Zhong K.; Nguyen H. L.; Do T. N.; Tan H.-S.; Knoester J.; Jansen T. L. C. Coarse-Grained Approach to Simulate Signatures of Excitation Energy Transfer in Two-Dimensional Electronic Spectroscopy of Large Molecular Systems. J. Chem. Theory Comput. 2024, 20, 6111–6124. 10.1021/acs.jctc.4c00413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fehér P. P.; Madarász Á.; Stirling A. Multiscale Modeling of Electronic Spectra Including Nuclear Quantum Effects. J. Chem. Theory Comput. 2021, 17, 6340–6352. 10.1021/acs.jctc.1c00531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuehlsdorff T. J.; Montoya-Castillo A.; Napoli J. A.; Markland T. E.; Isborn C. M. Optical Spectra in the Condensed Phase: Capturing Anharmonic and Vibronic Features Using Dynamic and Static Approaches. J. Chem. Phys. 2019, 151, 074111. 10.1063/1.5114818. [DOI] [PubMed] [Google Scholar]
- Chen M. S.; Mao Y.; Snider A.; Gupta P.; Montoya-Castillo A.; Zuehlsdorff T. J.; Isborn C. M.; Markland T. E. Elucidating the Role of Hydrogen Bonding in the Optical Spectroscopy of the Solvated Green Fluorescent Protein Chromophore: Using Machine Learning to Establish the Importance of High-Level Electronic Structure. J. Phys. Chem. Lett. 2023, 14, 6610–6619. 10.1021/acs.jpclett.3c01444. [DOI] [PubMed] [Google Scholar]
- Xu C.; Lin C.; Peng J.; Zhang J.; Lin S.; Gu F. L.; Gelin M. F.; Lan Z. On-the-Fly Simulation of Time-Resolved Fluorescence Spectra and Anisotropy. J. Chem. Phys. 2024, 160, 104109. 10.1063/5.0201204. [DOI] [PubMed] [Google Scholar]
- Isborn C. M.; Götz A. W.; Clark M. A.; Walker R. C.; Martínez T. J. Electronic Absorption Spectra from MM and ab Initio QM/MM Molecular Dynamics: Environmental Effects on the Absorption Spectrum of Photoactive Yellow Protein. J. Chem. Theory Comput. 2012, 8, 5092–5106. 10.1021/ct3006826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marenich A. V.; Cramer C. J.; Truhlar D. G. Electronic Absorption Spectra and Solvatochromic Shifts by the Vertical Excitation Model: Solvated Clusters and Molecular Dynamics Sampling. J. Phys. Chem. B 2015, 119, 958–967. 10.1021/jp506293w. [DOI] [PubMed] [Google Scholar]
- Crespo-Otero R.; Barbatti M. Spectrum simulation and decomposition with nuclear ensemble: formal derivation and application to benzene, furan and 2-phenylfuran. Theor Chem Acc 2012, 131, 1237. 10.1007/s00214-012-1237-4. [DOI] [Google Scholar]
- Warshel A.; Karplus M. Vibrational Structure of Electronic Transitions in Conjugated Molecules. Chem. Phys. Lett. 1972, 17, 7–14. 10.1016/0009-2614(72)80311-7. [DOI] [Google Scholar]
- Cederbaum L. S.; Domcke W. A many-body Approach to the Vibrational Structure in Molecular Electronic Spectra. I. Theory. J. Chem. Phys. 1976, 64, 603–611. 10.1063/1.432250. [DOI] [Google Scholar]
- Mukamel S.Principles of Nonlinear Optical Spectroscopy; Oxford University Press: 1995. [Google Scholar]
- Mukamel S.; Abramavicius D. Many-Body Approaches for Simulating Coherent Nonlinear Spectroscopies of Electronic and Vibrational Excitons. Chem. Rev. 2004, 104, 2073–2098. 10.1021/cr020681b. [DOI] [PubMed] [Google Scholar]
- Hu Z.; Brian D.; Sun X. Multi-State Harmonic Models with Globally Shared Bath for Nonadiabatic Dynamics in the Condensed Phase. J. Chem. Phys. 2021, 155, 124105. 10.1063/5.0064763. [DOI] [PubMed] [Google Scholar]
- Hu Z.; Sun X. All-Atom Nonadiabatic Semiclassical Mapping Dynamics for Photoinduced Charge Transfer of Organic Photovoltaic Molecules in Explicit Solvents. J. Chem. Theory Comput. 2022, 18, 5819–5836. 10.1021/acs.jctc.2c00631. [DOI] [PubMed] [Google Scholar]
- Fu Y.; Lee T. H.; Chin Y.-C.; Pacalaj R. A.; Labanti C.; Park S. Y.; Dong Y.; Cho H. W.; Kim J. Y.; Minami D.; et al. Molecular Orientation-Dependent Energetic Shifts in Solution-Processed Non-fullerene Acceptors and Their Impact on Organic Photovoltaic Performance. Nat. Commun. 2023, 14, 1870. 10.1038/s41467-023-37234-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kosco J.; Gonzalez-Carrero S.; Howells C. T.; Fei T.; Dong Y.; Sougrat R.; Harrison G. T.; Firdaus Y.; Sheelamanthula R.; Purushothaman B.; et al. Generation of Long-Lived Charges in Organic Semiconductor Heterojunction Nanoparticles for Efficient Photocatalytic Hydrogen Evolution. Nat. Energy 2022, 7, 340–351. 10.1038/s41560-022-00990-2. [DOI] [Google Scholar]
- Natsuda S.-i.; Sakamoto Y.; Takeyama T.; Shirouchi R.; Saito T.; Tamai Y.; Ohkita H. Singlet and Triplet Excited-State Dynamics of a Nonfullerene Electron Acceptor Y6. J. Phys. Chem. C 2021, 125, 20806–20813. 10.1021/acs.jpcc.1c06448. [DOI] [Google Scholar]
- Li J.; Ji Q.; Wang R.; Zhang Z.-G.; Wang X.; Xiao M.; Lu Y.-q.; Zhang C. Charge Generation Dynamics in Organic Photovoltaic Blends under One-Sun-Equivalent Illumination Detected by Highly Sensitive Terahertz Spectroscopy. J. Am. Chem. Soc. 2024, 146, 20312–20322. 10.1021/jacs.4c05786. [DOI] [PubMed] [Google Scholar]
- Guo Y.; Han G.; Yi Y. The Intrinsic Role of the Fusion Mode and Electron-Deficient Core in Fused-Ring Electron Acceptors for Organic Photovoltaics. Angew. Chem., Int. Ed. 2022, 61, e202205975. 10.1002/anie.202205975. [DOI] [PubMed] [Google Scholar]
- Mahadevan S.; Liu T.; Pratik S. M.; Li Y.; Ho H. Y.; Ouyang S.; Lu X.; Yip H.-L.; Chow P. C. Y.; Brédas J.-L.; et al. Assessing Intra- and Inter-Molecular Charge Transfer Excitations in Non-Fullerene Acceptors Using Electroabsorption Spectroscopy. Nat. Commun. 2024, 15, 2393. 10.1038/s41467-024-46462-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu J.; Fong P. W. K.; Liu H.; Huang C.-S.; Lu X.; Lu S.; Abdelsamie M.; Kodalle T.; Sutter-Fella C. M.; Yang Y.; et al. 19.31% Binary Organic Solar Cell and Low Non-radiative Recombination Enabled by Non-monotonic Intermediate State Transition. Nat. Commun. 2023, 14, 1760. 10.1038/s41467-023-37526-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seidner L.; Stock G.; Domcke W. Nonperturbative Approach to Femtosecond Spectroscopy: General Theory and Application to Multidimensional Nonadiabatic Photoisomerization Processes. J. Chem. Phys. 1995, 103, 3998–4011. 10.1063/1.469586. [DOI] [Google Scholar]
- Meyer H.-D.; Miller W. H. Classical Models for Electronic Degrees of Freedom: Derivation via Spin Analogy and Application to F*+ H2 → F + H2. J. Chem. Phys. 1979, 71, 2156–2169. 10.1063/1.438598. [DOI] [Google Scholar]
- Stock G.; Thoss M. Semiclassical Description of Nonadiabatic Quantum Dynamics. Phys. Rev. Lett. 1997, 78, 578–581. 10.1103/PhysRevLett.78.578. [DOI] [PubMed] [Google Scholar]
- Gao X.; Saller M. A. C.; Liu Y.; Kelly A.; Richardson J. O.; Geva E. Benchmarking Quasiclassical Mapping Hamiltonian Methods for Simulating Electronically Nonadiabatic Molecular Dynamics.. J. Chem. Theory Comput. 2020, 16, 2883–2895. 10.1021/acs.jctc.9b01267. [DOI] [PubMed] [Google Scholar]
- Wang H.; Sun X.; Miller W. H. Semiclassical Approximations for the Calculation of Thermal Rate Constants for Chemical Reactions in Complex Molecular Systems. J. Chem. Phys. 1998, 108, 9726–9736. 10.1063/1.476447. [DOI] [Google Scholar]
- Sun X.; Wang H.; Miller W. H. Semiclassical Theory of Electronically Nonadiabatic Dynamics: Results of a Linearized Approximation to the Initial Value Representation. J. Chem. Phys. 1998, 109, 7064–7074. 10.1063/1.477389. [DOI] [Google Scholar]
- Shi Q.; Geva E. Nonadiative Electronic Relaxation Rate Constants from Approximations Based on Linearizing the Path-Integral Forward-Backward Action. J. Phys. Chem. A 2004, 108, 6109–6116. 10.1021/jp049547g. [DOI] [Google Scholar]
- Kim H.; Nassimi A.; Kapral R. Quantum-Classical Liouville Dynamics in the Mapping Basis. J. Chem. Phys. 2008, 129, 084102. 10.1063/1.2971041. [DOI] [PubMed] [Google Scholar]
- Saller M. A. C.; Kelly A.; Richardson J. O. On the Identity of the Identity Operator in Nonadiabatic Linearized Semiclassical Dynamics. J. Chem. Phys. 2019, 150, 071101. 10.1063/1.5082596. [DOI] [PubMed] [Google Scholar]
- Cotton S. J.; Miller W. H. A New Symmetrical Quasi-Classical Model for Electronically Non-Adiabatic Processes: Application to the Case of Weak Non-Adiabatic Coupling. J. Chem. Phys. 2016, 145, 144108. 10.1063/1.4963914. [DOI] [PubMed] [Google Scholar]
- Cotton S. J.; Miller W. H. Symmetrical Windowing for Quantum States in Quasi-Classical Trajectory Simulations: Application to Electronically Non-Adiabatic Processes. J. Chem. Phys. 2013, 139, 234112. 10.1063/1.4845235. [DOI] [PubMed] [Google Scholar]
- Liu J. A Unified Theoretical Framework for Mapping Models for the Multi-State Hamiltonian. J. Chem. Phys. 2016, 145, 204105. 10.1063/1.4967815. [DOI] [PubMed] [Google Scholar]
- He X.; Liu J. A new perspective for Nonadiabatic Dynamics with Phase Space Mapping Models. J. Chem. Phys. 2019, 151, 024105. 10.1063/1.5108736. [DOI] [PubMed] [Google Scholar]
- He X.; Gong Z.; Wu B.; Liu J. Negative Zero-Point-Energy Parameter in the Meyer-Miller Mapping Model for Nonadiabatic Dynamics. J. Phys. Chem. Lett. 2021, 12, 2496–2501. 10.1021/acs.jpclett.1c00232. [DOI] [PubMed] [Google Scholar]
- Runeson J. E.; Richardson J. O. Generalized Spin Mapping for Quantum-Classical Dynamics. J. Chem. Phys. 2020, 152, 084110. 10.1063/1.5143412. [DOI] [PubMed] [Google Scholar]
- Mannouch J. R.; Richardson J. O. A Partially Linearized Spin-Mapping Approach for Simulating Nonlinear Optical Spectra. J. Chem. Phys. 2022, 156, 024108. 10.1063/5.0077744. [DOI] [PubMed] [Google Scholar]
- Ehrenfest P. Comment on the Approximate Validity of Classical Mechanics within Quantum Mechanics. Z. Phys. 1927, 45, 455–457. 10.1007/BF01329203. [DOI] [Google Scholar]
- Liu Z.; Lyu N.; Hu Z.; Zeng H.; Batista V. S.; Sun X. Benchmarking Various Nonadiabatic Semiclassical Mapping Dynamics Methods with Tensor-Train Thermo-Field Dynamics. J. Chem. Phys. 2024, 161, 024102. 10.1063/5.0208708. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.







