Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2025 Apr 18;58(9):4447–4458. doi: 10.1021/acs.macromol.5c00099

Effect of Ring Composition on the Statics and Dynamics of Block Copolyelectrolyte Catenanes

Pietro Chiarantoni †,‡, Andrea Tagliabue §,†,∥, Massimo Mella §, Cristian Micheletti †,*
PMCID: PMC12080470  PMID: 40386687

Abstract

graphic file with name ma5c00099_0010.jpg

We use Langevin simulations to study the effect of ring composition on the structure and dynamics of model polycatenanes with copolyelectrolyte rings, each made of one charged and one neutral block. Key observables have a nonmonotonic dependence on ring composition, including the radius of gyration, mechanical bond length, orientational correlations, and rotational relaxation times. Microscopic analysis shows that these nonmonotonicities arise from the competition between electrostatic repulsion, pulling rings apart, and topological constraints, enforcing the proximity of neighboring rings. By locking charged-neutral interfaces at the mechanically bonded regions, this interplay can induce a strong chemical orientational order along the catenane while also hindering the local relaxation dynamics. Chemical orientation defects, manifesting as neutral–neutral interfaces, can emerge too and migrate along the catenane via coupled reorientations of neighboring rings. Our results clarify how ring composition and mechanical bonds can define the properties of topological materials across different scales.

Introduction

Topological metamaterials, extended assemblies of mechanically interlocked molecules,1−4 were reportedly envisioned more than a century ago.5 However, it is only recently that breakthroughs in synthetic chemistry and combinatorial molecular design have enabled the high-yield production of supramolecular constructs with polymer-like connectivity through mechanical bonding. Examples range from linear catenanes6,7 and two-dimensional topological membranes8,9 to three-dimensional regular or irregular networks of interlocked molecules.10−12

Single-molecule probes, often complemented by modeling and simulations, are providing increasingly detailed insight into the fundamentally distinct properties of mechanically bonded systems and their covalently bonded counterparts. Differences have been reported across the main physical observables, such as metric scaling,13−16 intrinsic flexibility, writhe and curvature,17−20 relaxation dynamics,21−23 and the response to spatial confinement,24−26 molecular crowding27 or external forces.6,28−33 Besides being interesting per se, mechanically bonded structures are attracting interest for the possibility of harnessing topological constraints for tuning their physical properties in ways not available for conventional materials. A promising class of these tunable systems consists of interlocked block copolyelectrolytes (co-PEs), polymer chains with charged and neutral segments. These systems provide distinctive advantages for designability and external tunability.34,35 Charged blocks make the system’s size, shape, and dynamics responsive to external fields and to the concentration and valence of the ionic solution even in the presence of topological constraints.36−43 In addition, since topologically constrained co-PE strands primarily contact at their neutral regions,34,35 varying the neutral block length ought to allow for fine control over the geometry of mechanical bonding. Although these effects could provide considerable latitude for designing tunable topological materials, this potential has yet to be directly investigated. In fact, the notable properties of co-PE based materials44−48 have been mostly explored using the linear form of these molecules where, however, the effects of topological entanglements cannot be addressed.

Motivated by these considerations, here we examine the simplest type of topological materials comprising charged and neutral blocks: linear co-PE catenanes. Using Langevin molecular dynamics simulations, we study chains of interlocked ring polymers, each made of one charged and one neutral block, along with counterions that maintain the system’s overall charge neutrality. By systematically varying the relative size of these blocks, we analyze how this key design parameter influences the metric and dynamical properties of the catenane across various scales.

We show that several metric and dynamical observables have a nonmonotonic dependence on ring composition, including the radius of gyration, mechanical bond length, orientational correlations, and rotational relaxation times. Analysis of the catenane’s microscopic organization reveals that these nonmonotonicities arise from a competition between the intra- and inter-ring electrostatic repulsion and the mechanical bonding. This interplay favors the locking of charged-neutral interfaces at mechanically bonded regions, which can severely restrict the rings’ configurational space. This produces a strong chemical orientational order of the catenated rings while also hindering their rotational relaxation dynamics. Finally, our analysis reveals the presence of chemical orientation defects, manifesting as neutral–neutral interfaces at mechanically bonded regions. The defect dynamics involve concerted reorientations of neighboring rings, resulting in a cascade of defect hoppings. The cascade highlights the role of mechanical bonding in coupling structural reorganizations across various lengths and time scales.

Methods

Model and Simulation Setup

The simulated system consisted of a single linear polycatenane composed of n = 12 diblock copolyelectrolyte (co-PEs) rings, each made of m = 20 monomers, as illustrated in Figure 1, contained in a periodic cubic cell of side length Lbox. Each ring comprised two different blocks: a neutral segment of length mneu and a charged segment of length m-mneu, and was modeled via a coarse-grained beads-and-springs representation. The overall charge neutrality of the system was maintained by the presence of n(m – mneu) monovalent counterions.

Figure 1.

Figure 1

Open in a new tab

Typical configurations of the considered copolyelectrolyte linear catenanes at different ring compositions. The catenanes are made of n = 12 rings, each of m = 20 monomers, see sketch. The rings are diblock copolyelectrolytes, with one neutral block of mneu monomers (blue) and a charged one of 20 – mneu unit-charge monomers (red). Monovalent counterions (gray) ensure the overall charge neutrality of the system.

All particles had the same size, σ, and their excluded volume was modeled via the purely repulsive Weeks–Chandler–Anderson (WCA) interactions,49

graphic file with name ma5c00099_m001.jpg 1

where rij is the distance between beads i and j, the cutoff distance rcut = 21/6σ corresponds to the minimum of the 12–6 Lennard-Jones potential, and the interaction amplitude is set equal to the thermal energy of the system, ϵ = KbT.

Bonds between consecutive monomers in a ring were modeled via a finitely extensible nonlinear elastic (FENE) potential50

graphic file with name ma5c00099_m002.jpg 2

where rij is the distance between bonded monomers i and j, rmax = 3σ is the maximum allowed bond elongation, and kbond = 30 KbT/σ2. This parametrization, which differs from the Kremer-Grest one50 for the larger value of rmax, results in a probability distribution of intraring bond lengths that is largely independent of whether the consecutive monomers are neutral or charged, (i.e., whether they additionally interact via the Coulomb term described below), see Figure S1.

Electrostatic interactions between two charged particles i and j were accounted for with a Coulomb potential,

graphic file with name ma5c00099_m003.jpg 3

and were computed using the P3M method, a hybrid method combining direct short-range and mesh-based long-range force calculations,51 with an accuracy of 10–3.52 In eq 3, e is the elementary charge, lb is the Bjerrum length, ε0 is the vacuum dielectric constant, εr is the relative permittivity of the medium, and the ± prefactor reflects whether the particles carry charges with the same or opposite sign. The solvent is implicitly represented by a uniform dielectric continuum, as is common in primitive models of electrolytes. Setting σ = 3.55 Å and Lbox = 121.23σ results in a monomer concentration of 10–2 mol/L and a Bjerrum length lB = 2σ = 7.10 Å, the latter a value typical for diluted aqueous solutions of polyelectrolyte at room temperature.

The system was evolved via Langevin dynamics simulations in the canonical ensemble at T = 298 K with default values50 for the friction coefficient, γ, and particles’ mass, M. The dynamics was integrated with a velocity Verlet algorithm using a time step δt = 0.01τlj, where 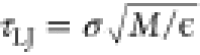Inline graphic is the characteristic Lennard-Jones time. Simulations were performed using the Molecular Dynamics software package ESPResSo v4.1.53 To avoid system instabilities and the rupture of the mechanical links due to Coulomb interactions, the system has been equilibrated as follows: after 100τLJ with electrostatics switched off, Coulomb interactions were gradually introduced by increasing the nominal ionization degree α of the charged monomers from 0 to 100% by means of a constant pH approach,54,55 in which the nominal pH was increased from −10 (α = 0) to 10 (α = 1) by ΔpH = 2 every 100τlj; then, the fully charged system was further equilibrated for 2 × 104τlj.

The neutral block length was varied from mneu = 0 (i.e., fully charged rings) to mneu = m = 20 (fully neutral rings). For each value of mneu, we equilibrated the system and ran 5 independent simulations of duration 105τlj, sampling configurations at 10τlj intervals.

Observables

To characterize the catenane’s properties across different scales, we computed canonical expectation values of various observables by taking averages over the sampled conformations.

Going from local to global metric observables, we considered: (i) the root mean squared gyration radius of individual rings, 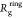Inline graphic; (ii) the average distance of the centers of mass of neighboring rings, i.e., the mechanical bond length, b; (iii) the distance of minimum approach of concatenated rings A and B, defined as the minimum distance between any monomer in ring A and any monomer in ring B, i.e., dmin = mini∈A,j∈Brij, and (iv) the charged/neutral character of the contacting monomers; the correlation of (v) mechanical bond vectors and (vi) the chemical orientation vectors v̂cn, defined as the (normalized) distance vectors between the midpoints of the charged and neutral blocks; (vii) the gyration radius and (viii) and end-to-end distance of the entire catenane’s backbone.

For the characteristic times of the catenane’s internal dynamics, we considered the reorientation time, that is, the decay time of the orientational correlation function of the normalized end-to-end vector, R̂ee,

graphic file with name ma5c00099_m006.jpg 4

where τ is the time lag and ⟨⟩t denotes the time average. The characteristic reorientation time of the catenane, Inline graphic, was obtained by integrating Cee(τ) from τ = 0 up to the smallest value of τ for which the correlation falls below 0.01.

For the relaxation dynamics at the local scale, we considered the characteristic reorientational time56 of the central ring, 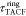Inline graphic. As customary,57 this was computed by averaging the orientational correlation functions of all its normalized diameter vectors.

Results

We first examined how the composition of the co-PE rings and their mechanical bonding influence the catenane metric properties across multiple scales.

Overall Catenane Size

We first analyzed the dependence on ring composition of the overall size of the catenane, which we measured via the root mean square values of the gyration radius, Rg, and end to end distance, Ree, of the catenanes’ backbone, as sketched in Figure 1. The data for Rg, are shown in Figure 2 and highlight two notable properties. First, Rg, has a nonmonotonic dependence on mneu, with a maximum at mneu = 3. The Rg fluctuations are similarly nonmonotonic (Figure S2). Second, the Rg curvature changes sign twice, with two concave regions flanking an intermediate convex one for 7 ≲ mneu ≲ 15. Analogous properties hold for the root mean squared end-to-end distance, Ree, which behaves similarly to Rg except for the milder decrease for mneu > 15, see Figure S3 and the inset of Figure 2. It is interesting to compare the dependence of the overall catenane size on the co-PE ring composition with that observed in mechanically bonded block copolymer rings with rigid and flexible segments. These systems have recently been studied in the context of two-dimensional chainmails, where the average size varied monotonically with ring composition.19 Although the systems’ dimensionalities differ, this result and others presented later suggest that the nonmonotonic behavior of Rg and Ree is specific to charged/neutral copolymers.

Figure 2.

Figure 2

Open in a new tab

Gyration radius of the catenane backbone, Rg, as a function of ring composition, mneu. The inset shows the dependence of the catenane’s gyration radius to end-to-end distance ratio, Ree/Rg, on the ring composition.

Rings’ Size and Compenetration

Turning to the local metric properties, we then considered the size and degree of compenetration of concatenated rings. To this end, we analyzed the root mean squared gyration radius of individual rings, Inline graphic, the average distance of minimum approach of linked rings, dmin, and the average distance of their centers of mass, also termed mechanical bond length, b, see sketch in Figure 3a. The dependence of these observables on mneu is illustrated in panels b–d of Figure 3.

Figure 3.

Figure 3

Open in a new tab

Local metric properties of catenanes as a function of ring composition. The profiled observables are the average ring’s gyration radius, Inline graphic; the average mechanical bond length, b (defined as the distance between the centers of mass of concatenated rings); and the average distance of minimum approach between monomers of two concatenated rings, dmin, see sketch in panel (a). The shaded band marks the interval 0 ≤ mneu ≤ 5 where the b and dmin curves exhibit qualitatively distinct behavior compared to longer neutral blocks.

Compared to the entire catenane, the gyration radius of individual concatenated rings has a different mneu dependence. In fact, it decreases monotonically and without significant changes in curvature. The decrease of Inline graphic with mneu reflects the diminishing intraring electrostatic repulsion, which maintains rings in an approximate planar circular state (Figure S7). Notice that Inline graphic decreases by only about 15% going from fully charged to fully neutral rings, whereas the catenane’s Rg decreases by nearly a factor of 2.

Interestingly, Figure 3c reveals a nonmonotonicity of the mechanical bond length, b, which has a maximum at mneu = 5. Although the peak location is similar to that of the catenane’s Rg, the b profile maintains the same curvature, unlike in the Rg case.

Finally, Figure 3d shows the profile of the average distance of minimum approach of monomers in mechanically linked rings, dmin, which we use as a measure of mechanical bond tightness. For mneu = 0, dmin is equal to 1.3σ, indicating that the inter-ring electrostatic repulsion, though lessened by the present counterions, prevents fully charged concatenated rings from being in tight contact. As the length of the neutral block increases, dmin decreases and eventually plateaus for mneu > 5 at 1.09σ. This value is approximately equal to the distance of bonded monomers in a ring; see Figure S1. This indicates that tight concatenation can already occur at mneu = 5, even though the rings are still mostly charged at this composition.

Overall, the results of Figure 3 point at two distinct regimes for the local metric properties. For mneu > 5, consecutive rings are in tight contact and their size and center of mass distance decrease significantly as the fully neutral case is approached. Instead, even though counterions are present for mneu < 5, the stronger electrostatic repulsion makes rings larger and keeps them more separated along the catenane’s backbone.

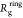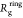The implications of the two effects for the nonmonotonicity of b is aptly conveyed by the following heuristic argument. Consider an idealized catenane composed of elliptic rings, with their longest axes aligned to the catenane backbone and lying in alternating orthogonal planes. Decreasing the rings’ size, Inline graphic via an affine transformation of the elliptic rings, clearly shortens the mechanical bond length b. Conversely, decreasing dmin while keeping Inline graphic constant causes b to increase. Thus, reducing Inline graphic and dmin has opposite effects on b. The nonmonotonicity of b(mneu) is precisely caused by such competition, since both Inline graphic and dmin decrease with mneu (Figure 3b,d). This point is quantitatively illustrated in Figure S4, which shows the mneu dependence of the approximate mechanical bond length, bapprox= 2l1 – dmin, where l1 is the square root of the largest eigenvalue of the average gyration tensor of individual rings.

The discussed interplay of b and Inline graphic provides an apt illustration of how global properties of the co-PE polycatenane are tied to local features underpinned by mechanical bonding.

Relative Orientation of Neighboring Rings

Next, we studied the relative orientation of concatenated rings and their neutral and charged blocks. Specifically, we analyzed the orientational correlations of mechanical bonds and the vectors connecting the midpoint monomers of the charged and neutral blocks on the same ring. For brevity, we shall refer to the latter as the chemical orientation vector, or charged-to-neutral vector, and indicate it as v⃗cn; see the sketch in Figure 4a.

Figure 4.

Figure 4

Open in a new tab

Internal orientational correlation of catenanes as a function of ring composition. The profiled observables involve scalar products of mechanical bond vectors, b̂, and charged-to-neutral vectors, v̂cn; see sketch in panel (a). Panels (b–d) show the mneu dependence of the orientational correlation of mechanical bonds and chemical orientation vectors for the same and consecutive rings. Data points represent the average scalar product value, while the shaded band indicates the Q1–Q3 interquartile range, spanning from the 25th (Q1) to the 75th (Q3) percentiles. Panel (e) shows the probability distributions for consecutive charged-to-neutral vectors at different mneu values.

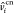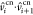As a measure of the effective rigidity of the catenane, we used the average scalar product of consecutive mechanical bonds, b̂i · b̂i+1, where the ^ symbol denotes that the vectors are normalized to unit length. To cover the possible combinations of mechanical bonds and charged-to-neutral vectors, we additionally analyzed the average scalar products Inline graphic · b̂i, and Inline graphic.

The dependence of these various measures of orientational order on ring composition is illustrated in Figure 4b–d.

The data in panel (b) show that b̂i · b̂i+1 remains above 0.5 for all values of mneu. This indicates that consecutive mechanical bonds have a strong alignment correlation across all ring compositions; see also Figure S8. In spite of this, it also emerges that b̂i · b̂i+1 has a minimum for intermediate values of mneu. Specifically, the alignment correlation decreases from a maximum of 0.86 for mneu = 0 (fully charged rings) to 0.66 for mneu = 10 (50–50 ring composition). Beyond this local minimum, b̂i · b̂i+1 rises to 0.75 for mneu = 16, before dropping to the global minimum of 0.6 for fully neutral rings, mneu = 20. This establishes the unexpected result that the effective bending rigidity of the catenane has a nonmonotonic dependence on the length of the neutral/charged segments. The corresponding mneu dependence of the effective persistence length of the catenane backbone is presented in Figure S5. The same figure shows that the nearly 2-fold variation in catenane size with mneu (Figure 2) is approximately captured by a Kratky–Porod model informed by the catenane’s persistence and mechanical bond lengths.

Panel (c) of Figure 4 shows that an opposite nonmonotonicity is present for 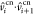Inline graphic. Note that the average scalar product of consecutive chemical orientation vectors is approximately zero for mneu equal to 1 and 19, which is close to the cases of uniformly charged/neutral rings, where v̂cn cannot be defined. The nonmonotonic curve bridging these limiting cases is strongly asymmetric with respect to the 50–50 composition. For mostly charged rings, mneu < 10, the average scalar product is unimodal, peaking at 0.5 for mneu = 5, while for mostly neutral rings it remains close to zero. The data thus indicate that the ″chemical orientation″ correlation of neighboring rings is strongest at mneu = 5 and negligible for mneu > 10.

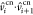This result is best understood by considering the probability distributions for the scalar products Inline graphic at different ring compositions, which are shown in panel (e). The distribution is bimodal for mneu = 3, with maxima corresponding to parallel and antiparallel chemical alignments. The parallel alignment is the dominant one and becomes even more so for mneu = 5, yielding the highest average scalar product. As mneu increases to 8, the statistical weight of the parallel order diminishes as intermediate negative values of the scalar product become populated, too. Finally, for mneu = 15, the curvature of the probability distribution of the scalar products changes sign. The parallel and antiparallel states become the least populated ones, while the distribution becomes broad and approximately symmetric with respect to zero. The same holds throughout the mneu > 10 interval, thus accounting for the observation in panel (c) of the flattening to zero of the Inline graphic curve for 12 ≤ mneu ≤ 19.

Finally, we discuss the relative orientation of the normalized chemical vector of a ring and one of its two mechanical bonds. We note that while the chemical orientation of individual rings is uniquely defined, the mechanical backbone is not oriented. Thus, inverting the orientation of all mechanical bonds b̂i → −b̂i provides a legitimate and entirely equivalent description of the catenane backbone, see also Figure S6. 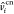To discount such inversion symmetry, we thus considered the modulus of the scalar product, Inline graphic. The data, which are plotted in panel (d), indicate that Inline graphic and b̂i are approximately parallel for mneu ≤ 5. As the neutral segment length increases, the good alignment of the chemical orientation vectors and the local backbone is progressively lost. In fact, throughout mneu ≥ 10 the average value and spread of Inline graphic are close to those expected for two randomly oriented vectors, a condition practically realized as the fully neutral case is approached.

All considered, the results of Figure 4b–d establish that (i) even small charged segments of as few as four monomers (mneu = 16) endow the catenane backbone with an effective bending rigidity that is significantly larger than the fully neutral case (mneu = 20), (ii) chemical orientation vectors are well aligned to the backbone for mneu ≤ 5, and (iii) the chemical orientation of neighboring rings is most correlated at mneu = 5, i.e., at the crossover between the two local metric regimes discussed in connection with Figure 3.

Chemical Orientation of Distant Rings, and Emerging Defects

To complete the analysis, we considered the correlation of chemical orientation vectors of ring pairs, i and j, at increasing backbone (sequence) distance, |i – j|. To avoid end effects, the first and last rings in the catenanes were not considered, so that the analysis is performed for |i – j| ranging from 1 to n – 3 = 9.

The results are shown in Figure 5. The average scalar products 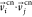Inline graphic remain close to zero for mneu > 10 at all backbone distances. This indicates that no significant chemical orientational correlation exists at any sequence separation between rings that are mostly neutral. We recall that in this same mneu range, the v⃗cn vectors are approximately randomly oriented with respect to the local backbone, too.

Figure 5.

Figure 5

Open in a new tab

Orientational correlation defects. Panel (a) shows the mneu dependence of the orientational correlation (average scalar product) of pairs of charged-to-neutral vectors, v⃗cn, at various distances along the catenane backbone. Negative values of the average scalar products are due to chemical orientation defects such as the one illustrated in panel (b) for a typical configuration at mneu = 5. The arrows sketched at the bottom represent the projections of the charged-to-neutral vectors along the end-to-end distance vector of the catenane. The defect separates oppositely oriented runs of the v⃗cn projections.

However, when the rings are mostly charged, a qualitative change occurs for increasing sequence separations. The data for the smallest possible distance, |i – j|=1, correspond to the same neighboring rings already discussed in Figure 4c, where the largest orientational correlation (+0.5) occurs at mneu = 5. As |i – j| increases, the correlation peak gradually diminishes, flattens to zero, and eventually turns into a negative peak, indicative of anticorrelation. Interestingly, the positive and negative peaks all occur near mneu = 5. The most negative correlation is about −0.25, i.e., half the magnitude of the largest positive one.

The results establish that, for the 3 ≲ mneu ≲ 8 compositions, the chemical orientation of distant rings is typically antiparallel, whereas that of neighboring rings is mostly parallel. This indicates that at these ring compositions catenanes are likely to contain defects, i.e., antiparallel pairs of consecutive charged-to-neutral vectors within a sequence of parallel-oriented pairs.

We recall that in this mneu range, the chemical orientation vectors are mostly aligned along the mechanical backbone that, in turn, has a high effective rigidity (Figure 4). These considerations suggest that a convenient representation of the defects can be achieved by considering the projections of the chemical orientation vectors along the catenane’s end-to-end vector. The illustration of one such defect is provided in Figure 5b, where it is noticed that the projected 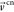Inline graphic vectors change directionality at the interface of rings i = 8 and i = 9. The resulting orientation pattern is reminiscent of the energetically costly domain walls in one-dimensional Ising chains. However, the analogy is only qualitative because, differently from Ising chains, domain walls in ordered PE-catenanes (featuring N–C interfaces only) can be introduced in different ways: either via a C–C interface, which is typically energetically costly, or via an N–N interface, as shown in Figure 5b.

The systematic presence of isolated defects for mneu ∼ 5 is underscored by the fact that the most probable orientations of consecutive chemical vectors are the parallel and antiparallel ones (Figure 4e). Detailed analysis, presented in the next subsection and in Figure S13, reveals that at the considered catenane’s length (n = 12), the most probable number of defects for mneu ∼ 3–5 is 1, although 0 and 2 defects have a sizable probability, too.

As evident from Figure 5b, the emergence of defects is associated with two neutral blocks interfacing at the mechanically bonded region.

Patterns of Contacting Monomers

To investigate the microscopic basis of the chemical orientational correlation, we analyzed the contact probability between charged and neutral monomers of neighboring rings as a function of ring composition. Our investigation involved two complementary approaches: first, we determined which contour regions of a ring are closest to the concatenated neighbors; next, we examined the contact probability between charged and neutral blocks of concatenated rings.

For the first analysis, we focused on the central ring in the catenane and identified the two monomers closest to the neighboring rings, as illustrated in the sketch in Figure 6. By repeating this procedure across the sampled conformations, we computed the joint probability distribution of the indices of the two mechanically bonded monomers. The results for various ring compositions are shown in Figure 6 as two-dimensional heatmaps with periodic boundary conditions; analogous plots for additional values of mneu are shown in Figure S11. The diagonal symmetry was not imposed a priori and reflects the statistical equivalence of the two neighboring rings. The color-coded sidebars denote the monomer types (charged or neutral), whereas dashed lines indicate the block boundaries. The top plots provide one-dimensional projections of the two-dimensional probability distributions and capture the probability that specific monomers within the neutral or charged blocks are in contact with one of the neighboring rings.

Figure 6.

Figure 6

Open in a new tab

Probability distribution of mechanically bonded monomers in a given ring. The heatmaps represent the joint probability distribution of the indices of the two monomers of the central ring in the catenane closest to each neighboring ring, as sketched on the left. The heatmaps are shown for three different values of mneu, with the neutral (blue) and charged (red) character of the monomers indicated by the colored sidebars. The profile at the top is the marginalized (one-dimensional) probability distribution. The diagonal symmetry of the heatmaps, reflecting the equivalence of the two monomers, was not imposed on the data.

The density plot for mneu = 5 reveals that mechanical bonding predominantly involves monomers located at the center of the neutral and charged blocks, thus corresponding to diametrically opposite positions on the ring contour. Interestingly, monomers close to the block boundaries are seldom in contact with the neighboring rings.

Two qualitative changes emerge with slightly longer neutral segments, mneu = 8. On the one hand, the boundary regions of the charged blocks become increasingly likely to participate in mechanical bonding. On the other hand, a significant probability density appears in the heatmap region where both contact points reside on the neutral segment, thus evidencing that the mneu = 8 segment is sufficiently long to occasionally accommodate mechanical bonds with both neighboring rings simultaneously, despite all rings being predominantly charged and therefore repelling one another. Due to this repulsion, the two contact points are at opposite edges of the neutral segment. This property makes the mneu = 10 composition consequential for various metric observables, as well as dynamical ones described later, that attain their local/global extremal values at the balanced composition. The significance of mneu = 10 is underscored by the analysis of the fraction of condensed counterions and the radial distribution functions of the system (see Figures S9 and S10). While the latter do not deviate from what commonly expected, the former exhibits a distinct regime shift at this nearby compositions.

These findings clarify key aspects of the considered system; in fact, the change in trend for the number of condensed counterions in Figure S10 could, in principle, be attributed to the decrease in probability that a charged segment on a ring sits relatively close to, or directly facing, a similar feature on another, mechanically linked, moiety. If so, the probability of counterions condensing “between two rings” (i.e., forming electrostatic bridges) due to the locally high electrostatic potential should also decrease, as it happens in knotted copolyelectrolytes.58 For the latter, we have already highlighted that essential crossings tend to foster a higher counterion condensation than the average,35 especially when in the presence of divalent ions. Importantly, the origin of the divalent species (i.e., whether coming as chain’s counterions or due to added salts) appears irrelevant.

This contact mode becomes dominant and typical as the neutral segment length increases, as illustrated by the mneu = 15 heatmap. In this case, the one-dimensional profile at the top reveals that contacts involving the central monomers of the blocks are suppressed, particularly in the charged region. Instead, the most probable contacting monomers are situated near the edges of the neutral block.

In the second type of analysis, for each pair of interlocked rings, we identified the type – neutral (N) or charged (C) – of the two closest monomers, one from each ring. We recall that these pairs correspond to those defining dmin in Figure 3d. We then calculated the total numbers of N–N, N–C, and C–C contacting pairs in the catenane and averaged them over the sampled conformations.

The resulting curves are shown in Figure 7, plotted as a function of mneu. Analogous data, but referred to the contacts types probabilities of individual mechanical bonds are shown in Figure S12. The data in Figure 7 reveal that C–C contacts decrease rapidly with the introduction of even a small number of neutral monomers and become negligible already at mneu = 5, despite the charged block being three times longer than the neutral one. The fact that the trend of the C–C curve parallels that of the minimum approach distance of concatenated rings (dmin curve in Figure 3d) suggests that mechanical links become taut for mneu > 5.

Figure 7.

Figure 7

Open in a new tab

Average number of contacting pair types in the catenane as a function of ring composition. The curves show the mneu dependence of the average number of neutral–neutral (N–N), charged–charged (C–C), and mixed (C–N or N–C) pairs of contacting monomers in the catenane. The contacts refer to the two closest monomers of concatenated rings. The average numbers of contact types sum to n – 1 = 11 at each mneu value. The three colored thin curves represent mean-field-like approximations, see main text. For 2 ≤ mneu ≤ 7, the N–N curves plateau at about the value of 1, marked by the dashed horizontal line.

For 2 ≤ mneu ≤ 10, C–N contacts are prevalent. Note that the peak in C–N contact number does not occur for the half-charged/half-neutral composition, but rather at mneu = 5, and N–N contacts become dominant for mneu > 10. Interestingly, for 2 ≤ mneu ≤ 7, the N–N curve plateaus near the value of 1. Consistently with the data of Figure 5, this indicates that, on average, there is one chemical orientation defect in the catenane. Indeed, detailed analysis of the distributions of contacting pairs type shows that, for mneu = 3–5, m = 12 catenanes are likely to feature from 0 to 2 defects, the single defect case being the most probably by far; see Figure S13.

For reference, in Figure 7 we also included baseline contact numbers (thin lines) computed from mean-field–like (MF) pairing combinatorics. The expressions, based on the fraction of neutral and charged monomers in a ring, are

graphic file with name ma5c00099_m027.jpg 5
graphic file with name ma5c00099_m028.jpg 6
graphic file with name ma5c00099_m029.jpg 7

All observed contact numbers deviate significantly from the MF estimates, with the largest discrepancy observed for the C–N case. The actual C–N peak at mneu = 5 is substantially shifted from the MF one (peaking at mneu = 10), and its value is nearly twice the MF one. As the neutral segment length increases, C–C contacts decay faster than predicted by the MF model. Finally, throughout the mneu > 10 interval, N–N contacts are over-represented compared to the MF curve, which also lacks the plateau associated with the chemical orientation defect.

Finally, we note that the curves for all three contact types in Figure 7 differ markedly from those observed in the aforementioned chainmails of copolymer rings with rigid and flexible segments.19 The latter are satisfactorily approximated by the MF curves, which exhibit mirror symmetry about the 50–50 composition, corresponding to an interchange of the two segment types. Conversely, the curves in Figure 7 are strongly asymmetric because electrostatic interactions introduce fundamental differences when neutral and charged monomers are interchanged. As a result, mechanically bonded systems made of co-PEs and neutral diblock copolymers have starkly different properties, reinforcing and generalizing the inequivalence previously established for conventionally bonded co-PEs and uncharged block copolymers.44,59

Dynamics

We now turn to the effects of the ring composition on the catenanes’ dynamics across different scales.

For the global dynamics, we analyzed the characteristic rotational time of the catenane, Inline graphic, which is defined as the correlation time of the end-to-end vector orientation; see Methods. This global relaxation mode was chosen for analysis because it decays much more slowly than the autocorrelation of other standard metric observables, such as the radius of gyration; see Figure S14.

Figure 8 shows that Inline graphic decreases steadily with mneu, dropping by approximately a factor of 3 from fully charged to fully neutral rings. The reduction is consistent with the relaxation becoming more rapid as the catenane shrinks with increasing mneu (Figure 2) to the reduced electrostatic repulsion. Indeed, Inline graphic and Inline graphic are approximately proportional, analogous to the behavior of Rouse-like models in the absence of hydrodynamic effects, see Figure S16. Interestingly, the rotational relaxation time of mechanical bond vectors is smaller but still comparable to Inline graphic throughout the entire mneu, see Figure S14. This is consistent with the observed overall stiffness of the catenane’s backbone at the considered length, n = 12.

Figure 8.

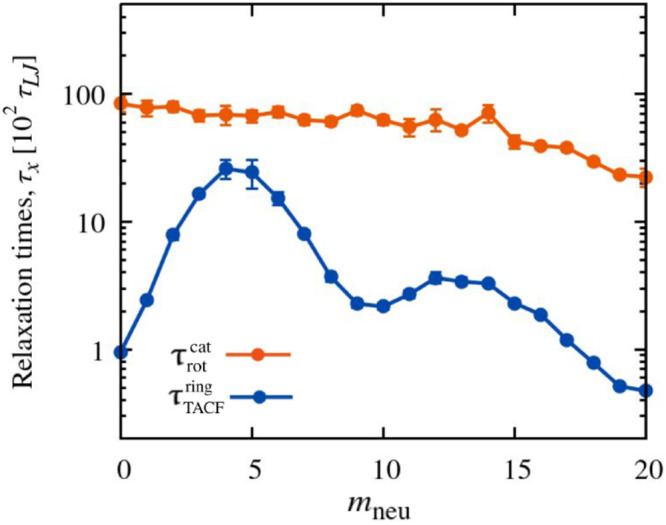
Figure 8

Open in a new tab

Characteristic times of global and local relaxation modes as a function of ring composition. The curves show the mneu dependence of the characteristic rotational times of the entire catenane and one of its rings. The former, 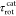Inline graphic, is the characteristic decay time of the orientational correlation function of the catenane end-to-end vector. The latter, Inline graphic is the characteristic decay time of the orientational correlation function of the ring’s diameter vectors, averaged over all diameters.

Differently from the global relaxation dynamics, the internal dynamics of individual rings exhibit a more varied and complex dependence on mneu. To characterize it, we analyzed the characteristic reorientational time56 of one of the two central rings, 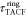Inline graphic, which we computed by averaging the rotational autocorrelation functions of all its diameter vectors;57 see Methods.

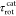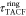Notably, Figure 8 shows that the Inline graphic (mneu) curve is bimodal, peaking at mneu ≈ 5 and mneu ≈ 15 and with an intervening local minimum at mneu = 10. Across most of the mneu range, Inline graphic is one to 2 orders of magnitude smaller than Inline graphic. An exception is mneu ≈ 5, where Inline graphic is of the same order as Inline graphic.

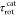The Inline graphic profile is best discussed starting from the limiting cases of fully charged and fully neutral rings. Inline graphic decreases by about a factor of 2 going from the former to the latter case. In relative terms, this slowdown is similar to that of the global rotational time, Inline graphic. 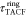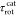However, due to the differing length scales of these two modes, Inline graphic is approximately 2 orders of magnitude shorter than Inline graphic.

The fact that local relaxation is significantly slower at mneu = 5 compared to fully charged rings reflects the particular structural organization of the catenane at this composition. As noted in connection with Figure 3c,d, the mneu = 5 neutral blocks are already sufficiently long to allow concatenated rings to form tight mechanical bonds at the charged-neutral clasped interfaces Figure 3c,d. At the same time, the electrostatic repulsion at mneu = 5 maintains a high rigidity of the catenane backbone while also locking their chemical alignment of neighboring rings (4b,c). These local geometrical constraints hinder the reorientational motion of the rings and reflect in their noticeably slow relaxation at mneu = 5.

As mneu is increased from 5 to 10, both the backbone rigidity and chemical alignment of neighboring rings decrease. As a result, the rings gain rotational freedom relative to each other without compromising the favorable charged-neutral interlockings. This reflects in the decrease of 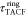Inline graphic in the same mneu range. At mneu = 10, the neutral segments become large enough to be co-opted in the mechanical bonding with both neighboring rings. 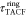At mneu ≈ 10, where N–N contacts dominate and the alignment between vcn and the catenane backbone is lost, a distinct Inline graphic regime emerges. 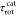Moving toward the fully neutral case, the widening gap between Inline graphic and Inline graphic highlights the progressive decoupling of the ring’s internal dynamics and the global dynamics of the catenane.

We conclude the analysis by discussing the dynamics of the chemical orientation defects. To this end, we examined the time evolution of the orientation of consecutive charged-to-neutral vectors relative to their local backbone direction, quantified by the scalar products 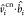Inline graphic.

Figure 9a shows typical traces of the scalar products over a timespan of 105τlj, several times longer than the global relaxation time 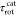Inline graphic. The data refer to four consecutive rings at mneu = 5, which is the neutral block length at which the incidence of defects is highest (Figure 5a). Analogous plots for different values of mneu are provided in Figure S15.

Figure 9.

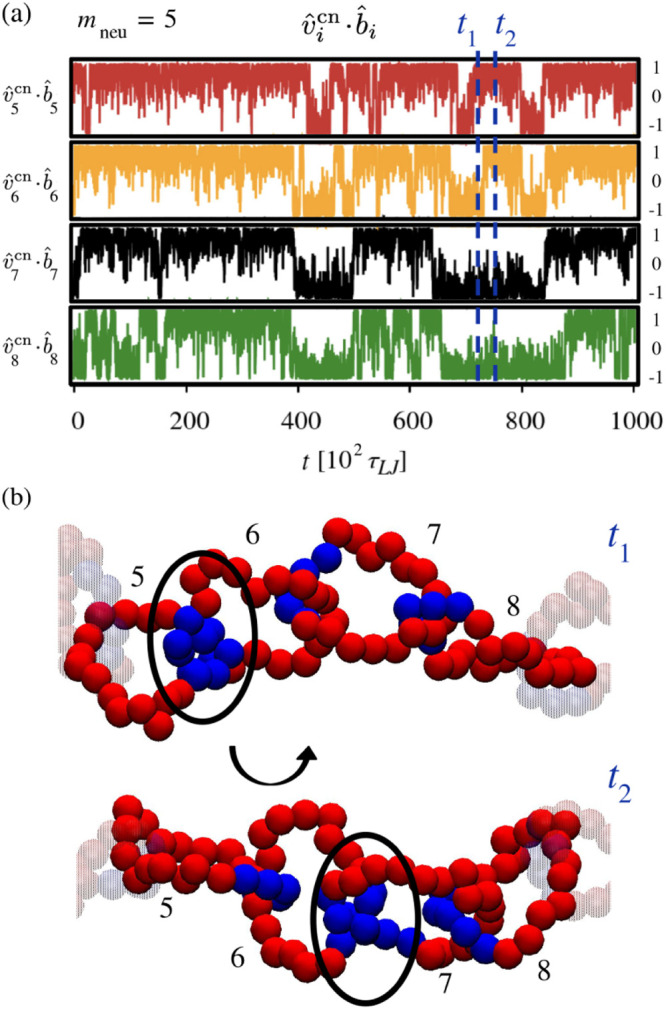
Figure 9

Open in a new tab

Dynamics of chemical orientation defects. The traces in panel (a) represent the time evolution of the orientational correlation (scalar product) of consecutive charged-to-neutral vectors, 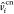Inline graphic and one of the two corresponding mechanical bonds b̂i. The data are for a stretch of a few consecutive rings at mneu = 5. The configurations corresponding to the two selected times (dashed lines) are shown in panel (b) and illustrate the hopping of the defect across neighboring rings.

The traces in Figure 9a present numerous switches between positive and negative values of Inline graphic, corresponding to inversions, or ″flips″, of the chemical orientation vectors. There are two key aspects of these stochastic inversions. First, the intervals between consecutive flips of a given ring vary widely, with an average duration of approximately 70× 102τlj. This time scale is of the same order as the ring rotational time, Inline graphic, discussed previously. Second, the flips often occur in a coordinated manner across concatenated rings. In fact, the traces show rapid sequences of flips involving multiple consecutive rings.

Figure 9b illustrates the elementary steps of the propagating chemical orientation inversions. The snapshots correspond to the two time points, t1 and t2, marked by vertical dashed lines in panel (a). The snapshots show the hopping of a defect between neighboring rings. At t1, the defect is located at the contact region of the two leftmost rings, i = 5 and 6, which interface through their neutral blocks. At t2, the defect has hopped to the right, i.e., to the interface of rings i = 6 and 7. This defect migration is driven by a half-turn rotation of ring 6, which flips the charged and neutral blocks in contact with its neighboring rings.

To summarize, the results of Figure 9 show that at mneu = 5, chemical reorientations of individual rings occur abruptly, with time separations of the order of Inline graphic, although with significant variance. These reorientations are typically part of a triggered cascade of defect hops that propagate across neighboring rings.

Conclusions

In this study, we considered model polycatenanes made of diblock copolyelectrolyte (co-PE) rings in solution with counterions. Using Langevin dynamics simulations, we investigate how the static and dynamic properties depend on ring composition. The latter was changed by systematically varying the number of monomers of the neutral block, mneu, while keeping fixed the number of ring monomers (m = 20) and of linearly concatenated rings (n = 12).

Our results revealed an unexpectedly complex dependence on ring composition of several metric and dynamical observables. Specifically, the catenane’s radius of gyration, the mechanical bond length, the chemical orientation of consecutive rings, and the rotational relaxation times of individual rings were found to be nonmonotonic with mneu, all presenting a maximum for mneu ≈ 5. These nonmonotonicities arise from the competition between the intra- and inter-ring electrostatic repulsion, which tends to pull rings away, and mechanical bonding, which maintains neighboring rings in spatial proximity.

This tug-of-war takes on different forms depending on the balance of charged and neutral block lengths, leading to qualitatively different properties. For mneu < 5, the repulsion of the like-charged monomers is sufficiently strong to keep rings swollen and prevent their contact. At mneu = 5, the neutral block length is large enough that neighboring rings can touch each other at their neutral-charged (or neutral–neutral) interfaces. At the same time, the inter-ring repulsion induces a tightening of the mechanical bonds. Because the neutral blocks co-opted in the succession of neutral-charged interlockings are short, consecutive rings are significantly restricted in their relative positioning, with two main consequences. On the one hand, consecutive chemical orientation vectors, defined as the distance vectors between the charged and neutral blocks midpoints, are strongly aligned. On the other hand, the local relaxation dynamics is hindered.

Increasing the neutral block length, mneu > 5, lessens these conformational constraints, and so does reducing mneu too, because going toward the fully charged limit eliminates the tight contacts of consecutive rings. It is for these reasons that the aforementioned metric and dynamic observables all present a maximum at mneu = 5.

Finally, for mneu > 10, where the majority of the monomers are neutral, the neutral blocks co-opted in the mechanically bonded regions are large enough, and the inter-ring repulsion is sufficiently small that consecutive rings are largely unrestricted, both orientationally and positionally, to the point that the neutral block of one ring is frequently interfaced with the charged blocks of both its neighbors. In such conditions, the variations of the metric observables, such as the ring’s and catenane’s size, are mainly ascribable to the progressive crumpling of the rings as the number of same-charged monomers is reduced.

Overall, two co-PE compositions, mneu = 5 and 10, emerge as particularly noteworthy, as various metric and dynamical observables exhibit extremal behavior at these values. The case mneu = 5 corresponds to the minimal neutral-block length needed to sufficiently reduce electrostatic repulsion so that rings can make contact at neutral-charged interfaces. Instead, mneu = 10 corresponds to the shortest neutral blocks that contact the charged segments of both neighboring rings. We expect that this physical rationale for singling out relevant co-PE compositions would remain valid when the length and number of concatenated rings are changed, although these specific numerical values of mneu would likely shift.

The findings open several avenues for further research. A natural extension would be varying the number of rings and monomers per ring, which are likely to influence the catenane’s flexibility, change the interplay of the local and global relaxation dynamics, and affect the number of defects and their interactions, too. Introducing rings with multiple alternating charged and neutral blocks could be a further design element for controlling the catenanes’ structural organization and dynamics. It would also be relevant to investigate how facile externally tunable conditions, such as solvent quality, pH,60 and concentration and nature of counterions in solution,35−37,41−43,58 could modulate the properties of co-PE catenanes across different scales, providing insights that could be transferrable to more general and complex classes of mechanically bonded supramolecular constructs. Furthermore, given that our dynamic characterization relied on conventional Langevin simulations, it would be worthwhile to assess in future studies whether significant differences arise when hydrodynamic effects are included.

As for the impact that varying solution composition may have, one may, de facto, attempt an educated guess on how the highlighted properties could be impacted basing on our previous results on knotted copolyelectrolytes and the pair distribution functions shown in Figure S9. Thus, adding monovalent salts is likely to “crumple” rings35,58 reducing their gyration radius, the mechanical bond lengths, and the inter-ring repulsion; in turn, this is likely to foster the decrease in the overall system’s gyration radius and “end to end” distance. As for the relative orientation of subsequent rings, the propensity of being positively correlated is expected to decrease, albeit it should not be vanquished as 1:1 salts do not appear able to completely neutralize charged segments due to condensation. The impact of divalent counterions or salts with divalent species with opposite charge than chains’ ones should, instead, be more marked (see ref (35) for knotted species) with respect to “ring crumpling” and all related metrics. Conversely, it appears difficult to predict the effect on the orientation of copolymer rings, as divalent species may effectively bridge charged segments, thus limiting the impact of neutral ones. Investigating the latter aspects may be of general interest, even though it is likely to be fraught with technical difficulties due to the possible increase in intra and inter-ring friction caused by the stronger electrostatic interaction between mobile ions and chains.

With respect to possible applications of the results discussed, one may envision the transfer of defects from one catenane end to the opposite one triggered by chemical-related or electrostatic stimuli. The system would, thus, act as a mechanically connected molecular wire (or switch61) rather than a covalently bonded one, as the defect migration could be interpreted in terms of an overall charge transfer. Moreover, one may harness the intrinsically polar nature of copolyelectrolyte catenanes in applications similar to the ones of covalently bound electrets62 when the macromolecular size range could be useful, for instance, as a separation layer or for its reorientation capability. Finally, the ability to control the number of defects may be exploited to trigger/impair energy or electron transfer along the catenane when the different chemical nature of the comonomers bestow them with the capability of acting as, alternatively, donors and acceptors.63,64

Acknowledgments

A.T. acknowledges postdoctoral fellowships from Università degli Studi dell’Insubria (assegno di ricerca junior, 2022) and SISSA. M.M. acknowledges funding from Università degli Studi dell’Insubria (Fondo d’Ateneo per la Ricerca, FAR2022). This study was funded in part by the European Union - NextGenerationEU, in the framework of the PRIN Project ″The Physics of Chromosome Folding″ (code: 2022R8YXMR, CUP: G53D23000820006), and by PNRR Mission 4, Component 2, Investment 1.4_CN_00000013_CN-HPC: National Centre for HPC, Big Data and Quantum Computing—Spoke 7 (CUP: G93C22000600001). The views and opinions expressed are solely those of the authors and do not necessarily reflect those of the European Union, nor can the European Union be held responsible for them.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.macromol.5c00099.

  • Additional results for the metric and dynamical properties of the considered block copolyelectrolyte catenanes (PDF)

Author Contributions

P.C., A.T., M.M., and C.M.: simulations, analysis, and writing.

The authors declare no competing financial interest.

Supplementary Material

ma5c00099_si_001.pdf (1.7MB, pdf)

References

  1. Niu Z.; Gibson H. W. Polycatenanes. Chem. Rev. 2009, 109, 6024–6046. 10.1021/cr900002h. [DOI] [PubMed] [Google Scholar]
  2. Gil-Ramírez G.; Leigh D. A.; Stephens A. J. Catenanes: Fifty Years of Molecular Links. Angew. Chem., Int. Ed. 2015, 54, 6110–6150. 10.1002/anie.201411619. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Hart L. F.; Hertzog J. E.; Rauscher P. M.; Rawe B. W.; Tranquilli M. M.; Rowan S. J. Material properties and applications of mechanically interlocked polymers. Nat. Rev. Mater. 2021, 6, 508–530. 10.1038/s41578-021-00278-z. [DOI] [Google Scholar]
  4. Orlandini E.; Micheletti C. Topological and physical links in soft matter systems. J. Phys.: Condens. Matter. 2022, 34, 013002. 10.1088/1361-648X/ac28bf. [DOI] [PubMed] [Google Scholar]
  5. Frisch H. L.; Wasserman E. Chemical Topology. J. Am. Chem. Soc. 1961, 83, 3789–3795. 10.1021/ja01479a015. [DOI] [Google Scholar]
  6. Wu Q.; Rauscher P. M.; Lang X.; Wojtecki R. J.; de Pablo J. J.; Hore M. J. A.; Rowan S. J. Poly[n]catenanes: Synthesis of molecular interlocked chains. Science 2017, 358, 1434–1439. 10.1126/science.aap7675. [DOI] [PubMed] [Google Scholar]
  7. Datta S.; Kato Y.; Higashiharaguchi S.; Aratsu K.; Isobe A.; Saito T.; Prabhu D. D.; Kitamoto Y.; Hollamby M. J.; Smith A. J. Self-assembled poly-catenanes from supramolecular toroidal building blocks. Nature 2020, 583, 400–405. 10.1038/s41586-020-2445-z. [DOI] [PubMed] [Google Scholar]
  8. Han X.; Ma T.; Nannenga B. L.; Yao X.; Neumann S. E.; Kumar P.; Kwon J.; Rong Z.; Wang K.; Zhang Y.; Navarro J. A.; Ritchie R. O.; Cui Y.; Yaghi O. M. Molecular weaving of chicken-wire covalent organic frameworks. Chem. 2023, 9, 2509–2517. 10.1016/j.chempr.2023.07.015. [DOI] [Google Scholar]
  9. Prakasam T. 2D covalent organic framework via catenation. Chem 2025, 11, 102307. 10.1016/j.chempr.2024.09.006. [DOI] [Google Scholar]
  10. Krajina B. A.; Zhu A.; Heilshorn S. C.; Spakowitz A. J. Active DNA Olympic Hydrogels Driven by Topoisomerase Activity. Phys. Rev. Lett. 2018, 121, 148001. 10.1103/PhysRevLett.121.148001. [DOI] [PubMed] [Google Scholar]
  11. Meng W.; Kondo S.; Ito T.; Komatsu K.; Pirillo J.; Hijikata Y.; Ikuhara Y.; Aida T.; Sato H. An elastic metal–organic crystal with a densely catenated backbone. Nature 2021, 598 (7880), 298–303. 10.1038/s41586-021-03880-x. [DOI] [PubMed] [Google Scholar]
  12. Speed S.; Atabay A.; Peng Y.-H.; Gupta K.; Müller T.; Fischer C.; Sommer J.-U.; Lang M.; Krieg E.. Assembling a true” Olympic Gel” from > 16,000 combinatorial DNA rings, bioRxiv, 2024, 2024–2027. 10.1101/2024.07.12.603212. [DOI] [Google Scholar]
  13. Ahmadian Dehaghani Z.; Chubak I.; Likos C. N.; Ejtehadi M. R. Effects of topological constraints on linked ring polymers in solvents of varying quality. Soft Matter 2020, 16, 3029–3038. 10.1039/C9SM02374G. [DOI] [PubMed] [Google Scholar]
  14. Li J.; Gu F.; Yao N.; Wang H.; Liao Q. Double Asymptotic Structures of Topologically Interlocked Molecules. ACS Macro Lett. 2021, 10, 1094–1098. 10.1021/acsmacrolett.1c00259. [DOI] [PubMed] [Google Scholar]
  15. Lei H.; Zhang J.; Wang L.; Zhang G. Dimensional and shape properties of a single linear polycatenane: Effect of catenation topology. Polymer 2021, 212, 123160. 10.1016/j.polymer.2020.123160. [DOI] [Google Scholar]
  16. Rauscher P. M.; Schweizer K. S.; Rowan S. J.; de Pablo J. J. Thermodynamics and Structure of Poly[n]catenane Melts. Macromolecules 2020, 53, 3390–3408. 10.1021/acs.macromol.9b02706. [DOI] [Google Scholar]
  17. Chiarantoni P.; Micheletti C. Effect of Ring Rigidity on the Statics and Dynamics of Linear Catenanes. Macromolecules 2022, 55, 4523–4532. 10.1021/acs.macromol.1c02542. [DOI] [Google Scholar]
  18. Tubiana L.; Ferrari F.; Orlandini E. Circular polycatenanes: Supramolecular structures with topologically tunable properties. Phys. Rev. Lett. 2022, 129, 227801. 10.1103/PhysRevLett.129.227801. [DOI] [PubMed] [Google Scholar]
  19. Luengo-Márquez J.; Assenza S.; Micheletti C. Shape and size tunability of sheets of interlocked ring copolymers. Soft Matter 2024, 20, 6595–6607. 10.1039/D4SM00694A. [DOI] [PubMed] [Google Scholar]
  20. Klotz A. R.; Anderson C. J.; Dimitriyev M. S. Chirality effects in molecular chainmail. Soft Matter 2024, 20, 7044–7058. 10.1039/D4SM00729H. [DOI] [PubMed] [Google Scholar]
  21. Rauscher P. M.; Rowan S. J.; de Pablo J. J. Topological Effects in Isolated Poly[n]catenanes: Molecular Dynamics Simulations and Rouse Mode Analysis. ACS Macro Lett. 2018, 7, 938–943. 10.1021/acsmacrolett.8b00393. [DOI] [PubMed] [Google Scholar]
  22. Klotz A. R.; Soh B. W.; Doyle P. S. Equilibrium structure and deformation response of 2D kinetoplast sheets. Proc. Natl. Acad. Sci. U. S. A. 2020, 117, 121–127. 10.1073/pnas.1911088116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Rauscher P. M.; Rowan S. J.; de Pablo J. J. Hydrodynamic interactions in topologically linked ring polymers. Phys. Rev. E. 2020, 102, 032502. 10.1103/PhysRevE.102.032502. [DOI] [PubMed] [Google Scholar]
  24. Soh B. W.; Doyle P. S. Equilibrium Conformation of Catenated DNA Networks in Slitlike Confinement. ACS Macro Lett. 2021, 10, 880–885. 10.1021/acsmacrolett.1c00299. [DOI] [PubMed] [Google Scholar]
  25. Amici G.; Caraglio M.; Orlandini E.; Micheletti C. Topological Friction and Relaxation Dynamics of Spatially Confined Catenated Polymers. ACS Macro Lett. 2022, 11, 1–6. 10.1021/acsmacrolett.1c00594. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Chiarantoni P.; Micheletti C. Linear Catenanes in Channel Confinement. Macromolecules 2023, 56, 2736–2746. 10.1021/acs.macromol.3c00249. [DOI] [Google Scholar]
  27. Rauscher P. M.; Schweizer K. S.; Rowan S. J.; de Pablo J. J. Dynamics of poly[n]catenane melts. J. Chem. Phys. 2020, 152, 214901. 10.1063/5.0007573. [DOI] [PubMed] [Google Scholar]
  28. Lee B.; Niu Z.; Craig S. L. The mechanical strength of a mechanical bond: sonochemical polymer mechanochemistry of poly (catenane) copolymers. Angew. Chem., Int. Ed. 2016, 55, 13086–13089. 10.1002/anie.201606893. [DOI] [PubMed] [Google Scholar]
  29. Caraglio M.; Orlandini E.; Whittington S. G. Driven Translocation of Linked Ring Polymers through a Pore. Macromolecules 2017, 50, 9437–9444. 10.1021/acs.macromol.7b02023. [DOI] [Google Scholar]
  30. Caraglio M.; Orlandini E.; Whittington S. G. Translocation of links through a pore: effects of link complexity and size. J. Stat. Mech.: Theory And Exp. 2020, 2020, 043203. 10.1088/1742-5468/ab7a20. [DOI] [Google Scholar]
  31. Soh B. W.; Doyle P. S. Deformation Response of Catenated DNA Networks in a Planar Elongational Field. ACS Macro Lett. 2020, 9, 944–949. 10.1021/acsmacrolett.0c00360. [DOI] [PubMed] [Google Scholar]
  32. Chen Y.-X.; Cai X.-Q.; Zhang G.-J. Topological Catenation Enhances Elastic Modulus of Single Linear Polycatenane. Chin. J. Polym. Sci. 2023, 41, 1486–1496. 10.1007/s10118-023-2902-x. [DOI] [Google Scholar]
  33. Rheaume S. N.; Klotz A. R. Nanopore translocation of topologically linked DNA catenanes. Phys. Rev. E. 2023, 107, 024504. 10.1103/PhysRevE.107.024504. [DOI] [PubMed] [Google Scholar]
  34. Tagliabue A.; Micheletti C.; Mella M. Tunable Knot Segregation in Copolyelectrolyte Rings Carrying a Neutral Segment. ACS Macro Lett. 2021, 10, 1365–1370. 10.1021/acsmacrolett.1c00453. [DOI] [PubMed] [Google Scholar]
  35. Tagliabue A.; Micheletti C.; Mella M. Tuning Knotted Copolyelectrolyte Conformations via Solution Properties. Macromolecules 2022, 55, 10761–10772. 10.1021/acs.macromol.2c01933. [DOI] [Google Scholar]
  36. Rybenkov V. V.; Vologodskii A. V.; Cozzarelli N. R. Probability of DNA knotting and the effective diameter of the DNA double helix. Proc. Natl. Acad. Sci. 1993, 90, 5307. 10.1073/pnas.90.11.5307. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Dommersnes P. G.; Kantor Y.; Kardar M. Knots in charged polymers. Phys. Rev. E. 2002, 66, 031802. 10.1103/PhysRevE.66.031802. [DOI] [PubMed] [Google Scholar]
  38. Tang J.; Du N.; Doyle P. S. Compression and self-entanglement of single DNA molecules under uniform electric field. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 16153–16158. 10.1073/pnas.1105547108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Ma Z.; Dorfman K. D. Diffusion of Knots along DNA Confined in Nanochannels. Macromolecules 2020, 53, 6461–6468. 10.1021/acs.macromol.0c00561. [DOI] [Google Scholar]
  40. Ma Z.; Dorfman K. D. Diffusion of knotted DNA molecules in nanochannels in the extended de Gennes regime. Macromolecules 2021, 54, 4211–4218. 10.1021/acs.macromol.1c00143. [DOI] [Google Scholar]
  41. Wettermann S.; Datta R.; Virnau P. Influence of ionic conditions on knotting in a coarse-grained model for DNA. Front. Chem. 2023, 10, 1096014. 10.3389/fchem.2022.1096014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Stano R.; Smrek J.; Likos C. N. Cluster Formation in Solutions of Polyelectrolyte Rings. ACS Nano 2023, 17, 21369–21382. 10.1021/acsnano.3c06083. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Aliakseyeu A.; Truong E.; Hu Y.-Y.; Sayko R.; Dobrynin A. V.; Sukhishvili S. A. Self-Diffusion of Star and Linear Polyelectrolytes in Salt-Free and Salt Solutions. Macromolecules 2025, 58, 240. 10.1021/acs.macromol.4c01374. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Wang X.; Goswami M.; Kumar R.; Sumpter B. G.; Mays J. Morphologies of block copolymers composed of charged and neutral blocks. Soft Matter 2012, 8, 3036–3052. 10.1039/C2SM07223H. [DOI] [Google Scholar]
  45. Min J.; Barpuzary D.; Ham H.; Kang G.-C.; Park M. J. Charged block copolymers: from fundamentals to electromechanical applications. Acc. Chem. Res. 2021, 54, 4024–4035. 10.1021/acs.accounts.1c00423. [DOI] [PubMed] [Google Scholar]
  46. Shen K.-H.; Fan M.; Hall L. M. Molecular dynamics simulations of ion-containing polymers using generic coarse-grained models. Macromolecules 2021, 54, 2031–2052. 10.1021/acs.macromol.0c02557. [DOI] [Google Scholar]
  47. Wang T.; Zhong L.; Xiao M.; Han D.; Wang S.; Huang Z.; Huang S.; Sun L.; Meng Y. Block copolymer electrolytes for lithium metal batteries: Strategies to boost both ionic conductivity and mechanical strength. Prog. Polym. Sci. 2023, 146, 101743. 10.1016/j.progpolymsci.2023.101743. [DOI] [Google Scholar]
  48. Sadeghi N.; Kim J.; Cavicchi K. A.; Khabaz F. Microscopic Morphology and Dynamics of Polyampholyte and Cationic Ionomers. Macromolecules 2024, 57, 3937–3948. 10.1021/acs.macromol.4c00039. [DOI] [Google Scholar]
  49. Weeks J. D.; Chandler D.; Andersen H. C. Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids. J. Chem. Phys. 1971, 54, 5237–5247. 10.1063/1.1674820. [DOI] [Google Scholar]
  50. Kremer K.; Grest G. S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. 10.1063/1.458541. [DOI] [Google Scholar]
  51. Hockney R. W.; Eastwood J. W.. Computer Simulation Using Particles; CRC Press, 1988. [Google Scholar]
  52. Deserno M.; Holm C. How to Mesh Up Ewald Sums. II. An Accurate Error Estimate for the Particle-Particle-Particle-Mesh Algorithm. J. Chem. Phys. 1998, 109, 7694–7701. 10.1063/1.477415. [DOI] [Google Scholar]
  53. Weik F.; Weeber R.; Szuttor K.; Breitsprecher K.; de Graaf J.; Kuron M.; Landsgesell J.; Menke H.; Sean D.; Holm C. ESPResSo 4.0 - an extensible software package for simulating soft matter systems. Eur. Phys. J.:Spec. Top. 2019, 227, 1789–1816. 10.1140/epjst/e2019-800186-9. [DOI] [Google Scholar]
  54. Reed C. E.; Reed W. F. Monte Carlo study of titration of linear polyelectrolytes. J. Chem. Phys. 1992, 96, 1609–1620. 10.1063/1.462145. [DOI] [Google Scholar]
  55. Tagliabue A.; Izzo L.; Mella M. Impact of Charge Correlation, Chain Rigidity, and Chemical Specific Interactions on the Behavior of Weak Polyelectrolytes in Solution. J. Phys. Chem. B 2019, 123, 8872–8888. 10.1021/acs.jpcb.9b06017. [DOI] [PubMed] [Google Scholar]
  56. Müller M.; Wittmer J.; Cates M. Topological effects in ring polymers: A computer simulation study. Phys. Rev. E. 1996, 53, 5063. 10.1103/PhysRevE.53.5063. [DOI] [PubMed] [Google Scholar]
  57. Katsarou A. F.; Tsamopoulos A. J.; Tsalikis D. G.; Mavrantzas V. G. Dynamic heterogeneity in ring-linear polymer blends. Polymers 2020, 12, 752. 10.3390/polym12040752. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Tagliabue A.; Micheletti C.; Mella M. Effect of Counterion Size on Knotted Polyelectrolyte Conformations. J. Phys. Chem. B 2024, 128, 4183–4194. 10.1021/acs.jpcb.3c07446. [DOI] [PubMed] [Google Scholar]
  59. Sing C. E.; Zwanikken J. W.; Olvera de La Cruz M. Electrostatic control of block copolymer morphology. Nat. Mater. 2014, 13, 694–698. 10.1038/nmat4001. [DOI] [PubMed] [Google Scholar]
  60. Tagliabue A.; Izzo L.; Mella M. Interface Counterion Localization Induces a Switch between Tight and Loose Configurations of Knotted Weak Polyacid Rings despite Intermonomer Coulomb Repulsions. J. Phys. Chem. B 2020, 124, 2930–2937. 10.1021/acs.jpcb.0c00620. [DOI] [PubMed] [Google Scholar]
  61. Molecular machines and motors; Sauvage J.-P.; Amendola V. Eds.;Springer Science & Business Media, 2001; Vol. 99. [Google Scholar]
  62. Sessler G. M. Physical principles of electrets. Electrets 1980, 33, 13–80. 10.1007/3540173358_10. [DOI] [Google Scholar]
  63. Charge and Energy Transfer Dynamics in Molecular Systems; John Wiley & Sons, Ltd, 2011, Chapter 7, pp. 309–433. 10.1002/9783527633791.ch7. [DOI] [Google Scholar]
  64. Charge and Energy Transfer Dynamics in Molecular Systems John Wiley & Sons, Ltd, 2011, Chapter 9 pp. 467–558. 10.1002/9783527633791.ch9 [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ma5c00099_si_001.pdf (1.7MB, pdf)

Articles from Macromolecules are provided here courtesy of American Chemical Society

RESOURCES