Abstract
To exploit the potential dosimetric advantages of intensity modulated radiation therapy (IMRT) and volumetric modulated arc therapy (VMAT), an in-depth approach is required to provide efficient computing methods. This needs to incorporate clinically related organ specific constraints, Monte Carlo (MC) dose calculations, and large-scale plan optimization. This paper describes our first steps towards a web-based real-time radiation treatment planning system in a cloud computing environment (CCE). The Amazon Elastic Compute Cloud (EC2) with a master node (named m2.xlarge containing 17.1 GB of memory, 2 virtual cores with 3.25 EC2 Compute Units each, 420 GB of instance storage, 64-bit platform) is used as the backbone of cloud computing for dose calculation and plan optimization. The master node is able to scale the workers on an “on-demand” basis. Monte Carlo dose calculation is employed to generate accurate beamlet dose kernels by parallel tasks. The intensity modulation optimization uses total-variation regulation (TVR) and generates piecewise constant fluence maps for each initial beam direction in a distributed manner over the CCE. The optimized fluence maps are segmented into deliverable apertures. The shape of each aperture is iteratively rectified to be a sequencing of arcs using the manufacture constraints. The output plan file from EC2 is sent to the Simple Storage Service (S3). Three de-identified clinical cancer treatment plans have been studied for evaluating the performance of the new planning platform with 6 MV flattening filter free (FFF) beams (40×40 cm2) from the Varian TrueBeam™ STx linear accelerator. A cloud computing environment leads to speed-ups of up to fourteen-fold for both dose kernel calculations and plan optimizations in the head and neck, lung, and prostate cancer cases considered in this study. The proposed system relies on a cloud computing environment that is able to provide an infrastructure for parallel and distributed computing. The resultant plans from the cloud computing are identical to PC-based IMRT and VMAT plans, confirming the reliability of the cloud computing platform. This cloud computing infrastructure has been established for a radiation treatment planning. It substantially improves the speed of inverse planning and makes future on-treatment adaptive re-planning possible.
1. Introduction
Intensity modulated radiation therapy (IMRT) and volumetric modulated arc therapy (VMAT) are increasingly used in radiation therapy. The complex radiation treatment planning (RTP) systems for clinical treatments demand efficient computing, such as non-deterministic Monte Carlo (MC) dose calculation and large-scale plan optimization. Parallel and distributed computing techniques have been applied to the complex computational tasks to perform the calculations in a time-efficient manner. One of the major studies published using parallel computing in radiotherapy employed the application of a graphics processing unit (GPU). A GPU provides a competitive computing platform to leverage massive parallel processing in many applications of medical physics (Men et al 2010, Jia et al 2011, Peng et al 2012). These studies have demonstrated a speed-up factor on a GPU implementation compared with a central processing unit (CPU). Although remarkably faster implementations have been achieved in GPU usages, a few limitations exist (Pratx and Xing 2011a). First, GPU programing requires an in-depth knowledge of single-instruction multiple-data (SIMD) architecture of the multiprocessors (MPs) for an adequate data parallelism to perform high computing efficiency. Second, GPU implementation is not always able to carry out a traditional CPU oriented task. A sequential code based algorithm on CPU is a challenge to convert into the different programming model in GPU and requires many parameters to configure and optimize complicated memory access patterns, data access patterns, and kernel workflows. Third, GPU code extension takes more time because of the consideration of the parameters with the difficulties of debugging and maintaining the primary code.
As an alternative parallel computing method, cloud computing technology has been used in several studies (Bateman and Wood 2009, Keyes et al 2010, Dudley et al 2010, Fox 2011, Schadt et al 2010, Wang et al 2011, Meng et al 2011, Pratx and Xing 2011b, Philbin et al 2011). These have shown that the cloud computing environment (CCE) can dynamically provide scalable applications and computational resources on an on-demand basis. A cloud infrastructure contains hardware, such as networks, servers, storages components, which are necessary to support cloud service, and software to provide cloud functions such as on-demand self-service, broad network access, resource pooling, rapid elasticity and measured service (Mell and Grance 2011).
The primary goal of cloud computing proposed in this paper is to establish and adapt a web-based treatment planning system (TPS) with the technical advantages of cloud computing. The proposed plan optimization method in CCE is an extension of our previous studies using the total-variation regularization (TVR) method (Zhu et al 2008, Zhu and Xing 2009, Kim et al 2011, Kim et al 2012) for fixed-gantry IMRT using more beam angles. A large number of incident beams are explicitly considered with the application of the TVR method to VMAT planning system for a TrueBeam™ linear accelerator (LINAC) beams (Varian Medical Systems, Palo Alto, CA) with/without the flattening filters available (Mok. et al 2010, Cho et al 2011, Cho et al 2013). Applying the TVR method to the proposed RTP system offers an effective interplay of planning and delivery to allow balancing the dose conformity and efficient delivery with flattening filter free (FFF) fields. FFF beams can improve the dose delivery rate with reduction of collimator scatter, head leakages, as well as out of field dose to patient (Kry et al 2010, Stevens et al 2011). In this paper, as our first steps towards a web-based real-time radiation treatment planning system, a detail cloud computing approach is described. Three de-identified clinical cases (Freymann et al 2012) of patients with head and neck, lung, and prostate cancers were used for evaluating the performance of the TPS with FFF beams.
2. Materials and Methods
2.1. Cloud computing infrastructure
The overall architecture of the web-based TPS is shown in Figure 1. The proposed TPS installed on Linux and running on a master node performs two major tasks: (1) non-deterministic MC simulation to generate accurate beamlet dose distributions and (2) large-scale optimization to create deliverable treatment plans. Amazon Elastic Compute Cloud (EC2) with a master node (named, m2.xlarge contains 17.1 GB of memory, 2 virtual cores with 3.25 EC2 Compute Units each, 420 GB of instance storage, 64-bit platform) is used as the backbone of cloud computing for those computations. The master is able to scale seamlessly the number of working group instances, called workers, based on the user-defined setting account for CPU usage. It can launch more workers if the CPU usage exceeds the upper limit for given time (e.g., over 90% usage for 2 minutes), and stop the workers when their tasks are finished. Since the user in a clinical site can control the master node through the virtual desktop mode, the TPS on the master node can be used in the same manner as using the PC-based TPS. When the user runs the TSP on the master, it distributes in-house developed software and application packages, such as MC simulations and optimization tools, to communicate with each worker. Once the connection between the master node and all workers is confirmed, the master can create a schedule to work the two major tasks in parallel. According to the schedules, the master can send the individual task to each worker and receive the results from the workers separately. If the number of tasks is larger than the number of workers, the master reschedules the distribution to wait for the next available workers while the other workers are performing the given tasks. The results are independently sent to the master node according to the performance ability of workers and/or the physical data transmission speed. The output plan file from EC2 is sent to the user computer from the Simple Storage Service (S3). The output plan file in S3 is then completely deleted from S3 in this study.
Figure 1.

Overall scheme for treatment planning system (TPS) distributed on cloud computing infrastructure (Elastic Compute Cloud (EC2); Simple Storage Service (S3)). The master schedules two major tasks, MC simulation and large-scale optimization, in parallel and distributed fashion with the workers.
2.2. Communications and networking environments
In-house developed software that facilitates building a communication network between user and EC2 is implemented in MATLAB®. The internet socket is employed for the proposed TPS to communicate between the master and each worker. The socket is usually referred to as the term of an application programming interface (API) for the Transmission Control Protocol (TCP)/Internet Protocol (IP) stack. It is able to deliver the data packet to the designated thread and process it as an endpoint of a communication object connected through an IP based computer network. The primary concept of the sockets is to use the transport layer with the interfaces between the application layer and the transport layer of the Open Systems Interconnection (OSI) model (Zimmermann 1980).
The master can identify and specify individual workers by their IP addresses and port numbers. The port numbers are designated to the workers through the Secure Shell (SSH) authorized by EC2 security groups. The SSH provides an open protocol for securing network communications over a public network. Each socket mapped by the proposed RTP system on the master is then able to communicate with a computational application process of workers. Figure 2 shows a diagram of TCP socket flow. The basic procedures are as follows: (1) Socket() creates a new socket with a designated integer number and allocates the system resources to it; (2) Bind () attaches a socket address associated with the port number and IP address of each worker; (3) Listen() keeps a listening state with bound TCP socket to be connected with the master and workers; (4) Connect() attempts and, when available, establishes a TCP connection between the master and available workers; (5) Accept() receives an incoming attempt and blocks the caller until the TCP connection established; (6) Send() & Receives() send and receive data through the established connection; and (7) Close() terminates the TCP connections.
Figure 2.

Diagram for TCP Socket flow; TCP connection between the master node and the workers are established through the internet socket.
2.3. Dose kernel calculation
To generate accurate beamlet dose kernels by parallel tasks, the voxel-based Monte Carlo algorithm (VMC++) (Kawrakow 1997, Kawrakow and Fippel 2000, Kawrakow 2001) is employed. VMC++ has been validated with the well-established MC simulation codes such as DOSXYZnrc and BEAMnrc (Gardner et al 2007, Hasenbalg et al 2008). VMC++ can be used for radiation transport through the beam modifiers such as jaws, wedges, blocks, and multileaf collimators (MLCs) (Tillikainen and Siljam ki 2008). In this study, the beam modifier is parameterized in the multisource model as an opened ratio factor through the edge of the blocks or MLCs (Cho et al 2011). The output of the multisource model is used as input for the VMC++ code. VMC++ is distributed on the workers and it is controlled by VMC++ input file. The file contains simulation geometry, dose scoring options, beamlet source position and edge coordinates, source spectrum, variance reduction parameter, and MC control parameter (number of particle tracks, batches to be used, initial random number seeds, cut-off energy and step size).
An in-house developed scheduler in the master node manages the workload distributing the VMC++ input file and collecting the simulation results. The distributed VMC++ on workers is set to run with the input file from the scheduler, and send back the simulation result to the master node. The scheduler supervises and administrates the computing resources connecting with the workers. The master node collects the results from all workers to update the dose kernel matrix in correct indices. Pseudocode (a) and (b) below illustrate how the dose kernel is calculated in serial and parallel fashions. The number of parallel tasks is approximately the same as the total number of beamlets in the iterative simulation. The output plan file from EC2 is sent to the Simple Storage Service (S3).
| Pseudocode (a): MC dose kernel calculation in a serial fashion: | |
| S1: | Set BEV of target for each beam direction |
| S2: | for beamlet 1 ← to |
| S3: | Set MC simulation input data: dose kernel calculation |
| S4: | for structure 1 ← to |
| S5: | Update dose kernel matrix in correct indices |
| S6: | end for |
| S7: | end for |
| S8: | Go for next beam direction |
| Pseudocode (b): MC dose kernel calculation in a parallel fashion: | |
| P1: | Set BEV of target for each beam direction |
| P2: | Distribute in parallel (Set MC simulation Input data: dose kernel calculation) |
| P3: | for structure 1 ← to |
| P4: | Update dose kernel matrix in correct indices |
| P5: | end for |
| P6: | Go for next beam direction |
2.4. Inverse treatment planning optimization
Inverse treatment planning has been increasingly used to optimize the desired dose distribution to the planning target volume and the organ at risks. The advantage of the total variation regularization (TVR) formulated as a quadratic programming (QP) problem permits the quadratic objective function with volumetric constraints to be expressed as a function of the aperture shapes and weights of the incident beams. The TVR based inverse treatment plan optimization problem is simply described in minimize , subject to , where the beamlet intensity , and the beamlet kernel , and the prescribed dose with of structure and total number of beamlets and are composed of and is regularization parameter, is difference matrix with and represent the number of MLC leaf positions and the number of pairs per field, is the number of fields.
As shown in our previous IMRT plan optimization studies (Zhu et al 2008, Zhu et al 2009, Kim et al 2011), the TVR based plan optimization solved as a QP problem was able to efficiently provide a piecewise constant fluence map for a relatively small number of fixed beams. However, the increasing number of beams for dynamic arcs in conjunction with the additional constraints for MLC leaf motions in arc therapy forces the plan optimization formulated as a QP problem to deal with expensive and intensive computational issues. These include a requirement for a large amount of memory and a slow convergence time. The employment in this study of a sparse optimization method utilizing a sparsity-inducing complex valued -minimization problem (Daubechies et al 2004, Combettes and Wajs 2006, Hale et al 2007) reduces the computational cost and time. If , and the objective function of the optimization problem can be decomposed by two functions as: , and if , the TVR based optimization problem is able to be rewritten with local variables and a global variable v:
| (1) |
From the resulting alternating direction method of multipliers (ADMM) algorithm(Gabay and Mercier 1976, Boyd et al 2011),
| (2) |
| (3) |
| (4) |
The framework of distributed computing of ADMM is summarized as follows:
| 1: | Set , and . |
| 2: | Distribute the initial settings to the workers |
| 3: | repeat |
| 4: | for all in parallel do |
| 5: | |
| 6: | Send to master |
| 7: | end for |
| 8: | Collect and from workers and broadcast the update v |
| 9: | |
| 10: | for all in parallel do |
| 11: | |
| 12: | end for |
| 13: | |
| 14: | until acceptance of stopping criterion¶ |
The iteration is terminated if .
The quadratic problems in steps 5 and 9 are solved by proximal operators. There are many reports on proximal operators with useful software packages available (Boyd et al 2011, Combettes and Pesquet 2011, Parikh and Boyd 2012). For parallel processing, a fixed row splitter is used to partition the beamlet kernel to a set of row blocks, with an assumption that there are workers and their stores. Three de-identified clinical cases in this study used different numbers of workers: 12, 8, and 6 for head and neck, lung, and prostate cancers, respectively. The optimized fluence maps in the master are segmented into deliverable apertures. The L-1 norm regularization on the weights of the derived segments in a solution space is then used for the final solution with re-optimization. An initial arc spacing of 6° creates 60 beams directions for a single 360° arc. The shape of each aperture is iteratively rectified to be a sequencing of arcs for rotational delivery using the manufacture’s constraint (Ma et al 2010, Bzdusek et al 2009). The constraint is
| (5) |
where, is leaf displacement, is MLC leaf travel speed, is gantry angular rotational speed, is the angular separation between adjacent angle.
2.5. Evaluation
The scalability of the proposed TPS associated with the type of virtual hardware specifications for the master and worker was evaluated for head and neck, lung, and prostate cancers. The de-identified clinical data encrypted with 256-bit AES algorithm are pre-uploaded to S3. After the MC dose calculation and plan optimization, the output plan file is encrypted with the same algorithm in S3 to be downloaded to the user computer. The worker was composed of a set of t1.micro instance, which has a 64-bit Linux platform, 613 MB memory with up to 2 EC2-compute units (to demonstrate the system performance with the basic compute unit in EC2). The time factors in the dose calculations are compared for 50,000 photon particles per beamlet for the different number of workers. The de-identified clinical studies for head and neck, lung, and prostate used 1.6 × 108, 2.9 × 108, 4.0 × 108 particles for IMRT, and 5.6 × 109, 8.6 × 109, 1.0 × 1010 particles for VMAT, respectively. The statistical uncertainty in the voxel for doses larger than 50% of maximum dose was found to be less than 0.5% for all the plans. To evaluate the quality of the treatment plans and efficiency of the planning platform of the proposed TPS, typical IMRT and VMAT plans are generated and compared for the three de-identified clinical cases.
The FFF beam profiles are generated by the multisource model (Cho et al 2011), and the photon spectra are generated by the spectrum model (Cho et al 2013). The calculated doses from the photon spectra are validated by the measured doses from 3×3 to 40×40 cm2 field sizes at 6 and 10 MV from a Varian TrueBeam™ STx linear accelerator (Cho et al 2011, Cho et al 2013). The 6MV FFF beams for a 40×40 cm2 field size are used for all plans. The head and neck cancer IMRT plan, with 66 Gy prescribed dose to the planning target volume (PTV), used step and shoot beams at seven fixed gantry angles. The lung cancer IMRT plan, with 74 Gy prescribed dose to PTV, was generated at six fixed gantry angles. The prostate cancer IMRT plan, with a 78 Gy prescribed dose to the PTV, used five fixed gantry angles. For all three of the cases, the VMAT plans used a single arc with a gantry spacing of 2°. All plans were normalized to cover the 95% volume of the PTV with the prescription doses.
3. Results
The calculation times for beamlet dose kernels of three de-identified clinical cases, head and neck, lung, prostate plans cancers, are compared. The speed-up factors (times for calculation on single worker cloud-based system divided by times for calculation on cloud-based system with multiple workers) for each beamlet dose kernel calculation for the cases can be improved up to 12.1-fold, 14.0-fold, and 10.6-fold, respectively, based on the current basic set of CCE (computing 1-worker to 100-worker). It is also observed that the computation efficiency tends to be improved as the total numbers of voxels are decreased as shown in Table 1.
Table 1.
Calculation times of beamlet dose kernels for one field in three de-identified clinical plans of head and neck, lung, and prostate cancers.
| Cancer location | Field size(cm) | Volume size | Resolution (mm) | Running time (sec) | Speedup factor | |
|---|---|---|---|---|---|---|
| Head Neck | 18 × 16 | 256 × 256 × 161 | 1.95 × 1.95 × 2.5 | 53.55 | 4.41 | 12.14 |
| Lung | 15 × 16 | 256 × 256 × 152 | 1.95 × 1.95 × 2.5 | 48.62 | 3.47 | 14.01 |
| Prostate | 12 × 13 | 256 × 256 × 308 | 1.95 × 1.95 × 2.5 | 68.44 | 6.48 | 10.56 |
A reciprocal regression model, , is used to fit the measured data in Figure 3 (a), where is the computing time, is the number of workers or instances, includes the times of overhead and data communication, and represents the primary computation time for difference cases, such as head and neck, lung, and prostate cancers. The models were fit to the data with for the head and neck cancer plan, for the lung cancer plan, and for the prostate cancer plan. The overall simulation time is limited by the term of . In a further analysis of , the measured data were fitted using the Amdahl’s Law formula, , where is the speed-up, is the number of workers or instances, and parallel fraction, , is the portion of computation which can be parallelized () (Amdahl 1967). To estimate pure overhead and data communication times in the cloud system, we assume that is 1 for the completely parallelized MC dose calculation in CCE. Figure 3(b) shows the total computing times based on this assumption. One stacked bar represents the total computing time with two execution regions, such as computation time (solid and hatched boxes) and overhead and data communication times (empty boxes), with varying number of workers for each type of case. The average amount of time spent on overhead and data communication with the ideal case of for all the different number of workers is 3.62±1.87, 3.36±1.84, 6.22±3.32 seconds for head and neck, lung, and prostate cancer cases, respectively. According to the Amdahl’s Law, the speed-up as a number of workers is shown in Figure 3(c). for the three cancer treatment plans were 0.92 with for the head and neck, 0.93 with for lung, and 0.896 with for prostate cancer cases. The insert in Figure 3(c) shows a linear regression model between the ratio of the total number of voxels for the prostate cancer case and , demonstrating a strong negative correlation. Small total numbers of voxels correspond to high portions of parallelization. The results shown in Figure 3 suggest that the restrictions are linearly related to the size of the transferring data, which implies that the workload to communicate large data in CCE limits the relative improvement in performance time. Figure 4 shows the dose distributions of VMAT (left) and IMRT (right) plans for the head and neck cancer in (a), lung cancer in (b), and prostate cancer in (c). These were all obtained with the cloud system.
Figure 3.

Computing times in (a) and (b) and speed-ups in (c) with varying number of workers for difference cases. The computation times can be approximated by the reciprocal regression model in (a). The pure computation times are depicted as solid and hatched boxes, and the empty boxes indicated the overhead and data communication times in (b). Insert graph in (c): a plot of the parallel fractions against ratio of total number of voxels to that of prostate. The measure data (diamonds, squares, circles) and fitted lines (solid, dashed, dotted) represent the prostate, lung, and head and neck cancer plans, respectively.
Figure 4.

Dose distributions calculated for de-identified clinical patients with head and neck cancer in (a), lung cancer in (b), and prostate cancer in (c); left for VMAT and right for IMRT plans.
The optimization times for IMRT and VMAT plans for the three cases are compared in Table 2. The IMRT and VMAT plan optimizations take less than a minute and three minutes respectively for the cases using the same CCE. Speed-up factors of the plan optimizations varied from 1.4-fold to 14.0-fold dependent on the specific case and plan type. Figure 5 shows the convergences of the proposed optimization with different number of iterations.
Table 2.
IMRT and VMAT optimization times comparison with three de-identified clinical cases.
| Cancer location | Plan type | Optimization time (sec) | Speed-up factor | |
|---|---|---|---|---|
| Head Neck | IMRT | 105.22 | 21.27 | 4.95 |
| VMAT | 154.86 | 110.91 | 1.40 | |
| Lung | IMRT | 404.36 | 58.03 | 6.97 |
| VMAT | 1858.21 | 147.46 | 12.60 | |
| Prostate | IMRT | 144.84 | 10.35 | 13.99 |
| VMAT | 245.31 | 24.57 | 9.98 | |
Figure 5.
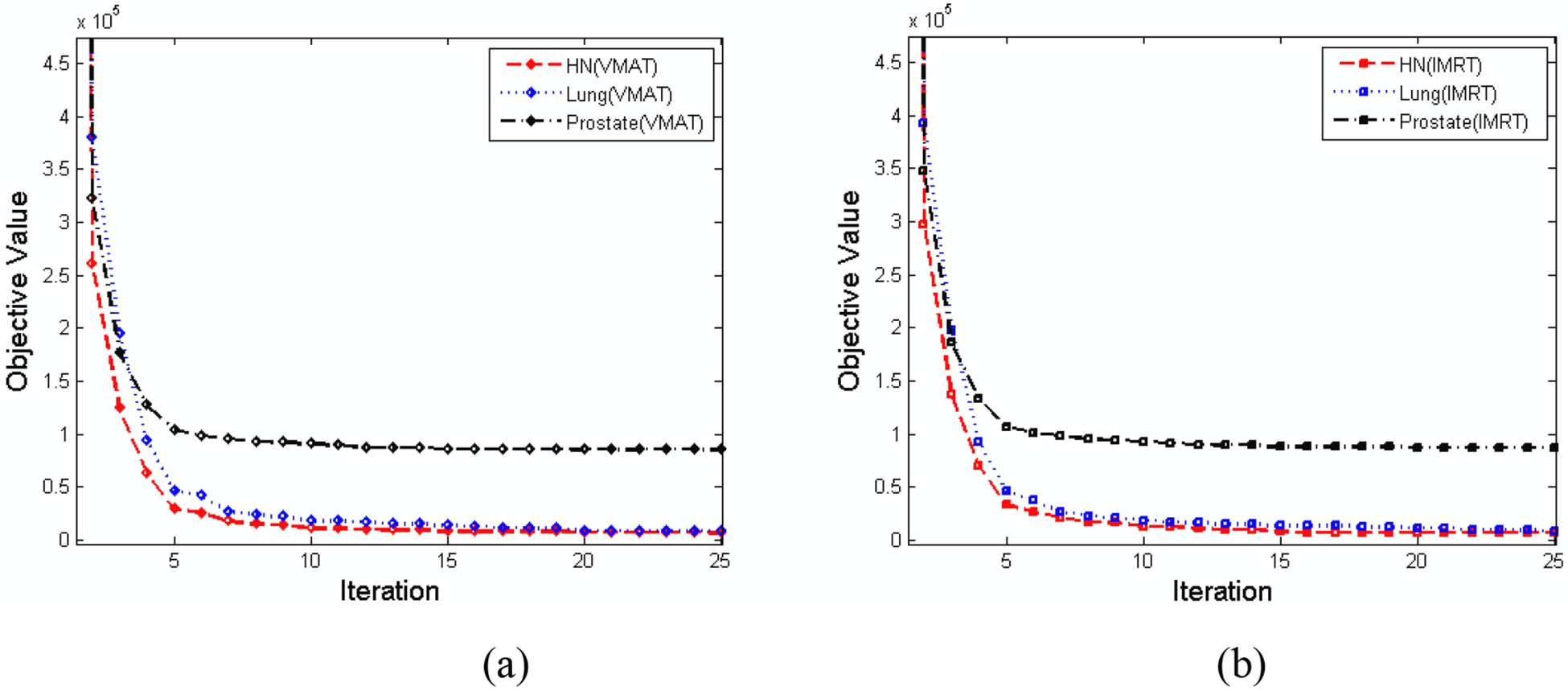
Convergences of (a) VMAT and (b) IMRT plans using the proposed optimization algorithm for the three different cases. The dashed, dotted, dash-dot lines represent the head and neck, lung, and prostate cancer plans, respectively.
Note that we assume that the total computation time on both PC- and cloud-based treatment plans is calculated by the sum of the dose calculation time and plan optimization time. Although the data transfer time between the user computer and S3 is not considered for the cloud-based calculation time in this study, it takes on average 46 seconds to upload and 29 seconds to download all de-identified clinical cases through the AWS Management Console. The average upload/download data transfer rate of the AWS Management Console is 17.32Mbps/28.91Mbps with 1Gbps network connection, which has 121.63Mbps/233.72Mbps upload/download Internet connection bandwidths. For the 130Mbps network connection which has 33.65Mbps/39.33Mbps upload/download Internet connection bandwidths, the AWS Management Console takes on average 80.36 seconds for upload and 54.44 seconds for download with the 9.92Mbps/15.37Mbps upload/download data transfer rate. As expected, the higher upload/download Internet connection bandwidths can reduce the data transfer time.
The Performance Ratios (PRs) (i.e., PC-based calculation time divided by cloud-based calculation times with a specific number of workers) indicate the actual amount of improvement of performances. Both VMAT and IMRT plans were done for the three de-identified clinical cases using the cloud-based system described in this report and compared with the plans obtained for the identical cases using the PC-based TPS. The isodose curves for the plans done on both systems were identical (the results not shown). This was to be expected since the software for the treatment planning voxel-based Monte Carlo algorithms and the treatment planning software used were the same for the cloud-based and PC-based systems. The time for the treatment planning was, however, shorter for both the IMRT and VMAT planning when the cloud-based system was compared with the PC-planning as summarized in Table 3.
Table 3.
Performance ratios (PC-based computing/Cloud-based computing) for VMAT and IMRT plans for three de-identified clinical cases
| Cancer location | Plan type | Performance Ratios (PRs) | ||
|---|---|---|---|---|
| 1-worker | 40-worker | 100-worker | ||
| Head Neck | IMRT | 1.17 | 8.02 | 8.94 |
| VMAT | 0.99 | 9.09 | 10.63 | |
| Lung | IMRT | 1.96 | 7.18 | 8.68 |
| VMAT | 1.15 | 8.10 | 13.28 | |
| Prostate | IMRT | 1.35 | 8.27 | 11.16 |
| VMAT | 0.99 | 7.06 | 10.25 | |
The PRs varied between the clinical sites studied. While the planning took longer for all of the VMAT plans compared with the site specific IMRT plans, the PRs were mostly better when the cloud-based system planning was compared to the PC-based system planning for the VMAT plans (0.99 ≤ PRs≤ 10.63 for the head and neck case, 1.15 ≤ PRs≤ 13.28 for lung case, and 0.99 ≤ PRs≤ 10.25 for prostate cancer cases). However, the PRs were approximately 1 for VMAT plans when the cloud-based system was used with only 1-worker for the planning of head and neck and prostate cancers. It is also observed that the PRs of VMAT plans still tend to be increased with large variances, while those of IMRT plans begin to plateau as the total number workers are increased past 40-worker for the lung and head and neck cancers, as shown in Figure 6.
Figure 6.

Performance ratios of (a) VMAT and (b) IMRT plans for the three different cases compared with different number of workers. The upload and download data transfer times are excluded. The dashed, dotted, dash-dot lines represent the head and neck, lung, and prostate cancer plans, respectively.
4. Discussion
The cloud computing resources in terms of virtual hardware specifications for the proposed TPS are composed of a master node and a computing work group, called workers or instances. The system installed on the master node is seamlessly able to communicate with workers through the internet sockets. Two major performance objectives, MC dose kernel calculation and large-scale optimization, are efficiently distributed and computed with parallel tasks under the supervision of the scheduler on the cloud. This proof of concept study shows that the speed-up is up to fourteen-fold for both dose kernel calculations and plan optimizations for different plan types and clinical evaluations. The factor was estimated with a given number of fundamental computing workers, such as 1 to 100 of t1.micro instances. The number of workers is scalable on an on-demand basis with the given capacity of Amazon Elastic Compute Cloud. The t1.micro instance in this study comes with the lowest computing price among all EC2 instances.
While, as demonstrated in this study, a cloud computing platform can improve computational performance, there are a few related issues that should be considered. First, the commercial cloud computing price is relatively high for pay-as-you-go. The Amazon EC2 computing cost depends on the type and number of instances in different regions. The price range between micro and high memory instances, such as t1.micro and m2.4xlarge varies from $0.025 to $1.840 per hour running Linux/UNIX for U.S. Northern California region (http://aws.amazon.com/ec2/pricing/). There is an additional charge for regional data transfers between the regions if a user wants to use instances in different regions. Currently, the cluster compute instances are not available in U.S. Northern California, Asia Pacific, and South America regions. However, the operation in CCE is more cost-effective than those of a dedicated in-house cluster (Zhai et al 2011). In general, there are significant savings, on average between 20% and 50%, depending on various cloud computing migrations, privacy and security protection, file server and storage utilization, and labor costs for maintenance and management (West 2010). This study demonstrated that the proposed TPS implemented in CCE (even with the basic computing group composed of micro instances), has improved computation efficiency, thus offering an opportunity to invest in the expansion of the computing work group involving high performance compute units. Second, although cloud service providers are still being studied concerning efficient big data transfer solutions, a network throughput should be carefully considered in CCE as compared with a GPU shared on-chip memory. If the multiple data packages are concurrently transferred to a master node across the network to be processed, the network can become congested. To avoid such data congestion, the scheduler in this study always maintains a global first-in-first-out (FIFO) data queue controlling the status of jobs and availability of workers in a given network throughput. Once one job has been completed in a worker, the scheduler immediately lets the distributed application be re-initiated for the next available job without unnecessary memory usage and other interrupts. Alternatively one of a type of queuing systems, the Simple Queue Service (SQS) provided by Amazon Web Services (AWS), can be used with simple APIs at an inexpensive cost. Third, a cloud service provider has to take account the safeguarding of patient privacy and security under the Health Insurance Portability and Accountability Act of 1996 (HIPAA) requirements subsequently expanded by the Health Information Technology for Economic and Clinical Health (HITECH) regulations. AWS provides technical information and prescriptive guidance for cloud application developers to comply with HIPAA and HITECH. In this pilot study implementing the web-based treatment planning system, each data package used three de-identified clinical cases which were encrypted by 256-bit AES algorithm (NIST-FIPS Standard 2001) before transmission. The package is transmitted to S3 through Secure Socket Layer (SSL) encrypted endpoints over the Internet from EC2. In order to secure access for EC2 data communication, a key pair with private and public keys created by 2048-bit RSA algorithm (Rivest et al 1978) is used for unique identification. Each output plan file package in S3 from EC2 is also encrypted by the same AES algorithm and transmitted to the user site. Such a data package of a de-identified clinical case can be transmitted to a third party organization in accordance with the agreement between the parties to use the same control mechanism.
From a technical point of view, the on-demand virtualized hardware resources along with a commercial CCE offer additional features with the distributable application packages associated with the advanced development of GPU-based computational methods in the radiotherapy community. The type of instance of computing work group in the proposed TPS can be easily updated and switched to the cluster GPU instances. The new computing work group is then able to employ such GPU-based dose calculation engines as well as GPU-based optimization algorithms through a simple modification of these methods.
5. Conclusion
This study has proposed a detailed strategy for developing a web-based TPS in CCE. The results demonstrate that the proposed TPS provides efficient computation for dose kernel calculation and large-scale plan optimization in cloud. The resultant plans of IMRT and VMAT plans from the cloud computing are found to be identical to those obtained using PC-based plans indicating the reliability of the cloud computing platform. The cloud computing environment substantially improves the speed of inverse planning and makes future on-treatment adaptive re-planning possible. Eventually, we plan on using the cloud computing environment approach of this study to enable interdisciplinary computing, sharing, and updating of the treatment planning system in a web-based environment.
Acknowledgment
This work was supported in part by the National Cancer Institute (1R01 CA133474) and by Leading Foreign Research Institute Recruitment Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (MSIP) (Grant No.2009-00420)
References
- Amdahl GM 1967. Validity of the single processor approach to achieving large scale computing capabilities. In AFIPS Conference Proceedings, Spring Joint Computer Conference: 30 483–5 [Google Scholar]
- Bateman A and Wood M 2009. Cloud computing Bioinformatics 25 1475. [DOI] [PubMed] [Google Scholar]
- Boyd S, Parikh N, Chu E, Peleato B and Eckstein J 2011. Distributed optimization and statistical learning via the alternating direction method of multipliers Foundations and Trends® in Machine Learning 3 1–122 [Google Scholar]
- Bzdusek K, Friberger H, Eriksson K, Hårdemark B, Robinson D and Kaus M 2009. Development and evaluation of an efficient approach to volumetric arc therapy planning Medical Physics 36 2328–39 [DOI] [PubMed] [Google Scholar]
- Cho W, Bush K, Mok E, Xing L and Suh TS 2013. Development of a fast and feasible spectrum modeling technique for flattening filter free beams. Medical Physics 40 041721-1-15 [DOI] [PubMed] [Google Scholar]
- Cho W, Kielar KN, Mok E, Xing L, Park JH, Jung WG and Suh TS 2011. Multisource modeling of flattening filter free (FFF) beam and the optimization of model parameters Medical Physics 38 1931–42 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Combettes PL and Pesquet J-C 2011. Proximal splitting methods in signal processing Fixed-Point Algorithms for Inverse Problems in Science and Engineering 49 185–212 [Google Scholar]
- Combettes PL and Wajs VR 2006. Signal recovery by proximal forward-backward splitting Multiscale Modeling and Simulation 4 1168–200 [Google Scholar]
- Daubechies I, Defrise M and De Mol C 2004. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint Communications on Pure and Applied Mathematics 57 1413–57 [Google Scholar]
- Dudley JT, Pouliot Y, Chen R, Morgan AA and Butte AJ 2010. Translational bioinformatics in the cloud: an affordable alternative Genome medicine 2 51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amazon Elastic Compute Cloud (Amazon EC2), http://aws.amazon.com/ec2/
- Fox A 2011. Cloud Computing—What’s in It for Me as a Scientist? Science 331 406–7 [DOI] [PubMed] [Google Scholar]
- Freymann JB, Kirby JS, Perry JH, Clunie DA and Jaffe CC 2012. Image data sharing for biomedical research—meeting HIPAA requirements for de-identification Journal of Digital Imaging 25 14–24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabay D and Mercier B 1976. A dual algorithm for the solution of nonlinear variational problems via finite element approximation Computers & Mathematics with Applications 2 17–40 [Google Scholar]
- Gardner J, Siebers J and Kawrakow I 2007. Dose calculation validation of VMC++ for photon beams Medical Physics 34 1809–18 [DOI] [PubMed] [Google Scholar]
- Hale ET, Yin W and Zhang Y 2007. A fixed-point continuation method for l1-regularized minimization with applications to compressed sensing CAAM TR07–07, Rice University [Google Scholar]
- Hasenbalg F, Fix M, Born E, Mini R and Kawrakow I 2008. VMC++ versus BEAMnrc: A comparison of simulated linear accelerator heads for photon beams Medical Physics 35 1521–31 [DOI] [PubMed] [Google Scholar]
- Amazon Elastic Compute Cloud Pricing, http://aws.amazon.com/ec2/pricing/
- Jia X, Gu X, Graves YJ, Folkerts M and Jiang SB 2011. GPU-based fast Monte Carlo simulation for radiotherapy dose calculation Physics in Medicine and Biology 56 7017–31 [DOI] [PubMed] [Google Scholar]
- Kawrakow I 1997. Improved modeling of multiple scattering in the Voxel Monte Carlo model Medical Physics 24 505–17 [DOI] [PubMed] [Google Scholar]
- Kawrakow I 2001. VMC++, electron and photon Monte Carlo calculations optimized for radiation treatment planning. Advanced Monte Carlo for Radiation Physics, Particle Transport Simulation and Applications: Proceedings of the Monte Carlo 2000 Meeting Lisbon, pp 229–36 [Google Scholar]
- Kawrakow I and Fippel M 2000. VMC++, a MC algorithm optimized for electron and photon beam dose calculations for RTP Proceedings of the 22nd Annual International Conference of the IEEE (Engineering in Medicine and Biology Society, Piscataway, NJ, 2000). 2 1490–3 [Google Scholar]
- Keyes R, Romano C, Arnold D and Luan S 2010. Medical physics calculations in the cloud: A new paradigm for clinical computing Medical Physics 37 3272 [Google Scholar]
- Kim H, Suh TS, Lee R, Xing L and Li R 2012. Efficient IMRT inverse planning with a new L1-solver: template for first-order conic solver Physics in Medicine and Biology 57 4139. [DOI] [PubMed] [Google Scholar]
- Kim T, Zhu L, Suh TS, Geneser S, Meng B and Xing L 2011. Inverse planning for IMRT with nonuniform beam profiles using total-variation regularization (TVR) Medical Physics 38 57–66 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kry SF, Vassiliev ON and Mohan R 2010. Out-of-field photon dose following removal of the flattening filter from a medical accelerator Physics in Medicine and Biology 55 2155–66 [DOI] [PubMed] [Google Scholar]
- Ma Y, Chang D, Keall P, Xie Y, Park JY, Suh TS and Xing L 2010. Inverse planning for four-dimensional (4D) volumetric modulated arc therapy Medical Physics 37 5627–33 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mell P and Grance T 2011. The NIST definition of cloud computing NIST Special Publication 800–145 1–7 [Google Scholar]
- Men C, Romeijn HE, Jia X and Jiang SB 2010. Ultrafast treatment plan optimization for volumetric modulated arc therapy (VMAT) Medical physics 37 5787–91 [DOI] [PubMed] [Google Scholar]
- Meng B, Pratx G and Xing L 2011. Ultrafast and scalable cone-beam CT reconstruction using MapReduce in a cloud computing environment Medical Physics 38 6603–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mok. E, Kielar. K, Hsu. A, Maxim. P and Xing L 2010. Dosimetric properties of flattening filter free photon beams from a new clinical accelerator Medical Physics 37 3248 [Google Scholar]
- NIST-FIPS Standard. Announcing the Advanced Encryption Standard (AES) Vol. 197 Federal Information Processing Standards Publication; 2001. [Google Scholar]
- Parikh N and Boyd S 2012. Proximal Algorithms
- Peng F, Jia X, Gu X, Epelman MA, Romeijn HE and Jiang SB 2012. A new column-generation-based algorithm for VMAT treatment plan optimization Physics in Medicine and Biology 57 4569. [DOI] [PubMed] [Google Scholar]
- Philbin J, Prior F and Nagy P 2011. Will the Next Generation of PACS Be Sitting on a Cloud? Journal of Digital Imaging 24 179–83 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pratx G and Xing L 2011a. GPU computing in medical physics: A review Medical Physics 38 2685–97 [DOI] [PubMed] [Google Scholar]
- Pratx G and Xing L 2011b. Monte Carlo simulation of photon migration in a cloud computing environment with MapReduce Biomedical Optics 16 125003-1-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivest RL, Shamir A and Adleman L 1978. A method for obtaining digital signatures and publickey cryptosystems Communications of the ACM 21 120–6 [Google Scholar]
- Schadt EE, Linderman MD, Sorenson J, Lee L and Nolan GP 2010. Computational solutions to large-scale data management and analysis Nature Reviews Genetics 11 647–57 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevens S, Rosser K and Bedford J 2011. A 4 MV flattening filter-free beam: commissioning and application to conformal therapy and volumetric modulated arc therapy Physics in Medicine and Biology 56 3809–24 [DOI] [PubMed] [Google Scholar]
- Tillikainen L and Siljamäki S 2008. A multiple-source photon beam model and its commissioning process for VMC++ Monte Carlo code. Journal of Physics: Conference Series: IOP Publishing pp 012024 1–6 [Google Scholar]
- Wang H, Ma Y, Pratx G and Xing L 2011. Toward real-time Monte Carlo simulation using a commercial cloud computing infrastructure Physics in Medicine and Biology 56 N175–N81 [DOI] [PMC free article] [PubMed] [Google Scholar]
- West DM. Saving money through cloud computing: Governance Studies at Brookings. 2010.
- Zhai Y, Liu M, Zhai J, Ma X and Chen W 2011. Cloud versus in-house cluster: evaluating Amazon cluster compute instances for running MPI applications. Proceeding SC’11 State of the Practice Reports, 2011 [Google Scholar]
- Zhu L, Lee L, Ma Y, Ye Y, Mazzeo R and Xing L 2008. Using total-variation regularization for intensity modulated radiation therapy inverse planning with field-specific numbers of segments Physics in Medicine and Biology 53 6653–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu L and Xing L 2009. Search for IMRT inverse plans with piecewise constant fluence maps using compressed sensing techniques Medical Physics 36 1895–905 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmermann H 1980. OSI reference model--The ISO model of architecture for open systems interconnection IEEE Transactions on Communications 28 425–32 [Google Scholar]


